2. 烟台大学 计算机与控制工程学院, 山东 烟台 264005
2. School of Computer and Control Engineering, Yantai University, Yantai 264005, China
粗糙集理论是由波兰学者Pawlak教授于1982年提出的一种用于处理和分析不确定、不精确数据的数学方法与工具[1-4]。目前,粗糙集理论在机器学习、决策分析、模式识别、数据挖掘和智能信息处理等领域得到了广泛应用。
属性约简或知识约简是粗糙集理论的重要研究内容之一,其本质是获取保持知识库某种分类能力在约简前后不发生改变的最小属性子集描述,国内外学者做了大量的相关研究工作。1992年,Skowron[5]提出了差别矩阵的概念,为获取信息系统或决策表的所有约简或最小约简提供了理论基础;1998年,Kryszkiewicz[6]讨论了基于差别矩阵的不完备信息系统广义决策保持属性约简问题;2003年,张文修等[7]给出了分布约简和分配约简的差别矩阵约简方法,并提出了最大分布约简;2007年,徐伟华等[8]给出了优势关系下基于差别矩阵的分布约简和最大分布约简;2009年,苗夺谦等[9]提出了不可分辨关系保持属性约简和相应的差别矩阵构造方法;2010年,张楠等[10]讨论了区间值信息系统下的属性约简问题。为了提高属性约简的算法效率,多种启发式属性约简算法相继被提出。1999年,苗夺谦等[11]从信息论的角度给出了属性重要度的度量方法,在此基础上提出了基于互信息的启发式约简算法;2002年,王国胤等[12]提出了基于条件信息熵的启发式属性约简算法;2010年,钱宇华等[13]提出了正向近似的基本概念并将其应用于启发式属性约简的构造过程,提高了属性约简的计算效率;2011年,钱宇华等[14-15]进一步将正向近似应用于不完备决策表的启发式属性约简,改善了不完备决策表下启发式属性约简的求取效率;陈红梅等[16-17]在动态属性约简方面做了大量的研究工作;文献[18-19]对现有的属性约简之间的关系进行了深入讨论与研究。
分布约简保证每个对象在约简前后的概率分布保持不变,即保证每条规则的置信度在约简前后不发生改变。在实际应用中,人们往往更关注可信度较高或较低的规则[20],分布约简的标准过于严格,很多对实际决策无用的规则的置信度在约简前后也要保持不变,很可能使得最终约简过于冗长,对实际决策造成一定的干扰。本文在分布约简的基础上,通过弱化分布约简的约简标准,提出了一种新的属性约简,即广义分布保持属性约简,该属性约简可以保证规则的置信度(P∈[0, α]或[β, 1])在约简前后不变,并对广义分布保持属性约简的方法和相关性质进行了研究和讨论。
1 广义分布保持属性约简定义1[7] 设决策表DT=(U, AT∪D, V, f),论域U={u1, u2, …, un},则∀ui∈U, A⊆ AT,对象ui在属性A下关于决策属性集D的概率分布定义为μA(ui)=(P(D1|[ui]A), (P(D2|[ui]A), …, (P(D |U/D||[ui]A))。其中,(P(Dj|[ui]A)=|Dj∩[ui]A|/|[ui]A|,i∈{1, 2, …, n},j∈{1, 2, …, |U/D|}。
定义2 设决策表DT=(U, AT∪D, V, f),U={u1, u2, …, un},U/D={D1, D2, …, D|U/D|},记dj为Dj对应的决策值,则∀ui∈U,A⊆ AT, ui在A下关于决策属性D的[α, β]决策-置信度序偶集定义为
| $ \begin{array}{*{20}{c}} {\Upsilon _A^{\left[ {\alpha ,\beta } \right]}\left( {{u_i}} \right) = \left\{ {\left\langle {{d_j},P\left( {{D_j}\left| {{{\left[ {{u_i}} \right]}_A}} \right.} \right)} \right\rangle |} \right.}\\ {\left. {\alpha \le P\left( {{D_j}\left| {{{\left[ {{u_i}} \right]}_A}} \right.} \right) \le \beta \wedge \alpha \le P\left( {{D_j}\left| {{{\left[ {{u_i}} \right]}_{{\rm{AT}}}}} \right.} \right) \le \beta } \right\}} \end{array} $ |
式中:i∈{1, 2, …, n},j∈{1, 2, …, U/D},α和β满足(α=0∧β∈[0, 1])或(α∈[0, 1]∧β=1)。
根据定义2,若对于∀u∈U,均满足
定义3 给定决策表DT=(U, AT∪D, V, f),U={u1, u2, …, un},∀A⊆ AT,若A是一个广义分布保持约简,当且仅当以下两个条件成立:
1)∀ui⊆ U,
2)∀B⊆ A,
式中:α和β满足(α=0∧β∈[0, 1])或(α∈[0, 1]∧β=1),i, j∈{1, 2, …, n}。
由定义3可知,对于置信度在[α, β]内的规则,它们的置信度在广义分布保持约简前后保持不变。
2 广义分布保持属性约简的判定与方法首先,给出广义分布协调集的等价证明。
定理1 设决策表DT=(U, AT∪D, V, f),U={u1, u2, …, un},∀A⊆ AT,则A是广义分布协调集当且仅当对于∀ui, uj∈U,当
证明 不妨记ρ([ui]A)={[uj]AT:[uj]AT⊆ [ui]A},其中i, j∈{1, 2, …, n}。由于A⊆ AT,故ρ([ui]A)构成[ui]A的一个划分。
“⇒”:设A是决策表DT上的广义分布协调集。∀ui, uj∈U,当[ui]A∩[uj]A≠Ø时,有[ui]A=[uj]A。因此
“⇐”:对于∀ui∈U,当[uj]AT⊆ [ui]A时,有[ui]A∩[uj]A≠Ø,故
| $ \begin{array}{*{20}{c}} {P\left( {{D_j}\left| {{{\left[ {{u_i}} \right]}_A}} \right.} \right) = \frac{{\sum\limits_{s = 1}^{\left| {\rho \left( {{{\left[ {{u_i}} \right]}_A}} \right)} \right|} {\left\{ {\left| {{\rho _s} \cap {D_k}} \right|:{\rho _s} \in \rho \left( {{{\left[ {{u_i}} \right]}_A}} \right)} \right\}} }}{{\left| {{{\left[ {{u_i}} \right]}_A}} \right|}} = }\\ {\sum\limits_{s = 1}^{\left| {\rho \left( {{{\left[ {{u_i}} \right]}_A}} \right)} \right|} {\left\{ {\frac{{\left| {{\rho _s} \cap {D_k}} \right|}}{{\left| {{\rho _s}} \right|}} \cdot \frac{{\left| {{\rho _s}} \right|}}{{\left| {{{\left[ {{u_i}} \right]}_A}} \right|}}:{\rho _s} \in \rho \left( {{{\left[ {{u_i}} \right]}_A}} \right)} \right\}} = }\\ {\sum\limits_{s = 1}^{\left| {\rho \left( {{{\left[ {{u_i}} \right]}_A}} \right)} \right|} {\left\{ {P\left( {{D_k}\left| {{\rho _s}} \right.} \right) \cdot \frac{{\left| {{\rho _s}} \right|}}{{\left| {{{\left[ {{u_i}} \right]}_A}} \right|}}:{\rho _s} \in \rho \left( {{{\left[ {{u_i}} \right]}_A}} \right)} \right\}} = }\\ {\sum\limits_{s = 1}^{\left| {\rho \left( {{{\left[ {{u_i}} \right]}_A}} \right)} \right|} {\left\{ {P\left( {{D_k}\left| {{{\left[ {{u_i}} \right]}_{{\rm{AT}}}}} \right.} \right) \cdot \frac{{\left| {{\rho _s}} \right|}}{{\left| {{{\left[ {{u_i}} \right]}_A}} \right|}}:{\rho _s} \in \rho \left( {{{\left[ {{u_i}} \right]}_A}} \right)} \right\}} = }\\ {P\left( {{D_k}\left| {{{\left[ {{u_i}} \right]}_{{\rm{AT}}}}} \right.} \right)} \end{array} $ |
因此,
定理1给出了判断属性子集是广义分布协调集的方法,由此可进一步得到广义分布保持约简的方法,在此可给出广义分布差别矩阵的概念。
定义4 给定决策表DT=(U, AT∪D, V, f),U={u1, u2, …, un},AT={a1, a2, …, a |AT|}为条件属性集,D={d}为决策属性,记
| $ {D^ * } = \left\{ {\left( {{u_i},{u_j}} \right)\left| {\Upsilon _{{\rm{AT}}}^{\left[ {\alpha ,\beta } \right]}\left( {{u_i}} \right) \ne \Upsilon _{{\rm{AT}}}^{\left[ {\alpha ,\beta } \right]}\left( {{u_j}} \right)} \right.} \right\} $ |
定义
| $ \mathit{\boldsymbol{M}}_{ij}^{\left[ {\alpha ,\beta } \right]} = \left\{ \begin{array}{l} \left\{ {a \in {\rm{AT}}\left| {f\left( {a,{u_i}} \right) \ne f\left( {a,{u_j}} \right)} \right.} \right\},\;\;\left( {{u_i},{u_j}} \right) \in {D^ * }\\ {\rm{AT,}}\;\;\;\;\left( {{u_i},{u_j}} \right) \notin {D^ * } \end{array} \right. $ |
为(ui, uj)的广义分布可辨识属性集,M [α, β]={Mij[α, β]i, j∈{1, 2, …, n}}为决策表的一个n×n的广义分布差别矩阵,其为对称矩阵,α和β满足(α=0∧β∈[0, 1])或(α∈[0, 1]∧β=1)。
定理2 设DT=(U, AT∪D, V, f),∀A⊆ AT,则A是广义分布协调集⇔ui, uj∈U,若Mij[α, β]≠Ø,有A∩Mij[α, β]≠Ø。其中,α和β满足(α=0∧β∈[0, 1])或(α∈[0, 1]∧β=1)。
证明 若(ui, uj)∉D*,显然有A∩Mij[α, β]≠Ø。反之,则有
“⇒”:由于A是广义分布协调集,故对于∀(ui, uj)∈D*,
“⇐”:不妨假设∃(ui, uj)∈D*,使得A∩Mij[α, β]=Ø,显然
定义5 设DT=(U, AT∪D, V, f),M[α, β]为广义分布保持约简的差别矩阵,其对应的差别函数为
| $ \text{DF}\left( {{\boldsymbol{M}}^{\left[\alpha, \beta \right]}} \right)=\wedge \left\{ \vee M_{ij}^{\left[\alpha, \beta \right]}\left| 1\le i\le j\le n \right. \right\} $ |
式中:∨Mij[α, β]=∨a(a∈Mij[α, β])表示Mij[α, β]中所有属性的析取,且α和β满足(α=0∧β∈[0, 1])或(α∈[0, 1]∧β=1)。
通过化DF(M[α, β])的主合取范式转化为主析取范式即可得到所有广义分布保持属性约简。
定理3 设DT=(U, AT∪D, V, f),M[α, β]为DT的广义分布保持约简的差别矩阵,且α和β满足(α=0∧β∈[0, 1])或(α∈[0, 1]∧β=1)。DF(M[α, β])是由M [α, β]导出的差别函数,DF(M[α, β])的极小析取范式为
| $ {\rm{DF}}\left( {{\mathit{\boldsymbol{M}}^{\left[ {\alpha ,\beta } \right]}}} \right) = \mathop \vee \limits_{k = 1}^t \left( {\mathop \wedge \limits_{s = 1}^{{q_k}} {a_{{i_s}}}} \right)。$ |
记Ak={ais|s=1, 2, …, qk},则{Ak|k=1, 2, …, t}是决策表的所有广义分布保持约简,其中t表示DF(M [α, β])的极小析取范式中的合取项数目。
证明 ∀k≤t,∀Mij[α, β]∈M[α, β],由极小析取范式的定义知Ak∩Mij[α, β]≠Ø,再由定理2可得Ak是广义分布协调集。同时,DF(M[α, β])=
由于DF(M[α, β])中包含了所有的Mij[α, β],因此不存在其他的广义分布保持约简,定理得证。
3 广义分布保持属性约简算法本节给出广义分布保持约简算法(generalized distribution preservation reduction algorithm,GDPRA),算法描述如下。
输入 决策表DT=(U, AT∪D, V, f),α和β。
输出 DT的所有广义分布保持属性约简。
1) 计算每个对象在条件属性集下关于决策属性的置信度分布μAT。
2) 根据每个对象的置信度分布μAT获取每个对象的[α, β]决策-置信度序偶集。
3) 根据对象之间的决策-置信度序偶集构造相应的广义分布差别矩阵。
4) 根据广义分布差别矩阵构造广义分布差别函数,并通过吸收率进行简化。
5) 在DF(M[α, β])基础上通过结合律获取所有的广义分布保持约简。
其中,α和β满足(α=0∧β∈[0, 1])或(α∈[0, 1]∧β=1)。
由于上述算法是通过差别矩阵获取决策表的所有的广义分布保持约简,故算法在最坏情况下的时间复杂度为O(|AT||U|2),最坏情况下的空间复杂度为O(|AT||U|2),其中|U|为样本空间中的对象数目,|AT|为条件属性数,下面通过例1简要说明GDPRA的执行过程。
例1 如表 1所示,论域为U={u1, u2, u3, u4},AT={a1, a2, a3, a4}为条件属性集,D={d}为决策属性,分别求[α, β]=[0, 0.3]以及[α, β]=[0.8, 1]时的所有广义分布保持约简。
| 表 1 决策表 Tab.1 Decision table |
1) 获取每个对象的置信度分布
| $ \begin{array}{*{20}{c}} {U/{\rm{AT = }}\left\{ {{E_1},{E_2},{E_3}} \right\}}\\ {U/D{\rm{ = }}\left\{ {{D_1},{D_2},{D_3}} \right\}} \end{array} $ |
| $ \begin{array}{*{20}{c}} {{E_1} = \left\{ {{u_1}} \right\}}\\ {{E_2} = \left\{ {{u_2}} \right\}}\\ {{E_3} = \left\{ {{u_3},{u_4}} \right\}} \end{array} $ |
| $ \begin{array}{*{20}{c}} {{D_1} = \left\{ {{u_1}} \right\}}\\ {{D_2} = \left\{ {{u_2},{u_4}} \right\}}\\ {{D_3} = \left\{ {{u_3}} \right\}} \end{array} $ |
| $ \begin{array}{*{20}{c}} {{\mu _{{\rm{AT}}}}\left( {{u_1}} \right) = \left( {1,0,0} \right)}\\ {{\mu _{{\rm{AT}}}}\left( {{u_2}} \right) = \left( {0,1,0} \right)}\\ {{\mu _{{\rm{AT}}}}\left( {{u_3}} \right) = \left( {0,0.5,0.5} \right)}\\ {{\mu _{{\rm{AT}}}}\left( {{u_4}} \right) = \left( {0,0.5,0.5} \right)} \end{array} $ |
2) 获取每个对象的[α, β]决策-置信度序偶集
当α=0,β=0.3时
| $ \begin{array}{l} \Upsilon _{{\rm{AT}}}^{\left[ {0,0.3} \right]}\left( {{u_1}} \right) = \left\{ {\left\langle {1,0} \right\rangle ,\left\langle {2,0} \right\rangle } \right\}\\ \Upsilon _{{\rm{AT}}}^{\left[ {0,0.3} \right]}\left( {{u_2}} \right) = \left\{ {\left\langle {0,0} \right\rangle ,\left\langle {2,0} \right\rangle } \right\} \end{array} $ |
| $ \begin{array}{l} \Upsilon _{{\rm{AT}}}^{\left[ {0,0.3} \right]}\left( {{u_3}} \right) = \left\{ {\left\langle {0,0} \right\rangle } \right\}\\ \Upsilon _{{\rm{AT}}}^{\left[ {0,0.3} \right]}\left( {{u_4}} \right) = \left\{ {\left\langle {0,0} \right\rangle } \right\} \end{array} $ |
当α=0.8,β=1时
| $ \begin{array}{l} \Upsilon _{{\rm{AT}}}^{\left[ {0.8,1} \right]}\left( {{u_1}} \right) = \left\{ {\left\langle {0,1} \right\rangle } \right\}\\ \Upsilon _{{\rm{AT}}}^{\left[ {0.8,1} \right]}\left( {{u_2}} \right) = \left\{ {\left\langle {1,1} \right\rangle } \right\} \end{array} $ |
| $ \begin{array}{l} \Upsilon _{{\rm{AT}}}^{\left[ {0.8,1} \right]}\left( {{u_3}} \right) = \emptyset \\ \Upsilon _{{\rm{AT}}}^{\left[ {0.8,1} \right]}\left( {{u_4}} \right) = \emptyset \end{array} $ |
3) 构造广义分布差别矩阵
[α, β]=[0, 0.3]时对应的广义分布差别矩阵如表 2所示,[α, β]=[0.8, 1]时对应的广义分布差别矩阵如表 3所示。
| 表 2 广义分布差别矩阵1 Tab.2 Generalized distribution discernibility matrix 1 |
| 表 3 广义分布差别矩阵2 Tab.3 Generalized distribution discernibility matrix 2 |
4) 获取差别函数并进行简化
| $ \begin{array}{l} {\rm{DF}}\left( {{\mathit{\boldsymbol{M}}^{\left[ {0,0.3} \right]}}} \right) = \left( {{a_2}} \right) \wedge \left( {{a_3}} \right)\\ {\rm{DF}}\left( {{\mathit{\boldsymbol{M}}^{\left[ {0.8,1} \right]}}} \right) = \left( {{a_2}} \right) \wedge \left( {{a_3}} \right) \end{array} $ |
5) 通过结合律获取所有的广义分布保持约简
由计算得,[α, β]=[0, 0.3]时和[α, β]=[0.8, 1]时的所有广义分布保持约简均为{a2, a3}。
4 一些特殊情形下的讨论值得注意的是,给定决策表DT=(U, AT∪D, V, f),当α和β取某些特殊值时,广义分布保持约简可以退化为目前已存在的一些约简,本节将根据α和β不同的特殊取值情况展开讨论,并给出相应的结论。其中,将MGEN、MPOS以及MDIS分别记为广义决策可辨识矩阵、正域可辨识矩阵以及分布可辨识矩阵,同时,将MijGEN、MijPOS以及MijDIS分别记为对象ui和uj对应在广义决策可辨识矩阵、正域可辨识矩阵以及分布可辨识矩阵的可辨识属性集,其中论域为U={u1, u2, …, un},i, j∈{1, 2, …, n}。
1)α=β=0时
当α和β取值均为0时,广义分布保持约简实质是保证对于置信度为0的规则在约简前后的置信度均为0,而对于置信度不为0的规则在约简前后的置信度均不为0,由此可得如下结论。
定理4 设决策表DT=(U, AT∪D, V, f),对于∀R⊆ AT且R≠Ø,α=β=0,若R是决策表DT的一个广义分布保持约简,则R必定同时是决策表DT的一个广义决策保持约简。
证明 不妨设∀ui, uj∈U,其中[ui]AT∩[uj]AT=Ø,同时设U/D={D1, D2, …, D|U/D|}。若有
2)α=β=1时
显然,当α=β=1时,广义分布保持约简实质是保证了置信度为1的规则在约简前后的置信度保持不变,由此可得如下结论。
定理5 决策表DT=(U, AT∪D, V, f),对于∀R⊆ AT且R≠Ø,令α=β=1,若R是决策表DT的一个广义分布保持约简,则R必定同时是决策表DT的一个正域保持约简。
证明 不妨设∀ui, uj∈U,其中,[ui]AT∩[uj]AT=Ø,U/D={D1, D2, …, D|U/D|},分情况进行如下讨论。
当
当
综上,由于∀ui, uj∈U,故在α=β=1的条件下,MPOS=M[1, 1]成立,故R是决策表DT的广义分布保持约简,则R必定同时是决策表DT的一个正域保持约简,证毕。
3) α=0,β=1时
当α=0,β=1时,广义分布保持约简实质是保证了置信度在[0, 1]内的所有规则在约简前后的置信度不变,同时易得,此时对象的[α, β]决策-置信度序偶集等价于在决策等价类划分上的置信度分布,由此可得如下结论。
定理6 决策表DT=(U, AT∪D, V, f),对于∀R⊆ AT且R≠Ø,α=0且β=1,若R是决策表DT的一个广义分布保持约简,则R必定同时是决策表DT的一个分布保持约简。
证明 不妨设∀ui, uj∈U,其中[ui]AT∩[uj]AT=Ø,U/D={D1, D2, …, D|U/D|};若
综上,图 1给出了广义分布保持约简与上述几种约简之间的关系。
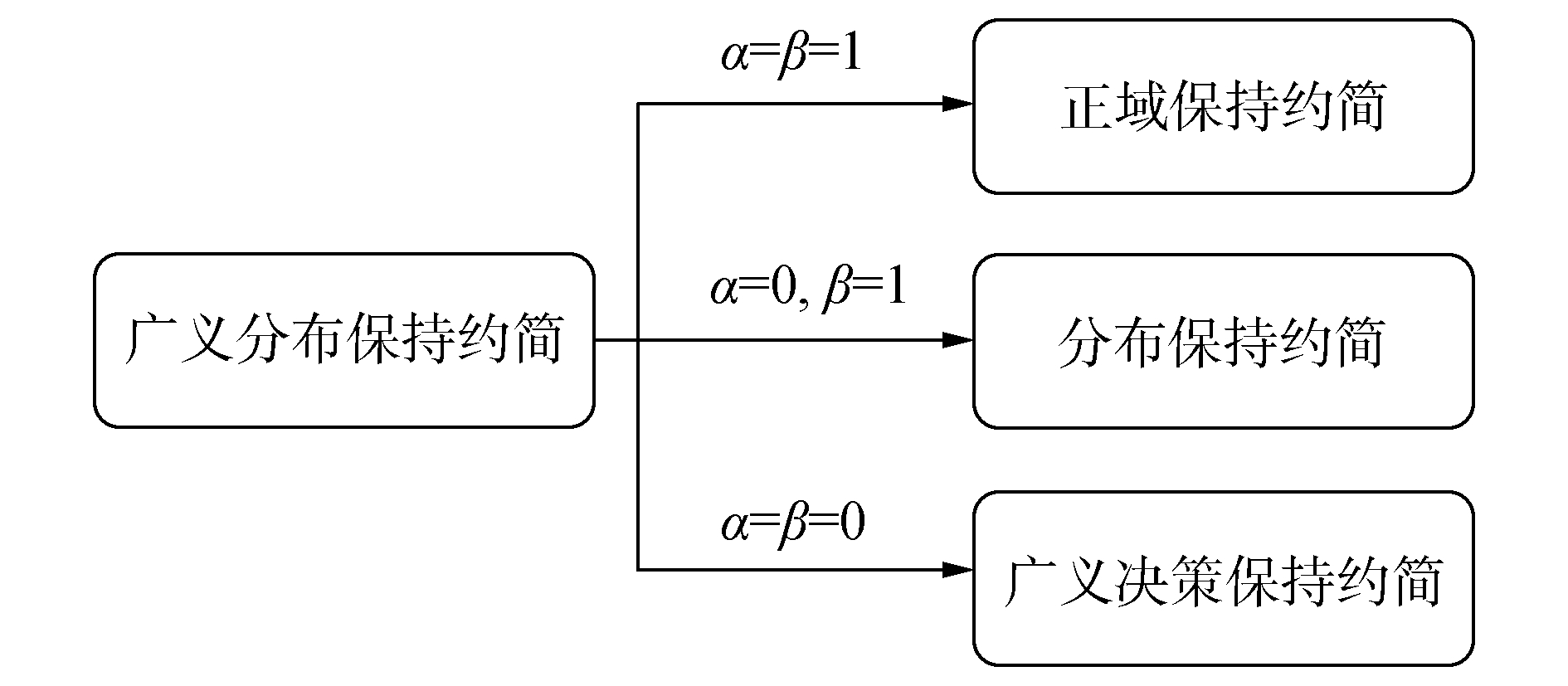
|
图 1 几种不同约简之间的关系 Fig.1 Relationships among different reductions |
例2 表 1所示决策表,论域U={u1, u2, u3, u4},AT={a1, a2, a3, a4}为条件属性集,D={d}为决策属性。由
| $ \begin{array}{*{20}{c}} {U/{\rm{AT = }}\left\{ {{E_1},{E_2},{E_3}} \right\}}\\ {{E_1} = \left\{ {{u_1}} \right\}}\\ {{E_2} = \left\{ {{u_2}} \right\}}\\ {{E_3} = \left\{ {{u_3},{u_4}} \right\}} \end{array} $ |
| $ \begin{array}{*{20}{c}} {U/D\left\{ {{D_1},{D_2},{D_3}} \right\}}\\ {{D_1} = \left\{ {{u_1}} \right\}}\\ {{D_2} = \left\{ {{u_2},{u_4}} \right\}}\\ {{D_3} = \left\{ {{u_3}} \right\}} \end{array} $ |
| $ \begin{array}{*{20}{c}} {{\rm{PO}}{{\rm{S}}_{{\rm{AT}}}}\left( D \right) = \left\{ {{u_1},{u_2}} \right\}}\\ {{\delta _{{\rm{AT}}}}\left( {{u_1}} \right) = \left\{ 0 \right\}}\\ {{\delta _{{\rm{AT}}}}\left( {{u_2}} \right) = \left\{ 1 \right\}}\\ {{\delta _{{\rm{AT}}}}\left( {{u_3}} \right) = \left\{ {1,2} \right\}}\\ {{\delta _{{\rm{AT}}}}\left( {{u_4}} \right) = \left\{ {1,2} \right\}} \end{array} $ |
| $ \begin{array}{*{20}{c}} {{\mu _{{\rm{AT}}}}\left( {{u_1}} \right) = \left( {1,0,0} \right)}\\ {{\mu _{{\rm{AT}}}}\left( {{u_2}} \right) = \left( {0,1,0} \right)}\\ {{\mu _{{\rm{AT}}}}\left( {{u_3}} \right) = \left( {0,0.5,0.5} \right)}\\ {{\mu _{{\rm{AT}}}}\left( {{u_4}} \right) = \left( {0,0.5,0.5} \right)} \end{array} $ |
求得正域保持约简为{a2, a3}, 广义决策保持约简为{a2, a3}, 分布保持约简为{a2, a3}。
因此,当α=β=1时,可得:
据此构造广义分布差别矩阵,如表 4所示。
| 表 4 广义分布差别矩阵 Tab.4 Generalized distribution discernibility matrix |
由广义分布差别矩阵可得所有的广义分布保持约简为{a2, a3},与正域约简一致。同理,α=β=0时的广义分布保持约简为{a2, a3},与广义决策约简一致; α=0, β=1时的广义分布保持约简为{a2, a3},与分布约简一致。
由定理4~6可得如下结论。
推论1 设DT=(U, AT∪D, V, f),置信度区间为[α, β],∀A⊆ AT,且A是置信度区间[α, β]下的一个广义分布保持约简,进一步,若给定置信度区间[α′, β′],且满足[α′, β′]⊆ [α, β],则∃A′⊆ A,使得A′是置信度区间[α′, β′]下的一个广义分布保持约简,且满足A′⊆ A。其中,α和β满足(α=0∧β∈[0, 1])或(α∈[0, 1]∧β=1)。
证明 由已知条件得,[α′, β′]⊆ [α, β],∀u∈U,有
本节采用4个UCI数据集进行实验,数据集信息如表 5所示,其中, |U|表示数据集的样本数,|AT|表示数据集的特征数,|D|表示分类数。对于数据集的预处理,处理策略如下:缺失特征值通过用该缺失特征值所对应特征下的多数特征值进行填充,连续型特征进行等频离散化,名词性特征值用整数进行替换,所有数据集的预处理均在Weka 3.6下进行。实验环境如下:Windows 7旗舰版32位操作系统,Intel Pentium G640C处理器,主频2.8 GHz,内存6.0 GB,所有算法均采用MATLAB R2010b编写实现。
| 表 5 UCI数据集信息 Tab.5 Information of UCI data sets |
实验分为两部分。第1部分验证置信度区间分别为[1.0, 1.0]、[0.0, 0.0]以及[0.0, 1.0]时,广义分布保持约简可分别退化为正域保持约简、广义决策保持约简以及分布约简,同时,也可验证广义分布保持约简算法的正确性;第2部分验证在较小的置信度区间下求得的广义分布保持约简是在较大的置信度区间下求得的广义分布保持约简的子集。
5.1 广义分布保持属性约简的退化情形本节中,分别令[α, β]取值为[1.0, 1.0]、[0.0, 0.0]和[0.0, 1.0],并求4个UCI数据集的广义分布保持约简,然后,分别求它们在正域保持约简算法(positive region preservation reduction algorithm,PRPRA),广义决策保持约简算法(algorithm of generalized decision preservation reduction,AGDPR)以及分布保持约简算法(distribution preservation reduction algorithm,DPRA)下的约简,通过前后对比,验证广义分布保持约简在3个特殊置信度区间下的退化情况,实验结果如表 6~8所示。
| 表 6 GDPRA和PRPRA的约简结果([α, β]=[1, 1]) Tab.6 Reduction results for GDPRA and PRPRA([α, β]=[1, 1]) |
| 表 7 GDPRA和GDECPRA的约简结果([α, β]=[0, 0]) Tab.7 Reduction results for GDPRA and GDECPRA([α, β]=[0, 0]) |
| 表 8 GDPRA和DPRA的约简结果([α, β]=[0, 1]) Tab.8 Reduction results for GDPRA and DPRA([α, β]=[0, 1]) |
当[α, β]分别为[1.0, 1.0]、[0.0, 0.0]以及[0.0, 1.0]时,GDPRA的约简结果分别同PRPRA、AGDPR以及DPRA的约简结果一致,验证了相关结论的正确性。
5.2 不同置信度区间下约简的包含关系本部分实验设置如下:首先,固定α的值为0.0,令β取值范围为0.0~1.0,取值间隔为0.2,记录随β取值的变化在不同置信度区间下求得的广义分布保持约简。同样的,固定β的值为1.0,令α取值范围为0.0~1.0,取值间隔为0.2,记录随α取值的变化在不同置信度区间下求得的广义分布保持约简,实验结果如表 9~12所示。
| 表 9 数据集1:Haberman’s survival Tab.9 Data set 1:Haberman's survival |
| 表 10 数据集2:blood transfusion service center Tab.10 Data set 2:blood transfusion service center |
| 表 11 数据集3:stone flakes Tab.11 Data set 3:stone flakes |
| 表 12 数据集4:airfoil self-noise Tab.12 Data set 4: airfoil self-noise |
实际中,具有较高或较低置信度的规则往往更易受到人们的关注,若通过分布约简进行规则提取,提取的规则可能过于冗长,不便于实际决策。因此,本文对分布约简的约简标准进行弱化,提出了广义分布保持约简的概念。理论与实验分析表明,当置信度区间取某些特殊值时,广义分布保持属性约简可退化为现有的一些属性约简,表明了广义分布保持属性约简具有一定的泛化性能,同时为深入研究不同属性约简之间的相互关系开阔了研究思路。实验数据表明,广义分布保持属性约简较分布约简可以获取更加简短的规则,且根据实际需要可以调整置信度区间以获取所需规则,使得广义分布保持属性约简可以适应不同的实际需求。但考虑到本文提出的算法主要是通过差别矩阵获取所有的广义分布保持属性约简,其时间和空间复杂度较高,不便于在实际应用中推广,具有一定的局限性,故开发更为高效的广义分布保持属性约简算法是未来主要的研究工作之一。
| [1] |
PAWLAK Z. Rough sets[J]. International journal of com-puter and information sciences, 1982, 11(5): 341-356. DOI:10.1007/BF01001956 ( 0) 0)
|
| [2] |
PAWLAK Z. Rough sets: theoretical aspects of reasoning about data[M]. Boston: Kluwer Academic Publishers, 1992.
( 0) 0)
|
| [3] |
张文修. 粗糙集理论与方法[M]. 北京: 科学出版社, 2001.
( 0) 0)
|
| [4] |
王国胤, 姚一豫, 于洪. 粗糙集理论与应用研究综述[J]. 计算机学报, 2009, 32(7): 1229-1246. WANG Guoyin, YAO Yiyu, YU Hong. A survey on rough set theory and applications[J]. Chinese journal of computers, 2009, 32(7): 1229-1246. (  0) 0)
|
| [5] |
SKOWRON A, RAUSZER C. The discernibility matrices and functions in information systems[J]. Theory and decision library, 1992, 11: 331-362. ( 0) 0)
|
| [6] |
KRYSZKIEWICZ M. Rough set approach to incomplete information systems[J]. Information sciences, 1998, 112(1/2/3/4): 39-49. ( 0) 0)
|
| [7] |
张文修, 米据生, 吴伟志. 不协调目标信息系统的知识约简[J]. 计算机学报, 2003, 26(1): 12-18. ZHANG Wenxiu, MI Jusheng, WU Weizhi. Knowledge reductions in inconsistent information systems[J]. Chinese journal of computers, 2003, 26(1): 12-18. (  0) 0)
|
| [8] |
徐伟华, 张文修. 基于优势关系下不协调目标信息系统的分布约简[J]. 模糊系统与数学, 2007, 21(4): 124-131. XU Weihua, ZHANG Wenxiu. Distribution reduction in inconsistent information systems based on dominance relations[J]. Fuzzy systems and mathematics, 2007, 21(4): 124-131. (  0) 0)
|
| [9] |
MIAO Duoqian, ZHAO Yan, YAO Yiyu, et al. Relative reducts in consistent and inconsistent decision tables of the Pawlak rough set model[J]. Information sciences, 2009, 179(24): 4140-4150. DOI:10.1016/j.ins.2009.08.020 ( 0) 0)
|
| [10] |
张楠, 苗夺谦, 岳晓冬. 区间值信息系统的知识约简[J]. 计算机研究与发展, 2010, 47(8): 1362-1371. ZHANG Nan, MIAO Duoqian, YUE Xiaodong. Approaches to knowledge reduction in interval-valued information systems[J]. Journal of computer research and development, 2010, 47(8): 1362-1371. (  0) 0)
|
| [11] |
苗夺谦, 胡桂荣. 知识约简的一种启发式算法[J]. 计算机研究与发展, 1999, 36(6): 681-684. MIAO Duoqian, HU Guirong. A heuristic algorithm for reduction of knowledge[J]. Journal of computer research and development, 1999, 36(6): 681-684. (  0) 0)
|
| [12] |
王国胤, 于洪, 杨大春. 基于条件信息熵的决策表约简[J]. 计算机学报, 2002, 25(7): 759-766. WANG Guoyin, YU Hong, YANG Dachun. Decision table reduction based on conditional information entropy[J]. Chinese journal of computers, 2002, 25(7): 759-766. (  0) 0)
|
| [13] |
QIAN Yuhua, LIANG Jiye, PEDRYCZ W, et al. Positive approximation: an accelerator for attribute reduction in rough set theory[J]. Artificial intelligence, 2010, 174(9): 597-618. ( 0) 0)
|
| [14] |
QIAN Yuhua, LIANG Jiye, PEDRYCZ W, et al. An efficient accelerator for attribute reduction from incom-plete data in rough set framework[J]. Pattern recognition, 2011, 44(8): 1658-1670. DOI:10.1016/j.patcog.2011.02.020 ( 0) 0)
|
| [15] |
钱宇华, 梁吉业, 王锋. 面向非完备决策表的正向近似特征选择加速算法[J]. 计算机学报, 2011, 34(3): 435-442. QIAN Yuhua, LIANG Jiye, WANG Feng. A positive approximation based accelerated algorithm to feature selection from incomplete decision tables[J]. Chinese journal of computers, 2011, 34(3): 435-442. (  0) 0)
|
| [16] |
CHEN Hongmei, LI Tianrui, RUAN Da, et al. A rough-set based incremental approach for updating approximations under dynamic maintenance environments[J]. IEEE transactions on knowledge and data engineering, 2013, 25(2): 274-284. DOI:10.1109/TKDE.2011.220 ( 0) 0)
|
| [17] |
CHEN Hongmei, LI Tianrui, LUO Chuan, et al. A rough set-based method for updating decision rules on attribute values' coarsening and refining[J]. IEEE transactions on knowledge and data engineering, 2014, 26(12): 2866-2899. ( 0) 0)
|
| [18] |
JIA Xiuyi, SHANG Lin, ZHOU Bing, et al. Generalized attribute reduct in rough set theory[J]. Knowledge-based systems, 2015, 91: 204-218. ( 0) 0)
|
| [19] |
ZHOU Jie, MIAO Duoqian, PEDRYCZ W, et al. Analysis of alternative objective functions for attribute reduction in complete decision tables[J]. Soft computing, 2011, 15(8): 1601-1616. DOI:10.1007/s00500-011-0690-7 ( 0) 0)
|
| [20] |
ZHANG Xiao, MEI Changlin, CHEN Degang, et al. Multi-confidence rule acquisition and confidence-preserved attribute reduction in interval-valued decision systems[J]. International journal of approximate reasoning, 2014, 55(8): 1787-1804. DOI:10.1016/j.ijar.2014.05.007 ( 0) 0)
|
 2017, Vol. 12
2017, Vol. 12


