现代经济发展中,大城市经济圈[1]内至少有一个或多个经济发达并具有较强城市功能的中心城市,以便带动周围其他城市的发展,这种经济圈模式现已成为城市经济圈发展的增长级。实践证明,经济圈中以三个地区为最好,例如京津冀经济圈、长江三角洲经济圈、珠三角经济圈等。另外,从数学方面分析,若将经济圈中每个城市视为一个顶点,城市间有路可达时连接为边,则一个经济圈为一个图。依据图论的知识可知,在多边形图中,三个顶点构成的圈(即三角形)是最稳定的,因此本文考虑的圈将以三角形为基本单元。
随着经济的发展,许多城市面临着严重的交通拥堵。若出行者对自己要经过交通网络的路径、费用、时间等能够以清晰地、直观地方式得到,则完成任务的效率将会大大提高。关于在复杂的交通网络的条件下,研究合理的出行路径模型和算法,请参见文献[2-9]。基于多属性条件路径选择问题,文献[2-9]以及目前掌握的材料中,均没有涉及对于交通网路信息提取的概念格[10]可视化研究。
概念格建立了对象和属性之间的一种概念层次结构,是数据分析和规则提取的一种有效工具。Whitney[11]在1935年首次提出的拟阵已经被广泛地应用于信息编码[12]和网络安全[13]等领域。将拟阵与概念格理论结合、图论[14-15]与概念格理论结合来解决问题,已有许多成功的案例[16-21]。
由于现实生活中,人们出行受多个属性条件的限制,针对这些限制,经过研究发现Kn简单图中形成三角形圈的一种特殊性质。由此,可以对复杂的交通网络进行分析、转化,形成Kn简单图。进而,能够建立网络模型,构建模型所对应的关联矩阵。依据Kn图所产生的特殊形式背景,建立概念格信息提取方法。从而,给出基于二元拟阵Kn图的一种建格方法,并利用具体实例验证方法的正确性与有效性。
1 预备知识本节主要介绍网络Kn图、拟阵和概念格一些定义与相关结论。有关图的基本概念和完全图的定义,读者请参见文献[14]。有关二元拟阵和图的拟阵可表示性请参见文献[11]。
定义1[22] 设任意(无向)图G=(V, E),其中顶点集V={v1, v2, …, vn},边集E= {e1, e2, …, ee}。用mij表示顶点vi与边ej关联的次数,可能取值为0, 1, 2,称所得矩阵M(G)=(mij)n×e为图G的关联矩阵。
定义2[14] V(G)=X∪Y, X∩Y=Ø, X中任二项不相邻,Y中任二项不相邻,则G为二部图;若X中每个顶点皆与Y中一切顶点相邻,则G为完全二部图,记Km, n,其中m=|X|,n=|Y|。
定义3[11] 设M是关于E={b1, b2, …, br, e1,e2,…, eq}的一个拟阵,其中B={b1, b2, …, br}是M的一个基。设Cj是B∪{ej}所含的基本圈,定义r×q阶矩阵D=(dij),其中
引理1[14] 在一个具有n个顶点的无向完全图中,包含的边数为
定义4[17] 形式背景K=(G, M, I)定义为一个三元数组,其中G中的元素被称为对象,M中的元素被称为属性。I⊆ G×M,用gIm表示(g, m)∈I,即对象g具有属性m。
定义5[17] 形式背景(G, M, I)中的概念定义为元素对(A, B),其中A⊆ G,B⊆ M,A称为概念的外延,B称为概念的内涵,并且满足以下条件:
1)B′={a∈G| ∀b∈B, aIb}, A′={b∈M | ∀a∈A, aIb};
2)A⊆ A″, B⊆ B″;
3)
定义6[17] 设(A1, B1)、(A2, B2)是L(G, M, I)中的两个概念,定义二元关系(A1, B1) ≤(A2, B2)⇔A1⊆ A2⇔B1⊆ B2, 称(A1, B1)是(A2, B2)的子概念,(A2, B2)是(A1, B1)的父概念。若不存在概念(A3, B3)使得(A1, B1)≤(A3, B3) ≤(A2, B2)成立,则称(A1, B1)是(A2, B2)的直接子概念,(A2, B2)是(A1, B1)的直接父概念。
不难证明这种父概念-子概念关系(也称泛化-特化关系)是L(G, M, I)上的一个偏序关系。事实上L(G, M, I)关于该偏序关系是一个完备格,称为形式背景(G, M, I)的概念格,记为L(G, M, I)。
引理2[17] 设(G, M, I)是一个形式背景,则L(G, M, I)关于上面定义的序“≤”构成的是完备格,其中上下确界由下式给出:
| $ \begin{align} & {{\vee }_{j\in J}}({{A}_{j}}, {{B}_{j}})=\left( {{\left( \underset{j\in J}{\mathop{\cup }}\, {{A}_{j}} \right)}^{\prime \prime }}, \underset{j\in J}{\mathop{\cap }}\, \text{ }{{B}_{j}} \right) \\ & {{\wedge }_{j\in J}}({{A}_{j}}, {{B}_{j}})=\left( \underset{j\in J}{\mathop{\cap }}\, \text{ }{{A}_{j}}, (\underset{j\in J}{\mathop{\cup }}\, {{B}_{j}}{)}'' \right) \\ \end{align} $ |
为了模型的建立和讨论表述简捷,给出如下几个定义。
定义7 含圈基:在Kn图中满足从一个顶点出发,到其他n-1个顶点的相连接的边叫做含圈基。
定义8 基顶点:在Kn图中满足从一个顶点出发包含的所有相连的含圈基的顶点叫做基顶点。
定义9 基最小圈:在一个三角形最小圈中,满足一个最小圈中包含两个基的三角形圈,叫做基最小圈。
2 模型的建立图论主要研究图的拓扑性质,为任何一个包含某种二元关系系统提供一种分析和描述模型。众所周知,交通网络可以用图表示出来,也可把交通网络里的距离当作两点之间的权值加入进去。
复杂网络中的交通网络对应图论里一类特殊的图结构,具有与应用相关的很多重要特征。对于一些网络中出现的复杂的网络,作如下处理。
1) 对于两个顶点之间具有多重边的情况,选择其中权值最小的边。
2) 当两个顶点之间的权值一样时,任意选择其中一条边,固定下来,成为最熟悉的一条道路。
3) 对于带环图的这种情况,因为实际问题考虑的是对于一个工厂的运输,自身运输没有任何实际的意义。例如:如果是一家超市,自身对于自身运输也没有意义,所以不予考虑。
具有重边或有环的图都可以转化为简单图应对出行问题,因此复杂网络图可以转化为简单图,用以讨论相应的出行问题。由于在具有n个顶点的简单图中,Kn图结构最复杂,所以只要解决了Kn图的出行问题,其他的简单图的出行问题将会迎刃而解。对于非Kn的n个顶点的简单图,因为它们是Kn的子图,所以可以通过加边,使其成为Kn图,只需将新加边的权值定义为0,采用本文的方法,完全可以解决出行问题。基于以上的讨论,只需解决具有Kn图这样的交通网络的出行问题,因此本文只研究Kn图。
现有n个城市,任意两个城市均由交通道路连接。一位出行者要从自己所居住的城市去其他n-1个城市办事情,要求到达其他任意两个城市后再回到自己所居住的城市,现在的问题是:如何找到以3个城市为三角形经济圈的一个出行方案。
首先建立一个网络模型,构建其关联矩阵。由于关联矩阵是一个0-1矩阵,信息提取中的任一个形式背景可视为一个0-1矩阵,因此依据形式背景的特殊性,建立概念格信息提取方法,进而找到人们所需的最适合出行方案。
2.1 问题的提出在不同城市间构建现代化交通网络,实现城市间交通一体化,将会极大方便交通出行。问题是:如何在众多出行方案中选取合适的方案,成为人们出行前需要解决的问题。交通运输网络错综复杂,很难给人们带来直接帮助,需要对交通运输网络进行简化和直观化,得到一个简化的网络。若出行者需要计算出自己所居住的城市和其他任意两个城市的距离和,即第1节定义9中的基最小圈,判断走哪个基最小圈距离和最短时,探究交通网络Kn图模型中的最小经济圈所需出行的路径距离就变得有意义了。
2.2 模型的条件设有n个城市,每个城市看作一个顶点,两个城市之间有路可达时,用一条线相连接,建立城市网络图。图中顶点用v1,v2,…,vn表示,组成集合V={v1, v2, …, vn}。网络图中vi,vj之间有路径可达,记相连接的边为eij,将此交通网络图记为G=(V, E),得G为一个有限无向图。出行者从给定的一个顶点城市v1出发去办事,要求路径中必须经过两个顶点城市(除去给定城市顶点以外的其他任意两个顶点城市),再返回到出发城市顶点v1。由于出行者走的道路为一个三角形,现在的问题是要选择一个三角形在距离和花费的时间都少的三角形作为出行者的最终出行方案,这就需要找到所有可能的出行方法,换句话说,出行者需要出行前找到所有需要走过的路径和出行方案,以便从中选择最佳方案,这些方案对决策者综合路径距离、时间、花费决策时有重要的意义,可以帮助其更加直观、快速地做决定,节约决策时间。
2.3 问题的分析交通城市之间的无向图G进行转化后是顶点为n的完全图,记G为Kn图。因Kn图对应的关联矩阵满足二元拟阵M,知定义7的含圈基满足定义3的拟阵M,即实际生活中人们出行方案里的最小三角形圈。于是在Kn图的二元拟阵的标准矩阵表示如下:在对应组成基本圈的三条边下标记1,没有组成基本圈的边下标记0,然后把得到的矩阵作为含0和1的形式背景。在上面进行概念格的探索和证明时发现,在Kn图中将二元拟阵中的基本圈即定义9的基最小圈,作为对象,每两个顶点之间相连的边作为属性,建立形式背景,找寻概念会遵循一定的数学规律,运用此规律进行建格,速度很快。
2.4 模型的解决 2.4.1 Kn图的建格模型根据定义3给出Kn图的标准矩阵表示。当顶点n=3时,根据引理1的公式得边数为3,含圈基的个数为n-1=2,与其中一个顶点相连接构成的基最小圈个数为边数
| 表 1 顶点数与基最小圈的规律 Tab.1 Vertex number and the basis of the smallest circle of the law |
将图G=(V, E)对应的拟阵M中定义9基最小圈集O视为形式背景中的对象集,将图G的边集E视为属性集P,圈Ci中含有某条边ej时,记Ciej值为1,否则为0,得到形式背景(O, P, I),对象集O={C1, C2, …, Cn},属性P={b1, b2, …, bn}。特别地,当图G=(V, E)为Kn图时,图G=(V, E)对应的形式背景L(Okn, Pkn, Ikn)如表 2所示。
| 表 2 Kn图的形式背景L(Okn, Pkn, Ikn) Tab.2 Formal context L(Okn, Pkn, Ikn) of Kn diagram |
定义10 在Kn图的形式背景L(Okn, Pkn, Ikn)对应的概念格L(O, P, I)中给出“层”的定义:
设L(O, P, I)最大元为A即第一层,对任意X∈L(O, P, I)|{A},设A到X的距离为n。也就是,当区间[X, A]⊆ L(O, P, I)最长链的长度为r,(r=1, 2, 3, …, n),则设X为第m层,m=r+1, 记第m层为m=L(m)。设概念格L(O, P, I)的Hasse示图记为H(L)。由表 2发现,当n=4时,根据L(Okn, Pkn, Ikn)={(P′, P)}得对应的概念为(C3C2C1, {})∈L(1);(C1C3, b1),(C3C2, b2),(C1C2, b3)∈L(2);(C3, b6b1b2),(C1, b4b1b3),(C2, b5b2b3)∈L(3);({}, b6b5b4b3b2b1)∈L(4)。
引理3 1) 根据完全图的定义和表 1知,当定义7含圈基个数为n-1时,与定义8基顶点相连接的每个基b1,b2,…,bn-1对应的对象个数为n-2个。
2) 根据定义9含两个基的基最小圈最多有一条重边。
证明 首先证明第1) 条。在表 2中,b1对应着的对象为n-2个,因为b1≠b2,所以对应的对象就为n-2个,即b1′≠b2′。其次,证明第2) 条。若两个基最小圈含有2个相同的边,根据定义9可知:假设C1≠C2,b1∈C1,b2∈C2,若(b1∪b2)∈(C1∩C2),则推出C1=C2,与条件中两个基最小圈含有2个相同的边矛盾,即C1 ≠C2矛盾。所以含两个基的基最小圈最多有一条重边。
定理1 Kn图对应的形式背景概念格有且仅有4层。
证明 根据定义4、定义5、定义6及引理3中的第1) 条的概念。第1层:O={C1, C2, …, CC2n-1}对应的属性集P={}可以表示为(C1 C2 …CC2n-1, {})∈L(1)。第2层:每个基对应n-2个圈,设为C1,C2, …,Cn-2。证任意基bi∈B={b1, b2, …, bn-1},(i=1, 2, …,n-1),设(C1C2…Cn-2, bi),其中bi′=C1C2…Cn-2,根据引理3中第1) 条,Ø ∩bi=Ø,|Ø|=0,|{bi}|=1且Ø⊄{bi}且不存在任意集合A满足⊄⊆ A⊆ {bi}。所以它们之间不会产生其他的概念。第3层:设(C1C2…Cn-2, b1)与(C1C2…Cn-3, b2)∈L(3),所以设(C1…Cn-3, (b1b2)″)=(C1C2…Cn-2, b1)∧(C1C2…Cn-3, b2),由引理3中第2) 条知C1=C2=…=Cn-3,取代表圈C1,由基最小圈定义当且仅当存在b3∈C1,则(C1, b1b2b3)是概念,由任意性知(Ci, Ci′)均为概念,其中Ci′为Ci包含的3条边。第4层:(C1, b1b2b3)与(C2, b1b3b4)∈L(4),(Ø, b1)。因为存在集合B={b1, b2, b3, …,
定理2 Kn图模型建立的概念格L(Kn)的第2层和第3层的Hasse示图组成一个二部图。
证明 根据定义2(二部图)的定义,二部图G=(V1, V2, E)由顶点集V1和V2及边集E⊆ V1×V2组成,V1={x1, x2, …, xs},V2={y1, y2, …, yt},则二部图G=(V1, V2, E)的伴随矩阵为二元矩阵A(aij),这里aij=1,当且仅当(xi, yj)∈E。设V1为对象集,V2为属性集,则二部图的伴随矩阵就是形式背景。二部图G=(V1, V2, E)由两个非交顶点集V1,V2组成,且G的每条边的顶点分别在V1,V2中。设V1是第2层概念的集合,V2是第3层概念的集合,则在Kn图中概念之间满足定义6,(C1, b1)≤(C2, b2)⇔C1⊆ C2(⇔b2⊆ b1),根据子概念-父概念的关系建立连线是一个二部图,如图 1所示。
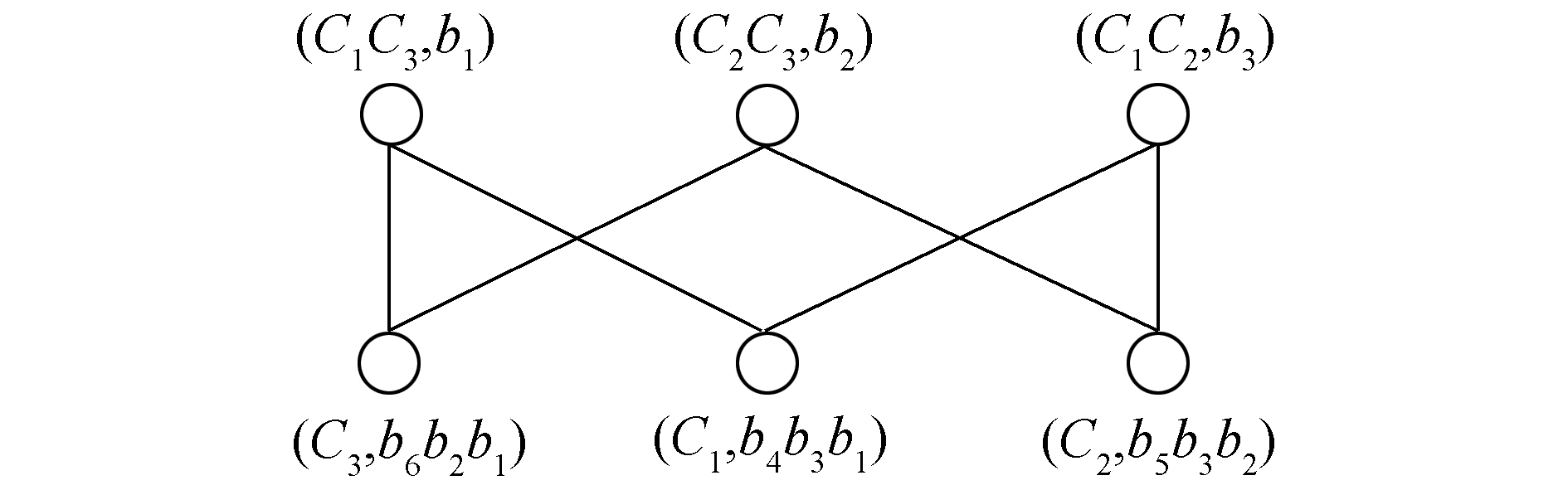
|
图 1 K4图的二部图 Fig.1 Bipartite graph of K4 diagram |
再把第1层和第4层概念(O, {})和({}, P)加进图 1,根据定理1建立概念格得Hasse示图,如图 2所示。Hasse图是利用概念之间的泛化和特化进行绘制的,由于概念格的完备性,概念格确定了,其Hasse图也唯一确定了。概念格最上层是全概念,最下层是空概念。Hasse图中的边分别连接在直接父概念和直接子概念之间。
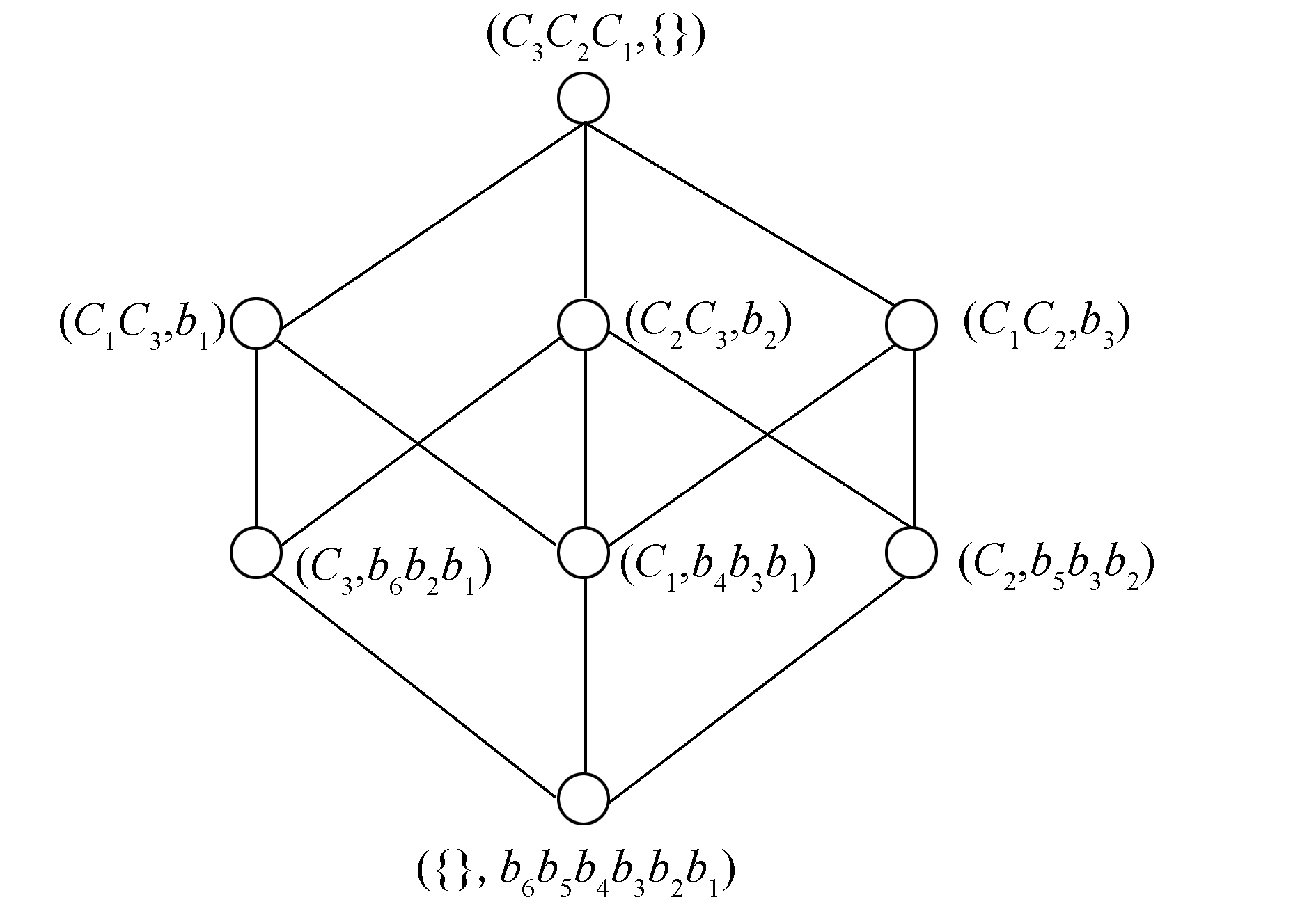
|
图 2 K4图的概念格 Fig.2 Concept lattice of K4 diagram |
根据K4图的格结构,利用数学归纳法分别对K5图、K6图、Kn图进行建格,得出Kn图建立概念格的一个算法过程。
2.4.2 算法过程通过对特殊限制Kn图的规律发现,满足Kn图二元标准矩阵特点的都可以建成一个Hasse示图。对于具有这种特定形式背景的概念,用上面的建格方法进行建格,速度很快。下面给出对象是基最小圈,属性是边的形式背景的建格过程。
输入 形式背景(O, P, I)。
输出 集合C,(O, P, I)所有的概念。
1)C:={P′, P}初始化属性集合B=Ø。
2) 找第2层的概念,根据规律知道,当完全图为Kn时,顶点数为n,与基顶点相连的边为n-1, 即第2层的概念为n-1个,根据属性b1, b2, …,bn-1找到所对应的基最小圈对象。
3) 找第3层的概念,根据完全图Kn的特点,基最小圈的个数为
4) 第1层中的元(概念),与且仅与第2层的每一个元分别连线,第4层的元与且仅与第3层的每一个元分别连线,第2层的元与第3层的元之间的连线关系可以根据定理2进行。这样就可以得到所有应该存在的连线。即根据定义6和引理2的偏序关系(C1, b1)≤(C2, b2)⇔C1 ⊆ C2(⇔b2⊆ b1),满足概念格子概念-父概念的关系,把第1层的概念(O, {})与第2层的概念建立连线,第4层的概念({}, P)与第3层概念建立连线加入到步骤2) 和3) 组成的二部图中。
2.4.3 算法的复杂度根据形式背景的特殊性,此处得到的概念格有且仅有4层。
第1层的概念和第四层的概念分别是(O, {})和({}, P)。
第2层的概念与基顶点连接的边个数为n-1(n表示顶点数)。
第3层的概念根据Kn图所产生的基最小圈个数N来决定,N=
与定义5和定义6找寻概念的方式(即参考文献[22]中13页概念格的生成算法1) 相比,本文提出的方法更有效。因为,如果存在|G |个对象,|M |个属性,那么相应的概念格将可能包含2|G|或2|M|个概念,计算量太大。而本文构造的概念的算法方式,由于具有一定的规律性,大大减少了计算量。
3 应用实例超市里冷冻猪肉和冷鲜猪肉因储存时间的长短不同,价格有很大差别。当决策者需要判断送货多少时,也许会出现这家超市里冷鲜猪肉已经卖完,而另一家超市里的冷鲜肉卖不出去,这时由于冷鲜猪肉放置太长时间,变成冷冻猪肉而导致价格下降,造成亏损。针对这种情况,为了减少亏损,合理决策冷鲜猪肉配送供给,变得十分重要。
因为供应超市里每个时间段内宰杀猪的数量一定,所以供货量一定; 又因为超市分配每辆货车行走的公里数一定,油费消耗一定。根据以上限制条件,需要货车从供应超市出发到达其他任意两个供给城市的连锁超市后,再返回原来的供应超市。为让决策者更快地给出供应超市的货车供给方案,应对其供货方案和距离进行概念格的可视化建格。
货物(冷鲜肉)将从石家庄市超市出发分别运往周边的县市超市。记石家庄市超市为v1,正定县超市记为v2,鹿泉市超市记为v3,新乐市超市记为v4,藁城市超市记为v5。但是货物运输时由于宰杀猪数量的限制只能带够发往两个县市超市的货物量,再回到出发地取货,为了选择出合适的运输方案,对其进行建格。
根据货车配送路线,v1超市距v2超市的距离为b1=15 km,v1超市距v3超市的距离为b2=15 km,v1超市距v4超市的距离为b3=38 km,v1超市距v5超市的距离为b4= 31 km,v2超市到v5超市的距离为b5= 39 km,v3超市到v5超市的距离为b6= 57 km,v4超市到v5超市的距离为b7= 52 km,v2超市到v4超市的距离为b8= 33 km,v3超市到v4超市的距离为b9= 60 km,v2超市到v3超市的距离为b10= 34 km。根据任意两个超市之间是否有路相连接,得无向图的关联矩阵(这里的距离是大约值,具体的取值可以根据用户的需求来定):
| $ \boldsymbol{A}=\begin{matrix} {} \\ {{v}_{2}} \\ {{v}_{3}} \\ {{v}_{4}} \\ {{v}_{5}} \\ \end{matrix}\left[\begin{matrix} {{b}_{1}} & {{b}_{2}} & {{b}_{3}} & {{b}_{4}} & {{b}_{5}} & {{b}_{6}} & {{b}_{7}} & {{b}_{8}} & {{b}_{9}} & {{b}_{10}} \\ 1 & 0 & 0 & 0 & 1 & 0 & 0 & 1 & 0 & 1 \\ 0 & 1 & 0 & 0 & 0 & 1 & 0 & 0 & 1 & 1 \\ 0 & 0 & 1 & 0 & 0 & 0 & 1 & 1 & 1 & 0 \\ 0 & 0 & 0 & 1 & 1 & 1 & 1 & 0 & 0 & 0 \\ \end{matrix} \right] $ |
根据出行人员的实际要求,从城市v1出发后要经过两个城市再返回原城市,符合基最小圈定义。建立数学模型,根据无向图的关联矩阵A得图 3所示K5图模型。以顶点v1为出发地,根据运送货物的实际情况,从顶点v1出发运送到其他两个顶点经过的距离,得送货所有可能的方案分别是C1={b1,b4,b5},C2={b2,b4, b6}和C3={b3, b4, b7},C4={b1,b3,b8},C 5={b2,b3, b9},C6={b1,b2,b10}。为在最短的距离内把货物送完,找出所有的送货路线,提取里面的规则进行建格。
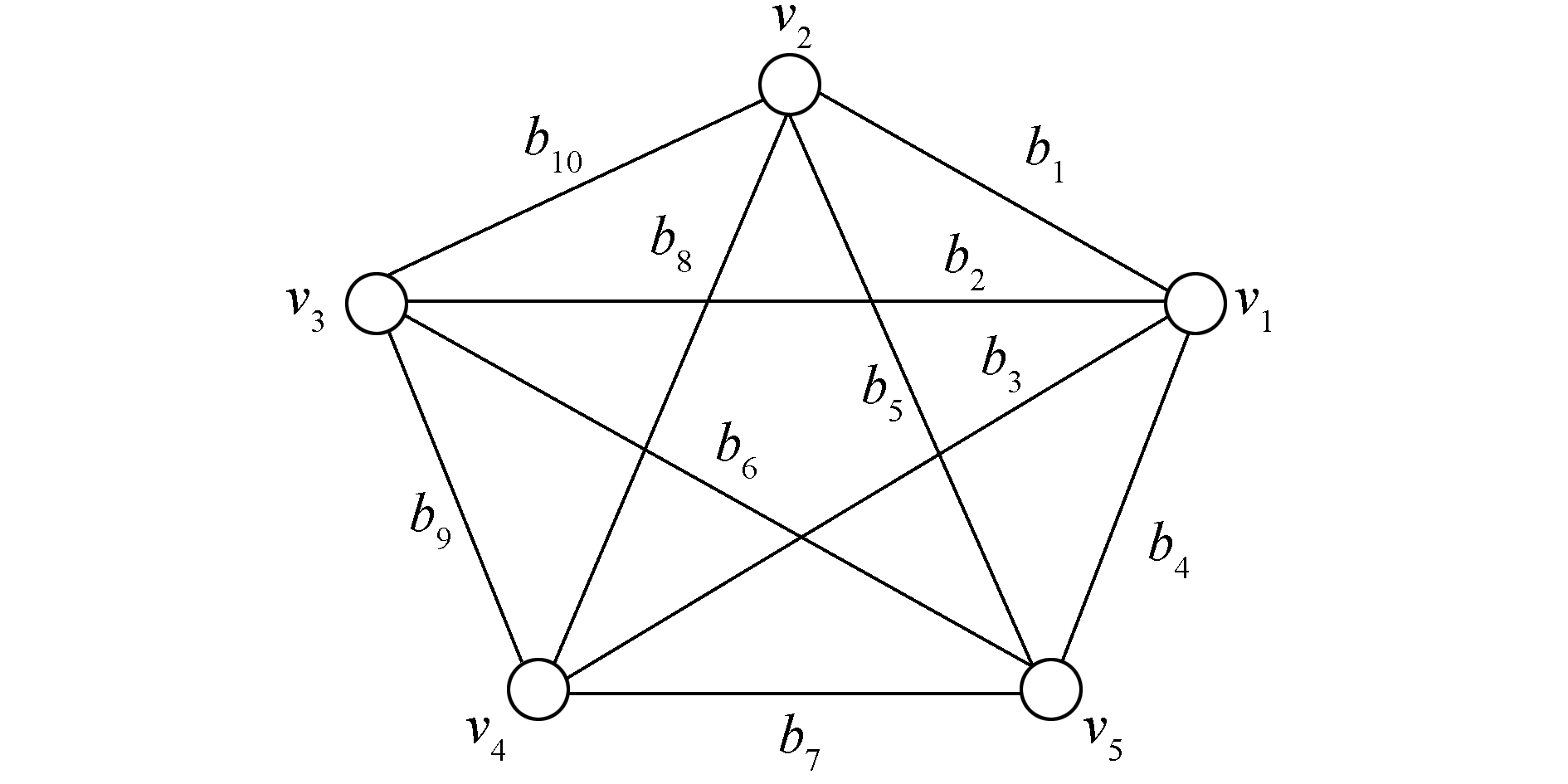
|
图 3 K5图 Fig.3 K5 diagram |
根据定义3得K5图的二元拟阵的标准矩阵:
| $ {{\boldsymbol{A}}^{*}}=\begin{matrix} {} \\ {{C}_{1}} \\ {{C}_{2}} \\ {{C}_{3}} \\ {{C}_{4}} \\ {{C}_{5}} \\ {{C}_{6}} \\ \end{matrix}\left[\begin{matrix} {{b}_{1}} & {{b}_{2}} & {{b}_{3}} & {{b}_{4}} & {{b}_{5}} & {{b}_{6}} & {{b}_{7}} & {{b}_{8}} & {{b}_{9}} & {{b}_{10}} \\ 1 & 0 & 0 & 1 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 1 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 1 & 0 & 0 & 1 & 0 & 0 & 0 \\ 1 & 0 & 1 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 1 & 1 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ \end{matrix} \right] $ |
根据概念格的定义4建立形式背景,如表 3。
| 表 3 K5图的形式背景 Tab.3 Formal context of K5 diagram |
利用表 3中K5图的形式背景,根据本文所给出算法过程,进行概念格Hasse图的建立。
1)C:={P′, P}初始化属性集合B=Ø。
2) 找第2层的概念,根据属性b1、b2、b3、b4、b5、b6找到所对应的基最小圈对象C1C4C6、C2C5C6、C3C4C5、C1C2C3得到概念(C1C4C6,b1)、(C2C5C6,b2)、(C3C4C5, b3)、(C1C2C3, b4)。
3) 找第3层的概念,根据完全图Kn的特点,由对象C1、C2、C3、C4、C5、C6找到所对应的属性b1b4b5、b2b4b6、b3b4b7、b1b3b8、b2b3b9、b1b2b10得到概念(C1, b1b4b5)、(C2,b2b4b6)、(C3, b3b4b7)、(C4, b1b3b8)、(C5,b2b3b9)、(C6, b1b2b10)。
4) 把第1层和第4层概念(O, {})和({}, P),根据定义6和引理2的偏序关系(C1, b1)≤(C2, b2)⇔C1⊆ C2(⇔b2⊆ b1),对满足概念格子概念-父概念的关系[23],把第1层的概念(O, {})与第2层的概念建立连线, 第4层的概念({}, P)与第3层概念建立连线加入到步骤2) 和3) 组成的二部图中,得到概念格的Hasse示图,如图 4。
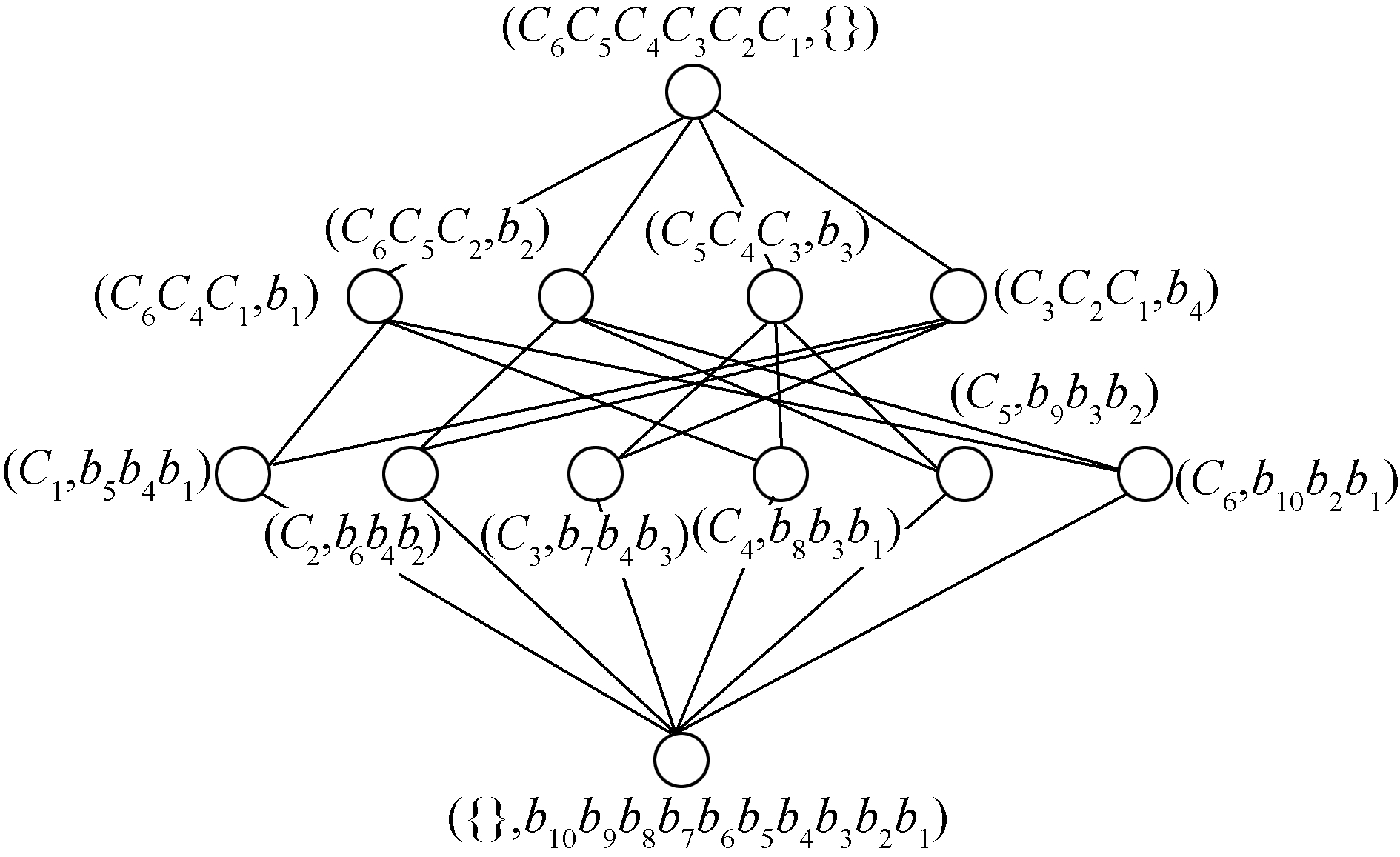
|
图 4 K5图的概念格 Fig.4 Concept lattice of K5 diagram |
从图 4中可以看出,满足b1这段距离油耗的货车有且仅有C1、C4、C6方案,满足b2这段距离油耗的货车有且仅有C2、C5、C6方案,满足b3这段距离油耗的货车有且仅有C3、C4、C5方案,满足b4这段距离油耗的货车有且仅有C1、C2、C3方案,还可以快速地计算出每个方案需要走的距离里程。若采用方案C1,需走的距离里程为b1+b4+b5=85 km;若采用方案C2,需走的距离里程为b2+b4+b6=103 km; 若采用方案C3,需走的距离里程为b4+b6+b7=140 km; 若采用方案C4,需走的距离里程为b1+b3+b8=86 km; 若采用方案C5,需走的距离里程为b2+b3+b9=113 km; 采用方案C6,需要走的距离里程为b1+b2+b10=64 km。从中比较可知,若运送货物途经距离最短,可以选择方案C6。
从图 4中可快速地筛选出运输最短路径的运输方案和最长路径的运输方案,方便出行者对出行方案的选择。在其他复杂网络中,两个顶点之间会出现两条边,比如重边的情况,在寻找哪种方案最优时,可能出现多种方案,而本文开始时就已经删除了那些对选择方案无用的边,因此从概念格的Hasse图中很容易看出哪个方案最优,不需要出行者进行2次或更多次的重新比较。
4 结束语根据京津冀紧密对接的一体化交通网络。基于出行者对于交通网络路径的选择,根据实际生活中的一些属性条件的限制,在Kn图模型中,根据三角形圈的一种特殊性,寻找规律,结果发现,对Kn图拟阵的标准矩阵的形式背景产生4层。根据此规律进行建格,提出利用二元拟阵的Kn图的概念格的建格方法。相比最基本的建格方法,此方法的计算量要少很多。通过实例发现,针对这种特殊的形式背景,出行者在提取有用的方案时,会更加快速、方便。由于研究背景和素材来源于实践,这类事件很多,因此提出的方法具有很好的推广意义和应用前景。在接下来的研究中,将会在Kn图中加入权值,进行距离和时间等多种属性的研究。
| [1] |
左锋. 经济学视野中大城市经济圈的形成与发展—论中国三大城市经济圈的现状及其发展[J]. 华东师范大学学报:哲学社会科学版, 2002, 34(5): 89-95. ZUO Feng. The formation and development of a metropolitan economic circle in the perspec-tive of economics[J]. Journal of east cluna normal university:philosophy and social sciences, 2002, 34(5): 89-95. (  0) 0)
|
| [2] |
胡一竑. 基于复杂网络的交通网络复杂性研究[D]. 上海: 复旦大学, 2008: 1-121. HU Yihong. Analysis of complex transportation networks[D].Shanghai: Fudan University, 2008: 1-121. http://d.wanfangdata.com.cn/Thesis/Y1965645 (  0) 0)
|
| [3] |
刘佳. 复杂网络中最短路径问题的优化算法研究[D]. 太原: 太原科技大学, 2007: 1-30. LIU Jia. Research on the algorithm for shortest path problem in complicated network[D]. Taiyuan: Taiyuan University of Science and Technology, 2007: 1-30. http://cdmd.cnki.com.cn/Article/CDMD-10109-2007127989.htm (  0) 0)
|
| [4] |
严寒冰, 刘迎春. 基于GIS的城市道路网最短路径算法探讨[J]. 计算机学报, 2000, 23(2): 210-215. YAN Hanbing, LIU Yingchun. A new algorithm for finding shortcut in a city's road net based on GIS technology[J]. Chinese journal of computers, 2000, 23(2): 210-215. (  0) 0)
|
| [5] |
谢政, 李建平. 网络算法与复杂性理论[M]. 北京: 国防科技大学出版社, 1995: 120-140.
( 0) 0)
|
| [6] |
LAM W H K, LI Zhichun, HUANG Haijun, et al. Modeling time-dependent travel choice problems in road networks with multiple user classes and multiple parking facilities[J]. Transportation research part B: methodological, 2006, 40(5): 368-395. DOI:10.1016/j.trb.2005.05.003 ( 0) 0)
|
| [7] |
GAO Song, Chabini I. Optimal routing policy problems in stochastic time-dependent networks[J]. Transportation research parB: methodological, 2006, 40(2): 93-122. DOI:10.1016/j.trb.2005.02.001 ( 0) 0)
|
| [8] |
于德新, 杨薇, 杨兆升. 重大灾害条件下基于GIS的最短路径改进算法[J]. 交通运输工程学报, 2011, 11(4): 123-126. YU Dexin, YANG Wei, YANG Zhaosheng. Shortest path improved algorithm based on GIS under large-scale disaster[J]. Journal of traffic and transportation engineering, 2011, 11(4): 123-126. (  0) 0)
|
| [9] |
陈京荣. 交通网络路径选择及应用研究[D]. 兰州: 兰州交通大学, 2009: 1-43. CHEN Jingrong. Research on route choice and its application in traffic networks[D]. Lanzhou: Lanzhou Jiaotong University, 2009: 1-43. http://cdmd.cnki.com.cn/Article/CDMD-10732-2010235726.htm (  0) 0)
|
| [10] |
GANTER B, Wille R. Formal concept analysis: mathematical foundations[M]. New York: Springer, 1999.
( 0) 0)
|
| [11] |
王树禾. 图论[M]. 北京: 科学出版社, 2009.
( 0) 0)
|
| [12] |
BONDY JA. Graph theory[M]. Berlin: Springer Press, 2008.
( 0) 0)
|
| [13] |
刘桂珍, 陈庆华. 拟阵[M]. 长沙: 国防科技大学出版社, 1994.
( 0) 0)
|
| [14] |
吉庆兵. 二元拟阵码及其对偶码[J]. 重庆师范学院学报:自然科学版, 2001, 18(4): 48-50. JI Qingbing. Binary matroid codes and their dual codes[J]. Journal of Chongqing normal university:natural science edition, 2001, 18(4): 48-50. (  0) 0)
|
| [15] |
马对霞, 林姿琼, 祝峰. 拟阵在网络安全中应用[J]. 小型微型计算机系统, 2015, 36(8): 1858-1860. MA Duixia, LIN Ziqiong, ZHU Feng. Application of matroids on network security[J]. Journal of Chinese computer systems, 2015, 36(8): 1858-1860. (  0) 0)
|
| [16] |
毛华. 拟阵与概念格的关系[J]. 数学进展, 2006, 35(3): 361-365. MAO Hua. The relation between matroid and concept Lattice[J]. Advances in mathematics, 2006, 35(3): 361-365. (  0) 0)
|
| [17] |
毛华, 李斌. 等价关系约束属性的形式概念分析[J]. 计算机工程与应用, 2010, 46(36): 158-160. Mao Hua, LI Bin. Formal concept analysis of attributes by equivalent relation[J]. Computer engineering applications, 2010, 46(36): 158-160. DOI:10.3778/j.issn.1002-8331.2010.36.043 (  0) 0)
|
| [18] |
李立峰, 刘三阳, 罗清君. 弦二部图的概念格表示[J]. 电子学报, 2013, 41(7): 1385-1388. LI Lifeng, LIU Sanyang, LUO Qingjun. Representing chordal bipartite graph using concept lattice theory[J]. Chinese journal of electronics, 2013, 41(7): 1385-1388. (  0) 0)
|
| [19] |
李立峰. 链图的概念格表示[J]. 计算机科学, 2014, 41(2): 264-266. LI Lifeng. Chain graph and their concept lattice representation[J]. Computer science, 2014, 41(2): 264-266. (  0) 0)
|
| [20] |
MAO Hua. A graph-theoretic method to representing a concept lattice[J]. Applied mathematics and information sciences, 2014, 8(2): 553-561. DOI:10.12785/amis/080213 ( 0) 0)
|
| [21] |
MAO Hua. Characterizing trees in property-oriented concept lattices[J]. Armenian journal of mathematics, 2016, 8(2): 86-95. ( 0) 0)
|
| [22] |
王海英, 黄强, 李传涛, 等. 图论算法及其MATLAB实现[M]. 北京: 北京航空航天大学出版社, 2010: 1-38.
( 0) 0)
|
| [23] |
李娜. 形式概念分析中若干算法的改进与实现[D]. 北京: 中央民族大学, 2007: 1-15. LI Na. Improvement and implementation of several algorithms about formal concept analysis[D]. Beijing: Minzu University of China, 2007: 1-15. http://cdmd.cnki.com.cn/Article/CDMD-10052-2007071298.htm (  0) 0)
|
 2017, Vol. 12
2017, Vol. 12


