云计算中心是基于超级计算机系统对外提供计算资源、存储资源等服务的机构或单位,以高性能计算机为基础面向各界提供高性能计算服务。当前,云计算中心主要面向大规模科学计算及工程计算应用,并在商业计算、互联网、电子政务、电子商务等领域拥有巨大发展潜力。对云计算中心的性能和能耗进行全面地分析具有十分重要的意义。
云计算中心作为服务机构,系统的性能指标(用户请求的等待时间、系统的堵塞程度等)是刻画服务质量的重要因素。将用户请求看作顾客,云计算中心的超级计算机的处理器作为服务器,而用户请求的处理过程作为服务过程,云计算中心是一个典型的排队系统。很多学者对云计算中心的性能及调度策略方面展开研究。廖倩文等[1]提出一种基于排队论的批量到达的云计算中心性能分析模型, 得到系统中用户请求队长的稳态概率分布、系统的阻塞概率、立即服务概率等指标。徐小龙等[2]研究了云计算系统任务调度和数据部署层面的节能机制, 提出一种面向绿色云计算中心的动态数据聚集算法。许丞[3]建议将Hadoop云平台的任务监控和任务调度管理功能分离,从而提升云平台的工作效率。倪志伟[4]综合考虑了用户最短等待时间资源负载均衡和经济原则,提出一种离散人工蜂群算法的云任务调度优化策略。
在云计算中心,能耗开销是不容忽视的问题,著名IT企业如Google、Microsoft、Amazon等云计算中心每年能耗超过百万美元,给云计算中心长期运营带来了巨大经济负担。云计算中心的能耗问题最近得到学者的广泛关注。罗亮等[5]从处理器性能计数器和系统使用情况入手,结合多元线性回归和非线性回归的数学方法,分析不同参数和方法对服务器能耗建模的影响,并提出适合云计算中心基础架构的服务器能耗模型。现有内存能耗模型研究发现,影响内存能耗的主要因素是内存读写的吞吐量[6]。何怀文等[7]在平均响应时间受限的条件下提出云计算中心异构服务器之间的优化能耗分配方法。针对云计算中心由于服务器空闲而产生大量空闲能耗,以及由于任务调度不匹配而产生大量“奢侈”能耗的问题,文献[8-10]提出通过任务调度的方式优化管理。文献[11]研究了云计算中心的动态迁移问题。文献[12]以利润最大化为目标,分析了云计算中心的优化配置。针对多个服务器切换过程存在大量冗余信号的问题,文献[13]提出了一种改进的多业务切换机制。文献[14]运用遗传算法分析用户请求的调度策略,从而提高云计算中心能源利用率。文献[15-16]对云计算中心的能耗和性能进行了联合优化。
以上关于云计算中心的相关研究都假设系统只有一类用户请求,但实际应用中,云计算中心根据用户请求的重要程度分为不同等级[17]。例如,云计算中心将实时用户请求赋予高优先权,将非实时用户请求赋予低优先权。另外,为了吸引更多客户,云计算中心为用户提供免费体验的服务,而付费的用户相对免费用户享有高优先权。Liu等[18]运用博弈论的方法研究具有多类用户请求的云计算中心的预约服务策略。
本文将研究具有两类用户请求的云计算中心能耗和性能的联合优化问题。假设两类用户请求的到达过程均为泊松过程,系统有多个平行的处理器,每个用户请求的处理时间服从指数分布,系统最多容纳有限的用户请求。我们将该系统构建为一个带非抢占优先权的马尔可夫过程,基于排队论对该系统的性能进行分析。将系统的能耗表示为处理器吞吐量和处理器个数的函数。最后,结合系统的性能和能耗构建系统的成本函数,对系统处理器的个数进行优化。
1 系统描述假设云计算中心有c个平行的服务器,按照用户的优先级别,将用户请求分为两类,第i类用户请求到达过程是参数为λi的泊松过程,i=1, 2。系统最多容纳N个用户请求,当系统中的用户请求个数小于N,用户请求的到达率为λ=λ1+λ2,否则到达率λ=0。用户请求到达云计算中心后,如果系统中有空闲的服务器,则用户请求直接进入空闲服务器接受服务,反之则需要在缓冲区中排队等待接受服务。第1类用户请求相对第2类用户请求具有非抢占优先权,即系统中的第1类用户请求被优先服务,但是第1类用户请求不能打断第2类用户请求的服务,对于每1类用户请求,系统按照先到先服务的规则(FCFS)进行服务。第i类用户请求的服务时间服从参数为μi的指数分布,i=1, 2。
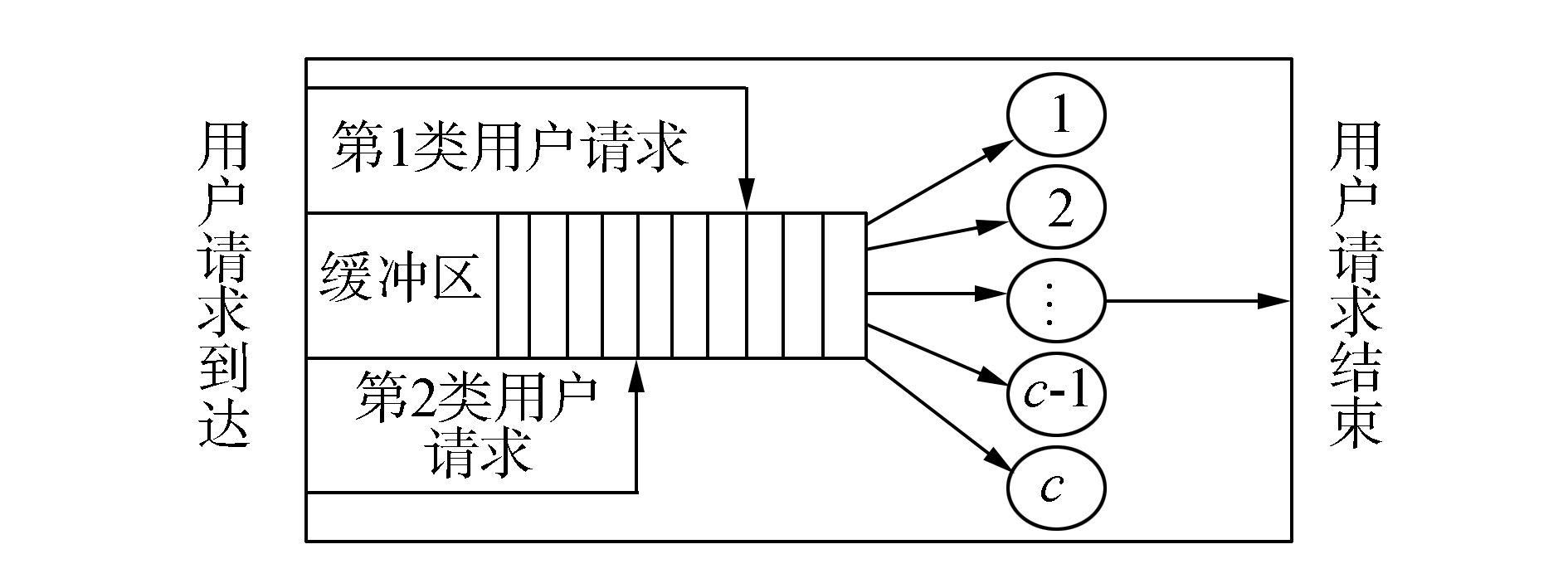
2 系统性能分析具有两类用户请求的云计算中心是一个非抢占优先权的M1, M2/M1, M2/(c/N)排队模型,如图 1所示。
|
图 1 具有两类用户请求的排队系统 Fig.1 Queueing system with two demand classes |
令(l1, l2)表示系统的状态,其中li表示系统中第i类用户请求的个数,该系统的状态空间为
| $ E = \left\{ {\left( {{l_1},{l_2}} \right),{l_1},{l_2} = 0,1, \cdots ,N,{l_1} + {l_2} = N} \right\}。$ |
系统被第i类用户请求占用系统的概率为
l=0的状态: 0,0。
l=1的状态: 1,0,0,1。
l=2的状态: (2, 0), (1, 1), (0, 2)。
l=N的状态:(N, 0),(N-1, 1),(N-2, 2),…,
(2, N-2),(1, N-1),(0, N)。
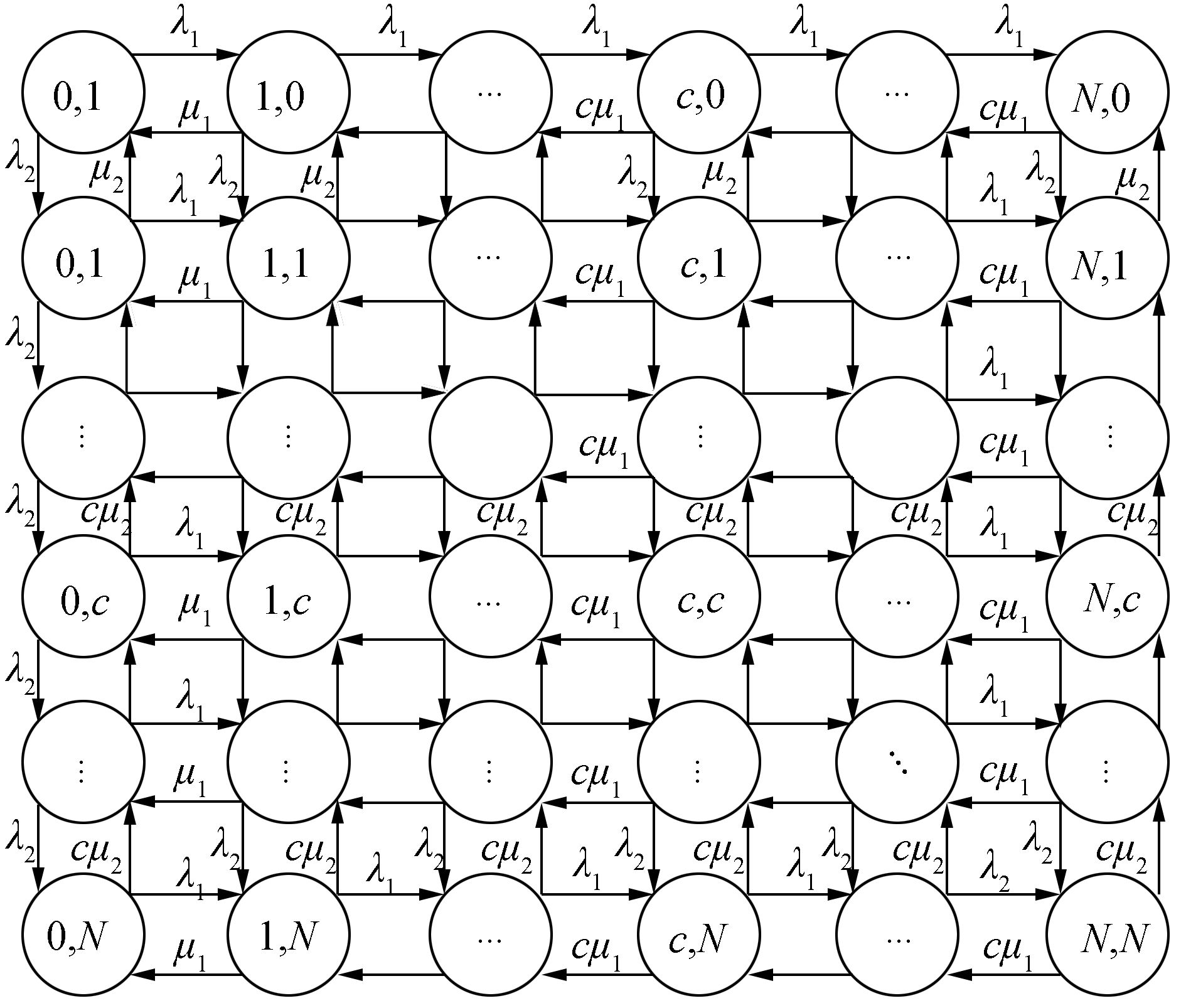
任意水平l可能存在的状态转移为l→l-1,l→l,l→l+1。状态转移如图 2所示。按照水平的顺序对所有状态排序,M1, M2/M1, M2/(c/N)排队模型的Q矩阵可表示为
| $ \mathit{\boldsymbol{Q = }}\left[ {\begin{array}{*{20}{c}} {{B_{00}}}&{{\mathit{\boldsymbol{B}}_{01}}}&0& \cdots &0&0&0\\ {{\mathit{\boldsymbol{A}}_{10}}}&{{\mathit{\boldsymbol{A}}_{11}}}&{{\mathit{\boldsymbol{A}}_{12}}}& \cdots &0&0&0\\ \vdots&\vdots&\vdots &{}& \vdots&\vdots&\vdots \\ 0&0&0& \cdots &{{\mathit{\boldsymbol{A}}_{N - 1,N - 2}}}&{{\mathit{\boldsymbol{A}}_{N - 1,N - 1}}}&{{\mathit{\boldsymbol{A}}_{N - 1,N}}}\\ 0&0&0& \cdots &0&{{\mathit{\boldsymbol{A}}_{N - 1,N}}}&{{\mathit{\boldsymbol{A}}_{N,N}}} \end{array}} \right] $ |
式中:Al, l-1对应水平l到水平l-1的矩阵块,Al, l对应水平l到水平l的矩阵块,Al, l+1对应水平l到水平l+1的矩阵块(1≤l≤N-1),B00对应l=0到l=0的值,B01对应l=0到l=1的矩阵块。Q矩阵的矩阵块随着水平l的增大而逐渐增大。令
| $ {\alpha _i} = \min \left( {i,c} \right) $ |
| $ {\beta _{l,i}} = \min \left( {l - i,c} \right),i = 0,1,2, \cdots ,l $ |
| $ {B_{00}} = - {\lambda _1} - {\lambda _2} $ |
| $ {\mathit{\boldsymbol{B}}_{01}} = \left[ {\begin{array}{*{20}{c}} {{\lambda _1}}&{{\lambda _2}} \end{array}} \right] $ |
| $ {\mathit{\boldsymbol{A}}_{l,l - 1}} = {\left[ {\begin{array}{*{20}{c}} {{\beta _{l,0}}{\mu _1}}&0&0& \cdots &0&0\\ {{\alpha _1}{\mu _2}}&{{\beta _{l,1}}{\mu _1}}&0& \cdots &0&0\\ 0&{{\alpha _2}{\mu _2}}&{{\beta _{l,2}}{\mu _1}}& \cdots &0&0\\ \vdots&\vdots&\vdots &{}& \vdots&\vdots \\ 0&0&0& \cdots &{{\alpha _{l - 1}}{\mu _2}}&{{\beta _{l,l - 1}}{\mu _1}}\\ 0&0&0& \cdots &0&{{\alpha _l}{\mu _2}} \end{array}} \right]_{l + 1,l}} $ |
| $ {\mathit{\boldsymbol{A}}_{l,l + 1}} = {\left[ {\begin{array}{*{20}{c}} {{\lambda _1}}&{{\lambda _2}}&0&0& \cdots &0&0&0\\ 0&{{\lambda _1}}&{{\lambda _2}}&0& \cdots &0&0&0\\ 0&0&{{\lambda _1}}&{{\lambda _2}}& \cdots &0&0&0\\ \vdots&\vdots&\vdots&\vdots &{}& \vdots&\vdots&\vdots \\ 0&0&0&0& \cdots &{{\lambda _1}}&{{\lambda _2}}&0\\ 0&0&0&0& \cdots &0&{{\lambda _1}}&{{\lambda _2}} \end{array}} \right]_{l + 1,l + 2}} $ |
| $ {\mathit{\boldsymbol{A}}_{l,l}} = \\ {\left[ {\begin{array}{*{20}{c}} { - {\beta _{l,0}}{\mu _1} - \lambda }&0&0& \cdots &0&0\\ 0&{ - {\alpha _1}{\mu _2} - {\beta _{l,1}}{\mu _1} - \lambda }&0& \cdots &0&0\\ 0&0&{ - {\alpha _2}{\mu _2} - {\beta _{l,2}}{\mu _1} - \lambda }& \cdots &0&0\\ \vdots&\vdots&\vdots &{}&0&0\\ 0&0&0& \cdots &{ - {\alpha _{l - 1}}{\mu _2} - {\beta _{l,l - 1}}{\mu _1} - \lambda }&0\\ 0&0&0& \cdots &0&{ - {\alpha _l}{\mu _2} - \lambda } \end{array}} \right]_{l + 1,l + 1}} $ |
|
图 2 系统状态转移图 Fig.2 Transitions among the system states |
令Li(t)表示t时刻系统中第i类用户请求的个数,
| $ \pi = \left( {{\pi _{0,0}},{\pi _{1,0}},{\pi _{0,1}}, \cdots ,{\pi _{N,0}},{\pi _{N - 1,1}}, \cdots ,{\pi _{0,N}}} \right) $ |
系统的稳态概率π分布可以通过求解如下方程组得到:
| $ \left\{ \begin{array}{l} \pi \mathit{\boldsymbol{Q}} = 0\\ \sum\limits_{j = 0}^N {\sum\limits_{i = 0}^N {{\pi _{i,j}} = 1} } \end{array} \right. $ |
系统中两类用户请求的平均队长分别为
| $ E\left( {{L_1}} \right) = \sum\limits_{i = 1}^N {i\sum\limits_{j = 0}^N {{\pi _{i,j}}} } $ |
| $ E\left( {{L_2}} \right) = \sum\limits_{j = 1}^N {j\sum\limits_{i = 0}^N {{\pi _{i,j}}} } $ |
根据Little法则,两类用户请求的平均等待时间分别为
| $ E\left( {{T_1}} \right) = E\left( {{L_1}} \right)/{\lambda _1} $ |
| $ E\left( {{T_2}} \right) = E\left( {{L_2}} \right)/{\lambda _2} $ |
系统中用户请求的平均等待时间为
| $ E\left( T \right) = \frac{{{\lambda _1}}}{{{\lambda _1} + {\lambda _2}}}E\left( {{T_1}} \right) + \frac{{{\lambda _2}}}{{{\lambda _1} + {\lambda _2}}}E\left( {{T_2}} \right) $ |
云计算中心服务器的能耗主要包括静态能耗和动态能耗。通常静态能耗比较稳定,假设每个服务器的静态能耗P*为常数,c个服务器的静态能耗为P静=cP*。
根据文献[19],当服务器的服务速率为μ时,单个服务器的动态能耗为kμα(单位为瓦),其中k为功耗比例因子,α≥3。由于系统中服务第i类用户请求的平均服务器数量为cρi(i=1, 2),因此系统的动态能耗为
| $ {P_{动}} = c{\rho _1}k\mu _1^\alpha + c{\rho _2}k\mu _2^\alpha = k{\lambda _1}\mu _1^{\alpha - 1} + k{\lambda _2}\mu _2^{\alpha - 1} $ |
系统的总体能耗为
| $ {P_{总}} = {P_{静}} + {P_{动}} = c{P^ * } + k{\lambda _1}\mu _1^{\alpha - 1} + k{\lambda _2}\mu _2^{\alpha - 1} $ |
云计算中心作为服务系统,用户请求的等待时间反应了的系统的服务质量,较长的等待时间必然影响用户对系统的评价,从而导致系统用户的丢失。系统可以通过增加服务器的方式减少用户请求的等待时间。但是服务器的增加,必然导致系统能耗增加。下面构建系统成本,对系统服务器的数量进行优化。
系统成本包括用户的等待成本和系统能耗成本。令hi表示一个第i类用户请求单位时间的逗留费用,则系统的等待成本为h1E(L1)+h2E(L2);令β为单位能耗价格,则系统的能耗成本为βP总,其中hi>0,β>0,i=1, 2。
因此,系统单位时间的成本为
| $ f\left( c \right) = {h_1}E\left( {{L_1}} \right) + {h_2}E\left( {{L_2}} \right) + \beta {P_{总}} $ |
系统最优成本可表示为如下数学规划问题:
| $ \left\{ \begin{array}{l} \min f\left( c \right)\\ {\rm{s}}{\rm{.t}}{\rm{.}}\;\;\;\;\frac{{{\lambda _1}}}{{c{\mu _1}}} + \frac{{{\lambda _2}}}{{c{\mu _2}}} < 1\\ c \in {{\bf{N}}^ + } \end{array} \right. $ |
对于任意的c∈N+,f(c)>0,且
| $ \left\{ \begin{array}{l} f\left( {{c^ * }} \right) < f\left( {{c^ * } - 1} \right)\\ f\left( {{c^ * }} \right) < f\left( {{c^ * } + 1} \right) \end{array} \right. $ |
下面针对具有两类用户请求的云计算中心的排队模型进行数值实验。假设h1=40,h2=20, β=0.8, N=100, μ1=μ2=1.5,调整参数λ1, λ2或服务器的数目c,计算系统的性能指标,并求解系统能耗及最优的服务器的数目。
例 1 假设两类用户请求的到达率不变,分析服务器数量c对系统的影响。假设h1=40,h2=20,β=0.8,N=100,μ1=μ2=1.5,λ1=1,λ2=2.5,c=1, 2, …, 7。表 1计算了服务器个数c取不同值的情况下,系统的服务强度ρ、平均队长E(L1)和E(L2)、平均等待时间E(T)、系统能耗P总及系统单位时间成本f(c)。表 1显示随着服务器个数c的增加,ρ、E(L1)、E(L2)、E(T)均减小,但是P总增加。随着c增加,系统的单位时间成本先增大后减小,在c=4时f(c)取得最小值,且f(c*)=77.671 8。实际上,对于任意的(λ1, λ2),最优值c*总是存在的,我们都可以通过表 1的方式求解最优值c*。
| 表 1 云计算中心的性能、能耗及成本分析(例1) Tab.1 The performance, power consumption and cost of cloud computing centers (example 1) |
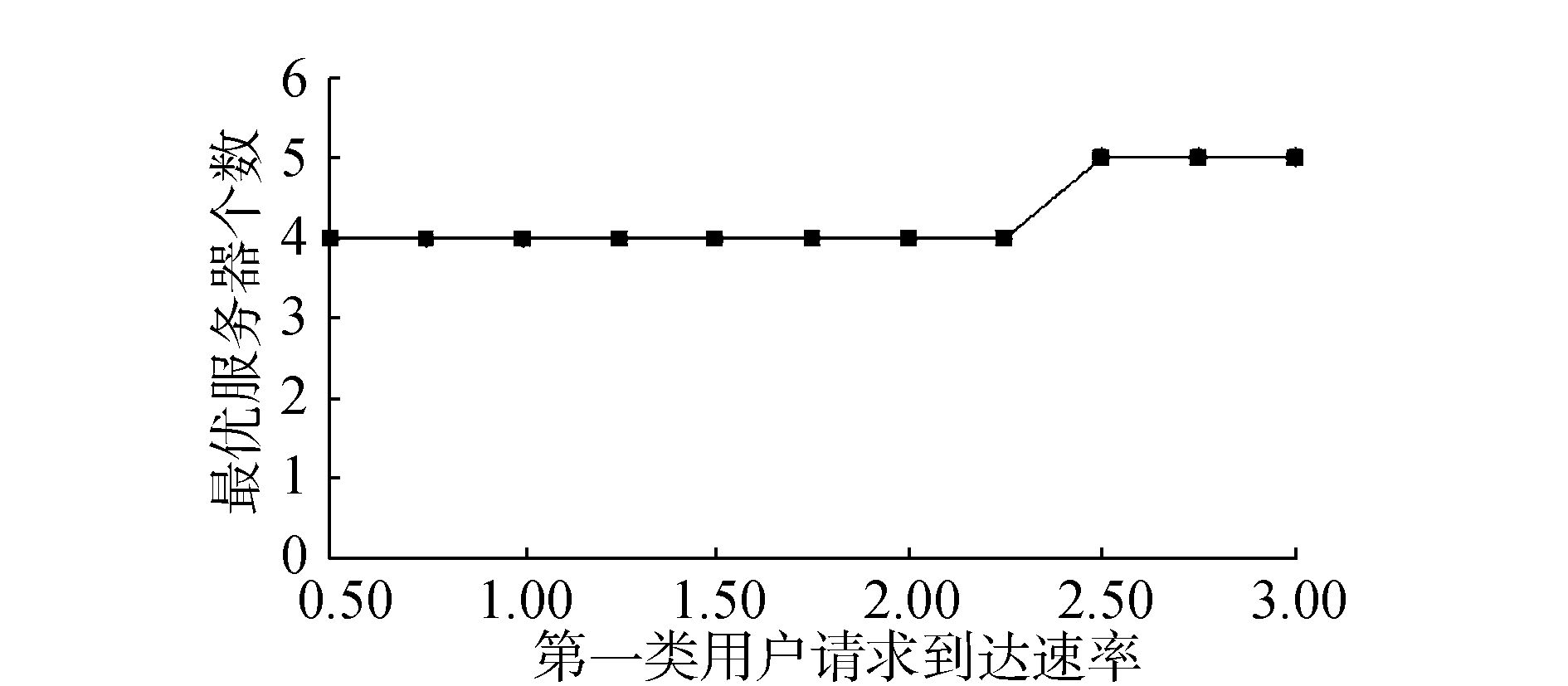
例 2 假设第二类用户请求的到达率不变,分析第一类用户请求的到达率增大对系统的影响。假设h1=40,h2=20,β=0.8,N=100, μ1=μ2=1.5,λ2=3,λ1∈0.5, 3。首先,对于给定的λ1,通过例1的方法求解最优值c*。其次,令c=c*,分析系统的如下性能参数:ρ、E(L1)、E(L2)、E(T)、P总及f(c*)。表 2的数值结果显示随着λ1增大,c*不变或增大(如图 3所示),E(L1)、P总及f(c*)均随着λ1增大而增大。
| 表 2 云计算中心的性能、能耗及成本分析(例2) Tab.2 The performance, power consumption and cost of cloud computing centers (example 2) |
|
图 3 最优服务器数量(例2) Fig.3 The optimal number of servers (example 2) |
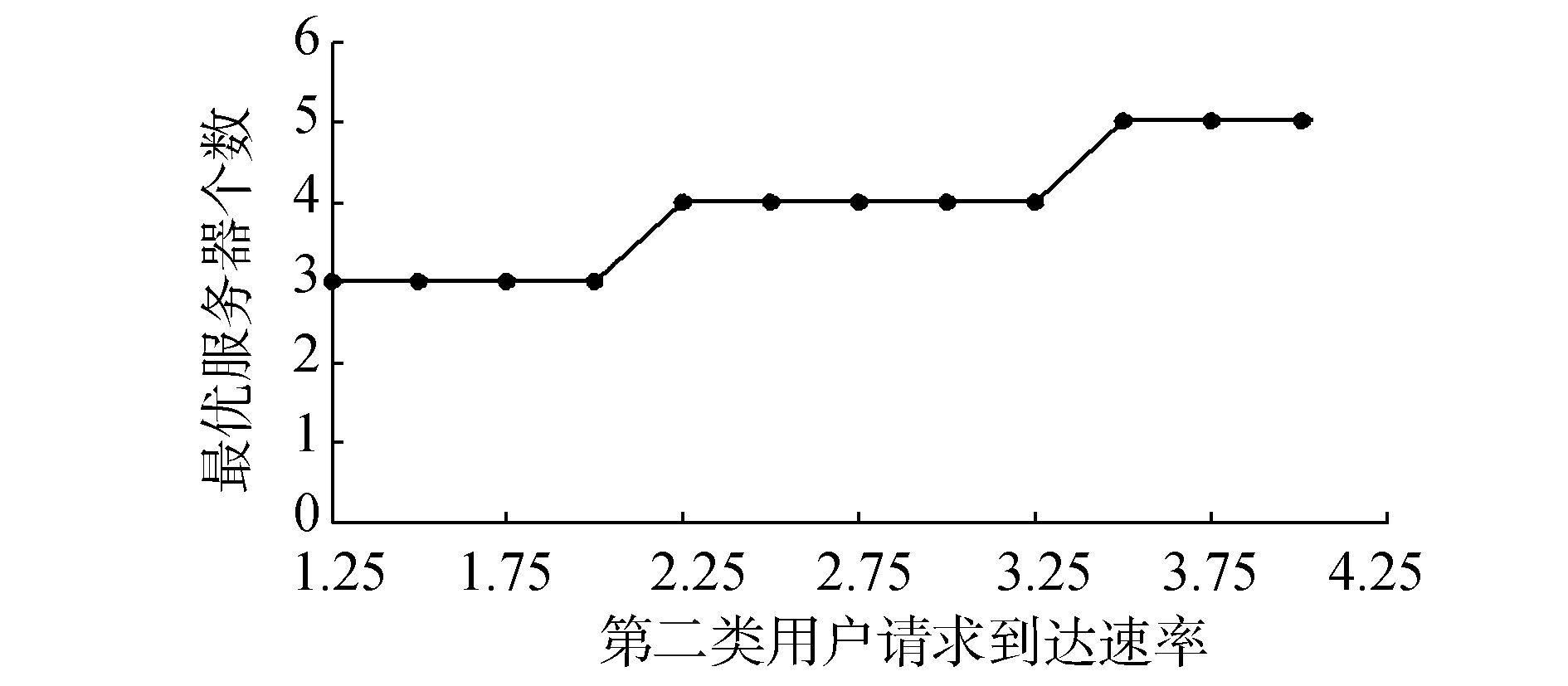
例 3 假设第一类用户请求的到达率不变,分析第二类用户请求的到达率增大对系统的影响。假设h1=40,h2=20,β=0.8,N=100, μ1=μ2=1.5,λ1=1,λ2∈[1.25, 4]。首先,对于给定的λ2,通过例1的方法求解最优值c*。其次,令c=c*,分析系统的如下性能指标:ρ、E(L1)、E(L2)、E(T)、P总及f(c*)。表 3的数值结果显示,随着λ2增大,c*不变或增大(如图 4所示),E(L2)、P总及f(c*)随着λ2增大而增大,而ρ、E(L1)、E(T)未呈现单调性。
| 表 3 云计算中心的性能、能耗及成本分析(例3) Tab.3 The performance, power consumption and cost of cloud computing centers (example 3) |
|
图 4 最优服务器数量(例3) Fig.4 The optimal number of servers (example 3) |
本文基于排队论分别对具有两类用户请求的云计算中心建立相应的排队模型,分析系统中用户请求的稳态概率分布、平均队长等性能指标;通过引入等待成本和能耗成本,构建系统单位时间的成本函数,分析系统的最优服务器的数量。研究发现,随着用户请求到达率变化,最优服务器数量可能会发生变化,服务器数量的最优值是用户请求到达率的非减函数。对于任意的到达率,都可以得到最优的服务器数量,这为云计算中心的资源配置提供理论依据。
本文讨论的云计算中心具有两类用户请求,服务规则是非抢占优先服务,然而,在实际中存在抢占服务规则的情况及多类型用户请求的云计算中心,在后续的研究中可以讨论更多类型的用户请求问题及抢占服务规则的情况,并对多类用户请求的调度策略进行分析。
| [1] |
廖倩文, 潘久辉, 王开杰. 基于排队理论的云计算中心性能分析模型[J]. 计算机工程, 2015, 41(9): 51-55. LIAO Qianwen, PAN Jiuhui, WANG Kaijie. Performance analysis model of cloud computing center based on queueing theory[J]. Computer engineering, 2015, 41(9): 51-55. (  0) 0)
|
| [2] |
徐小龙, 杨庚, 李玲娟, 等. 面向绿色云计算数据中心的动态数据聚集算法[J]. 系统工程与电子技术, 2012, 34(9): 1923-1929. XU Xiaolong, YANG Geng, LI Lingjuan. Dynamic data aggregation algorithm for data centers of green cloud computing[J]. Systems engineering and electronics, 2012, 34(9): 1923-1929. (  0) 0)
|
| [3] |
许丞, 刘洪, 谭良. Hadoop云平台的一种新的任务调度和监控机制[J]. 计算机科学, 2013, 40(1): 112-117. XU Chen, LIU Hong, TAN Liang. New mechanism of monitoring on Hadoop cloud platform[J]. Computer science, 2013, 40(1): 112-117. (  0) 0)
|
| [4] |
倪志伟, 李蓉蓉, 方清华, 等. 基于离散人工蜂群算法的云任务调度优化[J]. 计算机应用, 2016, 36(1): 107-112, 121. NI Zhiwei, LI Rongrong, FANG Qinghua, et al. Optimization of cloud task scheduling based on discrete artificaial bee colony algorithm[J]. Journal of computer applications, 2016, 36(1): 107-112, 121. DOI:10.11772/j.issn.1001-9081.2016.01.0107 (  0) 0)
|
| [5] |
罗亮, 吴文峻, 张飞. 面向云计算数据中心的能耗建模方法[J]. 软件学报, 2014, 25(7): 1371-1387. LUO Liang, WU Wenjun, ZHANG Fei. Energy modeling based on cloud data center[J]. Journal of software, 2014, 25(7): 1371-1387. (  0) 0)
|
| [6] |
CAO J, LI K, STOJMENOVIC I. Optimal power allocation and load distribution for multiple heterogeneous multicore server processors across clouds and data centers[J]. IEEE transactions on computers, 2014, 63(1): 45-58. DOI:10.1109/TC.2013.122 ( 0) 0)
|
| [7] |
何怀文, 傅瑜, 杨亮, 等. 性能受限下云中心异构服务器的能耗优化[J]. 计算机应用, 2015, 35(1): 39-42, 61. HE Huaiwen, FU Yu, YANG Liang, et al. Optimal power consumption of heterogeneous servers in cloud center under performance constraint[J]. Journal of computer applications, 2015, 35(1): 39-42, 61. DOI:10.11772/j.issn.1001-9081.2015.01.0039 (  0) 0)
|
| [8] |
谭一鸣, 曾国荪, 王伟. 随机任务在云计算平台中能耗的优化管理方法[J]. 软件学报, 2012, 23(2): 266-278. TAN Yiming, ZENG Guosun, WANG Wei. Policy of energy optimal management for cloud computing platform with stochastic tasks[J]. Journal of software, 2012, 23(2): 266-278. (  0) 0)
|
| [9] |
KE M, YEH C, SU C. Cloud computing platform for real-time measurement and verification of energy performance[J]. Applied energy, 2017, 188: 497-507. DOI:10.1016/j.apenergy.2016.12.034 ( 0) 0)
|
| [10] |
SINGH S, CHANA I. EARTH:Energy-aware autonomic resource scheduling in cloud computing[J]. Journal of intelligent & fuzzy systems, 2016, 30(3): 1581-1600. ( 0) 0)
|
| [11] |
TAO F, LI C, LIAO T, et al. BGM-BLA:a new algorithm for dynamic migration of virtual machines in cloud computing[J]. IEEE transactions on services computing, 2016, 9(6): 910-925. DOI:10.1109/TSC.2015.2416928 ( 0) 0)
|
| [12] |
MEI J, LI K, OUYANG A, et al. A profit maximization scheme with guaranteed quality of service in cloud computing[J]. IEEE transactions on computers, 2015, 64(11): 3064-3078. DOI:10.1109/TC.2015.2401021 ( 0) 0)
|
| [13] |
QI Q, LIAO J, WANG J. Integrated multi-service handoff mechanism with QoS-support strategy in mobile cloud computing[J]. Wireless personal communications, 2016, 87(2): 593-614. DOI:10.1007/s11277-016-3210-3 ( 0) 0)
|
| [14] |
HUANG Z, LU Y, OUYANG H. Scheduling strategy based on genetic algorithm for cloud computer energy optimization[C]//2015 IEEE International Conference on Communication Problem-Solving. Guilin, China, 2015:516-519.
( 0) 0)
|
| [15] |
YANG B, LI Z, CHEN S, et al. Stackelberg game approach for energy-aware resource allocation in data centers[J]. IEEE transactions on parallel and distributed systems, 2016, 27(12): 3646-3658. DOI:10.1109/TPDS.2016.2537809 ( 0) 0)
|
| [16] |
SURESH S, SAKTHIVEL S. System modeling and evaluation on factors influencing power and performance management of cloud load balancing algorithms[J]. Journal of web engineering, 2016, 15(5/6): 484-500. ( 0) 0)
|
| [17] |
李春艳, 何一舟, 戴彬. Hadoop平台的多队列作业调度优化方法研究[J]. 计算机应用研究, 2014(03): 705-707, 738. LI Chunyan, HE Yizhou, DAI Bin. Research on optimization of job scheduling based on multi-queue for Hadoop platform[J]. Application research of computers, 2014(3): 705-707, 738. (  0) 0)
|
| [18] |
LIU C, LI K, XU C, et al. Strategy configurations of multiple users competition for cloud service reservation[J]. IEEE transactions on parallel and distributed systems, 2016, 27(2): 508-520. DOI:10.1109/TPDS.2015.2398435 ( 0) 0)
|
| [19] |
ZHURAVLEV S, CARLOS SAEZ J, BLAGODUROV S. Survey of energy-cognizant scheduling techniques[J]. IEEE transactions on parallel and distributed systems, 2013, 24(7): 1447-1464. DOI:10.1109/TPDS.2012.20 ( 0) 0)
|
 2017, Vol. 12
2017, Vol. 12


