2. 江苏信息职业技术学院 物联网工程学院, 江苏 无锡 214153
2. School of Internet of Things Engineering, Jiangsu Vocational College of Information Technology, Wuxi 214153, China
聚类分析作为一种常见的无监督学习数据预处理方法,在数据挖掘、文件恢复、图像分割及模式分类等领域有着广泛的应用基础。随着现代技术发展的不断更新,传统的聚类模式已不再适应新的学习场景,如多视角学习场景[1-5]、迁移学习场景[6-9]、多任务学习场景[10-11]及子空间学习场景[12]等。本文将主要关注多视角学习场景,进而针对传统聚类模型如何在多视角学习场景下更好地学习优化及应用展开探讨。
对于传统聚类方法,主要有以FCM(fuzzy c-means)算法[13-16]为代表的划分型聚类算法, 还有以AP(affinity propagation)算法[17-18]为代表的图论型聚类算法等。相对于其他聚类模型,基于划分的聚类算法模型结构简单,优化过程亦不复杂,经常被用于实际应用。但在以FCM算法为族群的各种基于划分的算法中,如MEC(maximum entropy clustering, MEC)算法[19-20]及PCM(possibilistic c-means)算法[21-22]等,经实验验证PCM算法较之其他算法具备更好的噪声及孤立点鲁棒性,因此本文将以经典PCM算法模型为理论基础开展其在多视角学习场景下的模型优化及应用问题的研究。
目前针对多视角聚类问题,已有一些代表性的工作[2-5]被提出,如:1)基于概率论方法的多视角协同聚类Co-EM(collaborative expectation maximization)算法[2];2)基于FCM算法模型的Co-FC (collaborative fuzzy clustering)算法[3];3)针对Co-FC算法改进的Co-FKM(collaborative fuzzy k-means)算法[4];4) Tzortzis等[5]基于核聚类方法提出的两种多视角聚类算法MVKKM(multi-view kernel k-means)和MVSpec(multi-view spectral clustering)。尽管上述方法已使得一些传统聚类算法获得了多视角聚类的能力,但各方法在视角权重和视角内特征权重优化问题上的考量还是欠缺的,如基于协同学习思想提出的Co-EM、Co-FC及Co-FKM算法均未考虑视角权重和视角内特征权重优化问题,而MVKKM和MVSpec算法仅管采用了视角权重优化方法但在视角内特征权重优化问题上又未涉及。此外,上述大部分的算法是以FCM算法为基础提出的,鲁棒性较一般。为此,必须在多视角聚类领域提出一种新的具备较强鲁棒性及多视角聚类能力且兼顾视角权重及视角内特征权重优化问题的新聚类算法。为达此目的,本文拟针对传统PCM算法开展多视角聚类方面的模型优化工作,本文工作的创新主要涵盖以下几点:
1)针对传统可能性(PCM)算法无法解决多视角聚类场景的问题,提出了多视角PCM算法;
2)多视角PCM算法各视角之间的视角权重是一致的,这与客观事实不符。针对各视角之间视角权重应该不同的问题,引入视角间模糊加权机制;
3)多视角PCM算法各视角内的属性权重默认是一致的,这也与客观事实不符。针对各视角内的属性权重应该不同的问题,引入视角内属性模糊加权机制。
1 相关工作为了更好地说明本文所提之算法,首先本小节将对传统的PCM算法进行回顾,其次说明传统PCM算法在面对多视角聚类任务时所存在的问题,最后引出具备最佳视角及最优特征划分能力的多视角模糊双加权可能性聚类算法(MV-FDW- PCM)的迫切性。
1.1 传统PCM算法传统PCM算法于1996年被提出[1]。当时模糊C均值聚类FCM算法[2]是模糊聚类算法中最流行的聚类算法之一。随着FCM算法使用的推广,一些专家学者发现FCM算法中对隶属度的限制条件增大了噪声、例外点对聚类结果的影响。为了消除FCM算法中隶属度之和为1的限制,R.Krishnapuram等提出了PCM算法。该算法的优势在于去除了隶属度之和为1的限制条件,从而降低了噪声对聚类精度的影响。PCM算法的目标函数式为
| $\begin{aligned}&{J_{\rm PCM}}\left( {{\mathit{\boldsymbol{U}}},{\mathit{\boldsymbol{V}}}} \right) = \sum\limits_{i = 1}^C {\sum\limits_{j = 1}^N {u_{ij}^m||{{\mathit{\boldsymbol{x}}}_j} - {{\mathit{\boldsymbol{v}}}_i}|{|^2}} } + \sum\limits_{i = 1}^C {{\alpha _i}\sum\limits_{j = 1}^N {{{\left( {1 - {u_{ij}}} \right)}^m}} } \\&\quad\quad\quad\quad{\rm{s}}{\rm{.t}}. \;\; 0 \leqslant {u_{ij}} \leqslant 1,0 < \sum\limits_{j = 1}^N {{u_{ij}} < N} \end{aligned}$ | (1) |
式中:m是模糊系数,参数αi的计算公式为
| ${\alpha _i} = K\sum\limits_{j = 1}^N {u_{ij}||{{\mathit{\boldsymbol{x}}}_j} - {{\mathit{\boldsymbol{v}}}_i}|{|^2}/\sum\limits_{j = 1}^N {u_{ij}} } ,K = 1$ |
求解目标函数式(1)得到隶属度和聚类中心表达式为
| ${u_{ij}} = \exp \left( { - \frac{{||{{\mathit{\boldsymbol{x}}}_j} - {{\mathit{\boldsymbol{v}}}_i}|{|^2}}}{{{\alpha _i}}}} \right)$ | (2) |
| ${{\mathit{\boldsymbol{v}}}_i} = \sum\limits_{j = 1}^N {u_{ij}^m{{\mathit{\boldsymbol{x}}}_j}} /\sum\limits_{j = 1}^N {u_{ij}^m} $ | (3) |
随着多视角应用场景不断出现,传统聚类算法的单视角学习模式的局限性导致其在处理多视角聚类问题时性能往往无法令人满意。如传统PCM算法在处理多视角聚类任务时,其聚类原理如下:
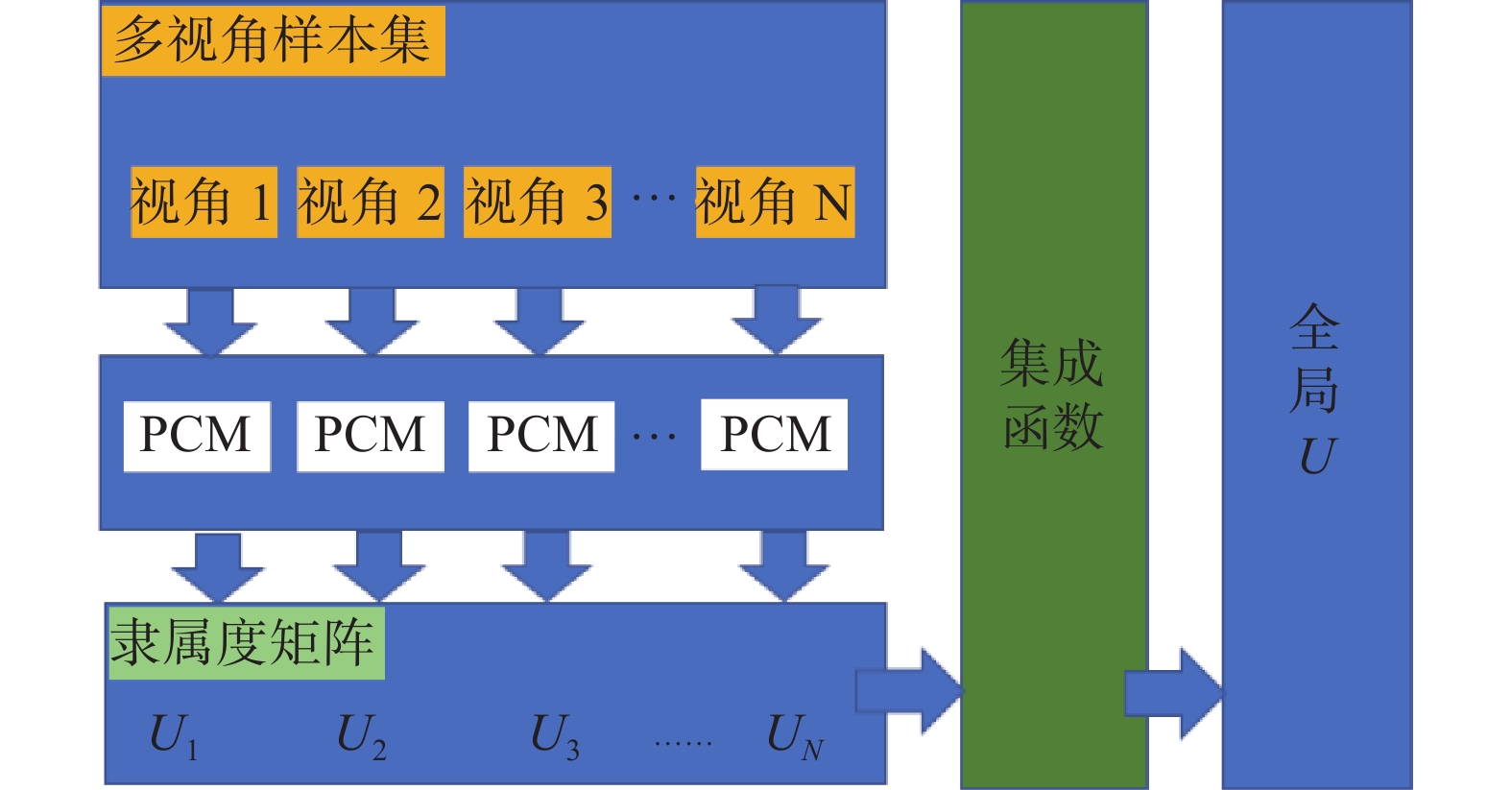
将多视角数据中每一个视角数据独立出来,作为多个不相干的样本进行独立聚类分析。具体实施时是将各视角的样本直接使用传统PCM算法聚类以分别获取各视角的划分结果
|
图 1 传统PCM算法聚类多视角数据原理图 Fig.1 The principle diagram of traditional PCM algorithm clustering multi-view data |
根据上述分析及图1所示的原理图可以看出,传统PCM算法在对多视角数据进行聚类任务时,存在以下问题:1)将各视角数据完全独立开来进行单独聚类,未考虑各视角间数据的关联性信息;2)对各视角聚类结果进行融合时,未考虑不同视角数据对聚类结果的差异化影响,即结果的融合策略采用平均策略不符合客观事实。综上,传统PCM算法受限于陈旧的聚类模式在处理多视角聚类任务时显得不再有效。
2 多视角模糊双加权可能性聚类算法针对传统PCM算法在处理多视角数据聚类任务时效果不理想的问题,本节首先提出了多视角PCM算法。考虑到实际的多视角聚类问题各视角的聚类特性应有差异(如图1所示),因而所设计的多视角聚类算法对于各视角的权重应根据实际情况进行优化获取,为此本节提出了视角间模糊加权机制。又由子空间聚类的原理可知各视角内属性的权重也应存在一定的差异性,于是本节又提出了视角内属性模糊加权机制。最后,基于上述两个机制,提出了具备最佳视角及最优特征划分能力的多视角模糊双加权可能性聚类算法。
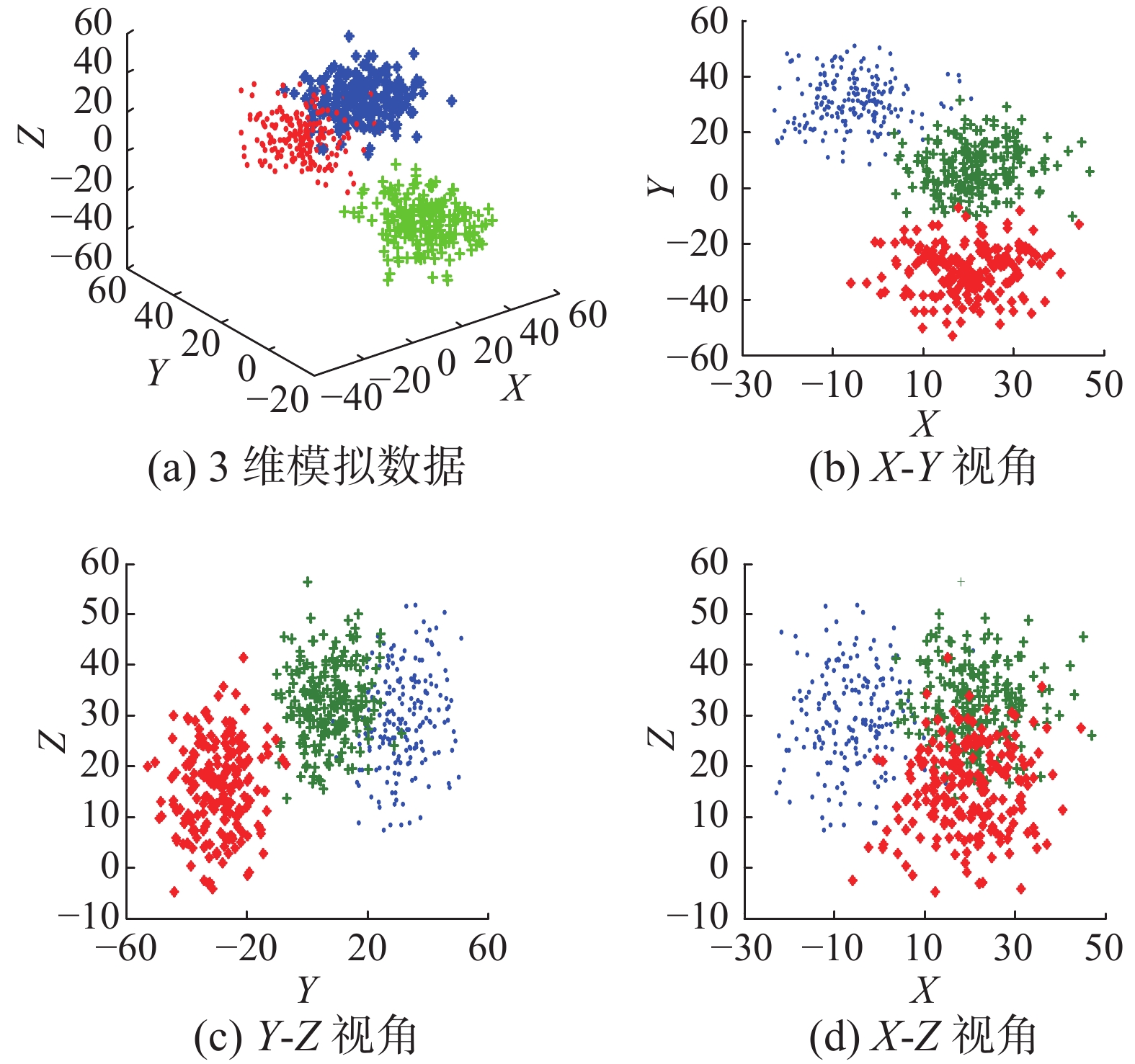
2.1 多视角聚类问题描述对于一个多视角聚类问题(如图2所示),其描述了一个3维(X维、Y维及Z维)的多视角模拟数据,若任意选择两维进行投影,可将一个3维数据变成2维且可视化程度更高的样本(如图2 (b)~(d)),同理对于4维以上的数据亦可如此。在投影后,可以清晰地发现由X维和Y维组成的X-Y视角具备较之其他两视角更好的可分性,其类别结构清晰且类与类之间划分亦较为清晰。因此,对于任意一个多视角聚类问题,各视角的权重应通过优化学习得到而并非强制的一致对待。此外,根据子空间聚类理论[12]可知样本特征的权重对于不同的聚类问题应是有差异的,这种特征权重的差异性反应到多视角聚类问题中将进一步延伸为视角内部各特征的权重也应是有所差异的,即同样以X-Y视角为例,若将X-Y视角的样本向X轴投影,那么“+”类将与“*”类严重重叠而不易区分,但若向Y轴投影则得到的3类的区分度(可分性)更佳。由此可知,在多视角聚类过程中,各视角下样本特征的权重与视角权重一样也需要得到优化,采用最佳的特征权重关系将进一步使得聚类结果得到显著提升。
|
图 2 问题描述 Fig.2 Problem description |
本文所用的符号说明如表1所示。
| 表 1 符号说明 Tab.1 The explanation of some notations |
为了让PCM算法能够更好地适应多视角聚类任务,本文首先提出了多视角PCM算法。该算法的目标函数式如下:
| $\begin{aligned} & \quad\quad\quad\quad\quad {J_{{\rm{MV {\text{-}} PCM}}}}\left( {{\mathit{\boldsymbol{U}}},{\mathit{\boldsymbol{V}}},{\mathit{\boldsymbol{W}}},{\mathit{\boldsymbol{Q}}}} \right) = \\[8pt]&\sum\limits_{k = 1}^K {\left( {\sum\limits_{i = 1}^C {\sum\limits_{j = 1}^N {\left[ {{{\tilde u}_{ij,k,\theta }}{{\left\| {{{\mathit{\boldsymbol{x}}}_{j,k}} - {{\mathit{\boldsymbol{v}}}_{i,k}}} \right\|}^2}} \right]} } + \sum\limits_{i = 1}^C {{\alpha _{i,k}}\sum\limits_{j = 1}^N {{{\left( {1 - {u_{ij,k}}} \right)}^{{m_3}}}} } } \right)} \end{aligned}$ | (4) |
| ${\tilde u_{ij,k,\theta }} = (1 - \theta )u_{ij,k}^{{m_3}} + \frac{\theta }{{K - 1}}\sum\limits_{{k'} \ne k,{k'} = 1}^K {u_{ij,{k'}}^{{m_3}}} $ | (5) |
s.t.
式(5)为视角隶属度融合项,θ为视角隶属度融合项的平衡系数。根据式(4)、(5)得到每个视角最终的隶属度矩阵。最终的划分结果用融合函数计算为
| ${{\mathit{\boldsymbol{U}}}_{ij}} = \sqrt[K]{{\mathop \prod \limits_{k \in k} {u_{ijk}}}}$ | (6) |
多视角PCM算法虽然改变了传统PCM算法的单视角聚类模型,使其能够解决多视角聚类任务,但该算法仍未考虑视角间的权重大小应当存在差异化的情况。因为现实生产生活中,多视角数据的每一个视角的数据存在聚类特性不相同的情况,即有些视角数据的聚类特性较好,有些视角数据的聚类特性较差。如果在聚类的过程中,无差别地将所有视角数据的权重默许一致,这种计算策略显然是不科学的。考虑到以上因素,本节提出了一种可行的视角间模糊加权机制。即赋予每一个视角一个合理的权重且所有视角权重之和为1。该机制的示意图如图3所示。

|
图 3 视角间加权机制示意图 Fig.3 The schematic diagram of weighting mechanism between perspectives |
视角间加权的表达式为
| ${J_{\rm{1}}}\left( {{\mathit{\boldsymbol{U}}},{\mathit{\boldsymbol{V}}},{\mathit{\boldsymbol{Q}}}} \right) = \sum\limits_{k = 1}^K {q_k^{{m_1}}\left( {{J_{{\rm{MV {\text{-}} PCM}}}}\left( {{\mathit{\boldsymbol{U}}},{\mathit{\boldsymbol{V}}},{\mathit{\boldsymbol{W}}},{\mathit{\boldsymbol{Q}}}} \right)} \right)} $ | (7) |
s.t.
考虑到各视角内各个属性权重默认相同的情况与客观现实不符,本文又提出了视角内属性加权机制。赋予聚类质量高的属性高的权重,聚类质量较差的属性低的权重。具体表达式为
| $\begin{aligned}{J_{\rm{2}}}\left( {{\mathit{\boldsymbol{U}}},{\mathit{\boldsymbol{V}}},{\mathit{\boldsymbol{Q}}}} \right) =& \sum\limits_{k = 1}^K {\left( {\sum\limits_{i = 1}^C {\sum\limits_{j = 1}^N {\left[ {{{\tilde u}_{ij,k,\theta }}\sum\limits_{l = 1}^{{D_k}} {w_{l,k}^{{m_{\rm{2}}}}{{\left\| {{{\mathit{\boldsymbol{x}}}_{jl,k}} - {{\mathit{\boldsymbol{v}}}_{il,k}}} \right\|}^2}} } \right]} } + } \right.} \\&\left. {\sum\limits_{i = 1}^C {{\alpha _{i,k}}\sum\limits_{j = 1}^N {{{\left( {1 - {u_{ij,k}}} \right)}^{{m_3}}}} } } \right)\end{aligned}$ | (8) |
| ${\tilde u_{ij,k,\theta }} = (1 - \theta )u_{ij,k}^{{m_3}} + \frac{\theta }{{K - 1}}\sum\limits_{{k'} \ne k,{k'} = 1}^K {u_{ij,{k'}}^{{m_3}}} $ | (9) |
式(9)为视角隶属度融合项,θ为视角隶属度融合项的平衡系数。
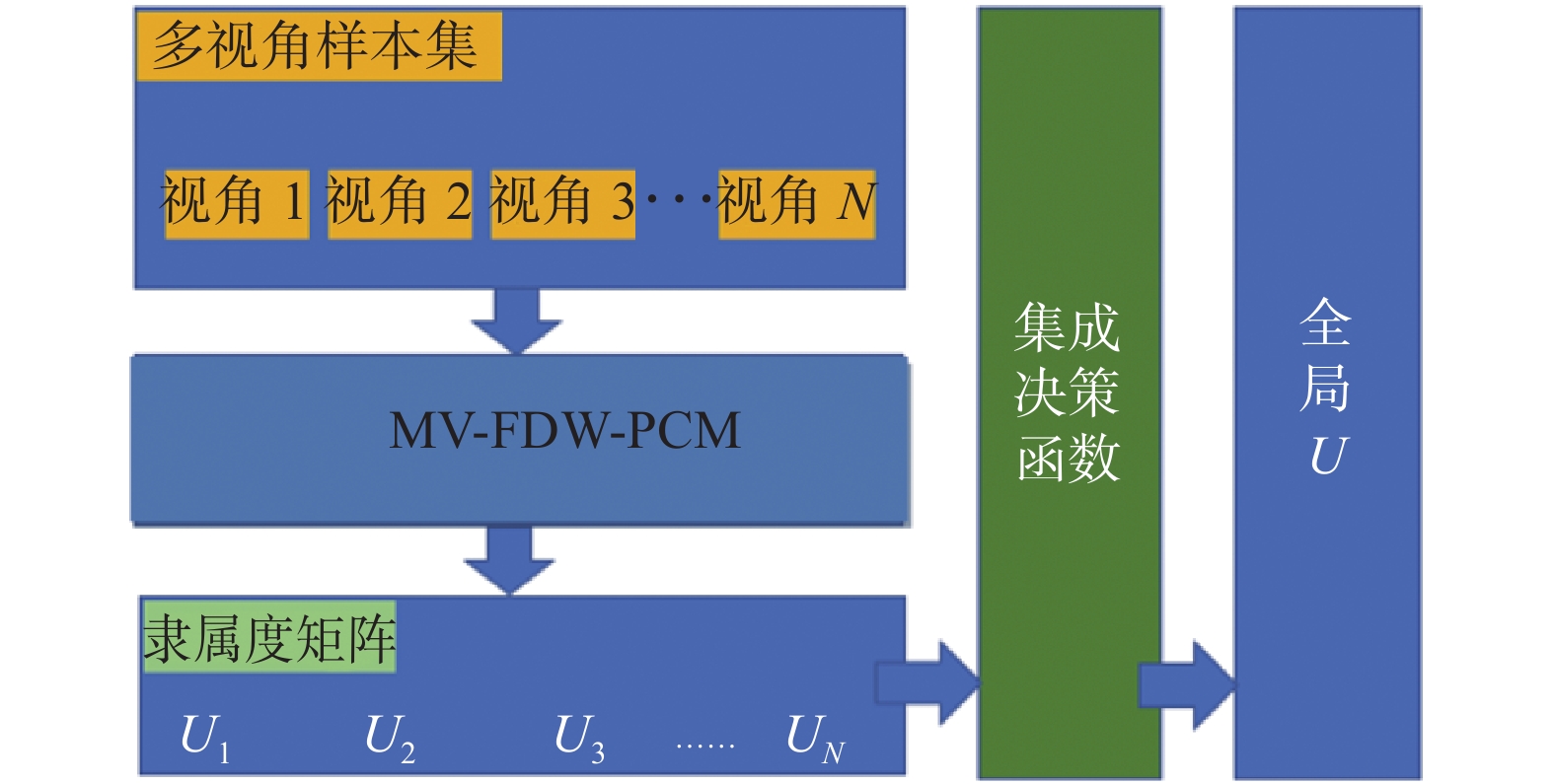
2.5 多视角模糊双加权可能性聚类算法在多视角PCM基础上,通过引入视角间模糊加权以及视角内属性模糊加权两种机制,本文提出了具备最佳视角及最优特征划分能力的多视角模糊双加权可能性聚类MV-FDW-PCM算法。该算法的原理如图4所示。
|
图 4 MV- FDW -PCM算法聚类多视角数据 Fig.4 The MV- FDW -PCM algorithm clustering multi-view data |
算法的目标函数式为
| $\begin{aligned}& \quad\quad\quad\quad {J_{{\rm{MV {\text{-}}FDW {\text{-}} PCM}}}}\left( {{\mathit{\boldsymbol{U}}},{\mathit{\boldsymbol{V}}},{\mathit{\boldsymbol{W}}},{\mathit{\boldsymbol{Q}}}} \right) = \\& \sum\limits_{k = 1}^K {q_k^{{m_{\rm{1}}}}\left( {\sum\limits_{i = 1}^C {\sum\limits_{j = 1}^N {\left[ {{{\tilde u}_{ij,k,\theta }}\sum\limits_{l = 1}^{{D_k}} {w_{l,k}^{{m_{\rm{2}}}}{{\left\| {{{\mathit{\boldsymbol{x}}}_{jl,k}} - {{\mathit{\boldsymbol{v}}}_{il,k}}} \right\|}^2}} } \right]} } + } \right.} \\& \quad\quad\quad\quad\quad\left. {\sum\limits_{i = 1}^C {{\alpha _{i,k}}\sum\limits_{j = 1}^N {{{\left( {1 - {u_{ij,k}}} \right)}^{{m_3}}}} } } \right)\end{aligned}$ | (10) |
| ${\tilde u_{ij,k,\theta }} = (1 - \theta )u_{ij,k}^{{m_3}} + \frac{\theta }{{K - 1}}\sum\limits_{{k'} \ne k,{k'} = 1}^K {u_{ij,{k'}}^{{m_3}}} $ | (11) |
s.t.
由于式(10)采用了属性加权机制以及多视角隶属度融合机制,所以
| ${\alpha _{i,k}} = G\sum\limits_{j = 1}^N {{{\tilde u}_{ij,k,\theta }}\sum\limits_{l = 1}^{{D_k}} {w_{l,k}^{{m_{\rm{2}}}}{{\left\| {{{\mathit{\boldsymbol{x}}}_{jl,k}} - {{\mathit{\boldsymbol{v}}}_{il,k}}} \right\|}^2}} } /\sum\limits_{j = 1}^N {{{\tilde u}_{ij,k,\theta }}} ,G = 1 \text{。}$ |
利用拉格朗日最小化目标函数式(10),得到聚类中心、隶属度、视角权重以及属性权重的计算式为
| ${v_{il,k}} = \sum\limits_{j = 1}^N {{{\tilde u}_{ij,k,\theta }}w_{l,k}^{{m_{\rm{2}}}}{{\mathit{\boldsymbol{x}}}_{jl,k}}} /\sum\limits_{j = 1}^N {{{\tilde u}_{ij,k,\theta }}w_{l,k}^{{m_{\rm{2}}}}} $ | (12) |
| ${u_{ij,k}} = \frac{1}{{1 + {{\left( {\displaystyle\frac{{(1 - \theta )\sum\limits_{l = 1}^{{D_k}} {w_{l,k}^{{m_{\rm{2}}}}{{\left\| {{{\mathit{\boldsymbol{x}}}_{jl,k}} - {{\mathit{\boldsymbol{v}}}_{il,k}}} \right\|}^2}} + \frac{\theta }{{K - 1}}\sum\limits_{{k'} \ne k,{k'} = 1}^K {\sum\limits_{l = 1}^{{D_k}} {w_{l,{k'}}^{{m_{\rm{2}}}}{{\left\| {{{\mathit{\boldsymbol{x}}}_{jl,{k'}}} - {{\mathit{\boldsymbol{v}}}_{il,{k'}}}} \right\|}^2}} } }}{{{\alpha _{i,k}}}}} \right)}^{\frac{1}{{{m_{_{_{3}}}} - 1}}}}}}$ | (13) |
| $q_k =\frac{1}{{\sum\limits_{h = 1}^K {{{\left( {\displaystyle\frac{{\left( {\sum\limits_{i = 1}^C {\sum\limits_{j = 1}^N {\left[ {{{\tilde u}_{ij,k,\theta }}\sum\limits_{l = 1}^{{D_r}} {w_{l,k}^{{m_{\rm{2}}}}{{\left\| {{{\mathit{\boldsymbol{x}}}_{jl,k}} - {{\mathit{\boldsymbol{v}}}_{il,k}}} \right\|}^2}} } \right]} } + \sum\limits_{i = 1}^C {{\alpha _{i,k}}\sum\limits_{j = 1}^N {{{\left( {1 - {u_{ij,k}}} \right)}^{{m_3}}}} } } \right)}}{{\left( {\sum\limits_{i = 1}^C {\sum\limits_{j = 1}^N {\left[ {{{\tilde u}_{ij,h,\theta }}\sum\limits_{l = 1}^{{D_r}} {w_{l,h}^{{m_{\rm{2}}}}{{\left\| {{{\mathit{\boldsymbol{x}}}_{jl,h}} - {{\mathit{\boldsymbol{v}}}_{il,h}}} \right\|}^2}} } \right]} } + \sum\limits_{i = 1}^C {{\alpha _{i,k}}\sum\limits_{j = 1}^N {{{\left( {1 - {u_{ij,k}}} \right)}^{{m_3}}}} } } \right)}}} \right)}^{\frac{1}{{{m_{_{_{1}}}} - 1}}}}} }}$ | (14) |
| $w_{l,k} = \frac{1}{{\sum\limits_{h = 1}^{{d_k}} {{{\left( {\displaystyle\frac{{\sum\limits_{i = 1}^C {\sum\limits_{j = 1}^N {\left( {{{\tilde u}_{ij,k,\theta }}{{\left\| {{{\mathit{\boldsymbol{x}}}_{jl,k}} - {{\mathit{\boldsymbol{v}}}_{il,k}}} \right\|}^2}} \right)} } }}{{\sum\limits_{i = 1}^C {\sum\limits_{j = 1}^N {\left( {{{\tilde u}_{ij,k,\theta }}{{\left\| {{{\mathit{\boldsymbol{x}}}_{jh,k}} - {{\mathit{\boldsymbol{v}}}_{ih,k}}} \right\|}^2}} \right)} } }}} \right)}^{\frac{1}{{{m_{_{_{2}}}} - 1}}}}} }}$ | (15) |
最终的划分结果用式(16)融合函数进行计算:
| ${{\mathit{\boldsymbol{U}}}_{ij}} = \sum\nolimits_{k = 1}^K {q_k} {u_{ij,k}}$ | (16) |
MV-FDW-PCM算法步骤如下:
1)给定聚类数C,样本总数N,视角总数K,聚类精度ε,最大迭代次数T,模糊系数m1,m2,m3,初始化隶属度矩阵U和聚类中心V;
2)根据式(12)更新聚类中心;
3)根据式(13)更新隶属度;
4)根据式(14)更新视角间权重系数;
5)根据式(15)更新视角内属性权重系数;
6)当
7)算法收敛后,输出各视角的隶属度矩阵uij,k;
8)利用式(16)计算出最终的划分结果。
3 实验与分析 3.1 实验环境及实验参数设置为了验证本文所提MV-FDW-PCM算法的性能,本文在以下几个数据集上进行了实验分析,实验数据集分别是:UCI标准数据集、Brodatz纹理图像[23]以及一组关于我实验室老师的真实人脸图像的实际应用效果展示。实验采用的对比算法主要有:经典的适用于单视角聚类环境的可能性C均值聚类算法PCM(Possibilistic c-means)、具备多视角模糊聚类性能的协同模糊K均值算法CoFKM[4](Collaborative fuzzy K-means)、具备聚类任务组合能力的K均值算法CombKM[24](Combine K-means)、具有多视角聚类算法代表性的多视角谱聚类算法MVSpec[5] (Multi-view spectral clustering)。所有实验运行平台的配置如下:酷睿i3 3.6 GHz CPU,3.42G RAM,32位Windows 7操作系统,MATLAB R2012b编程环境。
本文算法的评价指标如表2所示。
| 表 2 评价指标 Tab.2 The evaluation index |
表中两种评价指标分别为归一化互信息(normalized mutual information,NMI)和芮氏指标(rand index,RI),这两种指标为常用的评价聚类结果评价指标[5, 12],其取值范围均在[0, 1],指标数值越大(越接近1),代表该算法的性能表现越好。
实验中相关参数设置如下:本文MV-FDW-PCM算法中参数m1,m2,m3均在{1.1, 1.3, 1.5, 1.7, 1.9, 2.5}中寻优取得,参数θ设为1。MVSpec算法中指数p通过从{1, 1.1, ···, 1.9, 2, 3, ···, 6, 7}中进行网络搜索来设置最优值。实验结果均为算法运行20次的平均值与均方差, 因此实验结果部分对应的NMI-mean、NMI-std、RI-mean、RI-std分别为NMI和RI指标在20次运行后所得结果的均值和方差。
3.2 UCI标准数据实验本文使用了UCI数据集中经典的4种多视角表达的数据集,分别是手写数据集(MF)、图像分割数据集(IS)、污水处理数据集(WTP)及互联网广告数据集(IADS),表3中简要介绍了各数据集的基本信息。此外,各算法在这4种UCI数据集上的实验结果如表4所示。
| 表 3 UCI数据集介绍 Tab.3 Description of UCI data sets |
| 表 4 UCI数据集上的实验结果对比 Tab.4 The performance of clustering algorithm |
从实验结果可以观察出如下结论:
1) 通过观察各算法在MF数据集上的聚类结果,可以明显地看出CoFKM算法及本文所提的MV-FDW-PCM算法有着较大的性能优势。但是由于MF数据集本身所含的各视角样本的可分性均是比较均衡一致的,因此本文算法的视角加权的优势并不明显,其所得性能与CoFKM算法基本接近。
2) 当进一步观察本文算法在IS及WTP这两个多视角数据集上的聚类性能,本文所提的MV-FDW-PCM算法在IS数据集上性能优势较为明显,这是由于IS这类图像分割数据集不同视角间的特征差异明显、可分性也有一定的区分,这使得本文算法的属性加权机制和视角加权机制产生了一些积极的聚类效果,提高了聚类性能。而对于WTP这一水污染数据集,本文算法的性能与其他4种方法相比基本处于相同的性能水平,导致这一现象的原因主要是水污染数据集样本数较少各类之间的数据分布区分并不显著,此外该数据所含的类别较多,这对于采用欧式距离的算法而言是一种挑战,对于此类数据集,我们将在今后考虑使用其他的距离公式来替换欧氏距离改善聚类性能。
3) 观察IADS数据可发现具备多视角聚类能力的算法较之单视角的聚类算法如经典的PCM算法有着明显的聚类优势,但本文所提的MV-FDW-PCM算法的聚类性能却略差于基于谱聚类聚类原理的MVSpec算法。究其原因在于如IADS等广告类数据一般数据分布呈现非团状数据特征,而PCM、CombKM、CoFKM及MV-FDW-PCM均是基于c-means框架提出的方法,其对团状数据有效,对于非团状数据特别是凸型数据则显得无能为力。为了改善此类算法在非团状数据集上的聚类性能,一种有效的途径也是更换距离公式,今后我们也将在这部分研究内容上进行深入的探讨。
3.3 Brodatz纹理图像实验除了验证本文算法在UCI标准数据集上的聚类性能,本小节还在图像分割实验中验证了本文算法的性能。本文在著名的Brodatz纹理图库中(http://www.ux.uis.no/~tranden/brodatz.html)选择了7种具有常见的具备代表性的纹理图片组成了图5。两种不同的纹理组合图像的目标分割数均为7。对比算法不变,各算法对该纹理图的分割结果如图6所示。具体的聚类性能对比如表5所示。
根据图6各算法在两种不同的纹理组合图像上的实验结果可以观察出,本文算法MV-FDW-PCM所得的分割结果与理想分割结果图的效果最为接近。观察图6(a)、6(b)、6(f)及6(g)的实验结果,我们可以肉眼评价出单视角聚类算法的性能明显劣于3种多视角聚类算法,其分割结果的图像质量较差。而对于3种多视角聚类算法,本文方法由于其具备多视角加权和多视角属性加权机制,特别是多视角属性加权机制,该机制能够增大图像中重要属性的权重进而提高分割结果的质量使得本文算法获得了优于其他两种多视角聚类算法的更佳分割效果。综合图6与表5的结果,我们可以得出结论,本文提出的MV-FDW-PCM算法在图像分割实验中较其他算法具有更好的聚类性能。

|
图 5 纹理图像 Fig.5 Texture image |

|
图 6 各算法分割结果对比 Fig.6 Comparison of image segmentation results |
| 表 5 各算法的聚类性能对比 Tab.5 Comparison of clustering performance of each algorithm |

|
图 7 真实人脸图像 Fig.7 Real face image |

|
图 8 各算法在真实人脸图像上的分割结果 Fig.8 The segmentation results of the algorithm on the real face image |
在本节的实验中,我们针对一幅真人的证件照片图7(a)为例,以最基本的RGB通道分别获得3个视角样本如图7(b)、(c)所示,而后使用本文所提的MV-FDW-PCM算法与其他的4种相关算法做了进一步的性能比对分析。由于真人照片无法标定像素的真实标记,因此NMI指标和RI指标在该实验部分将无法使用,仅能够通过图8给出的分割结果从肉眼上进行评估。
从图8的分割结果可以明显地看出,3种具备多视角聚类能力的Co-FKM算法、MVSpec算法及本文所提的MV-FDW-PCM算法较之传统的单视角PCM算法及CombKM算法在分割性能上有着明显的优势。进而,对3种多视角聚类算法的结果进行分析,本文所提的MV-FDW-PCM算法在脸部及皮肤分割方面较之其他两种方法有着一定的分割优势,这也从侧面反映了两种加权策略(视角加权和属性加权)在聚类过程中起到了一定的作用, 改善了聚类结果。
3.5 算法运行性能分析根据表6的实验结果可知,本文所提方法的运行效率在所对比的5种方法中排名在后两位。因本文算法包含了4个参数(聚类中心、隶属度、视角内属性权重及视角权重)需要迭代优化,较之传统的PCM算法的2优化参数(类中心及隶属度)、组合K均值算法CombKM的2优化参数(类中心及隶属度)及多视角协同算法CoFKM的2优化参数(类中心及隶属度)均有着高出近1倍的优化迭代需求,而对于多视角谱聚类算法MVSpec,由于该算法基于谱聚类聚类原理和MV-FDW-PCM算法的C均值聚类原理有较大差别,两者的运行性能不具可比较性。综上,本文算法虽拥有较之其他相关算法更佳的聚类性能,但在运行效率上较之其他算法显得并不高效。为此,今后我们将进一步地探讨如何在更少的优化参数下保持当前聚类性能的多视角可能性聚类算法。
| 表 6 各算法的运行性能对比 Tab.6 Comparison of the running time of each algorithm |
为解决传统可能性聚类算法无法满足多视角学习场景聚类的实际问题,并进一步考虑到现有多视角聚类算法尚未重视的视角间权重及视角内特征权重优化问题,本文致力于提出一种新的具备最佳视角及最优特征划分能力的多视角模糊双加权可能性聚类算法(MV-FDW-PCM)。该算法基于传统的PCM算法,给出详细的多视角聚类学习框架,使得PCM算法具备多视角聚类能力,进而通过引入视角间模糊加权机制及视角内属性模糊加权机制以解决视角权重及视角内特征权重优化问题。本文在UCI中的标准多视角数据集、纹理图像分割实验以及真实人脸图像中,均进行了实验验证。实验结果表明,本文所提的MV-FDW-PCM算法在面对多视角聚类问题时较其他对比聚类算法具备更佳的聚类效果。
| [1] |
JIANG Y Z, DENG Z H, CHUNG F L, et al. Realizing two-view TSK fuzzy classification system by using collaborative learning[J]. IEEE transactions on systems, man, and cybernetics: systems, 2017, 47(1): 145-160. ( 0) 0)
|
| [2] |
YAMANISHI Y, VERT J P, KANEHISA M. Protein network inference from multiple genomic data: a supervised approach[J]. Bioinformatics, 2004, 20(1): 363-370. ( 0) 0)
|
| [3] |
PEDRYCZ W. Collaborative fuzzy clustering[J]. Pattern recognition letter, 2002, 23(14): 1675-1686. ( 0) 0)
|
| [4] |
CLEUZIOU G, EXBRAYAT M, MARTIN L, et al. CoFKM: a centralized method for multiple-view clustering [C]//Proc of the 9th IEEE International Conference on Data Mining (ICDM 2009). Miami, USA, 2009: 752–757.
( 0) 0)
|
| [5] |
TZORTZIS G F, LIKEAS A C. Kernel-based weighted multi-view clustering[C]//IEEE 12th International Conference on Data Mining. Brussels, Belgium, 2012: 675–684.
( 0) 0)
|
| [6] |
DENG Z H, JIANG Y Z, ISHIBUCHI H, et al. Enhanced knowledge-leverage-based tsk fuzzy system modeling for inductive transfer learning[J]. ACM transactions on intelligent systems and technology, 2016, 8(1): 1-21. ( 0) 0)
|
| [7] |
QIAN P J, JIANG Y Z, DENG Z H, et al. Cluster prototypes and fuzzy memberships jointly leveraged cross-domain maximum entropy clustering[J]. IEEE transaction on cybernetics, 2016, 46(1): 181-193. ( 0) 0)
|
| [8] |
DENG Z H, JIANG Y Z, CHUNG F L, et al. Transfer prototype-based fuzzy clustering[J]. IEEE transactions on fuzzy systems, 2016, 24(5): 1210-1232. ( 0) 0)
|
| [9] |
PAN S J, YANG Q. A survey on transfer learning[J]. IEEE transactions on knowledge and data engineering, 2010, 22(10): 1345-1359. ( 0) 0)
|
| [10] |
JIANG Y Z, CHUNG F L, ISHIBUCHI H, et al. Multitask TSK fuzzy system modeling by mining intertask common hidden structure[J]. IEEE transactions on cybernetics, 2015, 45(3): 548-561. ( 0) 0)
|
| [11] |
CARUANA R. Multitask learning[J]. Machine learning, 1997, 28(1): 41-75. ( 0) 0)
|
| [12] |
DENG Z H, CHOI K S, JIANG Y Z, et al. A survey on soft subspace clustering[J]. Information sciences, 2016, 348: 84-106. ( 0) 0)
|
| [13] |
HALL LO, GOLDGOF DB. Convergence of the single-pass and online fuzzy C-means algorithms[J]. IEEE transactions on fuzzy systems, 2011, 19(4): 792-794. ( 0) 0)
|
| [14] |
BEZDEK J C. Pattern recognition with fuzzy objective function algorithms[M]. New York, USA: Plenum Press, 1981: 65–79.
( 0) 0)
|
| [15] |
FREY B J, DUECK D. Clustering by passing messages between data points[J]. Science, 2007, 315(5814): 972-976. ( 0) 0)
|
| [16] |
曾令伟, 伍振兴, 杜文才. 基于改进自监督学习群体智能(ISLCI)的高性能聚类算法[J]. 重庆邮电大学学报: 自然科学版, 2016, 28(1): 131-137. ZENG Lingwei, WU Zhengxin, DU Wencai. Improved selfsupervised learning collection intelligence based high performance data clustering aproach[J]. Journal of Chongqing university of posts and telecommunications: natural science edition, 2016, 28(1): 131-137. (  0) 0)
|
| [17] |
程旸, 王士同. 基于局部保留投影的多可选聚类发掘算法[J]. 智能系统学报, 2016, 11(5): 600-607. CHENG Yang, WANG Shitong. A multiple alternative clusterings mining algorithm using locality preserving projections[J]. CAAI transactions on intelligent systems, 2016, 11(5): 600-607. (  0) 0)
|
| [18] |
杭文龙, 蒋亦樟, 刘解放, 等. 迁移近邻传播聚类算法[J]. 软件学报, 2016, 27(11): 2796-2813. HANG Wenlong, JIANG Yizhang, LIU Jiefang, et al. Transfer affinity propagation clustering algorithm[J]. Journal of software, 2016, 27(11): 2796-2813. (  0) 0)
|
| [19] |
邓赵红, 王士同, 吴锡生, 等. 鲁棒的极大熵聚类算法RMEC及其例外点标识[J]. 中国工程科学, 2004, 6(9): 38-45. DENG Zhaohong, WANG Shitong, WU Xisheng, et al. Robust maximum entropy clustering algorithm rmec and its outlier labeling[J]. Engineering science, 2004, 6(9): 38-45. (  0) 0)
|
| [20] |
KARAYIANNIS N B. MECA: maximum entropy clustering algorithm[C]//Proc of the 3rd IEEE Conf. on Fuzzy Systems. Orlando: IEEE Press, 1994: 630–635.
( 0) 0)
|
| [21] |
KRISHNAPURAM R, KELLER J. A possibilistic approach to clustering[J]. IEEE transactions on fuzzy systems, 1993, 1(2): 98-110. ( 0) 0)
|
| [22] |
KRISHNAPURAM R, KELLER J M. The possiblistic means algorithms: Insights and recommendation[J]. IEEE transactions on fuzzy systems, 1996, 4(3): 385-393. ( 0) 0)
|
| [23] |
TRYGVE R, BRODATZ T. Texture classification [EB/OL]. [2007-08-01]. http://www.ux.uis.no/tranden/brodatz.html.
( 0) 0)
|
| [24] |
GU Q Q, ZHOU J. Learning the shared subspace for multi-task clustering and transductive transfer classification [C]//Proc Int Conf Data Mining (ICDM). Miami, USA, 2009: 59–168.
( 0) 0)
|
 2017, Vol. 12
2017, Vol. 12

 ,
,