随着遥感技术的快速发展，高光谱图像分析也有了重大进展。高光谱数据因其波段众多可以提供地物更精确详尽的信息，但与此同时也带来了信息冗余，因而在对数据分析时会产生较高的计算复杂度以及Hughes现象，所以在高光谱图像处理过程中，降维是其重要环节。遥感数据降维有两种方法：特征提取和波段选择。特征提取是用映射的方法将原始数据变换为较少的新特征，常用的方法有主成分分析、独立成分分析、局部线性嵌入等^[1-3]。与特征提取不同，波段选择依据高光谱遥感数据的特点从原始数据集中选择合适的波段子集，在不改变原始数据的物理意义及光谱特性的同时降低数据维度，是一种有效的高光谱图像降维技术。

按照先验信息的有无，高光谱图像波段选择方法可分为监督波段选择和无监督波段选择^[4]。监督波段选择一般用一个准则函数来衡量已选波段与带标签数据之间的相似度，然后通过一些优化策略来搜索最优波段子集^[5]。无监督波段选择则只需要地物的原始高光谱图像信息，而无需带标签样本，因而更具有普适性，因此本文主要研究无监督的波段选择。

无监督的波段选择方法一般可分为如下几类:一类是按照信息量以及波段间相关程度排序的方法，一类是基于聚类的方法，此外由于端元选择与波段选择问题在模型上具有共性，一些端元选择方法也用于波段选择中^[6]。最大方差主成分分析方法(maximum-variance principle component analysis, MVPCA)是一种经典的基于信息量的方法，它利用PCA变换获取各波段的方差，将方差作为信息量的考量标准，然后按照方差的大小进行排序，以确定波段的优先级^[7]。基于信息散度(information divergence, ID)的波段选择方法是用信息散度对全波段计算概率密度分布与其所对应的高斯分布的偏离度，按照偏离度从大到小的顺序对波段进行排序，得到所需数目的波段子集^[8]。但鉴于高光谱数据的相邻波段具有较大相关性，按照信息量排序所选定的某波段，其相邻的波段也极有可能具有相近的信息量，因此也会被选入波段子集，造成冗余。于是，一些同时考虑信息量与相关系数的无监督波段选择方法被提出来，如最佳指数因子(optimal index factor, OIF)法计算波段的方差与相关系数的比值，再用这个数值来衡量波段的优先次序。但是OIF方法需要多次计算波段间的OIF，因此计算量庞大。自适应波段选择方法(adaptive band selection, ABS)与OIF方法类似，采用标准差与相关系数的比值作为考量标准，但较之OIF，ABS只计算相邻波段的相关系数，虽然计算复杂度较低，却忽视了所选波段子集的整体相关性^[9]。近些年，一些学者用聚类的方法进行波段选择，即将波段按照某衡量准则分成多个子集，用聚类中心代表子集内的其他波段，聚类数目根据所需的波段数确定。具有代表性的方法如基于K均值(K-means)算法的波段选择，基于谱聚类(spectral clustering, SC)的波段选择，使用仿射传播(affinity propagation, AP)的波段选择等^[10-12]。K均值算法简单易行，但是容易受初值影响，并且所选择的聚类中心是算术平均的位置，需要进一步处理。基于K-medoids的聚类直接选取候选波段作为波段的聚类中心，具有很好的鲁棒性，但该方法同样易受初始值影响，随着初值的不同而导致最后的聚类中心不同。基于SC的波段选择方法采用类内波段算术均值而非现实中存在的波段，对噪声敏感，且每类中随机选取的波段不一定能够最好地代表所在的类。基于AP算法的波段选择方法将每个样本点都视为候选类代表点，不受初始点选择的困扰，但相似矩阵的计算复杂度较高。而最大最小距离算法是一种基于试探的聚类算法，它以某种距离作为衡量标准，采用相距尽量远的样本作为聚类中心点，可以避免随机选取的初始聚类中心相距太近的情况^[13]。针对现有波段选择方法的不足，本文提出了一种基于最大最小距离的波段选择方法，该方法通过迭代计算得到一组初始的距离较远的波段子集，然后以这些波段为基础进行聚类更新，获取具有代表性的波段子集。

1 波段聚类的基础

高光谱数据的特点是具有极高的光谱分辨率，其相邻波段间具有较强的相关性，这里的谱间相关性就是指，对空间上某一相同位置，相邻波段的波段图像具有相似性。具有这种相似的原因主要是：同一地物在相邻波段的光反射率是非常相近的，因此产生了一定的相关性。这种相关性可以用相关系数矩阵来描述^[14]，以AVIRIS采集的印第安农林数据为例，计算其相关系数矩阵和相关系数向量，并将得到的矩阵和向量进行可视化，如图1。

图1中，(a)是以灰度图像的形式呈现，由灰度图像的取值特点可知，越明亮的区域其相关系数越大，而明亮区域主要集中于主对角线，因此可以说明相邻波段间的相关性更强，而从图1(b)可以直观看到相关性较强的各个波段范围。鉴于高光谱图像波段间具有的这种聚集特性，可以将其看作波段聚类问题，即将波段划分为具有相似特性的波段组成的集合，选择这些波段集合中具有代表性的聚类中心，就可以得到数据的一个波段子集，从而完成波段选择过程。

2 基于最大最小距离的波段选择

最大最小距离法是模式识别中一种基于试探的聚类算法，它以欧氏距离为基础，取尽可能远的对象作为聚类中心。因此它可以避免K-means算法初值选取时可能出现的聚类种子过于临近的情况，它不仅能智能确定初始聚类种子的个数，而且提高了划分初始数据集的效率。所以，本文尝试利用最大最小距离法进行高光谱图像的波段选择，以方差最大的波段作为第一个聚类中心，不断迭代计算最大最小距离获取所需数目的聚类中心集合，进而对集合外的剩余波段聚类，最后以K-medoids方法对聚类中心进行更新，获取最终波段子集，具体描述如下。

2.1 初始化聚类中心 2.1.1 第一个聚类中心的选取

在数据处理上，高光谱图像用集合 $B \!=\! \{ {b_1}, {b_2}, \cdots \!,{b_n}\} $ 表示，其中，n为波段个数， ${{\mathit{\boldsymbol{b}}}_i}(i = 1,2, \cdots \!,m)$ 为m行的列向量，代表第i个波段，m为波段图像包含的像素个数，则波段i的标准差值为

${s_i} = {\left( {\left( {1/m} \right)\sum\limits_{l = 1}^m {{{\left( {{b_{il}} - {\mu _i}} \right)}^2}} } \right)^{1/2}}$

(1)

式中 ${\mu _i}$ 为波段i的均值，即

${\mu _i} = \left( {1/m} \right)\sum\limits_{l = 1}^m {{b_{il}}} $

(2)

波段均值 ${\mu _i}$ 可以用于表征波段i各地物的平均强度；波段标准差 ${s_i}$ 可以反应波段i中像素强度与均值的偏离程度，一定程度上反映各波段图像的信息量，图像标准差越大，其所包含的信息越丰富，因此可以采用标准差值定量表示波段包含的信息量，并用标准差最大的波段作为最大最小距离算法第1个聚类中心 ${{\mathit{\boldsymbol{B}}}_1}$ 。

2.1.2 其他聚类中心的迭代选取

设最大最小距离算法最后得到的聚类中心为集合 ${{\mathit{\boldsymbol{B}}}_{{s}}} = \left\{ {{{\mathit{\boldsymbol{B}}}_1},{{\mathit{\boldsymbol{B}}}_2}, \cdots \! ,{{\mathit{\boldsymbol{B}}}_k}} \right\}$ ，其中k为聚类中心个数，即所选波段个数。根据2.1.1节的结果可知，第1个初始聚类中心 ${{\mathit{\boldsymbol{B}}}_1}$ 可表示为

${{\mathit{\boldsymbol{B}}}_1} = \arg \max {s_i}$

(3)

则 ${{\mathit{\boldsymbol{B}}}_{{s}}} = \left\{ {{{\mathit{\boldsymbol{B}}}_1}} \right\}$ 。然后计算B中其他波段与 ${{\mathit{\boldsymbol{B}}}_1}$ 的距离，选择距离最大的波段作为第2个类的聚类中心 ${{\mathit{\boldsymbol{B}}}_2}$ ，可表示为

${{\mathit{\boldsymbol{B}}}_2} = \arg \max {{d}}\left( {{{\mathit{\boldsymbol{b}}}_i},{{\mathit{\boldsymbol{B}}}_1}} \right)$

(4)

这里 ${{d}}\left( \cdot \right)$ 表示某种距离测度, 则 ${{\mathit{\boldsymbol{B}}}_s}$ 更新为 $\left\{ {{{\mathit{\boldsymbol{B}}}_1},{{\mathit{\boldsymbol{B}}}_2}} \right\}$ 。

当k大于2时，则第k个聚类中心 ${{\mathit{\boldsymbol{B}}}_k}$ 为B中剩余波段中 ${{\mathit{\boldsymbol{b}}}_i}$ 与 ${{\mathit{\boldsymbol{B}}}_s}$ 中的波段的最大最小距离，表示为

${{\mathit{\boldsymbol{B}}}_k} = \arg \max {{d}}\left( {{{\mathit{\boldsymbol{b}}}_i},{\rm{MI}}{{\rm{N}}_{k - 1}}} \right)$

(5)

式中 ${\rm{MI}}{{\rm{N}}_{k - 1}} = \min \{ d({{\mathit{\boldsymbol{b}}}_i},{{\mathit{\boldsymbol{B}}}_1}),d({{\mathit{\boldsymbol{b}}}_i},{{\mathit{\boldsymbol{B}}}_2}), \cdots \! ,d({{\mathit{\boldsymbol{b}}}_i},{{\mathit{\boldsymbol{B}}}_{k - 1}})\} $ ，此时 ${{\mathit{\boldsymbol{B}}}_s}$ 更新为 $\left\{ {{{\mathit{\boldsymbol{B}}}_1},{{\mathit{\boldsymbol{B}}}_2}, \cdots \! ,{{\mathit{\boldsymbol{B}}}_k}} \right\}$ 。

2.2 更新聚类中心

通过最大最小距离方法得到了相互距离较远的一组波段，在原本的最大最小距离算法中会将这组波段作为聚类中心，然后计算其他波段与这些中心的距离，以距离最小为原则划分类别。虽然这些波段间的区分度较高，但会导致聚类中心与簇内相距较远波段的相关性较低，而对于波段选择来说，其最终得到的应该是具有代表性的波段，也就是说，该波段到簇内其他波段间的代价函数应该最小。因此将这些“激进”但区分度又高的波段组合作为一个初始的聚类中心，然后采用对噪声较不敏感的K-medoids算法更新聚类中心，得到最终的波段组合。具体的步骤如下：

1)选择 ${{\mathit{\boldsymbol{B}}}_s}$ 作为初始中心点；

2)计算B中剩余波段与 ${{\mathit{\boldsymbol{B}}}_s}$ 中各波段的距离，以距离最小为准则进行分配；

3)在每一个类内，选择代价函数最小的波段作为新的聚类中心；

4)重复2)、3)直至各类的中心点稳定，此时算法结束。

算法的整体流程如下。

算法　基于最大最小距离的波段选择方法

输入　给定所需的波段数目k。

1)根据式(1)、(2)计算每个波段的标准差s_i，取标准差最大的波段作为1个聚类中心 ${{\mathit{\boldsymbol{B}}}_1}$ ；

2)计算剩余波段与 ${{\mathit{\boldsymbol{B}}}_1}$ 间距离，取距离最小的波段作为第2个聚类中心 ${{\mathit{\boldsymbol{B}}}_2}$ ；

3)当k>2时，按照式(5)迭代选择剩余的聚类中心， ${{\mathit{\boldsymbol{B}}}_s}$ 更新为 $\left\{ {{{\mathit{\boldsymbol{B}}}_1},{{\mathit{\boldsymbol{B}}}_2}, \cdots \! ,{{\mathit{\boldsymbol{B}}}_k}} \right\}$ ；

4)以最近邻原则将B中剩余波段划分给 ${{\mathit{\boldsymbol{B}}}_s}$ 中的各个聚类中心；

5)用K-medoids算法更新聚类中心 ${{\mathit{\boldsymbol{B}}}_s}$ ，输出最终的波段组合。

3 实验与分析

为验证本文算法的有效性，采用真实高光谱数据进行了仿真实验，同时与基于K-medoids，基于AP，以及基于ABS的典型波段选择算法进行比较。第1种和第2种是基于聚类方法的波段选择，第3种是同时考量了信息量与相关性的波段选择方法。实验环境为AMD双核处理器，主频2.47 Hz，有效内存3 GB，开发环境为MATLAB R2008a。

实验数据为去除噪声波段的200波段的AVIRIS印第安农林数据和103波段的ROSIS帕维亚大学数据：

1)印第安农林数据的波长范围为0.4～2.5 μm，空间分辨率为17 m，共有144×144个像素点。数据中剔除背景共包含16类地物，主要农作物是生长期的玉米和大豆，结合地面实际测量数据，其中7种地物样本量过少，对于该数据不具有代表性，因此选取另9种样本数目较多的主要类型地物用于实验。

2)帕维亚大学数据波长范围为0.43～0.86 μm，空间分辨率为1.3 m，共有610×340个像素点，共包含9类地物，实验中9种地物均用于实验。两组数据所对应的地物真实情况如图2、图3所示，9种地物类型及数目如表1所示。

3.1 评价标准

对于高光谱遥感图像，一般评价所选波段组合的优劣主要是面向应用的角度，其中地物的分类是一个重要的应用方法，因此本文以总体分类精度(overall accuracy, OA)为主评价波段选择方法的质量，同时辅助地考虑波段子集的平均相关性、信息贡献率、最佳指数(optimum index factor, OIF)，计算公式为

$\overline R = \frac{1}{{{C^2}}}\sum\limits_{i = 1}^{m - 1} {\sum\limits_{j = i + 1}^m {{R_{ij}}} } $

(6)

式中：C为样本总数，R_ij为波段i和波段j的相关系数，计算公式为

${R_{ij}} = \displaystyle\frac{{\sum\limits_{k = 1}^n {\left( {{x_{ik}} - {{\bar {\mathit{\boldsymbol{x}}}}_i}} \right)} \left( {{x_{jk}} - {{\bar {\mathit{\boldsymbol{x}}}}_j}} \right)}}{{\sqrt {\sum\limits_{k = 1}^n {{{\left( {{x_{ik}} - {{\bar {\mathit{\boldsymbol{x}}}}_i}} \right)}^2}\sum\limits_{k = 1}^n {{{\left( {{x_{jk}} - {{\bar {\mathit{\boldsymbol{x}}}}_j}} \right)}^2}} } } }}$

(7)

式中： ${{\mathit{\boldsymbol{x}}}_i} = {\left[ {{x_{i1}}\,{x_{i2}}\, \cdots \, {x_{in}}} \right]^{\rm{T}}}$ 为第 $i\left( {i = 1,2, \cdots ,m} \right)$ 个波段， ${\bar {\mathit{\boldsymbol{x}}}_i}$ 是第i个波段的均值。选择的m个波段的信息量贡献为

${o_{{{\rm{R}}_{{\mathop{\rm var}} }}}}\left( m \right) = \frac{{\sum\limits_{g = 1}^m {{\lambda _g}} }}{{\sum\limits_{k = 1}^n {{\lambda _k}} }} \times 100{\rm{\% }}$

(8)

式中：n为波段总数，m为所选波段的个数，通常 $m \leqslant n$ ， ${\lambda _g}\left( {g = 1,2, \cdots \! ,m} \right)$ 是所选波段经主成分变换后的特征值； ${\lambda _k}(k = 1,2, \cdots \! ,n)$ 是全波段主成分变换得到的特征值。

${O_{{\rm{OIF}}}} = \frac{{\sum\limits_{i = 1}^n {{S_i}} }}{{\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {\left| {{R_{ij}}} \right|} } }}$

(9)

式中：S_i是第i波段的标准差。

${O_{{\rm{OA}}}} = \frac{{\sum\limits_{i = 1}^c {{m_{ii}}} }}{C}$

(10)

式中：m_ii为第i类测试样本被正确分类的样本数，c为样本类别数^[15]。

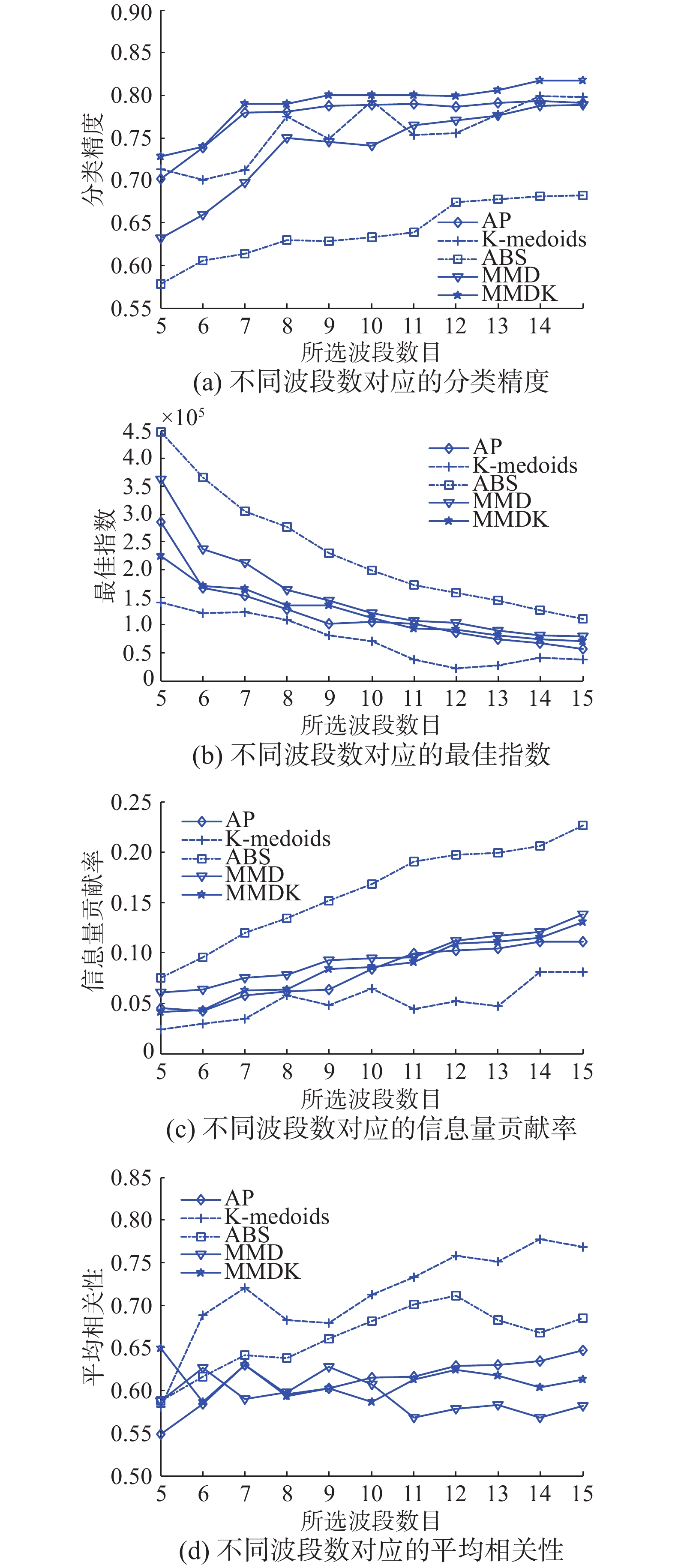
3.2 结果分析

为定量比较几种波段选择方法随所选波段数目的变化趋势，所以选择连续变化的波段数目。分类采用最大似然分类法，训练样本数目与测试样本数目各占总样本数目的一半。同时，也将只进行最大最小距离选择而未更新聚类中心的结果进行比较，在效果评价图中用MMD表示，本文算法记作MMDK。各波段选择算法在两组数据上所选波段子集的总体分类精度、最佳指数、信息贡献率、平均相关性和总体分类精度的结果分别绘制于图4、5中。下面分别对两组数据的实验结果进行分析。

3.2.1 Indian数据集

Indian数据集所选的波段数目为5~15，从两方面分析各算法在该数据集上所选波段的性能。

1)分类结果分析

从图4(a)中可以看到，AP、ABS、MMD和本文所提算法所得波段的总体分类精度随波段数目的增加而稳定上升，但无论所选的波段数目是多少，本文所提算法获取的波段组合总能够得到最高的分类精度。而MMD虽然选择了光谱维度上“距离”较远的波段，但分类效果并不理想，这也说明“激进”的波段并不能代表其所在的聚类，需要进一步更新聚类中心。K-medoids算法所选的波段组合随波段数目的增加具有波动性，再一次证明初始聚类中心对于保证波段选择效果的重要性。

2)信息量与相关性结果分析

对于信息量与相关性的考量则需要结合图4(b)、(c)、(d)一起分析。从图4中可以看出，ABS算法在信息量及综合考虑二者的OIF上均表现得很优秀，这是由于ABS是基于OIF而进行的改进，采用标准差与相关系数的比值作为考量标准，但ABS相较OIF是只计算相邻波段的相关系数，忽视了所选波段子集的整体相关性，因此其平均相关性较低。K-medoids算法受随机初始化的影响，所选的波段组合依然不稳定。本文所提算法在平均相关性与信息量上结果居中，与MMDK相比平均相关性稍高，信息量也较小，但却说明一个问题: 具有高信息量与低相关性的波段组合不一定是最能体现各波段聚类的，并且应用到实际问题中时的表现也不一定最优。这是因为，若以信息量大小排序来选择波段，当某波段入选，则相邻波段由于具有与其近似的波段图像，因此相邻波段也具有较高的入选优先性。虽然OIF考虑了相关性，但直接用方差与相关系数的比值来全面衡量二者，其结果较为生硬。

3.2.2 PaviaU数据集

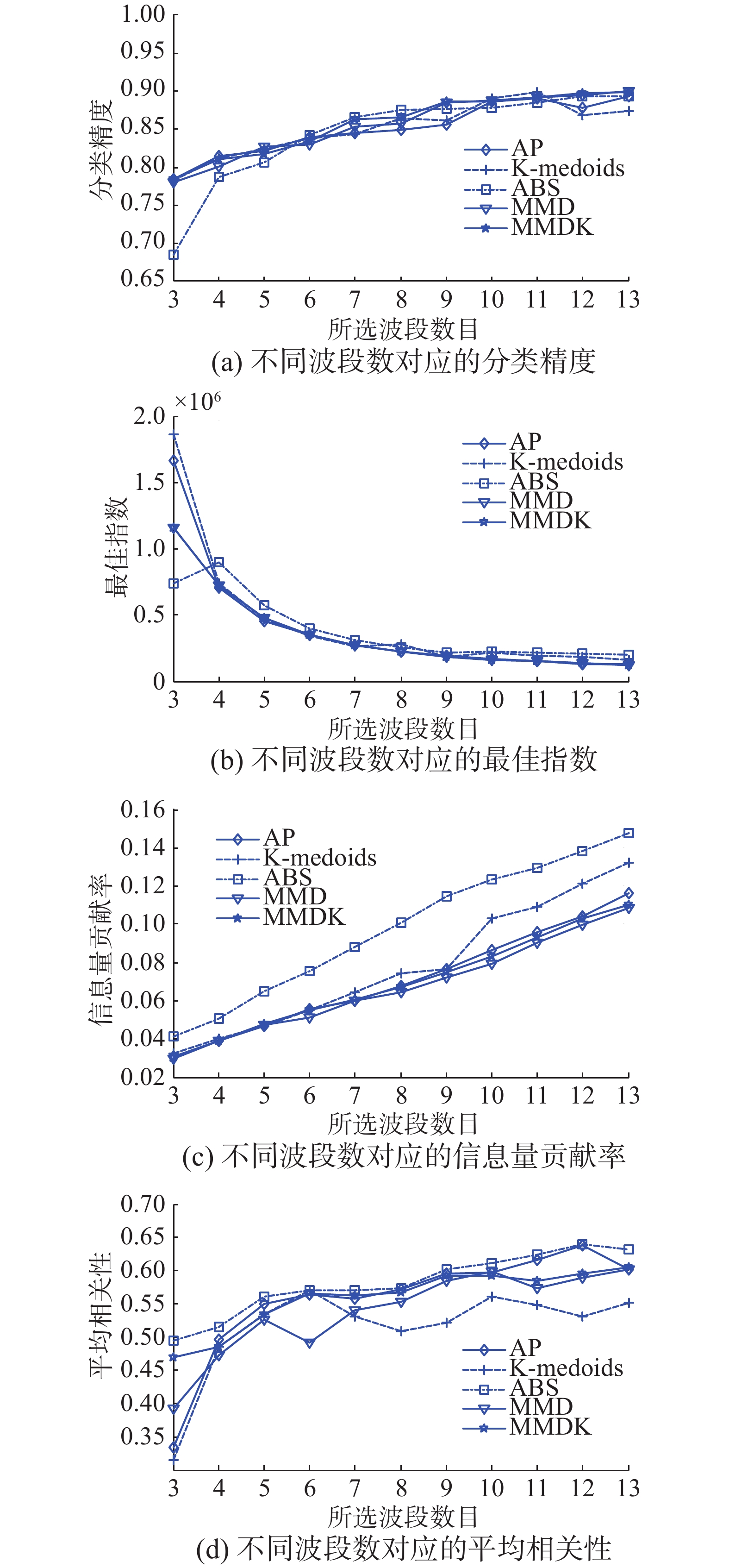
PaviaU数据集所选的波段数目为3~13，同样从两方面分析各算法在该数据集上所选波段的性能。

1) 分类性能分析

因为PaviaU数据集的空间分辨率较高，混合像素较少，并且地物种类与Indian数据相比，类别差异性更大，相对而言更容易区分，分类精度也更高。图5(a)中MMDK算法始终保持着较高的分类精度，而ABS算法在波段数目为3时分类精度较低，这是由于ABS算法虽以信息量与相关性为选择波段的标准，但其为计算便捷，会忽略波段组合整体相关性，因此容易选出相关性较高的波段子集，当所选波段数据较少时，这种差异性较其他方法会更明显。随机选择初始聚类中心的K-medoids算法整体依然存在波动性。AP算法在波段数目3~6区间时，具有较好的分类精度，但当大于6时相较MMDK分类精度低，这与AP算法中参考度p有关，p代表着相似度值，其值越大则簇越多，所以需要较多的簇时，p就需要取较大的相似度值，使得其各簇中心相似度较高，而对于波段选择来说，这是不利的。MMD算法整体分类精度与MMDK相仿，这主要是由于该数据相似波段之间距离较小，波段聚集密度较高，所以二者具有水平相当的分类能力。

2)信息量与相关性结果分析

结合图5(b)、(c)、(d)来分析各算法在PaviaU数据集所选波段子集包含的信息量与平均相关性可以看到，ABS算法在OIF值上依然整体占优，其他几种算法有着接近的OIF值。在信息量贡献率上ABS同样较其他算法得到较高的贡献率，但其平均相关性也更高，这依然由ABS算法优先将近似的但拥有较大信息量的波段选择到子集中，忽略波段子集的整体相关性导致。其他几种聚类算法除K-medoids具有波动性外，在各评价函数上均相差不大，这是由于PaviaU数据各波段簇较紧密所致。

通过两组数据的实验可以看出，MMDK算法所选的波段子集在两种数据集上均获得较高的分类精度，且其各性能随波段数目的增加均呈现平稳趋势，证明了算法的有效性与稳定性。而基于聚类的波段选择与基于信息属性的波段选择方法也有不同，基于聚类的波段选择更倾向于选择最具代表性的，而不是波段本身差异性大的，因此波段子集的信息量较基于信息属性所选择的波段子集低。而MMDK在信息量与相关性的评价中，虽始终居中，但这符合波段聚类中心需要更有代表性，而不是差异性大的选择标准。综上，可以得出结论，MMDK算法是一种行之有效的波段选择方法。

4 结束语

本文针对高光谱图像波段冗余问题，提出了基于最大最小距离的波段选择算法，该算法只需要输入待选波段的数目，不需要进行其他参数的设置，通过迭代计算已选波段与待选波段间的最大最小距离获取初始的聚类中心，然后用K-medoids更新此聚类中心，最终输出波段子集。此方法物理意义明确，便于实现。与基于K-medoids算法、基于AP算法、基于ABS算法的波段选择方法所进行的对比实验表明，基于MMDK算法的波段选择方法较其他3种典型波段选择算法在分类精度方面更理想，生成的波段组合也更稳定，更加能够满足实际需求。

未来的研究工作可从如下两方面展开：1)本文在计算距离时，采用的是欧氏距离，而衡量波段间区分性的还有光谱角距离、Bhattacharyya距离、JM距离等，不同的距离计算方式对聚类结果的影响如何，有待讨论；2)文中是通过给定波段子集大小的方式确定聚类中心的个数，而若给定的数目太小则不足以描述数据，给定的数目过多又会造成冗余，同样影响后续应用的效果，因此如何自动地确定不同数据集所需的波段数目也是一个值得研究的问题。