谱聚类作为聚类分析一种有效的方法,建立在谱图划分的基础上,可将数据集从原始空间转换到低维特征空间,使原始数据变成线性可分[1],目前已广泛应用于图像分割、人脸识别等领域[2-3]。另一方面,半监督学习是机器学习领域的研究热点,已被用于解决实际问题[4-6],在聚类分析中引入一些监督信息来指导聚类过程,能够提高聚类准确率。
半监督聚类算法的约束信息包括“必连”和“勿连”约束集合,引入这些约束信息可指导聚类过程。目前,针对半监督谱聚类算法已有大量的研究,Kamvar等[7]根据约束关系调整数据之间的相似度,将调整后的相似度矩阵用于改进谱聚类,但是不能充分利用初始有限的约束关系;蒋伟进等[8]提出一种纠错式主动学习成对约束算法,将挖掘到的监督信息用于调整数据点之间的距离矩阵,但约束集合对聚类结果影响较大;丁世飞等[9]通过优化高斯核参数和引入成对约束信息来调整相似度矩阵,但过多的约束信息会对聚类准确率造成负面的影响;Cucuringu等[10]将“必连”和“勿连”约束矩阵均视为图拉普拉斯矩阵,把约束聚类转化为广义特征值问题,针对2类划分效率和准确率显著提高。王翔等[11]提出一种柔性约束谱聚类框架,引入大量硬约束和软约束信息建立新的约束优化问题,有效提高聚类准确率,但是不具备约束关系传递。基于约束信息的半监督聚类算法,通常能获取数据的约束关系是非常有限的,通过约束传递来获得大量可靠的成对约束信息,可显著提高半监督聚类的性能。余志文等[12]提出一种增强型半监督聚类集成框架(incremental semi-supervised clustering ensemble,ISSCE),采用卢志武等[13]提出的约束传递方法,即基于k近邻图的标签传播方法,将少量标签样本的监督信息传递给未标签样本,但如果相似度错误反映数据点之间的相似性,会造成约束关系的错误传递。传统的谱聚类及上述大部分半监督谱聚类算法均需要存储数据的相似度矩阵且对拉普拉斯矩阵进行特征分解,空间和时间的计算复杂度比较高,在处理大规模数据集时计算代价难以承受。为了提升谱聚类的扩展性,蔡登等[14]提出基于地标点表示的谱聚类算法,通过数据点与地标点之间的相似度矩阵乘积来近似得到整体数据点的相似度矩阵,然后利用近似性质实现快速特征分解。
本文将采用基于地标点近似表示的方法,通过稀疏表示构造的相似度矩阵对柔性约束谱聚类算法模型[11]进行改进,并且根据约束集合内地标点的关系,利用Tarjan算法[15]自动检测连通区域,在每个连通区域内部动态调整近邻点,传递约束关系,从而更新稀疏表示矩阵提高聚类准确率。在5个大规模标准数据集上进行实验的结果表明,本文算法对这些大规模数据具有较好适应性,且在有效降低算法复杂度的同时,保证了约束谱聚类算法结果的准确率。
1 算法基本原理 1.1 约束NCut算法对于数据集
标准NCut的目标函数为
| $\mathop {\arg \min }\limits_{{{v}} \in {\mathbb{R}^n}} {{{v}}^{\rm{T}}}{{Lv}},{\rm{ }}\,{\rm{s}}{\rm{.t}}{\rm{. }}{{{v}}^{\rm{T}}}{{v}} = {{1}},{{v}} \bot {{1}}$ | (1) |
式中v表示松弛化的类指示向量。
假设已知“必连”约束集合M与“勿连”约束集合C,文献[11]根据约束信息生成约束矩阵
| $ {{{Q}}_{ij}}{\rm{ = }}\left\{ {\begin{aligned}& 1,\quad {({{{x}}_i},{{{x}}_j}) \in {M}}\\&- 1,\quad {({{{x}}_i},{{{x}}_j}) \in {C}}\\& 0,\quad {{\text{无约束信息}}}\end{aligned}} \right. $ | (2) |
通过式(3)来衡量
| ${{{v}}^{\rm{T}}}{{Qv}} = \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {{{{v}}_i}{{{v}}_j}{Q_{ij}}} } $ | (3) |
定义软约束
约束NCut的目标函数为
| $ \mathop {\arg \min }\limits_{{{v}} \in {^n}} {{{v}}^{\rm{T}}}{{Lv}},{\rm{ }}\,{\rm{s}}{\rm{.t}}{\rm{. }}{{{v}}^{\rm{T}}}{{Qv}} \geqslant \alpha ,{{{v}}^{\rm{T}}}{{v}} = {{1}},{{v}} \bot {{1}} $ | (4) |
上述问题可转化为求解矩阵的特征向量[11],但是空间和时间复杂度分别为
蔡登等[14]提出基于图稀疏表示的谱聚类算法,通过地标点的线性组合来实现所有数据点X的近似表示
| ${{{\hat x}}_i} = \sum\limits_{j = 1}^p {{{Z}_{ji}}{{{y}}_j}} $ | (5) |
式中:
如果
| $ {Z_{ji}} = \frac{{{{K}}({{{x}}_i},{{{y}}_j})}}{{\sum\nolimits_{j' \in \left\langle i \right\rangle } {{{K}}({{{x}}_i},{{{y}}_{j'}})} }},\quad i \in 1,2, \cdots ,n, j \in \left\langle i \right\rangle $ | (6) |
式中:
在获得矩阵Z后,可以构造两种形式的图,即
将在“必连”和“勿连”约束集合中的数据点视为地标点,其个数为p。根据约束关系生成一个
根据约束信息所生成的相似度矩阵,利用Tarjan算法检测生成
| ${{\hat Z}}\left( {{p_i},{p_j}} \right) = \left\{ {\begin{aligned}& {1,} \quad {\left\{ {{p_i} \in {T_a}|{p_j} \in {T_a}} \right\}} \\ & {0,} \quad {\left\{ {{p_i} \in {T_a}|{p_j} \in {{T_a^{\prime}}}} \right\}} \end{aligned}} \right.$ | (7) |
每个数据点均有r个近邻点,
| ${\bf{lookupVec}}_{i'} = \left\{ {\begin{aligned}& {\min + {\rm{fre}}{{\rm{q}}_{i'}} \times \displaystyle\frac{{\max - \min }}{{m - 1}},}\quad {m \ne 1} \\ & {\max ,}\quad {m = 1} \end{aligned}} \right.$ | (8) |
式中:min和max分别表示
| ${{{L}}_{{p_i}}} = \left\{ {{{{L}}_{{p_1}}} \cup {{{L}}_{{p_2}}} \cup \cdots \cup {{{L}}_{{p_{\left| a \right|}}}}} \right\}, \quad i \in 1,2, \cdots ,\left| {{T_a}} \right|$ | (9) |
根据式(8)、(9)进行约束关系的传递,对矩阵
| ${{\hat Z}}\left( {i,{p_j}} \right) = {\bf{lookupVec}}_{i'}$ | (10) |
式中:
根据1.2节所提出的基于稀疏表示建立的相似度矩阵可知,
依据稀疏表示的约束NCut目标函数可表示为
| $\mathop {\arg \min }\limits_{v \in {\mathbb{R}^n}} {{{v}}^{\rm{T}}}{{\bar Lv}},{\rm{ }}\,\,{\rm{s}}{\rm{.t}}{\rm{. }}{{{v}}^{\rm{T}}}{{Qv}} \geqslant \alpha ,{{{v}}^{\rm{T}}}{{v}} = {{1}},{{v}} \bot {{1}}$ | (11) |
式中
基于文献[11]提出的方法,上述问题的求解可以松弛为一般的特征值求解问题:
| ${{Lv}} = \lambda \left( {{{Q}} - \beta {{I}}} \right){{v}}$ | (12) |
式中
求解式(12)特征向量的时间复杂度为
| $\mathop {\arg \min }\limits_{{{u}} \in {\mathbb{R}^p}} {{{u}}^{\rm{T}}}{{Au}},{\rm{ }}\,{\rm{s}}{\rm{.t}}{\rm{. }}{{{u}}^{\rm{T}}}{{\hat Qu}} \geqslant \alpha ,{{{u}}^{\rm{T}}}{{\hat Su}} = {{1}},{{{1}}^{\rm{T}}}{{\hat Su}} = 0$ | (13) |
式中:
该模型等价于式(11)所表示的约束NCut目标函数,但是有两个改进:一是规范化的拉普拉斯矩阵
为了求解式(13),引入拉格朗日乘子,可扩展约束NCut问题转化为
| $\Lambda \left( {{{u}},\lambda ,\mu } \right) = {{{u}}^{\rm{T}}}{{Au}} - \lambda \left( {{{{u}}^{\rm{T}}}{{\hat Qu}} - \alpha } \right) - \mu \left( {{{{u}}^{\rm{T}}}{{\hat Su - 1}}} \right)$ | (14) |
需要满足KKT条件,即
| ${{Au}} - \lambda {{\hat Qu}} - \mu {{\hat Su}} = 0$ | (15) |
| ${{{u}}^{\rm{T}}}{{\hat Qu}} \geqslant \alpha $ |
| ${{{u}}^{\rm{T}}}{{\hat Su}} = {{1}}$ |
| ${{{1}}^{\rm{T}}}{{\hat Su}} = 0$ |
| $\lambda \geqslant 0$ |
| $\lambda \left( {{{{u}}^{\rm{T}}}{{\hat Qu}} - \alpha } \right) = 0$ |
当
假设
| ${{Au}} = \lambda \left( {{{\hat Q}} - \beta {{\hat S}}} \right){{u}}$ | (16) |
通过求解式(16)的特征值和特征向量,计算复杂度远远降低。
还需要考虑如何设置参数
| $\lambda {{{u}}^{\rm{T}}}\left( {{{\hat Q}} - \beta {{\hat S}}} \right){{u}} = \lambda \left( {\alpha - \beta } \right) \geqslant 0$ |
即参数
算法 结合稀疏表示与约束传递的半监督谱聚类算法
输入 数据集X,约束集合M和C,聚类个数k,参数
输出 类label。
1) 将在约束集合内的p个点选为地标点,并作为矩阵U的列向量;
2) 根据式(6)构造Z,并计算
3) 使用Tarjan算法,根据地标点之间的约束关系计算连通区域CC;
4) for 每个连通区域CC do:
计算连通区域的邻接子矩阵
根据近邻点出现频率的次数构建向量lookupVec;
根据式(9)将约束关系传递给该区域内剩余数据点;
根据lookupVec更新
end for
5) 依据约束关系生成约束矩阵
6) 求解
7) if
8) else求解式(16)的特征向量u;
9) 找出所有正特征值所对应的特征向量
10) 去掉
11) 计算
12) 计算
基于地标点近似表示的谱聚类算法需要构造稀疏矩阵
为了验证本文算法的性能,选取规模较大的数据集进行实验,依次为物体图像数据集COIL100,人脸数据集CMU-PIE,手写数字数据集USPS、MNIST和UCI标准库中的森林植被类数据集CoverType,数据集的特性如表1所示。仿真实验基于MATLAB2014b平台,计算机的硬件配置为Intel i7-4770 CPU 3.40 GHz、16 GB RAM。
| 表 1 实验数据集的特性 Tab.1 Experimental datasets features |
本文算法和文献[11]的约束谱聚类方法CSP,文献[14]的基于地标点采样的快速谱聚类算法LSC-R和LSC-K,文献[15]所提出的针对大规模数据集的半监督谱聚类算法SC-PC进行对比,LSC-R是通过随机采样来获取p个地标点,LSC-K是利用k-means算法来获得p个地标点。须指出,由于CSP算法在CMU-PIE、MNIST和CoverType数据集上计算负担过大,并没有进行相关实验的比较。
鉴于比较的公平性,具体的参数设置如下:其中文献[14-15]和本文算法的地标点个数p均设置为1 000,所有算法中k-means部分的迭代次数均设置为500,所有稀疏表示矩阵构造过程中的近邻点个数r设置为5。约束的下界即参数
通过数据集中每个样本预定义的类标签来实现对聚类结果的评价,采用聚类准确率ACC和归一化互信息NMI两种度量指标[14]对聚类结果进行评估和比较分析。两个评价指标的取值范围均是在0~1之间,值越大表示聚类效果越好。
3.2 实验分析各种算法在上述数据集的实验结果如表2所示。
| 表 2 各数据集实验结果 Tab.2 Experimental results of different datasets |
根据表2可以看出,约束谱聚类算法CSP在COIL100和USPS两个数据集上的ACC和NMI均取得最佳结果,因为其考虑引入约束矩阵建立约束优化问题,提高聚类准确率,但是在上述两个数据集上的运行时间太长,耗时将近5~7 h,对于更大的数据集CMU-PIE、MNIST和CoverType数据集,计算负担过大,没能进行验证。本文算法在COIL100和USPS数据集的ACC分别为0.666 0和0.843 5,NMI指标分别为0.797 5和0.773 1,和CSP相比稍有降低;但从运行时间上,本文算法的运行时间仅在秒级别,耗时分别为3.51 s和1.88 s,远远少于CSP的运行时间,而且在包含581 012个样本的大规模CoverType数据集上运行时间只需要747.36 s,所以本文算法基于稀疏表示矩阵来建立相似度矩阵,降低了矩阵分解的复杂度,提高了半监督聚类算法的可扩展性。
另一方面,本文算法和LSC-K、LSC-R、SC-PC三种均为提升谱聚类的效率的算法,即快速谱聚类算法相比,在准确率ACC和归一化互信息NMI两个指标上有所提高,且在CMU-PIE和CoverType数据集上两个指标具有明显的提升;和SC-PC算法相比,本文算法在CMU-PIE数据集上ACC、NMI分别提升了79.12%和38.58%,在CoverType数据集上ACC和NMI分别提升了15.02%和39.94%。因为在处理高维数据时,采用稀疏表示能够过滤一些异常点和噪声,同时指定约束下界,可去除一些噪声等约束关系的负面影响。因此,引入约束信息来改变谱聚类算法的目标函数,并通过在连通区域内进行约束关系传递,能够有效提高聚类的准确率。
为了分析初始约束信息对聚类结果的影响,添加了地标点个数p(对应半监督聚类中能获取的初始约束信息)对聚类指标影响的对比实验。同样,CSP算法只在USPS和COIL100两个数据集上实现。p依次取200、500、800和1 000。不同算法ACC和NMI的对比实验结果分别如图1、2所示。

|
Download:
|
| 图 1 不同算法的ACC比较 Fig. 1 Comparison of the ACCs of different algorithms | |
|
Download:
|
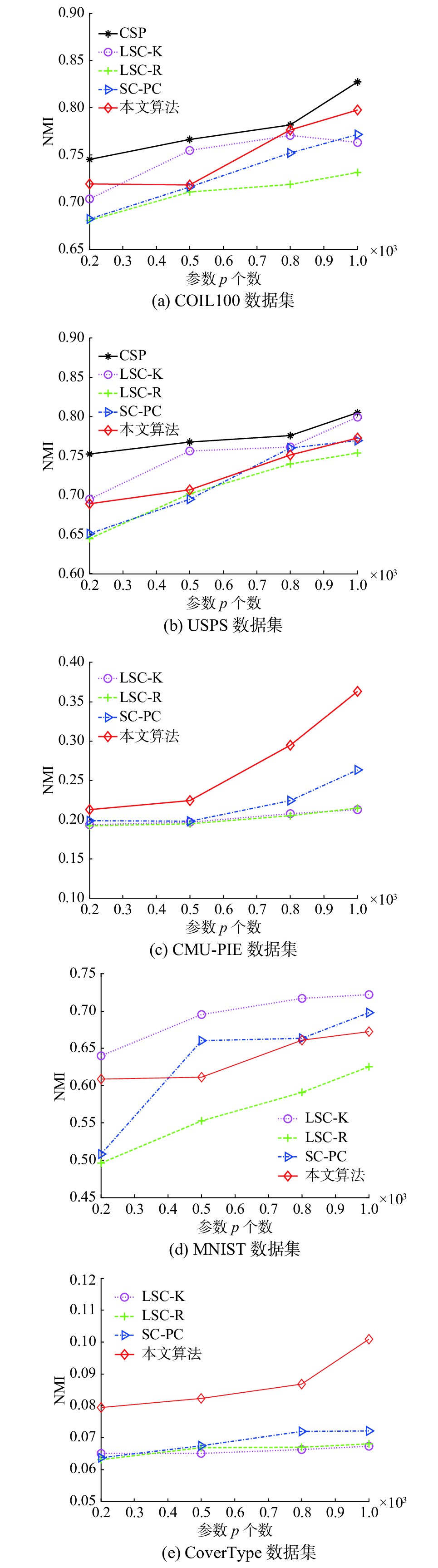
| 图 2 不同算法的NMI比较 Fig. 2 Comparison of the NMIs of different algorithms | |
由图1可知,本文算法在5个数据集上的ACC比LSC-K、LSC-R和SC-PC三种算法都要高,随着参数p个数增加,每种算法的ACC也随着增加,说明ACC受p的选取影响很大。由图2可知,在NMI指标上,本文算法和快速谱聚类算法相比,在CMU-PIE和CoverType两个数据集上具有明显的优越性,同样随着p个数增多,每种算法的NMI都随着提高。总的来说,在p的不同取值情况下,本文算法能取得最好的聚类效果。
4 结束语随着规模庞大、结构复杂数据的不断出现,对其聚类往往耗费大量的时间,同时多数半监督谱聚类算法存在没有充分利用初始约束信息的问题。本文通过稀疏表示改进约束谱聚类算法的目标函数,根据初始约束信息生成连通区域,在每个连通区域内动态调整近邻点进行约束关系传递。实验结果表明,本文算法在提高聚类准确率的同时能有效降低聚类复杂度,能够较好地适用于大规模数据集。但是本文算法的聚类准确率受采样地标点的个数和选取方法影响比较大,接下来可以针对该问题开展进一步的研究工作。
| [1] |
VON Luxburg U. A tutorial on spectral clustering[J]. Statistics and computing, 2007, 17(4): 395-416. DOI:10.1007/s11222-007-9033-z ( 0) 0)
|
| [2] |
SHI Jianbo, MALIK J. Normalized cuts and image segmentation[J]. IEEE transactions on pattern analysis and machine intelligence, 2000, 22(8): 888-905. DOI:10.1109/34.868688 ( 0) 0)
|
| [3] |
HU Han, FENG Jianjiang, YU Chuan, et al. Multi-class constrained normalized cut with hard, soft, unary and pairwise priors and its applications to object segmentation[J]. IEEE transactions on image processing, 2013, 22(11): 4328-4340. DOI:10.1109/TIP.2013.2271865 ( 0) 0)
|
| [4] |
刘建伟, 刘媛, 罗雄麟. 半监督学习方法[J]. 计算机学报, 2015, 38(8): 1592-1617. LIU Jianwei, LIU Yuan, LUO Xionglin. semi-supervised learning methods[J]. Chinese journal of computers, 2015, 38(8): 1592-1617. (  0) 0)
|
| [5] |
ALUSH A, FRIEDMAN A, Goldberger J. Pairwise clustering based on the mutual-information criterion[J]. Neurocomputing, 2016, 182: 284-293. DOI:10.1016/j.neucom.2015.12.025 ( 0) 0)
|
| [6] |
FORESTIER G, WEMMERT C. Semi-supervised learning using multiple clusterings with limited labeled data[J]. Information sciences, 2016, 361-362: 48-65. DOI:10.1016/j.ins.2016.04.040 ( 0) 0)
|
| [7] |
KAMVAR S D, KLEIN D, MANNING C D. Spectral learning[C]//Proceedings of the 18th International Joint Conference on Artificial Intelligence. Acapulco, Mexico, 2003: 561–566.
( 0) 0)
|
| [8] |
蒋伟进, 许宇晖, 王欣. 基于谱图和成对约束的主动半监督聚类算法[J]. 控制与决策, 2013, 28(6): 904-908. JIANG Weijin, XU Yuhui, WANG Xin. Active semi-supervised clustering algorithm based-on pair-wise constraints[J]. Control and decision, 2013, 28(6): 904-908. (  0) 0)
|
| [9] |
DING Shifei, JIA Hongjie, ZHANG Liwen, et al. Research of semi-supervised spectral clustering algorithm based on pairwise constraints[J]. Neural computing and applications, 2014, 24(1): 211-219. DOI:10.1007/s00521-012-1207-8 ( 0) 0)
|
| [10] |
CUCURINGU M, KOUTIS I, CHAWLA S, et al. Simple and scalable constrained clustering: a generalized spectral method[C]//Proceedings of the 19th International Conference on Artificial Intelligence and Statistics. Cadiz, Spain, 2016: 445–454.
( 0) 0)
|
| [11] |
WANG Xiang, QIAN Buyue, DAVIDSON I. On constrained spectral clustering and its applications[J]. Data mining and knowledge discovery, 2014, 28(1): 1-30. DOI:10.1007/s10618-012-0291-9 ( 0) 0)
|
| [12] |
YU Zhiwen, LUO Peinan, YOU J, et al. Incremental semi-supervised clustering ensemble for high dimensional data clustering[J]. IEEE transactions on knowledge and data engineering, 2016, 28(3): 701-714. DOI:10.1109/TKDE.2015.2499200 ( 0) 0)
|
| [13] |
LU Zhiwu, PENG Yuxin. Exhaustive and efficient constraint propagation: a graph-based learning approach and its applications[J]. International journal of computer vision, 2013, 103(3): 306-325. DOI:10.1007/s11263-012-0602-z ( 0) 0)
|
| [14] |
CAI Deng, CHEN Xinlei. Large scale spectral clustering via landmark-based sparse representation[J]. IEEE transactions on cybernetics, 2015, 45(8): 1669-1680. DOI:10.1109/TCYB.2014.2358564 ( 0) 0)
|
| [15] |
SEMERTZIDIS T, RAFAILIDIS D, STRINTZIS M G, et al. Large-scale spectral clustering based on pairwise constraints[J]. Information processing and management, 2015, 51(5): 616-624. DOI:10.1016/j.ipm.2015.05.007 ( 0) 0)
|
 2018, Vol. 13
2018, Vol. 13


