径向基函数(radial basis function，RBF)神经网络是一种模拟生物神经元局部响应特性的前馈神经网络，因其结构简单且具有良好的非线性映射能力而被广泛用于多个领域^[1-6]。RBF神经网络构建的核心问题在于结构设计^[7]。早期隐含层结构的确定多采用经验试凑法，但此类方法很难在保证神经网络精度的前提下得到一个紧凑的网络结构。因此，许多学者针对RBF神经网络的结构设计问题展开了大量研究。

聚类算法常被用来确定RBF神经网络的结构，如K-Means、Fuzzy C-Means (FCM)^[8-10]等，该类算法能根据各聚类中心之间的距离确定隐含层神经元的径向作用范围，但却无法确定隐含层神经元的个数，会影响神经网络的泛化能力。因此，根据研究对象自适应设计RBF神经网络中隐含层神经元的个数，提高网络性能已成为当前RBF神经网络研究的一个热点。Platt^[11]首次提出了一种结构自适应调整的RBF神经网络——资源分配网络(resource allocation network，RAN)，该网络能根据待处理任务动态增加RBF神经元，但容易导致网络结构过大的问题。在RAN的基础上，Yingwei等构建了最小资源神经网络(minimal resource allocation network，MRAN)^[12]。在自适应增加隐含层神经元的同时，MRAN能通过删减策略去除冗余神经元，但该网络收敛速度较慢。Huang等^[13]提出了一种增长修剪型RBF神经网络(growing and pruning RBF，GAP-RBF)，该网络基于神经元的显著性构建隐含层结构。文献[14]中构建了一种自组织RBF 神经网络(self-organizing RBF，SORBF)，SORBF网络基于RBF神经元径向作用范围对隐含层结构进行自适应增删。GAP-RBF网络和SORBF网络中涉及的算法参数较多，对算法最优参数的寻求会影响网络的性能。Wilamowski等^[15]基于误差补偿算法来构建RBF神经网络(error-correction RBF，ErrCor-RBF)，实验表明该方法能获得较精简的神经网络结构，但该网络仍然需要通过大量的迭代寻求最优结构。

鉴于以上存在的问题，结合RBF神经元激活函数本身的特性，本文对一种快速密度聚类算法进行了相应的改进，然后将其用于RBF神经网络的结构设计中。同时，针对传统梯度下降、算法收敛较慢且易陷入局部极小的问题，结合结构设计中确定的初始参数，选用改进的二阶梯度算法来训练RBF神经网络，提高了网络的收敛速度和泛化能力。最后，通过两个基准仿真实验验证，提出的基于快速密度聚类的RBF神经网络(fast density clustering RBF, FDC-RBF)，能够以紧凑的网络结构和较快的收敛速度获取较好的非线性映射能力。

1 RBF神经网络

RBF神经网络是一种典型的前馈型神经网络，其网络结构如图1所示(L个输入神经元，J个隐含层神经元，M个输出层神经元)。隐含层激活函数为径向基函数，常选用标准的高斯函数，即

${\theta _j}\left( {x} \right) = {{\rm{e}}^{{\rm{ - }}\frac{{{{\left\| {{x} - {c_j}} \right\|}^2}}}{{\sigma _j^2}}}}$

(1)

其中： ${{x}} = {\left[ {{x_1}\,\,\,{x_2} \,\,\, \cdots \,\,\, {x_L}} \right]^{\rm{T}}}$ 为网络输入向量， ${{{c}}_j}$ 为第j个神经元的中心向量， ${\sigma _j}$ 为第j个神经元的径向作用范围。输出层第m个神经元的输出 ${y_m}$ 为

${y_m} = \sum\limits_{j = 1}^J {{w_{jm}}{\theta _j}} $

(2)

式中： ${w_{jm}}$ 为第 $j$ 个隐层神经元到第m个输出神经元的连接权值。

2 基于快速密度聚类的RBF神经网络设计

RBF神经网络的设计包括结构构建和参数训练两部分。文中采用改进的快速密度聚类算法确定网络初始结构和初始参数，在此基础上，用一种改进的二阶梯度算法对网络进行训练。

2.1 快速密度聚类算法

聚类分析是基于相似度将样本划分成若干类别，目前大多数聚类算法普遍存在两点不足：需要提前确定聚类的类别数；需要通过大量迭代来寻求最优聚类结果。

针对以上问题，Alex等^[16]提出了一种快速密度聚类算法，该算法无需提前确定聚类类别数，通过寻找局部密度峰值作为聚类中心从而实现对数据样本的快速聚类。

快速密度聚类算法的核心思想在于聚类中心被其他密度值较小的点紧紧包围，且远离其他密度值较大的点。在聚类中心的寻找过程中，对于任一数据点i，需计算两个值：每个点的局部密度值 ${\rho _i}$ 和该点到其他密度值较大点的最小距离 ${\delta _i}$ 。数据点i的局部密度值计算公式为

${\rho _i} = \sum\limits_j {\chi \left( {{d_{ij}} - {d_c}} \right)} $

(3)

式中：当 $x < 0$ 时， $\chi \left( x \right) = 1$ ；当 $x \geqslant 0$ 时， $\chi \left( x \right) = 0$ ；d_c为需要提前设定的截断距离。

数据点i到其他密度值较大点的最小距离 ${\delta _i}$ 计算公式为

${\delta _i}{\rm{ = }}\mathop {{\rm{min}}}\limits_{j{\rm{:}}{\rho _j}{\rm{ > }}{\rho _i}} \left( {{d_{ij}}} \right)$

(4)

选出局部密度值较大和到其他点距离较小的点作为聚类中心，其他非中心数据样本依次分配到距离其最近且密度值较大的聚类中心所在类，由此完成整个聚类过程。

可见，该算法的聚类过程是一步完成的无需通过多次迭代来寻求最优结果。但其仍然存在两点不足：聚类前需要获取整个数据样本，因而不利于实现在线聚类；聚类的效果受到截断距离d_c的影响。

针对以上问题，结合高斯函数的特性，对该算法进行了一定的改进，并将其运用于RBF神经网络的结构设计中。

2.2 基于快速密度聚类算法的RBF网络结构设计

类似于快速密度聚类算法，本文通过寻找局部密度值较大的点作为隐含层神经元中心，进而确定RBF神经网络的结构。针对快速密度聚类算法需要预先知道所有的数据样本且聚类效果受到截断距离影响的问题，本文做出相应的改进。

1) 由于RBF神经元的激活函数为高斯函数，引入隐含层神经元活性评价指标如下：

${\rm{A}}{{\rm{C}}_{ij}}{\rm{ = }}{{\rm{e}}^{ - {{\left\| {{{{x}}_i} - {{{c}}_j}} \right\|}^2}/\sigma _j^2}} \geqslant V$

(5)

式中： ${\rm{A}}{{\rm{C}}_{ij}}$ 为第j个隐含层神经元被第i个样本激活后的活性，AC值越大，神经元的活性越强；V为神经元活性阈值，以保证隐含层神经元的活性足够大。输入向量、中心向量、径向作用范围需要满足以下关系：

$\frac{{\left\| {{{{x}}_i} - {{{c}}_j}} \right\|}}{{{\sigma _j}}} \leqslant \sqrt {\left\| {\ln V} \right\|} $

(6)

即输入向量与隐含层神经元的中心向量间的距离需要满足以下关系：

$\left\| {{{{x}}_i} - {{{c}}_j}} \right\| \leqslant {\sigma _j}\sqrt {\left\| {\ln V} \right\|} $

(7)

式中神经元活性阈值V根据实验进行取值。因此截断距离与神经元的径向作用范围以及神经元的活性相关。

2) 为了实现在线聚类，本文在确定神经网络结构时，训练样本依次进入神经网络对结构进行调整：增加一个隐含层神经元或对已有的隐含层神经元进行调整。

文中隐含层结构设计的核心思想在于：判断当前样本在激活其最近隐含层神经元时是否能保证该神经元具有足够的活性。如果能保证其活性则能归入当前隐含层神经元所在类，反之则不能；其次，通过密度比较，将密度较大的点作为隐含层神经元。

因此文中基于快速密度聚类的RBF神经网络结构设计可以分为两种情况：神经元增长机制；神经元调节机制。

设神经网络的训练样本是由P个输入输出对 $({{x}},{{{y}}_d})$ 组成，其中， ${{x}}$ 为L维输入向量， ${{{y}}_d}$ 为相对应的M维期望输出。初始时刻，网络隐含层的神经元个数为0。

①神经元增长机制

把第一个数据样本作为第一个隐含层神经元中心，同时设定相应的径向作用范围和输出权值。

${{{c}}_1} = {{{x}}_1}$

(8)

${\sigma _1} = 1$

(9)

${{{w}}_1} = {{{y}}_{d1}}$

(10)

在k时刻，假设已经存在j个隐含层神经元，当第k个数据样本进入网络时，找到距离当前样本最近的隐含层神经元k_min：

$k_{\min} = \arg \mathop {\min }\limits_{_{h \in [1,j]}} \left\{ {{\rm{dist}}({{{x}}_k},{{{c}}_h})} \right\}$

(11)

$D{\rm{ = dist}}\left( {{{{x}}_k},{{{c}}_{k_{\min }}}} \right)$

(12)

将此距离与该隐含层神经元的径向作用范围进行比较，如果 $D > {\sigma _{k_{\min} }}\sqrt {\left\| {\ln V} \right\|} $ ，则认为当前样本不能保证该神经元的活性，将第k个样本作为新增神经元的中心，同时设定其径向作用范围和输出权值：

${{{c}}_{j + 1}} = {{{x}}_k}$

(13)

${\sigma _{j + 1}} = 1$

(14)

${{{w}}_{j + 1}} = {{{y}}_{dk}}$

(15)

②神经元调整机制

在k时刻，若 $D \leqslant {\sigma _{k_{\min} }}\sqrt {\left\| {\ln V} \right\|} $ ，则认为当前网络能够对新样本进行学习，比较当前样本与该隐含层神经元的局部密度值，选出密度值较大的点作为新的隐含层神经元，数据点i的局部密度计算公式为

${P_i} = \sum\limits_{{{{c}}_i} \ne {{{x}}_j}} {\exp \left( { - {{\left\| {{{{c}}_i} - {{{x}}_j}} \right\|}^2}/{d_i}^2} \right)} $

(16)

式中： ${{x}}{}_j$ 是 ${{c}}{}_i$ 作用范围内所包括的样本点；d_i是该数据点的局部作用范围。

从式(16)可以看出，若一个数据点的局部密度值越大，代表该点附近聚集的样本点越多；同理，,隐含层神经元密度越大，则代表该神经元激活的样本数越多。

将当前输入样本点k的局部密度值与隐含层神经元k_min的局部密度值进行比较：

若 ${P_k} > {P_{k_{\min} }}$ ，则当前输入样本替换已有的隐含层神经元，成为新的隐含层神经元，初始参数设置为

${{{c}}_{k_{\min} }} = {{{x}}_k}$

(17)

${{{w}}_{k_{\min} }} = \frac{{{n_{k_{\min} }}{{{w}}_{k_{\min} }} + {{{y}}_{dj}}}}{{{n_{k_{\min} }} + 1}}$

(18)

${\sigma _{k_{\min} }}{\rm{ = max(dist(}}{{{c}}_{k_{\min} }},{{{x}}_{k_{\min} }}))$

(19)

式中： ${{x}}{}_{k_{\min} }$ 表示第k_min个隐含层神经元激活的所有样本； ${n_{k_{\min} }}$ 表示激活的样本数量。

反之，若 ${P_j} \leqslant {P_{k_{_{\min}} }}$ ，则已有的隐含层神经元不变，只需调整该神经元的径向作用范围以及到输出层的连接权值，见式(18)～(19)。

由此，可以得到FDC-RBF神经网络结构设计算法如下：

1)初始时刻，隐含层神经元个数为0。

2)当第1个样本进入网络后，将其作为第1个隐含层神经元，并按照式(8)～(10)对其中心、径向作用范围和连接权值进行设置。

3)当第k个样本进入网络后，计算其与当前所有隐含层神经元的距离，找出与第k个样本距离最近的隐含层神经元k_min。

4)判断输入样本是否能保证第k_min个神经元的活性，若不能保证则为网络新增加一个隐含层神经元，并按照式(13)～(15)赋予初始参数，然后转向6)；否则，执行下一步。

5)若能保证神经元活性，则比较当前样本与最近隐含层神经元的局部密度值，选出密度值较大的点作为新的隐含层神经元，按照式(17)～(19)对中心、径向作用范围和权值进行更新，转向6)。

6)若所有的样本比较完毕，则神经网络结构确定；否则，k=k+1，转向3)。

该算法将快速密度聚类的思想用于RBF网络结构设计中，并结合高斯函数特性进行相应改进，使网络具有紧凑的结构。同时，结构构建过程中设定的较优的初始参数又能提高网络的收敛速度。

2.3 神经网络学习算法

确定网络结构后，需要对网络参数进行调整。本文用一种改进的二阶算法对RBF网络进行训练，提高了网络的收敛速度和泛化能力。传统的LM算法更新规则如式(20)所示^[17]：

${{{\varDelta }}_{k + 1}} = {{{\varDelta }}_k} - {({{J}}_k^{\rm{T}}{{{J}}_k} + {\mu _k}{{I}})^{ - 1}}{{J}}_k^{\rm{T}}{{{e}}_k}$

(22)

式中： ${{\varDelta }}$ 指所有需要调整的参数(中心向量、径向作用范围、连接权值)；J为雅克比矩阵；e为误差向量；I是单位矩阵；μ为学习率参数。

误差向量计算公式为

${{e}} = {\left[ {{e_{11}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {e_{12}}...{e_{12}}...{e_{P1}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {e_{P2}}...{e_{PM}}{\kern 1pt} {\kern 1pt} } \right]^{\rm{T}}}$

(23)

${e_{pm}} = {y_{dpm}} - {y_{pm}}$

(24)

式中：P是样本数量，M是输出向量维数， ${y_{dpm}}$ 和 ${y_{pm}}$ 分别是第p个样本进入时第m个输出神经元对应的期望输出和实际输出。

雅克比矩阵计算公式为

${{J}} = \left[ {\begin{array}{*{20}{c}} {\displaystyle\frac{{\partial {e_{11}}}}{{\partial {{{\varDelta }}_1}}}}&{\displaystyle\frac{{\partial {e_{11}}}}{{\partial {{{\varDelta }}_2}}}}&{...}&{\displaystyle\frac{{\partial {e_{11}}}}{{\partial {{{\varDelta }}_N}}}} \\ \vdots & \vdots &{}& \vdots \\ {\displaystyle\frac{{\partial {e_{1M}}}}{{\partial {{{\varDelta }}_1}}}}&{\displaystyle\frac{{\partial {e_{1M}}}}{{\partial {{{\varDelta }}_2}}}}&{...}&{\displaystyle\frac{{\partial {e_{1M}}}}{{\partial {{{\varDelta }}_N}}}} \\ \vdots & \vdots &{}& \vdots \\ {\displaystyle\frac{{\partial {e_{P1}}}}{{\partial {{{\varDelta }}_1}}}}&{\displaystyle\frac{{\partial {e_{P1}}}}{{\partial {{{\varDelta }}_2}}}}&{...}&{\displaystyle\frac{{\partial {e_{P1}}}}{{\partial {{{\varDelta }}_N}}}} \\ \vdots & \vdots &{}& \vdots \\ {\displaystyle\frac{{\partial {e_{PM}}}}{{\partial {{{\varDelta }}_1}}}}&{\displaystyle\frac{{\partial {e_{PM}}}}{{\partial {{{\varDelta }}_2}}}}&{...}&{\displaystyle\frac{{\partial {e_{PM}}}}{{\partial {{{\varDelta }}_N}}}} \end{array}} \right]$

(25)

式中N是算法中所有参数的个数。

由式(23)可以看出，在LM算法的执行过程中，雅克比矩阵的计算与训练样本数量、参数个数以及输出向量的维数都有关。当样本数量过多时，则会影响算法的收敛速度。

针对以上问题，本文用一种改进的二阶算法对RBF网络进行训练，提高了神经网络的收敛速度。改进二阶算法的更新规则为^[18]

${{{\varDelta }}_{k + 1}} = {{{\varDelta }}_k} - {({{{Q}}_k} + {\mu _k}{{I}})^{ - 1}}{{{g}}_k}$

(26)

式中： ${{\varDelta }}$ 仍指所有需要调整的参数(中心向量，径向作用范围，连接权值)；Q为类海森矩阵；g为梯度向量；μ为学习率参数。

为了克服传统LM算法中存在的不足，减小存储空间，提高收敛速度，将类海森矩阵的计算转化为P×M个子矩阵的和，如式(25)、(26)所示：

${{Q}} = \sum\limits_{p = 1}^P {\sum\limits_{m = 1}^M {{{{q}}_{pm}}} } $

(27)

${{{q}}_{pm}} = {{j}}_{pm}^{\rm{T}}{{{j}}_{pm}}$

(28)

同样，将梯度向量的计算也转化为P×M个子向量的和：

${{g}} = \sum\limits_{p = 1}^P {\sum\limits_{m = 1}^M {{{{\eta }}_{pm}}} } $

(29)

${{{\eta }}_{pm}} = {{j}}_{pm}^{\rm{T}}{{{e}}_{pm}}$

(30)

这样，对类海森矩阵和梯度向量的计算就转化为对雅克比分量的计算：

${{{j}}_{pm}} = \left[ {\begin{array}{*{20}{c}} {\displaystyle\frac{{\partial {e_{pm}}}}{{\partial {w_{jm}}}}}&{...}&{\displaystyle\frac{{\partial {e_{pm}}}}{{\partial {\sigma _j}}}}&{...}&{\displaystyle\frac{{\partial {e_{pm}}}}{{\partial {c_{jm}}}}}&{...} \end{array}} \right]$

(31)

联立式(1)、(2)、(24)，对雅克比分量中每个参数的偏微分计算如下：

$\frac{{\partial {e_{pm}}}}{{\partial {w_{jm}}}} = - \frac{{\partial {y_{dpm}}}}{{\partial {w_{jm}}}} = - {\theta _j}\left( {{{{x}}_p}} \right)$

(32)

$\begin{array}{c} \displaystyle\frac{{\partial {e_{pm}}}}{{\partial {\sigma _j}}} = - \frac{{\partial {y_{dpm}}}}{{\partial {\sigma _j}}} = - \frac{{\partial {y_{dpm}}}}{{\partial {\theta _j}\left( {{{{x}}_p}} \right)}}\frac{{\partial {\theta _j}\left( {{{{x}}_p}} \right)}}{{\partial {\sigma _j}}} = \\ - \displaystyle\frac{{2{w_{jm}}{\theta _j}\left( {{{{x}}_p}} \right){{\left\| {{{{x}}_p} - {{{c}}_j}} \right\|}^2}}}{{\sigma _j^3}}\\ \end{array} $

(33)

$\begin{array}{c} \displaystyle\frac{{\partial {e_{pm}}}}{{\partial {c_{jm}}}} = - \frac{{\partial {y_{dpm}}}}{{\partial {c_{jm}}}} = - \frac{{\partial {y_{dpm}}}}{{\partial {\theta _j}\left( {{{{x}}_p}} \right)}}\frac{{\partial {\theta _j}\left( {{{{x}}_p}} \right)}}{{\partial {c_{jm}}}} = \\ - \displaystyle\frac{{2{w_{jm}}{\theta _j}\left( {{{{x}}_p}} \right)\left\| {{{{x}}_p} - {{{c}}_j}} \right\|}}{{\sigma _j^2}} \\ \end{array} $

(34)

训练过程中，学习率参数μ随着误差的变化自适应调整。如果后一时刻的误差小于前一时刻的误差，则μ值减小，并保留当前训练后的各参数值；反之，则μ值增大，各参数值恢复到调整前的值。

3 仿真实验

文中选用非线性函数逼近和非线性动态系统辨识两个基准实验对FDC-RBF网络进行仿真验证，并与其他算法进行了对比。

3.1 非线性函数sinE逼近

选取的典型非线性函数sinE为

$y = 0.8\exp ( - 0.2x)\sin (10x)$

(35)

式中 $0 \leqslant x \leqslant 2$ 。非线性函数sinE经常被用来检验RBF神经网络的性能。

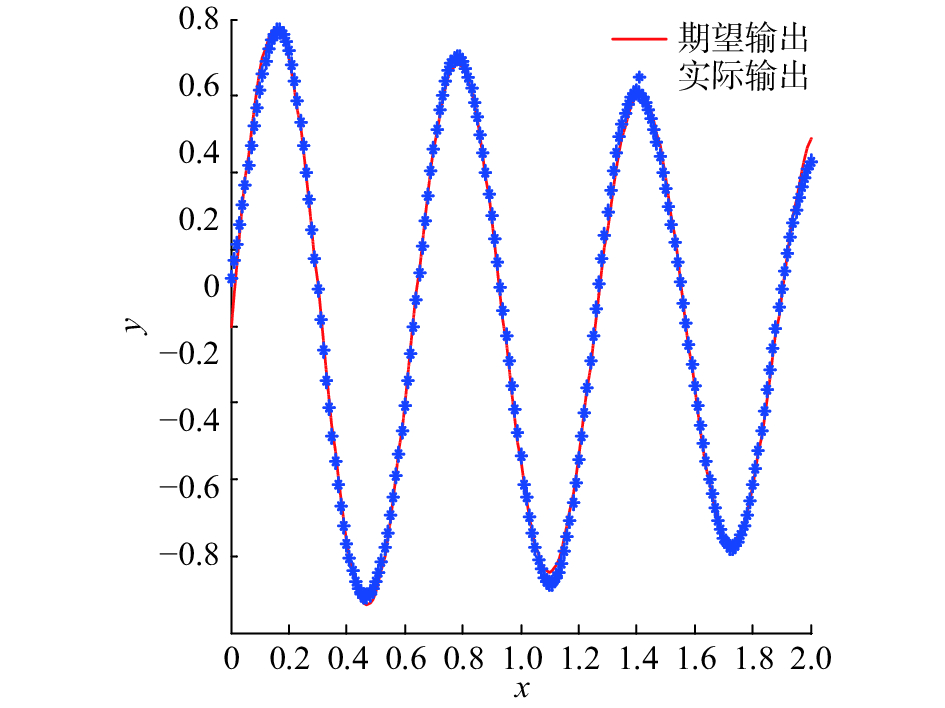
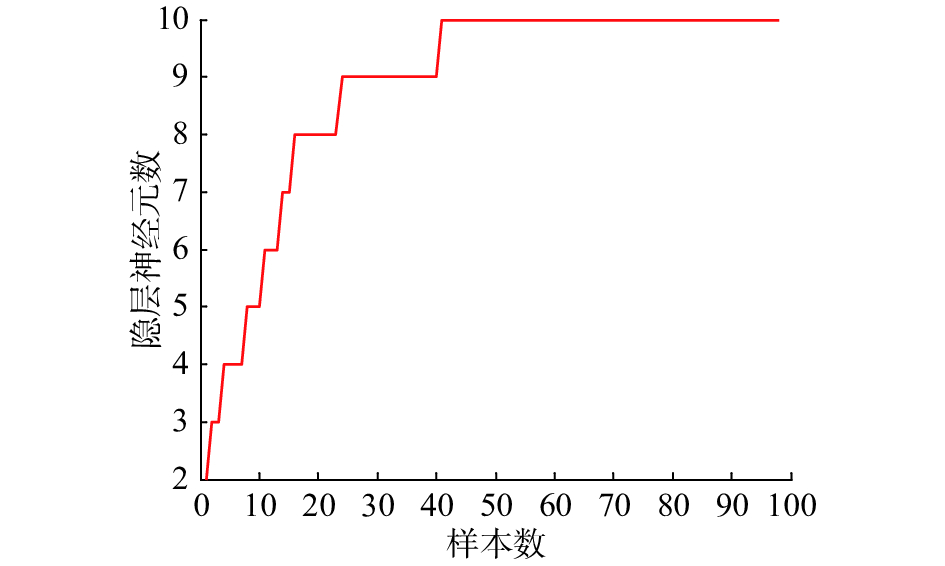
随机选取200个样本对神经网络进行训练，200个样本进行测试，训练的期望均方误差(mean square error，MSE)设为0.01，神经元活性阈值V设为0.55。用改进的二阶算法训练后的神经网络测试效果如图2所示，隐含层神经元数的变化如图3所示，二阶算法学习性能曲线如图4所示。此外，为了验证不同的学习算法对神经网络性能的影响，在RBF网络初始结构确定后，又用梯度下降法对该网络进行了训练，学习性能曲线如图5所示。

由图2可以看出，训练后的FDC-RBF网络能够较好地拟合sinE曲线。从图4和图5的对比可以看出，梯度下降算法需要在第45步左右才能完全收敛，而改进的二阶算法在第13步就已完全收敛。由此可以看出，当用改进的二阶算法训练该网络时，收敛速度大大提高了。

同时，为了显示FDC-RBF网络的优良性，本文将其与DFNN^[19]、GAP-RBF^[13]、SORBF^[14]、ART-RBF^[20]进行了对比，如表1所示。结果显示，与DFNN、GAP-RBF、SORBF相比，基于本文提出的算法设计的网络隐含层神经元个数要少于以上网络，结构要更为精简；同时，与其他4种网络相比，FDC-RBF网络收敛速度更快，训练时间更短；此外，从测试误差的对比可以看出，FDC-RBF网络的测试误差也要小于其他算法。因此可以得出，FDC-RBF神经网络在逼近该非线性函数时，网络结构较其他算法更为精简，收敛速度更快，泛化能力更好。

3.2 非线性系统动态辨识

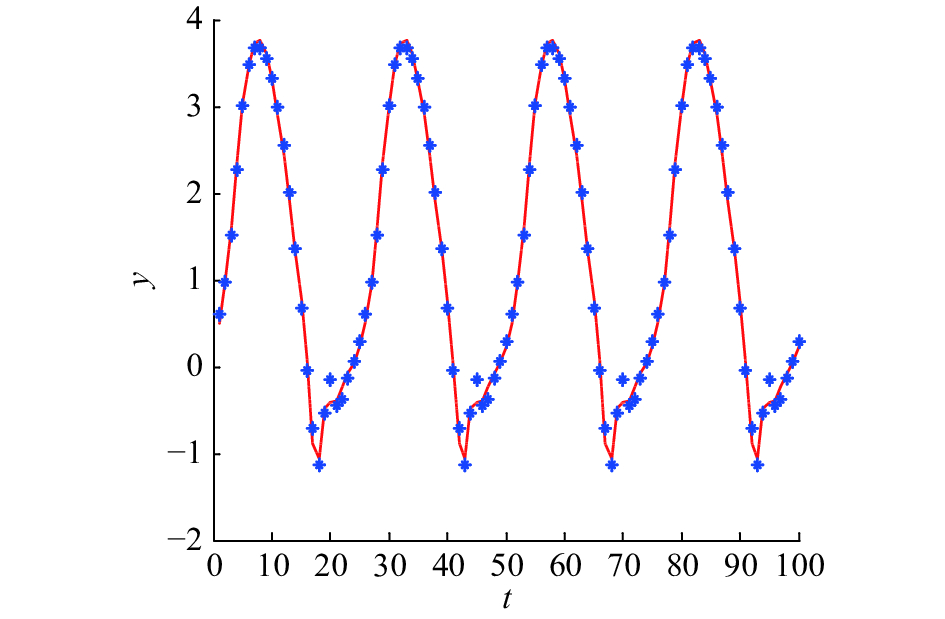
非线性动态系统辨识常被用来验证所设计的神经网络的性能，文中的非线性系统由式(34)表示：

$y\left( {t + 1} \right) = \frac{{y\left( t \right)y\left( {t - 1} \right)\left( {y\left( t \right) + 2.5} \right)}}{{1 + {y^2}\left( t \right) + {y^2}\left( {t - 1} \right)}} + u\left( t \right)$

(36)

式中： $u\left( t \right) = \sin \left( {2{{\text{π}}}t/25} \right),t \in [1,400],y(0) = 0,y(1) = 0$ 。选取100个点作为训练样本，其中 $t \in [1,100]$ ，另外选取100个点作为测试样本，其中 $t \in [301,400]$ ，训练的期望均方误差MSE设为0.01，神经元活性阈值V设为0.33。FDC-RBF网络的辨识结果如图6所示，其中用改进的二阶算法训练的神经网络学习性能曲线如图7所示，隐含层神经元个数的变化如图8所示。

由图6可以看出，FDC-RBF网络能够较好地辨识该非线性系统。同时，从图7的学习性能曲线变化可以看到，训练过程中，当迭代到第8步后网络完全收敛，由此可以看出，所设计网络的收敛速度非常快。

此外，本文还将FDC-RBF网络的非线性系统辨识结果与其他算法进行了对比，结果如表2所示。

从对比结果可以看出，与其他网络相比，FDC-RBF网络的训练时间要优于其他网络。同时，即使在期望的训练误差设为0.01的情况下，测试误差仍然能达到0.009 6，由此可以看到，该网络的辨识效果要好于其他网络。虽然隐含层神经元个数要多于SORBF和ART-RBF，但网络结构却仍然要比GAP-RBF与DFNN精简。由此可以得出，在用FDC-RBF神经网络进行非线性动态系统辨识时，能够在保证结构精简的前提下用较快的时间达到最好的泛化能力。

4 结束语

针对RBF网络的结构设计问题，本文将快速密度聚类算法进行了相应改进，在保证神经元活性的前提下通过寻找局部密度值较大的点来确定神经网络结构；同时，基于结构设计所确定的初始参数，用改进的二阶梯度算法对所设计的神经网络进行训练；最后，通过非线性函数逼近和非线性系统辨识两个基准实验进行仿真验证得到以下结论：

1)文中提出的RBF网络结构设计算法不依赖于全部的训练样本，能够根据实际任务自适应调整网络结构；

2)通过保证神经元活性和寻求密度最大的点作为隐含层神经元，最终获得的RBF神经网络结构精简且泛化能力好；

3)结合结构设计中所确定的初始参数，用改进的二阶梯度算法训练神经网络，大大提高了收敛速度，缩短了训练时间。

尽管FDC-RBF网络在非线性函数逼近和非线性系统动态辨识中取得了较好的效果，但其解决实际问题的能力还有待进一步验证。