2. 青岛大学 自动化与电气工程学院,山东 青岛 266071
2. School of Automation and Electrical Engineering, Qingdao University, Qingdao 266071, China
近几年,由于多智能体系统一致性问题在机器人编队问题[1]、群集运动问题[2]等方面得到广泛应用,这一问题成为了当前控制领域的研究重点。一致性控制就是设计一个一致性协议使得所有智能体的状态渐近达到一个共同的值。许多学者已经研究了在拓扑网络、非线性、时滞等约束条件下,以一阶、二阶或高阶动力学方程为模型的多智能体系统的一致性问题[3-7]。
用基于事件触发控制代替时间触发控制具有十分重要的意义[8]。通过与时间触发控制的比较发现,基于事件触发控制在减少通信次数方面具有明显的优点,在多数情况下,基于事件触发控制要优于传统的时间触发控制[9]。2013年,X.Y.Meng等[10]在固定拓扑网络下针对特定事件设计了一致性协议来探索多智能体系统的一致性问题,随后又提出了在切换拓扑网络下的基于事件的一致性协议。2014年,王航飞等[1]将基于事件触发控制应用到了环形编队问题中;2016年,K.Liu等[11]基于一致性理论研究成果研究了一阶和二阶多智能体系统在有向图下基于事件的包容控制问题,基于一定的事件,智能体决定何时传递状态给它的邻居,并且利用这些采样状态设计了分布式协议,从而使得跟随者最终收敛到领导者所形成的凸包中;Y.Fan等[12]对进行周期采样的多智能体系统设计了基于事件一致性协议,并且在此基础上设计了自触发一致性协议来减少通信次数和采样次数;2017年,W.Zhu等[13]研究了二阶多智能体系统在离散时间情况下的基于事件触发控制的一致性问题,通过自触发方式避免了观察智能体及其邻居在所有离散时刻的状态;文献[14]针对二阶多智能体系统提出了基于事件触发控制的一致性协议,对固定有向拓扑网络下的系统一致性问题进行了分析;2013年,胡春健[15]采用事件驱动控制方法,研究了一类一般线性多智能体系统的一致性问题,研究方法上不再要求拉普拉斯矩阵具有对称性,并获得了一类线性多智能体系统达到一致的充分条件;2016年,D.P.Yang等[16]研究了一般线性多智能体系统在有向图中的基于事件触发控制的一致性问题,基于状态反馈,采用分布式事件触发一致性协议使得所有智能体都实现了一致性,不需要智能体之间进行连续通信;文献[17]研究了一般线性模型多智能体系统在基于事件触发情况下的采样数据一致性问题,分别设计了固定和切换拓扑情况下的分布式事件触发策略。
虽然利用一阶邻居信息研究多智能体系统的一致性较为普遍,但由于系统的复杂性,为了提高系统的收敛速率,许多学者开始利用二阶邻居信息对多智能体系统的一致性问题进行研究。2010年,D.Yuan等[18]研究了一阶多智能体系统利用二阶邻居信息来加速分布式平均一致性的问题,解决了在离散和连续时间情况下的加速平均一致性问题,并发现了利用二阶邻居信息要比只使用一阶邻居信息的协议收敛速度快;不同于Z.Liu等[19]在2010年利用全局信息对多智能体系统的一致性进行研究的结果,文中只需要利用一阶和二阶邻居信息来研究一阶多智能体系统的一致性问题,结合二阶邻居信息和事件触发条件,通过对一阶多智能体系统加速平均一致性问题的研究来提高网络收敛速度;2017年,王康等[20]为了研究一阶多智能体系统的一致性特点及能控、能观性保持策略,分析了具有时变拓扑结构的多智能体系统在一阶邻居和二阶邻居协议下的一致性速度,并且得出了系统在二阶邻居协议下具有更快的收敛速度的结论;2014年,H.Pan等[21]证明了在二阶动力学方程下利用二阶邻居信息并不一定能够加速一致性速度,一致性速度还和二阶邻居协议的参数有关系。
本文将针对一类一阶多智能体系统的一致性问题展开研究,通过合理设计事件触发条件和一致性协议得到事件触发时刻序列,并获得使系统达到一致性的条件。本文采用的是文献[10]中的研究模型。
1 准备知识 1.1 代数图论令
考虑具有n个智能体的多智能体系统,且该系统由无向图
| ${\dot x_i}(t) = {u_i}(t),\,\, i = 1,2, \cdots ,n$ | (1) |
式中:
设智能体vi的事件触发判定条件为
| $||{e_i}(t_r^i + lh)||_2^2 \leqslant {\sigma _i}||{z_i}(t_r^i + lh)||_2^2,\,\, l = 1,2, \cdots $ | (2) |
式中:
在每个采样时刻,每个智能体都传递自己的状态信息给它的一阶邻居和二阶邻居并且也接收来自它一阶邻居和二阶邻居的状态信息用于事件检测。如果条件(2)满足,那么智能体vi不需要更新自己的控制输入;否则,vi将更新它自己的控制输入并且通知它的一阶邻居和二阶邻居利用vi当前的状态信息来更新它们的控制输入,同时将误差
| $t_{r + 1}^i = t_r^i + h\inf \{ l:||{e_i}(t_r^i + lh)||_2^2 > {\sigma _i}||{z_i}(t_r^i + lh)||_2^2\}$ |
式中:
为了减少符号的复杂程度,定义
| ${\hat x_i}(t) \buildrel \Delta \over = {x_i}(t_r^i),\;t_r^i \leqslant t < t_{r + 1}^i$ |
即通过在下一个事件出现之前都保持状态不变将离散时间信号
根据定义的符号,考虑利用二阶邻居信息构造一致性协议,由此给出下面的基于事件一致性协议:
| ${u_i}(t) = - (\sum\limits_{j \in {{\cal N}_i}} {({{\hat x}_i}(} t) - {\hat x_j}(t)) + \sum\limits_{k \in {\cal N}_i^2} {({{\hat x}_i}(} t) - {\hat x_k}(t)))$ | (3) |
暂且假设系统具有固定拓扑网络结构,由协议(3)式得到智能体vi的闭环系统为
| ${\dot x_i}(t) = - (\sum\limits_{j \in {{\cal N}_i}} {({{\hat x}_i}(} t) - {\hat x_j}(t)) + \sum\limits_{k \in {\cal N}_i^2} {({{\hat x}_i}(} t) - {\hat x_k}(t)))$ |
根据前面定义的
| $\begin{array}{c}{{\dot x}_i}(t) = - (\displaystyle\sum\limits_{j \in {{\cal N}_i}} {({x_i}(} t_r^i) - {x_j}(t_{r'}^j)) + \sum\limits_{k \in {\cal N}_i^2} {({x_i}(} t_r^i) - {x_k}(t_{r''}^k))) = \\ - \displaystyle\sum\limits_{j \in {{\cal N}_i}} {({x_i}(} t_r^i + lh) - {x_j}(t_r^i + lh)) - \\\sum\limits_{j \in {{\cal N}_i}} {({x_i}(} t_r^i) - {x_i}(t_r^i + lh)) + \displaystyle\sum\limits_{j \in {{\cal N}_i}} {({x_j}(} t_{r'}^j) - {x_j}(t_r^i + lh)) - \\\displaystyle\sum\limits_{k \in {\cal N}_i^2} {({x_i}(} t_r^i + lh) - {x_k}(t_r^i + lh)) - \\\displaystyle\sum\limits_{k \in {\cal N}_i^2} {({x_i}(} t_r^i) - {x_i}(t_r^i + lh)) + \sum\limits_{k \in {\cal N}_i^2} {({x_k}(} t_{r''}^k) - {x_k}(t_r^i + lh)) = \\ - \displaystyle\sum\limits_{j \in {{\cal N}_i}} {({x_i}(} t_r^i + lh) - {x_j}(t_r^i + lh)) - \sum\limits_{j \in {{\cal N}_i}} {({e_i}(} t_r^i + lh) - \\{e_j}(t_r^i + lh)) - \displaystyle\sum\limits_{k \in {\cal N}_i^2} {({x_i}(} t_r^i + lh) - {x_k}(t_r^i + lh)) - \\\displaystyle\sum\limits_{k \in {\cal N}_i^2} {({e_i}(} t_r^i + lh) - {e_k}(t_r^i + lh))\end{array}$ | (4) |
式中:
由式(4)可得,当
| ${\dot{x}}(t) = - ({\mathit{\boldsymbol{L}}} + {\tilde{L}}){\mathit{\boldsymbol{x}}}(rh) - ({\mathit{\boldsymbol{L}}} + {\tilde{L}}){\mathit{\boldsymbol{e}}}(rh)$ | (5) |
式中:
在无向连通图中,由于L的非对角线元素不大于零,主对角线元素大于等于零且行和为零,
引理1 对于半正定对称矩阵
| $|2{{\mathit{\boldsymbol{a}}}^{\rm{T}}}{\mathit{\boldsymbol{Ab}}}| \leqslant {{\mathit{\boldsymbol{a}}}^{\rm{T}}}{\mathit{\boldsymbol{Aa}}} + {{\mathit{\boldsymbol{b}}}^{\rm{T}}}{\mathit{\boldsymbol{Ab}}}$ |
证明 由于A是对称矩阵,所以存在正交矩阵U,使得
| ${{\mathit{\boldsymbol{a}}}^{\rm{T}}}{\mathit{\boldsymbol{Aa}}} = {{\mathit{\boldsymbol{a}}}^{\rm{T}}}{{\mathit{\boldsymbol{U}}}^{\rm{T}}}{\mathit{\boldsymbol{UA}}}{{\mathit{\boldsymbol{U}}}^{\rm{T}}}{\mathit{\boldsymbol{Ua}}} = {{\mathit{\boldsymbol{\alpha }}}^{\rm{T}}}{\mathit{\boldsymbol{\varLambda \alpha }}} = {\lambda _1}\alpha _1^2 + \cdots + {\lambda _n}\alpha _n^2$ |
记
| ${{\mathit{\boldsymbol{b}}}^{\rm{T}}}{\mathit{\boldsymbol{Ab}}} = {{\mathit{\boldsymbol{b}}}^{\rm{T}}}{{\mathit{\boldsymbol{U}}}^{\rm{T}}}{\mathit{\boldsymbol{UA}}}{{\mathit{\boldsymbol{U}}}^{\rm{T}}}{\mathit{\boldsymbol{Ub}}} = {{\mathit{\boldsymbol{\beta }}}^{\rm{T}}}{\mathit{\boldsymbol{\varLambda \beta }}} = {\lambda _1}\beta _1^2 + \cdots + {\lambda _n}\beta _n^2$ |
由于
| $\begin{array}{c}{{\mathit{\boldsymbol{a}}}^{\rm{T}}}{\mathit{\boldsymbol{Aa}}} + {{\mathit{\boldsymbol{b}}}^{\rm{T}}}{\mathit{\boldsymbol{Ab}}} = {{\mathit{\boldsymbol{\alpha }}}^{\rm{T}}}{\mathit{\boldsymbol{\varLambda \alpha }}} + {{\mathit{\boldsymbol{\beta }}}^{\rm{T}}}{\mathit{\boldsymbol{\varLambda \beta }}} = \\[3pt]{\lambda _1}\alpha _1^2 + \cdots + {\lambda _n}\alpha _n^2 + {\lambda _1}\beta _1^2 + \cdots + {\lambda _n}\beta _n^2 = \\[3pt]{\lambda _1}(\alpha _1^2 + \beta _1^2) + \cdots + {\lambda _n}(\alpha _n^2 + \beta _n^2) \geqslant \\[5pt]2({\lambda _1}|{\alpha _1}{\beta _1}| + \cdots + {\lambda _n}|{\alpha _n}{\beta _n}|) = 2|{{\mathit{\boldsymbol{\alpha }}}^{\rm{T}}}{\mathit{\boldsymbol{\varLambda \beta }}}| = \\[3pt]2|{{\mathit{\boldsymbol{a}}}^{\rm{T}}}{{\mathit{\boldsymbol{U}}}^{\rm{T}}}{\mathit{\boldsymbol{\varLambda Ub}}}| = 2|{{\mathit{\boldsymbol{a}}}^{\rm{T}}}{\mathit{\boldsymbol{Ab}}}|\end{array}$ |
考虑系统的平均状态:
| $\bar x(t) = \frac{1}{n}\sum\limits_{i = 1}^n {{x_i}} (t)$ |
在无向连通图中,
因此,
| $\delta (t) = {\mathit{\boldsymbol{x}}}(t) - \bar x(t){{\bf{1}}_n} = {\mathit{\boldsymbol{x}}}(t) - \bar x{{\bf{1}}_n}$ |
考虑李雅普诺夫函数
| $V(t) = \frac{1}{2}{{\mathit{\boldsymbol{x}}}^{\rm{T}}}(t){\mathit{\boldsymbol{x}}}(t)$ | (6) |
即状态的平方和的1/2。
引理 2 (Lasalle不变原理) 设C是有界闭集,从C内出发的系统
定理 1 设系统(1)具有连通通信拓扑,采用协议(3)的系统(1)在事件触发条件(2)的驱动下,若条件
| $0 < h \leqslant \frac{1}{{2{\lambda _n}}},0 < {\sigma _{\rm{max}}} < \frac{1}{{\lambda _n^2}}$ | (7) |
或者
| $\frac{1}{{2{\lambda _n}}} < h < \frac{3}{{4{\lambda _n}}},\;0 < {\sigma _{\rm{max}}} < \frac{{3 - 4h{\lambda _n}}}{{(4h{\lambda _n} - 1)\lambda _n^2}}$ | (8) |
成立,其中
证明 考虑函数(6)式在
| $\begin{array}{c}\dot V(t) = {{\mathit{\boldsymbol{x}}}^{\rm{T}}}(t){\dot{x}}(t) = - {{\mathit{\boldsymbol{x}}}^{\rm{T}}}(t)({\mathit{\boldsymbol{L}}} + {\tilde{L}})({\mathit{\boldsymbol{x}}}(rh) + {\mathit{\boldsymbol{e}}}(rh)) = \\[4pt](t - rh){({\mathit{\boldsymbol{x}}}(rh) + {\mathit{\boldsymbol{e}}}(rh))^{\rm{T}}}{({\mathit{\boldsymbol{L}}} + {\tilde{L}})^2}({\mathit{\boldsymbol{x}}}(rh) + {\mathit{\boldsymbol{e}}}(rh)) - \\[4pt]{{\mathit{\boldsymbol{x}}}^{\rm{T}}}(rh)({\mathit{\boldsymbol{L}}} + {\tilde{L}})({\mathit{\boldsymbol{x}}}(rh) + {\mathit{\boldsymbol{e}}}(rh)) \leqslant - {{\mathit{\boldsymbol{x}}}^{\rm{T}}}(rh)({\mathit{\boldsymbol{L}}} + \\[4pt]{\tilde{L}})({\mathit{\boldsymbol{x}}}(rh) + {\mathit{\boldsymbol{e}}}(rh)) + h{\lambda _n}{({\mathit{\boldsymbol{x}}}(rh) + {\mathit{\boldsymbol{e}}}(rh))^{\rm{T}}}({\mathit{\boldsymbol{L}}} + \\[4pt]{\tilde{L}})({\mathit{\boldsymbol{x}}}(rh) + {\mathit{\boldsymbol{e}}}(rh)) = - (1 - h{\lambda _n}){{\mathit{\boldsymbol{x}}}^{\rm{T}}}(rh)({\mathit{\boldsymbol{L}}} + {\tilde{L}}){\mathit{\boldsymbol{x}}}(rh) - \\[5pt]{{\mathit{\boldsymbol{x}}}^{\rm{T}}}(rh){\mathit{\boldsymbol{(L}}} + {\tilde{L}}){\mathit{\boldsymbol{e}}}(rh) + h{\lambda _n}{{\mathit{\boldsymbol{e}}}^{\rm{T}}}(rh)({\mathit{\boldsymbol{L}}} + {\tilde{L}}){\mathit{\boldsymbol{e}}}(rh) + \\[4pt]2h{\lambda _n}{{\mathit{\boldsymbol{x}}}^{\rm{T}}}(rh)({\mathit{\boldsymbol{L}}} + {\tilde{L}}){\mathit{\boldsymbol{e}}}(rh) = - (1 - h{\lambda _n}){{\mathit{\boldsymbol{x}}}^{\rm{T}}}(rh)({\mathit{\boldsymbol{L}}} + \\[5pt]{\tilde{L}}){\mathit{\boldsymbol{x}}}(rh) + (2h{\lambda _n} - 1){{\mathit{\boldsymbol{x}}}^{\rm{T}}}(rh)({\mathit{\boldsymbol{L}}} + {\tilde{L}}){\mathit{\boldsymbol{e}}}(rh) + \\[4pt]h{\lambda _n}{{\mathit{\boldsymbol{e}}}^{\rm{T}}}(rh)({\mathit{\boldsymbol{L}}} + {\tilde{L}}){\mathit{\boldsymbol{e}}}(rh)\end{array}$ |
应用引理 1,当
| $\begin{array}{c}\dot V(t) \leqslant - (1 - h{\lambda _n}){{\mathit{\boldsymbol{x}}}^{\rm{T}}}(rh)({\mathit{\boldsymbol{L}}} + {\tilde{L}}){\mathit{\boldsymbol{x}}}(rh) + (1 - 2h{\lambda _n})\\[5pt](\displaystyle\frac{1}{2}{{\mathit{\boldsymbol{x}}}^{\rm{T}}}(rh)({\mathit{\boldsymbol{L}}} + {\tilde{L}}){\mathit{\boldsymbol{x}}}(rh) + \displaystyle\frac{1}{2}{{\mathit{\boldsymbol{e}}}^{\rm{T}}}(rh)({\mathit{\boldsymbol{L}}} + {\tilde{L}}){\mathit{\boldsymbol{e}}}(rh)) + \\[5pt]h{\lambda _n}{{\mathit{\boldsymbol{e}}}^{\rm{T}}}(rh)({\mathit{\boldsymbol{L}}} + {\tilde{L}}){\mathit{\boldsymbol{e}}}(rh) = - \displaystyle\frac{1}{2}{{\mathit{\boldsymbol{x}}}^{\rm{T}}}(rh)({\mathit{\boldsymbol{L}}} + {\tilde{L}}){\mathit{\boldsymbol{x}}}(rh) + \\[5pt]\displaystyle\frac{1}{2}{{\mathit{\boldsymbol{e}}}^{\rm{T}}}(rh)({\mathit{\boldsymbol{L}}} + {\tilde{L}}){\mathit{\boldsymbol{e}}}(rh)\end{array}$ |
结合事件触发条件(2)得到
| $\begin{array}{c}\dot V(t) \leqslant - \displaystyle\frac{1}{2}{{\mathit{\boldsymbol{x}}}^{\rm{T}}}(rh)({\mathit{\boldsymbol{L}}} + {\tilde{L}}){\mathit{\boldsymbol{x}}}(rh) + \displaystyle\frac{1}{2}\lambda _n^2{\sigma _{\rm{max}}}{{\mathit{\boldsymbol{x}}}^{\rm{T}}}(rh)\\[5pt]({\mathit{\boldsymbol{L}}} + {\tilde{L}}){\mathit{\boldsymbol{x}}}(rh) = - \displaystyle\frac{1}{2}(1 - \lambda _n^2{\sigma _{\rm{max}}}){{\mathit{\boldsymbol{x}}}^{\rm{T}}}(rh)({\mathit{\boldsymbol{L}}} + {\tilde{L}}){\mathit{\boldsymbol{x}}}(rh)\end{array}$ |
当式(7)成立时,有
当
| $\begin{array}{c}\dot V(t) \leqslant - (1 - h{\lambda _n}){{\mathit{\boldsymbol{x}}}^{\rm{T}}}(rh)({\mathit{\boldsymbol{L}}} + {\tilde{L}}){\mathit{\boldsymbol{x}}}(rh) + (2h{\lambda _n} - 1)\\[5pt](\displaystyle\frac{1}{2}{{\mathit{\boldsymbol{x}}}^{\rm{T}}}(rh)({\mathit{\boldsymbol{L}}} + {\tilde{L}}){\mathit{\boldsymbol{x}}}(rh) + \displaystyle\frac{1}{2}{{\mathit{\boldsymbol{e}}}^{\rm{T}}}(rh)({\mathit{\boldsymbol{L}}} + {\tilde{L}}){\mathit{\boldsymbol{e}}}(rh)) + \end{array}$ |
| $\begin{array}{c}h{\lambda _n}{{\mathit{\boldsymbol{e}}}^{\rm{T}}}(rh)({\mathit{\boldsymbol{L}}} + {\tilde{L}}){\mathit{\boldsymbol{e}}}(rh) = (2h{\lambda _n} - \displaystyle\frac{3}{2}){{\mathit{\boldsymbol{x}}}^{\rm{T}}}(rh)({\mathit{\boldsymbol{L}}} + \\[5pt]{\tilde{L}}){\mathit{\boldsymbol{x}}}(rh) + (2h{\lambda _n} - \displaystyle\frac{1}{2}){{\mathit{\boldsymbol{e}}}^{\rm{T}}}(rh)({\mathit{\boldsymbol{L}}} + {\tilde{L}}){\mathit{\boldsymbol{e}}}(rh)\end{array}$ |
结合事件触发条件(2)得到
| $\begin{array}{c}\dot V(t) \leqslant (2h{\lambda _n} - \displaystyle\frac{3}{2}){{\mathit{\boldsymbol{x}}}^{\rm{T}}}(rh)({\mathit{\boldsymbol{L}}} + {\tilde{L}}){\mathit{\boldsymbol{x}}}(rh) + \\[5pt](2h{\lambda _n} - \displaystyle\frac{1}{2})\lambda _n^2{\sigma _{max}}{{\mathit{\boldsymbol{x}}}^{\rm{T}}}(rh)({\mathit{\boldsymbol{L}}} + {\tilde{L}}){\mathit{\boldsymbol{e}}}(rh) = \\[5pt](2h{\lambda _n} - \displaystyle\frac{3}{2} + (2h{\lambda _n} - \displaystyle\frac{1}{2})\lambda _n^2{\sigma _{max}}){{\mathit{\boldsymbol{x}}}^{\rm{T}}}(rh)({\mathit{\boldsymbol{L}}} + {\tilde{L}}){\mathit{\boldsymbol{x}}}(rh)\end{array}$ |
当式(8)成立时,有
由于G为连通图,
采样周期h和
| $0 < {\sigma _{\rm{max}}} < \frac{1}{{4{{(n - 1)}^2}}},\;0 < h < \frac{1}{{4(n - 1)}}。$ |
可以通过一个公共标量α,
在这部分中,将固定拓扑网络下的研究结果扩展到了G在连通图之间切换的情况,假定所有可能的连通图构成有限集
在切换拓扑情况下,根据(2)式和(3)式类似地定义事件触发条件和基于事件的一致性协议。在切换拓扑情形下,李雅普诺夫函数不变,仍是
定理 2 设系统(1)式的通信拓扑网络在有限个连通图之间进行切换,采用协议(3)式的系统(1)式在事件触发条件(2)式的驱动下,若满足下列条件
| $0 < h \leqslant \frac{1}{{2{\lambda _{\rm{max}}}}},\;0 < {\sigma _{\rm{max}}} < \frac{1}{{\lambda _{\rm{max}}^2}}$ |
或者
| $\frac{1}{{2{\lambda _{\rm{max}}}}} < h < \frac{3}{{4{\lambda _{\rm{max}}}}},\;0 < {\sigma _{\rm{max}}} < \frac{{3 - 4h{\lambda _{\rm{max}}}}}{{(4h{\lambda _{\rm{max}}} - 1)\lambda _{\rm{max}}^2}},$ |
其中
证明 类似于定理1的证明过程得到李雅普诺夫函数在区间
| $\dot V(t) = - {{\mathit{\boldsymbol{x}}}^{\rm{T}}}(t){({\mathit{\boldsymbol{L}}} + {\tilde{L}})_{s(rh)}}({\mathit{\boldsymbol{x}}}(rh) + {\mathit{\boldsymbol{e}}}(rh))$ |
若
| $0 < {\sigma _{\rm{max}}} <\displaystyle\frac{{3 - 4h{\lambda _n}({G_{s({{rh}})}})}}{{(4h{\lambda _n}({G_{s({{rh}})}}) - 1)\lambda _n^2({G_{s({{rh}})}})}} $ |
那么类似于固定拓扑情况,有
| $\lambda _n^2({G_{s(rh)}}){\sigma _{\rm{max}}}){{\mathit{\boldsymbol{x}}}^{\rm{T}}}(rh){({\mathit{\boldsymbol{L}}} + {\tilde{L}})_{s(rh)}}{\mathit{\boldsymbol{x}}}(rh)$ |
式中:
因为系统在有限个连通图之间切换,可得集合
通过与文献[10]的比较发现:即使多智能体系统(1)只采用一阶邻居信息用于研究系统的一致性收敛问题,与文献[10]的采样周期
在理论分析的基础上,本部分将通过仿真实验对所得出的理论结果进行验证。
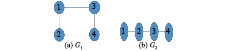
考虑由4个智能体组成的多智能体系统,为了便于比较,采用与文献[10]相同的通信拓扑和参数。图1是无向连通图,其利用二阶邻居信息所得的拉普拉斯矩阵为
| ${\mathit{\boldsymbol{L}}} + {\tilde{L}} = \left[ {\begin{array}{*{20}{c}}3 & { - 1} & { - 1} & { - 1}\\{ - 1} & 3 & { - 1} & { - 1}\\{ - 1} & { - 1} & 3 & { - 1}\\{ - 1} & { - 1} & { - 1} & 3\end{array}} \right]$ |
拉普拉斯矩阵的最大特征值
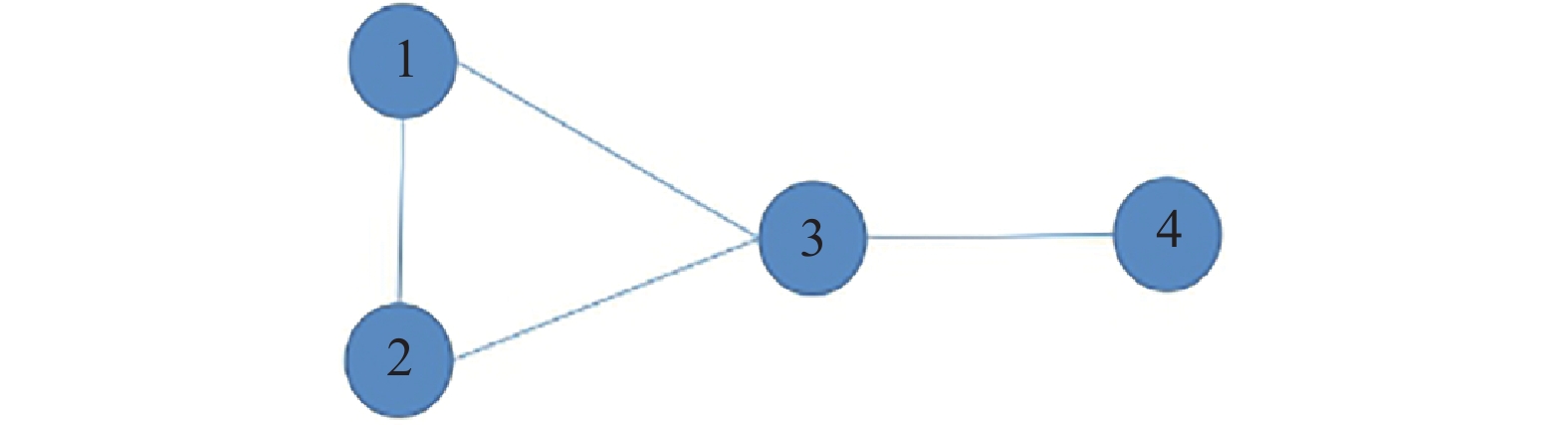
|
图 1 通信拓扑图 Fig.1 Communication topology |
图2是所有智能体在基于事件一致性协议(3)下的状态演变,从图2可以看出系统达到了一致,所有智能体的状态趋于一个共同的值。
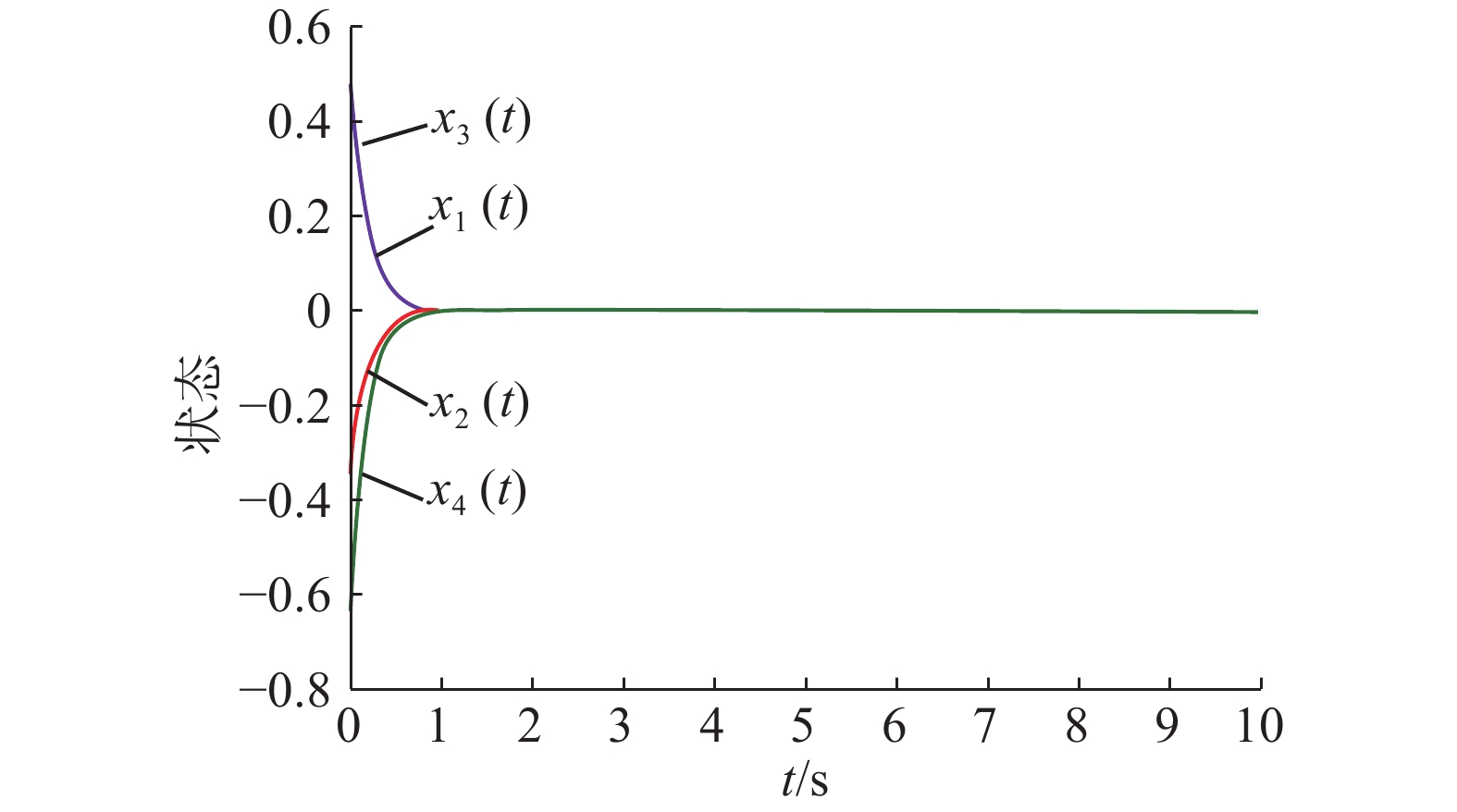
|
图 2 智能体的状态 Fig.2 States of the agents |
图3是所有智能体在基于事件一致性协议(3)下的非一致向量

|
图 3 非一致向量范数 Fig.3 Norm of the disagreement vector |
图4是所有智能体在基于事件一致性协议(3)下的控制输入的仿真结果,最终所有智能体的控制输入都趋于0。
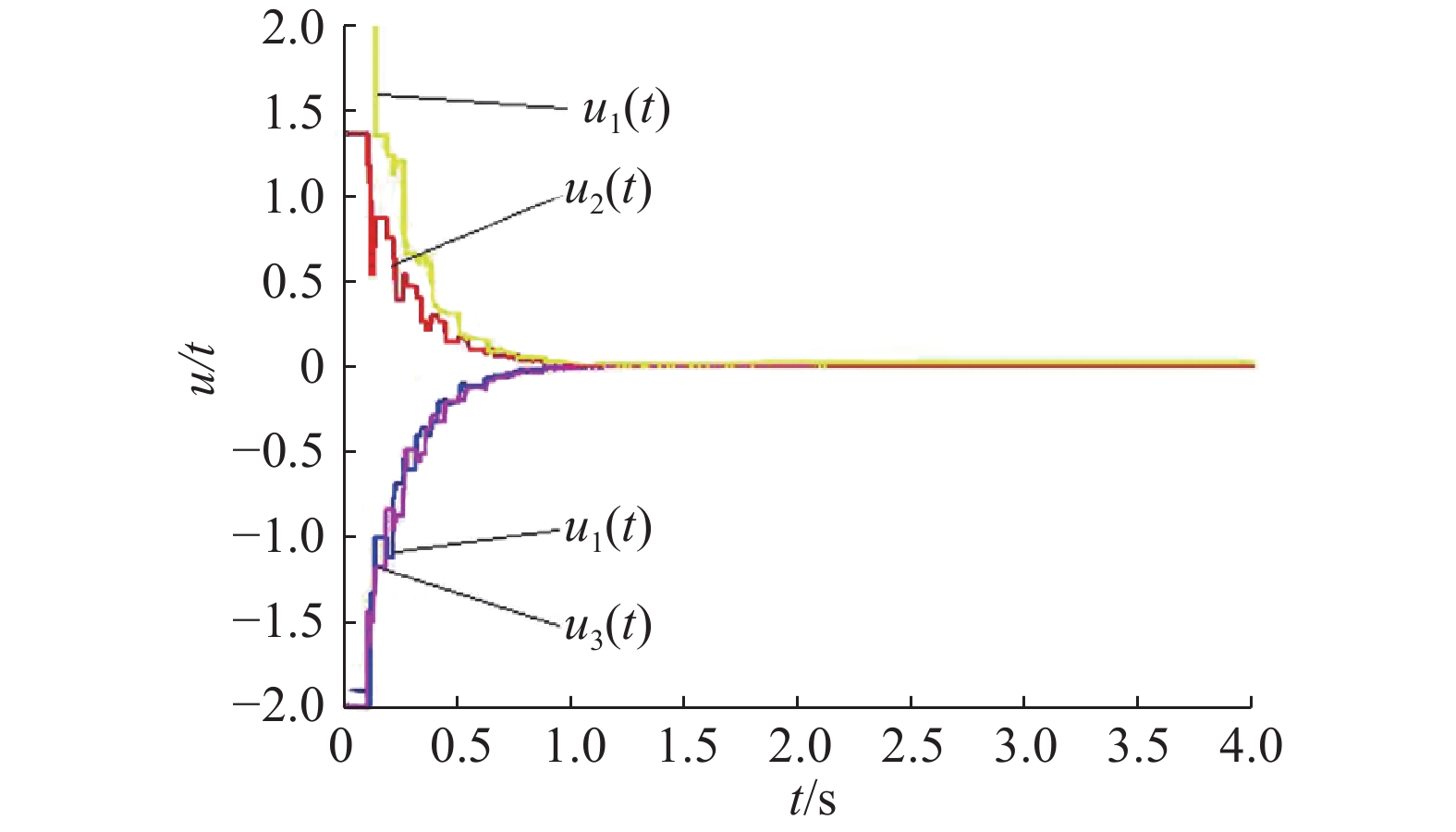
|
图 4 智能体的控制输入 Fig.4 Control inputs for the agents |
图5是所有智能体在基于事件一致性协议(3)下的事件触发时刻,说明只在特定时刻对智能体施加控制输入系统就能实现一致性。
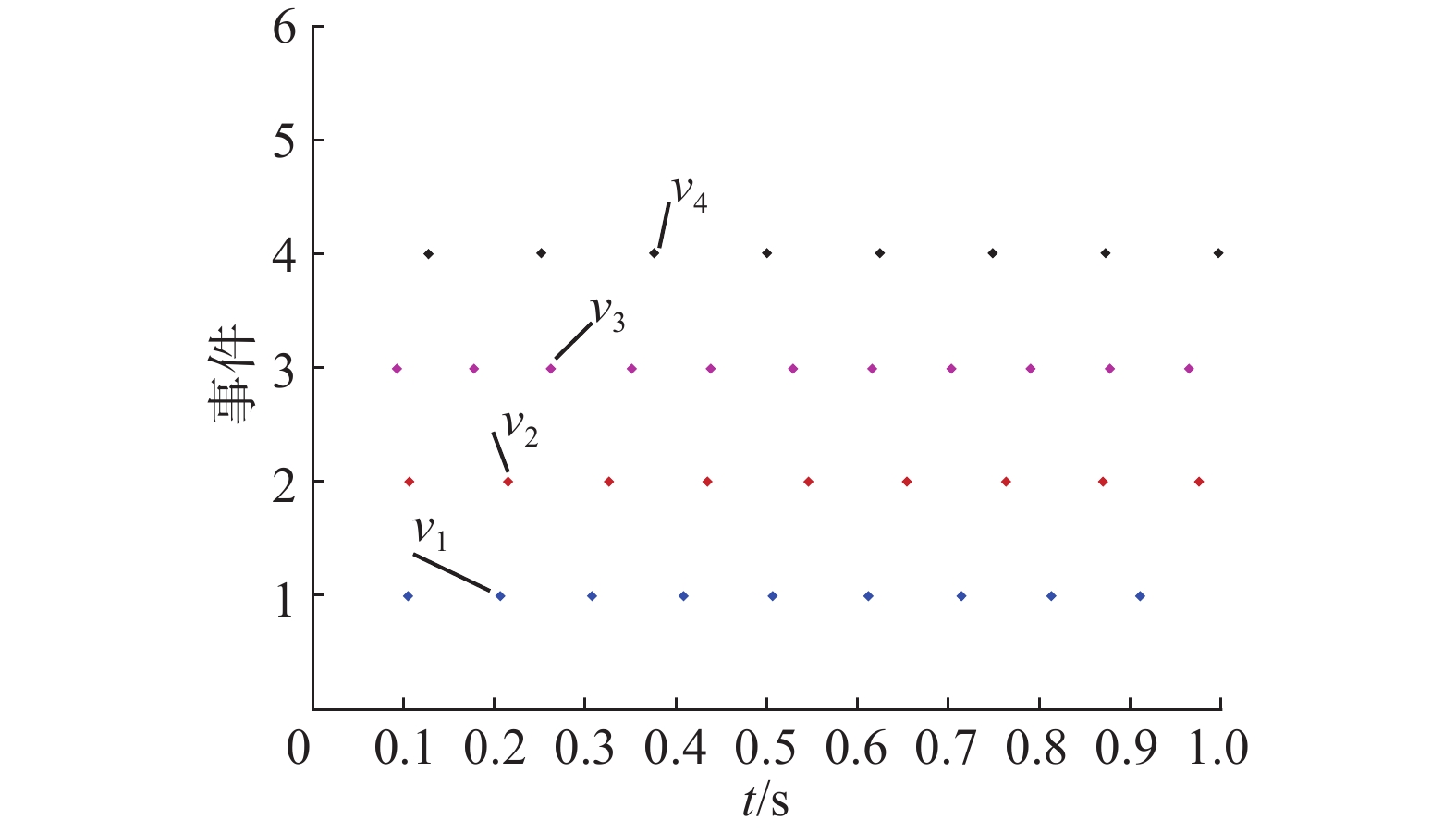
|
图 5 智能体的事件触发时刻 Fig.5 Event times for the agents |
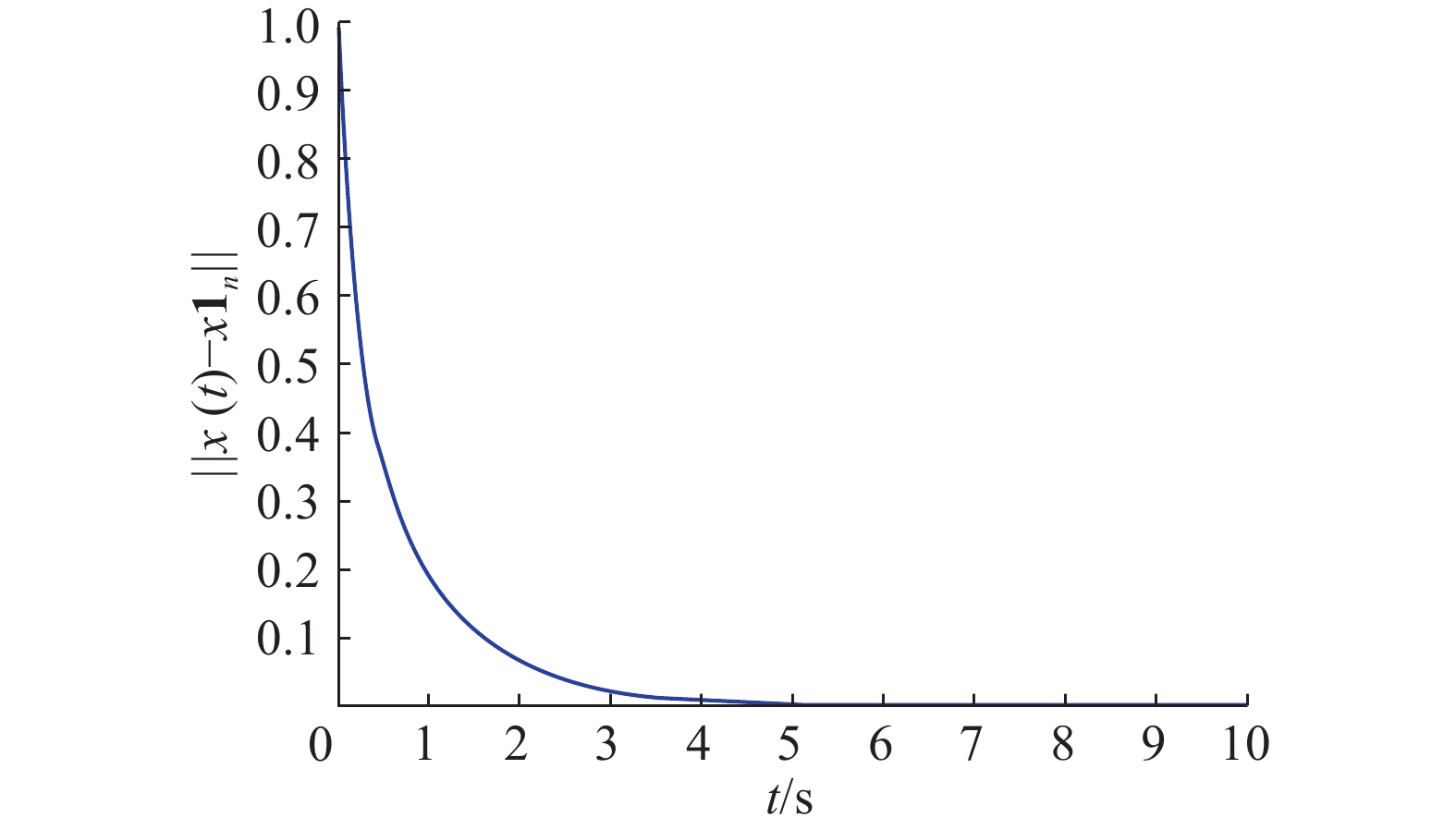
图6和图7分别是文献[7]中所有智能体利用一阶邻居信息在基于事件一致性协议下的状态和非一致向量

|
图 6 智能体的状态 Fig.6 States of the agents |
|
图 7 非一致向量范数 Fig.7 Norm of the disagreement vector |
从图2可以看出所有智能体大约在t=1 s这一时刻收敛到了相同的值,从图6可以看出所有智能体大约在t=3 s这一时刻收敛到了相同的值,通过比较可以发现利用二阶邻居信息之后所有智能体的状态达到一致性的速度更快。同样通过比较非一致性向量范数,我们发现图3在利用了二阶邻居信息之后所有智能体的状态趋于它们的初始状态平均值的速度明显比图7只利用一阶邻居信息时所有智能体的状态趋于它们的初始状态平均值的速度快。
下面给出在切换拓扑网络下的仿真实验。
考虑由4个智能体组成的多智能体系统在图G1和图G2之间进行切换,切换时刻是随机的,如图8所示。取智能体的事件检测器的参数为
|
图 8 切换拓扑图 Fig.8 Switching topology |
图9是所有智能体在基于事件一致性协议(3)下的状态演变,可以看出在切换拓扑网络下所有智能体的状态仍可以收敛到一个相同的值。

|
图 9 智能体的状态 Fig.9 States of the agents |
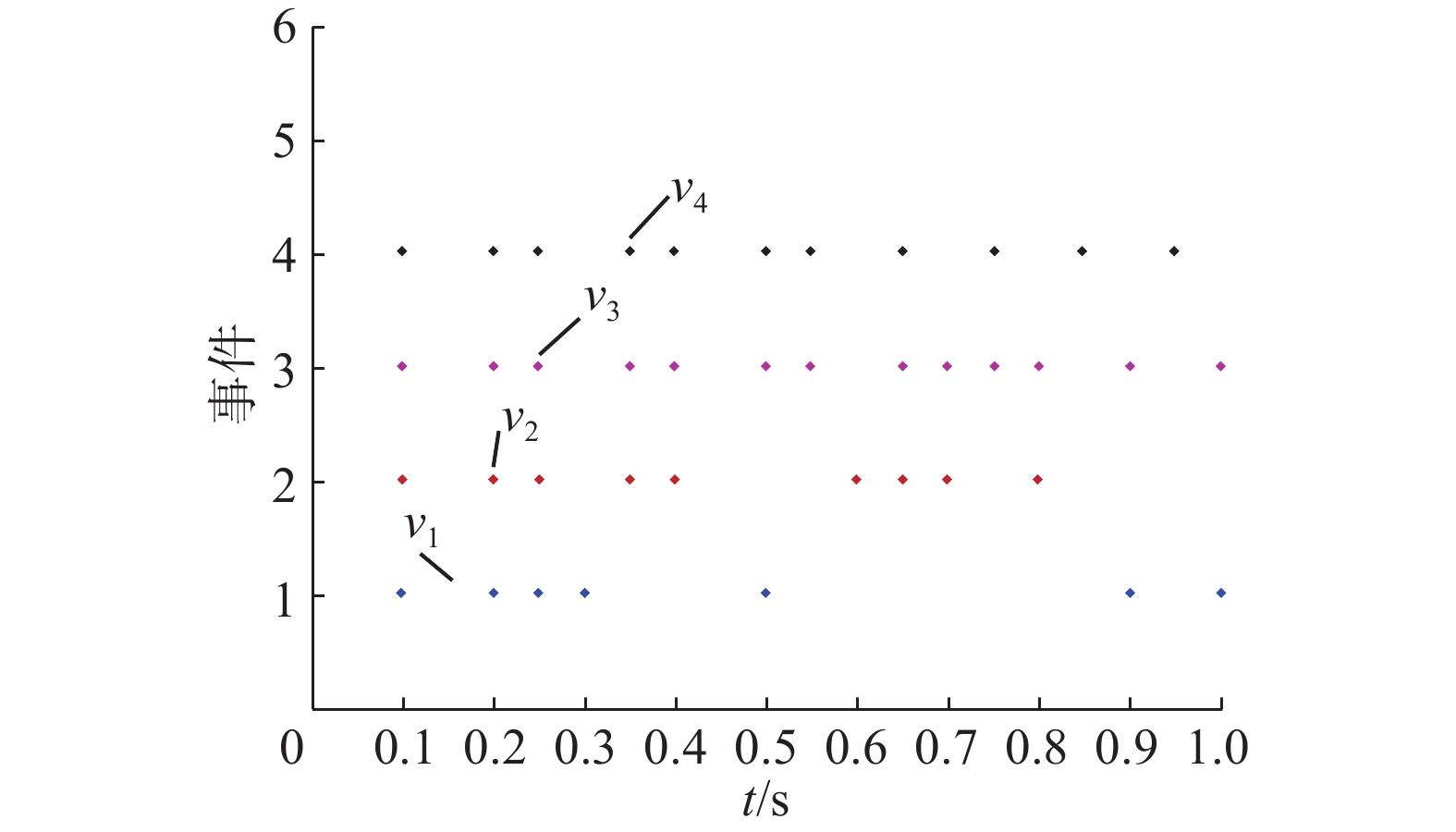
图10是所有智能体在基于事件一致性协议(3)下的事件触发时刻。
|
图 10 智能体的事件触发时刻 Fig.10 Event times for the agents |
本文首先在特定事件条件下利用二阶邻居信息设计了一阶多智能体系统在固定拓扑网络下的一致性协议,利用李雅普诺夫函数,设计采样数据事件检测器使状态渐近收敛到它们的初始状态平均值,发现多智能体系统利用二阶邻居信息能够加快一致性收敛速度。在固定拓扑网络研究结果的基础上,同样给出在切换拓扑网络下的基于事件一致性结果,最后利用仿真加以说明。以后将在二阶动力学方程下利用特定的事件触发条件来研究多智能体系统的一致性问题。
| [1] |
王航飞, 禹梅, 谢广明. 基于事件驱动的环形编队多智能体系统[J]. 系统科学与数学, 2014, 34(7): 815-827. WANG Hangfei, YU Mei, XIE Guangming. Event-driven circle formation control for multi-agent systems[J]. Journal of systems science and mathematical sciences, 2014, 34(7): 815-827. (  0) 0)
|
| [2] |
庄昊, 杨洪勇. 联合连通拓扑下的二阶多自主体系统有限时间包容控制[J]. 智能系统学报, 2017, 12(2): 188-195. ZHUANG Hao, YANG Hongyong. Finite-time containment control of second-order multi-agent systems with jointly connected topologies[J]. CAAI transactions on intelligent systems, 2017, 12(2): 188-195. (  0) 0)
|
| [3] |
OLFATI-SABER R, MURRAY R M. Consensus problems in networks of agents with switching topology and time-delays[J]. IEEE transactions on automatic control, 2004, 49(9): 1520-1533. ( 0) 0)
|
| [4] |
俞辉, 蹇继贵, 王永骥. 多智能体时滞网络的加权平均一致性[J]. 控制与决策, 2007, 22(5): 558-561. YU Hui, JIAN Jigui, WANG Yongji. Weighted average consensus for networks of multi-agent with time -delays[J]. Control and decision, 2007, 22(5): 558-561. (  0) 0)
|
| [5] |
GUO Meng, D V DIMAROGONAS. Nonlinear consensus via continuous, sampled, and aperiodic updates[J]. International journal of control, 2013, 86(4): 567-578. ( 0) 0)
|
| [6] |
LI Hongjie, ZHU Yinglian, WANG Jietai, et al. Consensus of nonlinear second-order multi-agent systems with mixed time-delays and intermittent communications[J]. Neurocomputing, 2017, 251(16): 115-126. ( 0) 0)
|
| [7] |
REZAEEA H, ABDOLLAHIA F. Discrete-time consensus strategy for a class of high-order linear multiagent systems under stochastic communication topologies[J]. Journal of the franklin institute, 2017, 354(9): 3690-3705. ( 0) 0)
|
| [8] |
LUNZE J, LEHMANN D. A state-feedback approach to event-based control[J]. Automatica, 2010, 46(1): 211-215. ( 0) 0)
|
| [9] |
MENG Xiangyu, CHEN Tongwen. Optimal sampling and performance comparison of periodic and event based impulse control[J]. IEEE transactions on automatic control, 2012, 57(12): 3252-3259. ( 0) 0)
|
| [10] |
MENG Xiangyu, CHEN Tongwen. Event based agreement protocols for multi-agent networks[J]. Automatica, 2013, 49(7): 2125-2132. ( 0) 0)
|
| [11] |
LIU Kaien, JI Zhijian, XIE Guangming, et al. Event-based broadcasting containment control for multi-agent systems under directed topology[J]. International journal of control, 2016, 89(11): 2360-2370. ( 0) 0)
|
| [12] |
FAN Yuan, YANG Yong, ZHANG Yang. Sampling-based event-triggered consensus for multi-agent systems[J]. Neurocomputing, 2016, 191: 141-147. ( 0) 0)
|
| [13] |
ZHU Wei, PU Huizhu, WANG Dandan, et al. Event-based consensus of second-order multi-agent systems with discrete time[J]. Automatica, 2017, 79: 78-83. ( 0) 0)
|
| [14] |
黄红伟, 黄天民. 基于事件触发的二阶多智能体领导跟随一致性[J]. 控制与决策, 2016, 31(5): 835-841. HUANG Hongwei, HUANG Tianmin. Leader-following consensus of second-order multi-agent systems via event- triggered control[J]. Control and decision, 2016, 31(5): 835-841. (  0) 0)
|
| [15] |
胡春健. 基于事件驱动的一般线性多智能体系统的一致性[J]. 重庆邮电大学学报: 自然科学版, 2013, 25(4): 549-562. HU Chunjian. Event-based consensus of general linear multi-agent systems[J]. Journal of chongqing university of posts and telecommunications: Natural science edition, 2013, 25(4): 549-562. (  0) 0)
|
| [16] |
YANG Dapeng, REN Wei, LIU Xiaodong, et al. Decentralized event-triggered consensus for linear multi-agent systems under general directed graphs[J]. Automatica, 2016, 69: 242-249. ( 0) 0)
|
| [17] |
张协衍. 网络化多智能体系统的一致性研究[D]. 长沙: 湖南大学, 2015: 75-102. ZHANG Xieyan. Consensus problem of network multi-agent systems[D]. Changsha: Hunan university, 2015: 75-102. (  0) 0)
|
| [18] |
YUAN Deming, XU Shengyuan. Accelerating distributed average consensus by exploring the information of second-order neighbors[J]. Physics letters A, 2010, 374(24): 2438-2445. ( 0) 0)
|
| [19] |
LIU Zhongxin, CHEN Zengqiang. Event-triggered average-consensus for multi-agent systems[J]. Proceedings of the 29th chinese control conference, 2010, 57(12): 4506-4511. ( 0) 0)
|
| [20] |
王康, 纪志坚, 晁永翠. 二阶邻居协议下多智能体系统能控能观性保持[J]. 智能系统学报, 2017, 12(02): 213-220. WANG Kang, JI Zhijian, CHAO Yongcui. A control Strategy for maitaining controllability and observability of a multi-agent system with the second-order neighborhood protocol[J]. CAAI transactions on intelligent systems, 2017, 12(02): 213-220. (  0) 0)
|
| [21] |
PAN Huan, NIAN Xiaohong. Second-order consensus in multi-agent systems based on second-order neighbours’information[J]. International journal of systems science, 2014, 45(5): 902-914. ( 0) 0)
|
| [22] |
HORN R A , JOHNSON C R. Matrix analysis[M]. Cambridge university press, 2012: 344.
( 0) 0)
|
 2017, Vol. 12
2017, Vol. 12


