近年来，智能移动机器人技术得到迅速发展，已广泛应用于工业、军事、物流、办公和家庭服务等领域^[1-2]。智能移动机器人在环境中自主运行，通常需要搭载激光雷达、GPS、声呐、单目或双目视觉设备等以获取环境信息，辅助移动机器人进行自主定位、建图、环境探测等任务^[3-4]。然而，采用大量传感器虽然可以提高系统的精度和鲁棒性，但也显著提高了机器人硬件和软件系统的复杂性以及成本，限制了移动机器人的进一步推广应用^[5]。为此，建立一个硬件结构简单、性能良好、经济性和通用性好的移动机器人系统，成为一个迫切需要解决的问题。

随着计算机视觉技术的进步，单目或双目视觉设备成为移动机器人的一种选择^[6-7]。RGB-D传感器能同时获取色彩与深度信息，易安装使用，成本低，被广泛应用于目标识别、跟踪等领域^[8-9]，利用RGB-D传感器进行SLAM的研究迅速发展。美国华盛顿大学与德国弗莱堡大学各自实现了基于RGB-D传感器的SLAM系统^[10-11]，利用图像特征估计图像间的变换关系，并利用ICP (iterative closest point)等算法优化。卡耐基梅隆大学开发出利用多边形重构和融合算法，在原始数据中提取平面特征，显著提高了算法的实时性^[12]。2007年Klein等^[13]首次提出了并行跟踪与建图算法PTAM (parallel tracking and mapping)，关键帧以及多线程处理方法被广泛采用。ORB-SLAM算法由西班牙萨拉戈萨大学Raul Mur-Artal等^[14]提出，由跟踪、局部建图和闭环检测3个并行线程组成，具备重新定位能力，取得了良好的稳定性、鲁棒性和实时性^[15]。

国内基于RGB-D信息的研究也迅猛发展。清华大学孙富春教授^[8-9]团队利用Kinect传感器和RGB-D信息完成了场景建模、机器人自主导航和人机协作等工作。北京工业大学贾松敏教授团队^[16]，通过提取Kinect RGB信息的特征点进行粗匹配，并结合深度信息，通过迭代最近点算法实时获取位姿，采用关键帧选取机制及线程并行处理的方法，提高了算法运行效率。上海交通大学曹其新教授团队^[17]，从两个方面对Kinect Fusion算法进行改进提高，通过使用环境中的边线特征点匹配提高了算法的定位鲁棒性，并通过在点云模型中预设地面点云提高了算法精度。第二炮兵工程大学张国良教授课题组^[18]提出了一种基于快速视觉里程计及大回环局部优化模型，提高配准精度并实现对累积误差快速优化的同步定位与三维点云地图创建方法。

本文使用基础运动底盘，搭载通用RGB-D传感器，通过开发整合相应算法，建立了一个硬件结构简单、易开发维护的自主移动机器人系统，实现了自主定位、障碍规避、运动规划与控制等功能。

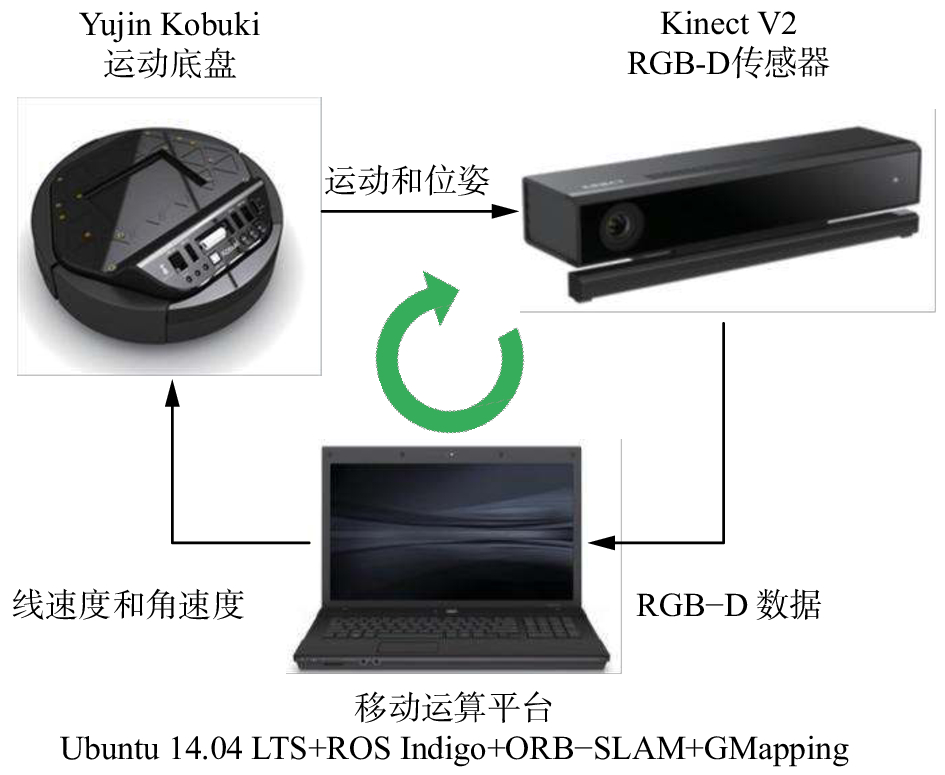
1 硬件平台与系统架构

本文建立的移动机器人系统由一个运动底盘、一个RGB-D传感器和一个移动运算平台组成，如图1所示。Yujin Kobuki运动底盘由两轮差速驱动，最大线速度可达70 cm/s，最大旋转速度为180 (°)/s，最大运载能力5 kg。采用Kinect V2传感器，TOF(time of flight)测量，水平可视角度为70.6°，垂直可视角度为60°，最大探测距离为8 m，最小探测距离为0.5 m，探测精度为2 cm。采用惠普ENVY 15-j105tx作为移动运算平台，配备了core i7 4 702 m中央处理器以及8 GB运行内存。基于Ubuntu 14.04 LTS操作系统，安装配置了机器人操作系统ROS Indigo、libfreenect2、PCL、OpenCV以及不莱梅大学提供的Kinect V2的ROS驱动等基础工具包^[19]。在此环境下，可方便地开发后续的移动机器人自主定位、障碍物检测规避与运动控制等算法。

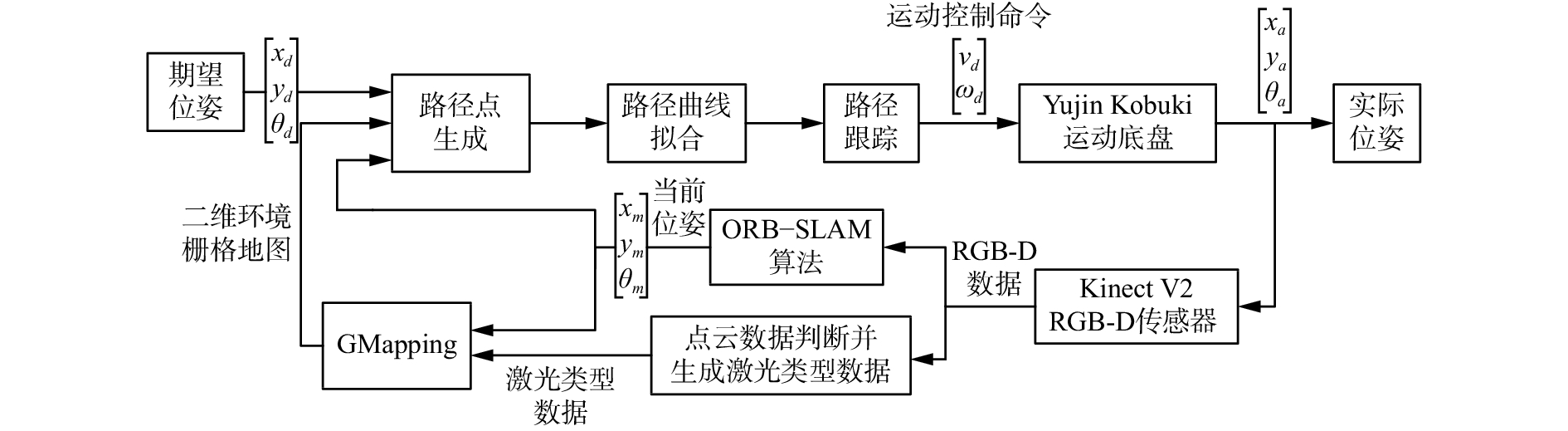
本文的移动机器人工作流程如图2所示，主要包括以下功能单元。

1)实时定位：根据Kinect V2获取的环境RGB-D信息，利用ORB-SLAM算法计算当前位姿。

2)环境地图创建：结合Kinect V2点云信息和当前位姿，利用GMapping建立二维栅格地图。

3)路径点生成：利用栅格地图，结合定位信息，利用改进人工势场法规划运动路径点。

4)路径曲线拟合：根据规划的路径点，利用二次规划进行曲线拟合，获得可解析的路径曲线。

5)路径跟踪：根据路径曲线，考虑运动约束，生成控制量，控制移动机器人运动。

2 主要研究方法 2.1 基于ORB-SLAM的实时定位

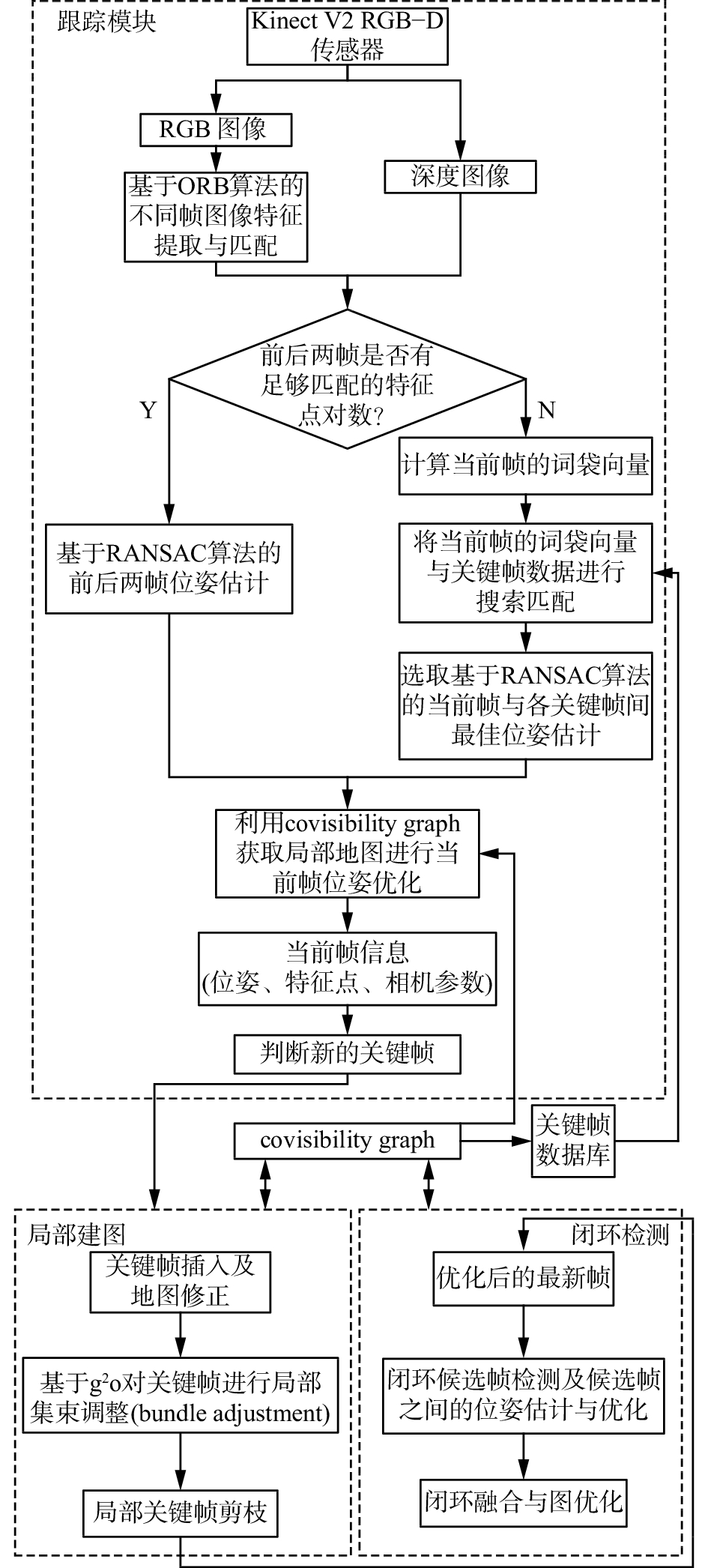
基于采用的移动机器人系统软硬件平台，实现了如图3所示的ORB-SLAM算法。

提取RGB-D数据中彩色图像的ORB图像特征，与上一帧图像特征点做初始匹配，得到初始点对，同时利用深度信息进行尺度判断。若存在足够的匹配点对，则对包含深度信息的当前帧与前一帧匹配点对进行基于RANSAC算法的前后两帧位姿估计。若没有足够的匹配点对，则首先使用DBoW2库建立关键帧ORB特征的词袋向量，在关键帧词袋数据库进行搜索匹配，选取最佳位姿估计。进而利用covisibility graph获取局部地图进行当前帧位姿优化，获得当前帧位姿等信息，然后判断是否为新的关键帧，用于进行局部建图，并采用g2o对当前正在处理的关键帧与相关联的covisibility graph内不同时刻的关键帧进行局部集束调整(bundle adjustment)，最后进行闭环检测。由此，实现了移动机器人的自主实时定位与特征地图创建。

2.2 基于GMapping的二维栅格地图创建

栅格地图用于表示二维平面坐标点存在障碍物的概率值，具有构建速度快、存储空间小、易扩展等优势^[20]。为实现路径规划，有必要建立二维栅格地图，对此GMapping算法具有良好性能^[21]。

GMapping算法的输入为当前位姿及二维激光类型观测数据，输出为二维栅格地图。当前实时位姿通过ORB-SLAM获取，而二维激光类型观测数据由RGB-D数据生成。利用获取的点云信息，根据移动机器人高度、RGB-D的实际观测视角及深度范围添加采样约束，取约束范围内离移动机器人最近的点集，降维生成在指定坐标系平面(移动机器人基坐标系平面)的激光类型数据。这种方法保留了环境立体信息，有利于自主移动机器人系统及时根据环境变化进行响应。

建图过程中，GMapping把订阅ORB-SLAM生成的移动机器人实时位姿作为里程计信息，通过RGB-D点云生成的激光类型数据，实时建立环境的二维栅格地图。基于建图环节的优化和闭环检测环节的约束，ORB-SLAM提供的实时位姿具有较好的稳定性与精确性，且位姿更新频率能达到20 Hz，满足需求；同时，根据移动机器人高度约束，取符合高度范围内的RGB-D点云用于地图构建。由于GMapping栅格地图构建的方式实时性较好，在本平台上能达到最少5 Hz的更新频率，为自主移动机器人平台实时进行路径规划与控制提供了保证。

2.3 基于人工势场法的路径点生成

对于移动机器人的路径规划，人工势场法是一种通用算法，传统人工势场法需处理势场中存在的局部最小、目标不可达等问题^[22]。为避免上述问题，本文采用改进人工势场法进行路径规划^[23]。

在空间中某个位置 ${{X}} = {[x\,\,y]^{\text{T}}}$ ，引力势场函数为

${U_{{\text{att}}}}(q) = \frac{1}{2}\varepsilon \rho (q,{q_{{\text{goal}}}})$

(1)

式中： $\varepsilon $ 是引力比例因子， $\rho (q,{q_{{\text{goal}}}})$ 为机器人 $q$ 与目标 ${q_{{\text{goal}}}}$ 之间的距离。引力可表示为势场的负梯度函数，如式(2)所示：

${F_{{\text{att}}}}(q) = - \nabla {U_{{\text{att}}}}(q) = \varepsilon \rho ({q_{{\text{goal}}}} - q)$

(2)

斥力对应的势场函数为

$\begin{array}{*{20}{c}}\!\!\!\!\! {{U_{{\text{req}}}}(q) = } \\ \!\!\!\!\! {\left\{ {\begin{array}{*{20}{l}} \!\!\!\!\! {\displaystyle\frac{1}{2}\eta { \, {\left( {\frac{1}{{\rho (q,{q_{{\text{obs}}}})}} - \frac{1}{{{\rho _0}}}} \right)}^2}{\rho ^n}(q,{q_{{\text{goal}}}}),}\quad{\;\rho (q,{q_{{\text{obs}}}}) \leqslant {\rho _0}} \!\!\!\!\! {0,}\quad {\;{\text{其他}}} \end{array}} \right.} \end{array}$

(3)

式中： $\eta $ 为斥力比例因子， $\rho (q,{q_{{\text{obs}}}})$ 为机器人 $q$ 与障碍物 ${q_{{\text{obs}}}}$ 之间的最小距离， ${\rho _0}$ 为障碍物的影响范围。进而斥力函数可表示为

${F_{{\text{rep}}}}(q) = \left\{ {\begin{array}{*{20}{l}} {{F_{{\text{rep}}1}} + {F_{{\text{rep2}}}},}\quad{\rho (q,{q_{{\text{obs}}}}) \leqslant {\rho _0}} \\ {0,}\quad{\rho (q,{q_{{\text{obs}}}}) > {\rho _0}} \end{array}} \right.$

(4)

式中：

${F_{{\text{rep1}}}} = \eta \left( {\frac{1}{{\rho (q,{q_{{\text{obs}}}})}} - \frac{1}{{{\rho _0}}}} \right)\frac{{{\rho ^n}(q,{q_{{\text{goal}}}})}}{{{\rho ^2}(q,{q_{{\text{obs}}}})}}$

(5)

${F_{{\text{rep2}}}} = \frac{n}{2}\eta {\left( {\frac{1}{{\rho (q,{q_{{\text{obs}}}})}} - \frac{1}{{{\rho _0}}}} \right)^2}{\rho ^{n - 1}}(q,{q_{{\text{goal}}}})$

(6)

分别为排斥机器人远离障碍物的分量和吸引机器人向目标运动的分量。

因此，移动机器人承受的总作用力由引力和斥力的合力构成，可表示为

${F_{{\text{sum}}}}(q) = {F_{{\text{att}}}}(q) + {F_{{\text{rep1}}}}\nabla \rho (q,{q_{{\text{obs}}}}) - {F_{{\text{rep2}}}}\nabla \rho (q,{q_{{\text{goal}}}})$

(7)

根据上述方法，结合定位信息以及栅格地图，可获得移动机器人的路径点。

2.4 基于二次规划的运动路径曲线拟合

前述获得的路径点存在曲线不平滑、不可解析的问题。为此，利用二次规划方法，将路径点进行曲线拟合，生成一条平滑可解析的路径曲线，并最终生成对移动机器人的控制量。

将生成的路径点表示为

$\left\{ {\begin{array}{*{20}{c}} {x(s) = {a_0} + {a_1}{s^1} + {a_2}{s^2} + \cdots + {a_n}{s^n}} \\ {y(s) = {b_0} + {b_1}{s^1} + {b_2}{s^2} + \cdots + {b_n}{s^n}} \end{array}} \right.$

(8)

式中： $s$ 为参数，假设路径点为 $m$ 个，进而可以将等式(8)表示为矩阵形式，即

${{A}}{{X}} = {{B}}$

(9)

式中：

${{A}} = \left[ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}}\!\!\!\!\! 1&{s_0^1}&{s_0^2}& \cdots &{s_0^n} \\ \!\!\!\!\! 1&{s_1^1}&{s_1^2}& \cdots &{s_1^n} \\ \!\!\!\!\! \vdots & \vdots & \vdots &{}& \vdots \\ \!\!\!\!\! 1&{s_m^1}&{s_m^2}& \cdots &{s_m^n} \end{array}}&0 \!\!\!\!\! \\ \!\!\!\!\! 0&{\begin{array}{*{20}{c}} 1&{s_0^1}&{s_0^2}& \cdots &{s_0^n} \!\!\!\!\! \\ 1&{s_1^1}&{s_1^2}& \cdots &{s_1^n} \!\!\!\!\! \\ \vdots & \vdots & \vdots &{}& \vdots \!\!\!\!\! \\ 1&{s_m^1}&{s_m^2}& \cdots &{s_m^n} \!\!\!\!\!\end{array}} \end{array}} \right]$

(10)

${{X}} = {\left[ {\begin{array}{*{20}{c}}\!\!\!\!\! {{a_0}}&{{a_1}}&{{a_2}}& \cdots &{{a_n}}&{{b_0}}&{{b_1}}&{{b_2}}& \cdots &{{b_n}} \!\!\!\!\!\end{array}} \right]^{\text{T}}}$

(11)

${{B}} = {\left[ {\begin{array}{*{20}{c}}\!\!\!\!\! {{x_0}}&{{x_1}}& \cdots &{{x_m}}&{{y_0}}&{{y_1}}& \cdots &{{y_m}} \!\!\!\!\!\end{array}} \right]^{\text{T}}}$

(12)

限定移动机器人路径曲线必须通过初始点以及终止点，有如下约束：

$\left[ {\begin{array}{*{20}{c}} \!\!\!\!\! {{x_0}} \!\!\!\!\! \\ \!\!\!\!\! {{x_m}} \!\!\!\!\! \\ \!\!\!\!\! {{y_0}} \!\!\!\!\! \\ \!\!\!\!\! {{y_m}} \!\!\!\!\!\end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}}\!\!\!\!\!\!\! 1&{s_0^1}&{s_0^2}& \cdots &{s_0^n} \\ \!\!\!\!\!\!\! 1&{s_m^1}&{s_m^2}& \cdots &{s_m^n} \end{array}}&0 \!\!\!\!\!\!\! \\ \!\!\!\!\!\!\! 0&{\begin{array}{*{20}{c}} 1&{s_0^1}&{s_0^2}& \cdots &{s_0^n} \!\!\!\!\!\!\! \\ 1&{s_m^1}&{s_m^2}& \cdots &{s_m^n} \!\!\!\!\!\!\!\end{array}} \end{array}} \right]{{X}}$

(13)

为了能够实现移动机器人的动态路径规划，在控制过程中采取分段规划的策略。因此，路径曲线还需满足起始角度和终止角度约束：

$\frac{{\partial x(s)}}{{\partial s}}\sin \theta - \frac{{\partial y(s)}}{{\partial s}}\cos \theta = 0$

(14)

根据式(8)可得

$\frac{{\partial x(s)}}{{\partial s}} = \left[ {\begin{array}{*{20}{c}} \!\!\! {{{{C}}^{\text{T}}}}&0 \!\!\!\end{array}} \right]{{X}}$

(15)

$\frac{{\partial y(s)}}{{\partial s}} = \left[ {\begin{array}{*{20}{c}} \!\!\! 0&{{{{C}}^{\text{T}}}} \!\!\!\end{array}} \right]{{X}}$

(16)

式中：

${{C}} = \left[ {\begin{array}{*{20}{c}} \!\!\! 0&1&{2{s^1}}& \cdots &{n{s^{n - 1}}} \!\!\!\end{array}} \right]$

(17)

设 $\tan {\theta _t}$ 为路径曲线上某一点角度的正切值，进而可得约束，即

$\left[ {\begin{array}{*{20}{c}} {{{R}}\tan {\theta _0}}&{ - {{R}}} \\ {{{T}}\tan {\theta _m}}&{ - {{T}}} \end{array}} \right]{{X}} = 0$

(18)

式中：

${{R}} = \left[ {\begin{array}{*{20}{c}} 0&1&{2s_0^1}& \cdots &{ns_0^{n - 1}} \end{array}} \right]$

(19)

${{T}} = \left[ {\begin{array}{*{20}{c}} 0&1&{2s_m^1}& \cdots &{ns_m^{n - 1}} \end{array}} \right]$

(20)

在上述条件下进行路径曲线拟合，即在满足上述约束下求解最优参数使得式(21)取最小值：

$\begin{array}{c}\min {\left\| {{AX} - {B}} \right\|^2} = \\\min {\left( {{AX} - {B}} \right)^{\rm{T}}}\left( {{AX} - {B}} \right) = \\\min \left( {{{X}^{\rm{T}}}{{A}^{\rm{T}}}{AX} - 2{{B}^{\rm{T}}}{AX}} \right) + {{B}^{\rm{T}}}{B}\end{array}$

(21)

式中 ${{{B}}^{\text{T}}}{{B}}$ 为标量。进而可将上述曲线拟合问题转化为二次规划问题，目标函数为

$\min \left( {{{{X}}^{\text{T}}}{{{A}}^{\text{T}}}{{AX}} - 2{{{B}}^{\text{T}}}{{AX}}} \right)$

(22)

需同时满足式(13)和式(18)的线性约束。

由此，可将路径点拟合成可解析的路径曲线。

2.5 移动机器人运动控制

移动机器人从初始位姿到目标位姿，可用经典的控制方法，如基于极坐标的点镇定控制方法^[24]。本文生成了可解析的路径曲线，能够采用非线性跟踪控制器^[25]。

使用的两轮差速驱动底盘运动学模型为

$\left\{ {\begin{array}{*{20}{l}} {\dot x = v\cos \theta } \\ {\dot y = v\sin \theta } \\ {\dot \theta = \omega \,\,\,\,\,\,\,\,\,} \end{array}} \right.$

(23)

式中 ${\left[ {x\,\,y\,\,\theta } \right]^{\text{T}}}$ 为当前位姿。位姿开环误差为

$\left[ {\begin{array}{*{20}{c}} {{e_x}} \\ {{e_y}} \\ {{e_\theta }} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\cos \theta }&{\sin \theta }&0 \\ { - \sin \theta }&{\cos \theta }&0 \\ 0&0&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{x_d} - x} \\ {{y_d} - y} \\ {{\theta _d} - \theta } \end{array}} \right]$

(24)

式中： ${\left[ {{e_x}\,\,{e_y}\,\,{e_\theta }} \right]^{\rm{T}}}$ 为误差， ${\left[ {{x_d}\,\,{y_d}\,\,{\theta _d}} \right]^{\text{T}}}$ 为期望位姿。对其进行求导并简化，可得

$\left\{ {\begin{array}{*{20}{l}} {{{\dot e}_x} = {v_d}\cos {e_\theta } - v + {e_y}\omega } \\ {{{\dot e}_y} = {v_d}\sin {e_\theta } - {e_x}\omega } \\ {{{\dot e}_\theta } = {\omega _d} - \omega } \end{array}} \right.$

(25)

采用如下的非线性控制器：

$\left\{ {\begin{array}{*{20}{l}} {v = {v_d}\cos {e_\theta } + {k_1}{e_x}} \\ {\omega = {\omega _d} + {e_y}{v_d}\displaystyle\frac{{\sin {e_\theta }}}{{{e_\theta }}} + {k_2}{e_\theta }} \end{array}} \right.$

(26)

式中 ${k_1},{k_2}$ 为参数，可以保证闭环系统渐进稳定^[25]。

3 实验结果与分析

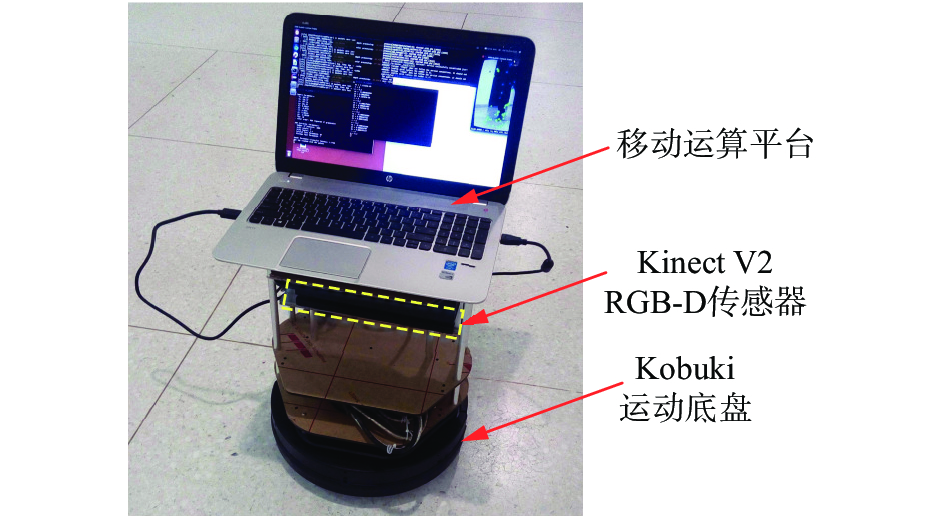
利用本文的自主移动机器人系统进行实验，以验证本文方法的有效性，如图4所示。

分别将移动机器人置于以下8个初始位姿： ${\left[ {0\,\,\,\, - 2.4\,\,\,\,0} \right]^{\text{T}}},{\left[ { - 2.4\,\,\,\, - 2.4\,\,\,\,0} \right]^{\text{T}}},{\left[ { - 2.4\,\,\,\,0\,\,\,\,0} \right]^{\text{T}}},{\left[ { - 2.4\,\,\,\,2.4\,\,\,\,0} \right]^{\text{T}}}$ ， ${\left[ {0\,\,\,\,2.4\,\,\,\,0} \right]^{\rm{T}}},{\left[ {2.4\,\,\,\,2.4\,\,\,\,0} \right]^{\rm{T}}},{\left[ {2.4\,\,\,\,{\rm{0}}\,\,\,\,0} \right]^{\rm{T}}},{\left[ {2.4\,\,\,\,{\rm{ - }}2.4\,\,\,\,0} \right]^{\rm{T}}}$ ，期望位姿设为 ${\left[ {0\,\,\,\,0\,\,\,\,{\text{π}}/2} \right]^{\rm{T}}}$ 。 $x,y$ 单位为m， $\theta $ 单位为弧度。

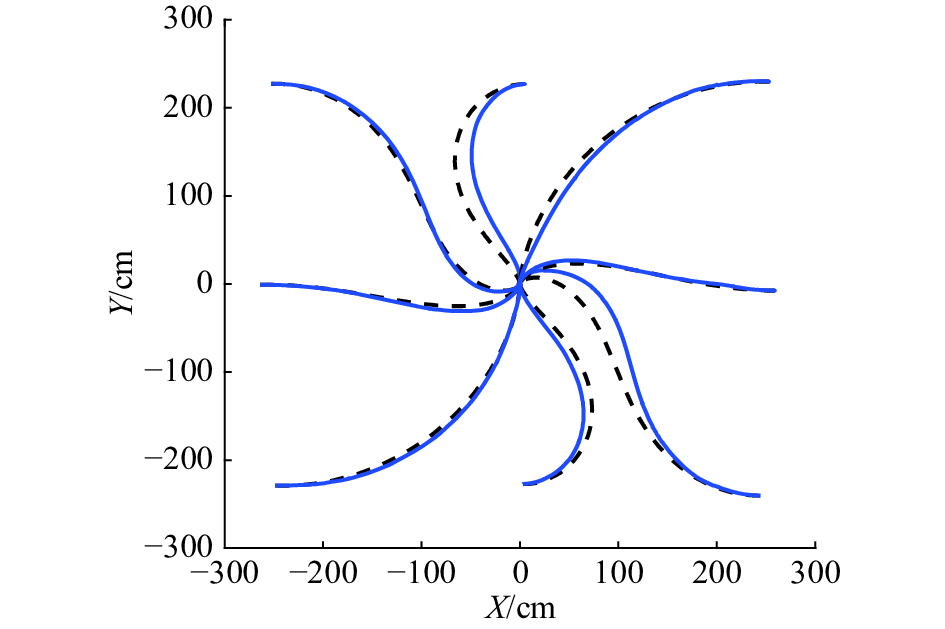
图5所示为实时定位与运动控制实验结果。虚线为基于理想模型和控制器的理论运动路径，实线为实验得到的实际运行路径。可以看出，两种路径趋势一致，且路径曲线平滑，定位平稳。

图6为8次实验中移动机器人到达期望位姿的位置和姿态误差，实心圆点代表位置误差，箭头方向代表姿态误差。移动机器人距离目标点 $X$ 轴方向的平均距离偏差为0.43 cm， $Y$ 轴方向的平均距离偏差为1.12 cm，总体距离误差都在3cm以内。姿态角偏差的绝对平均值为2.16°。实验表明，采用RGB-D信息和ORB-SLAM算法进行移动机器人实时定位确实有效，为后续的运动规划与控制打下了良好基础。

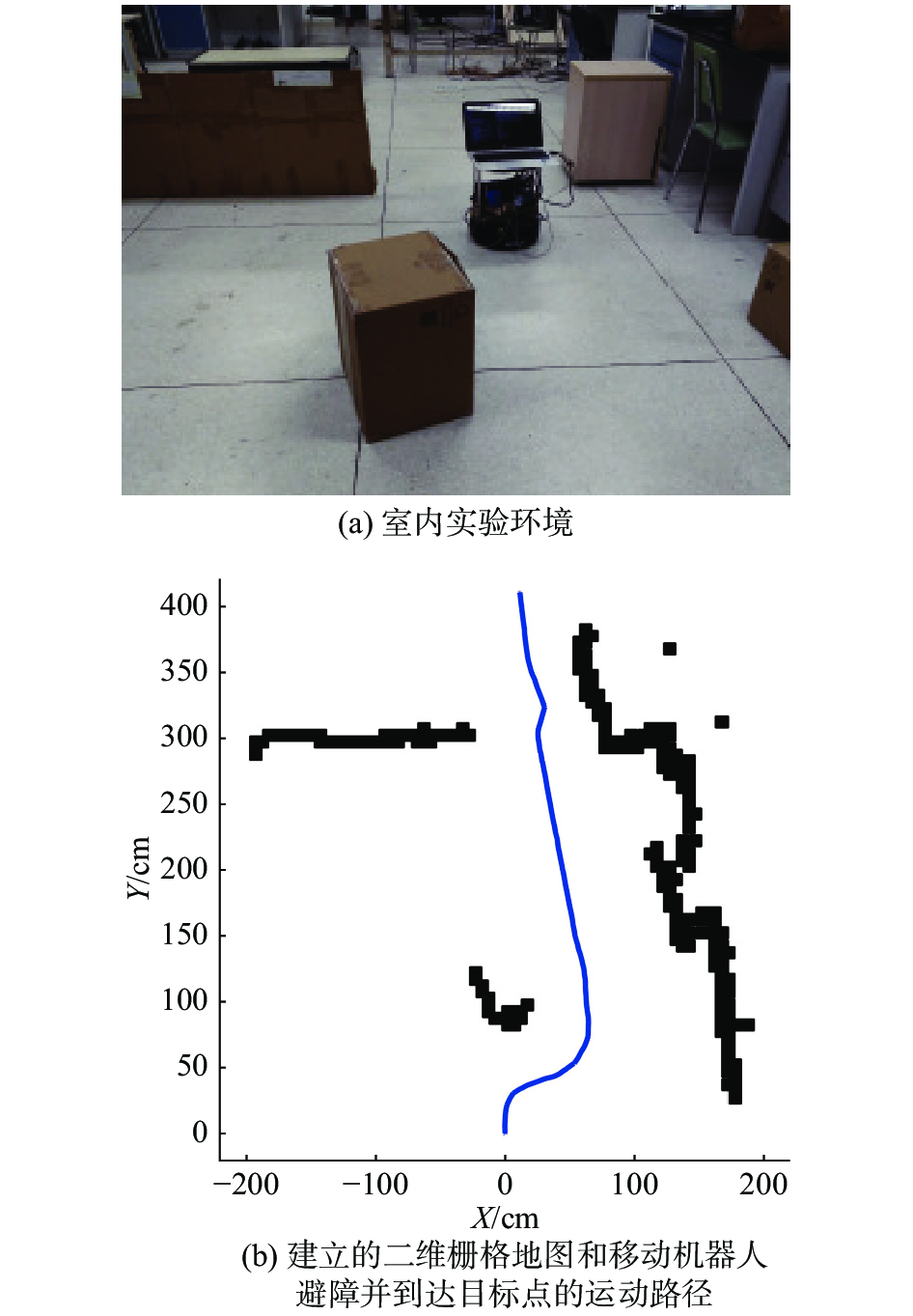
为验证本文方法和系统的有效性，在障碍环境下进行实验，结果如图7所示。图7(a)为实验环境，图7(b)为移动机器人在此存在障碍物的环境下进行地图创建和运动规划与控制的实验结果。可以看出，根据RGB-D点云生成的激光类型数据，通过GMapping算法成功建立了二维环境栅格地图，利用改进人工势场法以及二次规划和轨迹跟踪等算法，有效规避了障碍物，最终成功实现了从初始位置运动到目标位置运动，运动路径平滑。

4 结束语

本文利用基础运动底盘，搭载通用RGB-D传感器与移动计算平台，建立了一个架构简单、经济性好、易开发维护、性能强大、扩展性好的自主移动机器人系统。采用ORB-SLAM算法、GMapping算法、改进人工势场法、二次规划算法以及运动控制算法，实现了移动机器人的自主定位、路径规划、运动控制、障碍物规避等功能，并实时建立了环境二维栅格地图。由此，为移动机器人在家庭等各种场景下的推广应用提供了一个解决方案。

将来可以基于该系统的硬件和软件架构，面向具体应用有针对性地开发整合相关算法，提高系统的智能化程度与控制性能，进一步拓展移动机器人的功能和应用范围。