2. 北京工业大学 计算智能与智能系统北京市重点实验室,北京 100124
2. Beijing Key Laboratory of Computational Intelligence and Intelligence System, Beijing University of Technology, Beijing 100124, China
给水管网是城市重要基础设施,是整个城市得以生存和发展的命脉[1]。同时,给水管网投资巨大,往往占到整个供水系统的60%~80%,而且还涉及庞大的运行动力费和运行管理费[2]。
给水管网的优化设计,一般是在工程资金投入有限的情况下,寻求满足用户用水需求,且使整个系统的造价最低可靠性最高的设计方案。因此,管网的优化设计直接影响到整个供水系统的经济性和可靠性[3]。由于管网系统的非线性和管径的离散性,管网的多目标优化求解十分困难,成为了国内外众多学者研究的热点问题。文献[4]第一个将结构化混合遗传算法(structured messy genetic algorithm, SMGA)应用到给水管网多目标优化中,并将系统造价最低、收益最大作为两个目标,求得了一系列非支配解,但是SMGA算法的求解效率和所得解的多样性较差。文献[5]建立了以管网造价最小、管网压降最小为目标的优化模型,并采用多目标粒子群算法(multi-objective particle swarm optimization algorithm, MOPSO)进行优化,但是MOPSO算法不适合离散变量的优化问题。文献[6]建立了以管网造价最小、水质最优为目标的优化模型,且采用多目标遗传算法(multi-objective optimization genetic algorithm, MOGA)进行管网优化设计,其研究的重点主要为管网模型的设计。文献[7]以管网造价最低、可靠性最高为目标,建立了3个目标的管网优化模型,并采用快速非支配排序遗传算法(non-dominated sorting genetic algorithm II, NSGA-II)优化管网模型,取得了较好的效果,但是NSGA-II算法容易陷入局部最优,使获得的解分布不均匀。
目前,智能优化算法在解决管网多目标优化问题中取得了广泛的应用,但解的多样性和收敛性不好是其存在的主要问题,因此提高多目标优化算法解的多样性和收敛性成为重要的研究方向[8-10]。文献[11]提出了强度帕累托进化算法(strength Pareto evolutionary algorithm 2, SPEA2),通过引入密度估计策略和归档集截断算法,从一定程度上提高了算法解的多样性和收敛性。文献[12]提出的NSGA-II算法,其快速非支配排序和拥挤距离策略提高了多样性和收敛性。这两种算法均能从一定程度上提高算法的性能,但是都将多目标优化问题作为一个整体优化。因此当目标数大于2时,这两种算法的搜索性能急剧下降。文献[13]提出了基于分解的多目标进化算法(multi-objective evolutionary algorithm based on decomposition, MOEA/D),将一个多目标优化问题分解为多个单目标优化问题,通过同时优化所有的单目标子问题,提高了算法解的多样性和收敛性。但是,对于具有不同Pareto前沿的多目标优化问题,MOEA/D却使用了相同的权值向量。文献[14]基于支配和分解的框架,在NSGA-II算法基础上,结合一组提前设定的参考点,提出了NSGA-III算法。虽然NSGA-III算法进一步提高了解的多样性和收敛性,但是其收敛速度依然较慢,而且固定的参考点使得具有不同Pareto前沿的多目标优化问题难以达到相同的优化效果。
本文采用SPEA2算法[11]作为基础,结合NSGA-III中基于支配和分解的思想,提出了一种基于参考向量的强度帕累托进化算法(strength Pareto evolutionary algorithm 2 based on reference vectors, RVSPEA2),其目的是提高算法的多样性和收敛性,并采用文献[7]的3个目标作为管网优化模型,将其应用到双环管网、纽约管网以及实际的管网优化案例中。
1 给水管网优化模型描述给水管网优化设计的目的是在满足用户用水需求的前提下,使管网经济性最低和可靠性最高,并求出最优管线直径。本文中采用管网造价作为经济性目标,节点富余水头总和与节点富余水头方差作为可靠性目标,建立给水管网优化模型。
1.1 目标函数为了简化管网优化计算,本文采用管网造价作为经济性目标,其目标函数如式(1):
| $Z = \sum\limits_{j = 1}^P {{C_j}\left( {{D_j}} \right){L_j}} ,j = 1,2, \cdots \! ,P$ | (1) |
式中:Z为管网总造价;Dj、Lj分别为第j根管段的直径、长度;Cj (Dj)为管径为Dj的管段的单位长度造价;P为管网中管段总数。
管网的可靠性目标可用节点富余水头总和与节点富余水头方差表示。其相关定义如下。
每个节点的富余水头Isi计算如式(2):
| ${I_{si}} = {H_i} - {H_{\min }},i = 1,2, \cdots \! ,I$ | (2) |
式中:Hi为管网节点i的水压标高;Hmin为管网节点所要求的最小自由水压;I为管网中节点总数。
给水管网节点富余水头总和Is为
| ${I_s} = \sum\limits_{i = 1}^I {\left( {{H_i} - {H_{\min }} } \right)} $ | (3) |
节点富余水头均值
| $\overline {{I_s}} = \frac{{{I_{s1}} + {I_{s2}} + \cdots + {I_{sI}}}}{I}$ | (4) |
节点富余水头方差S为
| $S = \sum\limits_{i = 1}^I {{{\left( {{I_{si}} - \overline {{I_s}} } \right)}^2}} ,i = 1,2, \cdots \! ,I$ | (5) |
因此,给水管网多目标优化模型可表示为
| $\left\{ \begin{array}{l}\min Z = \sum\limits_{j = 1}^P {{C_j}\left( {{D_j}} \right){L_j}} ,j = 1,2, \cdots \! ,P\\\min Is = \sum\limits_{i = 1}^I {\left( {{H_i} - {H_{\min }}} \right),i = 1,2, \cdots \! ,I} \\\min S = \sum\limits_{i = 1}^I {{{\left( {{I_{si}} - \overline {{I_s}} } \right)}^2}} ,i = 1,2, \cdots \! ,I\end{array} \right.$ | (6) |
管网总造价Z越小,表明管网系统经济性越高。节点富余水头Is是指节点自由水头超过节点所要求的最小自由水头的部分水头,它与管网水压呈线性关系。在满足管网约束的条件下,节点富余水头越小,管网水压就越低。节点富余水头总和越大,即管网水压总和越大,一方面反映了资源浪费的情况,另一方面也代表了管网存在爆管的危险。另外,节点富余水头方差S反映了管网中各节点富余水头的分布情况。节点富余水头方差越大,说明了管网中各节点压力分布不均,亦存在爆管的危险。因此,节点富余水头总和与节点富余水头方差越小,表明管网系统可靠性越高。
1.2 约束条件除了优化目标之外,给水管网的优化还必须满足下列约束条件。
1) 节点流量连续性约束
管网中每个节点应满足:
| ${\mathit{\boldsymbol{Ag}}} + G = 0$ | (7) |
式中:A为节点关系矩阵,g为与该节点相连的管段流量,G为节点流量。
2) 能量平衡约束
管网中闭合回路水头损失代数和为零,即
| $\sum\limits_{k \in {\rm{Loop }}l} {\Delta {H_k} = 0} , \; \forall l \in L$ | (8) |
式中:ΔHk为闭合回路l中管段k的水头损失,L是管网中所有闭合回路。
3) 节点流量连续性约束
管网中每个节点应满足
| ${H_{\min }} \leqslant {H_i} \leqslant {H_{\max }}$ | (9) |
式中:Hi为节点i的水头,Hmin和Hmax分别为节点最小水头和最大水头。
4) 能量平衡约束
管网中每个管段直径应满足:
| ${D_j} \in \left\{ {{D_1},{D_2}, \cdots \! ,{D_m}} \right\}$ | (10) |
式中:Dj为管段j的直径,D1~Dm为标准管径。
2 基于参考向量的强度帕累托进化算法RVSPEA2本文基于SPEA2算法,与基于支配和基于分解的选择机制相结合,提出了一种基于参考向量的强度帕累托进化算法(RVSPEA2),旨在进一步提高算法解的多样性和收敛性,以解决给水管网的多目标优化问题。
2.1 基于参考向量的选择机制在SPEA2算法的环境选择过程中,当前种群中所有的非支配解被放入外部归档集中。如果外部归档集|Qt|≥N(预设值),则通过最小距离截断算法删除个体,直至|Qt|=N;如果外部归档集|Qt|<N(预设值),则随机选择支配解放入外部归档集,直至|Qt|=N。而在RVSPEA2中,当外部归档集|Qt|<N时,引入参考向量,根据非支配解与参考向量的关系,有目标地选择支配解放入外部归档集,其选择机制将在本节中详细介绍。
2.1.1 自适应目标归一化在实际的多目标优化问题中,各目标的范围往往差别很大,其对优化结果影响巨大[15]。因此,为了解决目标范围不同的优化问题,RVSPEA2采用了一种简单的目标归一化方法,即对于第j代种群的第i个目标函数
| ${f'_{i,j}}({\mathit{\boldsymbol{x}}}) = \frac{{{f_{i,j}}({\mathit{\boldsymbol{x}}}) - f_{i,j}^{\min }}}{{f_{i,j}^{\max } - f_{i,j}^{\min }}}$ | (11) |
式中:
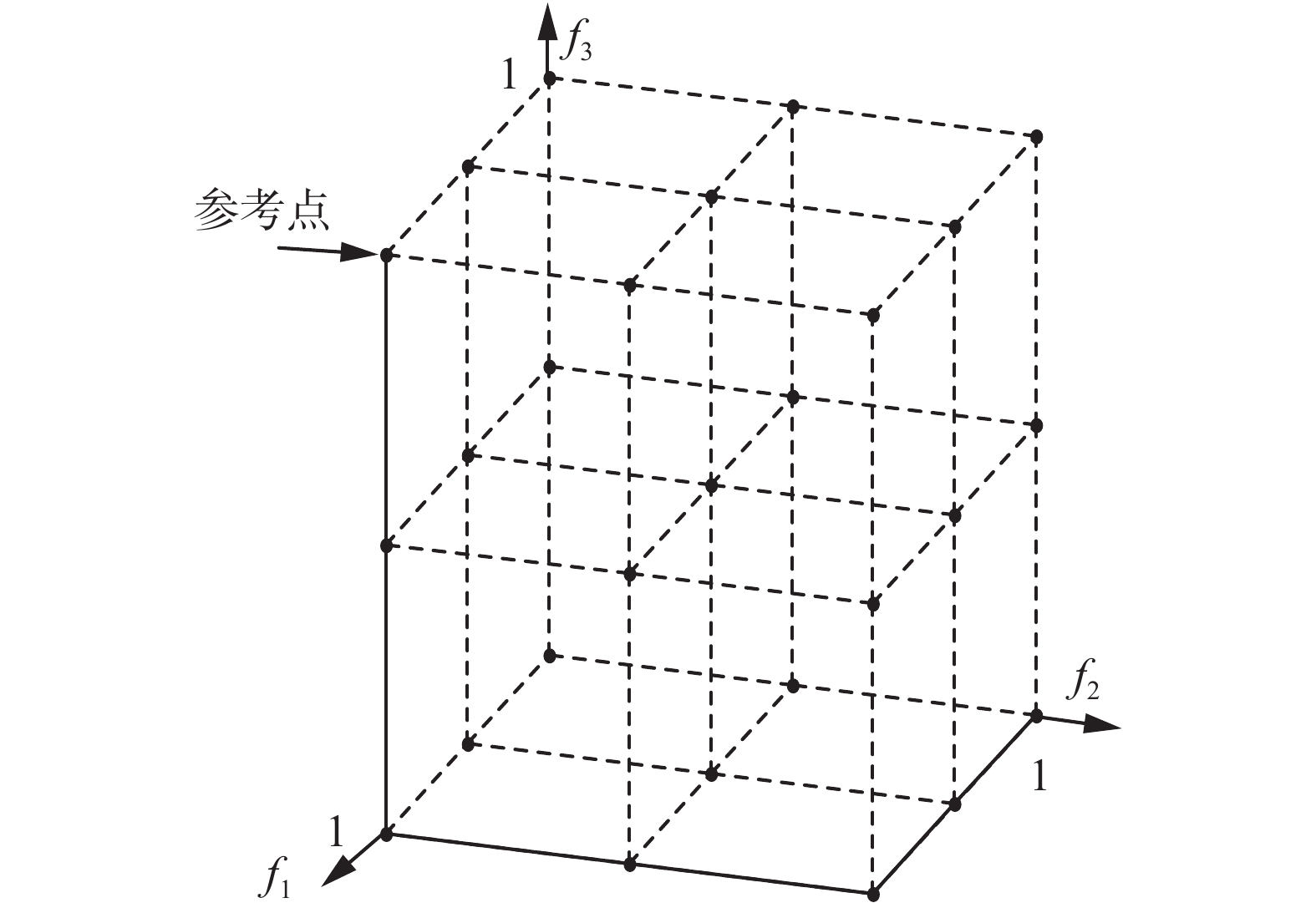
为了探索和开发整个搜索空间,RVSPEA2采用了一种简单且有效的方法用于生成参考向量。首先,在整个归一化目标空间生成Km个参考点,其中m为目标个数,K的计算公式如式(12):
| $K = \left\lfloor {\sqrt[m]{N} + 0.5} \right\rfloor $ | (12) |
式中:N为种群大小,
生成参考向量后,将种群中每个成员都关联一个参考向量。首先,计算种群成员与每一个参考向量的垂直距离,如式(13)所示。与每个成员垂直距离最近的参考向量将与该成员相关联,如式(14):
| ${d^ \bot }({\mathit{\boldsymbol{q}}},{\mathit{\boldsymbol{w}}}) = \left\| {{\mathit{\boldsymbol{q}}} - {{\mathit{\boldsymbol{w}}}^{\rm{T}}}{\mathit{\boldsymbol{qw}}}} \right\|$ | (13) |
| $r({\mathit{\boldsymbol{q}}}) = {\mathit{\boldsymbol{w}}}:{\rm{argmi}}{{\rm{n}}_{{\mathit{\boldsymbol{w}}} \in {R}}}{d^ \bot }({\mathit{\boldsymbol{q}}},{\mathit{\boldsymbol{w}}})$ | (14) |
|
Download:
|
| 图 1 当m=3,K=3时归一化空间中的27个参考点 Fig. 1 Twenty-seven reference points on the normalized objective space for a three-objective problem with K=3 | |

|
Download:
|
| 图 2 当m=3,K=3时归一化空间中的参考向量 Fig. 2 Reference vectors on the normalized objective space for a three-objective problem with K=3 | |
式中:q为种群成员,w为参考向量,
经过关联操作后,一个参考向量可能会有一个或多个种群成员与之相关联,甚至没有种群成员与之相关联[16]。当外部归档集|Qt|<N时,通过统计已有成员所关联的参考向量,排除这部分参考向量,从剩余参考向量所关联的种群成员中选择成员填满外部归档集。当外部归档集|Qt|≥N时,则依然通过最小距离截断算法删除个体[6],直至|Qt|=N。通过参考向量选择可以保证算法初期优化解的多样性,避免算法陷入局部最优;而在算法后期,在保证算法收敛性的同时,通过最小距离截断算法,进一步提高算法的多样性。
2.2 算法流程及性能测试设种群大小为N,最大进化代数为T,RVSPEA2算法的具体流程如下:
1) 初始化种群P0和外部归档集Q0,进化代数t=0;
2) 合并Pt和Qt为Qt+1;
3) 计算种群Qt+1中各成员的适应度;
4) 通过选择机制,从Qt+1中选出N个成员;
5) 进行锦标赛选择配对、单点交叉和均匀变异操作,得到Pt+1;
6) 计算t=t+1,并判断算法的终止条件,若满足则进行下一步,否则转至2);
7) 通过选择机制选出N个非支配解,并输出结果。
为了验证算法的性能,将RVSPEA2算法与SPEA2、NSGA-II和MOEA/D进行对比,用于优化双环管网和纽约管网,其布局图分别如图3和图4所示,其节点水压和管段长度等详细数据参照文献[17]。为了比较算法所得解的多样性和收敛性,本文采用了以下3个性能指标。
1) IGD(inverted generational distance)[18]
IGD的定义如式(15),其中P*为一组均匀分布在Pareto前沿上的解,P为算法所求得的非支配解,d(x, P)代表解x与P中解的最小欧式距离。如果P*中解的数量足够多,IGD在一定程度上能同时反映解的多样性和收敛性。IGD的值越小,算法所得解的多样性和收敛性越好。
| ${\rm{IGD}}({P^ * },P) = \frac{{\sum\limits_{x \in {P^ * }} {d(x,P)} }}{{\left| {{P^ * }} \right|}}$ | (15) |
2) GD(generational distance)[19]
GD的定义如式(16)所示,其用于计算非支配解与Pareto前沿之间的距离。GD的值越小,算法所得解的收敛性越好。
| ${\rm{GD}}(P,{P^ * }) = \frac{{\sqrt {\sum\limits_{x \in P} {d{{(x,{P^ * })}^2}} } }}{{\left| P \right|}}$ | (16) |

|
Download:
|
| 图 3 双环管网 Fig. 3 Two-loop network | |

|
Download:
|
| 图 4 纽约管网 Fig. 4 New York Tunnels network | |
3) SP(spacing)[20]
SP用于计算非支配解中相邻解之间距离的方差,其公式如式(17):
| ${\rm{SP}} = \sqrt {\frac{1}{{n - 1}}\sum\limits_{i = 1}^n {{{\left( {\bar d - {d_i}} \right)}^2}} } $ | (17) |
| ${d_i} = \min \left( {\sum\limits_{k = 1}^m {\left| {f_k^i\left( x \right) - f_k^j\left( x \right)} \right|} } \right),\;{\rm{ }}i,j = 1,2, \cdots \! ,n$ | (18) |
式中:
对于双环管网问题,RVSPEA2算法具体参数设置如表1所示,为了公平对比,SPEA2、NSGA-II和MOEA/D的参数设置与本文所提算法相同,每种算法均独立运行30次。表2列出了SPEA2、NSGA-II、MOEA/D与本文提出的RVSPEA2算法优化双环管网的结果。从表2中可以看出,在IGD、GD和SP3个指标的均值上,本文提出的RVSPEA2算法都优于其他算法,说明在双环管网问题上,RVSPEA2算法所得解的多样性和收敛性最好。
| 表 1 双环管网和纽约管网参数设置 Tab.1 Parameters of two-loop network and New York tunnels network |
| 表 2 双环管网优化结果 Tab.2 Optimization results for two-loop network |
对于纽约管网问题,RVSPEA2算法具体参数设置如表1所示,SPEA2、NSGA-II和MOEA/D的参数设置与RVSPEA2算法相同,每种算法均独立运行30次。表3列出了SPEA2、NSGA-II、MOEA/D与本文提出的RVSPEA2算法优化纽约管网的结果。从表3中可以看出,本文提出的RVSPEA2算法在IGD、GD和SP这3个指标的均值上,都优于其他算法。因此,在纽约管网问题上,RVSPEA2算法所得解的多样性和收敛性也优于SPEA2、NSGA-II和MOEA/D算法。
| 表 3 纽约管网优化结果 Tab.3 Optimization result for New York tunnels network |
通过双环管网和纽约管网的测试,验证了本文提出的RVSPEA2算法在解决管网多目标优化设计上的性能。
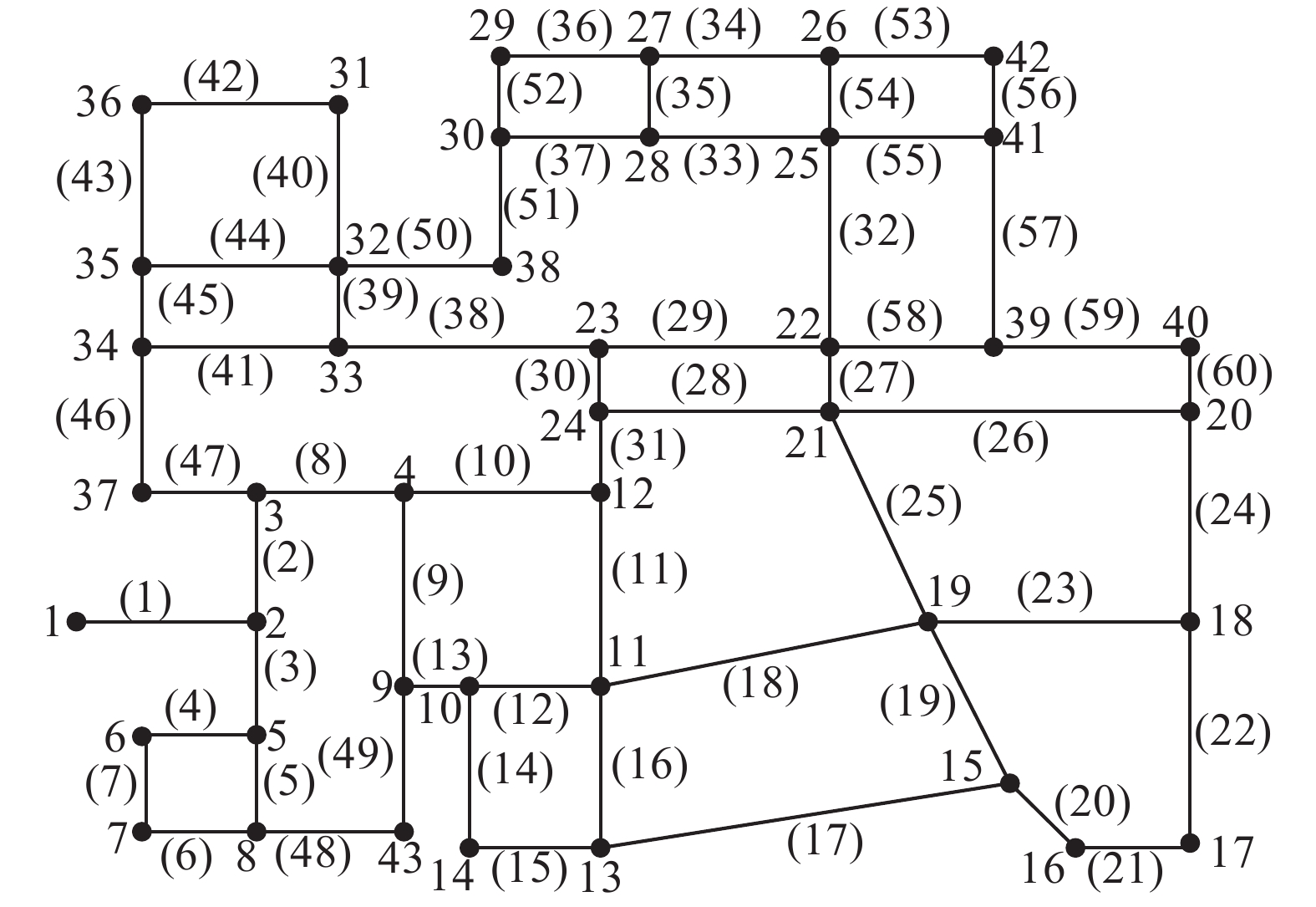
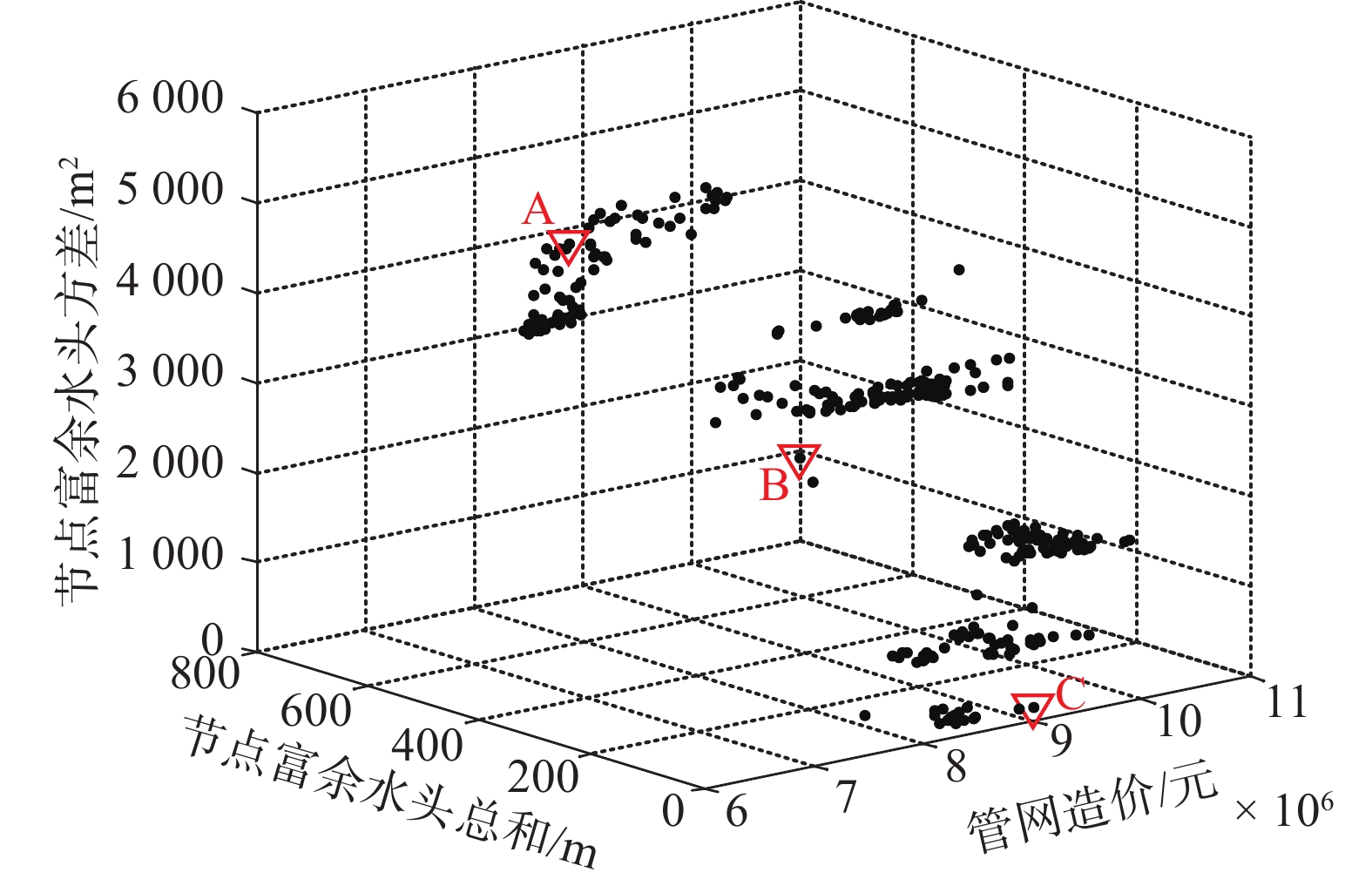
3 工程实例现将RVSPEA2算法应用于实际管网中。本实例为北京市某高校给水管网设计工程,管网布局如图5所示,管网中有1个水源、43个节点和60条管线。RVSPEA2算法参数设置如表4所示。图6画出了RVSPEA2算法所求出的非支配解。在实际工程应用中,应根据实际工程情况和决策者的经验,在保证供水基本可靠及居民正常用水的情况下,合理地选择一个施工方案。针对该实际工程问题,本文给出3个施工方案以供决策者选择,如表5所示。当资金有限时,应选择造价较低的方案,如方案A;当资金充足、管网可靠性更重要时,可采用节点富余水头总和小、节点富余水头方差小的方案,如方案C;当资金和管网可靠性同等重要时,可选择方案B。
|
Download:
|
| 图 5 工程实例 Fig. 5 Engineering example | |
| 表 4 工程实例参数设置 Tab.4 Parameters for engineering example |
|
Download:
|
| 图 6 工程实例的非支配解 Fig. 6 Non-dominated solutions for engineering example | |
| 表 5 3种不同情况下的施工方案 Tab.5 Construction schemes for three different cases |
针对管网多目标优化问题,本文结合选择机制中支配和分解的思想,提出了一种基于参考向量的强度帕累托进化算法——RVSPEA2。该算法通过在目标空间中生成均匀分布的点,生成一组参考向量,并基于SPEA2算法的选择机制,将进化产生的解与各参考向量相关联,通过参考向量配合支配强度进行解的选择,提高了算法解的多样性和收敛性。两个经典管网的验证表明了RVSPEA2算法解决管网多目标优化问题的有效性。最后,本文将RVSPEA2算法应用于工程实例,并给出3种施工方案以供决策者选择。
| [1] |
ALPEROVITS E, SHAMIR U. Design of optimal water distribution systems[J]. Water resources research, 1977, 13(6): 885-900. DOI:10.1029/WR013i006p00885 ( 0) 0)
|
| [2] |
MURPHY L J, SIMPSON A R, DANDY G C. Design of a pipe network using genetic algorithms[J]. Water-melbourne then artarmon, 1993, 20(4): 40-42. ( 0) 0)
|
| [3] |
MORGAN D R, GOULTER I C. Optimal urban water distribution design[J]. Water resources research, 1985, 21(5): 642-652. DOI:10.1029/WR021i005p00642 ( 0) 0)
|
| [4] |
HALHAL D, WALTERS G A, OUAZAR D, et al. Water network rehabilitation with structured messy genetic algorithm[J]. Journal of water resources planning and management, 1997, 123(3): 137-146. DOI:10.1061/(ASCE)0733-9496(1997)123:3(137) ( 0) 0)
|
| [5] |
MONTALVO I, IZQUIERDO J, SCHWARZE S, et al. Multi-objective particle swarm optimization applied to water distribution systems design: an approach with human interaction[J]. Mathematical and computer modelling, 2010, 52(7/8): 1219-1227. ( 0) 0)
|
| [6] |
LIU Haixing, YUAN Yixing, ZHAO Ming, et al. Hybrid multi-objective genetic algorithm for optimal design of water supply network[C]//Proceedings of the 12th Annual Conference on Water Distribution Systems Analysis. Tucson, United States, 2010: 899–908.
( 0) 0)
|
| [7] |
刘书明, 李明明, 王欢欢, 等. 基于NSGA-II算法的给水管网多目标优化设计[J]. 中国给水排水, 2015, 31(5): 50-53. LIU Shuming, LI Mingming, WANG Huanhuan, et al. Multi-objective optimization design of water distribution system based on non-dominated sorting genetic algorithm-II[J]. China water and wastewater, 2015, 31(5): 50-53. (  0) 0)
|
| [8] |
蒋怀德. 给水管网多目标优化设计[D]. 上海: 同济大学, 2007, 5–7. JIANG Huaide. Multi-objective optimization design of urban water distribution networks[D]. Shanghai: Tongji University, 2007, 5–7. (  0) 0)
|
| [9] |
LI Mingming, LIU Shuming, ZHANG Ling, et al. Non-dominated sorting genetic algorithms-iibased on multi-objective optimization model in the water distribution system[J]. Procedia engineering, 2012, 37: 309-313. DOI:10.1016/j.proeng.2012.04.245 ( 0) 0)
|
| [10] |
TOLSON B A, MAIER H R, SIMPSON A R, et al. Genetic algorithms for reliability-based optimization of water distribution systems[J]. Journal of water resources planning and management, 2004, 130(1): 63-72. DOI:10.1061/(ASCE)0733-9496(2004)130:1(63) ( 0) 0)
|
| [11] |
ZITZLER E, LAUMANNS M, THIELE L. SPEA2: improving the strength Pareto evolutionary algorithm: TIK-Report 103[R]. Swiss: Swiss Federal Institute of Technology, 2001.
( 0) 0)
|
| [12] |
DEB K, PRATAP A, AGARWAL S, et al. A fast and elitist multiobjective genetic algorithm: NSGA-II[J]. IEEE transactions on evolutionary computation, 2002, 6(2): 182-197. DOI:10.1109/4235.996017 ( 0) 0)
|
| [13] |
ZHANG Qingfu, LI Hui. MOEA/D: a multiobjective evolutionary algorithm based on decomposition[J]. IEEE transactions on evolutionary computation, 2007, 11(6): 712-731. DOI:10.1109/TEVC.2007.892759 ( 0) 0)
|
| [14] |
DEB K, JAIN H. An evolutionary many-objective optimization algorithm using reference-point-based nondominated sorting approach, part I: solving problems with box constraints[J]. IEEE transactions on evolutionary computation, 2014, 18(4): 577-601. DOI:10.1109/TEVC.2013.2281535 ( 0) 0)
|
| [15] |
PRASAD T D, PARK N S. Multiobjective genetic algorithms for design of water distribution networks[J]. Journal of water resources planning and management, 2004, 130(1): 73-82. DOI:10.1061/(ASCE)0733-9496(2004)130:1(73) ( 0) 0)
|
| [16] |
JIANG Siwei, CAI Zhihua, ZHANG Jie, et al. Multiobjective optimization by decomposition with Pareto-adaptive weight vectors[C]// International Conference on Natural Computation, Icnc 2011, Shanghai, China, 26–28 July. DBLP, 2011: 1260–1264.
( 0) 0)
|
| [17] |
SEDKI A, OUAZAR D. Hybrid particle swarm optimization and differential evolution for optimal design of water distribution systems[J]. Advanced engineering informatics, 2012, 26(3): 582-591. DOI:10.1016/j.aei.2012.03.007 ( 0) 0)
|
| [18] |
MA Xiaoliang, LIU Fang, QI Yutao, et al. A multiobjective evolutionary algorithm based on decision variable analyses for multiobjective optimization problems with large-scale variables[J]. IEEE transactions on evolutionary computation, 2016, 20(2): 275-298. DOI:10.1109/TEVC.2015.2455812 ( 0) 0)
|
| [19] |
TANG Lixin, WANG Xianpeng. A hybrid multiobjective evolutionary algorithm for multiobjective optimization problems[J]. IEEE transactions on evolutionary computation, 2013, 17(1): 20-45. DOI:10.1109/TEVC.2012.2185702 ( 0) 0)
|
| [20] |
JIANG Shouyong, YANG Shengxing. Evolutionary dynamic multiobjective optimization: benchmarks and algorithm comparisons[J]. IEEE transactions on cybernetics, 2017, 47(1): 198-211. DOI:10.1109/TCYB.2015.2510698 ( 0) 0)
|
 2018, Vol. 13
2018, Vol. 13


