视觉跟踪是计算机视觉领域的研究热点，在虚拟现实、人机交互、智能监控、增强现实、机器感知等场景中有着重要的研究与应用价值。视觉跟踪通过分析视频图片序列，对检测出的各个候选目标区域实施匹配，定位跟踪目标在视频序列中的位置。目前跟踪算法已经取得很多研究成果，但在实际中应对各类复杂场景时仍面临很大挑战，例如面对遮挡、形变、视频序列分辨率低等影响因素时，如何实现更加鲁棒和准确的跟踪仍然是目前研究的核心^[1]。

视觉跟踪算法一般分为两部分：目标表观建模和跟踪策略。

1)目标表观建模

根据对目标表观的建模方式可分为判别式模型和生成式模型两类^[2-3]。判别式模型将跟踪问题建模为一个二分类问题，用以区分前景和背景。B. Babenko等^[4]提出多示例学习算法(MIL)，针对跟踪中训练样本不足的问题，引入多示例学习机制，有效抑制跟踪过程中跟踪器的漂移问题；文献[5]提出具有元认知能力的粒子滤波(MCPF)目标跟踪算法，通过监控到突变，快速调节决策机制，实现稳定的目标跟踪。生成式模型不考虑背景信息直接为目标进行建模。文献[6]提出了L1跟踪系统，用稀疏方法表示跟踪目标，但算法运算复杂度高；K. Zhang等^[7]提出了压缩跟踪(CT)，用一个稀疏的测量矩阵提取特征以建立一个稀疏、健壮的目标表观模型，取得快速有效、鲁棒性好的跟踪效果；文献[8]引入小波纹理特征，改善单纯依靠颜色特征不能很好适应环境变化的情况，与单一特征相比能够实现更加稳健的跟踪。

2)跟踪策略

采用运动模型来估计目标可能的位置，通过先验知识来缩小搜索范围。代表性方法有隐马尔可夫模型^[9]、卡尔曼滤波^[10]、均值漂移算法^[11]和粒子滤波^[12]等。其中，粒子滤波算法因为对局部极小值相对不太敏感且计算非常有效而被广泛应用。另外，近几年相关滤波跟踪算法在目标领域也取得不错的成绩。D.S. Bolme等^[13]首次将相关滤波引入跟踪领域，通过设计一个误差最小平方和滤波器(MOSSE)，在跟踪过程中寻找目标最大响应值来实现跟踪。J.F. Henriques等^[14]提出的CSK算法使用循环矩阵结构进行相邻帧的相关性检测，利用灰度特征空间提高了算法的准确性。文献[15]在CSK的基础上，通过循环偏移构建分类器的训练样本，使数据矩阵变成一个循环矩阵，同时引入HOG、颜色、灰度多通道特征，提高了算法的速度和准确性。

传统跟踪算法大多数直接使用视频图像序列中的像素值特征进行建模，当跟踪过程中出现复杂场景等较大挑战时，浅层的像素级特征无法很好应对。针对卷积神经网络具有强大的特征提取功能，设计一种无需训练的卷积神经网络特征提取方法，在粒子滤波框架下，利用核函数加速卷积运算，实现了一种快速卷积神经网络跟踪算法，通过与其他算法的对比分析，最终验证了所提出算法的有效性。

1 相关工作

2013年以来，深度学习算法在跟踪领域已经取得了很大进展。如深度神经网络、卷积神经网络等深度学习方法能够挖掘出数据的多层表征，而高层级的表征更能够反映数据更深层的本质，相比传统浅层学习特征，基于高层次特征的跟踪算法可以提高目标的跟踪效率^[16]。

1.1 CNN特征提取结构

卷积神经网络(convolutional neural network，CNN)的网络结构类似于生物神经网络，采用局部连接、权值共享和时空下采样的思想降低了网络复杂度，减少了权值数量，使得 CNN 在处理高维图像时更具优势。

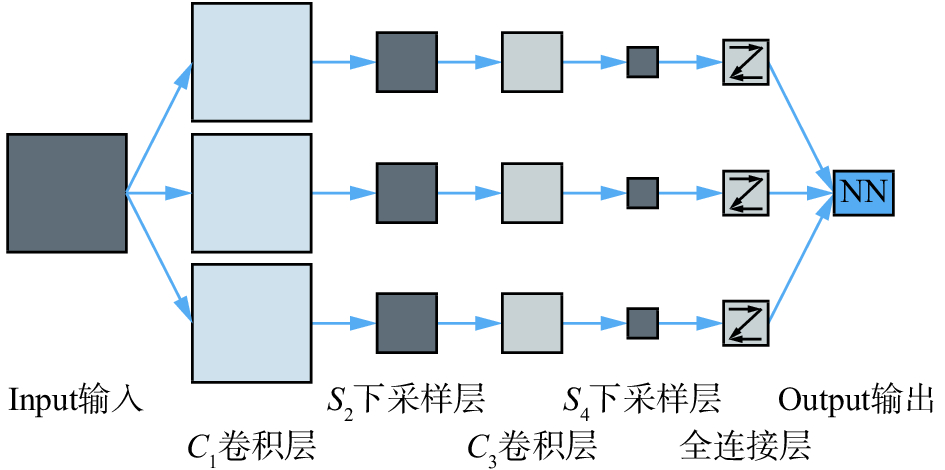
卷积神经网络具有多层性，在传统神经网络的基础上增加了特征提取的卷积层和保证位移不变的下采样层。每层由多个二维平面特征映射层组成，每个映射层由多个独立的神经元组成。卷积特征的提取首先对原始输入图像进行取片操作获取大量小的局部块，然后应用卷积网络模型对局部块进行训练，得到结果为各个卷积层的神经元卷积滤波器，与新输入的样本图像进行卷积滤波，提取样本图的抽象卷积特征从而得到原始图像的深度特征。如图1所示，给出了一个简单卷积特征提取结构，输入图像卷积后在C₁层产生若干特征映射图，然后特征映射图中每组的若干像素再进行求和，加权值与偏置，通过一个激活函数(Sigmoid、Relu)得到S₂层的特征映射图，这些映射图再经过滤波得到C₃层，这个层级结构再和S₂一样产生S₄。最终，这些像素值全连接成一个向量输入到传统的神经网络，得到输出。

1.2 基于深度学习的跟踪算法

深度学习在跟踪领域面临两个重要问题：1)深度学习网络在训练阶段需要大量的样本，而跟踪领域仅能够提供第一帧的目标进行训练，面临训练样本缺少问题；2)采用深度学习的网络模型运算时间复杂度大，跟踪实时性低。

针对以上问题，N.Y. Wang等^[17]提出DLT算法首次将深度学习算法应用到跟踪领域，在ImageNet数据集上使用栈式降噪自编码器离线预训练来获得通用的物体表征能力，并在跟踪过程中更新自编码器实现跟踪；K. Zhang等^[18]结合人脑视觉处理系统，简化了卷积网络结构，使用目标区域中随机提取的归一化图像块作为卷积神经网络的滤波器，从而实现了不用训练卷积神经网络的快速特征提取。文献[19]中的MDNet算法提出将训练方法和训练数据交叉运用的思路，在检测任务中重点关注背景中的难点样本，显著减轻了跟踪器漂移问题。

深度学习算法需要搭建专用的深度学习硬件平台，通过大量的前期预训练来训练神经网络提取深度特征，面临样本缺少，算法时间复杂度高，硬件运行平台要求高，跟踪实时性低等显著缺点。本文结合卷积神经网络在特征提取时能够获得一定的平移、尺度和旋转不变性且能够大幅降低神经网络规模的特性，结合文献[18]提出的无需训练的卷积特征提取方法，采用两层前馈处理方式简化卷积网络结构，通过分层滤波器卷积来抽取目标的高维抽象特征，利用高斯核函数进行运算加速，提出一种快速卷积神经网络跟踪算法。

2 高斯核函数卷积神经网络跟踪算法

针对卷积计算时间复杂度过高问题，本文引入高斯核函数进行变换，对算法的卷积运算实现加速；针对深度学习算法训练样本缺少的问题，本文采用简单两层前馈处理网络实现一种无需训练的特征提取方法。

2.1 核函数卷积

本文的卷积运算采用高斯核函数进行变换加速运算，文献[15]采用子窗口高斯核函数 $k({{x}},{{x}}')$ 的快速计算方法，其向量表达式为

${k({{x,\,x'}})} = \exp ( - \frac{1}{{{{{\sigma}} ^2}}}({\left\| {{x}} \right\|^2} + {\left\| {{{x}}'} \right\|^2} - 2{F^{ - 1}}(\sum\limits_d {{{{\hat{ x}}}^*}} \odot {\hat{ x}}')))$

(1)

式中：“*”表示复共轭， $d$ 表示滤波器的个数。

假设 ${{\varphi}} ({{x}})$ 是一个高维核希尔伯特空间的映射，则核函数 $k({{x}},{{x}}') = \left\langle {{{\varphi}} ({{x}}),({{x}}')} \right\rangle $ ，权重可表示为v = $ \displaystyle\sum\limits_i {{a_i}{{\varphi}} ({x_i})} $ ，系数向量为 ${{\alpha}} $ ，其元素为 ${a_i}$ ，最终要求解的参数由 ${{v}}$ 变为 ${{\alpha}} $ ，因此，核正则化最小二乘分类器(kernelized regularized least square，KRLS)具有一个简单的闭式解，即

${{\alpha }} = {({{K}} + \lambda {{I}})^{ - 1}}{{y}}$

(2)

式中： ${{K}}$ 是核函数矩阵，矩阵元素为 ${K_{i,j}} = k({x_i},{x_j})$ ； ${{I}}$ 是单位矩阵；向量 ${{y}}$ 的元素为 ${y_i}$ 。由于 ${{K}}$ 为循环矩阵，则式(2)可转换到DFT域，即

${{\hat{ \alpha }}^*} = {\hat{ y}} \times {({{\hat{ k}}^{xx'}} + \lambda )^{ - 1}}$

(3)

式中： ${{\hat{ k}}^{xx'}}$ 是核函数矩阵 ${{K}}$ 的第一行元素组成的向量，符号 $ \wedge $ 表示傅里叶变换。KRLS分类器的闭式解可利用FFT快速得到。

2.2 特征提取

本文利用卷积网络设计一个分层的目标表示结构。在第1帧中，将目标归一化到 $n \times n$ 大小，从中随机选取一部分重叠的小图像块组成一系列滤波器，用于同第 $t$ 帧候选目标框中所有抽取的图像块进行卷积，得到一系列局部特征的映射，提高候选目标全局特性的鲁棒性。

简单层特征，通过预处理将图像归一化到 $n \times n$ 大小，对目标区域利用 $w \times w$ 大小的滑动窗口进行采样，得到长度为 $L$ 的图像块组 $X$ ，然后用K-means聚类的方法从 $L = {(n - w + 1)^2}$ 个图像块中聚类出 $d$ 个图像块滤波器作为卷积核，记作F_d = $ \left\{ {{{F}}_1^o,{{F}}_2^o, \cdots ,{{F}}_d^o} \right\} \subset X$ 。输入图像I对应的响应为

${{S}}_i^o = {{F}}_i^o \otimes {{I}},\,\,{{S}}_i^o \in {R^{{{(n - w + 1)}^2}}}$

(4)

跟踪目标周围的上下文可为区分目标和背景提供大量有用信息，对目标周围的区域随机采样出 $l$ 个样本，同样进行K-means聚类获得一组背景模板：

${F_l} = \left\{ {{{F}}_1^b,{{F}}_2^b, \cdots ,{{F}}_l^b} \right\}$

(5)

最后，由目标卷积核减去背景卷积核与输入图像 ${{I}}$ 做卷积得到简单层的特征表达：

${{{S}}_i} = {{S}}_i^o - {{S}}_i^b = ({{F}}_i^o - {{F}}_i^b) \otimes {{I}},\,\,i \in \{ 1,2, \cdots ,d\} $

(6)

复杂层特征，为了加强对目标的特征表达，本文将 $d$ 个简单层的特征进行堆叠，构成一个3维张量来表示目标的复杂层特征，记作：

${{C}} \in {R^{(n - w + 1) \times (n - w + 1) \times d}}$

(7)

这种特征具有平移不变特性，由于图像归一化后，使得特征对目标的尺度具有鲁棒性，且复杂层特征保留不同尺度目标的局部几何信息。文献[20]表明可以通过一个浅层的神经机制实现跟踪，因此本文没有使用高层次的对象模型而是利用一个简单的模板匹配方案，结合粒子滤波实现跟踪。

2.3 粒子滤波

本文基于粒子滤波框架，设第 $t$ 帧时总的观测序列为 ${{{Z}}_t} = \{ {{{z}}_1},{{z}}_2, \cdots ,{{{z}}_t}\} $ ，则跟踪主要是求出后验概率 $p$ 的最大值，根据贝叶斯理论，可知：

$\begin{array}{c} p({{{S}}_t}|{{{Z}}_t}) \propto \\ p({{{Z}}_t}|{{{S}}_t})\int {p({{{S}}_t}|{{{S}}_{t - 1}})p({{{S}}_{t - 1}}|{{{Z}}_{t - 1}}){\text{d}}{{{S}}_{t - 1}}} \\ \end{array} $

(8)

式中： ${S_t} = {[{x_t}\,\,{y_t}\,\,{s_t}]^{\text{T}}}$ ， ${x_t}\text{、}{y_t}$ 为目标的位置， ${s_t}$ 为尺度参数； $p({{{S}}_t}|{{{S}}_{t - 1}})$ 为运动模型，用于根据第 $t - 1$ 帧的位置预测第 $t$ 帧的位置，假设目标状态参数是相互独立的，可用3个高斯分布来描述，从而运动模型即为布朗运动，于是

$p({{{S}}_t}|{{{S}}_{t - 1}}) = N({{{S}}_t}|{{{S}}_{t - 1}},\sum )$

(9)

式中： $\displaystyle\sum = {\text{diag}}({\sigma _x},{\sigma _y},{\sigma _t})$ 为对角协方差矩阵； $p({{{S}}_t}|{{{Z}}_{t}})$ 为观测模型，用于评估观测结果Z_t与目标的相似性。观测模型通过测量样本与目标之间的相似度来计算：

$p({{{Z}}_t}|{{S}}_t^i) \propto {{\text{e}}^{ - \left| {{\text{vec}}({{{C}}_t}) - {\text{vec}}({{C}}_t^i)} \right|_2^1}}$

(10)

于是，整个跟踪过程就是求最大响应：

${{\hat{ S}}_t} = \arg {\max _{\{ {{S}}_t^i\} _{i = 1}^{\text{N}}}}p({{{Z}}_t}|{{S}}_t^i)p({{S}}_t^i)$

(11)

2.4 跟踪算法

前文给出了简单前馈卷积网络的特征提取方式，并采用高斯核函数对卷积计算进行加速处理，获取目标的深层次复杂表示。基于这种卷积特征，结合粒子滤波，提出的跟踪算法流程如图2所示。

跟踪算法的主要步骤：

1)输入：输入视频序列，并给定跟踪目标。

2)初始化：归一化，粒子滤波，网络规模，样本容量等参数设置。

3)初始滤波器提取：利用第一帧的目标，通过滑动窗口和K-means聚类提取一个初始滤波器组用作后续网络的滤波器使用。

4)卷积特征提取：利用上文的卷积网络结构提取出各候选样本的深层抽象特征，并使用高斯核函数进行加速。

5)粒子滤波：按照粒子滤波算法，归一化后生成规定尺寸大小的候选图片样本集，并进行目标识别与匹配。

6)网络更新：采取限定阈值的方式，即当所有粒子中最高的置信值低于阈值时，认为目标特征发生较大表观变化，当前网络已无法适应，需要进行更新。利用初始滤波器组，结合跟踪过程中得到前景滤波器组，进行加权平均，得到全新的卷积网络滤波器。

7)模板更新：以第一帧中目标的中心点为中心，偏移量为±1个像素点范围内进行等尺寸采样，构成正样本集合。以当前帧目标的远近两类距离采样，构成负样本集合。跟踪过程中为了减轻漂移现象，预设一个更新阈值f=5，目标模板每5帧更新一次。

3 实验结果与分析

本文利用MATLAB2014a编程环境，PC配置为Inter Core i3-3220，3.3 GHz，8 GB内存，根据Database OTB2013^[3,21]中提供的测试视频序列对算法进行了仿真分析。本文仿真参数设置为：滑动窗口取片尺寸为6×6，滤波器个数为100，归一化尺寸为32×32，学习因子设置为0.95，粒子滤波器的目标状态的标准偏差设置为： ${\sigma _x} = 4,{\sigma _y} = 4,{\sigma _t} = 0.01$ ，使用N = 300个粒子。

3.1 定性分析

限于论文篇幅，本文仅给出几组代表性的跟踪实验结果。如图3(a)、(b)、(c)、(d)所示，比较的算法有CT^[7]、KCF^[15]、CNT^[18]与本文算法。图示给出Crossing、Football、Walking、Walking2四组序列，均存在目标形变问题，其中Crossing、Walking、Walking2均是在低分辨率场景下的跟踪，Football、Walking、Walking2均存在局部遮挡问题。对于Crossing序列，随着目标的运动导致目标本身的尺度变化，在低分辨率监控场景中，在第45帧，目标在行进过程中面临光线的干扰，并且出现运动车辆导致的背景干扰，在所有比较的算法中，同样跟踪成功，本算法性能都能达到最优。对于Football序列，目标在运动过程中，一直伴随着大量的形变问题，整个视频序列中大量的相似目标导致背景干扰问题，在第150帧目标进入人群中导致局部遮挡问题，本文算法在所有算法中表现最优。对于Walking序列，目标在监控的低分辨场景中，目标运动过程中伴随着一定的尺度变换，并在第90帧出现柱子遮挡目标的情况，本文算法在所有算法中表现最优。对于Walking2序列，在监控的低分辨场景中，目标运动途中伴随着尺度变换、遮挡、背景干扰。在第190帧与第360帧，目标均面临相似目标的背景干扰与遮挡，本文算法在所有算法中表现最优。

可见，本文算法在形变、遮挡、低分辨率等复杂背景干扰下均能取得有效的跟踪效果。

3.2 定量分析

为了测试算法性能，给出了部分序列的中心位置误差与距离精度的具体数据^[3,21]。中心位置误差(center location error，CLE)表示目标的中心位置与标准中心位置的欧氏距离的误差，表达式为ε = $ \displaystyle\frac{1}{n}\sum\limits_{i = 1}^n {\left\| {{{{C}}_i} - {{C}}_i^{\text{r}}} \right\|} $ ，n是图片序列的帧数， ${{{C}}_i}$ 为目标中心位置， ${{C}}_i^{\text{r}}$ 为标准中心位置；距离精度(distance precision，DP)表示中心误差小于一个给定阈值的帧的相对数量，表达式为 ${\rm{DP}} = \displaystyle\frac{m}{n}$ ，m为CLE小于某个固定阈值(实验中均选为20像素)的图片序列帧数。表1给出了算法的平均中心位置误差的对比数据，表2给出了算法的距离精度DP的对比数据。为保证数据真实性，本文所示数据均为5次实验后取平均值。

对于算法速度，同样采用卷积网络结构提取特征的CNT算法，与本文算法在相同实验环境下进行速度对比，CNT没有采用高斯核函数进行加速，算法速度为1~2 f/s，本文算法采用高斯核函数进行加速，算法平均速度为5 f/s。由实验可知，采用高斯核函数加速，在不影响跟踪精度的同时能够提升算法的速度。

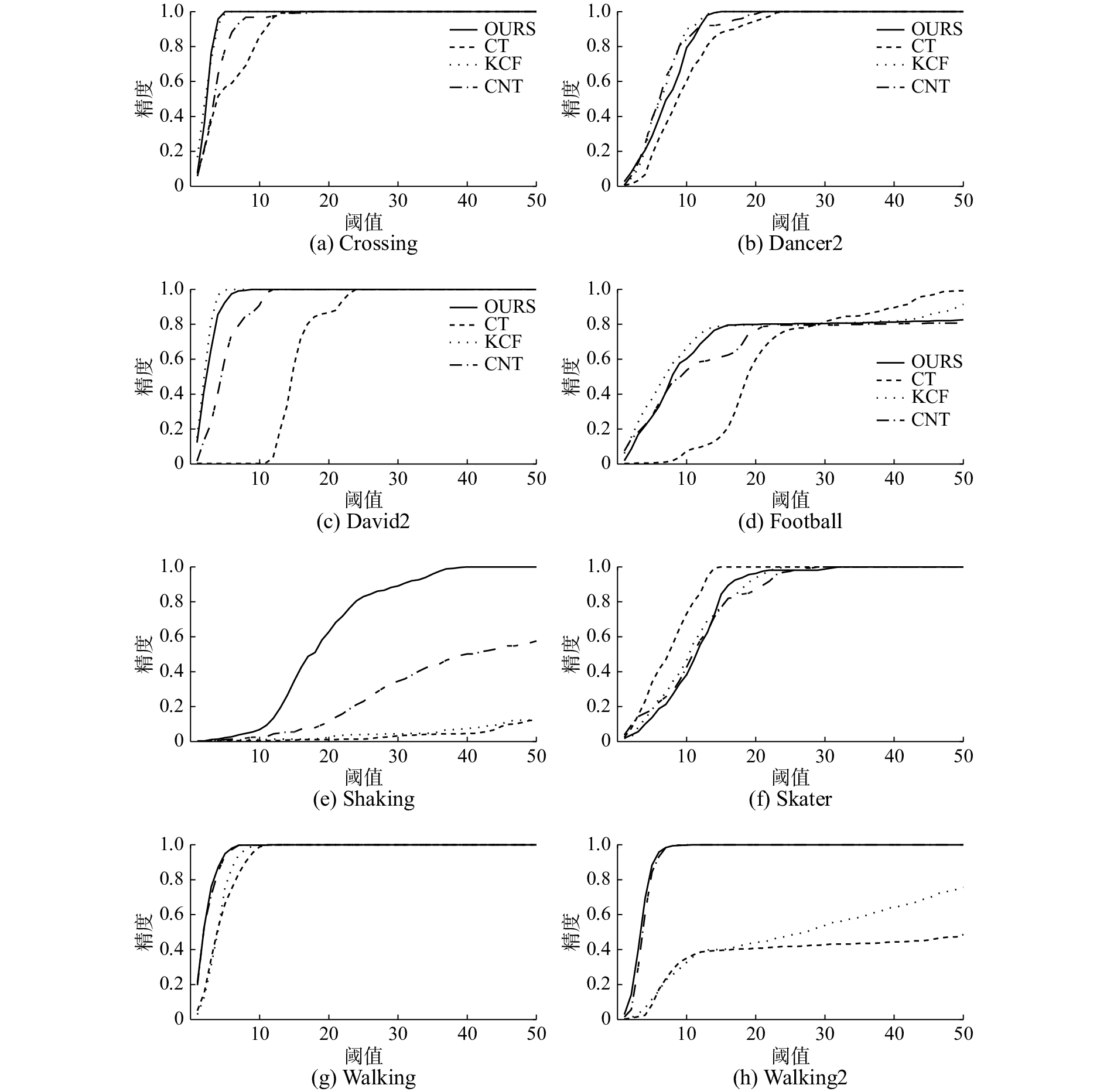
实验中，绘制了4种算法跟踪精度曲线图^[4]，跟踪精度曲线图首先设定一个目标估计位置与真实位置的阈值距离，在跟踪过程中，统计跟踪算法估计的目标位置与真实位置的距离小于阈值范围的帧数，并计算帧数占整个视频帧的百分比。图4给出了以上4种算法对应的8个视频序列的跟踪精度曲线，横坐标为阈值，纵坐标为精度，阈值越低而精度值越高的跟踪器性能越好。由曲线图可清晰地看到，本文算法具有较高的跟踪精度。

4 结束语

本文针对深度学习跟踪算法训练费时，硬件要求高等问题，采用高斯核函数加速计算，采用简单两层前馈卷积网络提取目标鲁棒性特征，基于简化的卷积神经网络提出跟踪算法，第一层利用K-means在第一帧中提取归一化图像块作为滤波器组提取目标的简单层特征，第二层将简单的单元特征图堆叠形成一个复杂的特征映射，并编码目标的局部结构位置信息，在粒子滤波框架下，在目标形变、遮挡、低分辨等场景下，脱离深度学习复杂的硬件环境，仍能取得较好跟踪效果。因为本文的特征提取方式采用卷积神经网络特征，所以本文算法在快速运动、目标出界等场景下仍面临很大挑战，在今后的工作中，将主要致力于解决此类场景的跟踪问题。