2. 华侨大学 计算机科学与技术学院, 福建 厦门 361021
2. School of Computer Science and Technology, Huaqiao University, Xiamen 361021, China
人工蜂群算法[1-3]是于2005年土耳其学者提出的用于解决优化问题的群智能算法。与其他智能算法相比,最大的优点在于:开采和开发同时进行,增加了寻找到最优解的概率。但它仍然存在收敛速度慢,易陷入局部最优,开采和开发能力不平衡等问题[4]。
针对以上问题,许多学者对该算法进行改进研究。G.Zhu和S. Kwong [5]受粒子群算法(particle swarm optimization,PSO)[6]的启发,提出了一种改进算法(gbest-guide ABC,GABC),通过把全局最优解加入到原始的搜索方程中,引导粒子向全局最优的方向更新,并通过测试函数验证了其有效性。Gao和Liu[7-11]对人工蜂群算法的改进进行了众多研究:在2011年,提出了IABC,采用logistic混沌映射进行初始化,并使用了ABC/best/1和ABC/rand/1两个搜索策略[7];2012年,提出MABC,通过正弦迭代器和反向学习方法进行初始化改进,并采用ABC/best/1进行迭代更新,具有很好的收敛性并得到了较高质量的解[8];2013年,提出PABC,采用Powell方法作为局部搜索工具以提高局部搜索能力[9];2014年,提出EABC,在采蜜蜂阶段和观察蜂阶段分别采用两种不同的搜索方程,以达到平衡开发和开采能力的效果[10];2015年,提出BABC,在观察蜂阶段采用高斯搜索方程生成新的候选个体提高开采能力[11]。虽然许多学者已对人工蜂群算法进行了各种改进,并取得了良好的效果,但是仍存在收敛速度慢、局部搜索能力弱的缺点,可继续改进。
针对以上问题,本文提出了一种收敛速度更快、局部搜索能力更强的人工蜂群算法。该算法采用高维混沌系统进行初始化,避免随机初始化带来的盲目性;并采用一种新的搜索策略,通过当前种群中的最优解引导进化方向,增强算法的局部搜索能力,进而达到提高解精度的效果,并且通过基于对数函数的适应度评价方式,增大个体间差异,减小选择压力,更容易选择出优秀个体。
1 基本的人工蜂群算法在人工蜂群算法中,把蜜蜂种群分为3种类型,即采蜜蜂、观察蜂和侦察蜂,把蜜蜂的行为分为以下3种,即搜索、招募和放弃[2]。在蜜蜂种群中取一半作为采蜜蜂,另一半作为观察蜂。蜜蜂种群在多维搜索空间中更新时,采蜜蜂负责根据自身经验搜索食物源,然后把食物源的具体信息告诉观察蜂;观察蜂根据采蜜蜂共享的信息选择将要跟随的蜜蜂;侦察蜂在食物源经过有限次搜索后仍未更新时发挥作用,重新初始化种群生成新的食物源。在优化问题中,食物源与优化问题的可行解相对应,采集食物源的过程相当于搜索最优解的过程。解的好坏取决于优化问题的适应度值,即较高的适应度值代表较好的食物源(可行解)。
首先,该算法根据公式(1)随机生成初始食物源(初始解):
| $ {x_i}^j = {x_{{\rm{min}}}}^j + {\rm{rand}}\left( {0, 1} \right)({x_{{\rm{max}}}}^j-{x_{{\rm{min}}}}^j) $ | (1) |
式中:i=1, 2, …, SN;j=1, 2, …, D;SN代表食物源(解)的个数;D表示解的维数;xminj和xmaxj分别表示解的下界和上界。
然后,采蜜蜂在食物源邻域进行搜索,寻找优良食物源的位置。当采蜜蜂搜索到食物源时,评估该食物源的适应度值。若该食物源具有较好的适应度值,则用新的食物源取代原来的食物源,否则不做更新。食物源邻域的搜索方程如式(2)所示:
| $ {v_i}^j = {x_i}^j + {\varphi _i}^j({x_i}^j-{x_k}^j) $ | (2) |
式中:xij表示第i个食物源的第j维,φij为[-1, 1]范围内的随机数,i∈[1, SN],j∈[1, D],k为随机选择的整数,k∈[1, SN],且k≠i。采用贪婪选择机制根据适应度值选择Vi和Xi。
对于最小化问题,适应度值的计算公式如式(3)所示:
| $ {\rm{fi}}{{\rm{t}}_i} = \left\{ \begin{array}{l} 1/(1 + {f_i}), {\rm{ }}{f_i} \ge 0\\ 1 + {\rm{abs}}({f_i}), {\rm{ }}{f_i} \le 0 \end{array} \right.{\rm{ }} $ | (3) |
式中:fi表示Vi对应的函数值,fi越小,则fiti越大。贪婪选择机制的公式如式(4)所示:
| $ P\{ {T_s}({X_i}, {V_i}) = {V_i}\} = \left\{ \begin{array}{l} 1, {\rm{ }}f({V_i}) \ge f({X_i})\\ 0, {\rm{ }}f({V_i}) < f({X_i}) \end{array} \right.{\rm{ }} $ | (4) |
式中:Ts表示蜜蜂个体间的一种映射关系,该式子能够确保种群中始终保留精英个体,即进化方向不会出现倒退现象。
采蜜蜂搜索结束后,进入观察峰阶段,该类蜜蜂指待在蜂巢内等待采蜜蜂采到食物源后返回分享食物源信息的个体。因此,观察蜂需要根据概率来选择将要跟随的采蜜蜂。概率选择公式如式(5)所示:
| $ {p_i} = \frac{{{\rm{fi}}{{\rm{t}}_i}}}{{\sum\limits_{i = 1}^{{\rm{SN}}} {{\rm{fi}}{{\rm{t}}_i}} }} $ | (5) |
当观察蜂根据式(5)选择到采蜜蜂进行跟随时,接下来观察蜂根据采蜜蜂共享的信息,到其附近进行局部深度搜索,搜索公式同式(2),然后再通过适应度值评估食物源的质量。
在经过一定次数的迭代之后(用limit表示迭代次数),若采蜜蜂或者观察蜂的食物源的质量一直没有更新,则认为该蜜蜂个体陷入了局部最优,此时放弃该食物源,并且采蜜蜂或观察蜂转变为侦察蜂,然后侦察蜂将会根据式(2)生成新的蜜蜂群体(新的可行解),进而跳出局部最优。
2 改进的人工蜂群算法在原始的人工蜂群算法中,初始种群由随机函数产生,所以该算法具有较强的全局搜索能力。但是,原始搜索方程的局部搜索能力比较弱,导致对解没有充分开采。全局搜索能力和局部搜索能力的不平衡是影响收敛速度和解质量的关键因素之一。另外,搜索进行到后期时,种群多样性会有所下降,严重影响算法的搜索效率。针对以上问题,本文提出3个改进策略提高算法的性能。
2.1 种群初始化种群初始解的质量在一定程度上影响最终解的质量,初始解分布越均匀,覆盖越广泛,在最优解邻域搜索的可能性就越大。所以,我们需要设计一种策略增加种群多样性。
混沌是一种非线性现象,具有随机性、遍历性和有界性。在一定范围内,根据规则可不重复地转变成所有状态。B. Alatas[12]已证明混沌映射是一种可有效地在整个搜索空间搜索解的方法。目前,应用在群智能算法上的混沌系统大多数为一维的,但是,一维混沌系统具有以下不足:1)迭代操作后产生单一序列;2)分布不均匀。因此,本文提出采用一种高维的混沌系统——洛伦兹混沌系统,该系统可产生3个不同的混沌迭代序列,增加了优良序列的可选择性,提高了序列的分布性。混沌迭代序列的生成公式如式(6)所示:
| $ \left\{ \begin{array}{l} \dot x = \delta \left( {y-x} \right)\\ \dot y = \gamma x-y-xz\\ \dot z = xy - \beta z \end{array} \right. $ | (6) |
式中:取x(0)、y(0)、z(0)为初始值;δ、γ、β为洛伦兹系统的参数,取值分别为δ=10,β=8/3, γ>24.74。最后,从产生的三组混沌序列中随机选一维,记作φ,把该参数代入式(1), 得到新的初始化方程,如式(7)所示:
| $ {x_i}^j = {x_{{\rm{min}}}}^j + \varphi ({x_{{\rm{max}}}}^j-{x_{{\rm{min}}}}^j) $ | (7) |
式中:i=1, 2, …, SN;j=1, 2, …, D;SN表示食物源(解)的数量;D表示解的维数;φ由混沌系统得到;xminj和xmaxj分别为函数的下界和上界。由混沌系统得出的φ与随机参数rand(0, 1)相比,可避免初始解的盲目性。
2.2 改进的适应度评价方式在原始人工蜂群算法中,观察蜂通过式(5)的概率选择优良食物源跟随,进行局部开采。概率的大小反映了采蜜蜂携带食物源的质量,食物源质量通过适应度值体现,适应度值越大,食物源质量越好,被选择的概率就越大。但是,在式(3)中,当函数值fi满足条件lim fi=0, lim fj=0, fi≠fj时,适应度值则lim fiti=1, lim fitj=1,那么公式(5)中的概率值也会相同,体现不出个体之间的差异[8]。为了解决该问题,本文采用基于对数的适应度评价方式,通过该方法把个体间差异明显化,进而把函数值相似但不同的种群个体区分开,使得优秀个体有更大的概率被跟随开采[13]。改进后的适应度评价方式如式(8)所示:
| $ {\rm{fi}}{{\rm{t}}_i} = 0.1/(0.1 + 1/\left| {{\rm{lg}}\;{f_i}} \right|), {\rm{ }}0 \le {f_i} \le {10^{-\lambda }} $ | (8) |
式中:λ由计算机的计算精度决定。此处,取λ=8。
2.3 新的搜索机制因为搜索能力不平衡会导致寻优能力下降,所以平衡算法的开发(全局搜索)和开采(局部搜索)能力是提高算法性能的措施之一。从原始人工蜂群算法的搜索方程式(2)可以看出:系数φij是[-1, 1]中的一个随机数,参数j和k为[1, D]中的随机整数,这些随机数使得算法具有较好的全局搜索能力,而局部搜索能力较弱。所以,需要设计一种局部搜索能力较强的搜索策略平衡搜索能力。受微分进化算法[14]的启发,本文提出了一种新的搜索策略,如
式(9)所示:
| $ {v_i}^j = {x_{{\rm{best}}}}^j + {\phi _i}^j({x_{{\rm{best}}}}^j-{x_r}^j) $ | (9) |
式中:r为{1, 2, …, SN}内的随机整数,且r≠i;i和j的含义同式(2);ϕij为[-1, 1]内的随机数;xrj为第r个蜜蜂的第j维;xbestj代表当代种群中最优个体的第j维,即当前种群最优解引导下一代个体的进化方向,可以达到增强局部搜索能力和提高解精度的效果。
2.4 改进算法流程图通过以上分析可得出:以上策略可以平衡算法的搜索能力,提高算法的性能。改进算法的具体流程如图 1所示。
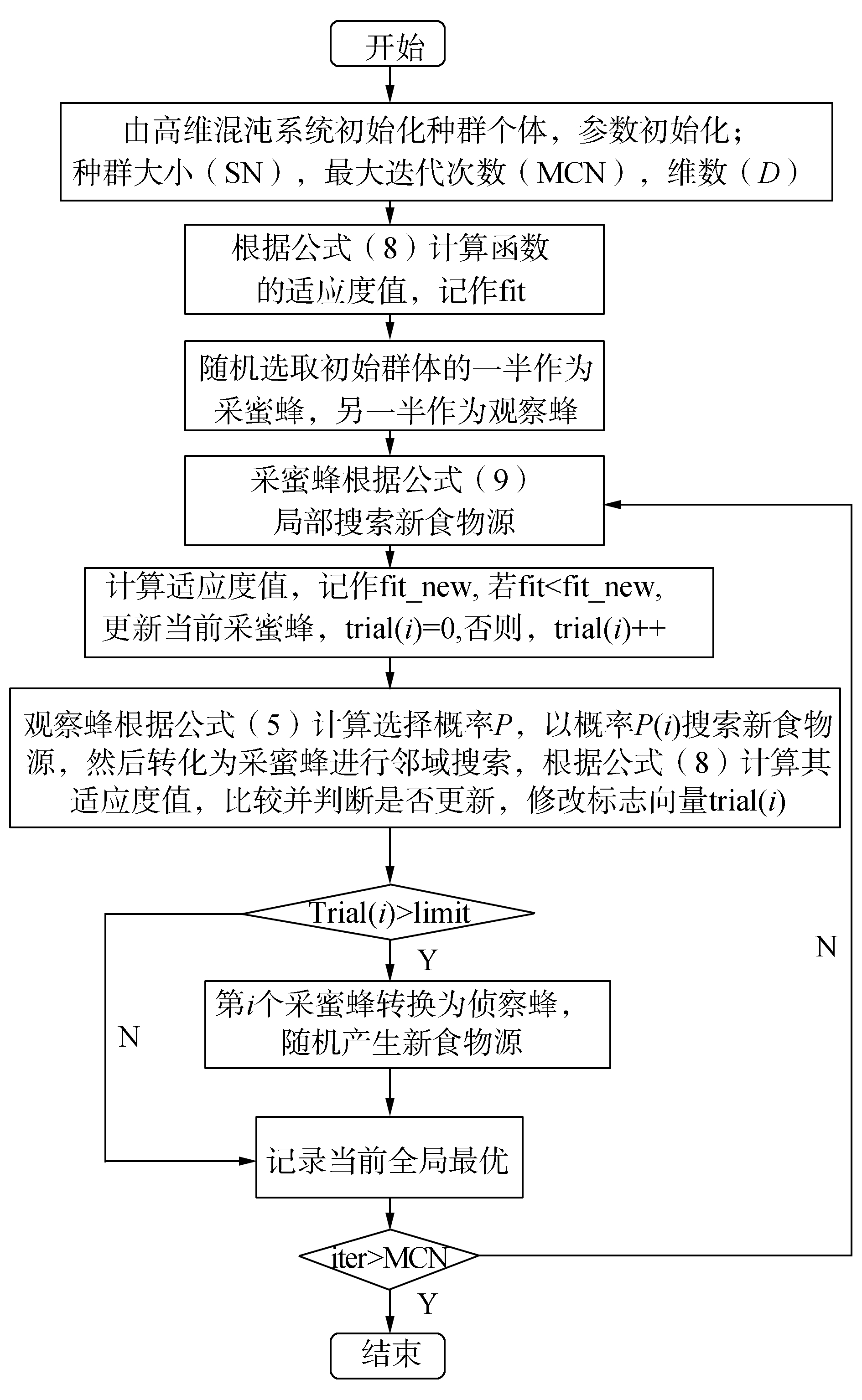
|
图 1 ESABC算法流程图 Fig.1 ESABC flowchat |
为了验证ESABC的性能,本文采用12个基准测试函数进行实验。表 1给出了测试函数的编号、名称、理论最优值和搜索范围。其中,F01~F04为单峰函数,F05~F12为多峰函数。函数的具体定义见参考文献[15-17]。
| 表 1 基准函数 Tab.1 Benchmark Functions |
本文改进算法ESABC与ABC[2]和GABC[5]进行对比,参数设置如下:SN=150,limit=100,MCN=1 000。3个算法在相同的实验背景下运行,且每个测试函数独立运行10次以避免偶然性,并记录最优值、最差值、平均值和方差。表 2和表 3分别为D=30和D=60的实验结果。其中,D=30的情况在11个函数进行测试,D=60的情况在10个函数进行测试。
| 表 2 实验结果(D=30) Tab.2 Experiential results(D=30) |
| 表 3 实验结果(D=60) Tab.3 Experiential results(D=60) |
由表 2可看出:对于单峰函数,ESABC解的精度和稳定性均优于ABC和GABC;对于多峰函数,除了himmelblau函数,ESABC的性能均优于ABC和GABC。除此之外,根据图 2可以更形象地比较3个算法的收敛速度,由图 2可以看出:对于himmelblau函数,3个算法的收敛精度一样,ESABC的收敛速度比GABC慢,比ABC快;对于其他函数,ESABC的收敛精度均好于ABC和GABC,收敛速度总体上快于另外两个算法。在图 2、3中,纵坐标平均误差为lg(|f(x)-f(x*)|,f(x)表示实际函数值,f(x*)表示理论函数值)。
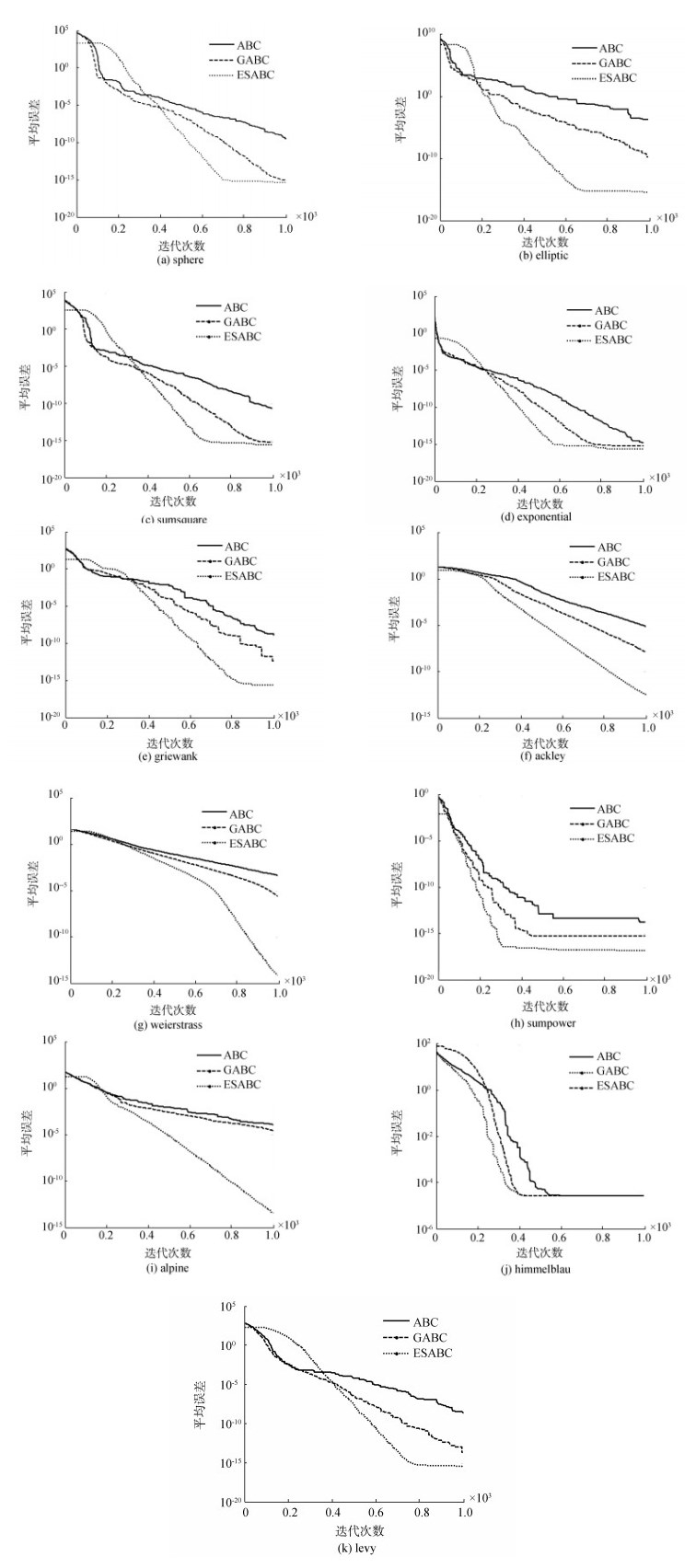
|
图 2 进化曲线(D=30) Fig.2 Evolution curves(D=30) |
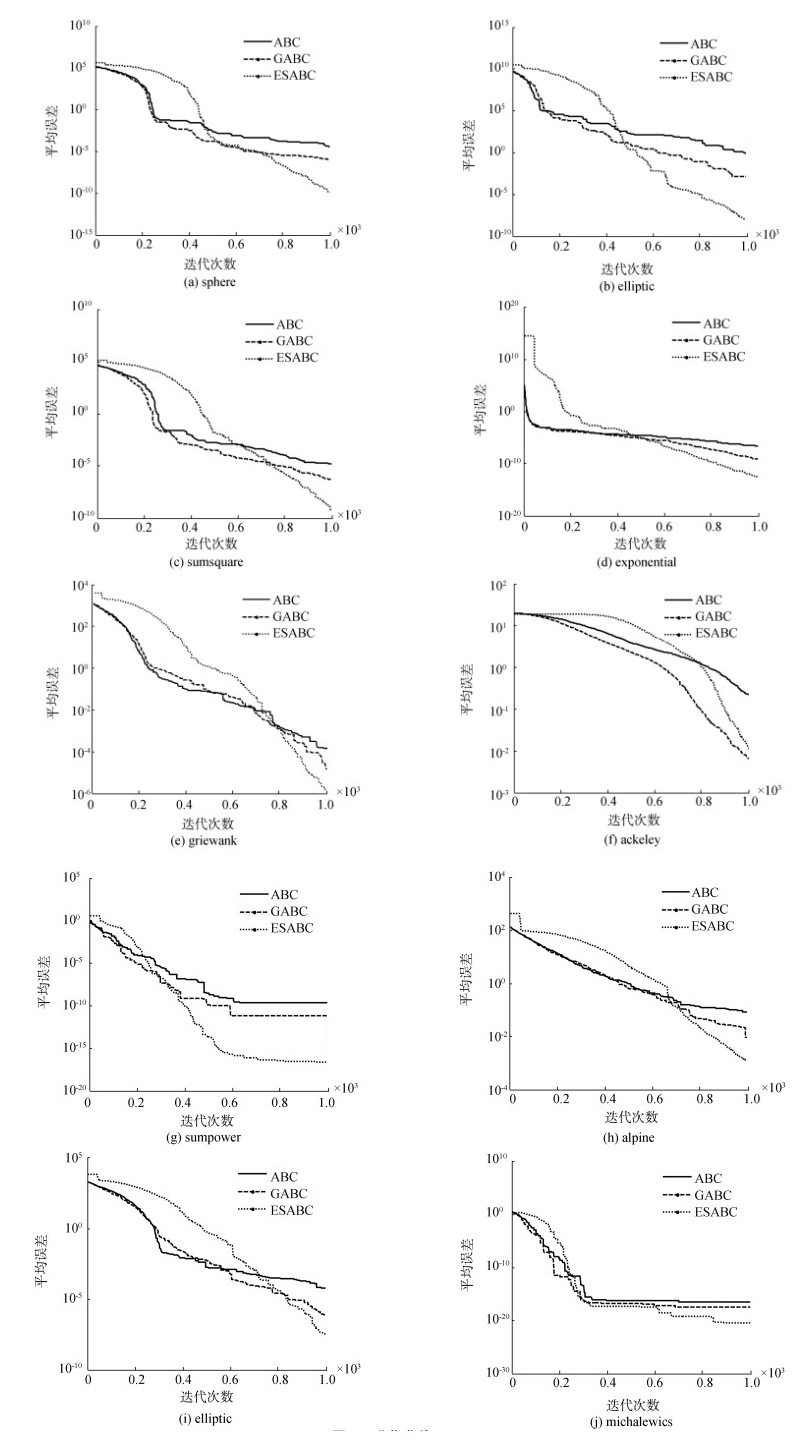
|
图 3 进化曲线(D=60) Fig.3 Evolution curves(D=60) |
由表 3可以看出:D=60时,除了ackley函数,ESABC的解均优于ABC和GABC。由图 3可看出:ackley函数的精度和收敛速度都差于GABC,优于ABC。
总体来说,ESABC在解的精度和收敛速度方面都有所提高。
4 结束语本文针对基本ABC算法存在初始化群体分布不均匀和局部搜索能力弱的问题,提出了一种基于增强局部搜索能力的人工蜂群算法。该算法首先采用洛伦兹混沌系统将初始解的分布尽量均匀化,然后采用改进的搜索策略以达到增强局部搜索能力的效果,并通过基于对数函数的适应度评价方式减小选择压力,更容易选择出优秀个体。通过12个测试函数的仿真实验表明,本文算法能够提高基本人工蜂群算法的性能,但该算法也有其局限性,并不能解决所有的问题。如何使算法能够有更好的普适性以及将所采用到的改进策略应用到多目标优化、机器人路径规划等领域是下一步的研究工作。
| [1] |
KARABOGA D. An idea based on honey bee swarm for numerical optimization. technical report-TR06[R]. Kayseri:Erciyes University, 2005.
( 0) 0)
|
| [2] |
KARABOGA D, BASTURK B. On the performance of artificial bee colony (ABC) algorithm[J]. Applied soft computing, 2008, 8(1): 687-697. DOI:10.1016/j.asoc.2007.05.007 ( 0) 0)
|
| [3] |
KARABOGA D, AKAY B. A comparative study of artificial bee colony algorithm[J]. Applied mathematics and computation, 2009, 214(1): 108-132. DOI:10.1016/j.amc.2009.03.090 ( 0) 0)
|
| [4] |
秦全德, 程适, 李丽, 等. 人工蜂群算法研究综述[J]. 智能系统学报, 2014, 9(2): 127-135. QIN Quande, CHENG Shi, LI Li, et al. Artificial bee colony algorithm:a survey[J]. CAAI transactions on intelligent systems, 2014, 9(2): 127-135. DOI:10.3969/j.issn.1673-4785.201307019 (  0) 0)
|
| [5] |
ZHU G, KWONG S. Gbest-guided artificial bee colony algorithm for numerical function optimization[J]. Applied mathematics & computation, 2010, 217(7): 3166-3173. ( 0) 0)
|
| [6] |
姜建国, 叶华, 刘慧敏, 等. 融合快速信息交流和局部搜索的粒子群算法[J]. 哈尔滨工程大学学报, 2015, 36(5): 687-691. JIANG Jianguo, YE Hua, LIU Huimin, et al. Particle swarm optimization method with combination of rapid information communication and local search[J]. Journal of Harbin engineering university, 2015, 36(5): 687-691. (  0) 0)
|
| [7] |
GAO Weifeng, Liu Sanyang, et al. Improved artificial bee colony algorithm for global optimization[J]. Information processing letters, 2011, 111(17): 871-882. DOI:10.1016/j.ipl.2011.06.002 ( 0) 0)
|
| [8] |
GAO Weifeng, LIU Sanyang. A modified artificial bee colony algorithm[J]. Computers and operations research, 2012, 39(3): 687-697. DOI:10.1016/j.cor.2011.06.007 ( 0) 0)
|
| [9] |
GAO W F, LIU S Y, HUANG L L. A novel artificial bee colony algorithm with method[J]. Applied soft computing, 2013, 13(9): 3763-3775. DOI:10.1016/j.asoc.2013.05.012 ( 0) 0)
|
| [10] |
GAO W F, LIU S Y, HUANG L L. Enhancing artificial bee colony algorithm using more information-based search equations[J]. Information sciences, 2014, 270(1): 112-133. ( 0) 0)
|
| [11] |
GAO W, CHAN F T S, HUANG L, et al. Bare bones artificial bee colony algorithm with parameter adaptation and fitness-based neighborhood[J]. Information sciences, 2015, 316(C): 180-200. ( 0) 0)
|
| [12] |
ALATAS B. Chaotic bee colony algorithms for global numerical optimization[J]. Expert systems with applications, 2010, 37(8): 5682-5687. DOI:10.1016/j.eswa.2010.02.042 ( 0) 0)
|
| [13] |
陈杰, 沈艳霞, 陆欣. 基于信息反馈和改进适应度评价的人工蜂群算法[J]. 智能系统学报, 2016, 11(2): 172-179. CHEN Jie, SHEN Yanxia, LU Xin. Artificial bee colony algorithm based on information feedback and an improved fitness value evaluation[J]. CAAI transactions on intelligent systems, 2016, 11(2): 172-179. (  0) 0)
|
| [14] |
YI, Wenchao, et al. Differential evolution algorithm with variable neighborhood search for hybrid flow shop scheduling problem[C]//IEEE, International Conference on Computer Supported Cooperative Work in Design IEEE. Nanchang, China 2016:233-238.
( 0) 0)
|
| [15] |
KIRAN M S, HAKLI H, GUNDUZ M, et al. Artificial bee colony algorithm with variable search strategy for continuous optimization[J]. Information sciences, 2015, 300: 140-157. DOI:10.1016/j.ins.2014.12.043 ( 0) 0)
|
| [16] |
SUGANTHAN P N, HANSEN N, LIANG J J, et al. Problem definitions and evaluation criteria for the CEC 2005 special session on real-parameter optimization[R]. KanGAL Report #2005005. India:ⅡT Kanpur, 2005.
( 0) 0)
|
| [17] |
王志刚, 王明刚. 基于符号函数的多搜索策略人工蜂群算法[J]. 控制与决策, 2016, 31(11): 2037-2044. WANG Zhigang, WANG Minggang. Multi-search strategy of artificial bee colony algorithm based on symbolic function[J]. Control and decision, 2016, 31(11): 2037-2044. (  0) 0)
|
 2017, Vol. 12
2017, Vol. 12


