随着复杂网络研究的兴起,许多现实世界中的系统都可以使用复杂网络进行描述。系统中的元素被视为网络中的节点,节点的边用来表示元素之间的相互作用和关系。例如,现实社会中的演员合作网、交通运输网、Internet网等都可以用复杂网络进行描述。现实网络规模巨大,节点间联系多而复杂的拓扑结构引起许多学者的极大兴趣,对其进行了大量的研究。
1 网络博弈研究现状最为成功的复杂网络模型当属WS小世界网络模型[1]和BA无标度网络模型[2]。许多复杂网络方面的研究都是基于这两个模型而展开的。然而这两个模型都有不足之处,不能真实再现现实中的网络结构。WS模型具有与现实网络相符合的高聚类系数特征,但其度分布为泊松分布,这与现实网络不符。BA模型的度分布具有与现实相符的幂律特点,但其聚类系数却很低,这一特征与现实网络尤其是社会网络的特征相去甚远。
有鉴于此,Holmes和Kim[3]构造了一种可调聚类系数的网络模型(HK模型),该模型利用一个可调参数
复杂网络上的博弈研究始于Nowak和May[14]研究的囚徒困境博弈在规则方格网络上的动态演化,研究发现合作者在方格网络上可以通过聚集来抵抗背叛策略入侵。受此影响,许多学者采用不同的博弈模型在不同的网络结构上进行研究,得到了丰富的理论成果。例如,文献[15]研究了可调聚类系数的无标度网络上的合作现象,研究发现高聚类系数有利于网络中合作行为的演化;文献[16]研究了齐次网络上的囚徒困境博弈,研究结果表明改变收益矩阵中的参数确实会影响系统的演化过程;Li等[17]在3种规则网络上研究了雪堆博弈,研究发现在复制动力学策略调整规则下可以抑制合作行为的参数区间;Zhang等[18]研究了随机规则网络上的雪崩博弈,研究发现当雪崩博弈成本收益率较小时,系统演化为全面合作状态,反之合作与背叛在系统中共生;文献[19]研究了基于记忆效应的囚徒博弈在相互依存网络中的合作现象,发现了与记忆长度和依赖程度相关的最优参数区间,可以极大地促进网络中合作现象的涌现;文献[20]研究了加权网络空间上的囚徒博弈,通过仿真实验发现网络中合作者密度会随网络耦合程度的升高而变大;文献[21]研究双复杂网络上的囚徒博弈,可以提高合作的水平,同时也揭示双网络模型下背叛领袖对合作水平的影响及其与合作领袖的互动机理。
受以上研究启发,本文提出了一种改进的HK网络模型,改进后的模型在服从幂律分布且幂律可调的情况下与HK网络模型相比具有更高的聚集系数。由于网络结构的改变是影响演化博弈的一个重要因素,本文在改进的HK网络模型上采用囚徒博弈模型,进一步研究了网络结构对博弈中合作行为的影响。
2 改进的HK网络模型 2.1 网络模型内部演化机制现实的社会网络中,相识的两个人可能同时认识一个新的朋友,进而有一定的机率同时认识这个新朋友的朋友,本文提出的改进后的HK模型正是反映了这种情况。
HK网络构造过程如下。
1)初始状态:网络初始状态有
2)增长机制:每一个时间步,向网络中加入一个带有
3)其余
在此基础上,本文提出了如下改进HK网络模型(EHK)的演化机制。
1)初始状态: 网络初始状态有
2)增长机制: 每一个时间步,加入两个连接在一起的节点,每个节点有
3)其余
4)若
5)终止条件: 重复2)、3)、4)步,直至网络规模
根据EHK网络模型演化机制,经过
| $\begin{array}{*{20}{c}}{\displaystyle\frac{{{\rm{d}}{k_i}}}{{{\rm{d}}t}}} = {\displaystyle\frac{{2{k_i}}}{{\sum\limits_l {{k_l}} }} + \left( {2m - 2} \right)p\left( {\frac{{{k_{{j_1}}}\displaystyle\frac{1}{{{k_{{j_1}}}}}}}{{\sum\limits_l {{k_l}} }} + \frac{{{k_{{j_2}}}\displaystyle\frac{1}{{{k_{{j_2}}}}}}}{{\sum\limits_l {{k_l}} }} + \cdots + \displaystyle\frac{{{k_{{j_v}}}\displaystyle\frac{1}{{{k_{{j_v}}}}}}}{{\sum\limits_l {{k_l}} }}} \right)}+\\{ \left( {2m - 2} \right)\left( {1 - p} \right)\displaystyle\frac{{{k_i}}}{{\sum\limits_l {{k_l}} }} = 2m\frac{{{k_i}}}{{\sum\limits_l {{k_l}} }}}\end{array}$ | (1) |
式中
网络中的节点每增加一条连边,网络中的度增加2。每一时刻网络中增加2个节点,网络中增加
| $\frac{{{\rm{d}}{k_i}}}{{{\rm{d}}t}} = 2m\frac{{{k_i}}}{{\sum\limits_l {{k_l}} }} = 2m\frac{{{k_i}}}{{\left( {4m + 2} \right)t}} = \frac{{m{k_i}}}{{\left( {2m + 1} \right)t}}$ | (2) |
解该方程:
| ${\rm{ln}}{k_i} = \frac{m}{{2m + 1}}{\rm{ln}}t + c$ | (3) |
将节点
| $c = {\rm{ln}}\frac{{m + 1}}{{t_i^{\frac{m}{{2m + 1}}}}},\;\;\;\;{k_i} = \left( {m + 1} \right){\left( {\frac{t}{{{t_i}}}} \right)^{\frac{m}{{2m + 1}}}}$ | (4) |
节点
| $\begin{array}{*{20}{c}} {P\left( {{k_i} < K} \right)} = {P\left( {\left( {m + 1} \right){{\left( {\displaystyle\frac{t}{{{t_i}}}} \right)}^{\frac{m}{{2m + 1}}}} < K} \right)} = \\ {P\left( {{t_i} > \displaystyle\frac{t}{{{{\left( {\displaystyle\frac{k}{{m + 1}}} \right)}^{2m + 1}}}}} \right)} \end{array} $ | (5) |
假设等时间间隔向网络中增加节点,则
| $\begin{array}{c}P\left( {{k_i} < K} \right) = P\left( {{t_i} > \displaystyle\frac{t}{{{{\left( {\displaystyle\frac{k}{{m + 1}}} \right)}^{2m + 1}}}}} \right) = \\1 - \displaystyle\frac{1}{{{m_0} + t}}\displaystyle\frac{t}{{{{\left( {\displaystyle\frac{k}{{m + 1}}} \right)}^{\frac{{2m + 1}}{m}}}}}\end{array}$ | (6) |
进而有
| $ {p\left( k \right)} = {\displaystyle\frac{{{\rm{d}}P\left( {{k_i} < K} \right)}}{{{\rm{d}}k}}} = {\displaystyle\frac{{t\left( {2m + 1} \right){{\left( {m + 1} \right)}^{\LARGE\frac{{2m + 1}}{m}}}}}{{m\left( {{m_0} + t} \right)}}{k^{ - 3 - \frac{1}{m}}}} $ | (7) |
由式
这表明,本文提出的EHK模型的度分布近似服从幂指数
由网络模型的构造算法可看出每一个时间步引入的节点与网络中已存在的节点每进行一次成功连接,必然构造出一个局部三角形结构,通过聚类系数的定义直观上可以看出由该演化机制构造的网络模型必然具有更高的聚类系数。
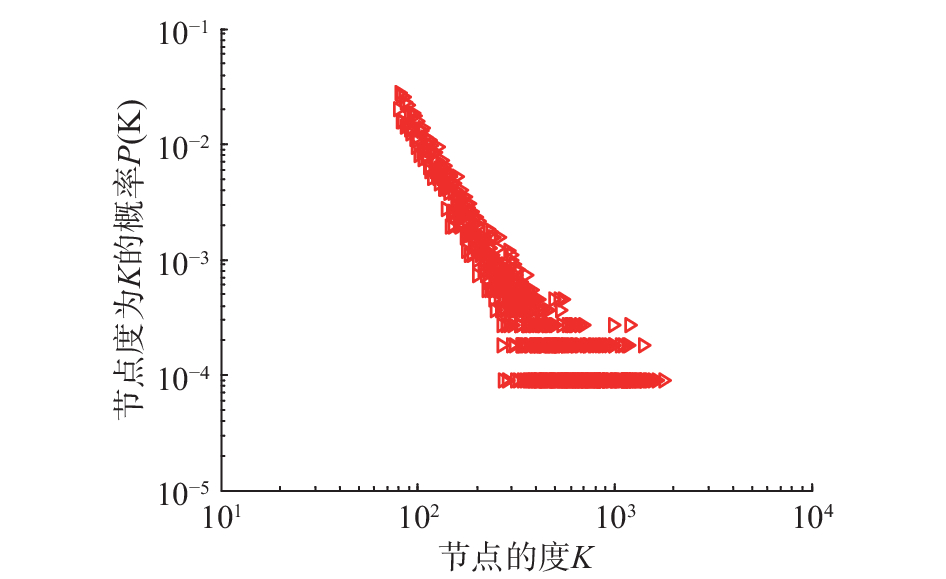
2.3 仿真分析为验证2.2节中的结论,检验提出的EHK网络模型是否会继承HK网络模型度分布服从幂律分布这一特性,本文通过仿真实验做出EHK网络的度分布图(见图1)。图1中网络初始状态为
|
Download:
|
| 图 1 EHK网络节点度分布图 Fig. 1 Degree distribution of EHK networks | |
此外,网络中节点
| ${C_i} = \frac{{\text{包含节点}i\text{的三角形的数目}}}{{\text{以节点}i\text{为中心的连通三元组的数目}}}$ | (8) |
对网络所有节点的聚类系数
| ${\rm{CC}} = \frac{1}{N}\sum\limits_{i = 1}^N {{C_i}} $ | (9) |
网络的平均聚类系数CC可以用来描述网络中节点之间形成三角形结构的趋势。其值反映了网络中三角结构连接的密度。由网络模型的构造算法可看出,每一个时间步引入的节点与网络中已存在的节点每进行一次成功连接,必然构造出一个局部三角形结构。通过聚类系数的定义直观上可以看出,由该演化机制构造的网络模型必然具有更高的聚类系数。
图2中的仿真结果显示了本文提出的网络模型的聚类系数与HK模型平均聚类系数的比较,初始条件为

|
Download:
|
| 图 2 EHK网络与HK网络平均聚类系数对比 Fig. 2 Comparison of the average clustering coefficient between EHK and HK | |
由仿真结果可见,相同条件下,聚类系数的值随可调节概率
| $C(k) = \frac{{\sum\limits_i {{C_i}{\omega _{{k_i}k}}} }}{{\sum\limits_i {{\omega _{{k_i}k}}} }}$ | (10) |
其中
| ${\omega _{{k_i}k}} = \left\{ {\begin{array}{*{20}{c}} {1,}&{{k_i} = k} \\ {0,}&{{k_i} \ne k} \end{array}} \right.$ | (11) |
研究表明,许多真实网络的

|
Download:
|
|
图 3 平均聚类系数
|
|
真实世界的网络往往为幂律网络,且具有高聚类的特性。由图1和图2的分析可知,本文构建的网络模型成功再现了这两个特征,并且图3的仿真结果也说明本文构建的网络符合现实网络的特征,由此可见本文所构建的网络模型能够很好地描述真实网络结构特性。
3 EHK网络上囚徒博弈 3.1 囚徒博弈模型在囚徒困境博弈模型(prisoner’s dilemma game,PDG)中,每个人都有两种选择合作(cooperation,C)与背叛(defection,D)。其收益矩阵为
| $\begin{array}{*{20}{c}} {}&{\begin{array}{*{20}{c}} C&D \end{array}} \\ {\begin{array}{*{20}{c}} C \\ D \end{array}}&{\left[ {\begin{array}{*{20}{c}} {{R}}&{{S}} \\ {{T}}&{{P}} \end{array}} \right]} \end{array}$ | (12) |
式中:最左侧一列代表自己的选择;最上面一行代表对方的选择;R为相互合作的奖励,即(C, C)策略组合中,选择C策略所获得的个体收益;S为给傻瓜的报酬,即(C, D)策略组合中选择D策略所获得的个体收益;T为背叛的诱惑(temptation to defect),即(D, C)策略组合中,选择D策略的个体收益;P为相互背叛的惩罚,即(D, D)策略组合中,采用D策略的个体收益,且满足T>R>P>S,2R>T+S。在上述情形下,理性的参与者总是会选择背叛策略作为自己的最佳策略,但从总体而言只有都选择合作策略才能使收益达到最大。然而当理性的参与者相互背叛时,没有参与者愿意单方面改变自己的策略,因为这样做会降低自身的收益,因此相互背叛状态(D, D)就构成了囚徒博弈的纳什均衡状态。
本文提出的EHK网络中每一个节点代表一个博弈个体。采用由Nowak和May提出的简化的单参数囚徒博弈模型,其收益矩阵为
| ${{P}} = \left[ {\begin{array}{*{20}{c}} 1&0 \\ b&0 \end{array}} \right]$ | (13) |
式中
| ${U_i} = \sum\limits_{j \in {\varOmega _i}} {{{S}}_i^{\rm{T}}{{P}}{{{S}}_j}} $ | (14) |
式中
| ${p_{i \leftarrow j}} = \frac{{{u_j} - {u_i}}}{{\left( {{{T}} - {{S}}} \right)\max \left( {{k_i},{k_j}} \right)}}$ | (15) |
式中
此外合作者密度
由第2节的研究可知,相同条件下可调节概率
|
Download:
|
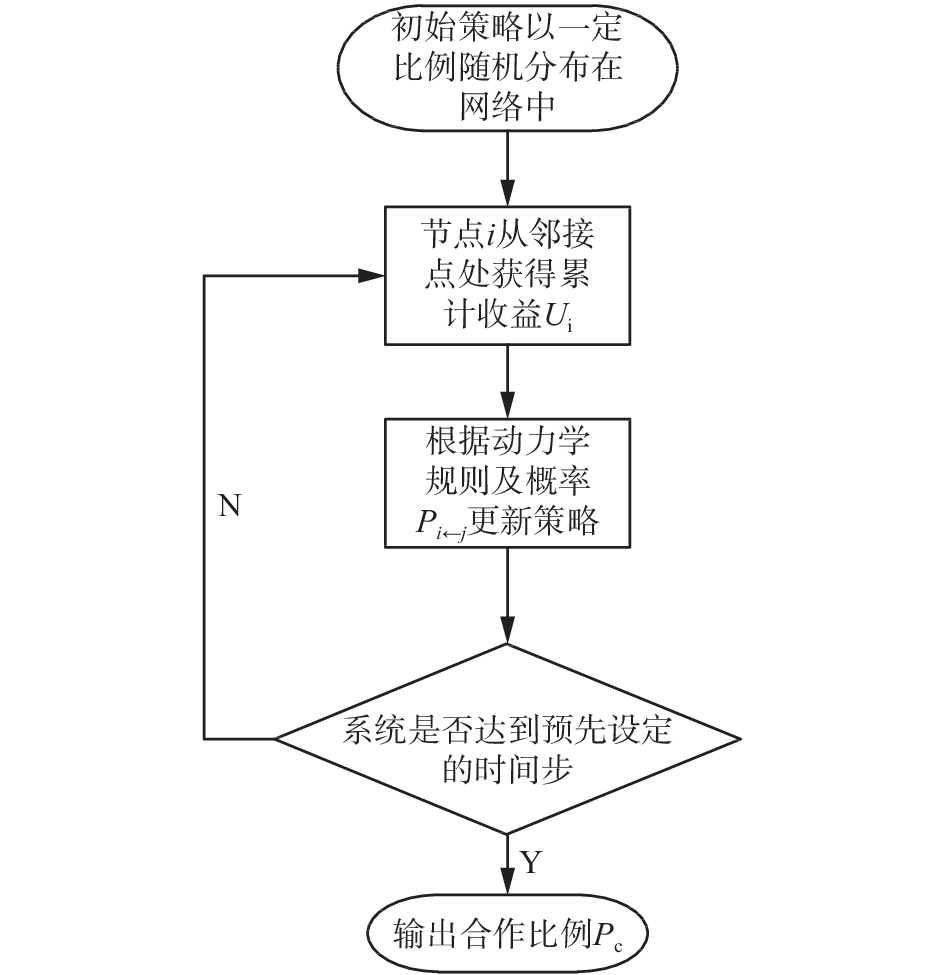
| 图 4 博弈演化流程 Fig. 4 Process of game evolution | |
|
Download:
|
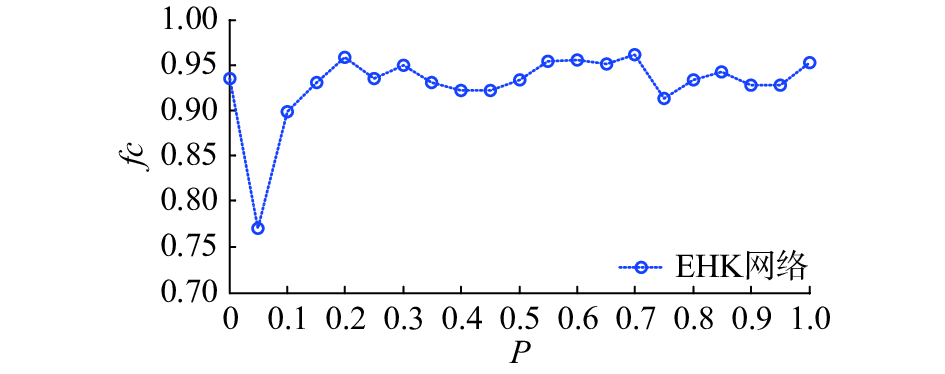
| 图 5 合作者比例随聚类系数变化 Fig. 5 Variation in the partner proportion and clustering coefficient | |
图5中每个数据是相同初始条件下10次重复实验所得到的平均值。由图5仿真结果可知合作者比例维持在0.75以上,这充分表明EHK网络对合作行为具有较大的促进作用。其原因是,EHK网络是高聚类异质网络,其中必然会存在许多具有多三角形结构的高连接度的hub节点,若hub节点选择合作策略,由于其采用累计收益的计算方式,会使hub节点获得较高的收益,由式(15)可知其所采用的合作策略容易被其低收益的邻居节点采纳。由式(13)可知采用(C, C)策略的双方收益都为1,而hub节点采用累计收益的计算方式,会使其始终成为被模仿的对象,这有利于合作行为在网络中进行传播。
若hub节点初始采用背叛策略,则由累计收益的计算方式和式(13)可知,hub节点会从其大量采用合作策略的邻居中获得较高的收益,由博弈演化策略可知,这些采用背叛策略的邻居在进行策略调整时会模仿hub节点的背叛策略,而由式(13)可知采用(D, D)策略的双方收益为零,故在下一次的网络博弈中hub节点的收益会随着采用背叛策略邻居增多而大幅下降。
随着网络博弈的进行,hub节点的收益会下降到使其本身所采用的背叛策略不再是其邻居节点模仿的对象,进而在某一时刻hub节点会模仿其邻居的合作策略,此时利用其hub节点本身具有的多连接的资源优势随着网络博弈的进一步演化会逐渐使其采用的合作策略成为被邻居节点模仿的对象。
由上述分析可知合作策略容易占据网络中的高度连接的hub节点,进而影响其周围邻居也采用合作策略,促进在EHK网络上合作现象的涌现。
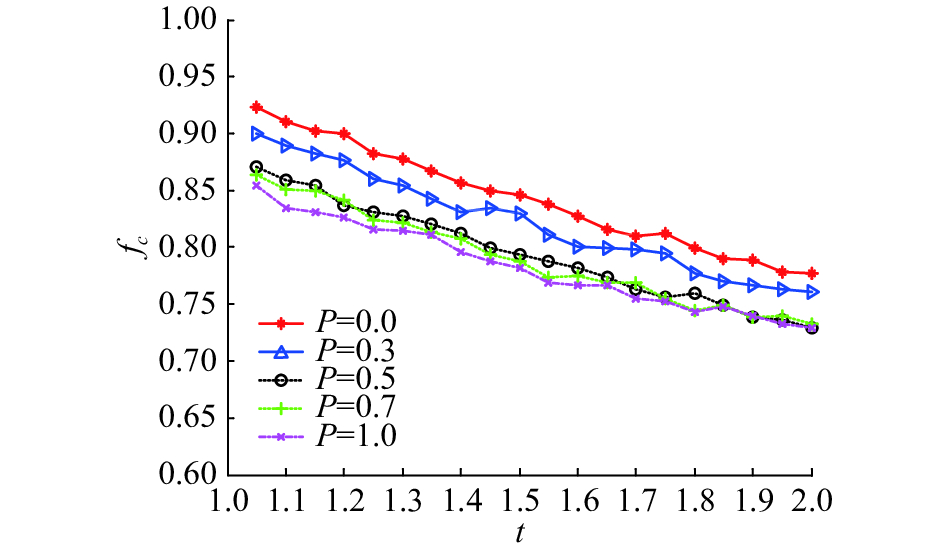
3.2.2 背叛的诱惑对合作行为的影响本节考虑收益矩阵式(13)中参数
|
Download:
|
| 图 6 合作者密度与欺骗诱惑关系 Fig. 6 Relationship between the partner density and deception temptation | |
此外,图6也从另一方面说明网络中这种拥有大量邻居节点的hub节点往往受到合作策略的眷顾,并且会在欺骗诱惑增大的情况下,起到阻碍背叛策略传播的作用。
4 结束语本文在HK网络基础上提出了一种高聚类幂律可调的网络结构模型,该模型与原HK网络模型相比具有更高的聚类系数。进一步在此模型基础上进行博弈演化策略的研究,研究结果表明高聚类幂律可调网络结构有利于促进博弈中合作现象的涌现,并且随着博弈模型中诱惑参数的增大合作者所占比例会随之降低。
| [1] |
WATTS D J, STROGATZ S H. Collective dynamics of ‘small-world’ networks[J]. Nature, 1998, 393(6684): 440-442. DOI:10.1038/30918 ( 0) 0)
|
| [2] |
BARABÁSI A L, ALBERT R, JEONG H. Mean-field theory for scale-free random networks[J]. Physica A: statistical mechanics and its applications, 1999, 272(1/2): 173-187. ( 0) 0)
|
| [3] |
HOLME P, KIM B J. Growing scale-free networks with tunable clustering[J]. Physical review E, 2001, 65(2 Pt 2): 026107. ( 0) 0)
|
| [4] |
李稳国, 王力虎, 陈明芳. HK网络演化模型的研究和改进[J]. 计算机工程, 2009, 35(3): 121-122, 125. LI Wenguo, WANG Lihu, CHEN Mingfang. Study and improvement on growing HK network model[J]. Computer engineering, 2009, 35(3): 121-122, 125. (  0) 0)
|
| [5] |
王丹, 井元伟, 郝彬彬. 扩展HK网络结构与同步能力的研究[J]. 物理学报, 2012, 61(22): 220511. WANG Dan, JING Yuanwei, HAO Binbin. Extended Holme-Kim network model and synchronizability[J]. Acta physica sinica, 2012, 61(22): 220511. DOI:10.7498/aps.61.220511 (  0) 0)
|
| [6] |
崔爱香, 傅彦. 加速增长的HK网络演化模型[J]. 计算机科学, 2015, 42(4): 37-39. CUI Aixiang, FU Yan. Accelerated-growth HK network evolution model[J]. Computer science, 2015, 42(4): 37-39. DOI:10.11896/j.issn.1002-137X.2015.04.005 (  0) 0)
|
| [7] |
徐玉珠, 张达敏, 曾成, 等. 改进HK网络演化模型的研究[J]. 电子科技, 2016, 29(3): 106-109. XU Yuzhu, ZHANG Damin, ZENG Cheng, et al. Research on and modeling of the improved HK network model[J]. Electronic science and technology, 2016, 29(3): 106-109. (  0) 0)
|
| [8] |
CHEN Liuqing, GAO Jinchun, XIE Gang, et al. Routing to enhance traffic capacity for scale-free networks with tunable clustering[C]//Proceedings of IEEE Advanced Information Technology, Electronic and Automation Control Conference. Chongqing, China, 2015: 110–113.
( 0) 0)
|
| [9] |
VARGA I, KOCSIS G. Novel model of social networks with tunable clustering coefficient[C]//Proceedings of the 9th International Conference on Applied Informatics. Eger, Hungary, 2014: 171–176.
( 0) 0)
|
| [10] |
ZHANG Xuejun, GU Bo, GUAN Xiangmin, et al. Cascading failure in scale-free networks with tunable clustering[J]. International journal of modern physics C, 2016, 27(8): 1650093. DOI:10.1142/S0129183116500935 ( 0) 0)
|
| [11] |
LI Ruiqi, SUN Shiwen, MA Yilin, et al. Effect of clustering on attack vulnerability of interdependent scale-free networks[J]. Chaos, solitons & fractals, 2015, 80: 109-116. ( 0) 0)
|
| [12] |
朱张祥, 刘咏梅. 在线社交网络谣言传播的仿真研究——基于聚类系数可变的无标度网络环境[J]. 复杂系统与复杂性科学, 2016, 13(2): 74-82. ZHU Zhangxiang, LIU Yongmei. Study of propagation of rumor in online social network based on scale-free network with tunable clustering[J]. Complex systems and complexity science, 2016, 13(2): 74-82. (  0) 0)
|
| [13] |
宋玉萍, 倪静. 网络集聚性对节点中心性指标准确性的影响[J]. 物理学报, 2016, 65(2): 028901. SONG Yuping, NI Jing. Effect of variable network clustering on the accuracy of node centrality[J]. Acta physica sinica, 2016, 65(2): 028901. (  0) 0)
|
| [14] |
NOWAK M A, MAY R M. Evolutionary games and spatial chaos[J]. Nature, 1992, 359(6398): 826-829. DOI:10.1038/359826a0 ( 0) 0)
|
| [15] |
ASSENZA S, GÓMEZ-GARDEÑES J, LATORA V. Enhancement of cooperation in highly clustered scale-free networks[J]. Physical review E, 2008, 78(1 Pt 2): 017101. ( 0) 0)
|
| [16] |
张文明. 网络演化博弈模型和仿真研究[D]. 哈尔滨: 哈尔滨工业大学, 2014. ZHANG Wenming. Model and simulation research on netwokded evolutionary games[D]. Harbin: Harbin Institute of Technology, 2014. (  0) 0)
|
| [17] |
LI Pingping, KE Jianhong, LIN Zhenquan, et al. Cooperative behavior in evolutionary snowdrift games with the unconditional imitation rule on regular lattices[J]. Physical review E, 2012, 85(2 Pt 1): 021111. ( 0) 0)
|
| [18] |
ZHANG Wen, XU Chen, HUI P M. Spatial structure enhanced cooperation in dissatisfied adaptive snowdrift game[J]. European physical journal B, 2013, 86(5): 196. DOI:10.1140/epjb/e2013-30997-2 ( 0) 0)
|
| [19] |
LUO Chao, ZHANG Xiaolin, LIU Hong, et al. Cooperation in memory-based prisoner’s dilemma game on interdependent networks[J]. Physica A: statistical mechanics and its applications, 2016, 450: 560-569. DOI:10.1016/j.physa.2016.01.032 ( 0) 0)
|
| [20] |
MENG Xiaokun, SUN Shiwen, LI Xiaoxuan, et al. Interdependency enriches the spatial reciprocity in prisoner’s dilemma game on weighted networks[J]. Physica A: statistical mechanics and its applications, 2016, 442: 388-396. DOI:10.1016/j.physa.2015.08.031 ( 0) 0)
|
| [21] |
向海涛, 梁世东. 双复杂网络间的演化博弈[J]. 物理学报, 2015, 64(1): 018902. XIANG Haitao, LIANG Shidong. Evolutionary gambling dynamics for two growing complex networks[J]. Acta physica sinica, 2015, 64(1): 018902. (  0) 0)
|
 2018, Vol. 13
2018, Vol. 13


