虽然互联网中存在海量的钢琴乐谱资源，但其难易程度不一，对于业余和初级乐器学习者来说，由于缺乏专业知识和指导，难以有效地找到与自身学习难度匹配的乐谱来学习。专业音乐学习者一般依据固定进阶教材，但缺乏个性化、灵活的学习方案。此外，一些经典但难度高的乐谱，会有诸多简化版本存在。因此，有必要对海量的钢琴乐谱资源的难度等级进行区分。

现在绝大部分乐谱难度等级仍然依赖于专业人士主观判断。对于海量的数字乐谱，人工判断难度等级会是一个耗时耗力的巨大工程。人工主观判断也很难稳定、可靠地把握每个难度等级之间的区别，尤其对于多类别问题。不同的人对于同一首乐谱可能会给出不同的难度等级，甚至对于同一首乐谱，同一个人在不同的时间也会给出不同的难度等级。因此，自动识别乐谱难度等级的系统具有重要的理论意义和应用价值。

为网络中存在的数字乐谱提供难度等级标签将会大大提高寻找合适难度等级乐谱的效率，并能提高音乐网站的用户体验。通常研究中将乐谱难度识别归为模式分类问题，从符号乐谱中定义并提取难度相关特征，利用分类思想实现乐谱难度等级的识别。下面将针对不同的技术来回顾钢琴乐谱难度等级识别领域的研究现状。

Shih-Chuan Chiu等^[1]最先开始钢琴乐谱难度等级识别研究。由于钢琴乐谱难度识别是一个相对较新的研究问题，现有的符号音乐特征(symbolic music feature)较少直接用于难度等级识别。所以他们首先定义8个与乐谱难度密切相关的特征，将此8个难度相关特征与语义特征一起作为特征空间。后用特征选择算法ReliefF^[2]按照特征重要程度(即各个特征对难度等级的辨别能力大小)分配权值，选择权值最大的10个特征作为后续实现难度等级识别的特征空间。最终用3个回归算法：多元线性回归、逐步回归^[3]、支持向量回归^[4]实现难度等级识别。实验中，支持向量回归算法得到最好的效果，其R²统计量为39.9%^[3]。

Véronique Sébastien等^[5]也将乐谱难度等级识别看作分类问题，他们利用无监督的聚类算法实现乐谱难度等级识别。首先定义7个难度相关特征，这些特征从MusicXML格式^[6]乐谱文件提取。之后用主成分分析 (principal component analysis，PCA)将特征投影到低维空间，以降低特征维数。然后，用分层聚类(hierarchical clustering)^[7]将乐谱聚成3类，即3个难度类别。

总的来说，无论是多元线性回归还是逐步回归都假设特征与难度等级之间为线性关系，此假设过于简化特征与难度等级之间的实际关系。而支持向量回归虽然可实现非线性拟合，但拟合结果尚不令人满意。与有监督算法相比，非监督算法，如分层聚类，虽能充分利用特征与难度等级之间的自然分布关系，但无法利用已有的难度等级标签作为先验知识提高识别效果。例如，实验中，原始乐谱数据是4个类别，Véronique Sébastien经过PCA降维，应用聚类算法，最终仅得到3个难度类别。

在现有有监督的回归拟合算法识别钢琴乐谱难度等级的研究中，支持向量回归有最好的拟合效果(其R²统计量值为39.9%)。但支持向量回归，更适合逼近、拟合连续分布数据，对于此离散类别的分类问题能力有限。所以本文利用一种与支持向量回归算法原理相近，但更适用于解决分类问题的支持向量机分类算法实现数字钢琴乐谱难度等级识别。

1 支持向量机理论

SVM是基于统计学习理论中经验风险最小化原则的一种机器学习算法^[8]。SVM已广泛应用于纹理分类(texture classification)^[9]、文本分类^[10]、人脸识别^[11]、语音识别^[12]等各个领域。理论和实践证明，SVM对噪声和离群点鲁棒性好，泛化能力强，经过扩展可解决多分类问题^[8]。

SVM实现分类的关键是核函数，利用核函数^[13]可以将低维线性不可分的问题转化到高维空间实现线性可分，同时避免因维数增加而导致过大的计算量。常用的核函数有线性核函数(linear kernel function)、多项式核函数(polynomial kernel function)、高斯径向基核函数(Gauss radical basis kernel function，GRB)等^[13]。由于本研究问题的特征数目远小于样本数目，并且为降低分类模型的参数复杂度，本文考虑采用高斯径向基核函数。

然而传统的基于高斯径向基核函数的SVM(GRB-SVM)算法假设特征不相关且权重相同，即不能根据特征对难度等级的贡献度差别对待。而在本应用问题中，特征对难度区分的贡献度不同。为弥补GRB-SVM不能根据特征重要程度差别对待的不足，本文结合测度学习(metric learning)理论，充分利用训练乐谱中关于难度等级的先验知识，从带难度等级标签的乐谱特征空间中有监督地学习到能更好区分钢琴难度的投影矩阵，保留特征之间的相关关系，从而利用该矩阵改进高斯径向基核函数，提出一种测度学习支持向量机分类算法——ML-SVM算法，实现数字钢琴乐谱难度等级识别。

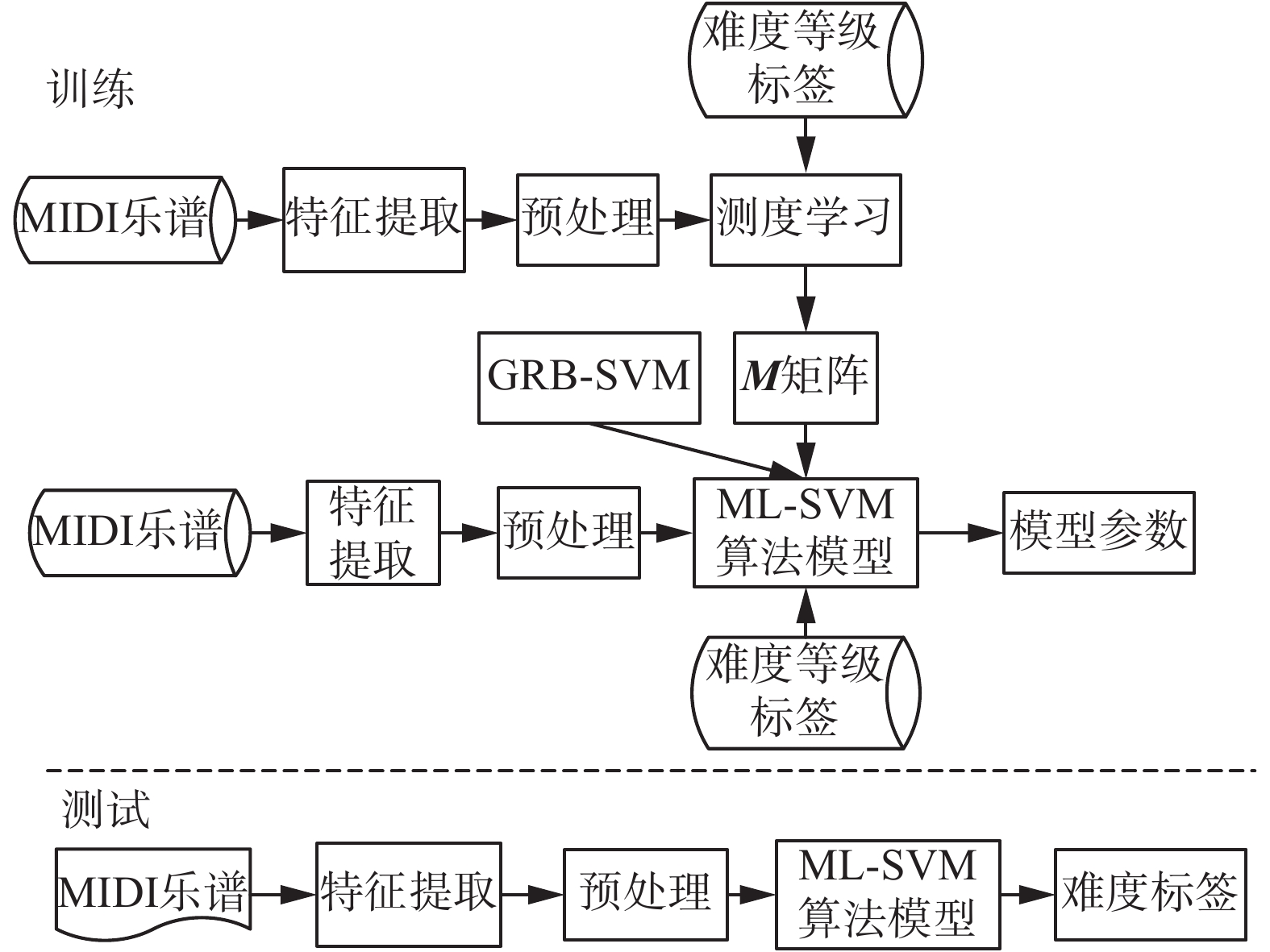
2 算法原理与算法描述

本文提出的ML-SVM乐谱难度识别算法主要包括以下3部分：基于测度学习从训练数据中有监督的学习到能增加钢琴乐谱难度区分度的投影矩阵；得到新的距离测度，并利用该测度改进高斯径向基核函数，建立ML-SVM算法模型；最后利用网格搜索算法得到核函数参数的最优组合，建立分类模型，实现数字钢琴乐谱难度等级的识别。ML-SVM乐谱难度识别算法框图，如图1所示。

2.1 特征空间的建立

为获取更多的钢琴乐谱难度相关特征，本文采用文献[1]与文献[5]中的难度相关特征作为本文的特征空间。所以本文中的特征空间包括：文献[1]中除指法复杂度(属于乐谱标注层面信息，MIDI乐谱中不包含此信息)，调号(key signature是元标签信息)之外的全部难度和语义特征；文献[5]中除去指法特征(同样属于标注层面特征)的全部特征，共22个特征，组成一个22维的特征向量来表示MIDI乐谱。

2.2 测度学习得到距离测度D_M，改进GRB核函数

由于传统的SVM算法无法根据特征对类别的辨别能力差别对待，所以本文考虑利用测度学习从训练乐谱中有监督地学习到一个投影矩阵，充分考虑特征对难度等级的贡献度，为特征分配不同的权重，进而得到新的距离测度D_M，改进原始高斯径向基核函数，改进后的高斯径向基核函数为

${k_M}({{{x}}_i},{{{x}}_j}) = \exp ( - \frac{1}{{2{\sigma ^2}}}{D_M}({{{x}}_i},{{{x}}_j}))$

(1)

式中：σ是高斯径向基核函数参数，可用网格搜索算法得到， ${{{x}}_i}\text{、}{{{x}}_j}$ 表示特征向量，exp表示以自然常数e为底的指数函数，D_M为新的距离测度：

${D_M} = {({{{x}}_i} - {{{x}}_j})^{{T}}}{{M}}({{{x}}_i} - {{{x}}_j})$

(2)

通过矩阵M，依据特征对难度等级的区别能力及特征之间的相关关系，将特征投影到一个类别区分度更高的空间^[14]。D_M的构建及投影矩阵 ${{L}}({{{L}}^{{T}}}{{L}} = $ M)的学习过程如下。

本算法的关键在于找到最佳的特征投影矩阵L。考虑用变换矩阵 ${{L}} \in {R^{n \times n}}$ (n表示特征的维数)实现特征投影：

${{x}}_i' = {{L}}{{{x}}_i}$

(3)

则投影后的特征向量 ${{x}}_i'$ 是原始特征向量 ${{{x}}_i}$ 和投影矩阵 ${{L}}$ 元素的一个线性组合，则投影空间中距离测度 ${d_L}$ 为

$\begin{array}{c} {d_L}({{{x}}_i},{{{x}}_j}) = ||{{L}}({{{x}}_i} - {{{x}}_j})|{|_2} = \\ \sqrt {{{{{[}}{{L}}({{{x}}_i} - {{{x}}_j})]}^{{T}}}{{[}}{{L}}({{{x}}_i} - {{{x}}_j})]} \\ \end{array} $

(4)

为避免求均方并保证距离为正值，取距离的平方并用矩阵形式表示，则新的距离测度D_M为

$\begin{array}{c} {D_M} = {d_L}^2 = {[{{L}}({{{x}}_i} - {{{x}}_j})]^{{T}}}[{{L}}({{{x}}_i} - {{{x}}_j})] = \\{({{{x}}_i} - {{{x}}_j})^{{T}}}{{{L}}^{{T}}}{{L}}({{{x}}_i} - {{{x}}_j}) = \\{({{{x}}_i} - {{{x}}_j})^{{T}}}{{M}}({{{x}}_i} - {{{x}}_j}) \\ \end{array} $

(5)

式中：矩阵 ${{M}} = {{{L}}^{{T}}}{{L}}$ 。希望投影后，相同难度标签的乐谱之间距离减小，不同难度标签的乐谱之间距离增大。求解M的过程归结为求解如下优化问题：

$\begin{array}{c} \mathop {\min }\limits_{{{M}} \geqslant 0} \sum\limits_{(i,j) \in s} {{D_M}({{{x}}_i},{{{x}}_j})} \\ { s.t.}\;\;\sum\limits_{(i,j,k) \in R} [ {D_M}({{{x}}_i},{{{x}}_j}) - {D_M}({{{x}}_i},{{{x}}_j})] \geqslant 1 \\ \end{array} $

(6)

式中：S表示由相同难度等级的两个乐谱组成的数据对集( ${{{x}}_i}\text{、}{{{x}}_j}$ 难度等级相同)，R表示在S的基础上，每个对集加入一个不同难度等级的乐谱组成的三集合( ${{{x}}_i}\text{、}{{{x}}_j}$ 难度等级相同， ${{{x}}_i}$ 和 ${{{x}}_k}$ 难度等级不同)。此优化目标与大间隔近邻算法(large margin nearest neighbor, LMNN)^[15]有相似之处。由于M是半正定对称矩阵，所以此优化问题是凸的，可以用梯度下降法有效求解^[15]，并且只有全局最优解。

2.3 ML-SVM算法

对于给定数据样本 $\{ ({{{x}}_i},{y_i}),i = 1,2, \cdots ,p\} $ ，其中 ${{{x}}_i} \in {R^n}$ 为 $n$ 维向量， ${y_i} \in \{ - 1, + 1\} $ 为样本标签，表示两个不同的类别，p为样本个数。则基于测度学习得到新的距离测度D_M，改进高斯径向基核函数后的ML-SVM算法模型求解最优超平面的问题即为求解下列目标函数：

$\begin{array}{c}\mathop {\max }\limits_\alpha f(\alpha ) = \sum\limits_{i = 1}^p {{\alpha _i}} - \displaystyle\frac{1}{2}\sum\limits_{i,j = 1}^p {{\alpha _i}{\alpha _j}{y_i}{y_j}} {k_M}\\{ s.t.}\;\;\;\;\;\;\sum\limits_{i = 1}^p {{\alpha _i}} {y_i} = 0\\0 \leqslant {\alpha _i} \leqslant C,\;\;i = 1,2,\cdots \!,p\end{array}$

(7)

式中 ${k_M} = \exp ( - \displaystyle\frac{1}{{2{\sigma ^2}}}{D_M}({{{x}}_i},{{{x}}_j}))$ 。

得到最优解 ${{{\alpha}} ^*} = {\left[ {(\alpha _1^* \,\, \alpha _2^*\, \cdots \, \alpha _n^*)} \right]^{{T}}}$ 。选择 ${{{\alpha}} ^{{*}}}$ 的一个小于C的正分量 $\alpha _j^*$ ，并据此计算：

${b^*} = {y_j} - \sum\limits_{i = 1}^p {{y_i}\alpha _i^*} k\left( {{{{x}}_i},{{{x}}_j}} \right)$

(8)

构造决策函数：

$f({{x}}) = \operatorname{sgn} (\sum\limits_{i = 1}^p {{y_i}\alpha _i^*} k\left( {{{x}},{{{x}}_i}} \right) + {b^*})$

(9)

依据决策函数可以得到待分类乐谱x所属类别^[8]。其中α是拉格朗日系数，C是错误分类的惩罚参数，k_M是改进后的高斯径向基核函数，核函数表达式中的 ${D_M}({{{x}}_i},{{{x}}_j})$ 是测度学习得到的距离测度。

另外，原始SVM是二分类的，本文采用一对余(one versus rest)方法^[8,16]将 ML-SVM扩展到多分类。主要思想是：对于一个m类分类问题，通过建立m个二分类ML-SVM模型，每一个ML-SVM模型需要训练所有的训练样本，但训练样本中只将某一个类别记为正，其余所有类别记为负。对于待识别的样本，依次调用训练好的m个ML-SVM模型，计算它在各个ML-SVM模型中决策函数的值，选择决策函数值最大的ML-SVM模型给出的类别，作为待识别乐谱难度类别。

3 实验

本文算法全部用MATLAB软件实现，所用的计算机环境为32位Windows 7操作系统，内置Intel I5-4200M处理器和4 GB的内存。

在实验中，为更好地评估本文提出的ML-SVM算法的分类性能和泛化能力，在9类和4类难度两个乐谱数据集中，将ML-SVM算法与逻辑回归、基于线性核函数的SVM、基于多项式核函数的SVM、基于原始高斯径向基核函数的SVM(均用one versus rest扩展到多分类)算法以及结合主成分分析的各个SVM算法进行对比试验，以识别准确率作为算法性能的评价指标。每个实验独立重复5次，并用五折交叉验证，取平均准确率作为最终识别准确率。同时为更全面评估识别算法性能，也给出各个算法结果的90%置信区间。

3.1 实验数据集

钢琴乐谱数据集采用包含音高、节拍、时间、和弦、速度和信道等钢琴乐谱信息的MIDI格式数字乐谱文件^[17]。MIDI文件小，易于获得。为和现有的研究作对比，我们采用了文献[1]中包含9个难度等级，共176个MIDI文件的数据集。

另外考虑到实际钢琴学习与教学中很多情况会将乐谱分为4个难度等级，大量音乐网站也普遍提供4个难度等级(easy，beginner，intermediate，advanced)的数字乐谱，所以为更好地评估本文算法的可拓展性，切合实际应用情况，我们还从大型音乐网站8notes^[18]收集到400首MIDI乐谱组成有4个难度等级的数据集，每一个难度等级有100个MIDI乐谱。为书写及引用方便，9个难度等级的数据集简称为NineS数据集，4个难度等级的数据集简称为FourS数据集。

3.2 数据预处理

特征提取后，一些特征对应的值较大，而另一些特征对应的值较小，甚至相差超过两个数量级，为避免数值较大的特征对整体分类的影响，利用Min-Max归一化方法：

${{{x}}^*} = \frac{{{{x}} - \min }}{{\max - \min }}$

(10)

将特征向量归一化到[0, 1]。其中min和max分别表示特征 ${{x}}$ 的最小和最大值， ${{{x}}^*}$ 表示特征 ${{x}}$ 经过归一化处理后的特征。

3.3 实验与结果分析

仿真试验中，将ML-SVM算法与逻辑回归(logistic regression，LR)^[19]，基于线性核函数的SVM(记为L-SVM)，基于多项式核函数的SVM(记为P-SVM)和基于高斯径向基核函数的SVM算法(记为GRB-SVM)^{[16, 20-21]}进行对比。每个实验独立重复5次，每次用5折交叉验证，取平均准确率作为分类性能指标，同时计算出结果的90%置信区间。

各个SVM算法中核函数参数利用网格搜索算法^[22]，在2^–10~2¹⁰内，以步长0.5，5折交叉验证寻找最优的参数设置。其中L-SVM，P-SVM(多项式阶数d=3)只需优化惩罚因子C，GRB-SVM与ML-SVM需要优化惩罚因子C与核函数参数g(g = $ \displaystyle\frac{1}{{{\sigma ^2}}}$ )的最优组合。最终的最优参数组合如表1所示。

表2给出了本文提出的ML-SVM算法与LR、L-SVM、P-SVM、GRB-SVM算法在NineS数据集和FourS数据集中的识别准确率及结果的90%置信区间。从表2中可以看出，在两个数据集上，本文提出的ML-SVM算法，识别准确率最高，分别达到68.74%和84.67%。两个数据集中，本文提出的算法最终识别准确率均高于GRB-SVM算法，尤其在FourS数据集中，本文所提算法得到84.67%的识别准确率，相对75.63%的GRB-SVM，识别准确率有较大提高。且更窄的置信区间表明结果更稳定、显著。基于线性核函数的SVM(L-SVM)一直表现欠佳，在两个数据集中识别效果不如逻辑回归(LR)，基于多项式核函数的SVM(P-SVM)表现良好，在FourS数据集中识别效果仅次于本文算法。

为进一步验证本文所提算法的有效性，我们将ML-SVM算法与另一种主要用来实现特征降维的投影算法——主成分分析结合SVM的分类准确率进行对比。在对原始特征数据进行PCA处理时，保留原始特征95%信息量的投影特征。PCA投影处理后，最终NineS数据集中的特征降到13维，而FourS数据集的特征降到8维。之后再用基于各个核函数的SVM算法对PCA降维后的数据进行分类。实验结果如表3所示。从表中可以看出，原始特征数据经过PCA处理后，最终各个SVM的分类准确率都有所提高。这是因为原始特征数据经过PCA投影、降维之后，可以有效减少混叠以及冗余信息，进而提高最终分类的准确率。

虽然原始特征数据经过PCA投影、降维处理后，利用GRB-SVM分类的准确率较之前有所提高，但分类准确率与本文提出的ML-SVM算法仍有差距，尤其在FourS数据集中，ML-SVM仍有较大优势，这也再次验证了本文提出的ML-SVM算法是有效的。

4 结束语

针对现有钢琴乐谱难度分类主要由人工方式完成，效率不高，区别于传统将乐谱难度等级识别归结为回归问题，本文直接将其建模为基于支持向量机的分类问题。并结合钢琴乐谱分类主观性强、特征之间普遍存在相关性等特点，利用测度学习改进高斯径向基核函数，从而提出一种测度学习支持向量机分类算法——ML-SVM算法。经过在9类和4类难度两个乐谱数据集上的对比实验，结果表明本文所提算法的识别准确率优于现有算法，且有效提高了基于高斯径向基核函数SVM的分类性能。实验结果说明，利用测度学习理论，保留特征之间的相关关系，更适合乐谱难度识别数据与分布特点，并能够有效识别算法的性能。未来的工作可以考虑应用半监督算法，以充分利用大量无难度标签数据，预期将会大大提高分类器的训练效果，进而提高算法的识别准确率。