同时定位与地图创建(SLAM)技术已经成为目前机器人研究领域的热点，随着SLAM问题研究的不断深入，对机器人位姿监测和环境地图创建的精确度、实时性也都有了更高的要求。因此，如何在精确度与实时性之间寻求一种平衡是目前众多SLAM算法中亟待解决的一个问题。而新型RGB-D摄像机Kinect^[1]，具有丰富3维空间信息与颜色纹理信息，为上述问题的解决提供了的可能。文献[2]提出的基于RGB-D相机的室内SLAM方法可实现对室内环境的稠密化建图，但论文中的SIFT特征提取算法较为费时，会占用较多的运算资源，因此其实时性较差。ORB-SLAM^[3]采用了基于单目摄像机的SLAM方案，以高效的ORB特征贯穿于系统中的特征处理、匹配、回环检测、重定位等方面，更侧重于系统处理的实时性，但因为单目相机的限制，ORB-SLAM算法在稠密化建图方面还有所欠缺。针对目前移动机器人视觉SLAM研究中存在的实时性差、精确度不高、无法稠密化建图等问题，本文提出了一种基于Kinect深度摄像机的移动机器人三维视觉SLAM算法，以实现对环境进行实时的、精确的稠密化建图。在本算法前端处理中，通过分析多种特征点检测算法的优劣，采用了鲁棒性与实时性更好的ORB特征检测。利用 RANSAC 算法^[4]对可能存在的误匹配点进行剔除完成初始匹配，以PNP(perspective-N-point)^[5]问题求解的方式实现了图像的快速配准。在后端优化中，通过对SLAM问题建模分析，遵循图优化思想，设计了一种非线性优化方法，实现对机器人位姿的优化。并与闭环检测^[6]机制相结合，提出了一种基于局部闭环与全局闭环约束的点云优化算法，同时完成对位姿与稠密化点云的优化，可有效地抑制系统的累积误差，进一步提升整个系统的精确性。最后通过实验，验证了本文SLAM方法的可行性和有效性。

1 系统结构

本文提出的室内环境下移动机器人三维视觉SLAM算法的总体框架如图1所示，主要分为前端的关键帧筛选、帧间配准、闭环检测和后端的图优化、点云融合、点云优化几个部分。

2 特征点的检测与配准 2.1 特征点的检测

特征点的检测与匹配是视觉SLAM问题中“图像前端”的部分，也是视觉SLAM中占用计算资源最多，最影响系统实时性的部分。基于FAST特征检测改进的ORB特征^[7]具有旋转不变和尺度不变特性的二进制特征，它是一种高效的具有良好针对视图不变的特征，比SIFT特征检测快两个数量级，同时特征点的质量较高、鲁棒性好。考虑到SLAM问题对鲁棒性、实时性的要求，本文采用了ORB特征提取算法。

2.2 特征点的配准

图像产生的本质是光线通过相机透镜投影到图像传感器上，这个过程是3-D场景到2-D平面的投影，因此场景与它的成像之间存在重要的联系，相同场景的不同成像之间也有联系。而通过这些联系，可以实现特征点的配准。

特征点配准算法可以分为以下5个步骤：

1) 提取特征点：Opencv提供了通用接口cv::FeatureDetector，这里将其设定为ORB特征。

2) 提取描述子：对于检测出的角点，用一些数学上的特征对其进行描述，这里通过cv::FeatureDetectorExtractor接口设置特征描述子提取器。

3) 匹配：通过各个角点的描述子来判断它们在两张图像中的对应关系。这里采用的方法为快速最近邻算法FLANN。

4) 去外点：利用RANSAC算法去除错误匹配的外点，保留正确的内点。

5) 位姿求解：调用Opencv的PnPsolver()函数，求解相机的位姿运动(R,t)。

3 位姿优化

针对传统的利用滤波方法估计位姿存在线性化误差、更新效率低下等问题，本文依据SLAM研究中的图优化^[8]思想，设计了一种基于非线性优化的位姿优化方法，同时实现局部位姿优化和全局位姿优化。

3.1 模型的建立

SLAM的经典数学模型通常分为3部分：状态变量、运动方程、观测方程。

${{X}} = [{x_1}\,{x_2}\,\cdots\,{x_N}\,{y_1}\,{y_2}\,\cdots\,{y_M}]$

(1)

${x_k} = {{f}}({x_{k - 1}},{u_k}) + {u_k}$

(2)

${z_{k,j}} = g({x_k},{y_j}) + {{{n}}_{k,{{j}}}}$

(3)

本文主要以Kinect作为主要的传感器输入，通过对视觉信号的处理，构建视觉里程计，用于位姿估计。所以这里只考虑状态变量和观测方程，构建出目标函数：

${{e}}({x_k},{y_j},{z_{k,j}}){{ = }}{z_{k,j}} - g({x_k},{y_j})$

(4)

$E({{X}}) = \sum\limits_{(k,j) \in C} {{{e}}{{({x_k},{y_j},{z_{k,j}})}^{{T}}}} {\varOmega _{kj}}^{ - 1}{{e}}({x_k},{y_j},{z_{k,j}})$

(5)

${{{X}}^*} = \mathop {\arg \min }\limits_X E({{X}})$

(6)

式中： ${x_k}$ 表示第k时刻的机器人位姿，也称为图优化的一个pose节点； ${y_j}$ 表示第k时刻机器人所能观测到的路标，也称为图优化的一个point节点； ${z_{k,j}}$ 表示pose节点与point节点的约束；特别地，在闭环检测优化过程中， ${z_{k,j}}$ 代表pose节点与pose节点的约束； $e({x_k},{y_j},{z_{kj}})$ 为由两顶点组成的边所产生的向量误差函数，代表两顶点满足约束条件 ${z_{k,j}}$ 的程度，当它的值为0时，表示两顶点完全满足匹配约束。

目标函数的物理意义：这里假设了误差函数e(·)符合高斯分布 $(0,\varOmega )$ ，则SLAM问题的贝叶斯概率描述为，求解适合的 $(x,y)$ ，使系统最有可能产生当前的观测数据Z，即最大似然(MLE)：

${(x,y)^*} = \mathop {\arg \max }\limits_{x,y} p(z|x,y)$

(7)

最终所求的 $e({x_k},{y_j},{z_{kj}})$ 的二次型(式(6))，实质上是在求解最大似然。即在假设噪声是高斯分布之后，将整个SLAM问题等效为一个最小二乘问题。进一步，利用李代数^[9]的扰动模型，求得目标函数关于pose和point的导数 ${J_x}$ 和 ${J_y}$ ，可对此最小二乘问题求解。以此建立最终的求解方程：

${{e}}(x + {\delta _x},y + {\delta _y}) \approx {{e}}(x,y) + {J_x}{\delta _x} + {J_y}{\delta _y}$

(8)

$H = \sum\limits_i {{{{J}}_i}^{{T}}} {{{\varOmega}} ^{ - 1}}{{{J}}_i}$

(9)

$b = \sum\limits_i {{{{J}}_i}^{{T}}} {{{\varOmega}} ^{ - 1}}{{{e}}_i}$

(10)

$H{\delta _{{x}}} = - b$

(11)

式中： ${J_x}$ 代表相机微小运动后，像素的变化； ${J_y}$ 代表空间点微小运动后，像素的变化。式(11)代表了考虑所有的变量与边的Full SLAM问题的求解。结合SLAM问题的稀疏性，选用合适的梯度下降方法^[10]，用求得的 ${\delta _{{x}}}$ 用于状态变量X的更新，通过多次迭代，最终求得满足目标方程的状态变量X的收敛值。可借助通用图优化工具g2o^[11]来解决上述非线性最小二乘问题，求解过程如图2所示。

3.2 图的建立与优化

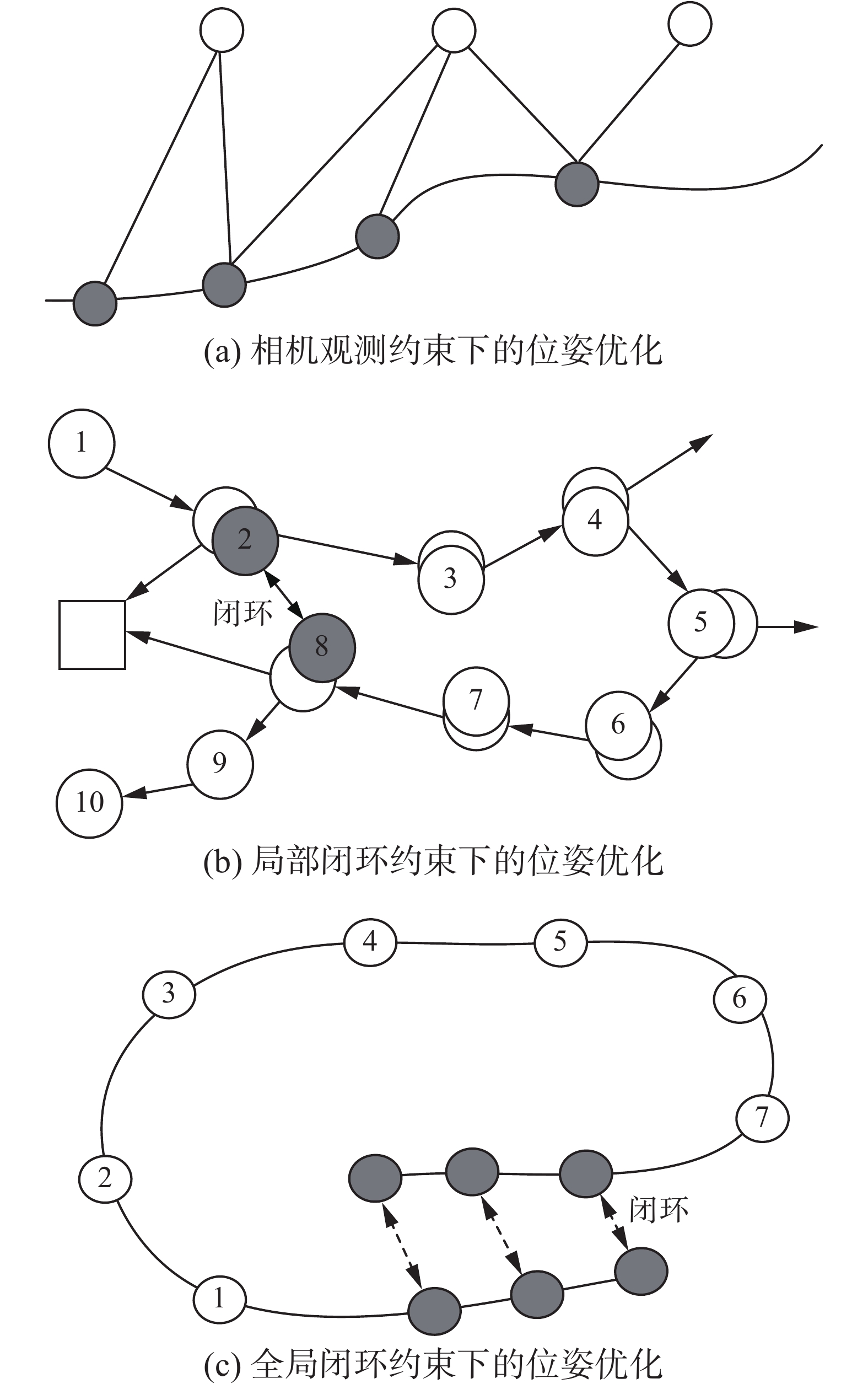
上述SLAM问题全部抽象成节点与边，节点代表了优化变量，包括pose节点和point节点。边代表了误差项约束条件，包括pose-point约束和pose-pose约束。pose-point约束依赖于相机观测产生的约束，如图3(a)所示。pose-pose约束则依赖于系统中闭环检测产生的约束，如图3(b)、(c)所示，可有效地抑制系统的累积误差，从而得到信息一致的地图。

4 闭环检测下的点云优化

在基于位姿增量估计的SLAM建图中，会产生误差的累积，则在长时间的大范围SLAM建图中，就需要闭环检测对位姿和生成的点云进行优化。RGBD-SLAM算法是在局部回环检测后，只使用局部回环优化后的位姿作为三维地图点云的重建。ORB-SLAM算法则是在运动跟踪过程中，时刻检测并维护关键帧之间的点云共视关系，同时实现对点云优化。但这种方法只适用于规模有限的稀疏点云，并不适用于稠密化点云的优化。基于此，提出了一种基于局部闭环与全局闭环约束的点云优化算法，同时完成对位姿与稠密化点云的优化。算法具体步骤如下：

1) 封装构造数据帧Frame，根据帧间的关联程度，筛选出关键帧序列。

2) 执行帧间配准。完成相机位姿初始估计。

3) 在相机观测约束下，直接应用式(6)，构建如图3(a)所示的图优化。求得优化后的相机的位姿变化 $(R,t)$ ，将原始点云进行坐标系变换，实现点云的拼接融合。

4) 执行闭环检测。通过动态计算闭环帧筛选阈值，得到匹配质量较高的闭环帧候选序列。

5) 闭环检测结束后，遍历闭环帧候选序列，在当前帧与闭环候选帧之间，进行Sim3(相似变换矩阵)求解与优化。当某一候选帧通过了Sim3求解与优化，则认为闭环检测成功，跳出对闭环帧候选序列的遍历。求得对应相似变换矩阵为

${{S}} = \left[ {\begin{array}{*{20}{c}} {sR}&t \\ 0&1 \end{array}} \right],R \in {{S}}O(3),s \in \mathbb{R},t \in {\mathbb{R}^3}$

(12)

6) 位姿优化的传播。当前帧坐标系与世界坐标系之间的变换在5)中已经确定并优化。通过一级相连关系的传播，可以确定这些相连的关键帧坐标系与世界坐标系之间的相似变换矩阵。

7) 点云优化。利用6)中的相似变换矩阵 ${{S}}$ ，将原始点云的世界坐标系转换到当前闭环帧处的坐标系，进行点云的拼接融合，实现点云的优化。

5 实验结果及分析 5.1 实验平台

为了验证算法的有效性，并保证本文实验的一致可对比性，故采用了知名的TUM标准数据集^[12]，并选用了基于Kinect视觉传感器采集的室内基准数据包。该基准数据包中包含Kinect 产生的彩色图像和深度图像序列，以及机器人的真实运动位姿。本文实验数据处理平台为一台Intel双核2.4 GHz主频的PC机，运行Ubuntu 14.04操作系统。程序均设定以30帧/秒的速度同时读取数据包中的RGB数据和深度数据。

5.2 室内环境下的三维视觉SLAM 5.2.1 特征提取与特征点配准

对两帧图像进行ORB特征提取后，在利用特征匹配算法(FLANN)获得相邻帧间对应关系的基础上，利用 RANSAC 算法对点云进行匹配，匹配结果如图4(c)所示。在图4(a)中，通过特征匹配算法，一共产生了929个匹配特征点，但误匹配点过多。因此，通过人工制定规则的筛选，去除了部分误匹配点，此时的匹配个数为250。为进一步提升匹配精读，通过RANSAC算法对图4(b)进行进一步的匹配筛选。最终，产生了97个经筛选后的匹配点，实验中整个匹配所耗时间为 0.003 5 s。

5.2.2 回环检测约束

通过回环检测，可以增加帧间的约束，进一步提升系统的鲁棒性，进而提升整个SLAM的轨迹与地图的质量。在本文算法中，通过筛选关键帧之后进行回环检测，并以PNP求解的结果作为对边的估计，增加到图优化中，如图5所示。

5.2.3 三维环境重构效果对比

图6(a)为采用了ORB-SLAM方法得到的三维环境重构结果，所构建的三维地图为稀疏点云。图6(b)为采用RGBD-SLAM方法得到的三维环境重构结果，物体轮廓可以辨别，但冗余点相对较多。图6(c)为采用本文的SLAM方法得到的三维环境重构结果，物体轮廓清晰可辨，冗余点明显减少。本算法实时性也远优于 RGBD-SLAM，与ORB-SLAM的实时性相当。RGBD-SLAM 处理一帧数据平均用时约为350 ms，每秒钟只能处理 3 帧数据，因此不适于实时 SLAM。而本算法前端处理一帧数据平均约为31 ms，后端经过位姿优化与点云优化，以约5帧/秒的频率更新点云地图。可以满足SLAM系统对实时性要求。

5.2.4 机器人运动轨迹跟踪

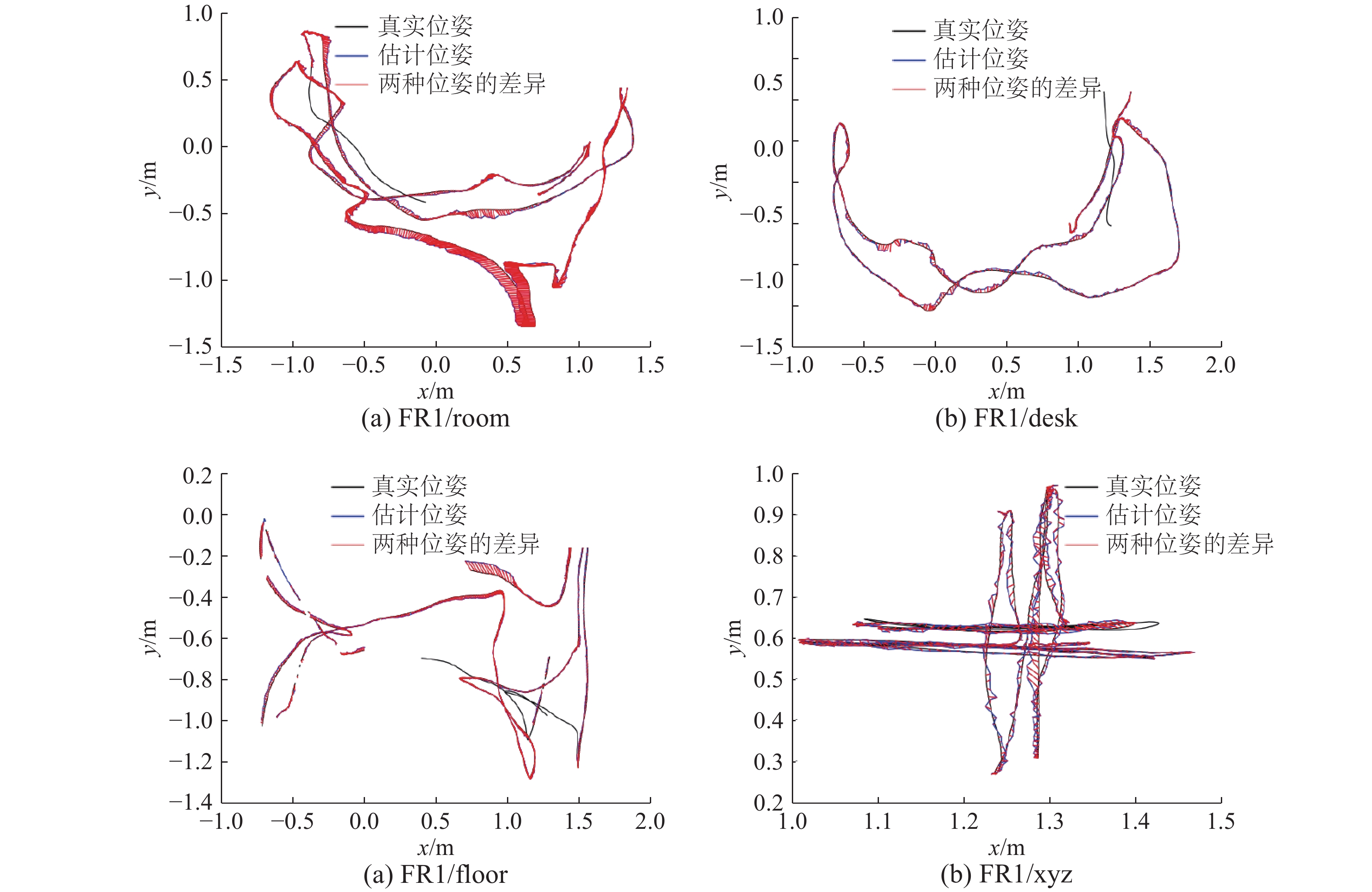
为了获得机器人位姿的变化，本文以3D-2D的特征点约束，采用PNP求解的方法对机器人相邻位姿进行估计，并借助图优化方法对估计位姿进行优化。为了使运动轨迹更为直观，实验给出了本文算法在不同数据集下，机器人运动轨迹在X/Y平面上的投影，如图7所示。表1则记录了不同算法在不同数据集下，由计算所得的机器人在三维空间中的运动轨迹的真实位姿之间的均方根误差(RMSE)。通过均方根误差的对比，可有效地评估算法对机器人位姿跟踪的误差大小。可以看出本文方法能较好地实现机器人的运动轨迹跟踪。

6 结束语

在本文基于图优化的视觉SLAM算法前端框架中，采用的ORB特征检测、RANSAC算法等方法，较好地解决了帧间配准过程中匹配误差较大、效率低下的问题。在三维地图生成部分，以图优化后的位姿为基础，进行点云构建，并引入闭环检测的机制，实现了对位姿与稠密化点云的双重优化。实验验证了本文所提方法能够准确、迅速地重构出稠密化的三维环境模型，并能精确估计出移动机器人的运动轨迹。下一步计划对系统进行两方面的改进: 1)改进前端的帧间配准方法，考虑采用直接法进行位姿跟踪，完成位姿估计；2)研究环境三维地图与语义信息的结合，实现更好的人机交互与导航。