图像分类是视觉领域研究的重要内容,基于表示的分类方法是图像分类方法中一种重要的分类方法,对表示方法而言,将目标图像恰当地表示出来,对于提高图像分类的性能非常有帮助[1-3]。因此,在基于表示的图像分类方法中,为图像找到一种合适的表示方法是非常重要且有意义的。
图像分类性能会受到很多因素的影响,其中的两个主要问题是由光照引起的像素强度变化和小样本问题。为解决光照问题带来的影响,文献[4]中提出光照补偿方法克服Lambertian模型的局限性;文献[2-3]通过对原始图像进行处理来得到其虚拟图像,减弱光照的影响,然后利用此互补图像来提高图像分类的准确率。为解决小样本问题,文献[5]通过提出基于虚拟样本图像的核协作表示分类方法来减小训练样本不足对图像分类带来的影响;文献[6]通过使用原始图像和其对应的镜像图像来克服小样本问题的影响提高分类识别率。此外,文献[7-8]的研究也表明,通过利用原始图像相邻列的像素得到虚拟图像对提高图像分类准确率非常有益。
传统的表示分类方法能直接利用原始图像来表示待测图像,且能够取得较为满意的分类结果,然而这是在具有充足的训练样本的前提下得到的结果,实际情况中经常会遇到训练样本不足(小样本问题)的情况,这时就会影响表示分类的效果。文献[2]虽然利用了虚拟图像和原始图像联合进行分类,一定程度缓解了小样本问题的影响,但是其得到的虚拟图像没有突出目标图像的特征信息。此外,传统的表示分类方法利用计算较为复杂的1范数进行求解,不利于实际应用。针对此情况,文献[9]提出的改进的表示方法利用2范数替代1范数,并使用两步策略得到了表示求解的快速实现。
针对以上问题以及原始图像中较大或较小像素过多给图像分类带来不良影响的问题,本文提出一种新的图像表示方法。本方法利用图像中相邻像素之间的联系,通过简单的数学方法将过大或过小像素转化为包含有目标更多特征信息的中等强度像素得到虚拟图像,然后同时在原始图像和虚拟图像上应用分类方法,最后融合得分进行分类。与其他传统方法相比,这种新的图像表示方法不仅能提高图像中等强度像素的占比,弱化光照变化带来的影响,而且可以较好地利用原始图像中相邻像素的相关性的特点,提高目标特征的辨识度。此外,联合方法还通过虚拟样本增加样本的数量,充分利用目标特征信息,提高了图像分类识别的准确率。
1 常用图像表示方法常用的图像表示方法有协作表示分类法(CRC)[10]和线性回归分类(LRC)[11]以及SRC[12]方法中的l1正则化最小二乘法(l1_ls)[13]等。
假设数据集中总共有c类样本,且每类样本都有n个列向量形式的训练样本。假设
| $y = x_1^1\alpha _1^1 + x_1^2\alpha _1^2 + \cdot \cdot \cdot + x_c^n\alpha _c^n$ | (1) |
式中:
| $y = { X { \alpha}} $ | (2) |
式中:
在SRC(l1_ls)中,为了获得稀疏解,式(2)转化为式(3)的最优化问题:
| ${\bf{ \hat { \alpha} }} = \arg \mathop {\min }\limits_\alpha \left\| {{ y} - { X}{\bf{{ \alpha} }}} \right\|_2^2\;{ s.t.}\;{\left\| {\bf{{ \alpha} }} \right\|_1} \leqslant \tau $ | (3) |
| ${\bf{\hat { \alpha} }} = L({ \alpha} ,\lambda ) = \arg \mathop {\min }\limits_\alpha \frac{1}{2}\left\| {{ y} - { X}{\bf{{ \alpha} }}} \right\|_2^2 + \lambda {\left\| {\bf{{ \alpha} }} \right\|_1}$ | (4) |
式中
由于
| $\begin{array}{c}{{\hat \alpha }} = \arg \mathop {\min }\limits_{{{\alpha }},{{\sigma }} \in {\Re ^N}} \displaystyle\frac{1}{2}\left\| {{{y }} - { X}{{\alpha }}} \right\|_2^2 + \lambda \sum\limits_{i = 1}^N {{{\bf{\sigma }}_i}} \\\;\;\;\;\;\;\;{ s.t.}\;\; - {{\bf{\sigma }}_i} \leqslant {{\bf{\alpha }}_i} \leqslant {{\bf{\sigma }}_i}\end{array}$ | (5) |
再根据平切牛顿法[13]来求解式(5)即可得到稀疏解
在CRC方法中是根据l2范数来求解式(2)的表示解的,所以式(2)可转化为式(6)所示的最优化问题:
| ${{\hat { \alpha} }} = L({{\alpha }},\lambda ) = \arg \mathop {\min }\limits_{{\alpha }} \frac{1}{2}\left\| {{ y} - { X}{{\alpha }}} \right\|_2^2 + \lambda \left\| {{\alpha }} \right\|_2^2$ | (6) |
然后求解表示系数矩阵
| ${{\alpha }} = {({{{X }}^{{T}}}{{X }} + \lambda {{I }})^{ - 1}}{{{X }}^{{T}}}{{y }}$ | (7) |
式中
SRC(l1_ls)和CRC方法在求解得到表示系数之后,分别计算测试样本和每类由训练样本和其表示系数构成的重构图像之间的残差:
| ${r_i} = \left\| {{{y }} - {{{X }}_i}{{{\alpha }}_i}} \right\|$ | (8) |
式中
| ${r_k} = \min {r_i}\left( {k,i = 1,2,\cdots \! ,c} \right)$ | (9) |
那么测试样本y就被分类到第k类。
LRC方法是用每一类训练样本表示测试样本:
| $y = {{{X }}_i}{{{\alpha }}_i}$ | (10) |
求解式(10)得到表示系数为
| ${{{\alpha }}_i} = {({{X }}_i^{{T}}{{{X }}_i})^{ - 1}}{{X }}_i^{{T}}{{y }}$ | (11) |
最后再按照式(8)和式(9)分类测试样本。
2 基于联合表示的图像分类方法基于联合表示的图像分类方法主要包含两个步骤:1)利用原始样本得到其对应的虚拟样本;2)联合原始样本和其对应的虚拟样本进行分类。
2.1 虚拟样本的产生令I表示原始灰度图像,Iij表示I的第i行第j列的像素强度;v表示一幅灰度图像中像素最大值,那么对于通常的灰度图像则有
| ${J_{i\!j}} = (v - {I_{i\!j}}) * {I_{(i + 1)j}}$ | (12) |
式中:Jij表示得到的虚拟样本J的第i行第j列的像素强度。由于得到的Jij远大于v,因而在计算得到Jij之后对其采取规范化措施,使其值范围处于灰度图像的像素范围内。从得到虚拟图像的定义知:
1)如果Iij很大,那么不论I(i+1)j的值是大还是小,计算得到的Jij都会很小;
2)如果Iij很小,那么Jij的值将会随着I(i+1)j的值得变化而变化;而且当Iij与I(i+1)j相差非常大时,Jij会很大,这时将会突出显示图像边缘信息;
3)如果Iij的值为中等大小,那么不论I(i+1)j的值是大还是小,计算得到的Jij的值也将会是中等大小。
2.2 原始样本和虚拟样本的联合表示在得到虚拟样本之后,将表示分类方法分别应用到原始样本和虚拟样本上,然后分别计算得到它们的测试样本和重构样本之间的残差。
假设
| $r_o^j = \left\| {{ y} - {{ X}_i}{{{\alpha }}_i}} \right\|,r_v^j = \left\| {{{ y}_v} - {{ J}_i}{\bf{\alpha }}_i^v} \right\|$ | (13) |
式中:
| $r_z^j = a \times r_o^j + (1 - a) \times r_v^j$ | (14) |
式中:
最后再将
1)将数据库分为两个子集,即训练样本子集、测试样本子集;
2)由式(12)计算得到两个子集中所有原始样本对应的虚拟样本,并将所有样本转换为单位列向量;
3)表示分类方法分别应用到原始样本和虚拟样本中求得表示系数后,按照式(13)分别得到对应的
4)由式(14)得到最后的联合表示残差;
5)由式(9)将测试样本分类到具有最小残差的类别。
3 基于联合表示的图像分类方法分析在图像分类中,可以利用所有图像像素的子集代表图像的主要特征来进行图像分类[15-16]。通常一幅图像的重要特征主要集中在中等强度像素区域[2],基于联合表示的图像分类方法正是基于上述思想进行图像分类。
3.1 方法原理对比分析 3.1.1 方法特点分析1) 由(12)式得出的结论中可知,在得到的新的表示(虚拟样本)中,中等强度像素区域将会增加;除了边缘区域之外,拥有非常大或小的像素区域在虚拟样本中的值相对较小。
2) 由原始样本得到虚拟样本的过程是一个非线性变换过程。相比于通过线性变换得到的虚拟样本,由非线性变换得到的虚拟样本与其对应的原始样本有更多的互补性,即原始样本和其虚拟样本合在一起比它们之中任何一个单独所包含的信息都要多。
3) 基于原始样本和虚拟样本的联合表示来完成图像分类时,可以通过式(14)中融合系数a的设置调整原始样本和虚拟样本的分类结果的可靠性。如:a值的设置较大时,原始样本的分类结果比虚拟样本的分类结果要可靠。
由于联合表示的方法是先通过产生虚拟样本,再联合虚拟样本与原始样本进行表示目标图像的,显然,联合表示的方法在算法的时间复杂度上和稀疏表示的复杂度相同,只是重复计算了图像的残差表示结果,因而使得计算时间比原始稀疏表示长。
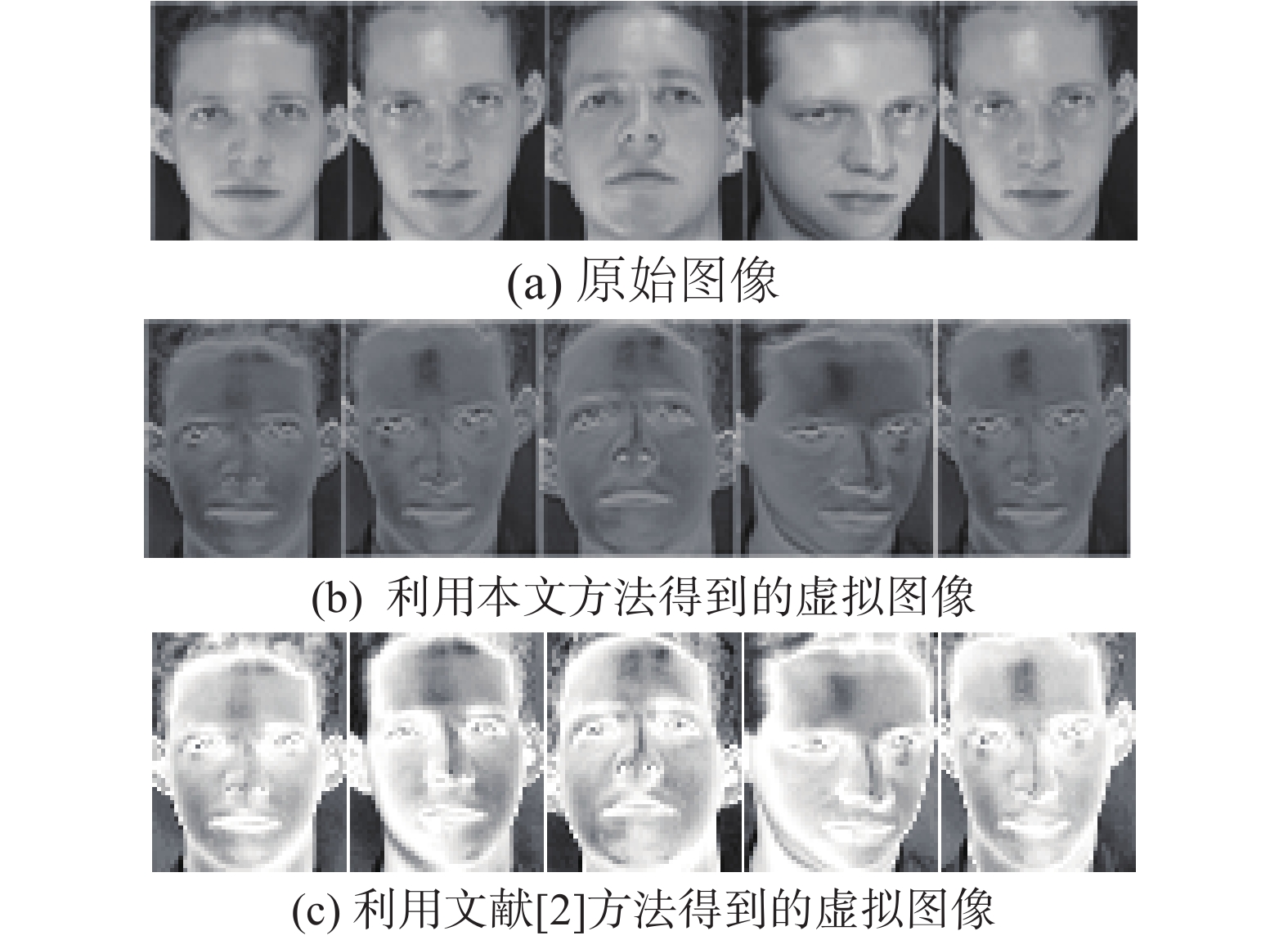
3.1.2 方法合理性分析以ORL数据库[17]为例进行方法合理性分析。ORL数据库包含来自40个人的总共400张图像,其中每个人均有10张不同的图像。数据库的所有图像均在不同时间、不同光照以及不同表情和细节(比如戴眼镜和不戴眼镜)下采集。图像大小均为92×112。图1中,第1行是ORL数据库中第1类图像的原始图像;第2行是采用本文方法得到的对应第1行的虚拟图像;第3行采用文献[2]方法得到的对应第1行的虚拟图像。
由图1中图像可以看出,虽然虚拟图像与原始图像直接相关,但是它们之间存在明显区别:本文方法得到的虚拟图像比原始图像对于光照细节的敏感度低,且在虚拟图像重要特征处(示例中的是眼睛和嘴巴等)比原始图像明显,而利用文献[2]方法得到的虚拟图像则更多地反映出光照信息,且在图像重要特征处的标示显示的不明显。由于原始图像和虚拟图像包含了同一类的不同方面的信息,因而同时使用它们能够得到更好的识别效果。
|
Download:
|
| 图 1 原始图像和利用本文方法以及文献[2]中方法得到的对应的虚拟图像 Fig. 1 The original images and their virtual images obtained by our method and the method proposed in literature [2] | |
ORL数据库中第1类的第1幅原始图像以及使用本文方法和文献[2]方法得到的其虚拟图像的灰度直方图如图2所示。可以看出本文方法得到虚拟图像的过程是一个非线性变换过程。此外,图2(b)和2(c)显示本文方法得到的虚拟图像的像素强度主要集中在中等强度区域,而文献[2]得到的虚拟图像的像素强度则主要偏向于高等强度区域。这说明在利用原始图像像素方面,本文方法更为合理。

|
Download:
|
| 图 2 原始图像和用不同方法得到的虚拟图像的灰度直方图 Fig. 2 The gray histograms of the original image and virtual images obtained by using different methods | |
虽然单独使用原始图像或虚拟图像进行分类可能得到满意的结果,但若能够将它们联合,识别率将得到明显提升,这是因为如果一个来自原始图像的测试图像被分类错误,但其虚拟图像对应的测试样本能够被正确分类,则按照式(14)将两种图像融合之后,测试样本也能被正确分类,识别率也更高;同样,当虚拟图像的测试样本分类错误,而其对应的原始图像的测试样本被正确分类时,按照式(14)的融合方法也能得到正确的分类结果。以ORL数据库为例来验证上述分析结果。
图3显示的是不同类别的重构样本与所有测试样本之间的距离。

|
Download:
|
| 图 3 不同类别的重构样本与所有的测试样本之间的距离 Fig. 3 The distances between reconstitution samples of different classes and all test samples | |
图3(a)是在训练样本数为8,测试样本数为2的情况下得到的;图3(b)是在训练样本数为7,测试样本数为3的情况下得到的。
在图3(a)中,重构图像属于第10类。在原始数据库下,可以明显看到第9个和第10个测试样本(这两个编号的测试样本属于第5类)下的距离最小,故在原始数据库中,给出的测试样本被识别为第5类,而事实上给出的测试样本属于第10类,所以在原始数据库上分类错误;在虚拟数据库下,第19个和第20个测试样本(这两个编号的测试样本属于第10类)下的距离最小,故在虚拟数据库中,给出的测试样本被识别为第10类,则分类正确;联合方法得到的结果与在虚拟库中得到的结果一致,因而最后的分类结果也是正确的。在图3(b)中,重构图像属于第31类。同理,在原始数据库下,第31类的测试样本被正确分类到第31类;在虚拟数据库下,测试样本被分类到第30类,分类错误;联合分类方法最后也将测试样本分类到第31类,即最后的结果也是正确的。
上述结果均表明,联合使用原始样本与虚拟样本一起来进行分类,比使用单一样本能够获得更好的分类结果。
4 实验研究为验证联合表示方法的优良性能,分别在ORL数据库、FERET数据库[18]、COIL-20数据库[19]和COIL-100数据库[20]上进行测试,所结合的表示方法为CRC、SRC(l1_ls)和LRC算法,对比方法为文献[2]所提出的方法。
FERET数据库包含超过200人的图像样本,本文实验中选取其中200个人的总计1 400张图像样本,其中每个人有7张不同的图像。数据库分别在不同光照和表情条件下,在相对正面人脸的±15°、±25°的条件下采集得到,图像的大小均为40×40;COIL-20数据库包含20个不同类别的物体图像,每类物体每隔5°采集一幅图像,每类物体包含72幅图像,整个数据库包含1 440张标准灰度图像。本文实验中挑选每类样本中的18幅图像共360幅图像,图像大小均为128×128;COIL-100数据库和COIL-20数据库类似,其中包含100个不同类别的物体的图像,本文实验中选择方式同COIL-20数据库,图像大小均为128×128。图4分别以这4种数据库中的一类图像作为代表展示了它们的特点。

|
Download:
|
| 图 4 种不同数据库中的原始图像 Fig. 4 The original images of the different four databases | |
在本实验中,对所有的数据库,联合表示方法在每类中均随机挑选若干样本作为训练样本,剩下的为测试样本,重复10次再取均值作为最终结果。对ORL数据库,每类分别选取3~5个样本作为训练样本,剩下的样本作为测试样本,且对于CRC、SRC(l1_ls)和LRC 3种分类方法均设置
| 表 1 ORL数据库上的不同方法的识别率 Tab.1 The classification rates of different methods on the ORL database |
对FERET数据库,每类分别选取2~4个图像作为训练样本,每类剩下的样本作为测试样本,且对于CRC、SRC(l1_ls)和LRC 3种分类方法均设置
| 表 2 FERET数据库上的不同算法的识别率 Tab.2 The classification rates of different methods on the FERET database |
对于COIL-20数据库,每类分别选取7~9个样本作为训练样本,每类剩下的样本作为测试样本,且对于CRC分类算法设置
| 表 3 COIL-20数据库上的不同算法的识别率 Tab.3 The classification rates of different methods on the COIL-20 database |
对于COIL-100数据库,每类分别选取5~7个图像作为训练样本,每类剩下的样本作为测试样本,且对于CRC分类算法设置
| 表 4 COIL-100数据库上的不同算法的识别率 Tab.4 The classification rates of different methods on the COIL-100 database |
在文献[2]的方法中,使用常规方式选取训练样本,即选取每类样本中编号的前若干个样本作为训练样本,剩下的则作为测试样本,则对于每一种训练样本,利用文献[2]中方法得出的实验结果只有一个。从表1~4可以看出,本文方法与CRC方法、LRC方法和SRC(l1_ls)方法结合之后,其分类正确率有明显提升。例如,对于ORL数据库,当每类的训练样本数为4时,单纯使用CRC算法进行分类得到的平均识别率为93.00%,而本文方法与CRC算法结合后进行分类,其平均识别率提升到为94.58%;对于FERET数据库,当每类的训练样本数为4时,单纯使用LRC方法分类得到的平均识别率为77.67%,而本文方法与LRC结合后进行分类时,其平均识别率提高到78.67%;对于COIL-100数据库,当每类的训练样本数为5时,单纯使用SRC(l1_ls)方法进行分类平均识别率为54.77%,本文方法与SRC(l1_ls)方法结合后进行分类时,其平均识别率提升到为56.28%。另外,相比于同样是使用虚拟样本的文献[2]的方法而言,在训练样本数相同的情况下,除了少数情况以外,本文方法得到的识别率都比其高。这些都充分说明了本文方法对于提升表示分类方法识别率具有优良性能。
5 结束语针对图像分类问题中的光照和小样本问题,提出了一种新的图像分类表示方法。这种方法能通过联合原始样本和虚拟样本的信息来提升分类性能。这里得到的虚拟图像不仅能够有效地利用原始图像中相邻像素之间的信息,突出显示目标的重要特征,且其对于光照信息不敏感。另外,由于同时利用了原始样本和虚拟样本,因而,其在增加训练样本个数,减小由小样本问题带来的影响方面也有帮助。本文方法还通过与其他表示分类方法相结合来提升该方法的分类效果。本文的方法的不足之处在于,不能自适应地选取联合系数,因此,下一阶段的工作就是找到一种方法,能够自适应地选取联合系数来进行分类。
| [1] |
CHEN Jie, SHAN Shiguang, HE Chu, et al. WLD: a robust local image descriptor[J]. IEEE transactions on pattern analysis and machine intelligence, 2010, 32(9): 1705-1720. DOI:10.1109/TPAMI.2009.155 ( 0) 0)
|
| [2] |
XU Yong, ZHANG B, ZHONG Zuofeng. Multiple representations and sparse representation for image classification[J]. Pattern recognition letters, 2015, 68: 9-14. DOI:10.1016/j.patrec.2015.07.032 ( 0) 0)
|
| [3] |
祝志远, 张庆辉. 基于视觉感知的人体轮廓捕获及自动调焦[J]. 应用科技, 2016, 6(2): 50-53. ZHU Zhiyuan, ZHANG Qinghui. An auto focus method for capturing body contours based on visual perception[J]. Applied science and technology, 2016, 6(2): 50-53. (  0) 0)
|
| [4] |
JIAN M, LAM K M, DONG J. Illumination compensation and enhancement for face recognition[C]//Proceedings of Asia—Pacific Signal and Information Processing Association Annual Summit and Conference. Xi’an: APSIPA, 2011.
( 0) 0)
|
| [5] |
HUANG Wei, WANG Xiaohui, MA Yanbo, et al. Robust kernel collaborative representation for face recognition[J]. Optical engineering, 2015, 54(5): 53103. DOI:10.1117/1.OE.54.5.053103 ( 0) 0)
|
| [6] |
XU Yong, LI Xuelong, YANG Jian, et al. Integrate the original face image and its mirror image for face recognition[J]. Neurocomputing, 2014, 131: 191-199. DOI:10.1016/j.neucom.2013.10.025 ( 0) 0)
|
| [7] |
PAYNE T, NICELY M C. Non-rectangular and/or non-orthogonal arrangement of gambling elements in a gaming apparatus[P]. US: US6241607, 2001.
( 0) 0)
|
| [8] |
MA Zhongli, LIU Quanyong, HAO Liangliang. Multiple collaborative representations for face recognition[C]//Proceedings of 2016 IEEE International Conference on Mechatronics and Automation. Harbin, China: 2016: 1655–1660.
( 0) 0)
|
| [9] |
XU Yong, ZHANG D, YANG Jian, et al. A two-phase test sample sparse representation method for use with face recognition[J]. IEEE transactions on circuits and systems for video technology, 2011, 21(9): 1255-1262. DOI:10.1109/TCSVT.2011.2138790 ( 0) 0)
|
| [10] |
ZHANG Lei, YANG Meng, FENG Xiangchun. Sparse representation or collaborative representation: which helps face recognition?[C]//Proceedings of 2011 International Conference on Computer Vision. Barcelona, Spain: IEEE, 2011: 471–478.
( 0) 0)
|
| [11] |
NASEEM I, TOGNERI R, BENNAMOUN M. Robust regression for face recognition[J]. Pattern recognition, 2012, 45(1): 104-118. DOI:10.1016/j.patcog.2011.07.003 ( 0) 0)
|
| [12] |
WRIGHT J, MA Yi, MAIRAL J, et al. Sparse representation for computer vision and pattern recognition[J]. Proceedings of the IEEE, 2010, 98(6): 1031-1044. DOI:10.1109/JPROC.2010.2044470 ( 0) 0)
|
| [13] |
KOH K, KIM S J, BOYD S. An interior-point method for large-scale l1-regularized logistic regression[J]. The journal of machine learning research, 2007, 8: 1519-1555. ( 0) 0)
|
| [14] |
PORTUGAL L F, RESENDE M G C, VEIGA G, et al. A truncated primal-infeasible dual-feasible network interior point method[J]. Networks, 2000, 35(2): 91-108. DOI:10.1002/(ISSN)1097-0037 ( 0) 0)
|
| [15] |
SMIELIK I, KUHNERT K D. Statistical dependence of pixel intensities for pattern recognition[C]//IEEE International Conference on Industrial Technology. Cape Town, South Africa: IEEE, 2013: 1179–1183.
( 0) 0)
|
| [16] |
吴鹏, 徐洪玲, 宋文龙. 结合小波金字塔的快速NCC图像匹配算法[J]. 哈尔滨工程大学学报, 2017, 5(38): 791-796. WU Peng, XU Hongling, SONG Wenlong. A fast NCC image matching algorithm based on wavelet pyramid search strategy[J]. Journal of harbin engineering university, 2017, 5(38): 791-796. (  0) 0)
|
| [17] |
SAMARIA F S, HARTER A C. Parameterisation of a stochastic model for human face identification[C]//Proceedings of 1994 IEEE Workshop on Applications of Computer Vision. Sarasota, FL: IEEE, 1994: 138–142.
( 0) 0)
|
| [18] |
PHILLIPS P J, MOON H, RIZVI S A, et al. The FERET evaluation methodology for face-recognition algorithms[J]. IEEE transactions on pattern analysis and machine intelligence, 2000, 22(10): 1090-1104. DOI:10.1109/34.879790 ( 0) 0)
|
| [19] |
NENE S A, NAYAR S K, MURASE H. Columbia object image library (COIL-20), CUCS-005-96[R]. 2011.
( 0) 0)
|
| [20] |
NENE S A, NAYAR S K, MURASE H. Columbia object image library (COIL-100), CUCS-006-96[R]. Columbia: Columbia University, 1996.
( 0) 0)
|
 2018, Vol. 13
2018, Vol. 13


