爬壁机器人的吸附方式中真空吸附应用普遍。真空吸附主要包括真空泵和吸盘。真空泵不断从吸盘腔中抽气，使吸盘腔内达到一定真空度，在大气压和摩擦力作用下，机器人不会倾覆^[1]。为了使吸盘和壁面紧密贴合，必须使吸盘平面和目标壁面平行，且两个平面间距足够小。足式真空吸附爬壁机器人通过接触传感器来感知吸盘和壁面的接触情况。美国密歇根州立大学研发的爬壁机器人Flipper和Crawler^[2]、中国科学院沈阳自动化研究所研发的机器人^[3–4]均采用单吸盘结构，在每个吸盘足安装了2个接触传感器，通过试探性地微调足端来使吸盘和壁面贴合，吸附动作缓慢；文献[5–6]采用吸盘组作为机器人的吸足，对吸盘与壁面的相对姿态要求更高；文献[7]爬壁机器人吸盘底部装有8个红外传感器组成的圆形阵列，用来判断吸盘和壁面的平行度，吸盘两侧装有光纤触觉传感器，用来感知吸盘和壁面的距离。机器人根据8个传感器的值，经位置逆解来使吸盘足和壁面平行。文献[8-9]通过在吸盘平面上安装距离传感器，来测量与壁面的距离。空间中确定吸盘平面至少需要安装3个距离传感器。根据3个距离传感器的值，计算出吸盘平面相对于壁面的夹角和距离。机器人基于运动学位置逆解调节关节角度，使吸盘和壁面贴合紧密。

在实际作业时，操作功能是机器人的关键。华南理工大学研发了爬杆机器人Climbot^[10–11]，使用摇杆控制机器人从6 m高的路灯杆上拧下灯泡，但是其摇杆和机器人动作映射过于复杂。文献[12]设计了混合坐标系来操作挖掘机，作者将挖斗和根部关节分开控制，使摇杆操作更直观。文献[13]为不同支撑足的情况分别建立了运动学模型。

本文首先介绍了自主研发的爬壁机器人机构；而后根据D-H参数，建立运动学模型、吸盘足至壁面的空间几何模型，分析可靠吸附的必要条件；然后设计了一种用于机构对称机器人的摇杆操作方法，摇杆轴数值映射为机器人摆动吸盘足在笛卡尔空间中的速度；最后开发了自适应吸附装置，在爬壁机器人上进行实物验证。

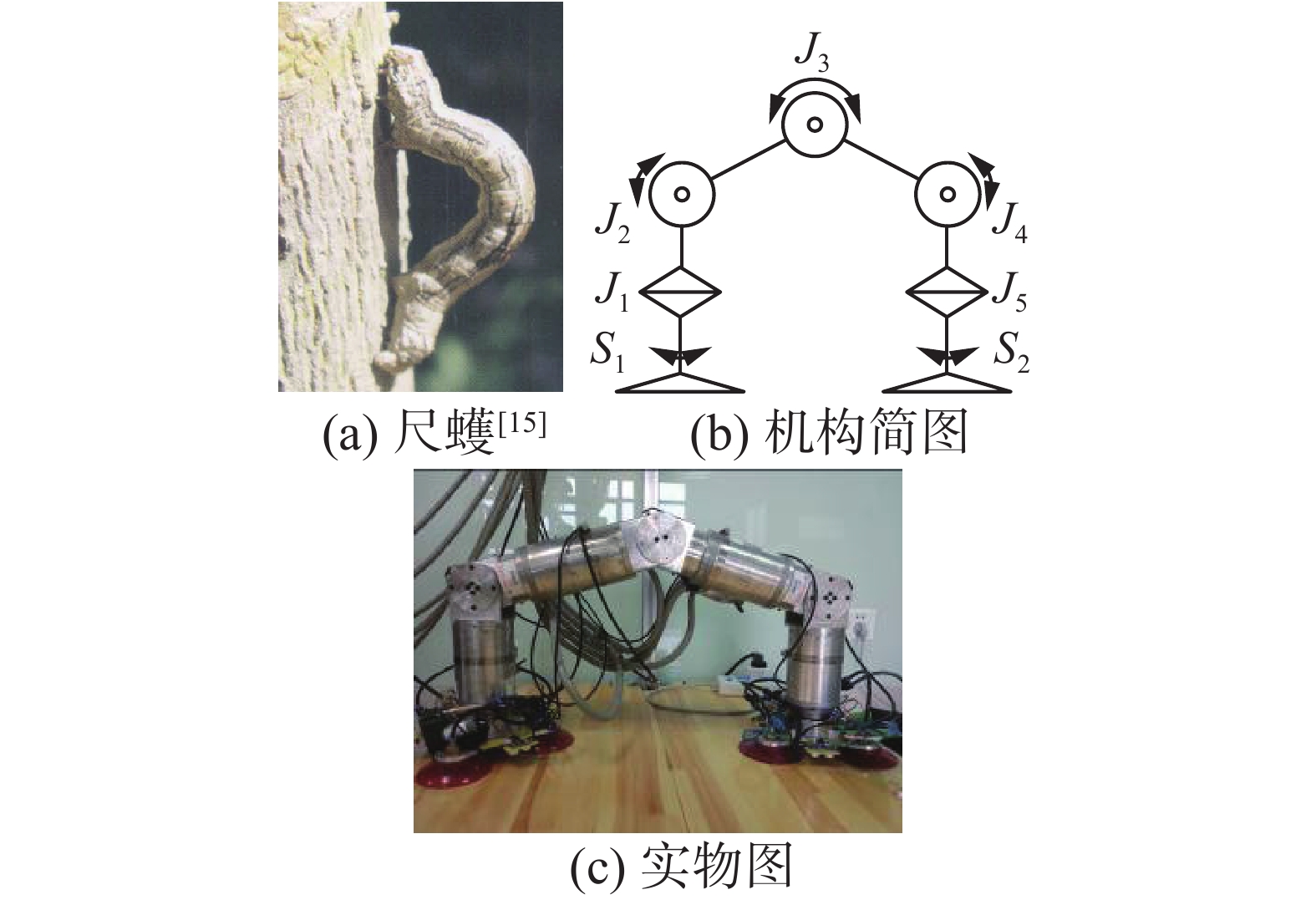
1 机器人机构

仿尺蠖爬壁机器人由5个旋转关节串联组成，结构对称，可以像图1(a)中的尺蠖一样蠕动爬行。图1(b)中，J₁和J₅关节轴线和连杆轴线重合，传动链是直流无刷电机+行星减速机+谐波减速机，用来模仿尺蠖转向；J₂、J₃和J₄关节轴线和连杆轴线垂直，传动链是直流无刷电机+谐波减速机+锥齿轮，用来模仿尺蠖躯体伸缩。S₁和S₂是两个吸盘足，对应于尺蠖头部和尾部用来附着植物的趾钩。每个吸盘足上安装有3个真空吸盘，以等边三角形分布，用以抵抗重力。多吸盘结构能够减小因吸盘形变导致的机器人倾斜^[14]。

2 机器人建模 2.1 位置运动学建模

J₂、J₃和J₄关节是爬行运动的关键，将爬壁机器人简化为一个平面三连杆机构。建立D-H坐标系，如图2所示。

建立摆动吸盘足到支撑吸盘足的齐次坐标变换矩阵：

${ T} = \left[ {\begin{array}{*{20}{c}} {{{{c}}_{{{123}}}}} & { - {{{s}}_{{{123}}}}} & 0 & {p{}_x} \\ {{{{s}}_{{{123}}}}} & {{{{c}}_{{{123}}}}} & 0 & {{p_y}} \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array}} \right]$

(1)

式中：

${p_x} = {a_1}{{{c}}_1} + {a_2}{{{c}}_{12}} + {a_3}{{c}}{}_{123}$

(2)

${p_y} = {a_1}{{{s}}_1} + {a_2}{{{s}}_{12}} + {a_3}{{{s}}_{123}}$

(3)

式中： ${{{s}}_1}$ 、 ${{{c}}_1}$ 分别为 $\sin {\theta _1}$ 和 $\cos {\theta _1}$ 的缩写， ${{{s}}_{12}}$ 、 ${{{c}}_{12}}$ 分别为 $\sin \left( {{\theta _1} + {\theta _2}} \right)$ 和 $\cos \left( {{\theta _1} + {\theta _2}} \right)$ 的缩写， ${{{s}}_{123}}$ 、 ${{{c}}_{123}}$ 分别为 $\sin \left( {{\theta _1} + {\theta _2} + {\theta _3}} \right)$ 和 $\cos \left( {{\theta _1} + {\theta _2} + {\theta _3}} \right)$ 的缩写， ${a_1}$ 、 ${a_2}$ 和 ${a_3}$ 均表示连杆长度。

设

$\varphi = {\theta _1} + {\theta _2} + {\theta _3}$

(4)

可得

$\varphi = \arctan \frac{s_{123}}{c_{123}}$

${\theta _2} = \pm {{arctan}}\frac{{w_x^2 + w_y^2 - a_1^2 - a_2^2}}{{2{a_1}{a_2}\sqrt {1 - {{c}}_2^2} }}$

(5)

${\theta _1} = {{arctan}}\frac{{({a_1} + {a_2}{{{c}}_2}){w_y} - {a_2}{{{s}}_2}{w_x}}}{{({a_1} + {a_2}{{{c}}_2}){w_y} + {a_2}{{{s}}_2}{w_x}}}$

(6)

${\theta _3} = \varphi - {\theta _1} - {\theta _2}$

(7)

式中： ${w_x} = {p_x} - {a_3}{{c}}\varphi $ ， ${w_y} = {p_y} - {a_3}{{s}}\varphi $ 。

由式(5)可知，运动学位置逆解有两组解： ${\theta _2}$ 为正值时，机器人如图2虚线所示，由于机构参数限制，J₂和J₄关节无法到达此位置，此解无效； ${\theta _2}$ 为负值时，机器人如图2实线所示，此解为有效解。

2.2 速度运动学建模

分别对式(2)~(4)求微分，并写成矩阵形式：

$\left[ \begin{array}{l} {{d}}{p_x} \\ {{d}}{p_y} \\ {{d}}\varphi \\ \end{array} \right] = {{J}}\left[ \begin{array}{l} {{d}}{\theta _1} \\ {{d}}{\theta _2} \\ {{d}}{\theta _3} \\ \end{array} \right]$

(8)

式中 ${{J}}$ 为雅各比矩阵。

式(8)中引入 $\varphi $ 是为了将 ${{J}}$ 凑成 $3 \times 3$ 方阵，以便于求逆。式(8)两边同时左乘雅各比逆矩阵 ${{{J}}^{ - 1}}$ ，并除以 ${{d}}t$ ，可得

$\left[ \begin{array}{l} {\omega _1} \\ {\omega _2} \\ {\omega _3} \\ \end{array} \right] = {{{J}}^{ - 1}}\left[ \begin{array}{l} {\nu _{{x}}} \\ {\nu _{{y}}} \\ {\omega _\varphi } \\ \end{array} \right]$

(9)

式中： ${\omega _1}$ 、 ${\omega _2}$ 和 ${\omega _3}$ 分别为关节J₂、J₃与J₄的转速， ${\nu _{{x}}}$ 和 ${\nu _{{y}}}$ 为机器人末端在笛卡尔空间中相对基坐标系X₁和Y₁方向上速度。

2.3 吸盘足与壁面夹角分析

如图3所示，S₁为支撑吸盘足，S₂为摆动吸盘足，下文分别简称为支撑足和摆动足。 ${{\alpha }}$ 为吸盘和距离传感器所在平面， ${{\beta }}$ 为目标壁面，点 ${{A}}$ 、 ${{B}}$ 和 ${{C}}$ 分别表示3个距离传感器的安装位置， $\Delta {{ABC}}$ 为等边三角形， ${l_1}$ 、 ${l_2}$ 和 ${l_3}$ 分别为点 ${{A}}$ 、 ${{B}}$ 和 ${{C}}$ 到目标平面 ${{\beta }}$ 的距离， $\Delta {{A'B'C'}}$ 为 $\Delta {{ABC}}$ 在平面 ${{\beta }}$ 上的投影。

在平面 ${{\alpha }}$ 内建立空间坐标系，以 $\Delta {{ABC}}$ 的中心作为坐标系原点 ${{O}}$ 。点 ${{O}}$ 到点 ${{A}}$ 、 ${{B}}$ 、 ${{C}}$ 的距离均为 $R$ 。 ${{\alpha }}$ 和 ${{\beta }}$ 平面方程分别为

$\begin{array}{c}{{\alpha }}:z = 0\\{{\beta }}:Mx + Ny + Pz + Q = 0\end{array}$

式中： $M \!=\! 2{l_2} - {l_1} - {l_3}$ ， $N \!=\! \sqrt 3 ({l_1} - {l_3})$ ， $P \!=\! 3R$ ， $Q \!=\! - R({l_1} + $ $ {l_2} + {l_3})$ 。

平面 ${{\alpha }}$ 和 ${{\beta }}$ 的法向量可表示为 ${{{n}}_{{\alpha }}}$ 和 ${{{n}}_{{\beta }}}$ ：

${{{n}}_{{\alpha }}} = {\left[ {\begin{array}{*{20}{c}} 0 & 0 & 1 \end{array}} \right]^{{T}}}, {{{n}}_{{\beta }}} = {\left[ {\begin{array}{*{20}{c}} M & N & P \end{array}} \right]^{{T}}}$

由此可得平面 ${{\alpha }}$ 和 ${{\beta }}$ 的夹角 $\theta $ ：

$\cos \theta = \cos \left\langle {{{{n}}_{{\alpha }}},{{{n}}_{{\beta }}}} \right\rangle = \frac{{| {{{{n}}_{{\alpha }}} \cdot {{{n}}_{{\beta }}}} |}}{{| {{{{n}}_{{\alpha }}}} || {{{{n}}_{{\beta }}}} |}}$

推导可得

$\theta = \arccos \frac{P}{{\sqrt {{M^2} + {N^2} + {P^2}} }}$

(10)

$\theta $ 的范围为 $0 \sim \text{π} /2$ 。 $\theta = 0$ 时，吸盘足和壁面平行，是可靠吸附的必要条件。

3 摇杆操作与自适应吸附设计 3.1 摇杆与机器人动作映射

吸盘足交替吸附时，机器人始终以X₁、Y₁作为基坐标系。将摇杆轴数值映射为摆动足的速度值。

根据式(9)，在已知机器人摆动足在笛卡尔空间中X₁和Y₁方向上速度情况下，可求得关节J₂、J₃与J₄的转速。机器人运动过程中有3种情况：

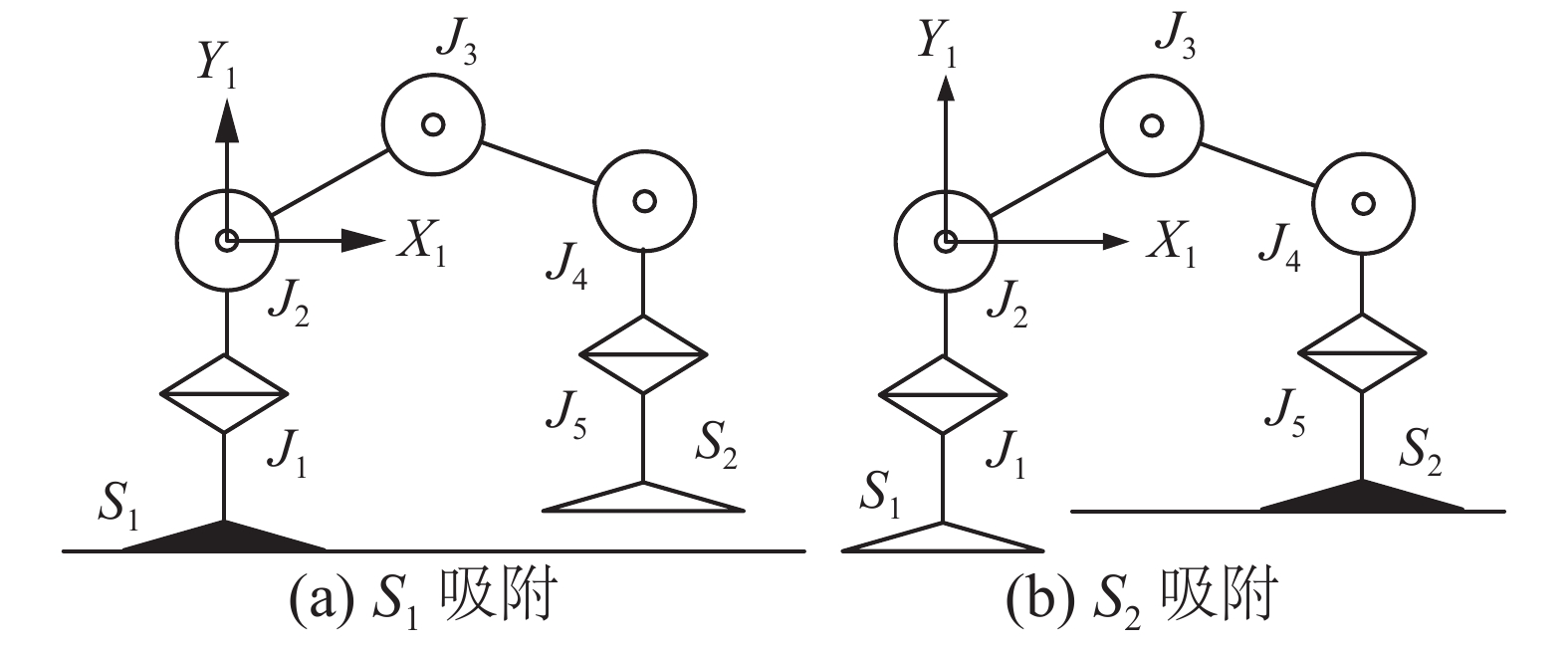
1) 吸盘足的抬起和放下。如图4(a)，当S₁为支撑足时，摆动足S₂向上抬起，若此时S₂为支撑足，如图4(b) ，可以看到摆动足S₁是向下运动的。支撑足不同时，相同的动作，导致摆动足在Y₁方向上的运动方向是相反的。为使摇杆轴和机器人运动之间的映射不因支撑足不同而改变，当S₁为支撑足时， $y \to {v_y}$ ；当S₂为支撑足时， $y \to - {v_y}$ 。其中， $y$ 表示摇杆 ${{y}}$ 轴的值， ${v_y}$ 表示机器人摆动足沿Y₁方向运动的速度，箭头表示映射。

2) 机器人躯干的伸缩。如图5，当S₁或S₂为支撑足时，躯干伸长代表前进，躯干缩短代表后退，摇杆与机器人动作映射为： $x \to {v_x}$ ，其中， $x$ 表示摇杆 ${{x}}$ 轴的值， ${v_x}$ 表示机器人摆动足沿X₁方向运动的速度。

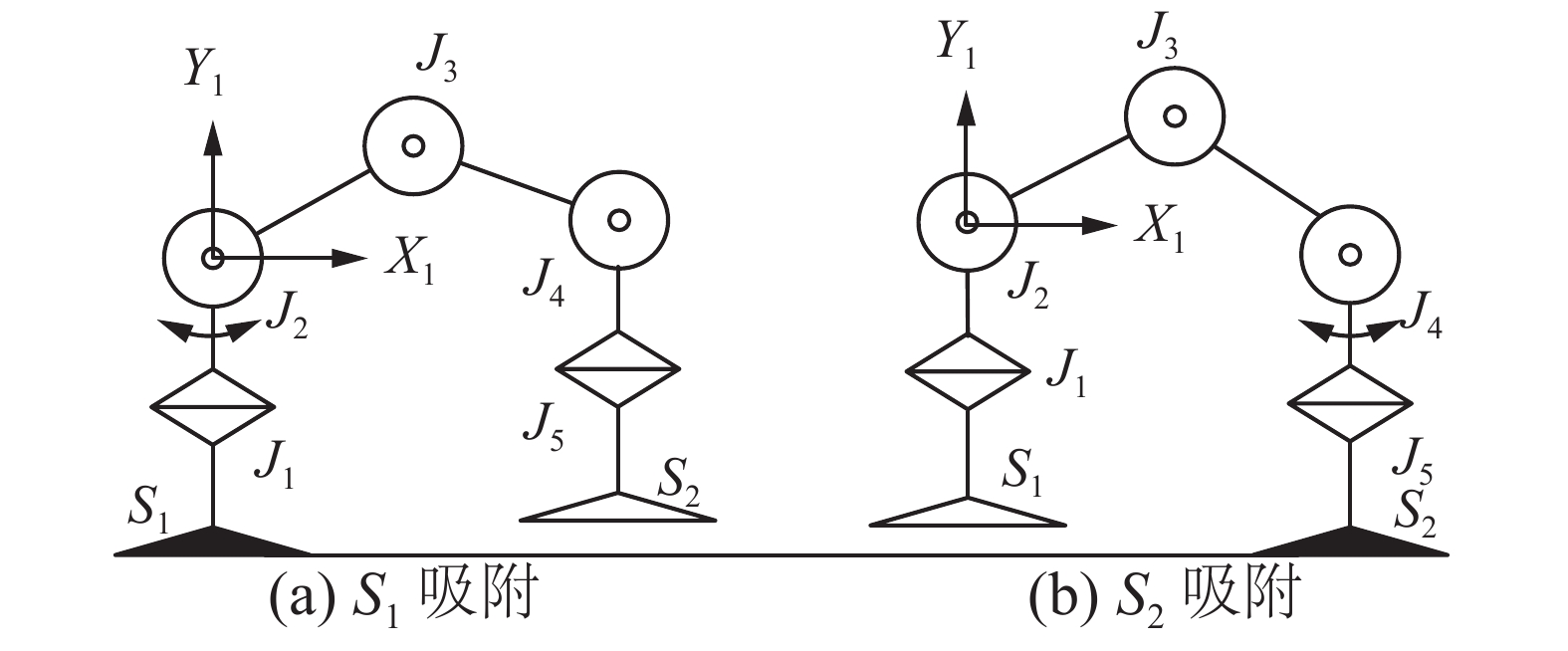
3) 机器人转向。如图6(a)，当S₁为支撑足时，摇杆控制J₁， $z \to {v_{{{J_1}}}}$ ；如图6(b)，当为S₂支撑足时，摇杆控制J₅， $z \to {v_{{{J_5}}}}$ 。其中， $z$ 表示摇杆 ${{z}}$ 轴的值， ${v_{{{J_1}}}}$ 表示机器人J₁关节转速， ${v_{{{J_5}}}}$ 表示机器人J₅关节转速。

机器人运动过程中，通过监测S₁和S₂中的气压来确定支撑足和摆动足。当摆动足至壁面距离小于设定阈值时，摇杆操作失效，机器人自动切换至自适应吸附动作。

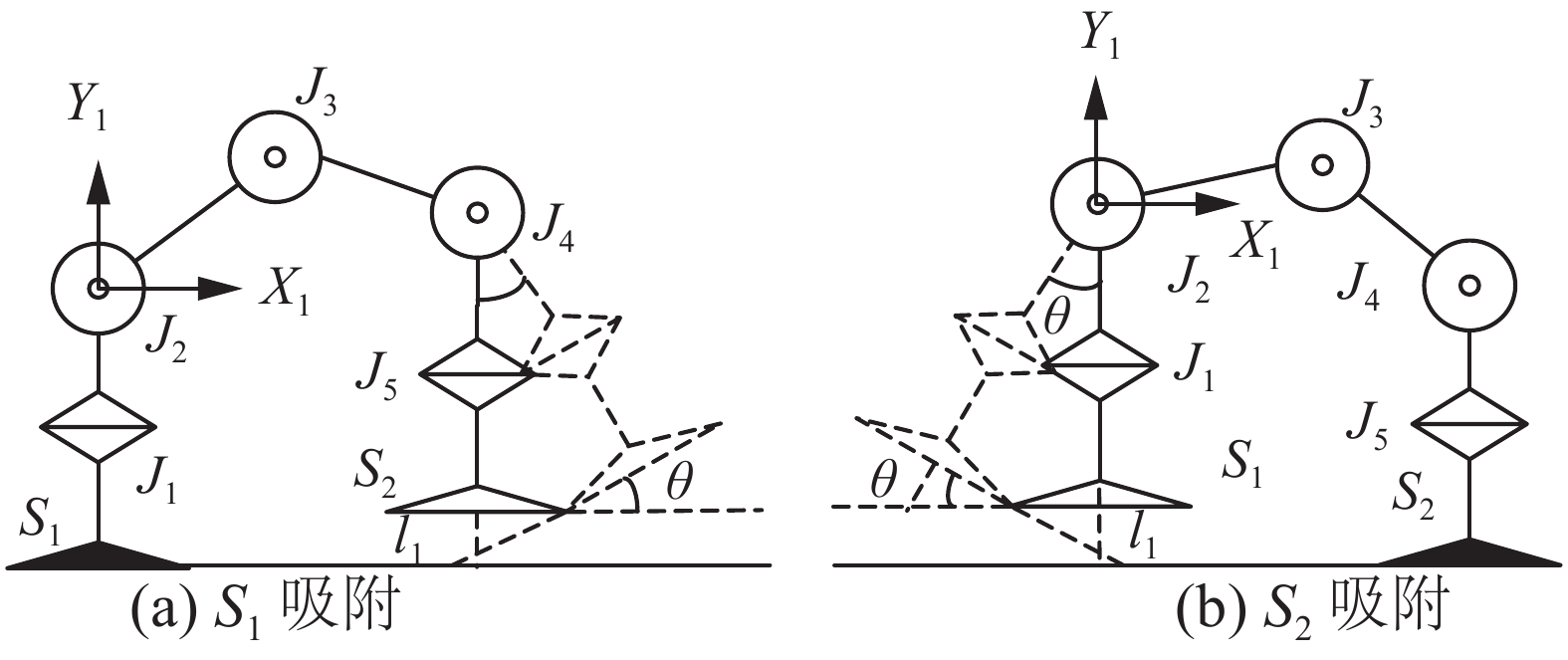
3.2 自适应吸附设计

如图7(a)，S₁为支撑足，根据式(10)求出 $\theta $ 的值；J₄关节旋转 $\theta $ ，使摆动足和壁面平行，此时 ${l_1} = {l_2} = {l_3}$ ；之后再次获取 ${l_1}$ 的值，根据式(5)~(7)求得J₃、J₄和J₅的角度，使 ${l_1} = 0$ ，此时S₂和壁面贴合紧密。如图7(b)，S₂为支撑足，不同于S₁为支撑足的情况：此时通过调节J₂使摆动足和壁面平行。

4 实验测试 4.1 控制系统

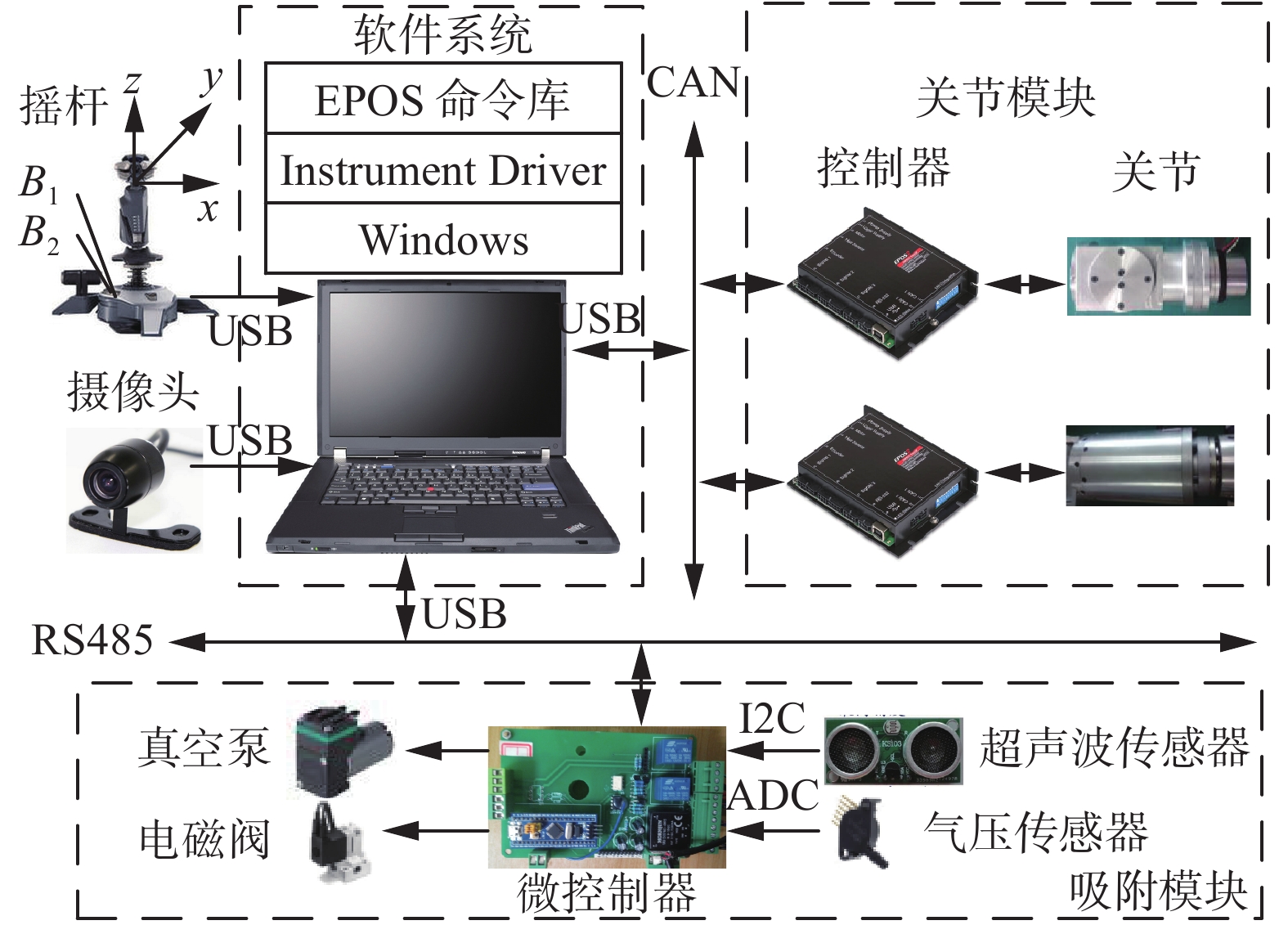
搭建了控制系统，如图8所示，控制系统包括PC、关节模块、摇杆、图像采集设备和吸附模块。

PC作为上位机负责机器人的运动规划、状态监控、人机交互和图像采集；关节模块中，每个电机上集成有相对式编码器，伺服控制器负责底层电流、速度及位置闭环运动控制；吸附模块由微控制器最小系统和外围电路组成，微控制器作为下位机，负责响应上位机命令。PC通过CAN和5个关节模块进行通信，通过RS485和2个吸盘足上的微控制器进行通信。摇杆和图像采集设备通过USB和PC连接。

吸盘足上的微控制器和上位机约定有6种命令：0x11、0x12、0x13、0x21、0x22和0x23，其中0x代表十六进制；第一位代表吸盘足，“1”代表吸盘足S₁，“2”代表吸盘足S₂；第二位代表命令，“1”代表读取距离，“2”代表读取气压，“3”代表吸盘足释放。

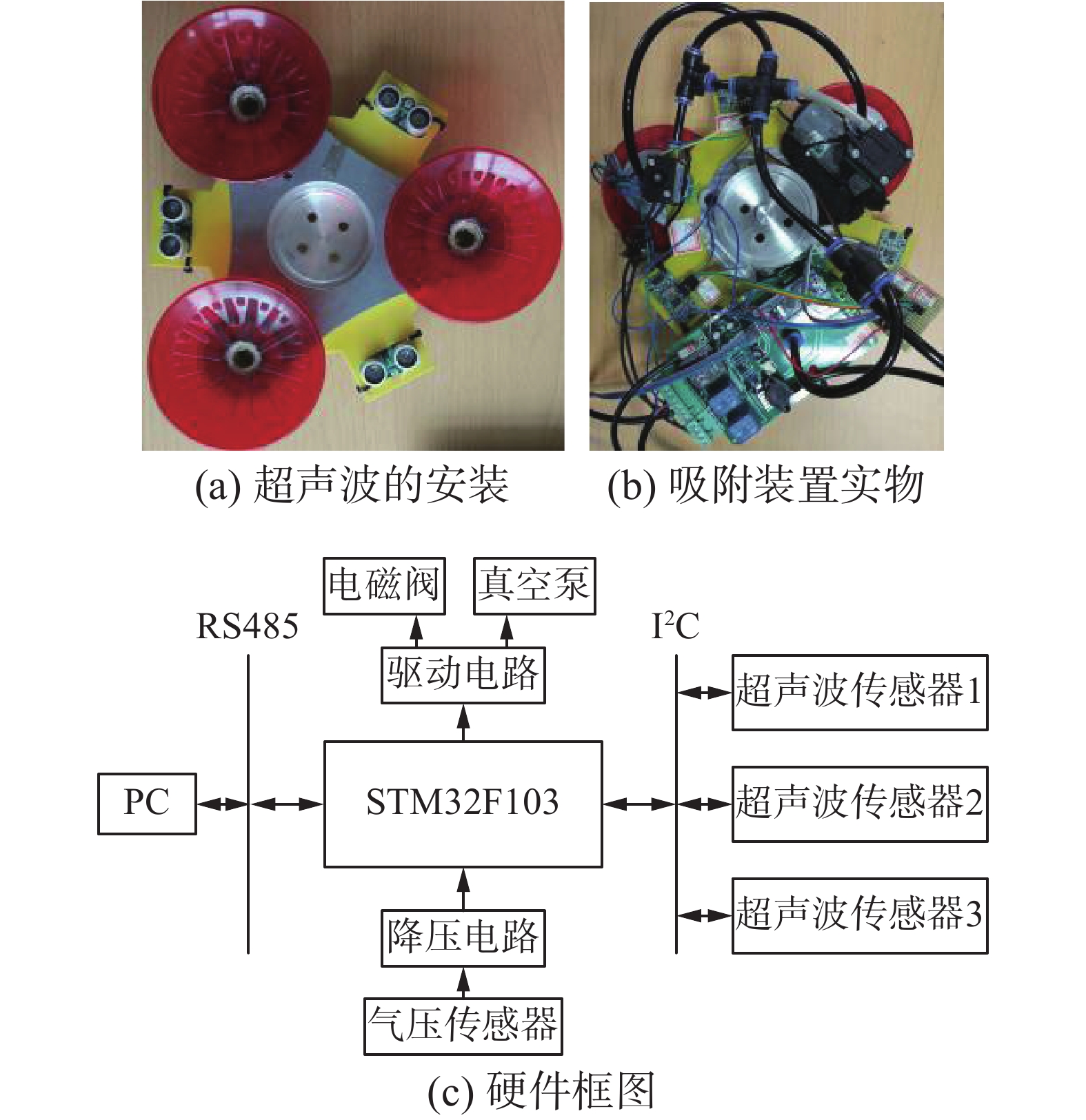
4.2 吸附装置

选用基于ARM的32位微控制器STM32F103作为足端传感和控制系统的控制器，运行频率72 MHz。距离传感器选用超声波传感器KS103，3个超声波传感器以等边三角形方式安装于吸盘足上，如图9(a)、(b)所示，微控制器通过I2C总线读取超声波传感器的数值。为了判断是否吸附成功，选用MPX5100气压传感器检测气路中气压，MPX5100输出0～5 V的模拟量，经过降压后接入微控制器的ADC端口。微控制器通过控制电磁阀和真空泵的开关，来控制吸盘足的吸附和释放。硬件框图如图9(c)所示。

机器人有两个吸盘足，每个吸盘足上都装有自适应吸附装置。以吸盘足S₁为例，微控制器上电后，经初始化进入循环，在循环中不断检查是否收到命令。微控制器收到0x11后分别测量3个超声波的值，并发送至上位机，满足设定阈值时，自动打开真空泵，开始吸附；收到0x12后测量气压传感器的值，并发送至上位机；收到0x13后，关闭真空泵，气路接大气。

4.3 爬行测试

机器人空载时，使用摇杆控制机器人在水平壁面上进行全向爬行运动。在图10(a)~(g)中，机器人前进了一个步长；在图10(h)~(n) 中，机器人改变了运动方向。操作方法如下：

1) 按下B₁按键，S₁释放；

2) 按下B₂按键，S₂释放；

3) 操作摇杆 ${{y}}$ 轴，抬起或放下摆动足，当摆动足至壁面距离小于自动吸附阈值时，摇杆轴失效，机器人自适应吸附至壁面；操作摇杆 ${{x}}$ 轴，机器躯体伸缩；操作摇杆 ${{z}}$ 轴，机器人转弯。

5 结束语

自适应吸附和摇杆控制设计，使机器人无需人工干预，自动调整吸盘足位姿，完成吸附动作，实验验证得出以下结论：1)在机器人吸盘足上安装3个距离传感器，测量吸盘足相对壁面的距离和倾角，经位置逆运动学求解，控制关节位置闭环，可使机器人自适应吸附至壁面；2)经逆速度运动学求解，将摇杆映射为机器人关节速度闭环，设定自适应吸附动作触发阈值，吸盘接近壁面时自动触发自适应吸附，降低了操控复杂度。由于超声波传感器的物理特性限制，当吸盘和壁面夹角大于超声波传感器波束角时，测距误差过大，无法正常使用，以后可选用其他类型的距离传感器。