2. 大连海事大学 船舶自动化仿真器研究所,辽宁 大连 116026
2. Institute of Ship Automation and Simulator, Dalian Maritime University, Dalian 116026, China
装备舵装置和螺旋桨推进器的水面船舶,通常由舵装置产生的转船力矩和螺旋桨的纵向推进力同时来控制船舶的位置和艏摇角3个自由度的状态,其中位置状态的控制是通过调节艏摇角间接实现的。这属于机械系统的广义坐标向量维数大于控制输入向量维数的情况,也就是说此时的船舶运动控制系统属于欠驱动系统。正常航行中的大多数船舶均处于欠驱动状态[1]。
近年来,随着控制理论的发展,欠驱船舶运动控制问题已经成为研究者关注的热点[2-4]。欠驱动船舶运动控制系统属于一类带有非完整加速度约束的非线性系统,传统非完整系统的控制方法不能直接应用于欠驱动船舶,因此深入研究欠驱动船舶运动控制问题具有理论和实际意义[5]。文献[6]在航向角速度持续激励的假设下,应用Lyapunov直接法设计出连续时变控制律,但是该控制律要求参考路径不能为直线;文献[7]通过适当的坐标变换,解决了持续激励问题,提出一种全局渐进稳定的路径跟踪控制律;文献[8]基于反演方法,提出了鲁棒非线性路径跟踪控制律,但是忽略了船舶模型中的非线性阻尼项。实现不依赖于船舶模型参数的路径跟踪控制是极为有意义的,可提高工程实用性。为了解决外部环境扰动和模型参数不确定性的影响,K.D.DO和他的团队利用LPA(Lipschitz projection algorithm)算法[9]对不确定项进行在线估计,设计出鲁棒自适应控制律[10]。由于神经网络对非线性函数具有很强的逼近能力[11],很多学者将其应用到欠驱动船舶跟踪控制中。文献[12]将迭代神经网络方法和动态面技术结合起来,提出一种速度控制律,可使得欠驱动船舶路径跟踪闭环系统所有误差信号最终一致有界;文献[13]为了补偿不确定模型参数以及外界风、浪、流所引起的干扰,将多层神经网络逼近器与鲁棒自适应控制方法相结合,设计出神经自适应鲁棒控制律;文献[14]基于自适应神经网络控制方法,提出了一种全局滑模路径跟踪控制律;文献[15]针对欠驱动船舶在稳定航速条件下的跟踪问题,利用神经网络逼近特性实现控制器中非线性部分的在线估计,提出了一种自适应神经网络与反步法结合的控制算法;文献[16]利用微分同胚变换和Lyapunov直接方法设计参考航向和速度,然后利用神经网络技术对操纵环路和推进环路分别设计自适应控制律,从而实现欠驱动船舶路径跟踪控制,该控制方法是针对船舶模型中惯性质量参数是已知的情况,但是在实际中,由于外界环境的干扰,一般惯性质量参数建模是不精确的。受以上研究的启发,考虑到船舶模型参数建模不精确的问题,区别文献[16]的方法,设计了欠驱动船舶路径跟踪的神经网络自适应控制律。该控制律无需已知船舶模型参数,利用RBF神经网络的万能逼近特性估计期望的前进速度和艏摇角的导数项,进而消除反演设计方法中的项数膨胀问题。应用Lyapunov函数证明了船舶路径跟踪闭环系统误差信号最终一致有界。最后基于一艘欠驱动船模的仿真对比实验验证了控制律的有效性。
1 船舶运动数学模型假定欠驱动船舶是
| $\left\{ \begin{array}{l}\dot x = u\cos \psi - v\sin \psi \\\dot y = u\sin \psi + v\cos \psi \\\dot \psi = r\end{array} \right.$ | (1-1) |
式中:
建立在船体坐标系下的船舶动力学模型具有不确定性和非线性特性,表示为[17]
| $\left\{ \begin{array}{l}\dot u = \displaystyle\frac{{{m_2}}}{{{m_1}}}vr - \frac{{{X_u}}}{{{m_1}}}u - \frac{{{X_{|u|u}}}}{{{m_1}}}|u|u + \frac{{{\tau _u}}}{{{m_1}}} + \frac{{{d_{wu}}}}{{{m_1}}}\\[7pt]\dot v = - \displaystyle\frac{{{m_1}}}{{{m_2}}}ur - \frac{{{Y_v}}}{{{m_2}}}v - \frac{{{Y_{|v|v}}}}{{{m_2}}}|v|v + \frac{{{d_{wv}}}}{{{m_2}}}\\[7pt]\dot r = \displaystyle\frac{{{m_1} - {m_2}}}{{{m_3}}}uv - \frac{{{N_r}}}{{{m_3}}}r - \frac{{{N_{|r|r}}}}{{{m_3}}}|r|r + \frac{{{\tau _r}}}{{{m_3}}} + \frac{{{d_{wr}}}}{{{m_3}}}\end{array} \right.$ | (2) |
式中:
假设1 船舶惯性质量参数的范围是确定的即
| ${m_{i,{{Min}}}} < {m_i} < {m_{i,{{Max}}}},i = 1,2,3$ | (3) |
式中:
假设2
| ${{|}}{d_{wu}}{{|}} < {d_{u{{Max}}}},\;\;\;{{|}}{d_{wv}}{{|}} < {d_{v{{Max}}}},\;\;\;{{|}}{d_{wr}}{{|}} < {d_{r{{Max}}}}$ | (4) |
式中:
船舶的惯性质量参数可通过建模得到,由于环境的干扰,一般测量值不精确,但是得到惯性质量参数的范围是相对容易的;船舶在海上航行,会受到风、浪、流等外界时变干扰,这些干扰的能量是有限的,作用到船舶的干扰力和力矩都是有界的量。因此,假设1和2合理。
欠驱动船舶的参考路径可由一条虚拟小船产生,受到文献[18]的启发,虚拟小船的数学模型可描述为
| $\left\{ \begin{array}{l}{{\dot x}_d} = {u_d}{{cos}}\,{\psi _d} - {v_d}\sin \,{\psi _d}\\{{\dot y}_d} = {u_d}\sin \,{\psi _d} + v\cos\, {\psi _d}\\{{\dot \psi }_d} = {r_d}\\{{\dot v}_d} = - \frac{{{m_1}}}{{{m_2}}}{u_d}{r_d} - \displaystyle\frac{{{Y_v}}}{{{m_2}}}{v_d} - \frac{{{Y_{|v|v}}}}{{{m_2}}}|{v_d}|{v_d}\end{array} \right.$ | (5) |
式中:
控制目标:考虑到船舶模型参数不确定以及受到外部时变扰动,设计神经网络自适应控制律,使得船舶的实际位置
根据运动学误差方程确定船舶辅助的前进速度和艏摇角,考虑到反演设计方法中存在“计算膨胀”问题,将辅助的前进速度和艏摇角的导数作为不确定项处理,利用RBF神经网络的万能逼近特性估计动力学方程中的不确定项[19],从而使得实际的前进速度和艏摇角有效地逼近辅助值。
2.1 运动学部分设计参考路径是由一条虚拟小船给出,定义误差项:
| ${x_e} = x - {x_d}, \;{y_e} = y - {y_d}$ | (6) |
根据实际船舶与虚拟小船的位置关系,考虑式(1)和式(5)并引入双曲正切函数
| $\begin{array}{c}{{\dot x}_{{e}}} + {k_1}\tanh ({k_{{3}}}{x_e}) = {D_x}\\{{\dot y}_{{e}}} + {k_2}\tanh ({k_{{4}}}{y_e}) = {D_y}\end{array}$ | (7) |
式中
| $\begin{array}{c}{D_{{x}}} = u\cos \, \psi - v\sin \, \psi - {u_d}\cos \, {\psi _d} + {v_d}\sin \, {\psi _d} + \\\;\;\;\;\;\;\;\; {k_1}\tanh ({k_{{3}}}{x_e})\\{D_{{y}}} = u\sin \, \psi + v\cos \, \psi - {u_d}\sin \, {\psi _d} - {v_d}\cos \, {\psi _d}+ \\\;\;\;\;\;\;\;\; {k_{{2}}}\tanh ({k_{{4}}}{{{y}}_e})\end{array}$ | (8) |
式中:
| ${E_u} = u - {\alpha _u},\;{\psi _e} = \psi - {\psi _d},\;{E_\psi } = {\psi _e} - {\alpha _{{\psi _e}}}$ | (9) |
式中:
| $\begin{array}{c}\left[ {\begin{array}{*{20}{c}}{{D_x}}\\{{D_y}}\end{array}} \right] = J(\psi )\left[ {\begin{array}{*{20}{c}}{{E_u}}\\0\end{array}} \right] + J(\psi ) \times \\[9pt]\;\;\;\;\;\;\;\;\;\;\;\left[ {\begin{array}{*{20}{c}}{{\alpha _u} - \cos ({E_\psi } + {\alpha _{{\psi _e}}}){{\bar D}_x} - \sin ({E_\psi } + {\alpha _{{\psi _e}}}){{\bar D}_y}}\\[3pt]{v + \sin ({E_\psi } + {\alpha _{{\psi _e}}}){{\bar D}_x} - \cos ({E_\psi } + {\alpha _{{\psi _e}}}){{\bar D}_y}}\end{array}} \right]\end{array}$ | (10) |
式中
| $\begin{array}{c}J(\psi ) = \left[ {\begin{array}{*{20}{c}}{\cos \, \psi }&{ - \sin \, \psi }\\{\sin \, \psi }&{\cos \, \psi }\end{array}} \right]\\{{\bar D}_x} = {u_d} - \cos ({\psi _d}){k_1}\tanh ({k_{{3}}}{x_e}) - \\\;\;\;\;\;\;\sin ({\psi _d}){k_2}\tanh ({k_{{4}}}{y_e})\\{{\bar D}_y} = {v_d} + \sin ({\psi _d}){k_1}\tanh ({k_{{3}}}{x_e}) - \\\;\;\;\;\;\;\cos ({\psi _d}){k_2}\tanh ({k_{{4}}}{y_e})\end{array}$ | (11) |
式中:
| $\begin{array}{c}{\alpha _u} = \cos \, {\alpha _{{\psi _e}}}{{\bar D}_x} + \sin \, {\alpha _{{\psi _e}}}{{\bar D}_y}\\{\alpha _{{\psi _e}}} = \theta - \varphi \end{array}$ | (12) |
式中:
| $\theta = \arctan ({\bar D_y}/{\bar D_x}),\phi = \arctan (v/u)$ | (13) |
可以看出
| ${k_1} > 0,{k_2} > 0,{k_1} + {k_2} < {u_d}$ | (14) |
保证
| ${\alpha _u} = \cos ({\alpha _{{\psi _e}}} - \theta )\sqrt {\bar D_x^2 + \bar D_y^2} $ | (15) |
由于
| $v = u\beta ({\alpha _{{\psi _e}}})$ | (16) |
式中:
| $\begin{array}{c}\beta ({\alpha _{{\psi _e}}}) = ({{\bar D}_y}\cos \, {\alpha _{{\psi _e}}} - {{\bar D}_x}\sin \, {\alpha _{{\psi _e}}})/\\\;\;\;\;\;\;\;\;\;\;\;\;\;({{\bar D}_x}\cos \, {\alpha _{{\psi _e}}} + {{\bar D}_y}\sin \, {\alpha _{{\psi _e}}})\end{array}$ | (17) |
由于
| $v = {\bar D_y}\cos \, {\alpha _{{\psi _e}}} - {\bar D_x}\sin \, {\alpha _{{\psi _e}}} + \beta ({\alpha _{{\psi _e}}}){E_u}$ | (18) |
将式(9)、(11)和(17)代入式(6)并进行三角函数变换得运动学误差方程:
| $\begin{array}{c}\left[ {\begin{array}{*{20}{c}}{{{\dot x}_e}}\\{{{\dot y}_e}}\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}{ - {k_1}\tanh ({k_3}{x_e})}\\{ - {k_2}\tanh ({k_4}{y_e})}\end{array}} \right] + J(\psi )\left[ {\begin{array}{*{20}{c}}{{E_u}}\\{\beta ({\alpha _{{\psi _e}}}){E_u}}\end{array}} \right] + 2J(\psi )\; \times \\[9pt]\left[ {\begin{array}{*{20}{c}}{\sin ({E_\psi }/2 + {\alpha _{{\psi _e}}})}&{ - \cos ({E_\psi }/2 + {\alpha _{{\psi _e}}})}\\{\cos ({E_\psi }/2 + {\alpha _{{\psi _e}}})}&{\sin ({E_\psi }/2 + {\alpha _{{\psi _e}}})}\end{array}} \right]\left[ {\begin{array}{*{20}{c}}{{{\bar D}_x}}\\{{{\bar D}_y}}\end{array}} \right] \times \\[9pt] \sin ({E_\psi }/2)\end{array}$ | (19) |
为了稳定
| ${S_\psi } = {\dot E_\psi } + {k_\psi }{E_\psi }$ | (20) |
式中:
| $\begin{array}{c}{{\dot E}_u} = \displaystyle\frac{1}{{{m_{1,M}}\Delta {m_1}}}{\tau _u} + {f_u}\\{{\dot S}_\psi } = \displaystyle\frac{1}{{{m_{3,M}}\Delta {m_3}}}{\tau _r} - {{\dot r}_d} + {k_\psi }(r - {r_d}) + {f_r}\end{array}$ | (21) |
式中:
| $\begin{array}{c}{f_u} = \displaystyle\frac{{{m_2}}}{{{m_1}}}vr - \frac{{{X_u}}}{{{m_1}}}u - \frac{{{X_{|u|u}}}}{{{m_1}}}|u|u + \frac{{{d_{wu}}}}{{{m_1}}} - {{\dot \alpha }_u}\\{f_r} = \displaystyle\frac{{{m_1} - {m_2}}}{{{m_3}}}uv - \frac{{{N_r}}}{{{m_3}}}r - \frac{{{N_{|r|r}}}}{{{m_3}}}|r|r + \frac{{{d_{wr}}}}{{{m_3}}} - {{\ddot \alpha }_{{\psi _e}}} - {k_\psi }{{\dot \alpha }_{{\psi _e}}}\\{m_{1,M}} = \sqrt {{m_{1,{{Min}}}}{m_{1,{{Max}}}}} \;\;\;{m_{3,M}} = \sqrt {{m_{3,{{Min}}}}{m_{3,{{Max}}}}} \end{array}$ | (22) |
式中:
| $\begin{array}{c}\displaystyle\frac{{{m_{1,{{Min}}}}}}{{{m_{1,M}}}} \leqslant \Delta {m_1} \leqslant \frac{{{m_{1,{{Max}}}}}}{{{m_{1,M}}}}\\\displaystyle\frac{{{m_{3,{{Min}}}}}}{{{m_{3,M}}}} \leqslant \Delta {m_3} \leqslant \frac{{{m_{3,{{Max}}}}}}{{{m_{3,M}}}}\end{array}$ | (23) |
的两个值。
2.2 动力学部分设计由于动力学误差方程中存在不确定函数
| $\begin{array}{c}{f_u} = {{{W}}_u}^{{T}}{{\sigma}} ({\eta }) + {\varepsilon _u}\\{f_r} = {{{W}}_r}^{{T}}{{\sigma}} ({\eta }) + {\varepsilon _r}\end{array}$ | (24) |
式中:网络的输入信号
| $\begin{array}{c}||{{{W}}_u}|{|_F} \leqslant {W_{u,M}},\;\;\;\;\;||{{{W}}_r}|{|_F} \leqslant {W_{r,M}}\\{\varepsilon _u} \leqslant {\varepsilon _{u,M}},\;\;\;\;\;{\varepsilon _r} \leqslant {\varepsilon _{r,M}}\end{array}$ | (25) |
未知函数
| $\begin{array}{c}{{\hat f}_u} = {{\hat{ {W}}}^{{T}}}_u{\sigma }({\eta })\\{{\hat f}_r} = {{\hat{ {W}}}^{{T}}}_r{\sigma }({\eta })\end{array}$ | (26) |
将式(23)和(25)代入(20)并作适当变换得
| $\begin{array}{c}{{\dot E}_u} = - {k_u}{E_u} + {k_u}{E_u} + { {\hat{{W}}}_u^{{T}}}{\sigma }({{\eta} }) + \displaystyle\frac{1}{{{m_{1,M}}\Delta {m_1}}}{\tau _u} + \tilde{{{W}}_u}^{{T}}{\sigma }({\eta }) + {\varepsilon _u}\\{{\dot S}_\psi } = - {k_r}{S_\psi } + {k_r}{S_\psi } + \hat{{{W}}_r}^{{T}}{\sigma }({\eta }) + \displaystyle\frac{1}{{{m_{3,M}}\Delta {m_3}}}{\tau _r} - {{\dot r}_d} + {k_\psi }(r - \\\;\;\;\;\;\;\;\;{r_d}) + \tilde{{{W}}_r}^{{T}}\sigma ({\eta }) + {\varepsilon _u}\end{array}$ | (27) |
式中:
| $\begin{array}{c}{\tau _u} = {m_{1,M}}( - {k_u}{E_u} - \hat{ {{{W}}_u}}^{{T}}{\sigma }({\eta }) - \left| {\hat{ {{{W}}_u}}^{{T}}{\sigma }({\eta }) + {k_u}{E_u}} \right| \times \\\;\;\;\;\;\;\;{\mathop{ sgn}} ({E_u})(1 + {\delta _{u,{{Max}}}}))\end{array}$ | (28) |
| $\begin{array}{c}{\tau _r} = {m_{3,M}}( - {k_r}{S_\psi } - \hat{ {{{W}}_r}}^{{T}}{\sigma }({\eta }) + {{\dot r}_d} - {k_\psi }(r - {r_d}) - \\\;\;\;\;\;\;\left| {\hat{ {W_r}}^{{T}}{\sigma }({\eta }) + {k_r}{S_\psi } - {{\dot r}_d} + {k_\psi }(r - {r_d})} \right|{\mathop{ sgn}} ({S_\psi }) \times \\\;\;\;\;\;\;(1 + {\delta _{r,{{Max}}}}))\end{array}$ | (29) |
| ${\dot {\hat{ {{W}}_u}}}= {{{{F}}_u}}({E_u}{\sigma }({\eta }) - {\gamma _u}{\hat{ {{{W}}_u}}})$ | (30) |
| ${\dot{ \hat{{{{W}}_r}}}} = {{{{F}}_r}}({S_\psi }{\sigma }({\eta }) - {\gamma _r}{\hat{ {W}}_r})$ | (31) |
式中:
| ${\delta _{u,{{Max}}}} = \frac{{{m_{1,{{Max}}}}}}{{{m_{1,M}}}}, \,\, {\delta _{r,{{Max}}}} = \frac{{{m_{3,{{Max}}}}}}{{{m_{3,M}}}}$ | (32) |
式中:
定理 针对式(1)和(2)描述的欠驱动船舶,设计的路径跟踪控制律式(27)~(28)和参数自适应律式(29)~(30)能够保证闭环系统的所有误差信号
证明 首先分析动力学部分的稳定性,引入Lyapunov函数:
| ${L_1} = 0.5{E_u}^{\!\!\!\! 2} + 0.5{S_\psi }^{\!\!\!\!\! 2} + 0.5\tilde{ {{{W}}_u}}^{{T}}{{{F}}_u}^{ - 1}{\tilde{ {W}}_u} + 0.5\tilde{ {{{W}}_r}}^{{T}}{{{F}}_r}^{ - 1}{\tilde{ {W}}_r}$ | (33) |
对式(32)取时间导数并考虑式(26)~(30)得
| $\begin{array}{c}{{\dot L}_1} = {E_u}[ - {k_u}{E_u} + {\varepsilon _u} + (1 - \displaystyle\frac{1}{{\Delta {m_1}}})({{\hat f}_u} + {k_u}{E_u}) - \displaystyle\frac{1}{{\Delta {m_1}}}\times \\[5pt] |{{\hat f}_u} + {k_u}{E_u}|{\mathop{ sgn}} ({E_u})(1 + {\delta _{u,{{max}}}})] + {S_\psi }[ - {k_r}{S_\psi } + \\ [5pt]{\varepsilon _r} + (1 - \displaystyle\frac{1}{{\Delta {m_3}}})({{\hat f}_r} + {k_r}{S_\psi } - {{\dot r}_d} + {k_4}(r - {r_d})] - \\ [5pt]\displaystyle\frac{1}{{\Delta {m_3}}}|{{\hat f}_r} + {k_r}{S_r} - {{\dot r}_d} + {k_4}(r - {r_d})|{\mathop{ sgn}} ({S_\psi }) \times \\ [5pt](1 + {\delta _{r,{{Max}}}})) + {\gamma _u}\tilde{ {{{W}}_u}}^{{T}}{\hat{ {{{W}}_u}}} + {\gamma _r}\tilde{ {{{W}}_r}}^{{T}}{\hat{ {{{W}}_r}}} \leqslant \\ [5pt]- {k_u}E_u^2 + {\varepsilon _{u,M}}|{E_u}| + \displaystyle\frac{{1 + \Delta {m_1}}}{{\Delta {m_1}}}|{{\hat f}_u} + {k_u}{E_u}||{E_u}| - \\[5pt]\displaystyle\frac{{1 + {\delta _{u,{{Max}}}}}}{{\Delta {m_1}}}|{{\hat f}_u} + {k_u}{E_u}||{E_u}| - {k_r}S_\psi ^2 + {\varepsilon _{r,M}}|{S_\psi }| + \\[5pt]\displaystyle\frac{{1 + \Delta {m_3}}}{{\Delta {m_3}}}|{{\hat f}_r} + {k_r}{S_\psi } - {{\dot r}_d} + {k_4}(r - {r_d})||{S_\psi }| - \\[5pt]\displaystyle\frac{{1 + {\delta _{r,{{Max}}}}}}{{\Delta {m_3}}}|{{\hat f}_r} + {k_r}{S_r} - {{\dot r}_d} + {k_4}(r - {r_d})||{S_\psi }| + \\[7pt]{\gamma _u}(\tilde{{{{W}}_u}}^{{T}}{{{{W}}_u}} - ||{\tilde{{{{W}}_u}}}|{|^2})\; + {\gamma _r}(\tilde{{{{W}}_r}}^{{T}}{{W}_r} - ||{\tilde{{{{W}}_r}}}|{|^2})\end{array}$ | (34) |
根据式(22)和(31),得
| $\begin{array}{c}{{\dot L}_1} \leqslant - {k_u}E_u^2 - {k_r}S_\psi ^2 + {\varepsilon _{u,M}}|{E_u}| + {\varepsilon _{r,M}}|{S_\psi }|\; + \\[5pt]{\gamma _u}\tilde{{{{W}}_u}}^{{T}}{\hat{{{{W}}_u}}} + {\gamma _r}\tilde{{{{W}}_r}}^{{T}}{\hat{{{{W}}_r}}}\end{array}$ | (35) |
根据杨氏不等式得
| $\begin{array}{c}{{\dot L}_1} \leqslant - \displaystyle\frac{1}{2}({k_u}E_u^2 - \displaystyle\frac{{{\varepsilon ^2}_{u,M}}}{{{k_u}}}) - \frac{1}{2}({k_r}S_\psi ^2 - \displaystyle\frac{{{\varepsilon ^2}_{r,M}}}{{{k_r}}}) - \\[7pt]\displaystyle\frac{{{\gamma _u}}}{2}(||{\tilde{{{{W}}_u}}}|{|^2} - ||{{{{W}}_u}}|{|^2}) - \frac{{{\gamma _r}}}{2}(||{\tilde{{{{W}}_r}}}|{|^2} - ||{{{{W}}_r}}|{|^2}) \leqslant \\[7pt]- \eta {L_1} + (\displaystyle\frac{\eta }{2} - \displaystyle\frac{{{k_u}}}{2})E_u^2 + (\displaystyle\frac{\eta }{2} - \frac{{{k_r}}}{2})S_\psi ^2 + [\frac{\eta }{2}{\lambda _{\max }}({{{F}}_u}^{ - {{1}}}) - \\[7pt]\displaystyle\frac{{{\gamma _u}}}{2}]||{\tilde{{{{W}}_u}}}|{|^2} + [\frac{\eta }{2}{\lambda _{\max }}({F}_r^{ - 1}) - \displaystyle\frac{{{\gamma _r}}}{2}]||{\tilde{{{{W}}_r}}}|{|^2} + \mu \leqslant \\[5pt]- \eta {L_1} + \mu \end{array}$ | (36) |
式中:
| $\begin{array}{c}\eta \leqslant \min \left\{ {k_u},{k_r},\displaystyle\frac{{{\gamma _u}}}{{{\lambda _{\max }}({F}_u^{ - 1})}},\frac{{{\gamma _r}}}{{{\lambda _{\max }}({F}_r^{ - 1})}}\right\} \\[7pt]\mu = \displaystyle\frac{{{\gamma _u}}}{2}||{{{{W}}_u}}|{|^2} + \frac{{{\gamma _r}}}{2}||{{W}_r}|{|^2} + \frac{{{\varepsilon ^2}_{u,M}}}{{2{k_u}}} + \frac{{{\varepsilon ^2}_{r,M}}}{{2{k_\psi }}}\end{array}$ | (37) |
令
| ${L_1} \leqslant \rho + ({L_1}(0) - \rho ){{{e}}^{ - \eta t}}$ | (38) |
可知动力学部分的误差信号
接下来分析路径误差信号
| ${L_2} = \ln \{ \cosh ({k_3}{x_e})\} + \ln \{ \cosh ({k_4}{y_e})\} $ | (39) |
对式(38)取时间导数并考虑式(18)得:
| ${\dot L_2} \leqslant - {k_1}{k_{{3}}}{\tanh ^2}({k_3}{x_e}) - {k_2}{k_{{4}}}{\tanh ^2}({k_4}{y_e}) + {\mu _2}$ | (40) |
式中:
| ${\mu _{{2}}} = ({k_3} + {k_4})((1 + \beta ({\alpha _{{\psi _e}}}))|{E_u}| + 4(|{\bar D_x}| + |{\bar D_y}|)|\sin ({E_\psi }/2)|)$ | (41) |
由于
为验证路径跟踪控制器的控制性能,采用文献[21]介绍的船舶模型参数,其中参数为
| $\begin{array}{c}{m_1} = 25.8\,\,{{kg}},\,{m_2} = 33.8\,\,{{kg}},\,{m_3} = 2.76\,\,{{kg}} \cdot {{{m}}^2},\\[3pt]{X_u} = 12\,\,{{kg/s}},\,{Y_v} = 17\,\,{{kg/s}},\,{N_r} = 0.5\,\,{{kg}} \cdot {{{m}}^2}/{{s}},\\[3pt]{X_{|u|u}} = 2.5\,\,{{kg/s}},\,{Y_{|v|v}} = 4.5\,{{kg/s}},\,{N_{|r|r}} = 0.1\,\,{{kg}} \cdot {{{m}}^2}\end{array}$ |
参考路径是由式(4)所示的虚拟小船产生的,虚拟船的初始状态
为验证控制律的鲁棒性,采用同文献[22]相似的方式产生外界环境的干扰力和力矩。
| $\begin{array}{c}W' = \displaystyle\frac{{H \times S}}{{100}}\\[3pt]H = {H_0} \times (1 + {H_r} \times {{{Rand}}_b}) \times A{H_0}\end{array}$ |
式中:
|
Download:
|
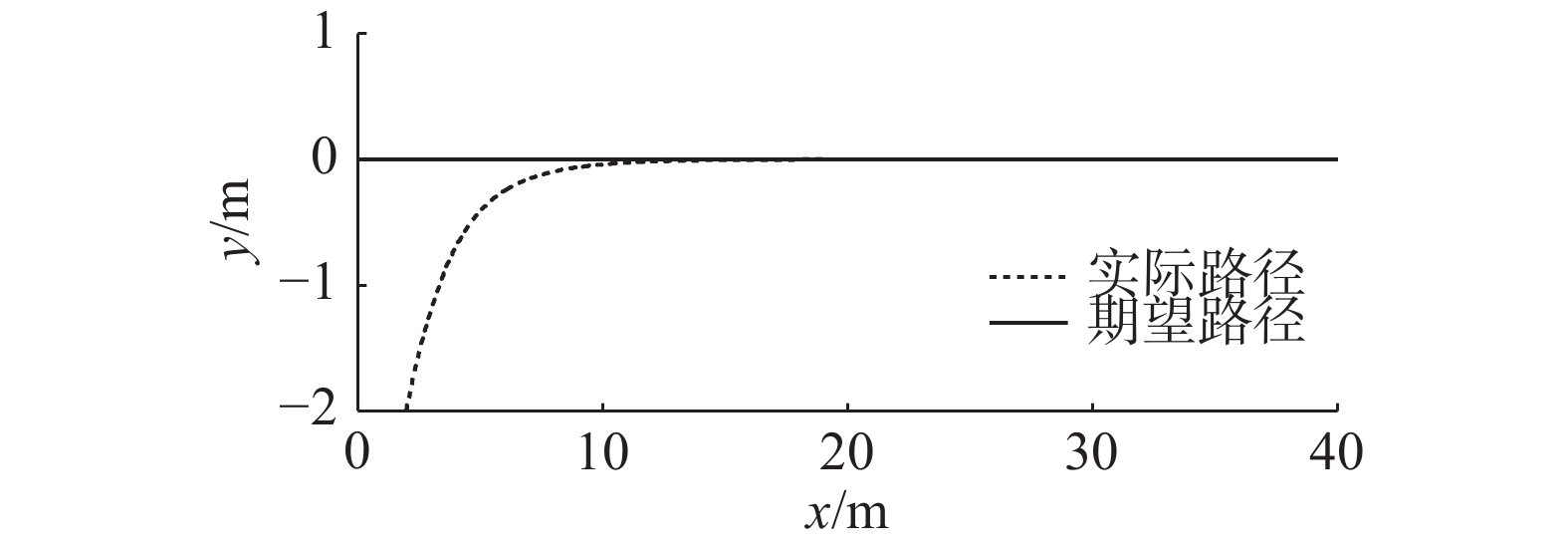
| 图 1 直线路径跟踪控制对比曲线 Fig. 1 Comparsion of straight path-following control | |
|
Download:
|
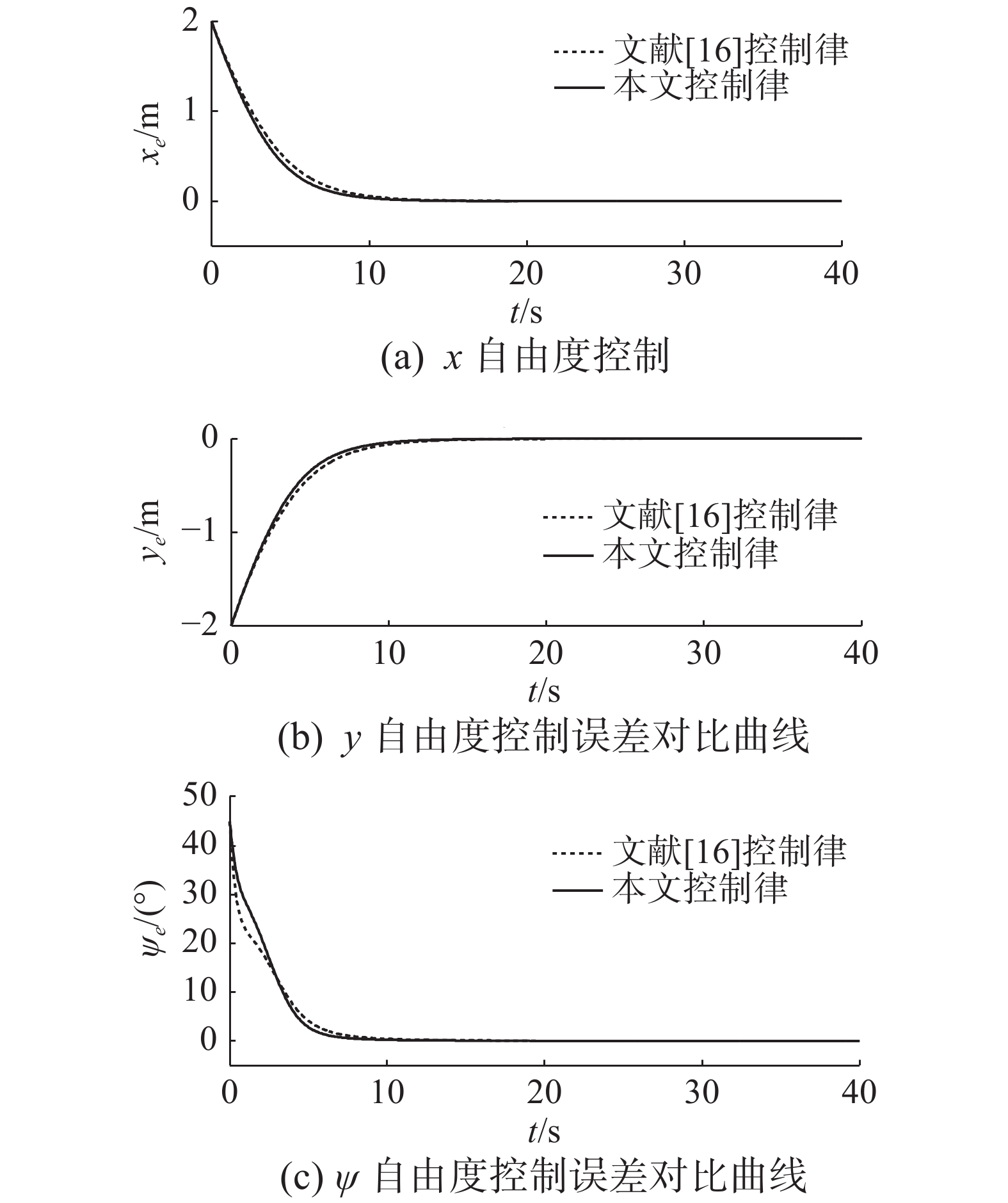
| 图 2 船舶位置、艏摇角跟踪误差对比曲线 Fig. 2 Comparsions of position and heading angle errors | |
|
Download:
|
|
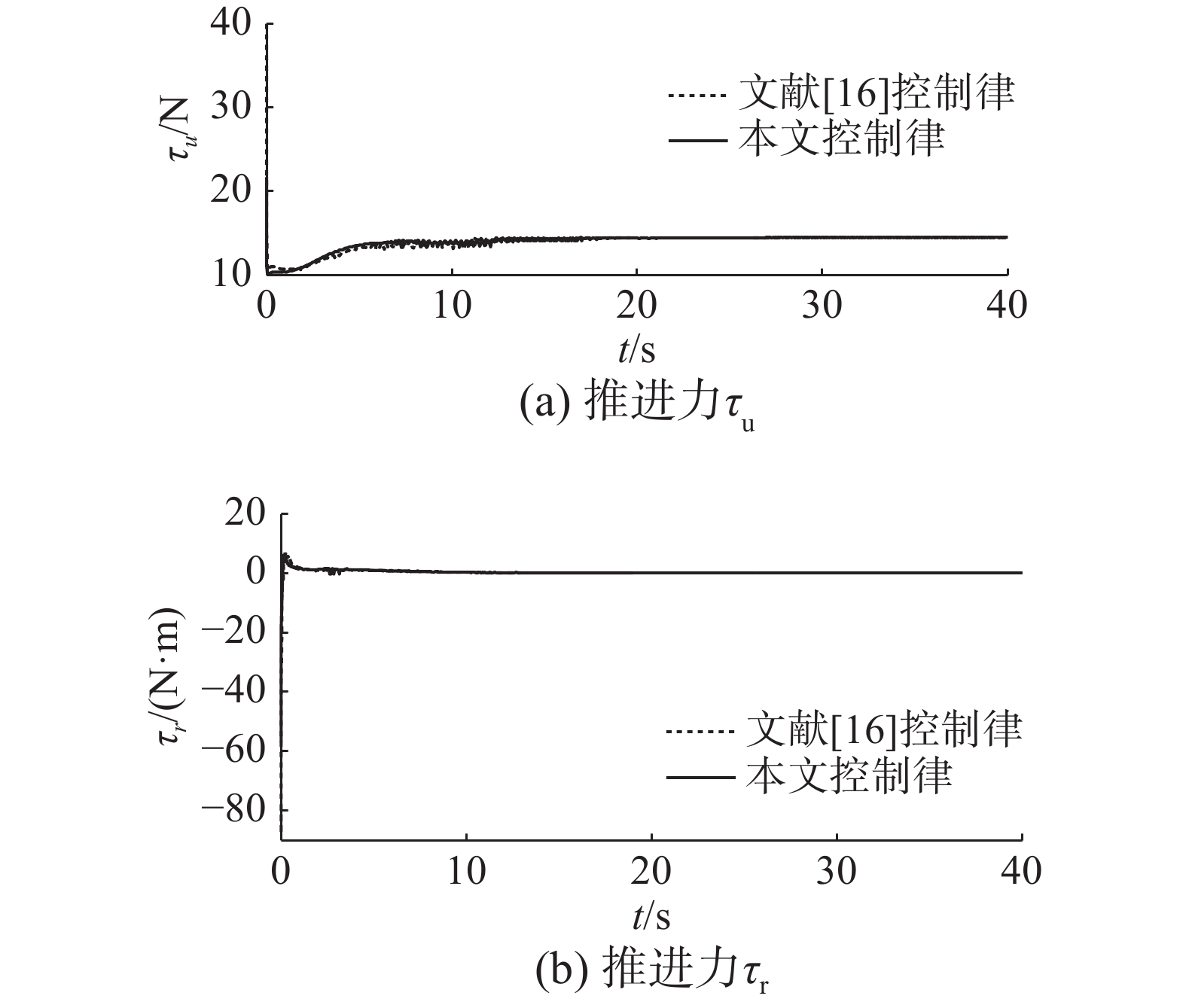
图 3 制输入
|
|
在本小结,验证所设计的控制律可以使欠驱动船舶跟踪曲线路径。参考路径同样由虚拟小船产生,虚拟小船的初始状态
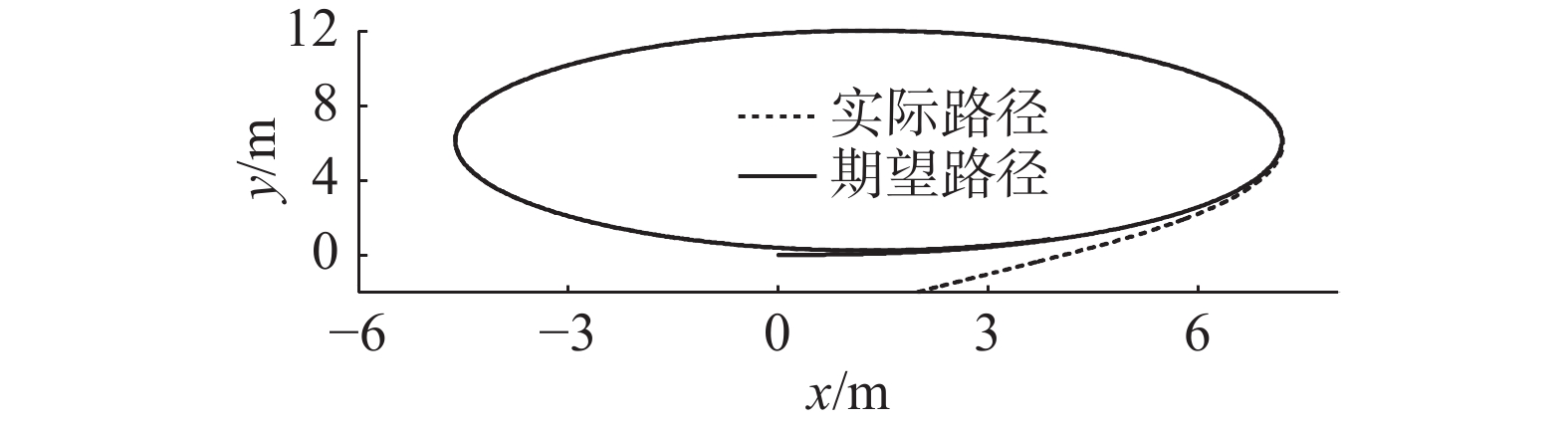
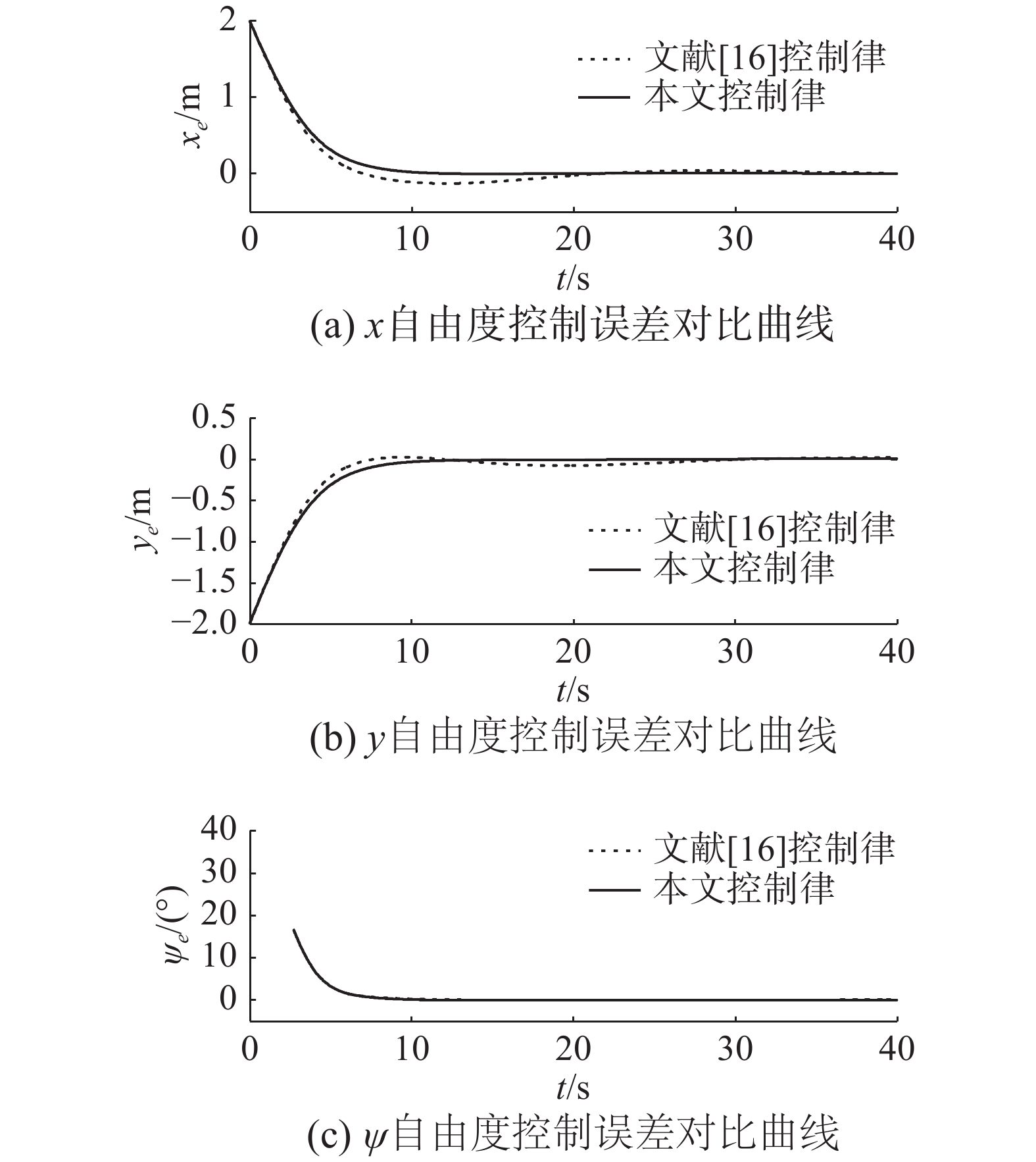
为验证控制律的有效性,船舶惯性质量参数较3.1节有10%的波动,但是外界环境干扰以及控制律参数与3.1节相同。图4~6给出了本文提出的控制律实现欠驱动船舶曲线路径跟踪的结果曲线,该曲线表明,无论船舶惯性质量参数是否有波动,所设计的神经网络控制律可以使得欠驱动船舶跟踪曲线路径,再次证明了控制律的鲁棒性。结合图1可知,无论参考路径是曲线还是直线,在控制律参数不改变的情况下都可以实现跟踪控制,验证了控制律的有效性。图5给出了船舶位置和艏摇角跟踪误差的对比曲线,曲线表明,在惯性质量参数发生波动但是控制律参数不发生调整的情况下,文献[16]的误差曲线发生较大的波动,而本文的误差曲线并没有发生较大的变化,从而验证了本文的神经网络控制律具有较强的鲁棒性。
|
Download:
|
| 图 4 曲线路径跟踪控制对比曲线 Fig. 4 Comparsion of curve path-following control | |
|
Download:
|
| 图 5 船舶位置、艏摇角跟踪误差对比曲线 Fig. 5 Comparsions of position and heading angle errors | |
|
Download:
|
|
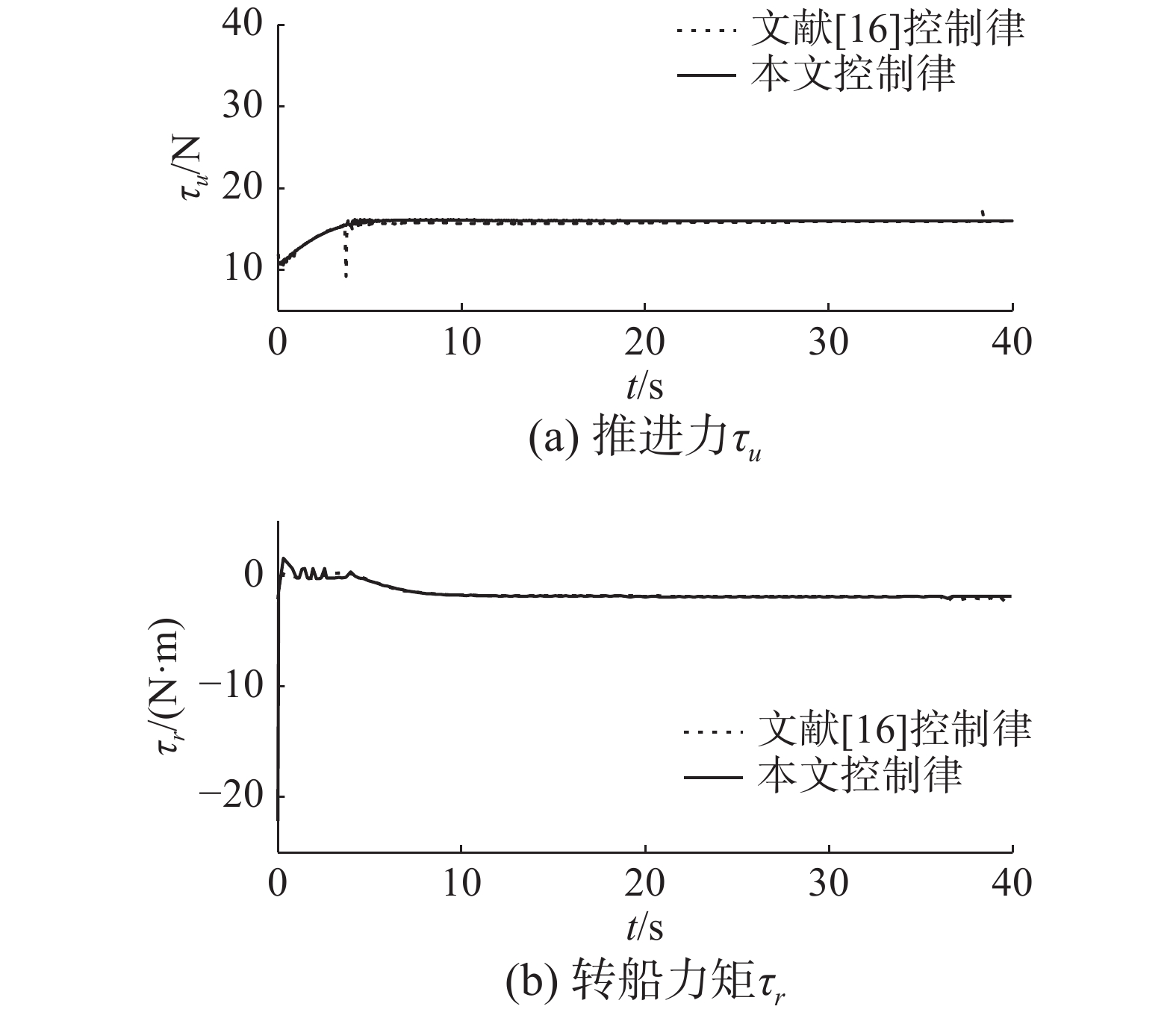
图 6 制输入
|
|
本文针对欠驱动船舶路径跟踪问题,提出了一种神经网络稳定的自适应控制律。引入神经网络万能逼近技术消除了传统反演方法中固有的计算膨胀问题,该控制律在设计过程中不需要船舶模型中的具体参数值,并且对外界环境干扰具有一定的抑制能力,对船舶运动控制领域中自动化装置的研制具有重要的现实意义。
| [1] |
郭晨, 汪洋, 孙富春, 等. 欠驱动水面船舶运动控制研究综述[J]. 控制与决策, 2009, 24(3): 321-329. GUO Chen, WANG Yang, SUN Funchun, et al. Survey for motion control of underactuated surface vessels[J]. Control and decision, 2009, 24(3): 321-329. (  0) 0)
|
| [2] |
ZHENG Zewei, SUN Liang. Path following control for marine surface vessel with uncertainties and input saturation[J]. Neurocomputing, 2016, 177: 158-167. DOI:10.1016/j.neucom.2015.11.017 ( 0) 0)
|
| [3] |
FOSSEN T I, PETTERSEN K Y, GALEAZZI R. Line-of-sight path following for dubins paths with adaptive sideslip compensation of drift forces[J]. IEEE transactions on control systems technology, 2015, 23(2): 820-827. DOI:10.1109/TCST.2014.2338354 ( 0) 0)
|
| [4] |
CHOMMAM J, MNIF F, DERBEL N. Global stabilisation and tracking control of underactuated surface vessels[J]. IET control theory and applications, 2010, 4(1): 71-88. DOI:10.1049/iet-cta.2008.0131 ( 0) 0)
|
| [5] |
DO K D, PAN J. Underactuated ships follow smooth paths with integral actions and without velocity measurements for feedback: theory and experiments[J]. IEEE transactions on control systems technology, 2006, 14(2): 308-322. DOI:10.1109/TCST.2005.863665 ( 0) 0)
|
| [6] |
JIANG Zhongping. Global tracking control of underactuated ships by Lyapunov’s direct method[J]. Automatica, 2002, 38(2): 301-309. DOI:10.1016/S0005-1098(01)00199-6 ( 0) 0)
|
| [7] |
DO K D, JIANG Z P, PAN J. Underactuated ship global tracking under relaxed conditions[J]. IEEE transactions on automatic control, 2002, 47(9): 1529-1536. DOI:10.1109/TAC.2002.802755 ( 0) 0)
|
| [8] |
LI Zhen, SUN Jing, OH S. Design, analysis and experimental validation of a robust nonlinear path following controller for marine surface vessels[J]. Automatica, 2009, 45(7): 1649-1658. DOI:10.1016/j.automatica.2009.03.010 ( 0) 0)
|
| [9] |
POMET J B, PRALY L. Adaptive nonlinear regulation: estimation from the Lyapunov equation[J]. IEEE transactions on automatic control, 1992, 37(6): 729-740. DOI:10.1109/9.256328 ( 0) 0)
|
| [10] |
DO K D, PAN J. Global robust adaptive path following of underactuated ships[J]. Automatica, 2006, 42(10): 1713-1722. DOI:10.1016/j.automatica.2006.04.026 ( 0) 0)
|
| [11] |
DO K D, PAN J. Global tracking control of underactuated ships with nonzero off-diagonal terms in their system matrices[J]. Automatica, 2005, 41(1): 87-95. ( 0) 0)
|
| [12] |
LIU Lu, WANG Dan, PENG Zhouhua. Path following of marine surface vehicles with dynamical uncertainty and time-varying ocean disturbances[J]. Neurocomputing, 2016, 173: 799-808. DOI:10.1016/j.neucom.2015.08.033 ( 0) 0)
|
| [13] |
SHOJAEI K. Neural adaptive robust control of underactuated marine surface vehicles with input saturation[J]. Applied ocean research, 2015, 53: 267-278. DOI:10.1016/j.apor.2015.09.010 ( 0) 0)
|
| [14] |
MENG Wei, GUO Chen. Global sliding mode based adaptive neural network path following control for underactuated surface vessels with uncertain dynamics[C]//Proceedings of the 3th International conference on Intelligent Control and Information Processing. [S.l.], 2012: 40–45.
( 0) 0)
|
| [15] |
段海庆, 朱齐丹. 基于反步自适应神经网络的船舶航迹控制[J]. 智能系统学报, 2012, 7(3): 259-264. DUAN Haiqing, ZHU Qidan. Trajectory tracking control of ships based on an adaptive backstepping neural network[J]. CAAI transactions on intelligent systems, 2012, 7(3): 259-264. (  0) 0)
|
| [16] |
刘杨, 郭晨, 沈智鹏, 等. 欠驱动船舶路径跟踪的神经网络稳定自适应控制[J]. 控制理论与应用, 2010, 27(2): 169-174. LIU Yang, GUO Chen, SHEN Zhipeng, et al. Stable adaptive neural network control of path following for underactuated ships[J]. Control theory and applications, 2010, 27(2): 169-174. (  0) 0)
|
| [17] |
FOSSEN T I. Marine control systems: guidance, navigation and control of ships, rigs and underwater vehicles[M]. Trondheim, Norway: Marine Cybernetics, 2002: 35–129.
( 0) 0)
|
| [18] |
DO K D, JIANG Z P, PAN J. Universal controllers for stabilization and tracking of underactuated ships[J]. Systems and control letters, 2002, 47(4): 299-317. DOI:10.1016/S0167-6911(02)00214-1 ( 0) 0)
|
| [19] |
PARK J, SANDBERG I W. Universal approximation using radial-basis-function networks[J]. Neural computation, 1991, 3(2): 246-257. DOI:10.1162/neco.1991.3.2.246 ( 0) 0)
|
| [20] |
CHWA D. Global tracking control of underactuated ships with input and velocity constraints using dynamic surface control method[J]. IEEE transactions on control systems technology, 2011, 19(6): 1357-1370. DOI:10.1109/TCST.2010.2090526 ( 0) 0)
|
| [21] |
DO K D, PAN J. Robust path-following of underactuated ships: theory and experiments on a model ship[J]. Ocean engineering, 2006, 33(10): 1354-1372. DOI:10.1016/j.oceaneng.2005.07.011 ( 0) 0)
|
| [22] |
叶松, 陈永冰, 周岗, 等. 海浪干扰对船舶航向影响规律研究[J]. 舰船电子工程, 2015, 35(1): 65-67. YE Song, CHEN Yongbing, ZHOU Gang, et al. Effect of waves interference on ship course[J]. Ship electronic engineering, 2015, 35(1): 65-67. (  0) 0)
|
 2018, Vol. 13
2018, Vol. 13


