随着社会的进步，科学技术的飞速发展，当今各种社会生产活动中每时每刻都在产生大量的数据信息，而随着计算机技术的不断进步，互联网的出现使得全球数据共享成为现实，从而全面进入了大数据时代。因此如何将海量数据进行充分有效地挖掘和利用从而指导社会生产是当前数据挖掘领域的核心任务。数据挖掘是20世纪80年代后期出现的一类数学、计算机和管理等多学科相结合的交叉科学。其旨在从海量数据中识别、提取有效的、新颖的甚至潜在有用的以及最终可被识别、理解的知识，从而作为管理决策者进行决策的科学决策依据。数据挖掘作为一个热门研究领域，涉及的新方法有神经网络、决策树、随机森林、支持向量机、深度学习等。

可拓数据挖掘^[1-6]是将可拓学的理论和方法^[7-8]与挖掘数据的方法、技术相结合的一门新技术。它在发现事物的类别转化以及识别潜在的变换知识等方面有着广阔的应用前景。

本文吸取了可拓学寻找变换知识的思想，考虑事物的某种性质的变化所带来的问题转化，结合当前已经非常成熟的支持向量机模型，从而提出了可拓支持向量机这一新的可拓数据挖掘新方法。

1 支持向量机

支持向量机(support vector machine, SVM)^[9-18]是一种通用的、有效的机器学习算法，主要建立在统计理论(statistical learning theory, SLT)、最优化理论及核理论的三大理论基础之上。以分类问题为例，SVM首先把输入映射到某一个高维的特征空间中，利用统计学习理论中的结构风险最小化原则把分类问题转化为一个凸二次规划问题来解决；然后利用最优化理论中的对偶理论，得到该凸规划的对偶问题，使得引入核函数成为可能；最后再利用核理论来处理非线性分类的情况。与数据挖掘中的其他方法相比，SVM理论相对完备，较好地解决了其他方法中经常出现的一些棘手问题。随着科学技术的进步和完善，支持向量机的研究也更为深入广泛，许多新的理论、算法层出不穷，应用领域更为广阔。

标准的两类分类问题为：给定训练集

$\mathit{\boldsymbol{S}} = \left\{ {{\rm{(}}{x_{\rm{1}}}{\rm{,}}{y_{\rm{1}}}{\rm{), }}{(x_2, y_2),}\cdots \! {\rm{ ,\, (}}{x_l}{\rm{,}}{y_l}{\rm{)}}} \right\} \subseteq {\mathbb{R}^n}$

(1)

式中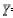： ${x_i} \in {\mathbb{R}^n}{\rm{, }}\,{y_i} \in $ $ = {\rm{\{ 1, - 1\} , }}i = {\rm{1, 2,}}\cdots \! {\rm{ , }}\, l{\rm{}}$ 。在此基础上，试寻找定义在 ${\mathbb{R}^n}$ 空间上的一个实值函数 $g(x)$ ，从而得到决策函数：

$f(x) = {\mathop{\rm sgn}} {\kern 1pt} {\kern 1pt} \left( {g(x)} \right)$

(2)

以便推断任意x对应的输出y。若 $g(x)$ 是线性函数 ${\rm{g}}(x) = ({\mathit{\boldsymbol{w}}} \cdot x) + b$ ，则式(2)对应着用超平面 $({\mathit{\boldsymbol{w}}} \cdot x) + $ $b = 0$ 将空间 ${\mathbb{R}^n}$ 分成两部分，称为线性分类机。

基于结构风险最小化原则，SVM构造出的线性分类机的原始最优化问题为

$\mathop {{\rm{min}}}\limits_{{{w},b,{\xi}} } {\kern 1pt} \frac{1}{2}{\left\| {\mathit{\boldsymbol{w}}} \right\|^2} + C\sum\limits_{i = 1}^l {{\xi _i}} $

(3)

${\mathop{\rm s}\nolimits} .{\rm{t}}.{\kern 1pt} \quad{y_i}({\mathit{\boldsymbol{w}}} \cdot x + b) \geqslant 1 - \xi {}_i{\kern 1pt} ,i = 1, 2, \cdots \! ,\, l$

(4)

${\xi _i} \geqslant 0,i = 1, 2, \cdots \! ,\, l$

(5)

式中 ${\mathit{\boldsymbol{\xi}}} = {[{\xi _1} \cdots \! \, {\xi _l}]^{\rm{T}}},C \geqslant 0$ 是一个惩罚参数。通过求解上述问题的对偶问题(见算法1中的优化问题)，SVM建立了处理二分类的线性算法(算法1)。

算法1　SVM

输入　输入训练集(见(1)式)；

输出　分划超平面以及决策函数。

1) 输入训练集(见式(1))，并选择合适的惩罚参数 $C \geqslant 0$ 。

2) 构造并求解凸二次规划问题：

$\begin{array}{c}\mathop {{\rm{min}}}\limits_{{\mathit{\boldsymbol{w}}},b,{\mathit{\boldsymbol{\xi}}} } \frac{1}{2}{\kern 1pt} \sum\limits_{i = 1}^l {\sum\limits_{j = 1}^l {{y_i}{y_j}({x_i} \cdot {x_j}){\kern 1pt} {\alpha _i}{\alpha _j}} } {\rm{ - }}\sum\limits_{j = 1}^l {\kern 1pt} {\alpha _i}\\{\rm{s.t.}} \quad \sum\limits_{j = 1}^l {{y_i}} {\alpha _i} = 0\\0 \leqslant {\alpha _i} \leqslant C,i = 1, \cdots \! , \, l\end{array}$

得到解 ${\mathit{\boldsymbol{\alpha}}^*} = {[\alpha _1^*{\kern 1pt} {x_2^*} , \cdots \! , \, \alpha _l^*]^{\rm{T}}}$ 。

3) 计算最优超平面参数 $({{\mathit{\boldsymbol{w}}}^*},{b^*})$ ：

$\begin{array}{c}{{\mathit{\boldsymbol{w}}}^*} = \sum\limits_{i = 1}^l {\alpha _i^*} {y_i}{x_i};\\{{{b}}^*} = {y_j}{\rm{ - }}({{\mathit{\boldsymbol{w}}}^*} \cdot {x_j}),j \in \left\{ {{\kern 1pt} j|{\kern 1pt} 0 \leqslant \alpha _i^* \leqslant C{\kern 1pt} } \right\}\end{array}$

4) 构造分划超平面 $({{w}^{\rm{*}}} \cdot x) + b = 0$ , 从而求出决策函数 $f(x) = {\mathop{\rm sgn}} (({{w}^{\rm{*}}} \cdot x) + b)$ 。

算法1为针对线性分类问题的SVM算法，事实上在很多实际问题中，分类问题并不能被线性分划。这时需引入从空间 ${\mathbb{R}^n}$ 到Hilbert空间的变换 $x = \varPhi (x)$ ，将训练集变换到特征空间并在该空间执行算法1，相应地， $({x_i},{y_i})$ 转化为 $(\varPhi ({x_i}),\varPhi ({x_j}))$ ，而 $(\varPhi ({x_i}),\varPhi ({x_j}))$ 的计算可以通过引进核函数 ${K}(x,x') = $ $ (\varPhi (x),\varPhi (x'))$ 代替计算。通常，常用的核函数有RBF核函数、多项式核函数、B样条核函数等。

2 可拓支持向量机

在实际问题中，我们不仅关注对未知样本的类别预测，更关心已有类别或被预测了类别的样本能否转化到相反的类别，在什么条件下会转化，所付出的代价有多大。这些在可拓学里被称为变换的知识。挖掘这些变换的知识的一个途径，就是找到那些可以变换的特征或变量。以疾病的辅助诊断为例，患者患有疾病的相关特征(变量)有很多，比如性别、年龄、身高、体重、血压(低压)、胆固醇、血常规等，这些变量中，对某个患者来说，其性别就是不可变换的变量，而血压则可以通过吃药等治疗手段变高或变低。那么在解决疾病辅助诊断的分类问题时，我们一方面希望决策函数能准确地预测未知样本的类别，另一方面希望这个决策函数能找到那些可以互相转换类别的样本，这样就可以找到更多的变换的知识。首先给出以下定义。

可拓变量 若向量 ${\mathit{\boldsymbol{x}}} = ({\kern 1pt} {[x]_1}{\kern 1pt} , \, \cdots \! , \, {[x]_n})$ 中分量 ${[x]_j}$ 的值可以变化，则称 ${[x]_j}$ 为可拓变量。

可拓变量集合 由全体可拓变量构成的集合则称为可拓变量集合，记为E。

可拓变量区间 可拓变量 ${[x]_j}$ 的值所变化的区间 $[{a_j},{b_j}]$ 称为可拓变量区间。

可拓分类问题 给定训练集

$\mathit{\boldsymbol{S}} = {\rm{\{ (}}{x_{\rm{1}}}{\rm{,}}{y_{\rm{1}}}{\rm{),}} \,(x_2,y_2), \cdots \! {\rm{, \, (}}{x_l}{\rm{,}}{y_l}{\rm{)\} }} \subseteq {({\mathbb{R}^n} \times \mathbb{Y})^l}$

(6)

式中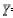： ${x_i} \in {\mathbb{R} ^n},{\kern 1pt} {[{x_i}]_j},j \in \mathit{\boldsymbol{E}}$ ，可在某个区间内变化， ${{\rm{y}}_i} \in $ = $ \{ 1,{\rm{ - }}1\} ,i = 1, 2,\, \cdots \! , \, l$ 。基于此，在 ${\mathbb{R}^n}$ 空间上寻找一个实值函数 ${\rm{g}}(x)$ ，得到决策函数：

$f(x) = {\mathop{\rm sgn}} \left( {g(x)} \right)$

(7)

以便推断任意x对应的输出y，并判断其是否可以变换为相反的输出–y。

可拓样本　若样本点x可以通过改变某个或某些可拓变量的值而改变类别标号，则称x为可拓样本。

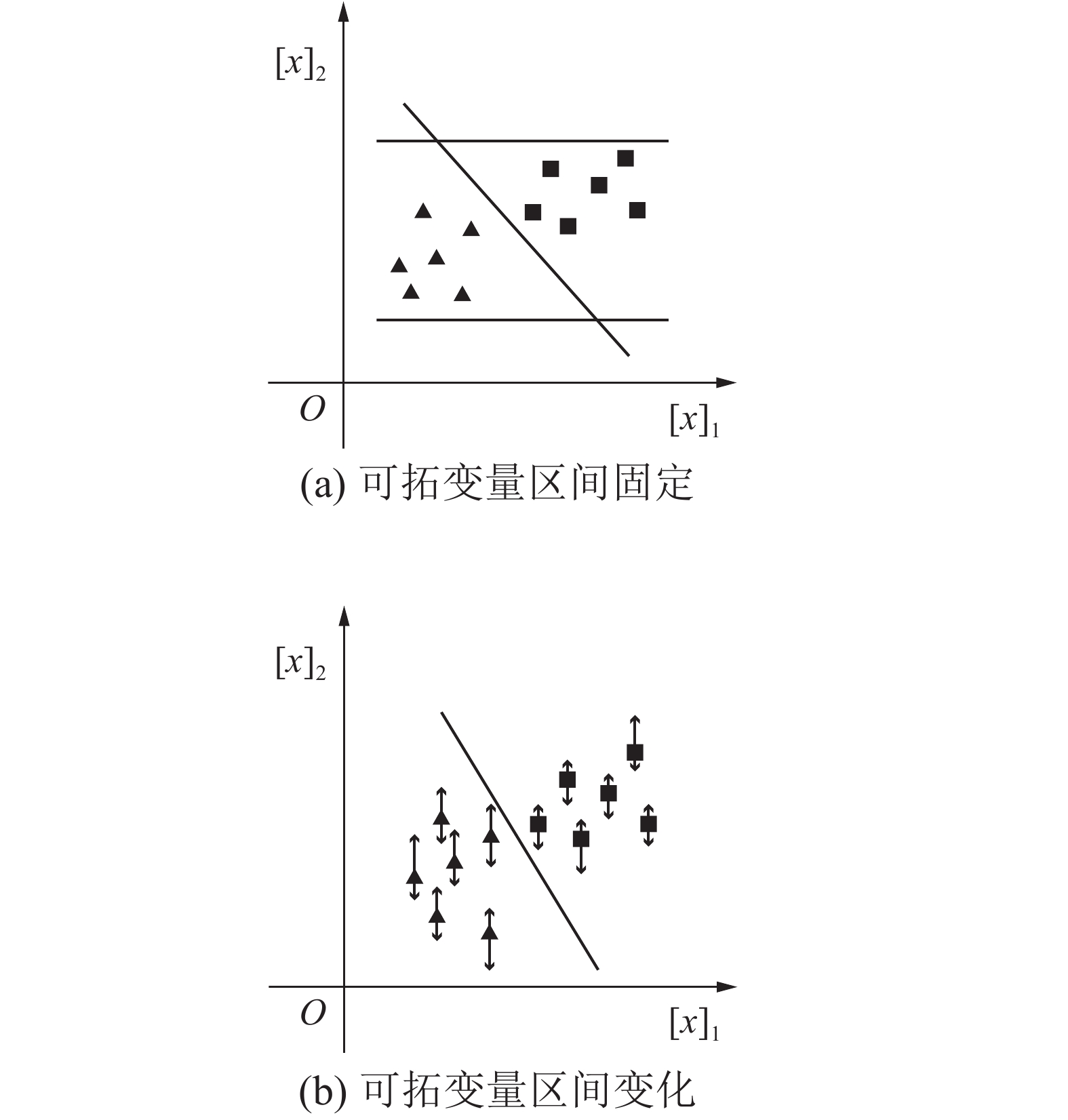
下面给出可拓分类问题示意性的例子。图1中给出了两类点，分别用▲和■表示，分量 ${[x]_2}$ 为可拓变量。图1(a) 所示的是所有点的可拓变量区间均满足 ${[x]_2} \in [a, \, b]$ 的情况，即所有点被上下两条直线 ${[x]_2} = a$ 和 ${[x]_2} = b$ 所控制；图1(b) 所示的是每个点的可拓变量区间不同的情况，即满足 ${[{x_i}]_j} \in $ $ [a_j^i, \, b_j^i]$ ，在图中就是每个点分别被双箭头线段所控制。

注意，与标准的两类分类问题不同，这里除了给出标准的训练集外，还给出了每个点的可拓变量区间。据此可以构建算法2：可拓SVM1。

算法2　可拓SVM1

输入　输入训练集(见式(1))；

输出　决策函数。

1) 输入训练集(见式(1))，并选择合适的惩罚参数C >0。

2) 构造并求解凸二次规划问题：

$\begin{array}{c}\mathop {{\rm{min}}}\limits_{{{w},b,{\xi}} } \frac{1}{2}\sum\limits_{i = 1}^l {\sum\limits_{j = 1}^l {{y_i}{y_j}({x_i} \cdot {x_j}){\kern 1pt} {\alpha _i}{\alpha _j}} } {\rm{ - }}\sum\limits_{j = 1}^l {{\alpha _i}} \\{\rm s.t.}\;\;\;\;\sum\limits_{j = 1}^l {{y_i}} {\alpha _i} = 0\\0 \leqslant {\alpha _i} \leqslant C, \, i = 1, 2, \, \cdots \! , \, l\end{array}$

得到解 ${\mathit{\boldsymbol{\alpha }}^*} = {[\alpha _1^* {x_2^*},\cdots, \! \, \alpha _l^*]^{\rm{T}}}$ 。

3) 计算最优超平面参数:

$\begin{array}{c}{{w}^*} = \sum\limits_{i = 1}^l {\kern 1pt} \alpha _i^*{\kern 1pt} {y_i}{x_i}\\{b^*} = {y_j}{\rm{ - }}({{w}^*} \cdot {x_j}),j \in \{ j \big|0 \leqslant \alpha _i^* \leqslant C\} \end{array}$

4) 构造分划超平面 $({{w}^{\rm{*}}} \cdot x) + b = 0$ , 从而求出决策函数 $f(x) = {\mathop{\rm sgn}} \left( {({{w}^{\rm{*}}} \cdot x) + b} \right)$ 。

5) 对输入 ${x_k}$ , 首先用决策函数 $f({x_k})$ 得到其对应的预测类别y_k，然后用其可拓变量对应的可拓区间 $a_j^k$ 和 $b_j^k$ 分别代替 ${[{x_k}]_j}$ ，这样对 $\left| \mathit{\boldsymbol{E}} \right|$ 个可拓变量，会得到 ${2^{\left| \mathit{\boldsymbol{E}} \right|}}$ 个不同的组合值，相应的，我们基于x_k得到了 ${2^{\left| \mathit{\boldsymbol{E}} \right|}}$ 个新的输入，分别用决策函数来判断，若有一个被判断为-y_k，则认为该输入是可变换的。

对图1(a) 所示的例子，可以用算法2得到图2(a) 所示的分划线，因该问题的可拓变量区间为定值，所以可以直接得到两条垂直的线，在这两条垂直线中间的点都是可拓样本(用圆圈标注)，并用箭头表示该样本在可拓变量的变化方向。对图1(a) 所示的例子，用算法2得到图2(b) 所示的分划线，可以看出没有可拓样本点，即没有点可以通过可拓变量的区间变化来达到类别标号的改变。

进一步，考虑稍微复杂的情况，若对上述的可拓分类问题，增加了先验知识。该先验知识为：在给定的训练集S中，训练点x_i的可拓变量 ${[{x_i}]_j},i = 1, 2, \, \cdots \! , \, l \, ,j \in \mathit{\boldsymbol{E}}$ 在可拓区间内变化时，其y_i没有变化，如何寻找决策函数来推断任意x对应的输出y，并判断其是否可以变换为相反的输出–y。

可以看出，这时候训练点的输入就不再是一个点，而是一个集合。如果限定该集合是一个凸集，比如为一个球体，则训练集变为

$\mathit{\boldsymbol{S}} = \left\{ {{\rm{(}}{X_{\rm{1}}}{\rm{,}}\, {{\rm{y}}_{\rm{1}}}{\rm{),}} \, \left(X_2,y_2 \right), \cdots \! {\rm{, \, (}}{X_i},{y_l}{\rm{)}}} \right\}$

(8)

式中输入集合X_i是一个以X_i为球心、以r_i为半径的球体, ${{\rm{y}}_i} \in $ $ = \{ 1, \, {\rm{ - }}1\} , \, i = 1, 2,\, \cdots \! , \, l$ 。那么该分类问题就转化为鲁棒支持向量机所求解的问题^[15]，此时构造的原始最优化问题为

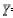
$\mathop {{\rm{min}}}\limits_{{w},b,{\xi} } {\kern 1pt} \frac{1}{2}{\kern 1pt} \left\| {w} \right\|{{\kern 1pt} ^2} + C\sum\limits_{i = 1}^l {{\xi _i}} $

(9)

$\begin{array}{c}{\rm s.t.}{\kern 1pt} \quad {y_i}\left( {{w} \cdot ({x_i} + {x_i}{u_i}) + b} \right) \geqslant 1 - \xi {}_i,\\\forall \left\| {{u_i}} \right\|{\kern 1pt} \leqslant 1,i = 1, 2,\cdots \! ,l\end{array}$

(10)

${\xi _i} \geqslant 0,i = 1{\kern 1pt} , 2, \cdots \! ,l$

(11)

因为约束式(10)含有无穷多个约束，一般做法是把它转化成一个仅含有有限个约束的问题，并求解相应的对偶问题^[15]，据此构造可拓SVM2，见算法3。

算法3　可拓SVM2

输入　输入训练集(见式(8))；

输出　决策函数。

1) 输入训练集(见式(8))，并选择合适的惩罚参数C >0。

2) 构造并求解二阶锥规划：

$\begin{array}{c}\mathop {{\rm{min}}}\limits_{{w}, b,\,{\xi} ,u, v,t} \quad\frac{1}{2} (u {\rm{ - }}v) + C\sum\limits_{i = 1}^l { {\xi _i}} \\{\rm{s. t.}} \quad{y_i}\left( {{w}{\kern 1pt} \cdot ({x_i} + {x_i}{u_i}) + b} \right) \geqslant 1 - {\xi _i}, \, i = 1, \, 2, \cdots \! , \, l \\{\xi _i} \geqslant 0, \, i = 1, 2,\, \cdots \! , \, l\\u + v = 1\\{[u\;v{\kern 1pt}\;t]^{\rm{T}}} \in \mathit{\boldsymbol{L}}{{\kern 1pt} ^3}\\{[t\;{\kern 1pt} {w}]^{\rm{T}}} \in {\mathit{\boldsymbol{L}}^{n + 1}}\end{array}$

3) 计算 $\bar b $ ，构造决策函数：

$f(x) = {\rm{sgn}}(\sum\limits_{i = 1}^l {{\alpha _i}{y_i}({x_i} \cdot x) + \sum\limits_{i = 1}^l {{y_i}{\rm{}}{{\mathit{\boldsymbol{B}}}_i}^{\rm{T}}(\bar {\beta} _i^*{\rm{ - }}{{\bar {\beta} }_i})} + \bar b} )$

(12)

式中 ${\left( {{B^i}} \right)_q} = \left( {x \cdot ({\Delta _i}).{,_q}} \right),q = 1,2, \cdots ,n$ 。

4) 对输入x_k, 首先用决策函数 $f({x_k})$ 得到其对应的预测类别y_k，然后在其可拓变量对应的可拓区间内随机取值m次，这样对 $\left| \mathit{\boldsymbol{E}} \right|$ 个可拓变量，会得到 ${m^{\left| \mathit{\boldsymbol{E}} \right|}}$ 个不同的组合值，相应的，基于x_k得到了 ${m^{\left| \mathit{\boldsymbol{E}} \right|}}$ 个新的输入，分别用决策函数来判断，若有一个被判断为–y_k，则认为该输入是可变换的。

如图3(a)所示，设 ${[x]_1}{\text{、}}\, {[x]_2}$ 均为可拓变量，每个点的可拓区间为半径不同的球体，空心圆是正类，实心圆是负类。根据算法3可得到图中的分划线，则可知虚线所示的圆的圆心点为正类，但当该点在圆内变化时，它的类别会改变。

如果先验知识为：在给定的训练集S中，训练点x_i的可拓变量 ${[{x_i}]_j},i = 1,2, \cdots \! , \, l, \, j \in \mathit{\boldsymbol{E}}$ 在可拓区间内变化时，其y_i产生了变化，如图3(b)所示。 ${[x]_1},\, {[x]_2}$ 均为可拓变量，每个点的可拓区间为不同大小的矩形，白色为正类，黑色为负类。而黑白相间的矩形则为点在这些区间内变化时，类别发生了变化。这时问题就变得复杂，需要引入可拓集的概念和关联函数来处理，这是进一步的研究方向。并且还可以将其拓展到应用广泛的多示例、多标签学习等方面^[19-22]。

3 结束语

本文提出了一种新的分类方法——可拓支持向量机，可拓支持向量机在进行分类预测时较标准的支持向量分类机有所不同，它更注重于找到那些通过变化特征值而转换类别的样本。文中给出了可拓变量和可拓分类问题的定义，并构建了求解可拓分类问题的两种算法。基于此模型，我们可以在理论和方法上做一系列研究。理论上，包括对其相应的统计学习理论基础研究，可拓决策函数集的VC维估计，推广能力的上界估计，可拓结构风险的实现原理等；方法上，包括如何在标准的支持向量机模型中引入关联函数，构造可拓的核函数，对其相应的大规模最优化问题的快速求解算法，模型参数选择问题等。