2. 广东工业大学 机电工程学院, 广东 广州 510006
2. School of Electromechanical Engineering, Guangdong University of Technology, Guangzhou 510006, China
相关网方法是可拓学中建立的利用基元模型研究基元之间的相关关系的方法[1]。目前对于复杂系统下相关网的量化研究较少,而对于复杂系统的研究而言,相关分析是一个很有用的分析方法。文献[2]研究了复杂系统下相关分析中不同相关特征量值之间的函数关系,为复杂系统中相关网的进一步研究打下了坚实的基础。文献[3-7]基于基元的相关性介绍了传导变换的概念以及传导效应的计算方法。然而,对于复杂系统的相关网,如果能用更简单系统化的方法进行分析和研究,为相关函数的近似构造提供依据,将会为可拓创意的生成和优选提供现实依据。
系统动力学是由美国麻省理工学院J.W.Forrester教授提出的一种对社会经济问题进行系统分析的方法论和定性与定量相结合的分析方法。其目的在于综合控制论、信息论和决策论的成果,以计算机为工具,分析研究信息反馈系统的结构和行为。系统动力学研究的是组成系统的内部若干因素相互间的影响,并加以模拟分析,得出最优的决策,使系统更加完善或者更好地发挥系统的功能。当然,这里的系统指的是对于分析的问题所建立的模型。文献[8-13]对近年来系统动力学的广泛运用领域进行了综述,并且可以得出系统动力学作为一种系统的科学分析方法,实践证明其在各种领域的应用研究效果显著,在很多领域都具有很高的应用价值。
可拓学中相关分析理论虽然比较直观地表述了各相关基元相关特征的量值之间的函数关系,但需要依赖于已有领域知识确定函数关系。根据文献[14-19]可知,如果缺乏领域知识,目前有两种处理方法:1) 如果有相关的数据积累,则可以利用数据挖掘方法或统计方法获得规则知识;2) 如果没有相关的数据积累,则只能用规则表示,不能定量地准确表示出来,也就不可能将相关影响过程用函数进行模拟。文献[20]有效利用系统动力学进行数据挖掘工作,取得了很好的效果。
在分析时如果能直接通过将可拓学中相关分析和系统动力学有机结合,对相关分析而言,就可以使相关网能够进行时间连续的动态仿真模拟,得出更加全面准确的分析,为生成更有价值、更准确的决策方案提供依据。
从系统动力学模型的组成部分来说,包括“流”与“元素”。“流”即为系统内传递的内容:信息或者实物。“元素”表示系统内全体属性的一个表征量。一般来说,将所有状态变量在某个时刻的取值视为系统当时的状态即为状态变量;系统输入作用后在系统输出端所出现的变量,是属于不可控变量即为“速率”;“辅助变量”则是一个可以控制的变量,形成系统的输入。
可拓学中的相关分析,可以形式化、定量化分析若干物元之间的相互作用和相互影响。本文研究的相关网是由具有相关关系的物元组成的网络,在网络内传递的内容可以是信息,也可以是实物,即为“流”。对于由多个动态物元组成的相关网,如果相关网内的每个动态物元都只有一个特征cm,该动态物元可表示为M(t)=(O(t), c, v(t))。设该特征在某一时刻t0的量值为v(t0),且在时刻t1有v(t1)=v (t0)+Δv,此时,称v (t0)为时刻t0处的状态量,v (t1)为时刻t1的状态量,Δv为状态变化量。该物元的特征cm可以是“速率”或“辅助变量”,也可以是其他特征。
本文基于系统动力学模型和可拓学中的相关分析理论,针对一维物元,提出了建立物元相关网的一种方法,初步确定了本方法的使用步骤,并说明其应用领域。在此基础上运用系统动力学理论对相关函数进行近似构造。案例分析说明了相关网方法与系统动力学进行结合的可行性以及该方法的优点。
1 相关分析与系统动力学建模 1.1 相关分析理论为了让人们更清晰、直观地了解事物之间的相关关系和相互作用的关系,可拓学中研究了相关分析理论。相关分析是根据物、事和关系之间的相关性,利用基元作为形式化工具,对基元与基元之间的相关关系进行的形式化定量化分析。
基元描述了事物所有的特征及其相应的量值,如果没有目的性地进行相关分析,则分析工作难以展开,同时工作量也异常大。而其中大部分的工作都是无用功。所以需要根据要分析的目标,选取与其相关基元中的相关特征进行分析,将不相关的特征摒弃,从而使分析工作简单高效。本文仅以物元作为研究对象。
文献[1]给出了基元相关的一般定义和相关分析原理。本文重点研究动态物元的相关,对动态物元而言,常用的相关关系包括同物异特征物元相关、异物同特征物元相关和异物异特征物元相关。
定义 对于动态物元M1(t)=(O1(t), c1, v1(t)), M2(t)=(O2(t), c2, v2(t)),若v2(t)=f(v1(t)),则称物元M1(t)与M2(t)是相关的,记作
动态物元的相关具有如下原理:
给定物元M(t)=(O(t), c, v(t)),则至少存在一个异物同特征物元Mc(t)=(O′(t), c, v′ (t))或同物异特征物元Mo(t)=(O(t), c′, v′(t))或异物异特征物元M′(t)=(O′ (t), c′, v′ (t)),使M(t)~Mc(t), 或M(t)~ Mo(t),或M(t)~ M′(t)。
1.2 相关网方法在可拓学中,物元可以形式化表示世间万物,物元之间的相关关系都可以利用可拓学的相关理论对其进行形式化、定量化地分析。当某个物元并不能有效地用来研究问题时,可以考虑利用物元之间的相关关系,采用其他与之相关的物元来研究。另外,一个物元某个特征的量值发生变化,必将导致与其相关的物元的某些特征的量值发生变化,从而使物元发生变化。
由于一个物元可能与很多物元存在相关关系,用模型表述,就会形成一个网状的结构,称之为相关网,如图 1所示。相关树是相关网的一种特殊情况。
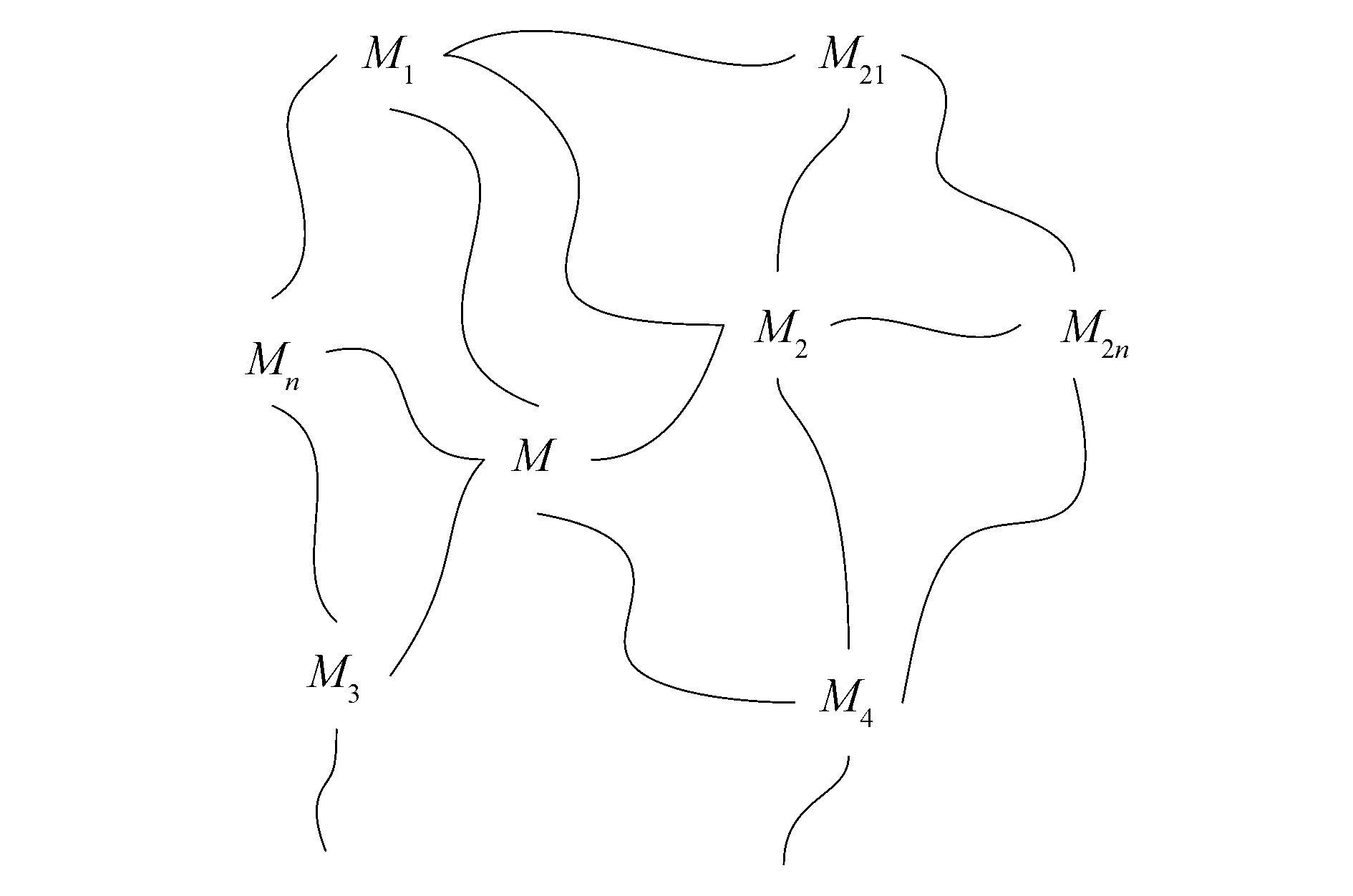
|
图 1 相关网符号表示 Fig.1 Symbolic representation of correlated network |
由于世间万物是在不断变化的,所以相关网中的物元也会发生动态变化。当一个物元发生改变时,会导致网中与其相关的其他物元发生相应变化。由此可知,相关网应该是动态的。在某一时刻,物元是固定的,所以相关网也是唯一确定的。
建立相关网和初步分析的基本步骤如下:
1) 将要分析的事物,建立初始物元模型Mi(t);
2) 利用相关分析原理和专业知识列出物元Mi(t)的相关网;
3) 对相关网进行分析,确定引起物元Mi(t)变化的物元Mj(t),或由于物元Mi(t)的变化而引起变化的物元Mj(t)。
在物元相关网中,由于物元都与其他物元存在着某种相关关系,所以不同物元之间的相关关系错综复杂。所以将相关网的表示进行变形[2],单向箭头表示有向相关,双箭头表示互为相关。例如,给定6个物元之间的相关关系,则相关网变成如图 2所示的相关关系图。
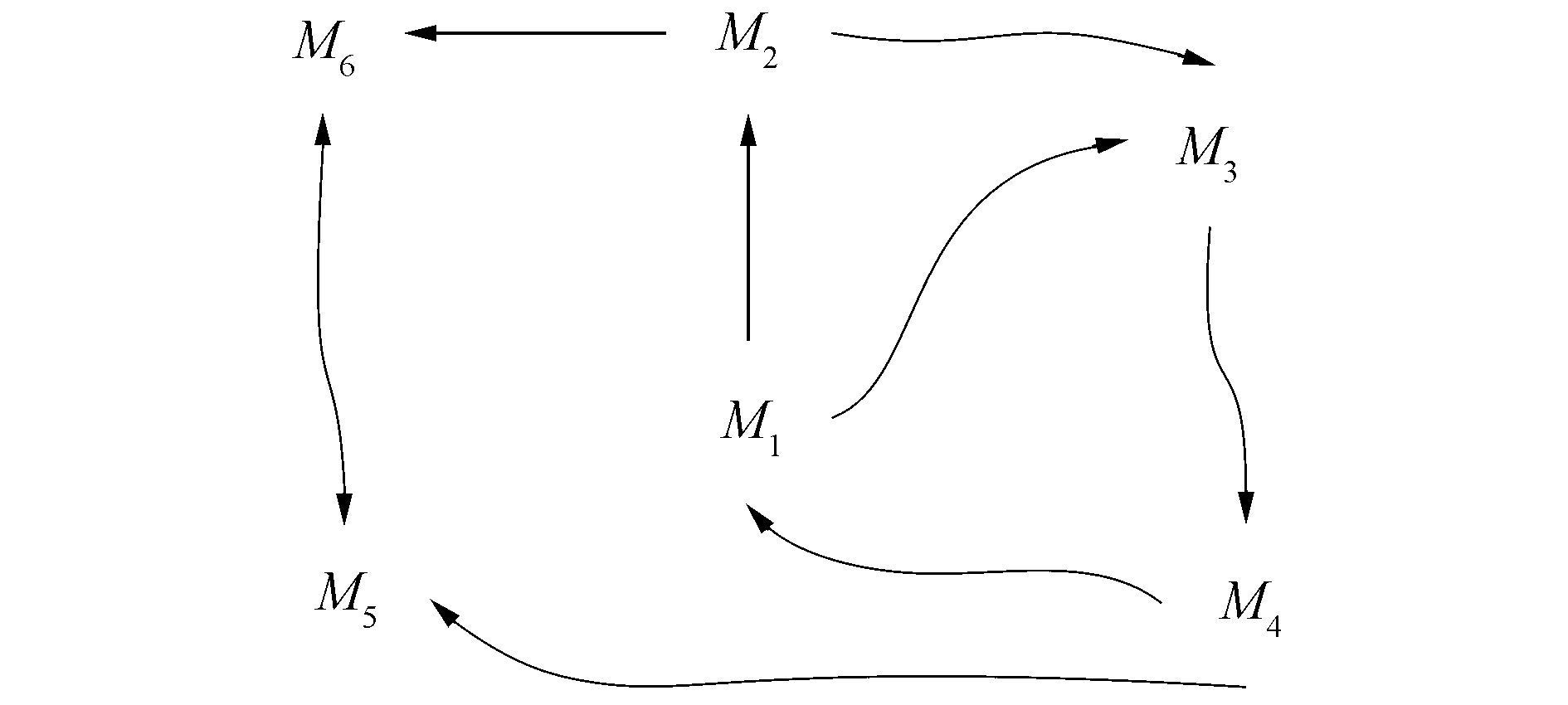
|
图 2 6个物元形成的相关网 Fig.2 The correlative network between six matter-elements |
系统动力学模型由“流”与“元素”构成。“流”分为“实体流”和“信息流”;“元素”包括“状态变量”、“速率”和“辅助变量”等6个要素。
系统动力学建模的过程为[3]:1) 了解问题、界定问题、确认研究目标;2) 绘制所研究系统的相关反馈图;3) 建立对应的系统动力学模型;4) 对模型进行测试,验证模型是否可以再现真实系统的行为;5) 利用模型模拟策略,选出最佳策略;6) 执行策略。
建模流程如图 3所示。
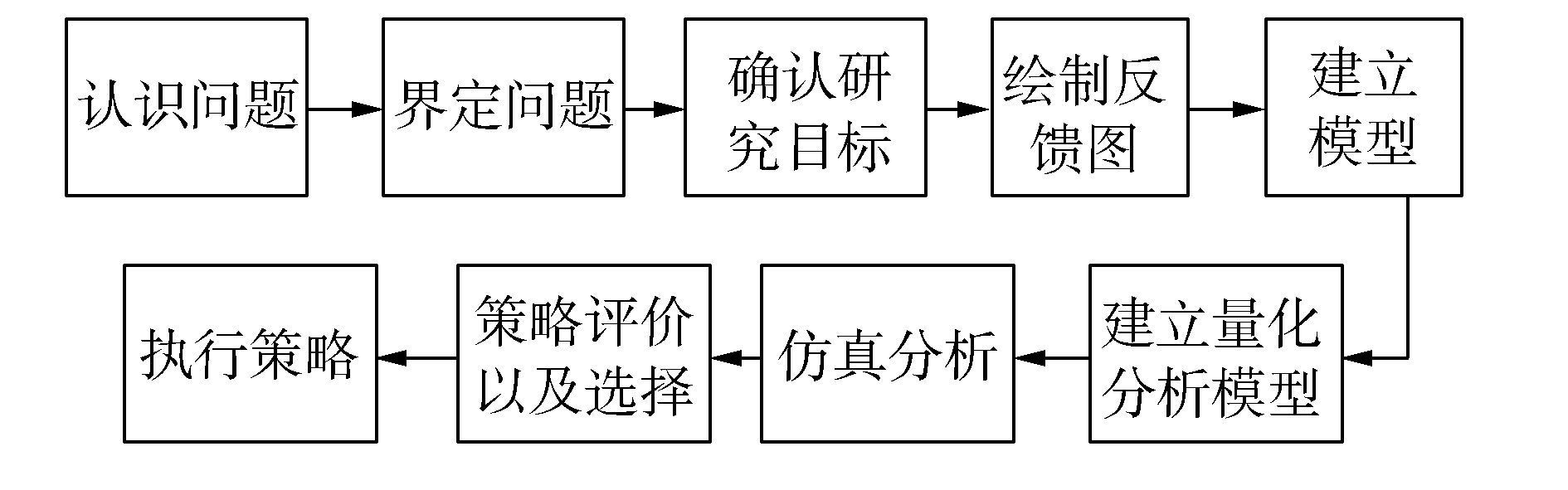
|
图 3 建模流程图 Fig.3 Flow of modeling process |
对于系统模型来说,反馈环的存在使模型的正确表示以及分析工作得以进行,从而得出准确有用的结论。可以说,反馈环是系统动力学中最重要的部分。本文中通过利用已建立的相关网,建立反馈环,以此找到模型中物元之间存在的循环关系。在此基础上,便可选取其中的循环关系,建立流率流量图,进行模拟和仿真。
2 基于系统动力学模型的相关网建模方法基于系统动力学模型建立相关网的具体操作步骤如下:
1) 针对具体研究对象的建立原始物元模型Mi(t)=(O (t), C, V(t)),建立的物元模型的维数和个数依具体研究对象而定,可以是若干个物元模型,其中的模型可以是一维模型,也可以是多维模型。
由于需要对研究对象进行动力学分析,就要求在建立相关网的时候必须包括所有与研究对象相关的物元。只有把研究对象的所有相关的物元组合在一起,共同建立模型,进行模拟分析后才能得出准确、实用的决策。
2) 根据建立的物元模型选取相关的同物物元和异物物元,建立相关网,然后分析各物元的量值之间的函数关系。
但是如果要把物元相关分析过程用系统动力学模型描述,并且进行模拟分析,就必须对参与模拟分析的物元进行变形。变形需要满足的要求是必须具有变量、参数和函数关系。
多维物元可以分解为多个一维物元。多维物元包括的信息量很大,对于那些没有相关关系的一维物元可以直接省去。此时,任意两个一维物元Mi(t)=(Oi(t), ci, vi (t))和Mj(t)=(Oj(t), cj, vj(t))便有了可以进行系统动力学分析的条件,即变量vi (t)、函数关系vi(t)=fij(vj(t))或vj(t)=fji(vi(t))以及函数方程中的参数。
3) 建立物元相关网图。相关网是在相关的物元中表示有关系的符号连起来所组成的网状图形。但是相关网中并不能表示一个线段的两个端点物元的特征ci和cj的量值之间具体的关系:函数关系、模糊函数关系以及ci与cj两者的量值之间谁是自变量,谁是因变量等关系。在明确所有相关物元的量值之间的函数关系的情况下,才能做进一步的模拟分析。
4) 以包含特征ci的一维物元为研究对象,利用系统动力学软件Venple对相关网图进行变形,称其为“动力学相关网”。
对相关网进行变形的方法:找出相关网中量值之间具有相关函数关系的物元之间的线段,结合相互之间自变量与因变量的关系将线段变成有向线段,单箭头表示有向相关,双箭头表示互为相关,如图 2。需要注意的是:这里的相关包括同对象异特征相关、异对象同特征相关、异对象异特征相关。
在此基础上,利用系统动力学软件,将表示互为相关的双向箭头变成两个单向相关箭头,即相关箭。就变成了动力学相关关系网,如图 4。这样做的目的是为了方便系统动力学建模,所以对相关网变形是必要的。
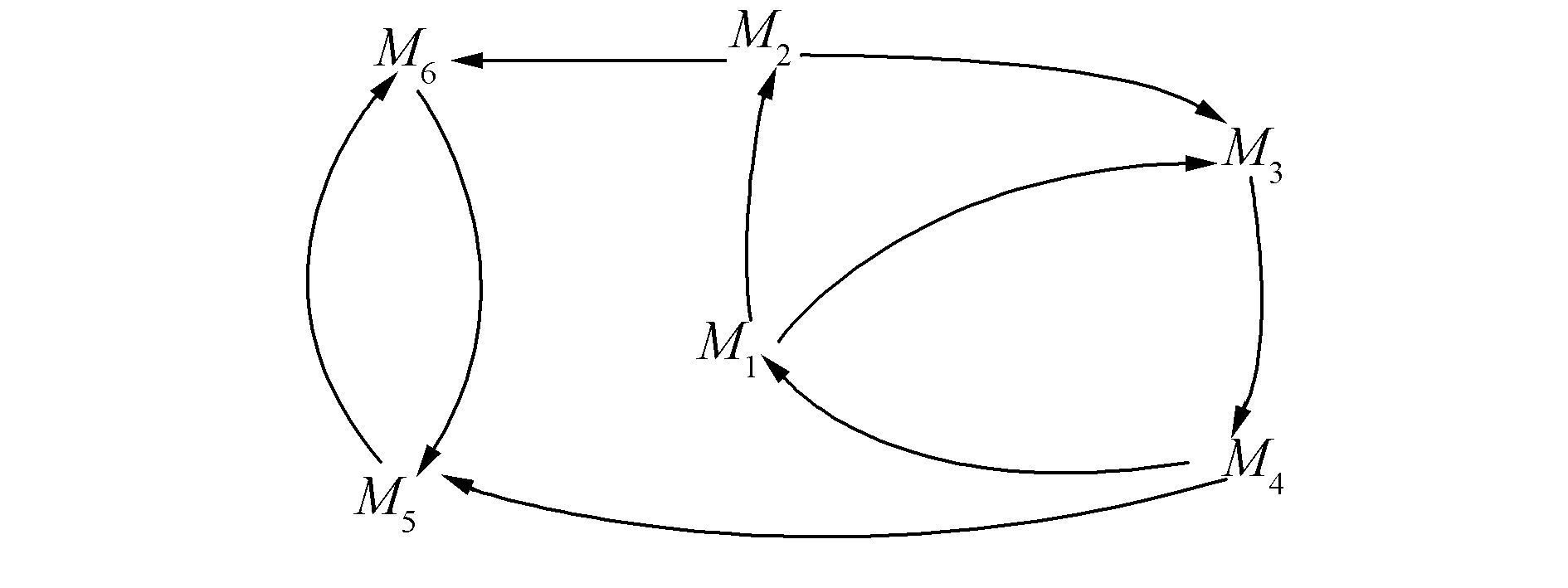
|
图 4 动力学相关关系网 Fig.4 The correlation network of dynamics |
5) 结合特征之间的关联传递关系,建立动力学模型,并进行模拟分析。
在4) 的基础上,整个相关网经过分析、变形已经逐渐走向可以直接建立系统动力学模型的方向。
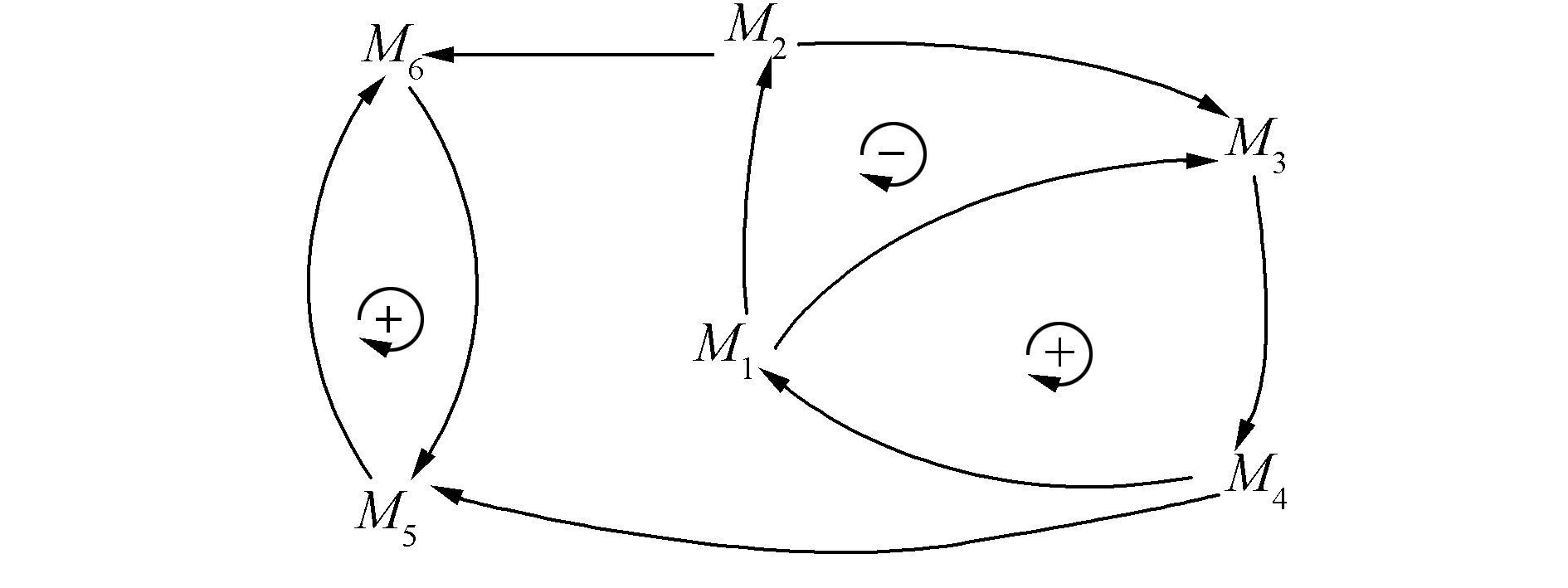
① 根据有向线段两端的物元的特征ci和cj之间的正影响和负影响关系,在线段的箭头处用符号“+”和“-”标出,调整相关回路,并将回路用符号表示,如图 5。
|
图 5 动力学相关回路图 Fig.5 The correlation loop of dynamics |
② 建立相关分析目标的存量流量图。
假设以M4为研究对象,则其对应的存量流量图如图 6。

|
图 6 M4的存量流量图 Fig.6 The stock and flow diagram of M4 |
③ 量化分析模型及仿真计算。
6) 初步得出模拟结果,用于后续的分析。
3 利用SD模型的DYNAMO基本方程近似构造相关函数 3.1 SD模型的DYNAMO的基本方程SD的主要过程之一是通过确定对象系统的水准变量、速率变量、参量、辅助变量等,分析各变量之间存在的函数关系,建立DYNAMO仿真模型,进行人工计算或者仿真[7]。这是得到描述系统内部反馈机制的流程图后建立动力学模型并进行定量分析的主要工作。DYNAMO方程就是SD的数学模型或者量化分析模型。
DYNAMO主要采用差分方程式描述有反馈的社会系统的宏观动态行为,并通过差分及代数方程式的求解(简单迭代)进行计算机仿真的专用语言。其最大特点是简单明了,容易使用。
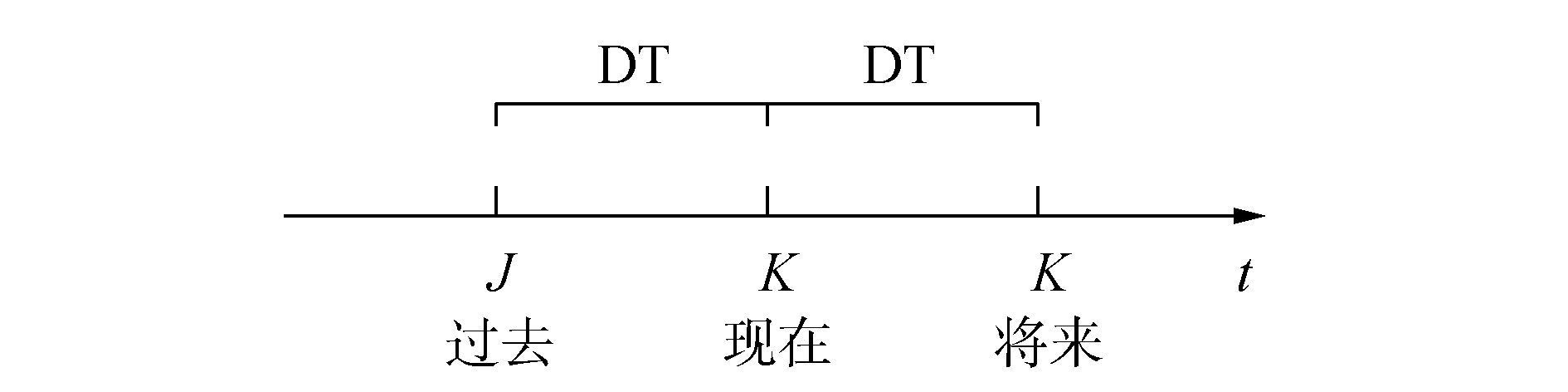
SD的对象系统是随时间变化的动态系统。在DYNAMO方程中,变量一般都有时间标号,规定如图 7。SD使用逐步仿真的方法,仿真的时间步长记为DT。
|
图 7 DYNAMO方程时间标号及其含义 Fig.7 Time label of DYNAMO equation and it's meaning |
DYNAMO方程是SD的数学模型或者量化分析模型。基本的DYNAMO方程主要有以下3个[12]:
1) 水准方程。它是计算水准变量的方程,也就是计算一维物元特征量值的方程。它的标准形式为
| ${\rm{LEVE}}{{\rm{L}}_{{t_2}}} = {\rm{LEVE}}{{\rm{L}}_{{t_1}}} + {\rm{DT}} \cdot \left( {{\rm{RI}}{{\rm{N}}_{{t_1}{t_2}}} - {\rm{ROU}}{{\rm{T}}_{{t_1}{t_2}}}} \right)$ | (1) |
式中:LEVELt1表示过去t1时刻的水准量,即此时一维物元M(t1)=(O(t1), c, v(t1))的量值;LEVELt2表示现在t2时刻的水准量,即此时一维物元M(t2)=(O(t2), c, v(t2))的量值;DT表示两个时刻t1和t2之间的时间间隔;RINt1t2表示该时间段内量值的增加速率;ROUTt1t2表示该时间段内量值的减少的速率。
2) 速率方程。它是计算速率变化量的方程,用来计算从t1到t2时间段内一维物元特征量值变化速率的量值。
| ${\rm{RATE}} \cdot {t_2}L = f\left( {L \cdot {t_2},A \cdot {t_2},C, \cdots } \right)$ | (2) |
式中:L·t2表示t2时刻的水准量,即一维物元M(t2)的特征c的量值v(t2);A·t2表示t2时刻描述水准变量的辅助变量;C为常数。
该速率方程并没有标准的形式,根据要分析的对象而定。速率的值在DT内不变,速率方程是在t2时刻进行计算,而在自t1至t2的时间间隔(即DT)中假定保持不变。
3) 辅助方程。它是用来辅助说明速率变量的方程。
| ${\rm{AUX}} \cdot {t_2} = g\left( {A \cdot {t_2},L \cdot {t_2},{R_{{t_1}{t_2}}},C, \cdots } \right)$ | (3) |
式中:Rt1t2表示在时刻t1和t2之间的时间间隔内,一维物元M(t)关于特征c的量值v(t)变化的速率。
该辅助方程没有统一的标准格式,有时需要其他参数方程来进一步说明。
另外还有赋值方程和常量方程,本文没有涉及,此不赘述。
3.2 近似构造相关函数的操作步骤由于SD的基本函数模型已经概括性地刻画了影响系统的所有相关函数关系,该模型在大多数相关领域都是很实用的,也说明了该基本函数模型的准确性。所以,在进行相关分析时,准确相关函数未知的情况下,就可以利用SD的基本函数模型对该相关关系进行判定,并且进行近似的构造,以便于进行相关分析。同时,为了方便相关分析能够利用系统建模这个简单的工具进行操作,可以考虑按着系统动力学的规范来操作。这样的好处是能够运用系统动力学的领域,相关网的实际运用就可以拓宽到该领域。具体步骤如下:
1) 近似构造某研究对象的相关关系时,首先要根据物元的构造规范,正确建立研究对象关于其特征和相应的量值构成的多个一维物元。确定相关的一维物元。
2) 根据领域知识,搜集研究对象关于其特征的量值变化的一些数据,需要注意这些数据的变化规律。不同的函数曲线代表着不同的函数类型。作为佐证确定的相关函数是否符合事实并且可用的依据。
3) 根据SD的基本函数模型,在符合相关数学规则的情况下,尽量从最简单的函数方程出发来近似构造特征的相关函数。如果上一次确定相关函数没有成功的话,根据上一次函数方程模拟得到的信息作为依据,逐渐将方程复杂化,继续模拟分析,直到找到可以描述事实规律的近似相关函数。
4) 利用已经建好的相关网动力学模型,在参数相同的情况下,对近似构造的函数进行建模仿真,根据搜集的数据,判断函数的正确性,如果不正确,重复上述操作,直到找到符合实际规律的近似相关函数。
需要补充一点,在有数据支撑的情况下,尽量把相关网建得详细一些,将有助于确定更加准确的相关函数。
根据客观事实,可以确定相关因素并且在数据详实的情况下运用本方法比较方便。对于受很多复杂因素影响的物元相关网,该方法并不适合使用。
4 案例分析W公司是一家数字教学器材公司。VAX系列微型计算机是这家公司很成功的产品。每台VAX微型计算机的售价在100 000~150 000美元之间。VAX11/750型微型计算机于1980年试制成功。其销售主要是靠用户的口头传播。通过对一定数量的数据样本进行分析可知:销售曲线成正态分布,产品累计销售曲线呈现为S型结构。
为了让产品的销售过程持续保持良好的状态。下面利用本文提出的方法来研究该新产品的销售过程中与产品的销售相关的因素,并且找寻相互之间的相关函数。对于企业来说,这样就可以细致准确地模拟产品销售过程的各种情况,为进一步做出正确的决策提供依据,使产品的销售过程满足企业的利润诉求。
4.1 建模与相关分析1) 根据案例背景以及相关资料,建立产品的物元模型如下:
| $\begin{array}{l} M\left( t \right) = \left[ {\begin{array}{*{20}{l}} {{\rm{产品}}{O_1}\left( t \right),}&{{\rm{目标用户群总数}}{c_1},}&{{v_1}\left( t \right)}\\ {}&{{\rm{当前用户}}{c_2},}&{{v_2}\left( t \right)}\\ {}&{{\rm{潜在用户}}{c_3},}&{{v_3}\left( t \right)}\\ {}&{{\rm{销售速率}}{c_4},}&{{v_4}\left( t \right)}\\ {}&{{\rm{用户接触速率}}{c_5},}&{{v_5}\left( t \right)} \end{array}} \right] \buildrel \Delta \over = \\ \left[ {\begin{array}{*{20}{l}} {{O_1}\left( t \right),}&{{c_1},}&{{v_1}\left( t \right)}\\ {}&{{c_2},}&{{v_2}\left( t \right)}\\ {}&{{c_3},}&{{v_3}\left( t \right)}\\ {}&{{c_4},}&{{v_4}\left( t \right)}\\ {}&{{c_5},}&{{v_5}\left( t \right)} \end{array}} \right] = \left[ {\begin{array}{*{20}{l}} {{M_1}\left( t \right)}\\ {{M_2}\left( t \right)}\\ {{M_3}\left( t \right)}\\ {{M_4}\left( t \right)}\\ {{M_5}\left( t \right)} \end{array}} \right] \end{array}$ |
2) 根据领域知识和相关分析原理分析各分物元之间的相关关系如下:
产品的当前用户数量与产品的目标用户群总数相关, 即
根据上述分析,可建立如图 8所示的相关网。

|
图 8 相关网 Fig.8 The correlation network |
对上述相关网进行分析,可以得出如下分析结果:在新产品的销售过程中,要强提高销量,即当前用户的数量,就必须提高产品的销售速率。同时,潜在用户与用户接触产品的速率存在间接相关关系。它们也会影响当前用户数量的变化,即M3(t)~M1(t)~M2(t),M5(t)~M4(t)~M2(t)。
3) 建立相关关系图如图 9。

|
图 9 相关关系图 Fig.9 The correlations of matter-elements |
4) 对相关网变形得到系统动力学相关网。并分析各相关物元的量值之间的函数关系。系统动力学相关网如图 10。

|
图 10 系统动力学相关网 Fig.10 The correlation network of dynamics |
5) 结合特征之间的关联传递关系,建立动力学模型,并进行模拟分析。
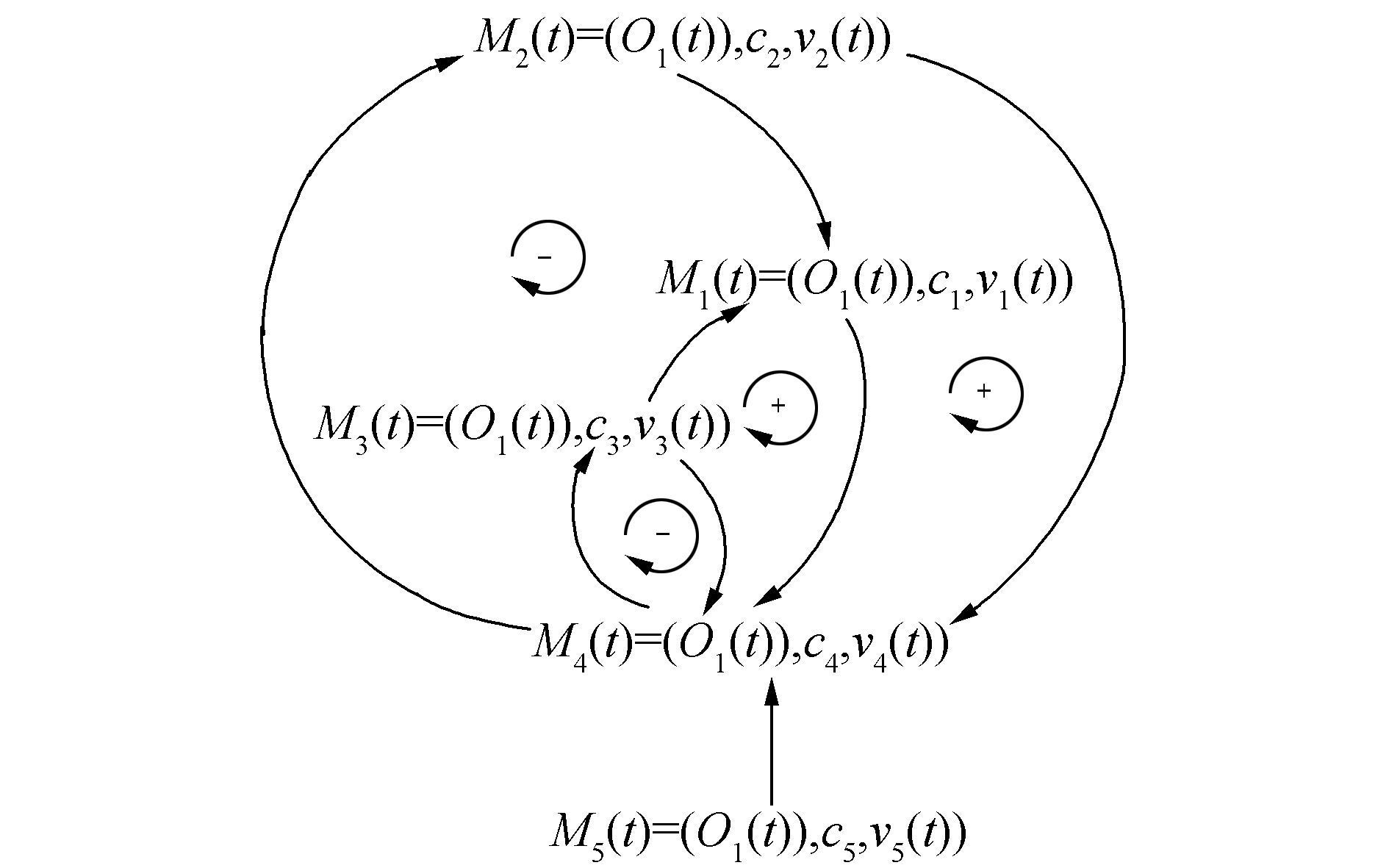
根据上述步骤可得出相关网回路图如图 11。
|
图 11 动力学相关网回路图 Fig.11 The correlation loop of dynamics |
6) 根据相关回路图,找出回路中存在的反馈环(回路),并且以系统的目标为重点,提取主要回路进行分析。
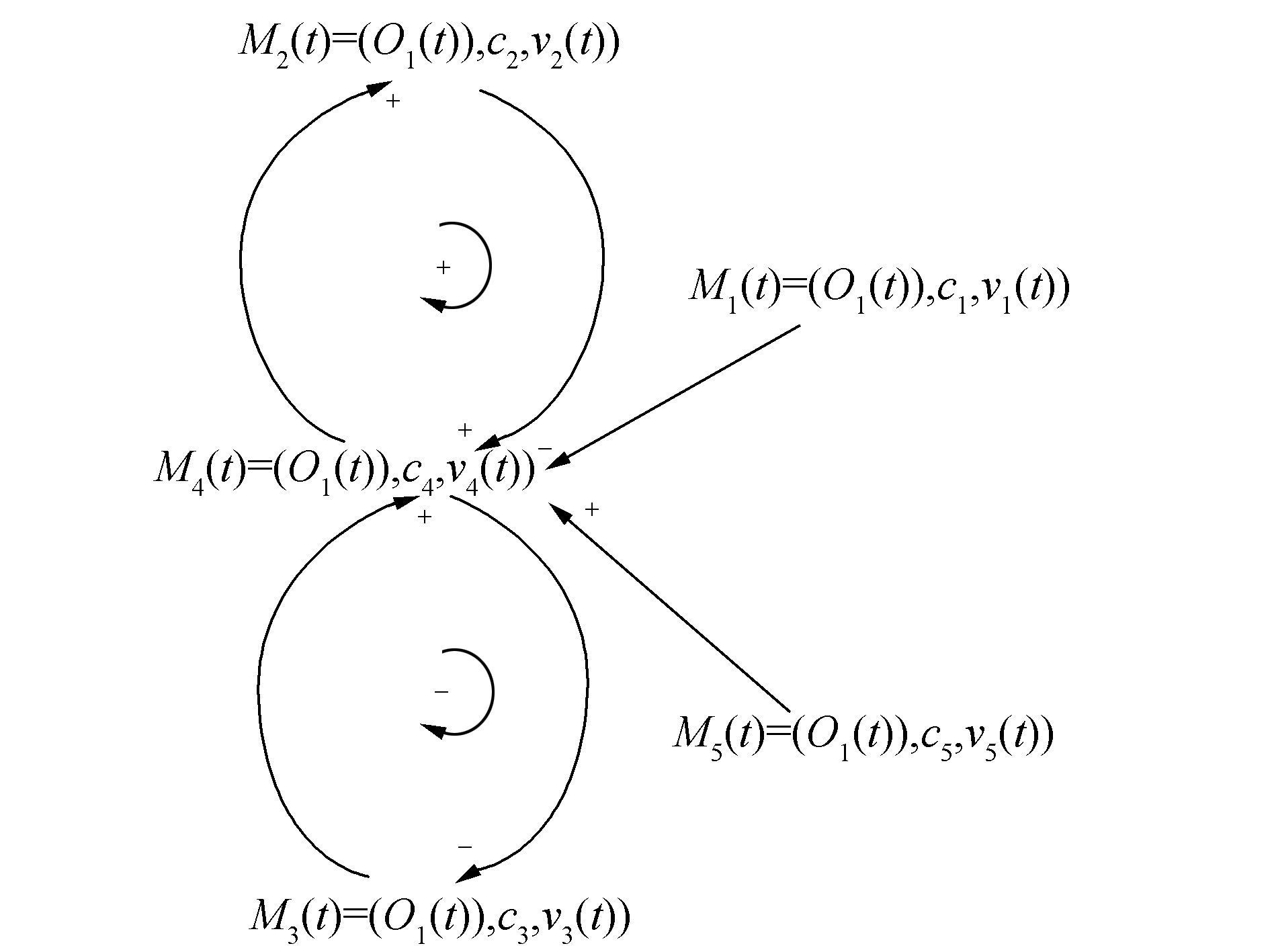
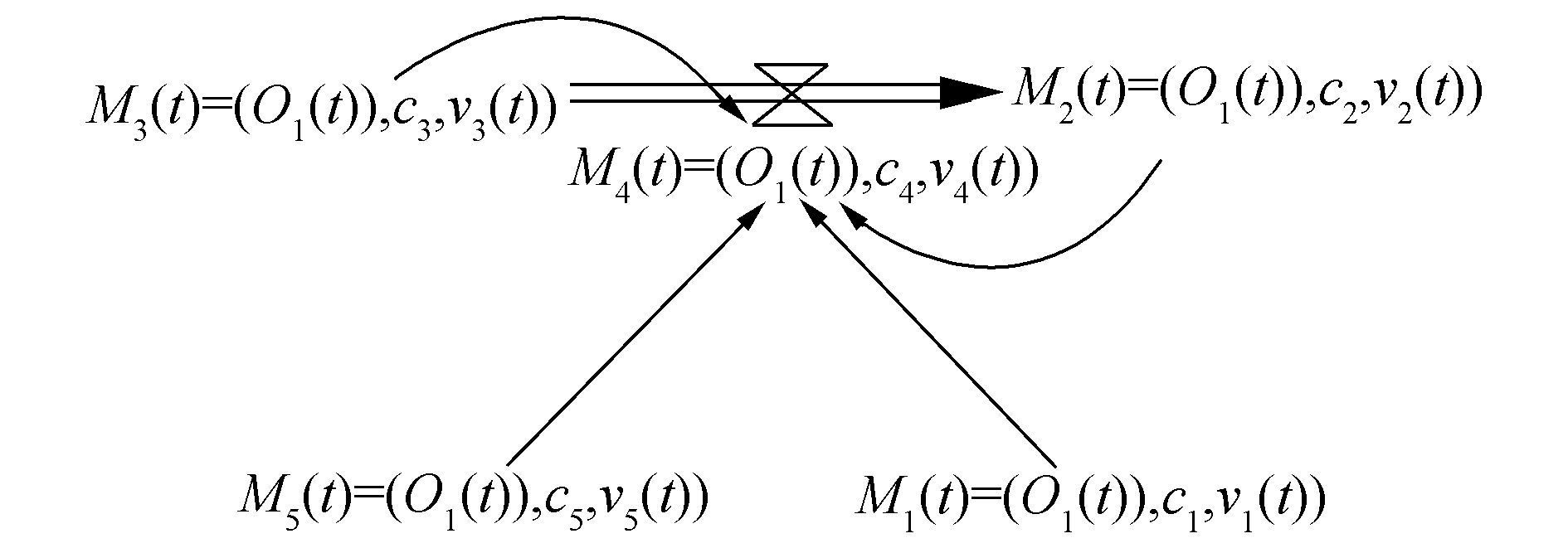
根据图 11可知,本系统存在4个反馈环,以销售过程的现有用户数量为目标,存在两个反馈环如图 12。建立存量流量图,如图 13。
|
图 12 销售系统回路图 Fig.12 Flow of sales system |
|
图 13 销售过程存量流量图 Fig.13 The stock and flow diagram of selling progress |
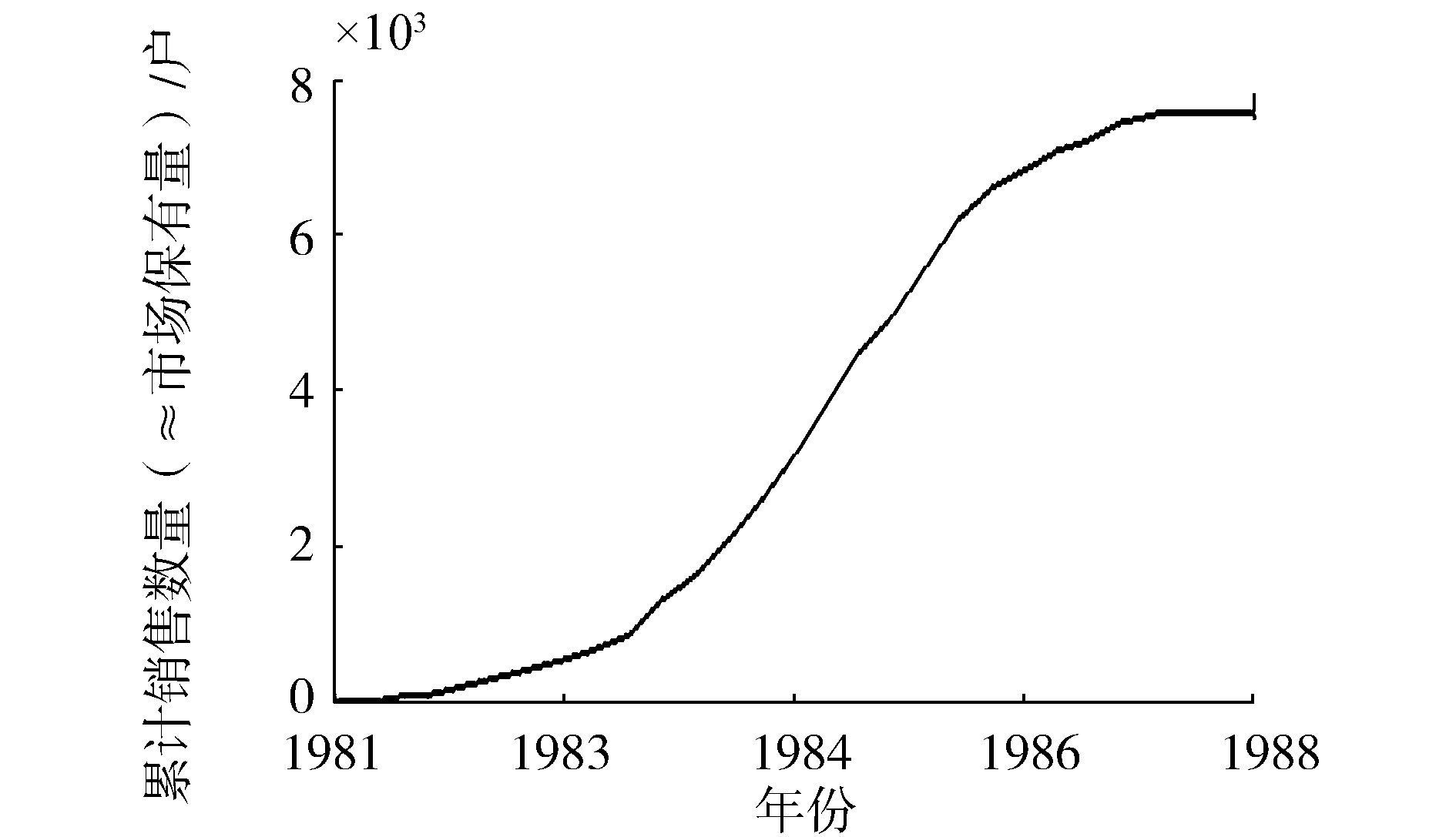
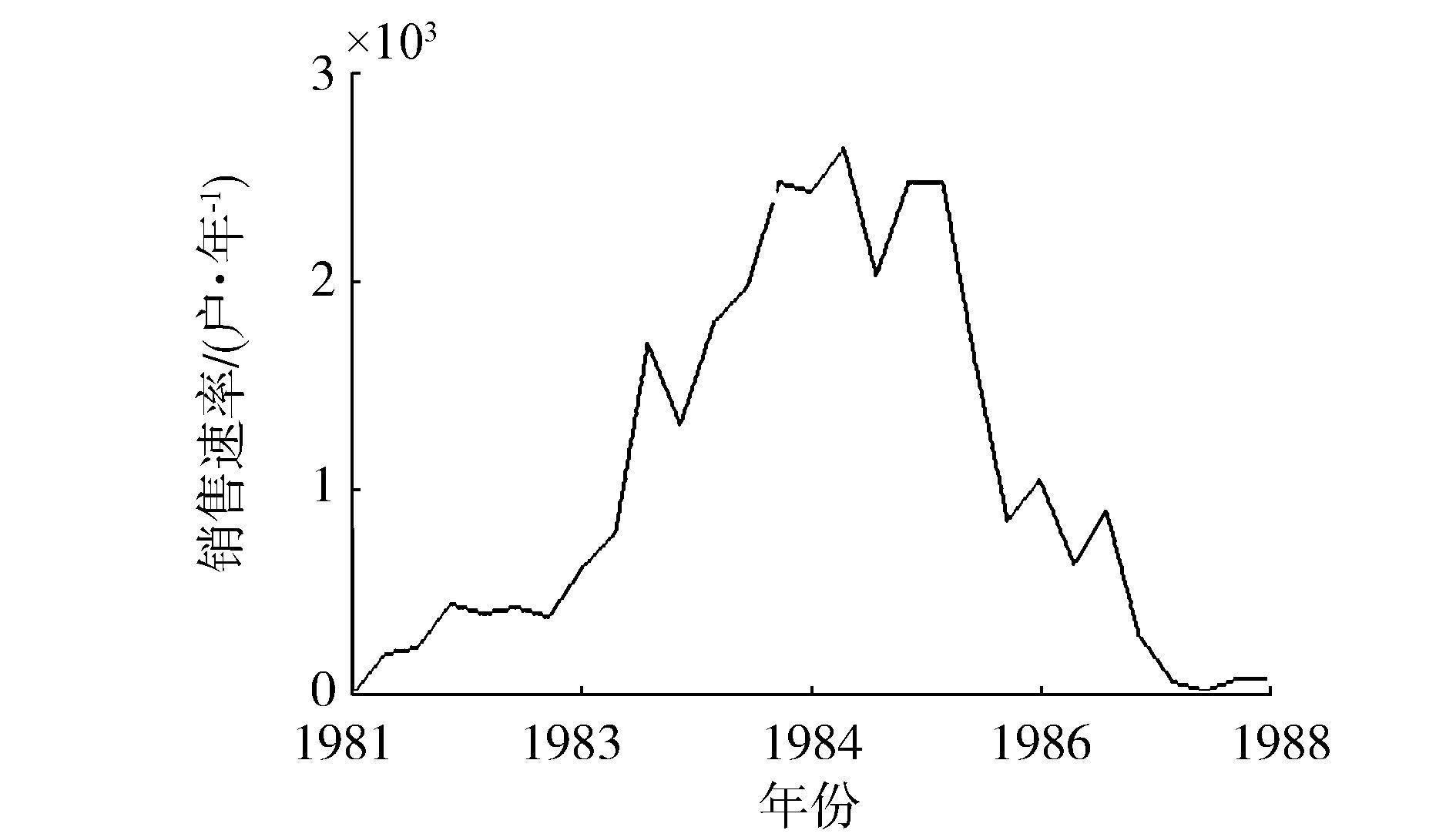
1) 对于不易确定的相关特征之间的相关函数,查阅并分析公司的历年的相关数据,部分如图 14、15。
|
图 14 累计销售量增长图 Fig.14 The growth label of total sales |
|
图 15 历年销售速率 Fig.15 The selling rate of calendar year |
2) 以SD的DYNAMO方程为依据,近似构造相关网内各物元特征的相关函数,并通过模拟,初步验证相关函数的可用性。
根据专业资料可知:用户群总数=当前用户数量+潜在用户数量,即v1(t)=v2(t)+v3(t)。
t+1时刻的潜在用户数量=t时刻的潜在用户数量-从t时刻到t+1时刻的时间间隔内产品的销售速率·时间间隔,即v3(t+1)=v3(t)-v4(t)·DT。
t+1时刻的当前用户数量=t时刻的当前用户数量+从t时刻到t+1时刻的时间间隔内产品的销售速率·时间间隔,即v2(t+1)=v2(t)+v4(t)·DT。
由于销售速率受很多因素的影响,而且在数学函数无法获得的情况下,根据收集的历史销售数据与领域知识可知:用户接触速率v5(t)、当前用户数量v2(t)和潜在用户数量v3(t)与销售速率v4(t)成正比,可假设:v4(t)=v5(t)·v2(t)·v3(t)·ℜ(t)·f(v1(t))
其中, ℜ(t)为未知的影响因素函数。
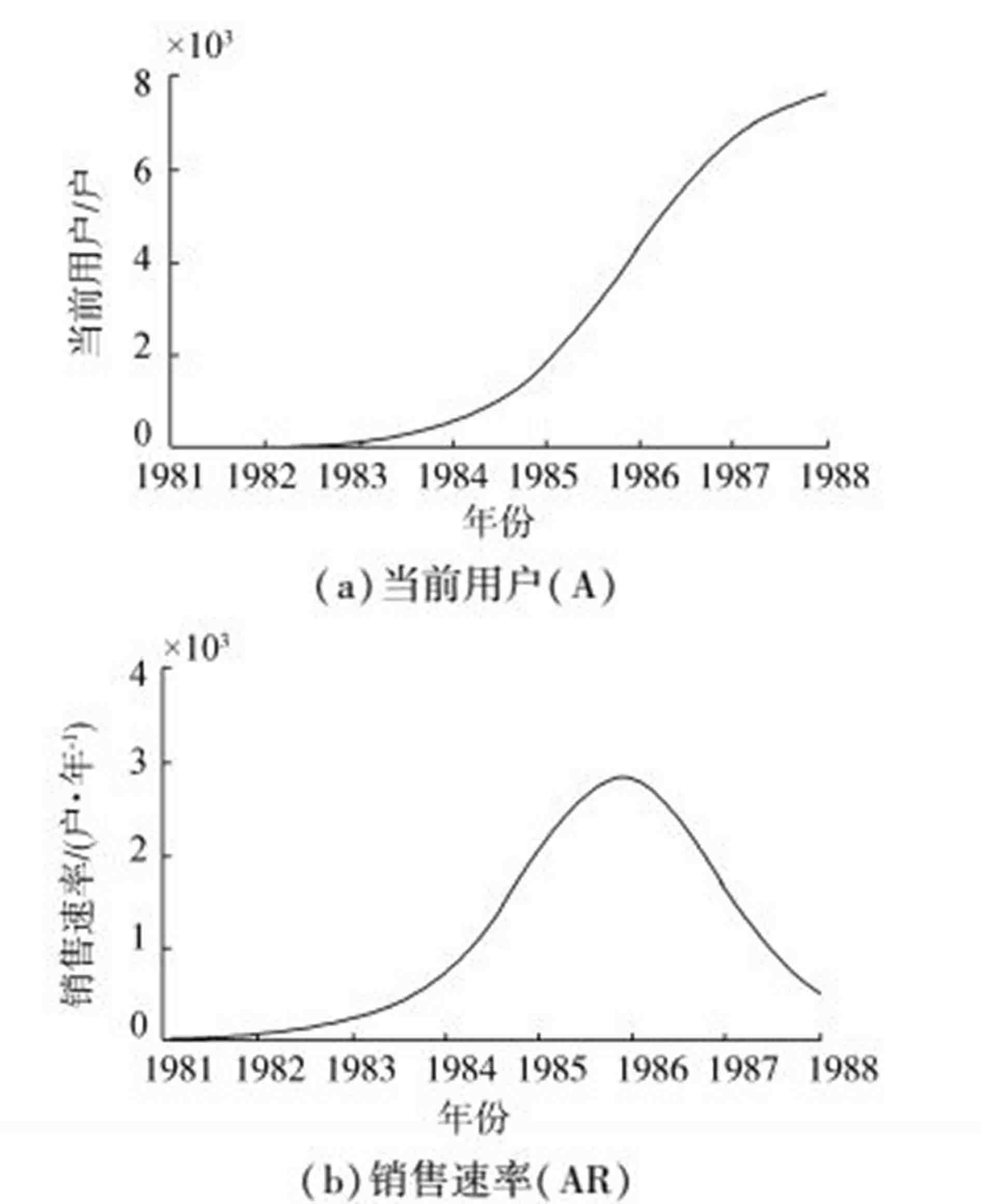
经过反复的分析和模拟,最后一次模拟结果如下图 16所示。
|
图 16 模型运行结果 Fig.16 The results of the model |
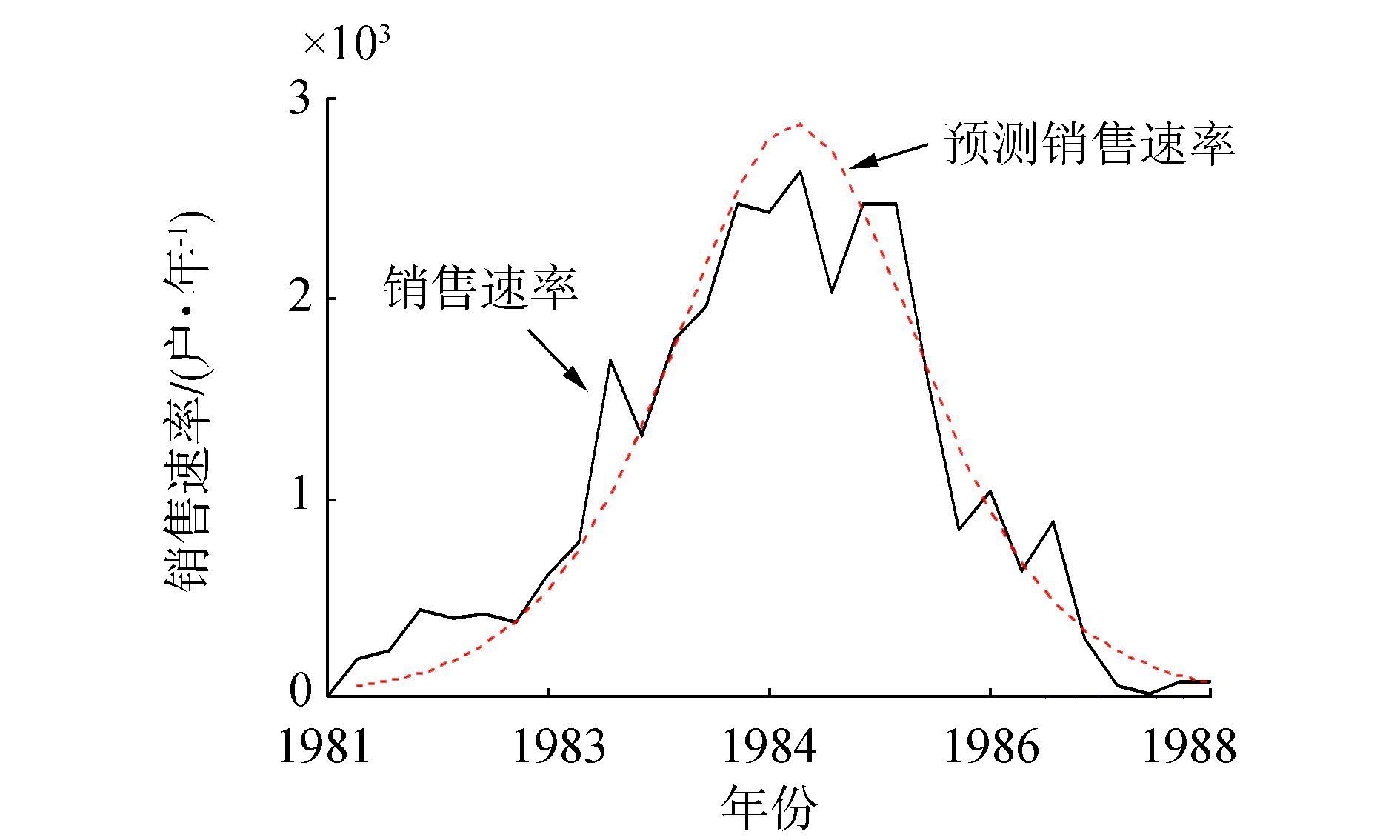
在参数相同的情况下,将模拟结果与搜集的历史资料进行对比,可以确定近似构造的函数基本上可以比较准确的描述各相关特征之间的关系,近似构造对比结果如图 17~18。

|
图 17 销售量模拟对比 Fig.17 The comparison of modeling result of total sales |
|
图 18 销售速率模拟对比图 Fig.18 The comparison of modeling result of sales rate |
所以,最终可以确定:
| $\Re \left( t \right) \cdot f\left( {{v_5}\left( t \right)} \right) = \frac{1}{{{v_5}\left( t \right)}}$ |
则各物元的量值之间的近似函数关系如下:
| $\begin{array}{*{20}{c}} {{v_1}\left( t \right) = {v_2}\left( t \right) + {v_3}\left( t \right)}\\ {{v_3}\left( {t + 1} \right) = {v_3}\left( t \right) - {v_4}\left( t \right) \cdot {\rm{DT}}}\\ {{v_2}\left( {t + 1} \right) = {v_2}\left( t \right) + {v_4}\left( t \right) \cdot {\rm{DT}}}\\ {{v_4}\left( t \right) = \frac{{{v_5}\left( t \right) \cdot {v_2}\left( t \right) \cdot {v_3}\left( t \right)}}{{{v_1}\left( t \right)}}} \end{array}$ |
可拓学中的相关分析理论为研究可拓变换的传导变换提供了前提,在相关分析的基础上实施可拓变换,可以避免传导变换的负效应的产生,以获得可行的创意,为创新、创造以及具体领域问题的研究提供了一种分析工具,为了更好地将相关分析理论运用到更广泛的领域,以提高相关分析方法的可操作性,相关分析理论有待于在普适性以及运用的广泛性方面进一步发展:
1) 本文针对物元相关网,提出了相关网的系统动力学模型建模方法,为相关分析的实施提供了可智能化模拟分析的工具,在一定程度上为相关分析理论应用领域的拓展提供了可能。
2) 在此基础上提出了在动力学相关网模型中近似构造相关函数的方法。为相关函数未知情况下相关分析的实施提供了工具,在一定程度上弥补了相关分析理论运用中的局限性。
3) 以W公司新产品销售过程为例,通过对其建立相关网动力学模型,进行模拟分析以及近似构造未知相关函数,通过与对现实数据进行初步分析得出的信息对比,验证了其有效性。
本文对相关分析的智能化模拟分析和相关函数的确定研究,可以为未来相关领域的应用及对相关网的进一步理论深入研究作打下基础性工作。
| [1] |
杨春燕, 蔡文. 可拓学[M]. 北京: 科学出版社, 2014: 43-133.
( 0) 0)
|
| [2] |
汤龙, 杨春燕. 复杂基元相关网下的传导变换[J]. 智能系统学报, 2016, 11(1): 1-9. TANG Long, YANG Chunyan. Conductive transformation under complicated basic-element correlative network[J]. CAAI transactions on intelligent systems, 2016, 11(1): 1-9. (  0) 0)
|
| [3] |
杨春燕, 蔡文. 可拓学与矛盾问题智能化处理[J]. 科技导报, 2014, 32(36): 15-20. YANG Chunyan, CAI Wen. Extenics and intelligent processing of contradictory problems[J]. Science and technology review, 2014, 32(36): 15-20. DOI:10.3981/j.issn.1000-7857.2014.36.001 (  0) 0)
|
| [4] |
YANG Chunyan, CAI Wen. Extenics:theory, method and application[M]. Beijing: Science Press, 2013.
( 0) 0)
|
| [5] |
蔡文, 杨春燕, 何斌. 可拓逻辑初步[M]. 北京: 科学出版社, 2004: 55-56.
( 0) 0)
|
| [6] |
李立希, 杨春燕, 李铧汶. 可拓策略生成系统[M]. 北京: 科学出版社, 2006: 46-62.
( 0) 0)
|
| [7] |
汪应洛. 系统工程[M]. 北京: 机械工业出版社, 2008: 86-102.
( 0) 0)
|
| [8] |
张波, 虞朝晖, 孙强, 等. 系统动力学简介及其相关软件综述[J]. 环境与可持续发展, 2010(2): 1-4. ZHANG Bo, YUN Chaohui, SHUN Qiang, et al. Overview of system dynamics and related software[J]. Environment and sustanable development, 2010(2): 1-4. (  0) 0)
|
| [9] |
张力菠. 基于系统动力学的管理决策建模研究[D]. 南京: 南京理工大学, 2001: 8-19. ZHANG Libo. Research of management decision-making based on system dynamics modeling[D]. Nanjing:Nanjing University of Science and Engineering, 2001:8-19. http://cdmd.cnki.com.cn/Article/CDMD-10288-2002052955.htm (  0) 0)
|
| [10] |
陈国卫. 系统动力学应用研究综述[J]. 控制工程, 2012, 19(6): 921-928. CHEN Guowei. Application research overview of system dynamics[J]. Control engineering of China, 2012, 19(6): 921-928. (  0) 0)
|
| [11] |
毕克新, 孙德花, 李柏洲. 基于系统动力学的制造业企业产品创新与工艺创新互动关系仿真研究[J]. 创新管理, 2008(12): 75-80. BI Kexin, SUN Dehua, LI Baizhou. Product innovation and process innovation-a system dynamics-based simulation of the interaction in manufacturing enterprise[J]. Innovation management, 2008(12): 75-80. (  0) 0)
|
| [12] |
吴振华, 黎芸, 贵文龙, 等. 基于系统动力学的住宅价格预测研究[J]. 技术经济与管理研究, 2013(8): 101-105. WU Zhenghua, LI Yun, GUI Wenlong, et al. The forecast research of urban commodity residence price based on system dynamics[J]. Techno economics and management research, 2013(8): 101-105. (  0) 0)
|
| [13] |
郑士源. 基于系统动力学的两厂商投资微分博弈模拟[J]. 上海海事大学学报, 2006, 27(4): 70-74. ZHENG Shiyuan. Duopoly investment differential game simulation based on system dynamics[J]. Journal of Shanghai maritme university, 2006, 27(4): 70-74. (  0) 0)
|
| [14] |
梁吉业, 冯晨娇, 宋鹏. 大数据相关分析综述[J]. 计算机学报, 2016, 39(1): 1-18. LIANG Jiye, FENG Chenjiao, SONG Peng. A survey on correlation analysis of big data[J]. Chinese Journal of Computers, 2016, 39(1): 1-18. DOI:10.11897/SP.J.1016.2016.00001 (  0) 0)
|
| [15] |
夏幼明, 解敏, 周雯. 数据挖掘方法分析与评价[J]. 云南师范法学学报, 2003, 23(2): 7-16. XIA Youming, XIE Min, ZHOU Wen. Analysis and evaluation of data mining[J]. Journal of Yunnan normal university, 2003, 23(2): 7-16. (  0) 0)
|
| [16] |
郭秀娟. 数据挖掘方法综述[J]. 吉林建筑工程学院学报, 2004, 21(1): 49-53. GUO Xiujuan. Summary of data mining[J]. Journal of Jilin architectural and civil engineering, 2004, 21(1): 49-53. (  0) 0)
|
| [17] |
王惠忠, 彭安群. 数据挖掘研究现状及发展趋势[J]. 工矿自动化, 2011, 37(2): 29-32. WANG Huizhong, PENG Anqun. Study on status and development trends of data mining[J]. Industry and mine automation, 2011, 37(2): 29-32. (  0) 0)
|
| [18] |
胡文瑜, 孙志辉, 吴英杰. 数据挖掘取样方法研究[J]. 计算机研究与发展, 2011, 48(1): 45-54. HU Wenyu, SUN Zhihui, WU Yingjie. Study of sampling methods on data mining and stream mining[J]. Journal of computer research and development, 2011, 48(1): 45-54. (  0) 0)
|
| [19] |
崔广风. 数据挖掘中的统计方法及其应用研究[D]. 成都: 西南石油大学, 2014: 8-25. CUI Guangfeng. Study on statistical method and Its application in data mining[D]. Chengdu:Southwest Petroleum University, 2014:8-25. http://cdmd.cnki.com.cn/Article/CDMD-10615-1014411446.htm (  0) 0)
|
| [20] |
党辉. 基于系统动力学和云模型模糊数据挖掘的生态安全仿真预警[D]. 兰州: 西北师范大学, 2013: 29-49. DANG Hui. Ecological security simulation early warning based on system dynamics and fuzzy data mining on cloud model[D].Lanzhou:Northwest Normal University, 2013:29-49. http://cdmd.cnki.com.cn/Article/CDMD-10736-1014018998.htm (  0) 0)
|
 2017, Vol. 12
2017, Vol. 12


