移动机器人全覆盖路径规划是地形探测、地面资源勘探、地面清洁、战地侦查等任务的重要组成部分[1-3]。作为移动机器人领域核心研究问题之一,全覆盖路径规划一直受到广泛关注。移动机器人完成全覆盖路径规划需要解决3个问题[4-7]:1)需遍历工作区域内除障碍物以外的全部区域;2)在遍历过程中有效避开所有障碍物;3)在遍历过程中要尽量避免路径重复,缩短移动距离。迄今为止,关于全覆盖路径规划的方法多种多样,各有优劣,主要的方法可以分为:行为覆盖法[8-9]、区域分割法[10-12]、神经网络法[13-16]等。
2000年Balch等[8]提出一种移动机器人行为覆盖路径规划方法,机器人根据简单的移动行为,尝试性地覆盖工作区域,如果遇到障碍物,则执行对应的转向命令。这种方法是一种以时间换空间的低成本策略,如不计时间可以达到全覆盖。该算法无需了解整个作业区全貌,也不用依赖过多的传感器,处理器运算量也很小,是一种性价比很高的方案。但是,行为全覆盖算法工作效率低,路径规划策略过于简单,面对复杂地形机器人经常无法逃离死区[9]。
为了使机器人能够逃离死区,同时减少算法的计算量,Jin等[10]提出一种基于时空信息的全局导航与局部导航组合的算法。该算法一方面能够通过局部计算代替不必要的全局计算,减少了实时决策时局部最优导航的计算量;另一方面通过分层的方式使机器人能够逃离死区。但是在局部与全局的转换过程中,当周围没有未覆盖的区域时,机器人需要扩大邻近区域的面积来寻找未覆盖区域,这将导致覆盖效率的降低,尤其是当未覆盖区域距离机器人较远时[11-12]。
近年来,神经网络算法被应用到全覆盖路径规划中[13-14]。利用神经网络的自学习、并行性等特性,增强机器人的“智能”,提高覆盖效率。受神经网络结构与栅格地图单元类似的启发,加拿大学者S. X. Yang [15-16]等提出一种基于生物启发神经网络的移动机器人全覆盖路径规划算法,将需要全覆盖的二维栅格地图单元与生物启发神经网络的神经元一一对应起来,机器人实现全覆盖的实时路径规划是由神经元的活性值和机器人的上一位置产生的。该算法完全根据栅格地图单元的性质(未搜索单元、已搜索单元还是障碍物),决定神经元的输入,直接计算神经元的活性值,不存在神经网络学习过程,算法实时性好,同时可以自动避障与逃离死区。
最近,Yan[17]等在文献[15-16]的基础上,进一步将生物启发神经网络应用到水下机器人全覆盖路径规划中。该算法根据声呐传感器获取的信息,利用信息融合技术构建动态水下环境地图,根据水下感知的环境地图性质确定生物启发神经网络中神经元的活性值,水下机器人通过比较邻近神经元活性值进行路径规划,完成对工作区域的全覆盖,该方法将水下环境的地图构建与全覆盖路径规划有机结合,得到一套完整的水下机器人感知环境与全覆盖搜救方法。
但是基于生物启发神经网络的全覆盖算法计算量大,同时此种方法中神经网络模型的衰减率等参数没有最优值,在实现算法时只能通过反复实验确定,参数的设定存在人为不确定因素,从而影响其在线应用[18]。
对此,本文在栅格地图的基础上,引入方向信度函数的概念,提出一种移动机器人全覆盖信度函数路径规划策略。该策略计算量小、路径重复率低,使得机器人不仅能够完成工作区域全覆盖任务,而且能够快速逃离死区。算法包括3个部分:1)根据地面环境的状态对栅格地图进行赋值,使用不同的函数值表示障碍物、已覆盖栅格和未覆盖栅格;2)引入方向信度函数对栅格信度函数值进行优化;3)机器人根据栅格信度函数进行覆盖路径规划。本文提出的基于栅格信度函数的移动机器人全覆盖路径规划算法能够实现动态工作区域的全覆盖,与生物启发神经网络算法相比有更短的覆盖路径。
1 基于栅格信度函数的全覆盖路径规划算法全覆盖路径规划是指移动机器人以尽可能低的路径重复率遍历工作区域中的全部可到达点,它包含两个方面的技术指标,即区域覆盖率和路径重复率。本文以弓形路径移动方式为基础,引入方向信度函数对机器人移动路径进行优化,完成对工作区域的全覆盖的同时降低路径重复率。
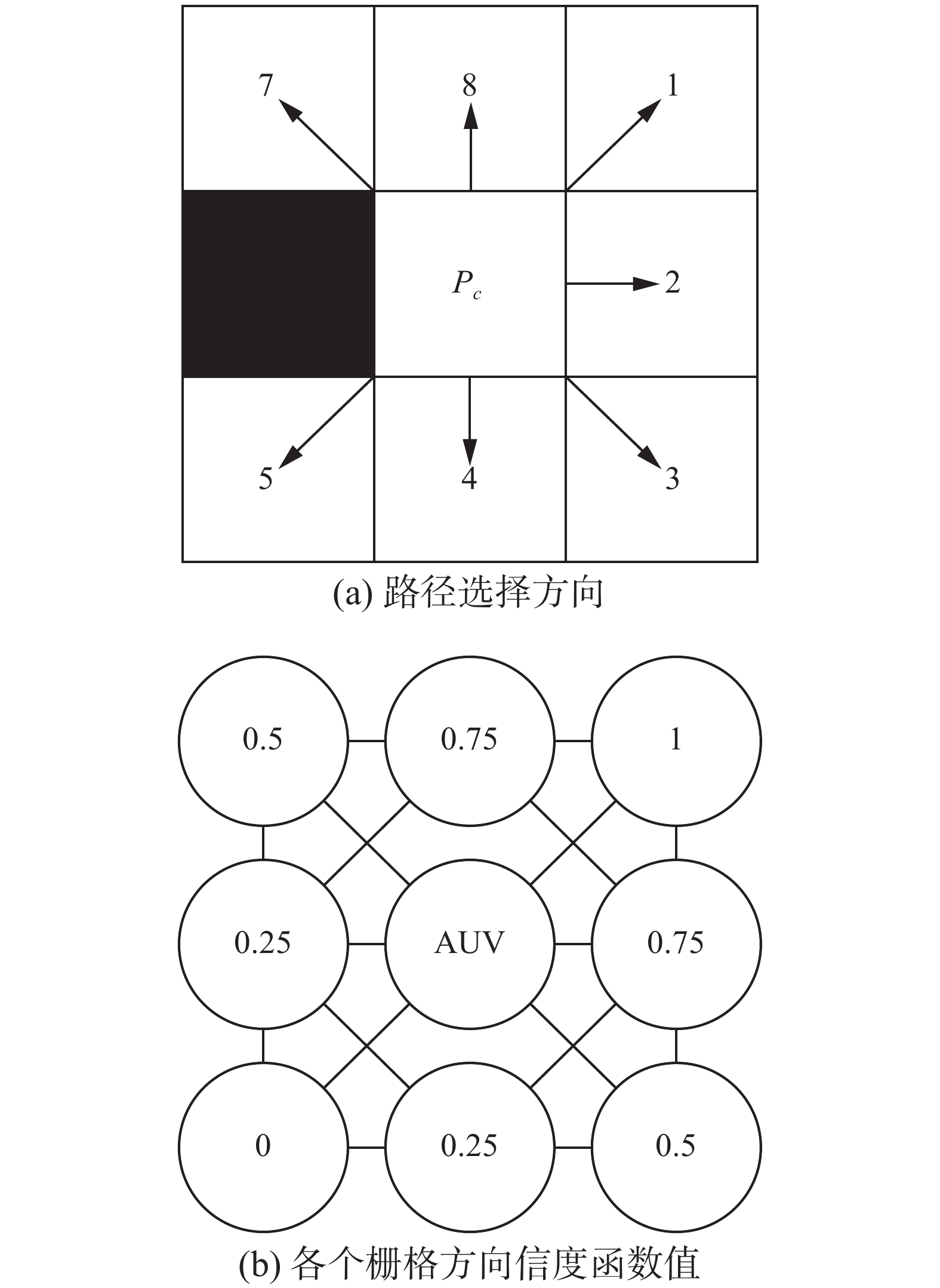
1.1 栅格位置性质函数为了避免机器人与障碍物发生碰撞,防止机器人对同一栅格单元重复覆盖,将对栅格地图进行赋值。依据每个栅格的性质赋不同的信度函数值,表示出每个栅格的状态信息[19-22]。本节以二维的栅格地图为例说明怎样对栅格进行信度赋值。图1(a)显示的是一个二维的栅格地图,工作区域被分成了9个栅格,其中黑色栅格表示被障碍物占领,白色栅格表示自由空间,Pc表示机器人当前所在的位置。根据式(1)对栅格位置性质函数xj赋值,如栅格6表示障碍物,则被赋值为-
| ${x_j} = \left\{ {\begin{array}{*{20}{l}}{1,\quad \text{该单元未覆盖}}\\{0.5,\quad \text{该单元被覆盖}}\\{ - \infty ,\quad \text{该单元是障碍物}}\end{array}} \right.$ | (1) |
式中xj表示第j个栅格的位置性质函数值。同时为了避免同一个栅格的反复覆盖,在此约定栅格被多覆盖一次,其位置性质函数值就减少0.5。假如栅格Pc被覆盖过一次,其位置性质函数值为0.5;如果栅格Pc被覆盖了两次,其位置性质函数值为0。
|
Download:
|
| 图 1 栅格地图 Fig. 1 The grid map | |
为了降低路径重复率,提高覆盖效率,对机器人的移动路径进行优化,引入方向信度函数
| ${y_j} = \left\{ {\begin{array}{*{20}{l}}{1 - \displaystyle\frac{{\Delta {\theta _j}}}{\text{π} },\quad \text{机器人未陷入死区}}\\{\cos \Delta {\varphi _j},\quad \text{机器人陷入死区}}\end{array}} \right.$ | (2) |
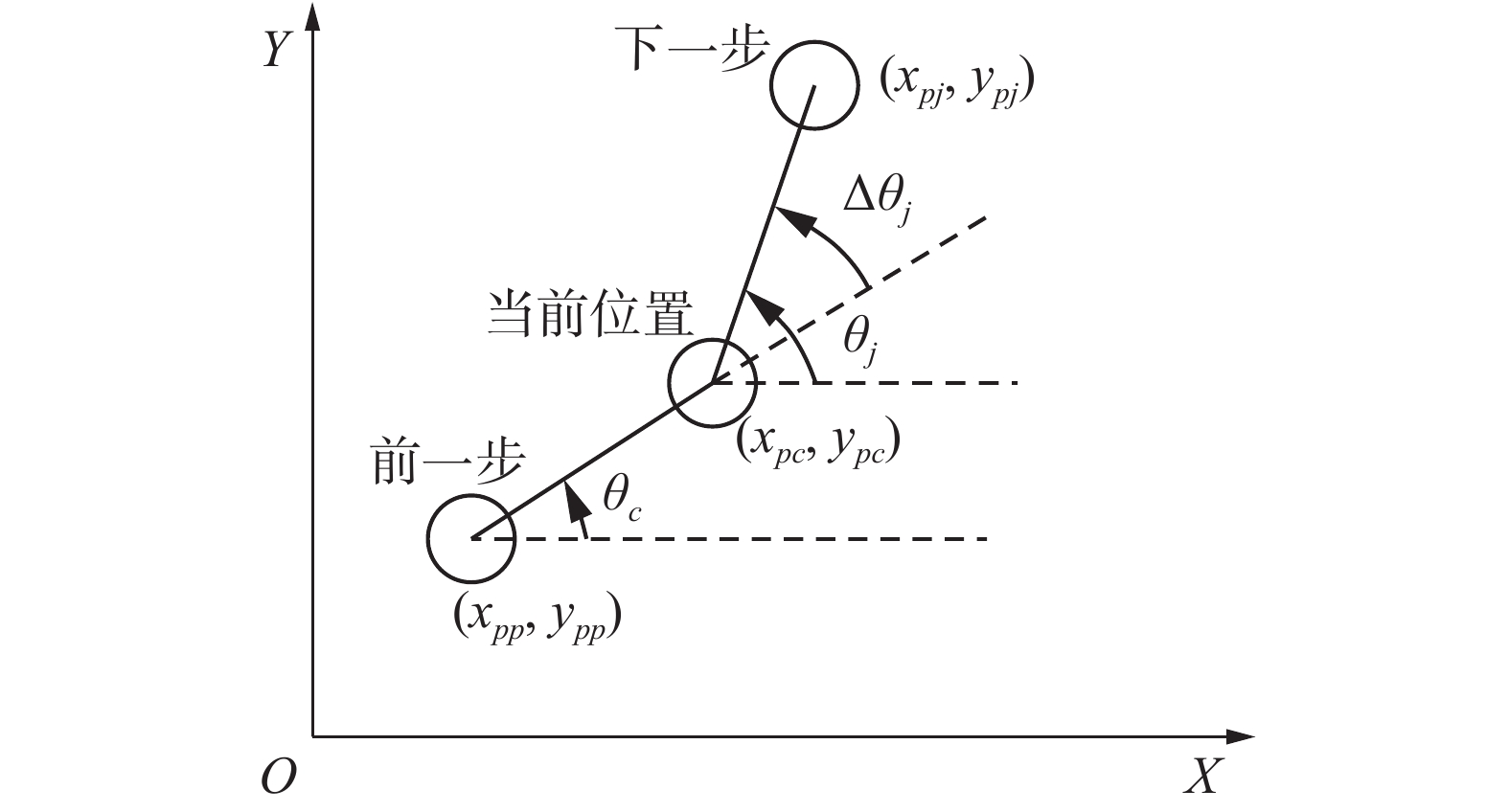
式(2)中方向信度函数的定义分为两种情况,当机器人未陷入死区时,
| $\begin{array}{c}\!\!\!\!\!\!\!\!\! \Delta {\theta _j} = \left| {{\theta _j} - {\theta _c}} \right| = \\\!\!\!\!\!\!\!\!\! |a\tan 2({y_{{p_j}}} - {y_{{p_c}}},{x_{{p_j}}} - {x_{{p_c}}}) - a\tan 2({y_{{p_c}}} - {y_{{p_p}}},{x_{{p_c}}} - {x_{{p_p}}})|\end{array}$ | (3) |
式中:
|
Download:
|
| 图 2 未陷入死区方向信度函数 Fig. 2 The direction belief function in the free zone | |
|
Download:
|
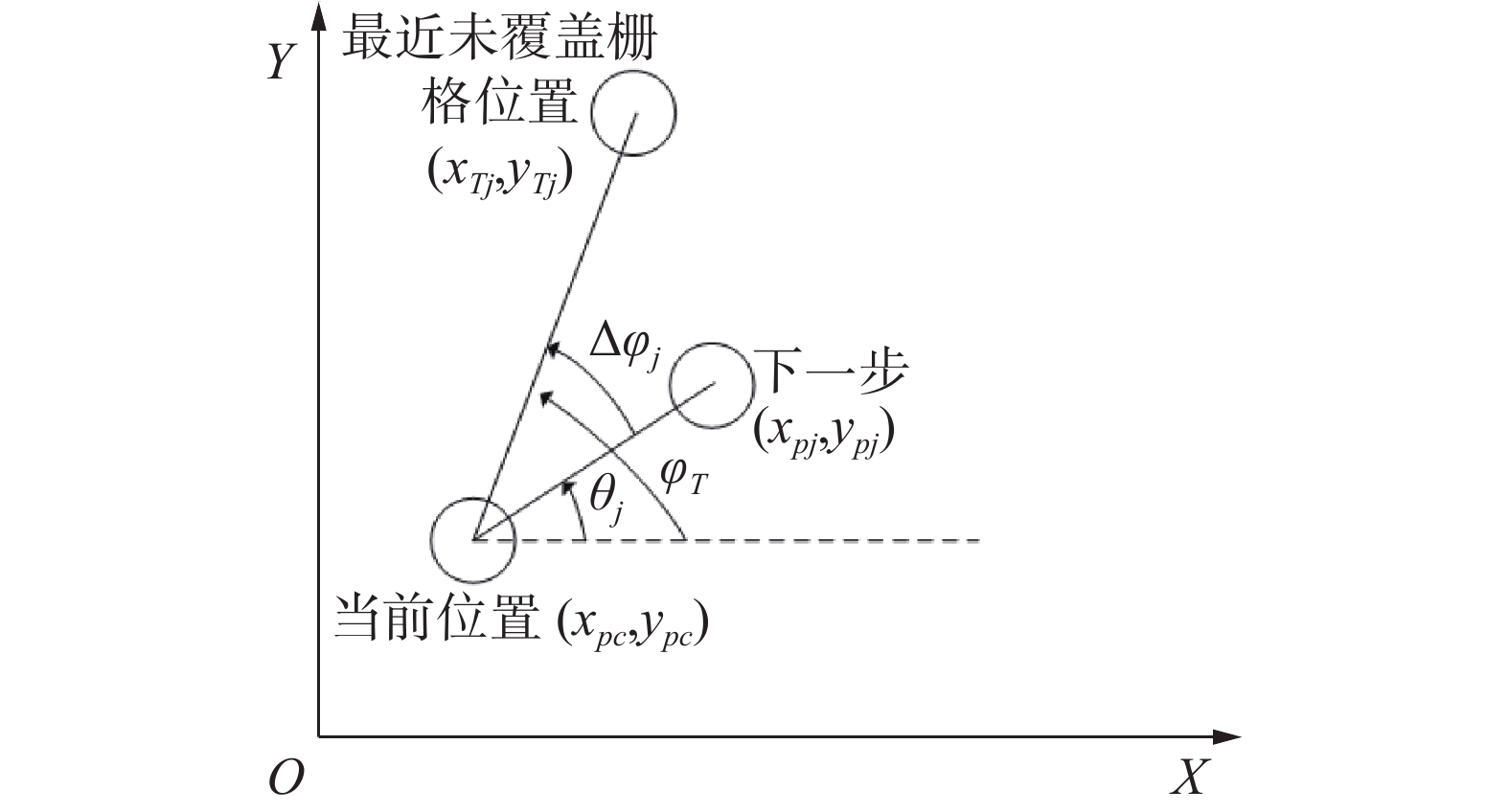
| 图 3 陷入死区方向信度函数 Fig. 3 The direction belief function in the dead zone | |
机器人陷入死区是指它的周边相邻区域,或者是边界,或者是障碍物,或者是已覆盖过的区域。只有从死区逃离出来,才能继续完成全覆盖任务,而逃离死区的路径,直接决定着全覆盖的路径重复率。当机器人陷入死区后,为了让机器人以尽可能短的路径逃离死区,本文提及的算法不再以当前位置与下一步位置的移动角之差作为方向向导,而是将当前位置与距离最近未覆盖栅格位置和下一步位置的角度差作为移动的方向向导,引导机器人快速逃离死区。机器人陷入死区后的方向信度函数定义为
| $\begin{array}{c}\Delta {\varphi _j} = \left| {{\varphi _T} - {\theta _j}} \right| = |a\tan 2({y_{{T_j}}} - {y_{{p_c}}},{x_{{T_j}}} - {x_{{p_c}}}){\kern 1pt} - \\{\kern 1pt} \;\;\;\;\;\;\;\;\;a\tan 2({y_{{p_j}}} - {y_{{p_c}}},{x_{{p_j}}} - {x_{{p_c}}})|\end{array}$ | (4) |
式中:
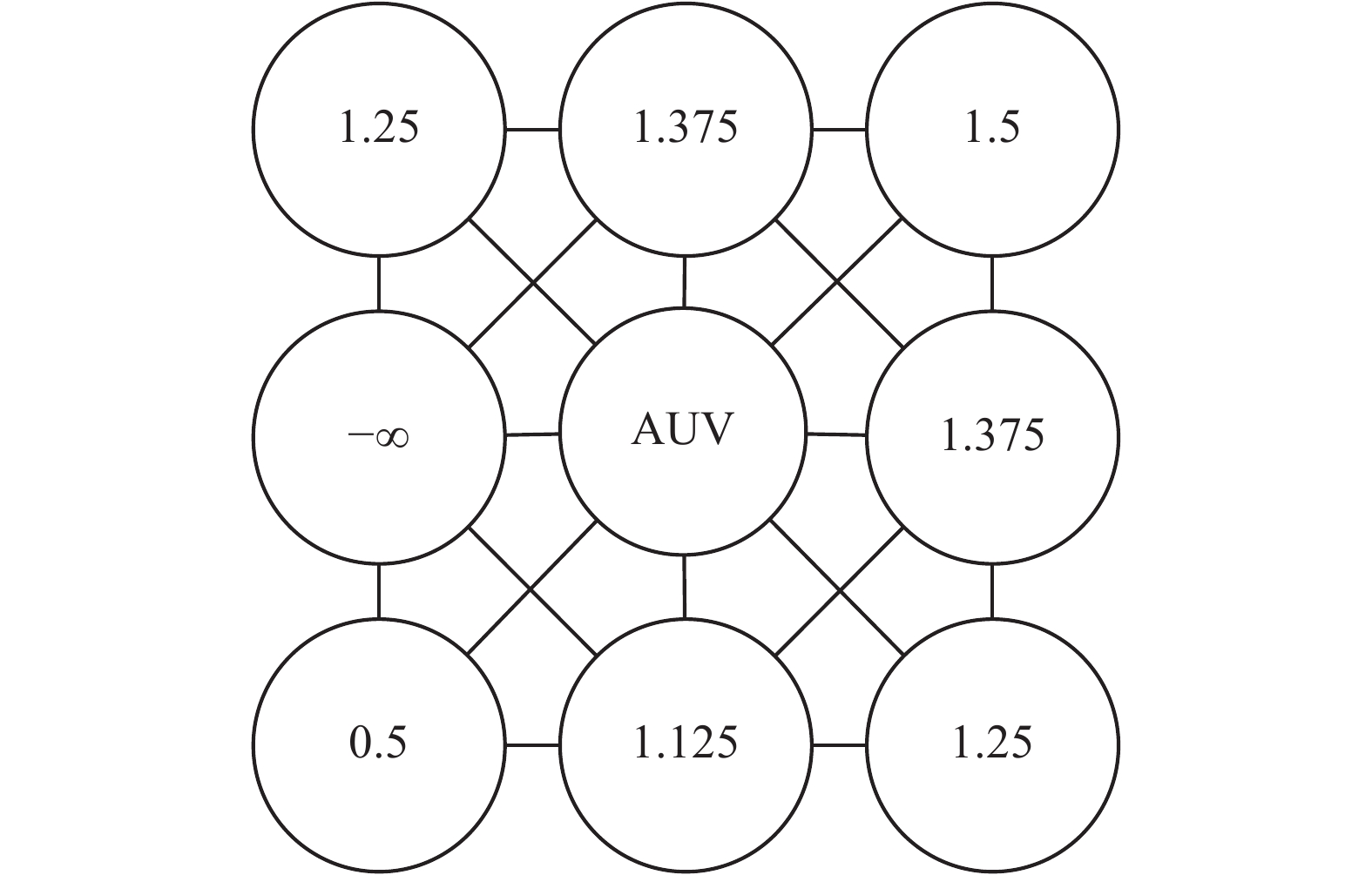
在栅格地图中,全覆盖路径规划问题就演变为寻找机器人的下一个移动位置,只有准确找出了该位置,才能使机器人自主规划出一条切实可行的无碰撞且重复率低的移动路径。为了避开障碍物并且能够完成工作区域的全覆盖,根据栅格位置性质函数和方向信度函数,定义一个综合栅格信度函数
| ${p_j} \Leftarrow {F_{{P_j}}} = \max \{ {F_j} = {x_j} + c{y_j},{\kern 1pt} \;\;\;j = 1,2,\cdots \!,k\} $ | (5) |
式中:
|
Download:
|
| 图 4 各个栅格综合信度函数值 Fig. 4 The comprehensive belief function of each grid | |
为了进一步说明机器人的路径选择策略,图5显示了二维环境中基于栅格信度函数路径选择策略的路径规划效果(设置参数

|
Download:
|
| 图 5 机器人路径选择过程 Fig. 5 The process of robot’s path selection | |
进一步分析机器人未陷入死区时每一步路径选择,表1列出了图5(a)中前6步机器人邻近位置的栅格信度函数值。如表所示,机器人初始位置是(1,1),由于靠近边界只有3个邻近栅格可以作为下一步的位置,根据式(1)、(2)、(5)计算出其邻近栅格信度函数值分别为1.375、1.250和1.500,根据路径选择策略选择最大值1.500对应的
| 表 1 机器人前7步的栅格信度函数值 Tab.1 The grid belief function of robot for the first seven steps |
当机器人陷入死区以后,采用
| 表 2 机器人逃离死区的栅格信度函数值 Tab.2 The grid belief function of robot escaping from the dead zone |
仿真实验设置工作区域的大小为
工作区域中,动态障碍物对机器人的路径规划具有不容忽视的影响,尤其是机器人在执行地面全覆盖式的地形勘探和数据测量等任务时,动态障碍物的出现不仅威胁机器人安全,还会妨碍其对整个区域的全覆盖效果。本节针对动态障碍物对区域全覆盖的影响进行研究。如图6(a)所示,机器人从(1,1)位置出发执行全覆盖任务。障碍物3是动态的,起初在地图上占据着相关区域,机器人无法对该区域进行覆盖,如图6(b)所示。
随着机器人任务的继续执行,当机器人移动至300步时,障碍物3离开(图6(b)所示),地图上相关区域的栅格性质函数值变为1。当机器人移动到(20,4)时,正好执行完障碍物3离开前的地图覆盖,如图6(c)所示。但是此时由于障碍物离开留下的区域需要覆盖,因此根据快速逃离死区的规则,机器人从(20,4)再度出发,前往最近未覆盖栅格(14,11),此时机器人采用

|
Download:
|
| 图 6 动态障碍物环境中的机器人全覆盖路径规划 Fig. 6 Complete-coverage path planning of robot in the dynamic obstacle environment | |
为了进一步考察本文所提算法的性能,本节将与其他算法对区域覆盖率、路径重复率、总行程等指标进行比较。图7显示了两种不同算法对20×20且存在不规则障碍物的栅格区域进行全覆盖路径规划的结果。采用文献[17]的生物启发神经网络全覆盖方式得到的路径规划效果如图7(a)所示。采用本文提及的栅格信度函数算法的路径规划结果如图7(b)所示。两种路径规划方法进行效果对比的评价指标如表3所示。通过图7和表3的结果可知,虽然两种方法的区域覆盖率均达到100%,但是机器人逃离死区的路径有较大的区别。生物启发神经网络算法由于陷入死区的位置离未覆盖区域较远,神经元的活性传递需要较长时间,使得机器人长期停留在死区,需要更长的路径才能逃离死区。而栅格信度函数算法在机器人陷入死区后能通过调整方向信度函数的方法快速的逃离死区。图7中黑色线段显示了两种不同算法逃离死区的路径。虽然两种算法在未陷入死区前机器人移动路径相同,但是由于逃离死区的路径不同,导致两种算法的重复覆盖栅格数,路径重复率、总行程等指标的差异。从表3可见生物启发神经网络算法的重复覆盖的栅格有39块,而栅格信度函数算法只有23块;生物启发神经网络算法的路径重复率几乎是本文算法的2倍;总行程后者比前者少16步。结果表明基于栅格信度函数的算法可以有效降低路径重复率,缩短行程,对于机器人来说路径规划更适合控制,更节省能源。

|
Download:
|
| 图 7 不同算法全覆盖路径规划结果 Fig. 7 The results of complete-coverage path planning with different algorithms | |
| 表 3 不同算法全覆盖路径规划性能比较 Tab.3 Performance comparison of complete-coverage path planning with different algorithms |
本文采用栅格信度函数算法解决了移动机器人全覆盖路径规划问题。仿真实验证明本文所提算法在二维障碍物环境中,不仅能够实现动态障碍物工作区域的全覆盖,而且还能够快速逃离死区,降低了机器人路径的重复率,提高了覆盖效率。限于篇幅,本文未讨论实际的二维环境栅格地图的构建以及机器人的形状、转向幅度、定位对全覆盖路径规划的影响,后续研究将把栅格地图构建与全覆盖路径规划结合,研究移动机器人对真实环境的感知与路径规划方法。
| [1] |
简毅, 张月. 移动机器人全局覆盖路径规划算法研究进展与展望[J]. 计算机应用, 2014, 34(10): 2844-2849, 2864. JIAN Yi, ZHANG Yue. Complete coverage path planning algorithm for mobile robot: progress and prospect[J]. Journal of computer applications, 2014, 34(10): 2844-2849, 2864. DOI:10.11772/j.issn.1001-9081.2014.10.2844 (  0) 0)
|
| [2] |
YAN Mingzhong, ZHU Daqi. An algorithm of complete coverage path planning for autonomous underwater vehicles[J]. Key engineering materials, 2011, 467-469: 1377-1385. DOI:10.4028/www.scientific.net/KEM.467-469 ( 0) 0)
|
| [3] |
莫宏伟, 马靖雯. 一种生物地理学移动机器人路径规划算法[J]. 智能系统学报, 2015, 10(5): 705-711. MO Hongwei, MA Jingwen. A biogeography-based mobile robot path planning algorithm[J]. CAAI transactions on intelligent systems, 2015, 10(5): 705-711. (  0) 0)
|
| [4] |
LI Yan, CHEN Hai, JOO ER MENG, et al. Coverage path planning for UAVs based on enhanced exact cellular decomposition method[J]. Mechatronics, 2011, 21(5): 876-885. DOI:10.1016/j.mechatronics.2010.10.009 ( 0) 0)
|
| [5] |
蒲兴成, 赵红全, 张毅. 细菌趋化行为的移动机器人路径规划[J]. 智能系统学报, 2014, 9(1): 69-75. PU Xingcheng, ZHAO Hongquan, ZHANG Yi. Mobile robot path planning research based on bacterial chemotaxis[J]. CAAI transactions on intelligent systems, 2014, 9(1): 69-75. (  0) 0)
|
| [6] |
KAPANOGLU M, ALIKALFA M, OZKAN M, et al. A pattern-based genetic algorithm for multi-robot coverage path planning minimizing completion time[J]. Journal of intelligent manufacturing, 2012, 23(4): 1035-1045. DOI:10.1007/s10845-010-0404-5 ( 0) 0)
|
| [7] |
杜鹏桢, 唐振民, 陆建峰, 等. 不确定环境下基于改进萤火虫算法的地面自主车辆全局路径规划方法[J]. 电子学报, 2014, 42(3): 616-624. DU Pengzhen, TANG Zhenmin, LU Jianfeng, et al. Global path planning for ALV based on improved glowworm swarm optimization under uncertain environment[J]. Acta electronica sinica, 2014, 42(3): 616-624. (  0) 0)
|
| [8] |
BALCH T. The case for randomized search[C]//Proceedings of Workshop on Sensors and Motion, IEEE International Conference on Robotics and Automation. San Francisco, CA: IEEE Press, 2000: 213–215.
( 0) 0)
|
| [9] |
HABIB M A, ALAM M S, SIDDQUE N H. Optimizing coverage performance of multiple random path-planning robots[J]. Paladyn, 2012, 3(1): 11-22. ( 0) 0)
|
| [10] |
JIN Xin, GUPTA S, LUFF J M, et al. Multi-resolution navigation of mobile robots with complete coverage of unknown and complex environments[C]//Proceedings of 2012 American Control Conference. Montreal: IEEE Press, 2012: 4867–4872.
( 0) 0)
|
| [11] |
YAZICI A, KIRLIK G, PARLAKTUNA O, et al. A dynamic path planning approach for multirobot sensor-based coverage considering energy constraints[J]. IEEE transactions on cybernetics, 2014, 44(3): 305-314. DOI:10.1109/TCYB.2013.2253605 ( 0) 0)
|
| [12] |
HSU P M, LIN Chunliang, YANG Mengyao. On the complete coverage path planning for mobile robots[J]. Journal of intelligent and robotic systems, 2014, 74(3/4): 945-963. ( 0) 0)
|
| [13] |
邱雪娜, 刘士荣, 宋加涛, 等. 不确定动态环境下移动机器人的完全遍历路径规划[J]. 机器人, 2006, 28(6): 586-592. QIU Xuena, LIU Shirong, SONG Jiatao, et al. A complete coverage path planning method for mobile robots in uncertain dynamic environments[J]. Robot, 2006, 28(6): 586-592. (  0) 0)
|
| [14] |
GUO Yi, BALAKRISHNAN M. Complete coverage control for nonholonomic mobile robots in dynamic environments[C]//Proceedings of 2006 IEEE International Conference on Robotics and Automation. Orlando, FL, USA: IEEE Press, 2006: 1704–1709.
( 0) 0)
|
| [15] |
YANG S X, LUO Chaomin. A neural network approach to complete coverage path planning[J]. IEEE transactions on systems, man, and cybernetics, part B: cybernetics, 2004, 34(1): 718-724. DOI:10.1109/TSMCB.2003.811769 ( 0) 0)
|
| [16] |
LUO Chaomin, YANG S X. A bioinspired neural network for real-time concurrent map building and complete coverage robot navigation in unknown environments[J]. IEEE transactions on neural networks, 2008, 19(7): 1279-1298. DOI:10.1109/TNN.2008.2000394 ( 0) 0)
|
| [17] |
YAN Mingzhong, ZHU Daqi, YANG S X. Complete coverage path planning in an unknown underwater environment based on D-S data fusion real-time map building[J]. International journal of distributed sensor networks, 2012, 2012: 567959. DOI:10.1155/2012/567959 ( 0) 0)
|
| [18] |
朱大奇, 颜明重. 移动机器人路径规划技术综述[J]. 控制与决策, 2010, 25(7): 961-967. Zhu Daqi, Yan Mingzhong. Survey on technology of mobile robot path planning[J]. Control and decision, 2010, 25(7): 961-967. (  0) 0)
|
| [19] |
LEE T K, BAEK S H, CHOI Y H, et al. Smooth coverage path planning and control of mobile robots based on high-resolution grid map representation[J]. Robotics and autonomous systems, 2011, 59(10): 801-812. DOI:10.1016/j.robot.2011.06.002 ( 0) 0)
|
| [20] |
欧阳鑫玉, 杨曙光. 基于势场栅格法的移动机器人避障路径规划[J]. 控制工程, 2014, 21(1): 134-137. OUYANG Xinyu, YANG Shuguang. Obstacle avoidance path planning of mobile robots based on potential grid method[J]. Control engineering of china, 2014, 21(1): 134-137. (  0) 0)
|
| [21] |
郝宗波, 洪炳镕, 黄庆成. 基于栅格地图的机器人覆盖路径规划研究[J]. 计算机应用研究, 2007, 24(10): 56-58. HAO Zongbo, HONG Bingrong, HUANG Qingcheng. Study of coverage path planning based on grid-map[J]. Application research of computers, 2007, 24(10): 56-58. DOI:10.3969/j.issn.1001-3695.2007.10.016 (  0) 0)
|
| [22] |
SIPAHIOGLU A, KIRLIK G, PARLAKTUNA O, et al. Energy constrained multi-robot sensor-based coverage path planning using capacitated arc routing approach[J]. Robotics and autonomous systems, 2010, 58(5): 529-538. DOI:10.1016/j.robot.2010.01.005 ( 0) 0)
|
 2018, Vol. 13
2018, Vol. 13


