随着遥感技术的飞速发展，利用卫星遥感和飞机遥感等方式实时获取的地物图像质量也越来越高。从人工地物的遥感图像中提取信息，可以避免传统的实地勘测，大大提高工作效率。城区作为遥感图像中一类重要的人工地物目标，其自动提取在城市规划、地理信息系统更新、数字化城市以及军事侦察等实际领域均有重要的应用^[1-3]。遥感图像分割是遥感图像处理中最为基础和关键的环节之一，是对图像进行分析和识别的前提，对图像描述和特征测量有重要的影响^[4]。

阈值分割是一类常用的遥感图像分割方法，因其简单快速和易于实现，成为研究热点^[5-6]。该方法主要是依据直方图的概率分布计算相应的准则函数，同时运用智能优化算法加快阈值搜索速度，从而选取合适的阈值进行分割。其中基于熵的方法最受关注，主要包含最大熵法^[7]、最大指数熵法^[8]和最小交叉熵法^[9]等。城区遥感图像通常由密集的建筑物群、草坪树丛、湖泊河流以及贯穿其中的道路交通网所构成。对含有灰度值位于明显不同区间的多类目标的图像进行分割时，采用单阈值分割方法无法取得令人满意的效果^[10]。而模糊聚类法一般是根据特定的相似性度量方式和隶属度准则函数，实现对多类目标的分割^[11]。但该算法针对样本量较大、内容复杂的图像，尤其是对高空间分辨率遥感图像，所需的运行时间远远超过阈值分割法。因此，为了提高城区遥感图像的分割精度和速度，可以考虑将基于熵的单阈值选取推广到多阈值的情况，以此对城区遥感图像进行多阈值分割。

在单阈值选取中，文献[12]提出的直方图最大熵阈值分割方法简单、易操作、效果较好，一经提出就受到关注，并被推广到多阈值分割^[13]。然而在该类方法中采用的对数熵在零点处存在无定义值的问题，且其计算仅仅依赖于直方图的分布情况，没有顾及图像中目标和背景区域内灰度的均匀性。为了克服这一缺点，文献[14]定义了倒数灰度熵，并由此提出了倒数灰度熵阈值分割方法，弥补了零点处无定义值及不能反映类内灰度均匀性的缺陷，能获得更好的分割效果。但目前基于熵的多阈值分割方法大多只利用了图像的一维灰度级信息，抗噪性能差。为此，二维直方图被应用到多阈值分割上，增强了方法的抗噪能力^[15]。但由于利用了图像的灰度级——邻域平均灰度级直方图，增加了算法的复杂度，导致占用的内存空间剧增，运行速度大大降低，使得基于二维熵的多阈值分割方法无法满足实时性的要求，适用范围受到限制。另外，若采用传统穷举算法搜索最优多阈值，其运算量会随所需分割的处于不同灰度区间的目标种类数量增多呈指数形式增长。为了保证方法的实时性，条件迭代^[16]、遗传^[17]、粒子群^[18]等优化算子被引入，以此对多阈值选取方法进行加速，一定程度上缩短了所需的运行时间。其中，粒子群优化算法(particle swarm optimization, PSO)操作简单、搜索速度较快，但在搜索过程中易陷入局部极值，且在进化后期阶段收敛精度较低、速度较慢^[19]。而近年来提出的人工蜂群优化算法(artificial bee colony optimization, ABC)具有计算简单、收敛速度快、需要调整参数少等优点^[20]，有望进一步提高阈值搜索的准确性和实时性。

基于上述分析，本文提出了一种基于直线截距直方图倒数灰度熵和人工蜂群优化的城区遥感图像多阈值分割方法。该方法依据遥感图像中各个像素点的灰度级——邻域平均灰度级联合信息，建立该图像的直线截距直方图，并将倒数灰度熵的单阈值选取准则运用到此直方图中，将此推广得到基于直线截距直方图的多阈值选取公式，再利用人工蜂群优化算法，搜索最优多阈值，以此对城区遥感图像进行分割。针对大量城区遥感图像进行实验，并与近年来提出的改进核模糊C均值聚类(kernel fuzzy C means clustering, KFCM)分割法^[11]、基于粒子群优化的指数熵单、多阈值分割法^[18]以及本文提出的单阈值分割法进行了对比，给出了相应的评价，验证了本文方法的优越性。

1 直线截距直方图

对于一幅大小为 $M \times N$ 、灰度级数为 $L$ 的图像， $f(m, n)$ 表示图像中像素点 $\left( {m, n} \right)$ 的灰度级， $f\left( {m,n} \right) \in $ $ \left[ {0,1, \cdots \! ,L - 1} \right]$ ； $g\left( {m, n} \right)$ 表示其邻域平均灰度级， $g\left( {m,n} \right) \in $ $ \left[ {0,1, \cdots \! ,L - 1} \right]$ 。

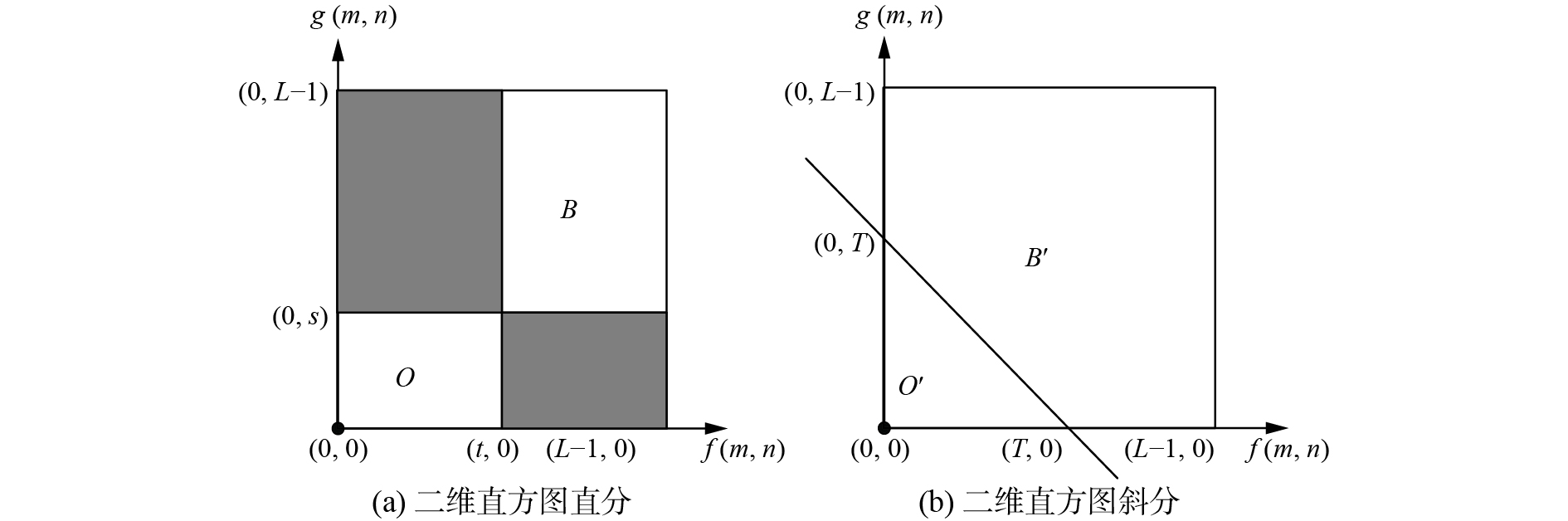
现有的二维直方图划分方式通常分为直分和斜分两种，如图1所示。

其中直分法依据相互垂直的两条直线，将二维直方图分为4个区域。一般情况下，假设边缘和噪声区域(图1(a)中阴影部分)的概率分布为零，则目标、背景对应图1(a)中的区域O、区域B。但因忽略了阴影部分，分割结果的准确性有所下降。鉴于此，为了使图像分割更加准确，斜分法随后被提出^[21]，由于其对阈值的搜索空间仍为二维，运行速度有待进一步的提升。该方法，如图1(b)所示，通过在二维直方图中确定一条与主对角线垂直的以 $T$ 为截距的阈值直线，将直方图区域分为目标(O′)和背景(B′)两个部分。从图1中可以看出，二维直方图中共有2L–1条阈值直线。实际上由于斜分法划分直方图时，阈值直线的斜率是固定的^[22-23]，只要确定该直线的截距，该直线即被唯一确定，则可将整个二维直方图区域向其对角线方向做投影，以此得到该图像的直线截距直方图。

令 $f\left( {m, n} \right) + g\left( {m, n} \right) = F\left( {m, n} \right)$ ，现以一幅城区遥感图像(图2(a), 1 111像素×741像素)为例，建立其直线截距直方图的基本思路如下：1)将原始城区遥感图像进行灰度化处理，得到灰度图像 $f\left( {m, n} \right)$ (图2(b))；2)以 $f\left( {m, n} \right)$ 为依据求遥感图像中像素点的邻域平均灰度级大小，得到其邻域平均灰度图像 $g\left( {m, n} \right)$ (图2(d))；3)对灰度图像和邻域平均灰度图像分别进行直方图统计，得到其灰度级直方图(图2(c))和邻域平均灰度级直方图(图2(e))；(4)将灰度图像 $f\left( {m, n} \right)$ 与其邻域平均灰度图像 $g\left( {m, n} \right)$ 叠加，则叠加后的 $F\left( {m, n} \right)$ 可以看作一幅大小 $M \times N$ 、灰度级数 $2L$ 的灰度+邻域平均灰度图像。据此，对 $F\left( {m, n} \right)$ 进行灰度直方图统计，得到城区遥感图像的直线截距直方图(图2(f))。

基于上述分析可知，利用斜分法获取最优阈值的过程可转化为在直线截距直方图的基础上，选取合适的阈值选取准则，求解最优截距阈值的过程。以此有望在保证分割结果准确性的同时，将阈值搜索空间由二维转化为一维，进一步提高斜分法的运行速度。

2 基于直线截距直方图倒数灰度熵和人工蜂群优化的多阈值选取 2.1 基于直线截距直方图倒数灰度熵的多阈值选取

设一幅城区遥感图像中像素 $(m, n)$ 的灰度级为 $f(m, n)$ ，其邻域平均灰度级为 $g\left( {m, n} \right)$ ， $h\left( k \right)$ 为该图像中满足 $F\left( {m, n} \right) = f\left( {m, n} \right) + g\left( {m, n} \right) = k$ 的像素点频数。

设图1(b)中阈值直线左下方的区域为目标区域，阈值直线右上方的区域为背景区域。则可以用阈值 $T$ 将该城区遥感图像按灰度级 $F\left( {m, n} \right)$ 分为目标类 ${\varOmega _{{o}}}$ 和背景类 ${\varOmega _{{b}}}$

${\varOmega _{{o}}} = \left\{ {\left( {m,n} \right){{|}}F\left( {m,n} \right) = 0,1, \cdots \! ,T} \right\}$ ， ${\varOmega _{{b}}} = \left\{ {\left( {m,n} \right){{|}}F\left( {m,n} \right) = T + 1,T + 2, \cdots \! ,2L - 1} \right\}$

并设

${P_{m,n}} = \left\{ {\begin{array}{*{20}{c}}{\displaystyle\frac{{F(m,n)}}{{\displaystyle\sum\limits_{(x,y) \in {\varOmega _{{o}}}} {F(x,y)} }},\quad (m,n) \in {\varOmega _{{o}}}}\\[20pt]{\displaystyle\frac{{F(m,n)}}{{\displaystyle\sum\limits_{(x,y) \in {\varOmega _{{b}}}} {F(x,y)} }},\quad (m,n) \in {\varOmega _{{b}}}}\end{array}} \right.$

(1)

则基于直线截距直方图的城区遥感图像的总倒数灰度熵 $E(T)$ 为

$\begin{array}{c} E(T) = {E_{{o}}} + {E_{{b}}} = \\[3pt] \displaystyle\sum\limits_{(m, n) \in {\varOmega _{{o}}}} {{P_{m, n}}} \frac{1}{{1 + {P_{m, n}}}} + \sum\limits_{(m, n) \in {\varOmega _{{o}}}} {{P_{m, n}}} \frac{1}{{1 + {P_{m, n}}}} = \\[12pt] \displaystyle \sum\limits_{k = 0}^T {h(k)\frac{k}{{k + {u_{{o}}}(T)}}} + \sum\limits_{k = T + 1}^{2L - 1} {h(k)\frac{k}{{k + {u_{{b}}}(T)}}} \\ \end{array} $

(2)

式中： ${E_{{o}}}$ 和 ${E_{{b}}}$ 分别表示目标、背景区域的倒数灰度熵， ${u_{{o}}}(T) = \displaystyle\sum\limits_{k = 0}^T {h{{(}}k{{)}}k} $ ， ${u_{{b}}}(T) = \displaystyle\sum\limits_{k = T + 1}^{2L - 1} {h{{(}}k{{)}}k} $ ，其可以反映目标、背景区域的类内灰度均匀性。当总倒数灰度熵 $E(T)$ 取最大时，表明目标区域内像素灰度级大小差异与背景区域内像素灰度级东西差异之和最小，即图像分割的效果最理想，此时对应的灰度级阈值 ${T^*}$ 即为最优阈值。

${T^*} = \arg \mathop {\max }\limits_{0 \leqslant T \leqslant 2L - 1} \{ E(T)\} $

(3)

可根据此最优阈值 ${T^*}$ 对城区遥感图像进行单阈值分割：

$f'(m, n) = \left\{ \begin{gathered} 0, \;\;\;\;f\left( {m, n} \right) + g\left( {m, n} \right) \leqslant {T^*} \hfill \\ L - 1, \;\;\;f\left( {m, n} \right) + g\left( {m, n} \right) > {T^*} \hfill \\ \end{gathered} \right.$

(4)

若图像中只含有单类目标或多类目标区域与其他区域的灰度级差异较明显时，采用单阈值选取方法是有效的。但是实际上，城区遥感图像中可能含有植被、道路、湖泊河流、建筑区域等多类目标，且各目标的灰度值也有差异。因此，现将式(2)推广，以 $N$ 个阈值 ${T_1},{T_2}, \cdots \! ,{T_N}$ $(0 \leqslant {T_1} < {T_2} \cdots < {T_N} < 2L - 1)$ 将城区遥感图像分成 $N + 1$ 个灰度级区间。

设 $u(0, {T_1}) =\!\!\! \displaystyle\sum\limits_{k = 0}^{{T_1}} {h(k)k} $ ， $u({T_{q - 1}} + 1, {T_q}) =\!\!\! \displaystyle\sum\limits_{j = {T_{q - 1}}}^{{T_q}} {h(k)k}, q =$ $ 2, 3, \cdots \!, N$ ， $u({T_N} + 1, 2L - 1) = \!\!\! \displaystyle\sum\limits_{k = {T_N} + 1}^{2L - 1} {h(k)k} $ ，则基于直线截距直方图的城区遥感图像的总倒数灰度熵 ${E_M}\left( {{T_1},} \right.$ $\left. {{T_2}, \cdots ,{T_N}} \right)$ 为

$\begin{array}{c} {E_{{M}}}({T_1}, {T_2}, \cdots, {T_N}) = \\ \displaystyle\sum\limits_{k = 0}^{{T_1}} {\frac{{h(k)k}}{{u(0, {T_1}) + k}}} + \sum\limits_{k = {T_1} + 1}^{{T_2}} {\frac{{h(k)k}}{{u({T_1} + 1, {T_2}) + k}}} + \cdots + \\ \displaystyle\sum\limits_{k = {T_{N - 1}} + 1}^{{T_N}} {\frac{{h(k)k}}{{u({T_{N - 1}} + 1, {T_N}) + k}}} + \sum\limits_{k = {T_N} + 1}^{2L - 1} {\frac{{h(k)k}}{{u({T_N} + 1, 2L - 1) + k}}}\end{array} $

(5)

${E_{{M}}}({T_1},{T_2}, \cdots \! ,{T_N})$ 的值越大，意味着城区遥感图像中同一类区域内像素点灰度级的差值越小。当总倒数灰度熵 ${E_{{M}}}({T_1}, {T_2}, \cdots \!, {T_N})$ 最大时，此时的 $N$ 个阈值即为最优多阈值，即基于直线截距直方图的倒数灰度熵多阈值选取公式为

$({T_1}^*,{T_2}^*, \cdots ,{T_N}^*) = \mathop {\arg \max \left\{ {{E_{{M}}}({T_1},{T_2}, \cdots ,{T_N})} \right\}}\limits_{0 \leqslant {T_1} < {T_2} < \cdots < {T_N} < 2L - 1} $

(6)

另外，为了进一步缩短阈值选取的时间，本文采用人工蜂群算法对多阈值的搜索进行优化。

2.2 多阈值选取的人工蜂群优化算法

人工蜂群算法是受蜂群觅食行为启发建立的群智能优化算法，主要由以下3部分循环迭代：

1)引领。引领蜂的总数设为S_L，每只引领蜂对应1个食物源的位置，在目标函数的可行域中任意取值，本文采用适应度函数 $F({X_i})$ 对食物源的花蜜收益度进行评价

$F({X_i}) = \left\{ {\begin{array}{*{20}{c}}{\displaystyle\frac{1}{{1 - {E_{{M}}}({T_1},{T_2}, \cdots \! ,{T_N})}},\quad {E_{{M}}}({T_1},{T_2}, \cdots \! ,{T_N}) \leqslant 0}\\[7pt]{1 + |{E_{{M}}}({T_1},{T_2}, \cdots ,{T_N})|,\quad {E_{{M}}}({T_1},{T_2}, \cdots ,{T_N}) > 0}\end{array}} \right.$

(7)

式中： ${X_i}(i = 1,2, \cdots \! ,{S_{{L}}})$ 表示第i个引领蜂的位置，即对应的可能解。在评估当前食物源收益情况的同时，每只引领蜂会观察周围的食物，并在附近随机搜索另一个食物源

${Z_i} = {X_i} + \varepsilon ({X_i} - {X_l})$

(8)

式中: $\varepsilon $ 是范围在 $[-1, \;1]$ 的随机数， ${X_l}$ 表示第 $l(l \ne i)$ 个引领蜂的位置。在当前食物源和随机搜索的食物源之间，引领蜂依据适应度值择优选取。

2)观察。引领蜂经过对食物源的初步探索，向观察蜂发出信号，信号强弱由引领蜂所在食物源的花蜜收益度确定，观察蜂依据信号强弱比例以概率P_i选取所要跟随的引领蜂

${P_i} = \frac{{F({X_i})}}{{\displaystyle\sum\limits_{j = 1}^{{S_L}} {F({X_j})} }}$

(9)

式中： ${X_j}$ 表示第 $j$ 个引领蜂的位置。

在所跟随引领蜂的周围，观察蜂随机搜索另一个食物源，搜索方式同样依照式(7)。然后将该食物源信息传达给引领蜂，引领蜂再次依据适应度值飞到较优的那个位置。

3)侦查。侦查蜂是引领蜂的变种，当引领蜂陷入局部极值时，该引领蜂将会变为侦查蜂，对新的位置进行搜索，以跳出该局部最优解。

通过上述3个部分的循环迭代，可搜索到全局最优解，即基于直线截距直方图的倒数灰度熵最优多阈值。

3 方法步骤与流程图

本文提出的基于直线截距直方图倒数灰度熵和人工蜂群优化的城区遥感图像多阈值分割方法的基本思路为：根据图像像素点的二维信息，建立一维直线截距直方图，并通过人工蜂群算法对最大倒数灰度熵多阈值选取进行优化，从而完成城区遥感图像的多阈值分割。本文方法的流程图如图3所示。

1) 输入待分割城区遥感图像，设置蜂群的种群规模为10 (引领蜂和观察蜂分别占据一半)。ABC算法的最大迭代次数 ${C_{{M}}}$ 为10，判断局部极值的条件为当前循环次数 ${C_{{L}}} \geqslant 3$ 。将引领蜂位置 ${X_i}(i = 1,2, \cdots \! ,$ $5)$ 初始化，并依据式(7)计算每个位置的适应度函数值。

2) 引领蜂按照式(8)更新位置 ${Z_i}$ ，若 ${Z_i}$ 的适应度优于当前 ${X_i}$ 的适应度，则将 ${Z_i}$ 替代 ${X_i}$ 。

3) 引领蜂发出的信号，观察蜂通过信号择优选择部分引领蜂进行跟随，并在所选引领蜂周边随机探查一个新的食物源。再比较两者的适应度值，将适应度值高的位置赋值给 ${X_i}$ 。

4) 如果引领蜂在 ${C_{{L}}}$ 次循环中食物源位置不变，则该引领蜂变为侦查蜂，搜索新的解取代 ${X_i}$ 。

5) 在一次循环迭代结束时，该循环的最优解将会被记录下来，循环次数加1。

6) 当循环次数达到 ${C_{{M}}}$ 时，运算停止，所得解即为本文方法的最优多阈值，以此对城区遥感图像进行分割，否则跳到3)。

4 实验结果与分析

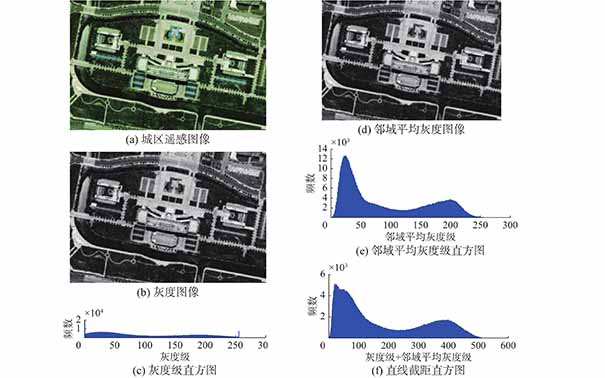
利用本文提出的基于直线截距直方图的倒数灰度熵和人工蜂群优化的多阈值分割方法对大量城区遥感图像进行了实验，并与文献[11]提出的改进KFCM聚类分割法、文献[18]提出的基于PSO的指数熵单阈值分割法、基于PSO的指数熵多阈值分割法、本文提出的单阈值分割法在分割效果和运行时间等方面进行了比较。实验中，KFCM聚类数目为3；PSO中的粒子个数为30，最大迭代次数为100；ABC中的蜂群种群规模为10，最大迭代次数为10，局部循环最大次数为3。实验运行环境为Intel(R) Core(TM) i5 CPU 2.0 GHz、2GB RAM、MATLAB R2013a。因篇幅限制，现以其中大小不一、特点不同的3幅城区遥感图像为例说明本文方法的性能，分别为城区遥感图像1 (219像素×221像素)、城区遥感图像2 (249像素×305像素)、城区遥感图像3 (2 499像素×2 393像素)。图4～6中的(a)和(i)为分别为这3幅城区遥感图像的原始图像及其直线截距直方图，(b)～(h)图分别为采用KFCM、基于PSO的指数熵单阈值、基于PSO的指数熵多阈值(双阈值、三阈值)、本文方法单阈值、本文方法多阈值(双阈值、三阈值)等5种方法所得到的3幅遥感图像的分割结果。

城区遥感图像1主要含有建筑物、河流、道路等多类目标，基于熵的单阈值分割法中，本文提出的单阈值法的效果较好，然而利用单一的阈值难以有效地将多类目标区分出来。基于PSO的指数熵单阈值分割法所得结果的误分割率很高，其中的建筑物、道路连成一片，完全丢失各自的特征，且存在严重的欠分割，目标背景均无法辨识。KFCM聚类分割法和基于PSO的指数熵多阈值分割法在一定程度上改善了分割效果，但是相比本文提出的多阈值分割法，其结果中目标边缘粗糙，河流区域灰度不均匀，且含有部分噪声斑。

城区遥感图像2反映的是建筑物群呈块状分布且相对集中，其余部分较为空旷的城市区域，道路、草坪等多类目标的灰度值较为相近。基于PSO的指数熵单阈值和双阈值分割法，能较为准确地将建筑物与地面区分开，但却无法提取道路、草坪等其他多类目标，分割后图像的大量细节信息丢失，这势必影响后续的地物目标检测。本文提出的单阈值和多阈值选取方法获得了很好的分割效果，其中，相比于单阈值方法，本文提出的多阈值选取方法的分割结果中，多类目标边缘完整、特征鲜明。KFCM聚类分割法和基于PSO的指数熵三阈值分割法的分割结果受噪声干扰，有少许虚警点，且存在目标模糊和边缘残缺的现象，如图中右下角建筑物的阴影信息被湮没。

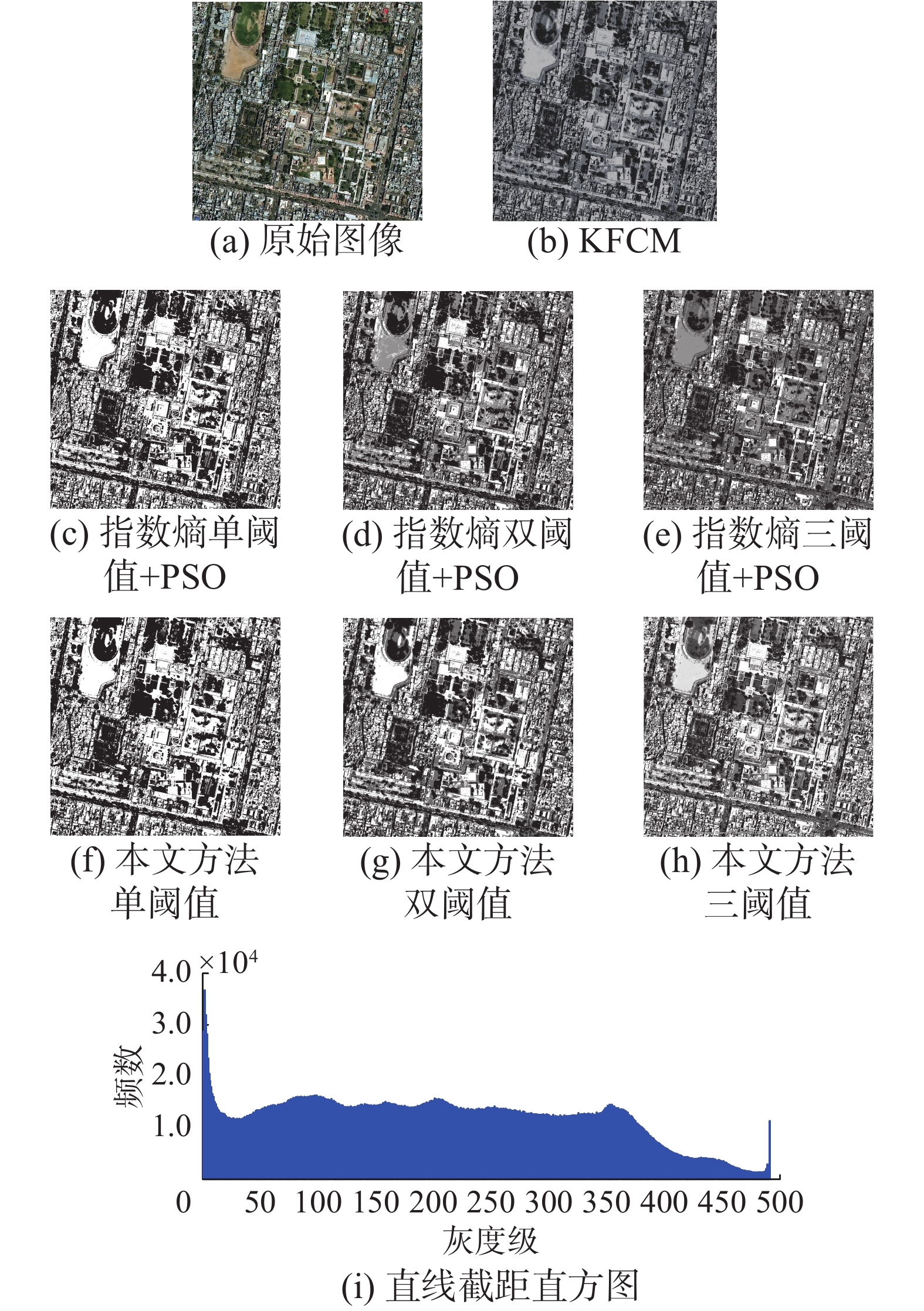
城区遥感图像3中建筑物密集，道路网交织，且有多处草坪、树丛覆盖，具有较高的复杂度。由分割结果可以看出，对于此类图像而言，基于熵的单阈值分割法虽能较为准确地将建筑物与背景分离，但却无法准确地提取其他目标的边界形状。采用KFCM聚类分割法和基于PSO的指数熵多阈值分割法时，背景地面的边界轮廓不清晰，对位于图像中间的树丛区域分割不准确，含有大量阴影。而本文提出的基于直线截距直方图倒数灰度熵和人工蜂群优化的三阈值分割法则能较为准确地提取建筑物的边界形状，草坪、道路网和树丛的轮廓均清晰可辨，且树丛的纹理、边缘和细节特征更为丰富。这是由于倒数灰度熵同时考虑了图像中目标区域和背景区域内的灰度均匀性，对纹理丰富的区域分割效果更优。

下面再根据正确分割率对5种方法的分割效果进行定量评价。以人工分割结果为标准，这里正确分割率定义为正确分割像素数目与像素总数的比值，正确分割像素数目是指分割后的图像与经人工精确分割后的图像相比存在差异的像素个数。正确分割率越大，表示分割结果越准确。表1所示为上述5种方法的正确分割率比较。从表中可以看出，本文方法的正确分割率最大，即分割效果最优。

上述主观视觉效果分析和客观定量评价指标两方面均表明，无论是针对灰度层次较简单的图像(如图5(a))，还是针对纹理细节丰富、数据量较大的图像(如图6(a))，与KFCM聚类分割法、基于熵的单阈值分割法、基于PSO的指数熵多阈值分割法相比，本文提出的基于直线截距直方图倒数灰度熵和人工蜂群优化的多阈值分割方法在分割效果上均有明显的优势。

表2给出了基于PSO的指数熵单阈值、多阈值分割方法与本文提出的基于直线截距直方图倒数灰度熵和人工蜂群优化的单阈值、多阈值分割方法的最优阈值比较，可以看出基于PSO的指数熵单阈值、多阈值分割方法是建立于一维灰度级直方图的基础上，最优阈值的范围为(0, 255)。而本文方法是建立于直线截距直方图的基础上，同时考虑了灰度级和邻域平均灰度级信息，最优阈值的范围为(0, 511)。

表3为5种分割方法所需的运行时间对比。从表中可以看出，KFCM聚类分割法的运行时间受图像大小影响严重，针对数据量大的图像，分割时间过长，无法满足实时性的要求。而本文提出的单阈值方法耗时最少，但从上述对分割效果的分析可知，其分割效果欠佳。本文提出的多阈值分割法的耗时与基于PSO的指数熵单阈值分割法相当，而与基于PSO的指数熵多阈值分割法相比，仅为其运行时间的25%。这主要是由于本文方法是基于灰度级、邻域平均灰度级联合信息所建立的一维直线截距直方图，将原有的阈值搜索空间由二维转化为一维，减小了运算量，缩短了所需运行时间，且采用ABC优化算法加速了最优多阈值的搜索过程。综上所述，本文提出的多阈值分割方法在进一步改善分割效果的同时，大幅度提高了方法的运行速度。

5 结束语

本文提出的基于直线截距直方图倒数灰度熵和ABC的多阈值分割方法，以城区遥感图像像素的二维联合信息为基础建立直线截距直方图，以此将阈值搜索空间转化为一维。另一方面，以倒数灰度熵作为城区遥感图像的阈值选取准则函数，并采用ABC算法对最优阈值的搜寻进行优化，大大减少了方法的运行时间。本文方法是对基于熵理论的城区遥感图像分割技术的进一步扩展和补充。实验结果表明，与KFCM聚类分割法、基于PSO的指数熵阈值分割法等进行对比，在主观视觉效果和客观评价指标两个方面，证明了本文方法的准确性和实时性。本文提出的方法，已应用于地物识别中的城区、建筑物分割，取得了极佳的分割效果。