人脸表情识别技术是生理学、心理学、图像处理、模式识别和计算机视觉等领域的一个具有挑战性的交叉学科^[1]。为了确保信息的完整性，研究人员们使用不存在遮挡人脸表情图像在受控的实验室条件下进行实验和研究^[2]。然而，人脸遮挡在现实生活中很常见，例如，太阳镜可以遮挡眼睛区域、一条围巾或外科口罩遮挡嘴部区^[3]。因此，在人脸存在遮挡的表情识别仍然是人脸表情识别系统在实际应用中最重要的瓶颈之一。

近年来，针对部分遮挡人脸表情识别，研究人员已经提出了许多方法来减少遮挡对表情识别的影响。Kotsia等^[4]受Fisher的线性判别分析和支持向量机(support vector machine，SVM)的启发，提出了一种新颖的最小类内方差的多类分类器来研究在不同人脸器官遮挡的情况下对人脸表情识别的影响。Tarrés等^[5]提出了基于PCA(principal component analysis)和LDA(linear discriminant analysis)，并结合直方图均衡化和均值、方差归一化预处理的方法，减少了遮挡部分对人脸识别过程的影响。Kotsia等^[6]对遮挡的人脸图像进行Gabor小波滤波提取纹理特征，利用监督的判别非负矩阵因子分解(discriminant non-negative matrix factorization，DNMF)进行图像分解，再采用基于模型的方法来描述特定面部特征的几何位移来完成遮挡图像的特征表征。Zhang等^[7]利用蒙特卡罗算法对表情图像提取Gabor特征，并遍历表情图像的每个区域进行模板匹配以产生对遮挡具有鲁棒性的特征向量。Wang等^[8]利用改进的中心对称局部二值模式和梯度中心对称局部方向模式GCS-LDP，利用卡方距离求取测试集图像与训练集图像特征直方图之间的距离。但是，上述方法主要研究眼部遮挡和嘴部遮挡对人脸表情识别效果的影响，没有充分考虑遮挡在现实生活中出现的特点，对随机遮挡情况的适应性较弱。人脸遮挡的特点是遮挡可以在人脸的任何地方发生，并且遮挡范围的大小和遮挡的形状都是未知的，没有任何关于它的先验知识^[9]。因此，不能只考虑脸部某个区域对人脸表情识别的影响情况，应该根据遮挡的特点来展开研究，并提出一些可以克服这个问题的方法。Wright等^[10]采用稀疏编码方法完成人脸识别任务，并提出使用已知类别的训练人脸图像对测试人脸图像进行稀疏表示的方法，在随机遮挡人脸识别系统中取得了较为理想的识别效果。M. Zhu等^[11]利用稀疏分解求出待测图像的稀疏表示系数，并在待测图像所在的子空间内实现表情类别判断，该方法使待测图像的分解系数变得更稀疏，同时避免身份特征对表情分类的干扰。

为了提高稀疏表示的鲁棒性和有效性，本文提出了基于鲁棒的正则化编码和自动更新权重的随机遮挡表情识别方法。受鲁棒回归理论的启发^[10]，即通过自适应地不断迭代的方法来给残差分配不同的权重，直到估计过程收敛。本文通过假设编码残差和编码系数分别是独立同分布的，并基于最大后验估计的原则来对给定的信号进行鲁棒回归，为了方便实现，正则化编码的最小化问题将转换成一个自动更新权重的问题，通过设计合理的权重函数可以鲁棒地识别出遮挡部分从而减小它们对编码过程的影响。在JAFFE和Cohn-Kanade数据库上，本文方法对随机遮挡表情识别的鲁棒性进行了验证，取得了较理想的识别效果。

1 鲁棒的正则化编码

通常情况下，稀疏编码问题可以定义为

${\hat{ \alpha }} = \arg \min {\left\| {{\alpha }} \right\|_1}{{s.t}}.\left\| {{{y}} - {{T\alpha }}} \right\|_2^2 \leqslant \varepsilon $

(1)

式中： ${{y}}$ 是待测的表情图像, ${{T}}$ 是训练表情图像字典， ${{\alpha }}$ 是待测的表情图像 ${{y}}$ 在训练表情图像字典 ${{T}}$ 上的编码向量,并且ε>0。保真项定义为 $\left\| {{{y}} - {{T\alpha }}} \right\|_2^2$ 。

如果事先假设编码残差 ${{e}} = {{y}} - {{T\alpha }}$ 服从高斯分布，式(1)的解将变成最大似然估计的解，如果 ${{e}}$ 服从拉普拉斯分布，l₁稀疏限制的最大似然估计解变为 ${\hat{ \alpha }} = \arg \min {\left\| {{\alpha }} \right\|_1}{{s.t.}}{\left\| {{{y}} - {{T\alpha }}} \right\|_{{1}}} \leqslant \varepsilon $ 。

其实， ${\hat{ \alpha }} = \arg \min {\left\| {{\alpha }} \right\|_1}{{s.t.}}{\left\| {{{y}} - {{T\alpha }}} \right\|_{{1}}} \leqslant \varepsilon $ 是式(1)的另一种表现形式，因为它们都具有相同的拉格朗日公式： $\arg \min \left\{ {{{\left\| {{\alpha }} \right\|}_1} + \lambda {{\left\| {{{y}} - {{T\alpha }}} \right\|}_1}} \right\}$ 。

在实际应用中这种假设是不成立的，尤其是当人脸表情图像 ${{y}}$ 被遮挡时。为了构建一个鲁棒性更强的人脸表情图像的稀疏编码模型，本文提出了一个更通用的而且效率更高的鲁棒正则化编码模型。

1.1 鲁棒的正则化编码模型

贝叶斯估计的观点确切地说是从最大后验概率估计观点考虑人脸表示的问题。通过字典 ${{T}}$ 对待测表情图像 ${{y}}$ 进行编码，编码向量 ${{\alpha }}$ 的最大后验概率估计变成 ${\hat{ \alpha }} = \arg \max \ln P\left( {{{\alpha }}|\left. {{y}} \right)} \right.$ 。利用贝叶斯公式得

${\hat{ \alpha }} = \arg \max \left\{ {\ln P\left( {{{y}}|\left. {{\alpha }} \right) + \ln P\left( {{\alpha }} \right)} \right.} \right\}$

(2)

将式(1)中的字典 ${{T}}$ 改写成 ${{T}} = \left[ {{{{r}}_{{1}}};{{{r}}_{{2}}}; \cdots ;{{{r}}_{{n}}}} \right]$ ，其中， ${{{r}}_{{i}}}$ 表示 ${{T}}$ 的第 $i$ 列，而且 ${{e}} = {{y}} - {{T\alpha }} = \left[ {{{{e}}_{{1}}};{{{e}}_{{2}}}; \cdots; {{{e}}_{{n}}}} \right]$ ，其中， ${{{e}}_{{i}}} = {{{y}}_{{i}}} - {{{r}}_{{i}}}{{\alpha }},i = 1,2, \cdots ,n$ 。假设元素 ${{{e}}_{{i}}}$ 是独立同分布的，并且概率密度函数为 ${f_\theta }\left( {{{{e}}_{{i}}}} \right)$ ，而且 $P\left( {{{y}}|\left. {{\alpha }} \right)} \right. = \displaystyle\prod\limits_{i = 1}^n {{f_\theta }} \cdot$ $ ( {{y}}_{{i}}-{{r}}_{{i}}{{\alpha }}) $ 。

与此同时，假设编码向量 ${{\alpha }} = \left[ {{\alpha _1};{\alpha _2}; \cdots ;{\alpha _m}} \right]$ 中的元素 ${{{\alpha }}_{{j}}},j = 1,2, \cdots ,m$ 是独立同分布的并且概率密度函数为 ${f_0}\left( {{{{\alpha }}_{{j}}}} \right)$ ，而且 $P\left( {\left. {{\alpha }} \right)} \right. = \displaystyle\prod\limits_{j = 1}^m {{f_0}} \left( {{{{\alpha }}_{{j}}}} \right)$ 。从而式(2)中 ${{\alpha }}$ 的最大后验概率估计为

${\hat{\alpha }} = \arg \max \left\{ {\prod\limits_{i = 1}^n {{f_\theta }} \left( {{{{y}}_{{i}}} - {{{r}}_{{i}}}{{\alpha }}} \right)} + \prod\limits_{j = 1}^m {{f_0}} \left( {{{{\alpha }}_{{j}}}} \right)\right\}$

(3)

令 $\,{\rho _\theta }\left( {{e}} \right) = - \ln {f_\theta }\left( {{e}} \right)$ 和 $\,{\rho _0}\left( {{\alpha }} \right) = - \ln {f_0}\left( {{\alpha }} \right)$ 式(3)转成：

${\hat{ \alpha }} = \arg \min \left\{ {\sum\limits_{i = 1}^n {{\rho _\theta }\left( {{{{y}}_{{i}}} - {{{r}}_{{i}}}{{\alpha }}} \right) + \sum\limits_{j = 1}^m {{\rho _0}\left( {{{{\alpha }}_{{j}}}} \right)} } } \right\}$

(4)

本文把式(4)的模型称为鲁棒的正则编码，由于保真项 ${\rho _\theta }\left( {{{{y}}_{{i}}} - {{{r}}_{{i}}}{{\alpha }}} \right)$ 对遮挡造成的异常值具有鲁棒性，且根据先验概率 $P\left( {{\alpha }} \right)$ ， $\displaystyle\sum\limits_{j = 1}^m {{\rho _0}\left( {{{{\alpha }}_{{j}}}} \right)} $ 是正则化项。

因此当 ${{{\alpha }}_{{j}}}$ 服从拉普拉斯分布的时候有： $P\left( {{\alpha }} \right) =$ $ \displaystyle\prod\limits_{j = 1}^m {\exp \left( { - {{\left\| {{{{\alpha }}_{{j}}}} \right\|}_1}/{\sigma _\alpha }} \right)} /2{\sigma _\alpha }$ ； $\sum\nolimits_{j = 1}^m {{\rho _0}\left( {{{{\alpha }}_{{j}}}} \right)} $ 将变成稀疏限制l₁范数。对于分类问题，理想的结果是只有待测表情图像与训练样本组成的完备字典中对应的目标类别的表示系数有很大的绝对值。由于事先不知道待测图像属于哪个类别，可以进行一个合理的推理，是只有很少一部分的稀疏表示系数具有显著值。因此，假设稀疏表示系数 ${{{\alpha }}_{{j}}}$ 服从高斯分布，则有：

${f_0}\left( {{{{\alpha }}_{{j}}}} \right) = \beta \exp \left\{ { - {{\left( {\left| {{{{\alpha }}_{{j}}}} \right|/{\sigma _\alpha }} \right)}^\beta }} \right\}/\left( {2{\sigma _\alpha }\Gamma \left( {1/\beta } \right)} \right)$

(5)

式中 $\Gamma $ 表示伽马函数。

由于表情图像的变化多样性，很难预先确定稀疏表示残差的分布。通常，假设概率密度函数 ${f_\theta }\left( {{e}} \right)$ 是对称的、单调并且可微的。因此， ${\rho _\theta }\left( {{e}} \right)$ 具有以下性质：

1) ${\rho _\theta }\left( {0} \right)$ 是 ${\rho _\theta }\left( {{e}} \right)$ 的局部最小值；

2) 对称性： ${\rho _\theta }\left( {{{{e}}_{{i}}}} \right) = {\rho _\theta }\left( { - {{{e}}_{{i}}}} \right)$ ；

3) 单调性：当 $\left| {{{{e}}_{{1}}}} \right| > \left| {{{{e}}_{{2}}}} \right|$ 时， ${\rho _\theta }\left( {{{{e}}_{{1}}}} \right) > {\rho _\theta }\left( {{{{e}}_{{2}}}} \right)$ 。不失一般性，令 ${\rho _\theta }\left( {0} \right) =0$ 。

鲁棒的正则化编码模型需要解决的两个关键问题：如何确定 ${{{\rho }}_{{\theta }}}$ (或者 ${f_\theta }$ )的分布和最小化能量函数。如果只是简单的使 ${f_\theta }$ 服从高斯分布或者拉普拉斯分布并且 ${f_o}$ 服从拉普拉斯分布，本文提出的模型将退化成式(1)所示的传统的稀疏表示问题。为了解决这两个问题并更有效地获得鲁棒的正则化编码模型的最大后验概率，本文将式(4)的最小化问题转换成迭代权重正则编码问题。

1.2 迭代权重优化鲁棒的正则化编码模型

定义 ${F_\theta }\left( {{e}} \right) = \sum\nolimits_{i = 1}^n {{\rho _\theta }} \left( {{{{e}}_{{i}}}} \right)$ 。 ${F_\theta }\left( {{e}} \right)$ 在定义域内某点 ${{{e}}_{{0}}}$ 处的一阶泰勒展开公式：

${\tilde F_\theta }\left( {{e}} \right) = {F_\theta }\left( {{{{e}}_{{0}}}} \right) + {\left( {{{e}} - {{{e}}_{{0}}}} \right)^{ T}}{F'_\theta }\left( {{{{e}}_{{0}}}} \right) + {R_1}\left( {{e}} \right)$

(6)

式中： ${F'_\theta }\left( {{e}} \right)$ 是 ${F_\theta }\left( {{e}} \right)$ 的一阶导数， ${R_1}\left( {{e}} \right)$ 是 ${F_\theta }\left( {{e}} \right)$ 的高阶导数的余项式。定义 $\,{\rho '_\theta }$ 是 ${\rho _\theta }$ 的一阶导数，并且有： ${F'_\theta }\left( {{{{e}}_{{0}}}} \right) = \left[ {{{\rho '}_\theta }\left( {{{{e}}_{{{0}},{{1}}}}} \right);{{\rho '}_\theta }\left( {{{{e}}_{{{{0}},{{2}}}}}} \right); \cdots {{\rho '}_\theta }\left( {{{{e}}_{{{{0}},{{n}}}}}} \right)} \right]$ ； ${{{e}}_{0,i}}$ 是 ${{{e}}_{{0}}}$ 的第i个元素。使 ${F'_\theta }\left( {{e}} \right)$ 严格显凸性便于最小化，近似余项为 ${R_1}\left( {{e}} \right) \approx \frac{1}{2}{\left( {{{e}} - {{{e}}_{{0}}}} \right)^{{T}}}{{W}}\left( {{{e}} - {{{e}}_{{0}}}} \right)$ 其中， ${{W}}$ 是对角矩阵，使 ${{e}}$ 中的元素独立且在 ${F_\theta }\left( {{e}} \right)$ 中 ${{{e}}_{{i}}}$ 和 ${{{e}}_{{j}}} \left( {i \ne j} \right)$ 没有交叉项。

${F_\theta }\left( {{e}} \right)$ 在 ${{e}} = 0$ 取得最小值的同时，它的近似值 ${\tilde F_\theta }\left( {{e}} \right)$ 在 ${{e}} = 0$ 也应取得最小值。令 ${F'_\theta }\left( 0 \right) = 0$ ，可以得到 ${{W}}$ 的对角元素如式(7)：

${{{W}}_{{{{i}},{{i}}}}} = {\rho '_\theta }\left( {{{{e}}_{{{{0}},{{i}}}}}} \right)/{{{e}}_{{{{0}},{{i}}}}}$

(7)

根据ρ_θ的性质， ${\rho '_\theta }\left( {{{{e}}_{{i}}}} \right)$ 和 ${{{e}}_{{i}}}$ 符号相同，所以 ${{{W}}_{{{{i}},{{i}}}}}$ 是非负的标量。因此进一步，从而 ${\tilde F_\theta }\left( {{e}} \right)$ 可以写成 ${\tilde F_\theta }\left( {{e}} \right) = \frac{1}{2}\left\| {{{{W}}^{1/2}}{{e}}} \right\|_2^2 + {b_{{{{e}}_{{o}}}}}$ 。

式中： ${b_{{{{e}}_{{o}}}}} = \displaystyle\sum\limits_{i = 1}^n {\left( {{\rho _\theta }\left( {{{{e}}_{{{{0}},{{i}}}}}} \right) - {{\rho '}_\theta }\left( {{{{e}}_{{{{0}},{{i}}}}}} \right){{{e}}_{{{{0}},{{i}}}}}/2} \right)} $ 是由 ${{{e}}_{{0}}}$ 决定的标量常量。不考虑 ${b_{{e_o}}}$ ，式(4)模型可近似为式(8)：

${\hat{ \alpha }} = \arg \min \left\{ {\frac{1}{2}\left\| {{{{W}}^{1/2}}\left( {{{y}} - {{T\alpha }}} \right)} \right\|_2^2 + \sum\limits_{j = 1}^m {{\rho _0}\left( {{{{\alpha }}_{{j}}}} \right)} } \right\}$

(8)

虽然，式(8)是式(4)的局部近似值，但是这样做可以将鲁棒的正则化编码模型的最小化问题通过迭代再加权重l₂正则编码来解决，也就是通过式(7)不断更新权重 ${{W}}$ 。这样最小化问题转变成了如何计算对角权重矩阵 ${{W}}$ 。

1.3 权重W

${{{W}}_{{{{i}},{{i}}}}}$ 表示分配给待测表情图像 ${{y}}$ 每个像素点 $i$ 的权值。从人的感官认识出发，被遮挡部分的像素点应该具有较低的权重，这样可以减少它们对编码过程的影响。由于完备字典是由非遮挡的人脸表情图像构成的，可以很好地表征人脸表情，然而遮挡部分像素造成的异常值将具有较大的编码残差，因此，这些具有较大的编码残差像素点应具有较小的权重。通过观察式(7)可以得到 ${{{W}}_{{{{i}},{{i}}}}}$ 与 ${{{e}}_{{i}}}$ 成反比，与 ${\rho '_\theta }\left( {{{{e}}_{{i}}}} \right)$ 成正比。由于ρ_θ可微、对称、单调并且在原点取得最小值，可以假设 ${{{W}}_{{{{i}},{{i}}}}}$ 是连续且对称的，与 ${{{e}}_{{i}}}$ 成反比而且有界。不失一般性，令 ${{{W}}_{{{{i}},{{i}}}}} \in \left[ {0,1} \right]$ ，综合多方面的考虑，逻辑函数是权重函数的最好选择。本文选用与逻辑函数具有相似性质的SVM hinge loss函数^[12]作为权重函数。

初值对人脸表情识别取得较理想的识别效果至关重要。为了对待测表情图像 ${{y}}$ 设置初值，首先应该初始化 ${{y}}$ 的编码残差 ${{e}}$ 。本文对 ${{e}}$ 初始化为 ${{e}} \!=\! {{y}} \!-\! {{T}}{{\hat{ \alpha }}^{\left( {{0}} \right)}}$ ； ${{{\alpha }}^{\left( {{0}} \right)}}$ 是初始编码向量。由于待测表情图像 ${{y}}$ 所属类别事先未知，因此 ${{{\alpha }}^{\left( {{0}} \right)}}$ 的合理初始编码向量可以设置为 ${{{\alpha }}^{\left( {{0}} \right)}} = \left[ {\displaystyle\frac{1}{m};\frac{1}{m}; \cdots; \frac{1}{m}} \right]$ 。这样 ${{T}}{{{\alpha }}^{\left( {{0}} \right)}}$ 表示的就是所有训练表情图像的平均表情图像。

通过不断迭代优化更新权重 ${{W}}$ ，直到权重收敛为止, 即相邻迭代权重之间的差异足够小。具体来说，应当式(9)成立时停止迭代:

${\left\| {{{{W}}^{\left( t \right)}} - {{{W}}^{\left( {t - 1} \right)}}} \right\|_2}/{\left\| {{{{W}}^{\left( {t - 1} \right)}}} \right\|_2} < \gamma $

(9)

式中： $\gamma $ 是较小的正数. 本文迭代15次权重就趋于收敛。得到收敛后的权重矩阵 ${{W}}$ 后，最优的稀疏表示 ${\hat{ \alpha }}$ 可以通过式(8)计算得到。最后, 通过式(10)计算每类训练表情图像逼近待测表情图像 ${{y}}$ 的逼近残差。

${r_i}\left( {{y}} \right) = {\left\| {{{W}}_{{final}}^{1/2}\left( {{{y}} - {{T}}{{{\delta }}_{{i}}}\left( {{\hat{ \alpha }}} \right)} \right)} \right\|_2},i = 1,2, \cdots ,k$

(10)

式中： ${{{\delta }}_{{i}}}\left( {{\hat{ \alpha }}} \right)$ 是 ${\hat{ \alpha }}$ 第i类训练样本空间最终编码向量， ${{{W}}_{{{final}}}}$ 是最终的权重矩阵， $k$ 表示表情类别数。

根据最小逼近残差的准则公式(11)，待测表情图像 ${{y}}$ 最终将被分类到训练表情图像逼近待测表情图像残差最小的类别。可由式(11)进行判断：

${{identity}}\left( {{y}} \right) = \arg \mathop {\min }\limits_{i \in \left( {1, 2, \cdots ,k} \right)} \left( {{r_i}\left( {{y}} \right)} \right)$

(11)

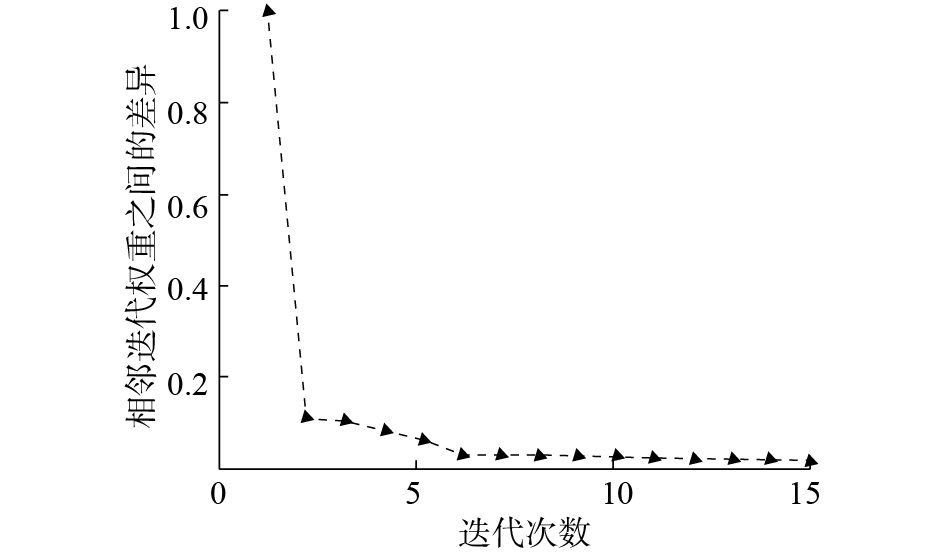
因此，本文方法的流程如图1所示。首先，待测的人脸表情图像的每个像素点赋予不同的权重。其次，通过连续迭代得到收敛的权重矩阵。权重随着每次迭代的收敛曲线如图2所示。然后, 得到收敛的权重矩阵 ${{W}}$ 后，待测表情图像的最优稀疏表示也可以通过计算得到。最后，计算每类训练表情图像逼近待测表情图像 ${{y}}$ 的编码残差，并根据最小逼近残差的准则将待测表情图像 ${{y}}$ 分类到训练表情图像逼近待测表情图像最小逼近残差所对应的类别。每类训练表情图像逼近待测表情图像的逼近残差如图3所示。为了减少原始表情特性的特征维数，本文应用PCA的方法对特征进行降维处理，Eigenface特征应用到与本文方法进行对比的其他算法中。定义 $P$ 为PCA的投影矩阵，那么，式(8)将变为

${\hat{ \alpha }} = \arg \min \left\{ {\frac{1}{2}\left\| {{{P}}{{{W}}^{1/2}}\left( {{{y}} - {{T\alpha }}} \right)} \right\|_2^2 + \sum\limits_{j = 1}^m {{\rho _0}\left( {{{{\alpha }}_{{j}}}} \right)} } \right\}$

(12)

2 实验描述与结果分析

实验采用日本女性表情图像JAFFE数据库和Cohn-Kanade数据库来验证本文所提方法的可行性和有效性。JAFFE数据库包含10个女性共213张人脸表情图像，并且每个人都有7种表情，每种表情有3或4张表情图像样本。实验时选用10个人共137表情图像作为训练样本，其中(高兴-19，惊讶-20，悲伤-20，恐惧-20，厌恶-18，愤怒-20和中性-20)。其余的76张人脸表情图像作为测试样本。基于JAFFE数据库的表情图像数量少，实验将遍历3种情况来取得平均识别率。而 Cohn-Kanade人脸表情数据库是由100名大学生按照指定的方式来从中性表情呈现23幅表情序列，这些人都来自18~30岁的大学心理系的学生。其中15%为欧洲人(包括黑种人和白种人)，3%为亚洲人或拉丁人种，65%为女性。该数据库也包含与JAFFE数据库一样的7种表情类别。对于Cohn-Kanade数据库,选用10个人7种表情(高兴-6，惊讶-6，悲伤-6，恐惧-6，厌恶-6，愤怒-6和中性-6)共420张表情序列进行实验。其中，10个人7种表情共210张表情图像作为训练样本，其余的作为测试样本。为了验证算法在Cohn-Kanade数据库的泛化性能实验遍历6种情况来取得平均识别率。

2.1 实验描述

由于JAFFE数据库和Cohn-Kanade数据库中的表情图像稍有头部倾斜和尺寸大小不一，需要经过预处理来消除这些差异。本文采用类似文献[12]的预处理方法：通过旋转使眼睛水平面对准，并根据两眼间的距离来从原始的表情图像裁剪出实验用的只含正面人脸表情的矩形区域。JAFFE数据库中的原始人脸表情图像的尺寸为256×256，Cohn-Kanade数据库中的原始人脸表情图像尺寸为640×490。两数据库中的表情图像进行尺寸归一化128×104，利用直方图均衡化来增强表情图像某些区域的局部对比度，如图4所示。

与其他的影响因素不同，如姿势的变化，它的变化特点是可以事先预测判别出来的。然而，面部遮挡是特别难以处理的，因为它具有随机性的特点，也就是说，遮挡可以发生在人脸表情图像的任意位置并且大小也是任意的。我们对于遮挡发生的位置和遮挡面积的大小没有任何明确的先验知识。关于遮挡唯一有的先验信息就是遮挡毁坏的像素点可能是彼此相邻的，就是说某个区域的像素点可能是连续毁坏。图4表示的两个表情数据中一些在不同遮挡程度块遮挡级别下的人脸表情图像。遮挡级别表示的是遮挡的部分占整个人脸表情图像的百分比是多少。所以遮挡级别是正数并且处于[0,1]，遮挡级别为0表示图像没有被遮挡，1表示图像全部被遮挡，例如：遮挡级别0.1表示图像的10%被遮挡。基于稀疏表示的人脸表情识别方法最重要特点是对于人脸遮挡具有鲁棒性。为更好地验证本文提出的方法对于随机遮挡的鲁棒性，采用表情识别方法：KNN^[14](K-nearest neighbor)、SVM^[15]、SRC^[10](sparse representation-based classifier)、GSRC^[16](gabor feature based sparse representation)与本文方法在以下两种数据库进行对比。

2.2 结果分析

表1和表2分别表示的是本文提出的方法与其他方法分别在JAFFE数据库上和在Cohn-Kanade数据库上对应不同遮挡级别的平均识别率。

从表1和表2可看出，随遮挡级别增大人脸表情的识别率逐渐减小，符合人们的感性认识。表情识别方法在遮挡级别为0.1~0.5会取得较理想的识别效果。由于训练样本和测试样本用自身像素值不需特征提取过程，KNN^[16]和SVM^[17]方法在遮挡级别很大时没有很好的识别效果。且这两种方法要结合提取较好区分性特征的提取方法才可发挥较好的分类效果，可看出本文的方法比SRC^[10]和GSRC^[12]表情识别率略高。

本方法在随机遮挡的情况下取得比其他方法较为理想的识别效果，接下来分析本文在不同遮挡级别对于每种表情识别的影响大小。两种数据库不同遮挡级别对每种表情的遮挡情况如表3和表4。

从表3和表4可以看出，随着表中给出的人脸表情图像的随机遮挡级别的增大，两种数据库上不同的人脸表情识别率随之降低。在两种数据库中，生气、高兴、中性、悲伤和惊讶表情在图像遮挡级别为0~0.1取得了较为理想的识别效果。这是由于遮挡级别较小，这些表情图像的决策信息缺失的少。在这两种数据库上所有表情只有惊讶表情的识别效果在遮挡级别为0.2时受到了影响，其他表情都没有受到影响。当图像遮挡级别为0.3时，在这两种数据库上所有表情只有生气、悲伤和惊讶表情识别效果受到了影响。当图像遮挡级别为0.4~0.5，在JAFFE数据库上高兴和中性表情取得了较好的识别效果，在图像遮挡级别为0.6时中性表情取得了较好的识别效果。然而在Cohn-Kanade数据库上，当图像遮挡级别为0.4~0.6时，恐惧和中性表情取得了较好的识别效果。当图像遮挡级别为0.7~0.9时，所有的表情的识别率(除了中性表情外)都受到了较为严重的影响。

从两表中可以看出中性表情识别率在不同的图像遮挡级别下都可以保持了较高的识别率。即使在遮挡级别为0.9的JAFFE数据库上，中性表情的识别率仍为60%。这是由于本文在赋予编码残差 $e$ 的初值时，选用的是所有训练表情图像的平均表情作为 $e$ 的初值，中性表情和平均人脸表情很相似。因此，即使在遮挡级别很大是，中性表情也较其他表情更容易更有效地识别。

图5表示的是JAFFE数据库上所有测试的中性表情图像和所有训练表情图像的平均表情图像。虽然在JAFFE数据库上中性表情的识别效果在遮挡级别很高的时候也能取得较好识别效果，但是在Cohn-Kanade数据库上这种现象表现的并不是十分明显。在遮挡级别为0.9时的中性表情识别率为46.67%。尽管中性表情的识别率较其他的表情识别率高，但是与在JAFFE数据上的识别率相比还是相差较大。这是由于JAFFE数据库上的人脸表情图像都是女性，并且都属于同一国家的。

而Cohn-Kanade数据库中的人脸表情图像是来自不同的国籍和不同性别的。这将造成如图6所示的中性表情和平均人脸表情之间的相似性较小。因此，当遮挡级别为0.7~0.9时，在Cohn-Kanade数据库上的中性表情较JAFFE上的中性表情的识别率低。尽管，中性表情的识别率在两种表情数据库上相差较大，但是Cohn-Kanade数据库中的表情图像来自不同的国籍和性别更符合实际情况，在该数据库上进行实验更有利于算法的推广和实际应用。

3 结束语

本文提出了基于鲁棒的正则化编码模型和自动更新权重的随机遮挡表情识别方法。根据人脸表情遮挡随机性的特点，提高了稀疏表示的鲁棒性和有效性并且减少随机遮挡部分对人脸表情识别的影响。本文方法使用原始图像数据(像素点)即可不需要采用特征降维、特征提取、综合训练样本和特定领域信息等，通过求取编码问题的最大后验概率，从而来实现对遮挡的鲁棒性。根据编码残差来对待测图像的所有像素点自适应的分配和反复迭代权重，这样可以鲁棒地辨别出遮挡造成的奇异值并减少它们对编码过程的影响。在JAFFE数据库和Cohn-Kanade数据库上与其他几种方法进行了不同遮挡级别情况下识别率的对比实验，由结果可以看出本文提出的方法取得了较好的识别效果，较其他几种方法有效并对随机遮挡具有较强的鲁棒性。