SCADA系统[1]是工业控制系统的核心,也是油气田安全稳定运行的关键,其安全性关系到整个油气田的生产运行。而高速发展的信息技术以及工业技术使我们快速进入了 “工业4.0”时代。信息网络化分布式智能生产成为了潮流和趋势,这使得针对工控系统的恶意攻击数量有迅猛增加的趋势,如“Stuxnet”、“Flame”、“Duqu”、“Havex”等各种攻击工业控制系统的病毒层出不穷。因此,对油气SCADA系统定期地开展系统信息安全评价是针对工控系统信息安全问题的首要应对措施。为了深入分析和防范工业信息系统的安全问题,各国先后成立了专门的研究机构。例如,美国针对信息安全问题,成立了相应的网络应急部门ICS-CERT[2-4],对工业控制系统中的问题进行分析后,及时发出警报并提供相关的解决办法,从而及时解决当前遇到的安全问题。
目前针对油气SCADA系统信息安全的评价方法主要存在评价规范不够完善、评估对象模糊等问题。为此本文进行积极地探索,提出云模型评价方法,最终通过MATLAB的仿真实验,发现该方法起到较好的评价作用,在一定程度上提高了系统的安全性。
1 SCADA系统信息安全评价条件因素在油气SCADA系统中,为了保障系统生产、控制和管理过程的安全性,需要采取一些相关的信息安全技术和措施。事前、事中、事后防御体系[5]是一种常用的安全评价技术路线,本文将采取这种防御技术体系。
油气SCADA工控系统的信息安全评价包括事件发生前期、中期和后期三个过程。事件发生前主要针对网络分段[6]、信息加密等过程进行评价。事件发生时主要对资源,通信的完整性、实时稳定性[7]等进行评价。而事件发生后的评价包括系统的异常恢复,分析和审计等过程。本文主要针对事中因素的资源控制进行评价。工控系统主机的资源占用的大小,不仅会影响到系统的实时性和稳定性,还可能对工业生产带来不可估量的损失。本文首先建立了油气SCADA系统的因素空间评价模型,再针对SCADA信息安全事中因素的资源控制采用云模型评价方法,系统的资源占用为其评价因素,最后通过MATLAB仿真得到评价结果。
2 因素空间模型的建立 2.1 因素空间理论因素空间[8] 是一个坐标架,它以因素为轴。它是信息描述普适性框架,所有对象均可以看作该空间上的一个点。
因素空间的定义:如果满足公理
1)
2)
3)若因素族
| $f:U \to X(f),u \mapsto \left\{ {\begin{array}{*{20}{c}} {f(u),\,\,u \in D(f)}&{\begin{array}{*{20}{c}} {}&{} \end{array}} \\ {\theta ,\,\,u \in U\backslash D(f)}&{\begin{array}{*{20}{c}} {}&{} \end{array}} \end{array}} \right.$ | (1) |
根据因素空间理论,定义因素
| $X({f_0}){{ = }}\left\{ {{\text{事前}};\;{\text{事中}};\;{\text{事后}}} \right\}$ |
在事前因素族中,定义
在事中因素族中,定义
在事后因素族中,定义
从而可建立如图1所示的油气SCADA信息安全的“因素滕网[9]”评价模型。

|
Download:
|
| 图 1 SCADA系统信息安全“因素藤网”评价模型 Fig. 1 “Factor rattan net” evaluation model of information security of SCADA system | |
在因素藤网中,每个节点都是一个因素空间也是一个因素神经元,神经元可以存储与评价相关的操作或算法,它们既有输入也有输出,输入即是条件因素的状态空间,而输出是评价因素的状态。
在上述评价模型中,每个神经元的都有其相应的算法且其计算不仅可采用因素分析法,还可采用其他算法,而本文采用云模型推理法对系统进行评价。
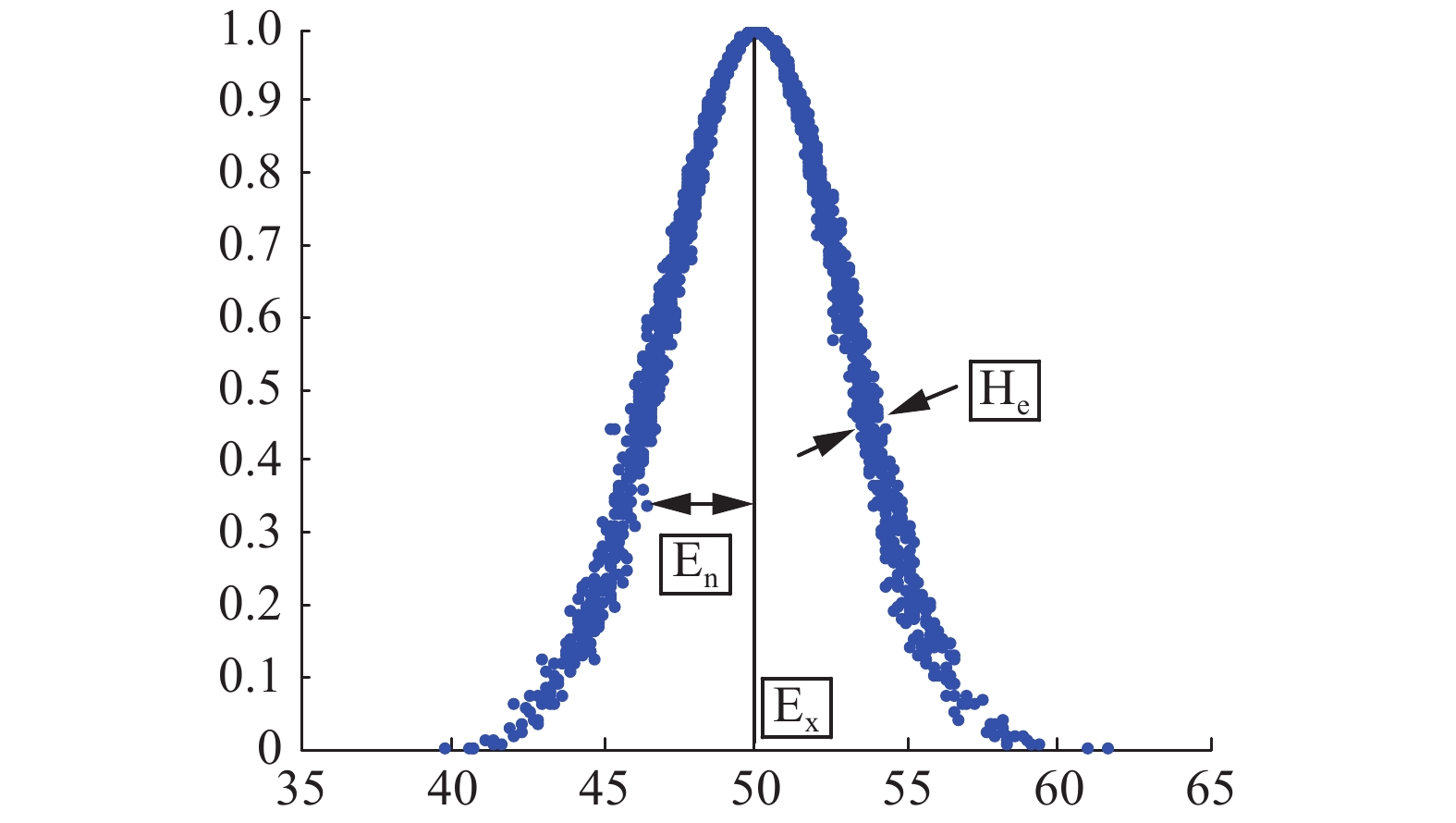
3 云模型推理信息安全评价 3.1 正态云模型理论正态云模型[10]采用3个定量的参数:期望
设
| $\begin{array}{l}\mu :\;U \to [0,1]\\\forall x \in U,x \mapsto \mu (x)\end{array}$ | (2) |
|
Download:
|
| 图 2 云及云的数字特征 Fig. 2 Cloud and Cloud’s Digital Features | |
前向云生成器(FCG)的原理是由参数
后向云生成器(BCG)的原理是由已知的云滴
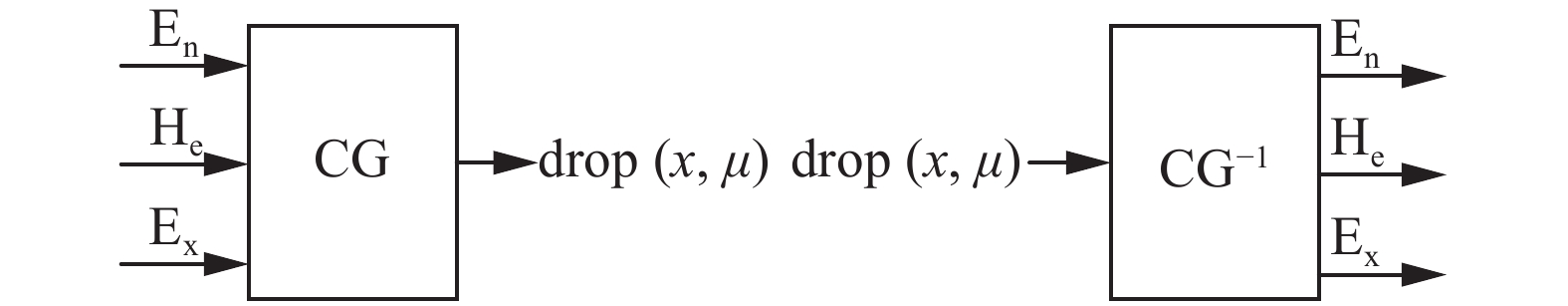
|
Download:
|
| 图 3 FCG和BCG Fig. 3 FCG and BCG | |
二维云规则生成器的工作原理:
由条件A和B得到结果C(A、B、C都是由
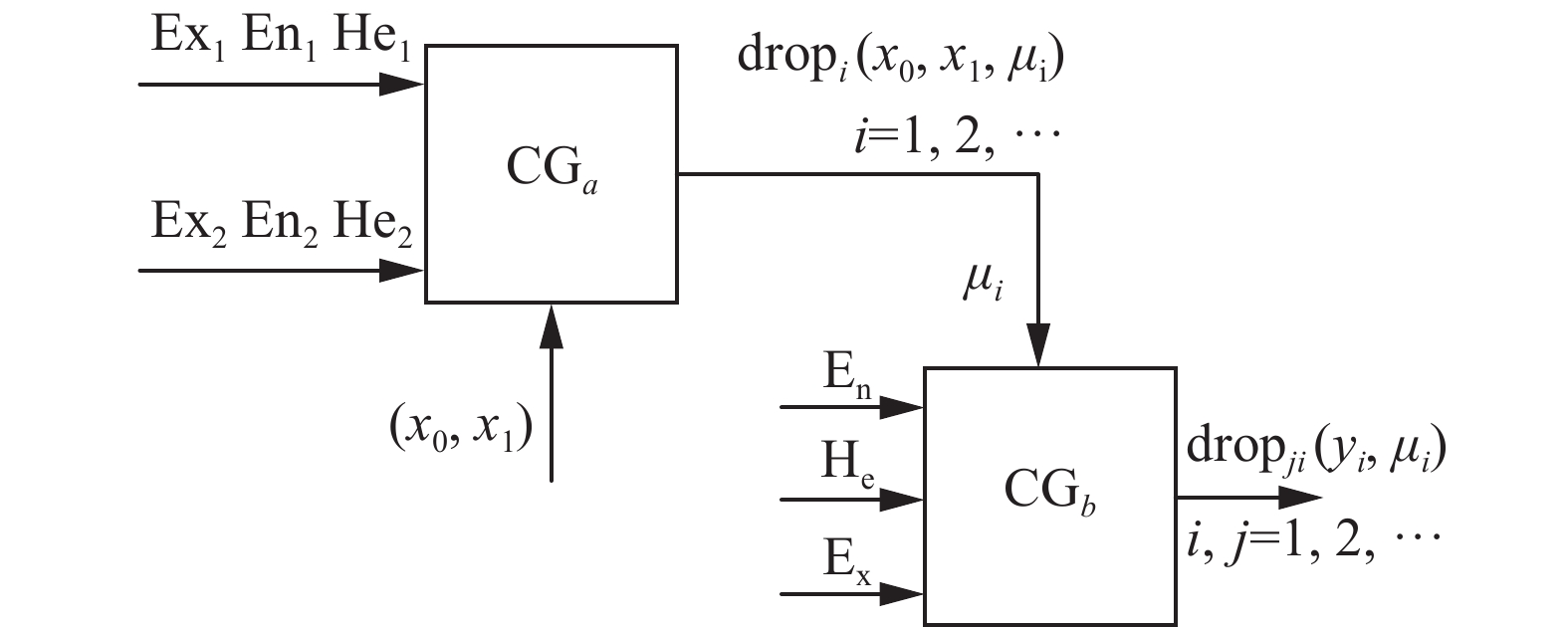
将前向云生成器与后向云生成器按照给定规则相结合得到如图4所示的单条件规则生成器。
|
Download:
|
| 图 4 单条件规则生成器 Fig. 4 Single condition rule generator | |
规则1:If
规则2:If
规则n:If
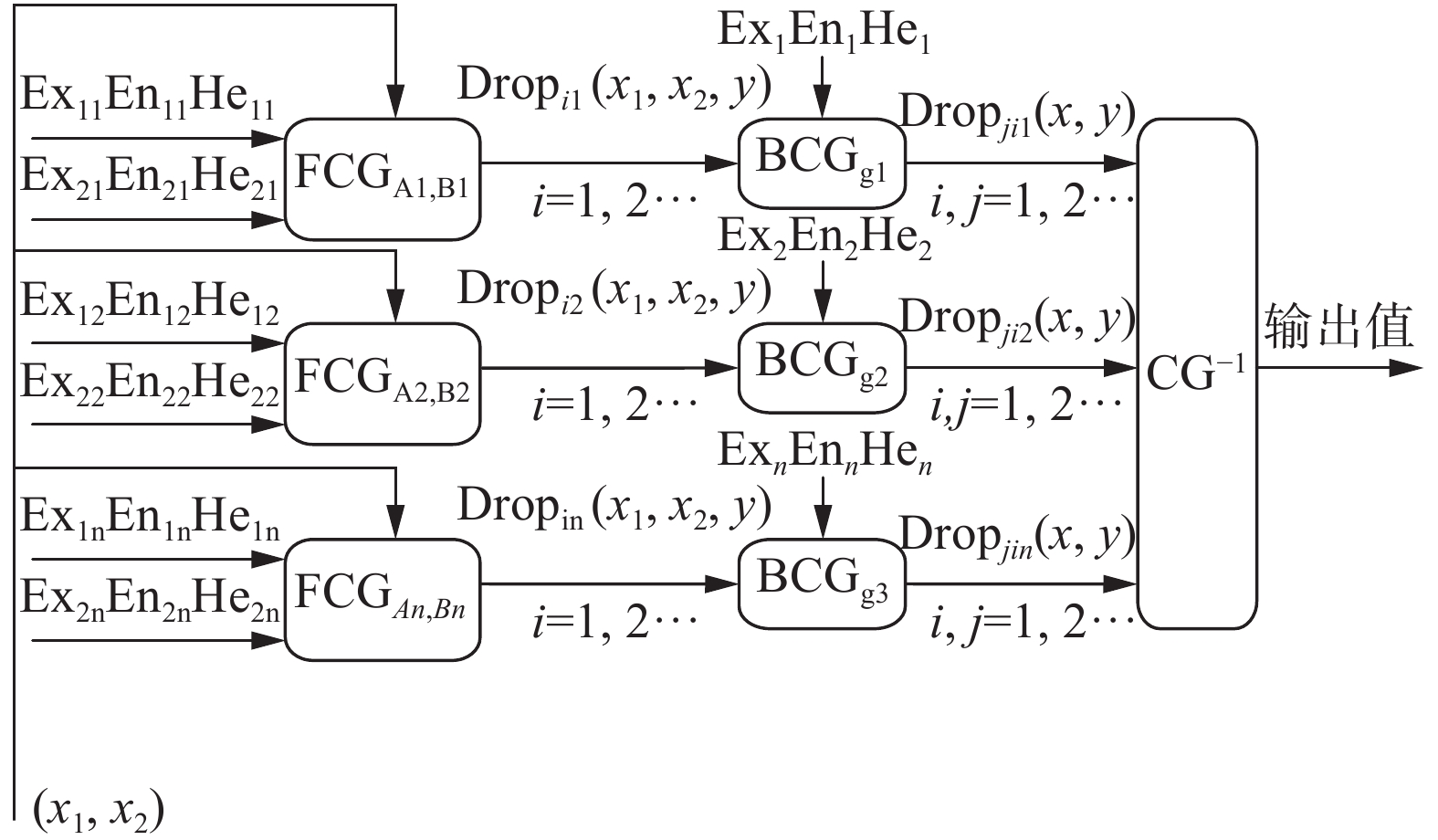
用n条上述形式表示的规则相结合组成一个二维多规则云生成器,其结构示意图如图5所示。
|
Download:
|
| 图 5 二维多规则生成器 Fig. 5 Two-dimensional multiple rule generator | |
本文引入云模型推理方法对事中因素的资源占用进行评价,其基本思路是:资源占用中的 “很高、高、中、低、很低”分别表示评价指标中的“很差、差、一般、好、很好”,资源占用由CPU和内存在“因素占用率”映射下的状态空间共同决定。本文在资源占用的评价中,根据CPU占用和内存占用这两个条件因素构造二维
对于资源占用的评价,本文设计了一个二维多规则的云模型推理机,输入二维值
通过对大量的数据的聚类处理[13],本文得到10条定性规则如表1所示。
| 表 1 聚类处理资源占用规则表 Tab.1 Cluster processing resource occupancy rule table |
其中设定资源占用率[0,25]、(25,40]、(40,65]、(65,85] 、(85,100]依次为:很低、低、中、高、很高。如表1中的由条件得到结果的过程称为变量云化。将表1的10条定性规则用云对象[14]进行处理后得到表2所示的数字特征和参数。
| 表 2 处理后的数字特征和参数 Tab.2 Digital features and parameters after processing |
云对象输入云化的方法有定量、定性两种。当输入为定量输入云化时,输入的变量需满足双边限制条件或者单边限制条件。然后利用正态云规则“
双边限制的计算可按照式(3)进行计算:
| $\begin{array}{c}{{E_x}}{{ = }}({B_{{{max}}}} + {B_{\min }}){{/2}}\\{{E_n}}{{ = }}({B_{{{max}}}}{{ - }}{B_{\min }}){{/6}}\\{{H_e}} = k\end{array}$ | (3) |
而当输入为定性输入云化
| $\begin{array}{c}{E_x}{{ = }}\displaystyle\frac{{{{{E}}_{{{x}}1}} \times {{{E}}_{{{n}}1}} + {{{E}}_{{{x}}2}} \times {{{E}}_{{{n}}2}} + \cdot \cdot \cdot + {{{E}}_{{xn}}} \times {{{E}}_{{nn}}}}}{{{{{E}}_{{{n}}1}} + {{{E}}_{{{n}}2}} + \cdot \cdot \cdot + {{{E}}_{{nn}}}}}\\[6pt]{E_n} = {{{E}}_{{{n}}1}}{{ + }}{{{E}}_{{{n}}1}}{{ + }} \cdot \cdot \cdot {{ + }}{{{E}}_{{nn}}}\\[2pt]{H_e} = \displaystyle\frac{{{{{H}}_{{{e}}1}} \times {{{E}}_{{{n}}1}} + {{{H}}_{{{e}}2}} \times {{{E}}_{{{n}}2}} + \cdot \cdot \cdot + {{{H}}_{{en}}} \times {{{E}}_{{nn}}}}}{{{{{E}}_{{{n}}1}} + {{{E}}_{{{n}}2}} + \cdot \cdot \cdot + {{{E}}_{{nn}}}}}\end{array}$ | (4) |
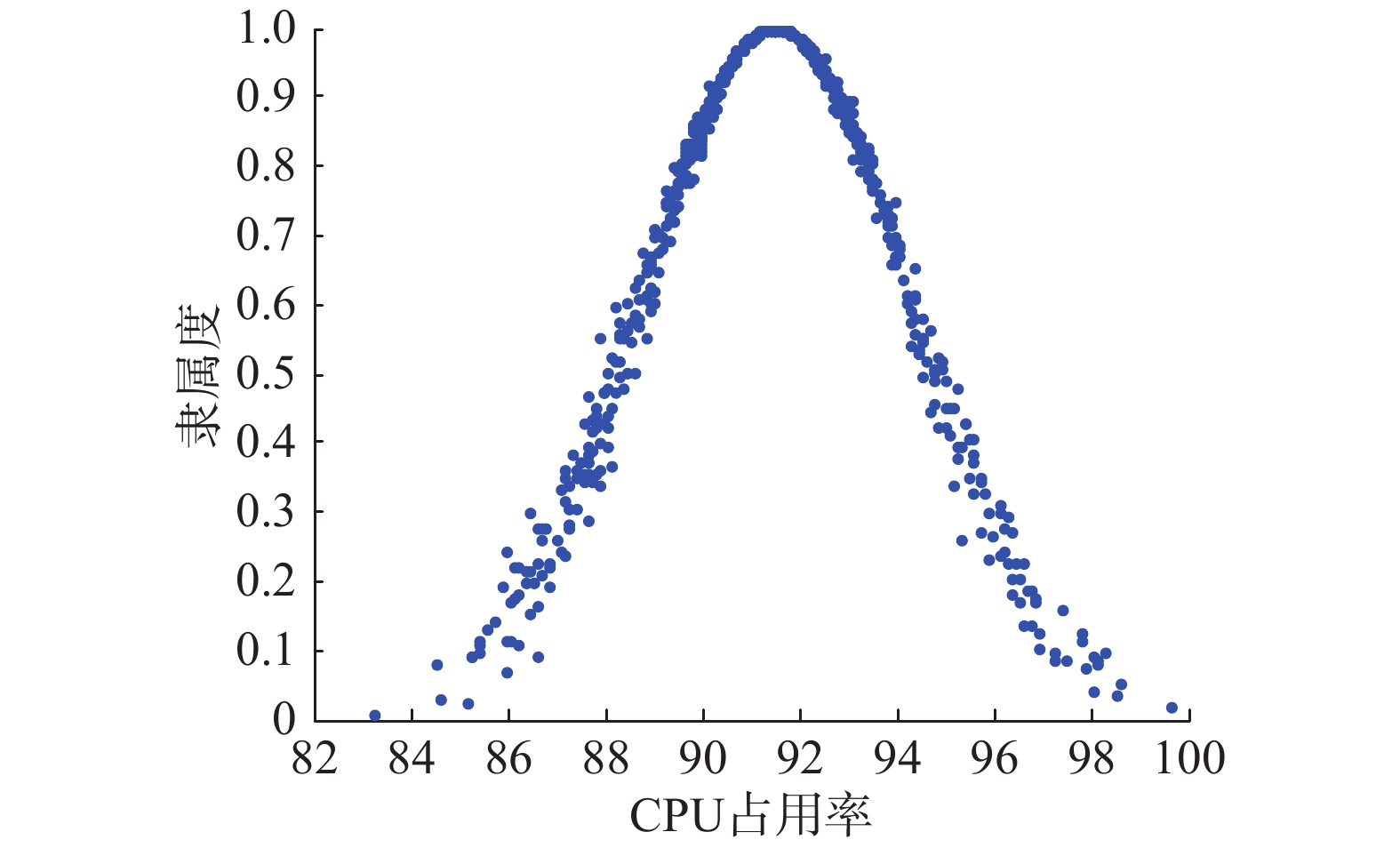
在CPU占用很高的情况下,用式(3)可以计算出
|
Download:
|
| 图 6 一维云分布 Fig. 6 One dimensional cloud distribution | |
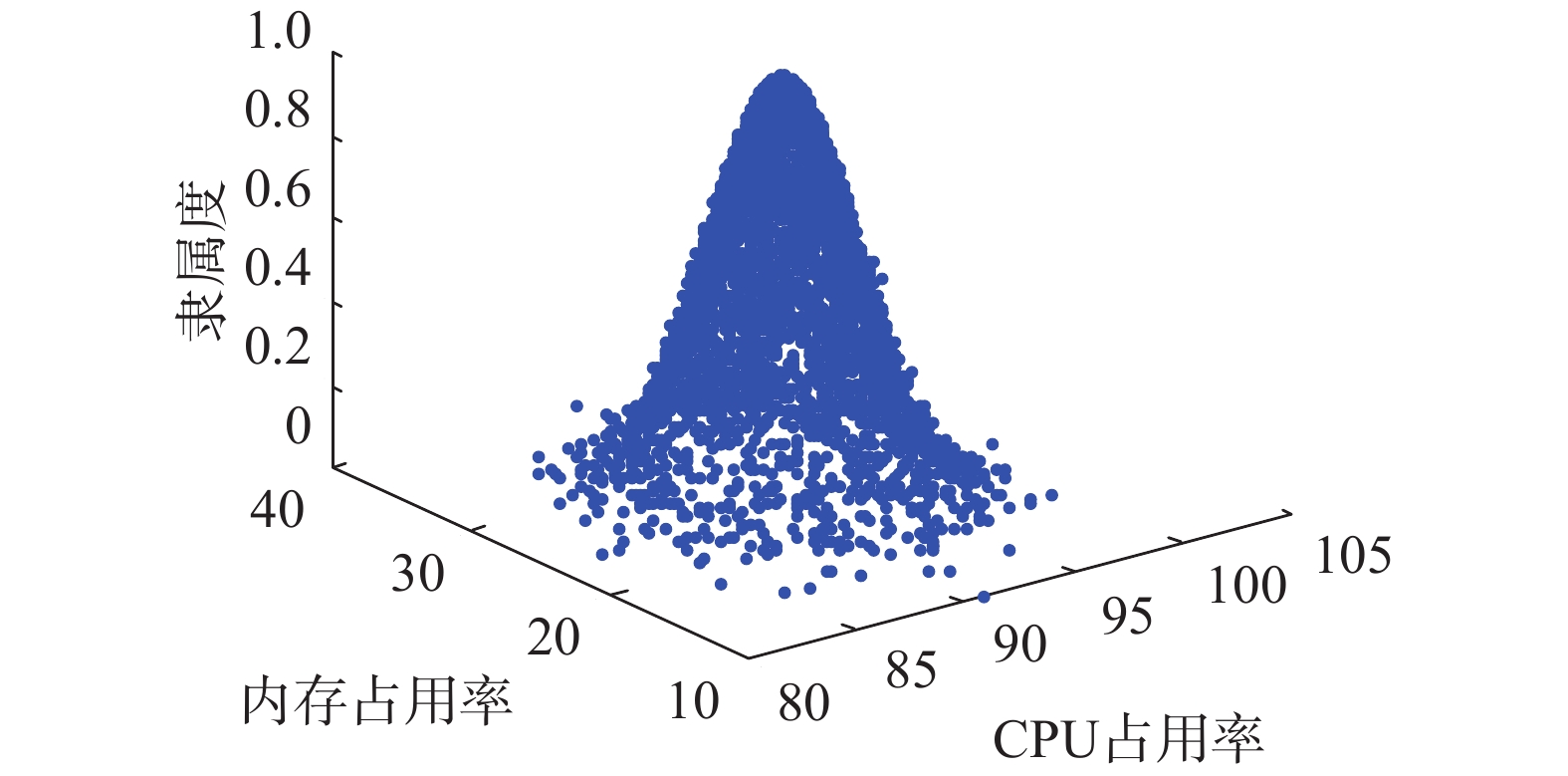
同样的用规则9依据正态二维云发生器形成的CPU占用率很高且内存占用很低的二维云模型的三维云图如图7所示。
|
Download:
|
| 图 7 规则9的正态二维云分布 Fig. 7 Rule 9 normal two-dimensional cloud distribution | |
推理的步骤如下:
1)假设CPU和内存占用率都是0.5,即
2)将
3)计算最大隶属度
4)将3)得到的两个云滴送入逆向云发生器,得到一组定量值
单规则的前向云生成器(FCG)过程:
输入:规则的前向云参数。
输出
Begin{
//对于表中的每条规则,
| $({{{E}}_1},{{{E}}_2}) = {{binormrnd}}({{{E}}_{{{n}}1}},{{{E}}_{{{n}}2}},{{{H}}_{{{e}}1}},{{{H}}_{{{e}}2}})$ |
//在前件规则生成器输入
| $q = {({x_1} - {{{E}}_{{x_1}}})^2}/{{{E}}_{12}}$ |
| $d = {({x_2} - {{{E}}_{{x_2}}})^2}/{{{E}}_{22}}$ |
| $\mu = \exp ( - (1/2)*(q + d))$ |
}END
针对单规则的后向云生成器(BCG)的具体实现过程:
输入:规则后件云参数
输出:
Begin {
//通过后向云生成器
| ${{{E}}_{n31}} = {{normrnd}}({{{E}}_{n3}},{{{H}}_{e3}})\text{;}$ |
//根据激活强度和正态随机数En31按公式
| ${y_1} = {{{E}}_x} + {{{E}}_{nn}}*{{sqrt}}( - 2*\log ({\mu _1}))\text{;}$ |
| ${y_2} = {{{E}}_x} - {{{E}}_{nn}}*{{sqrt}}( - 2*\log ({\mu _1}))$ |
}END
4.2 传统隶属度函数法对比实验传统隶属度函数法[15]是系统评价的传统方法之一,而本文使用的云模型评价法也是以传统隶属度函数法为基础。因此用传统隶属度方法做对比实验,可以更好地分析云模型的优缺点。使用MATLAB做仿真分析,操作步骤如下:
1)运用模糊工具箱,由表2中数据选择隶属度函数为Gauss型(正态型),规则共10条,每条规则有2个输入,一个输出,均按照期望(
2)隶属度函数的推理规则为:
如果条件
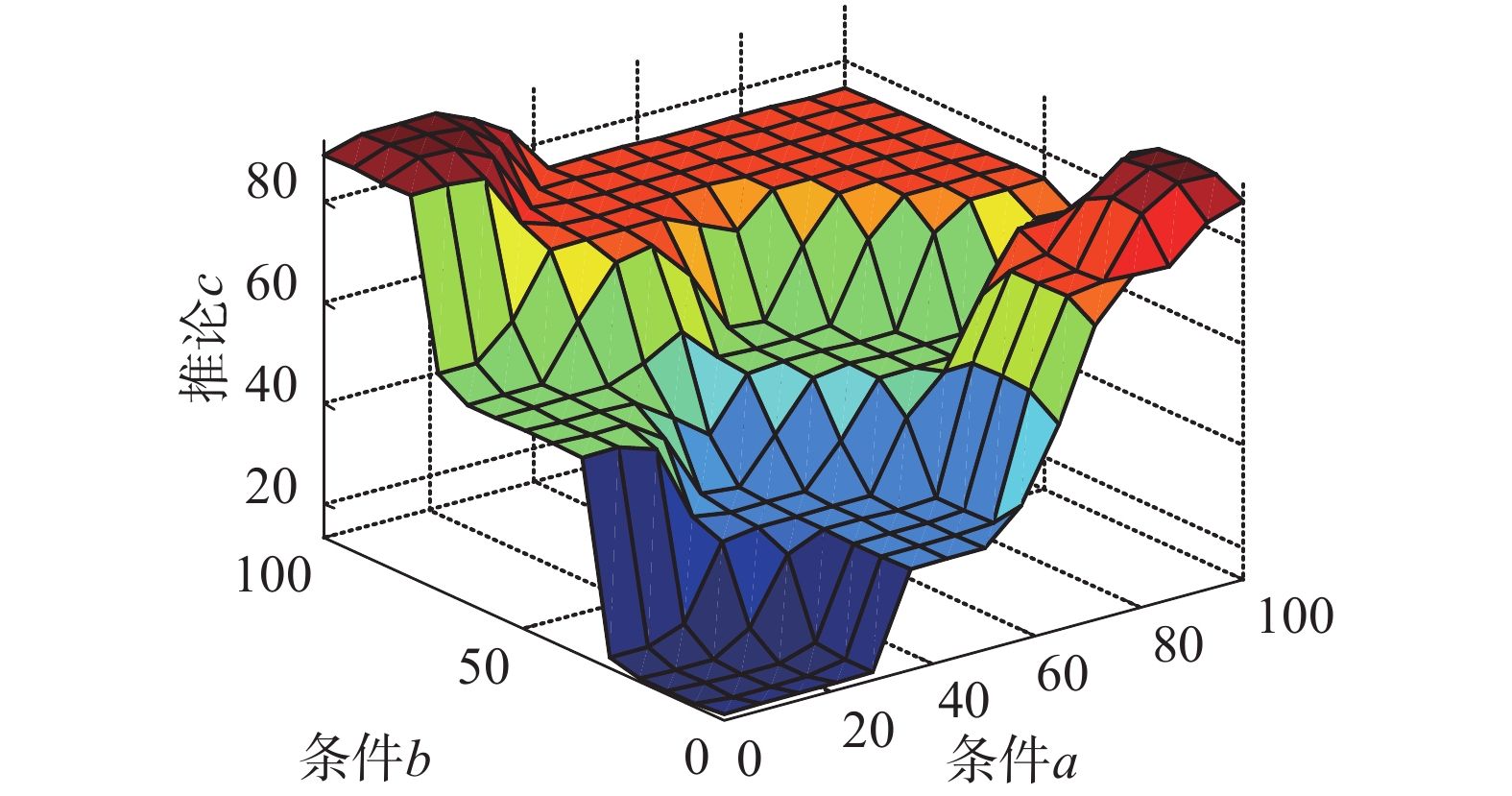
3)传统隶属度函数法得到Surface图如图8所示,输入数据后可得到结果并与云模型得到的结果进行对比分析。
|
Download:
|
| 图 8 传统隶属度函数法surface图 Fig. 8 FIS surface | |
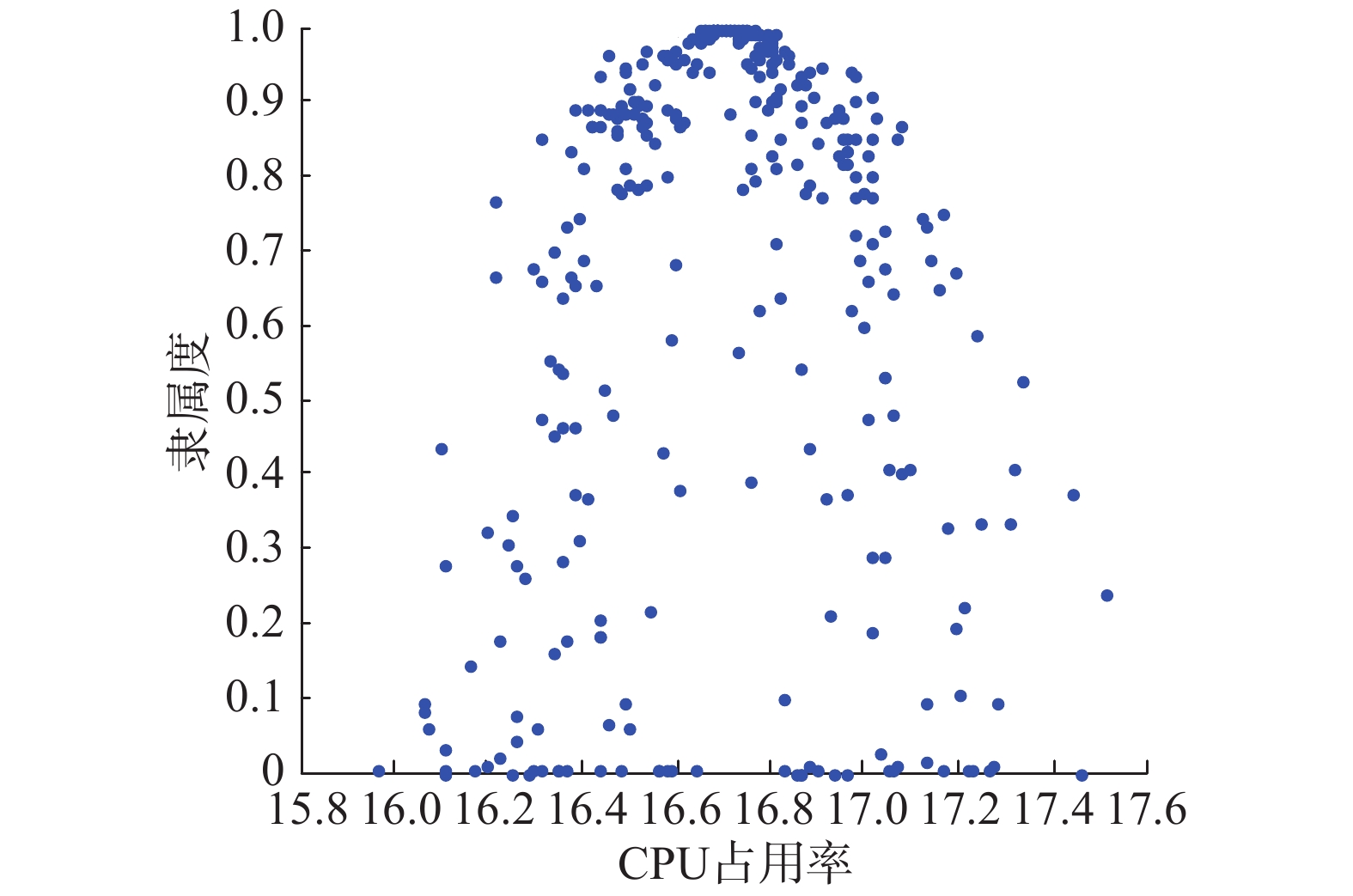
假设资源占用的CPU和内存占用率分别为10%、25%,即输入(10,25),得到云模型推理资源占用结果如图9所示。
|
Download:
|
| 图 9 云模型推理得到资源占用评价 Fig. 9 Resource occupancy evaluation based on cloud model reasoning | |
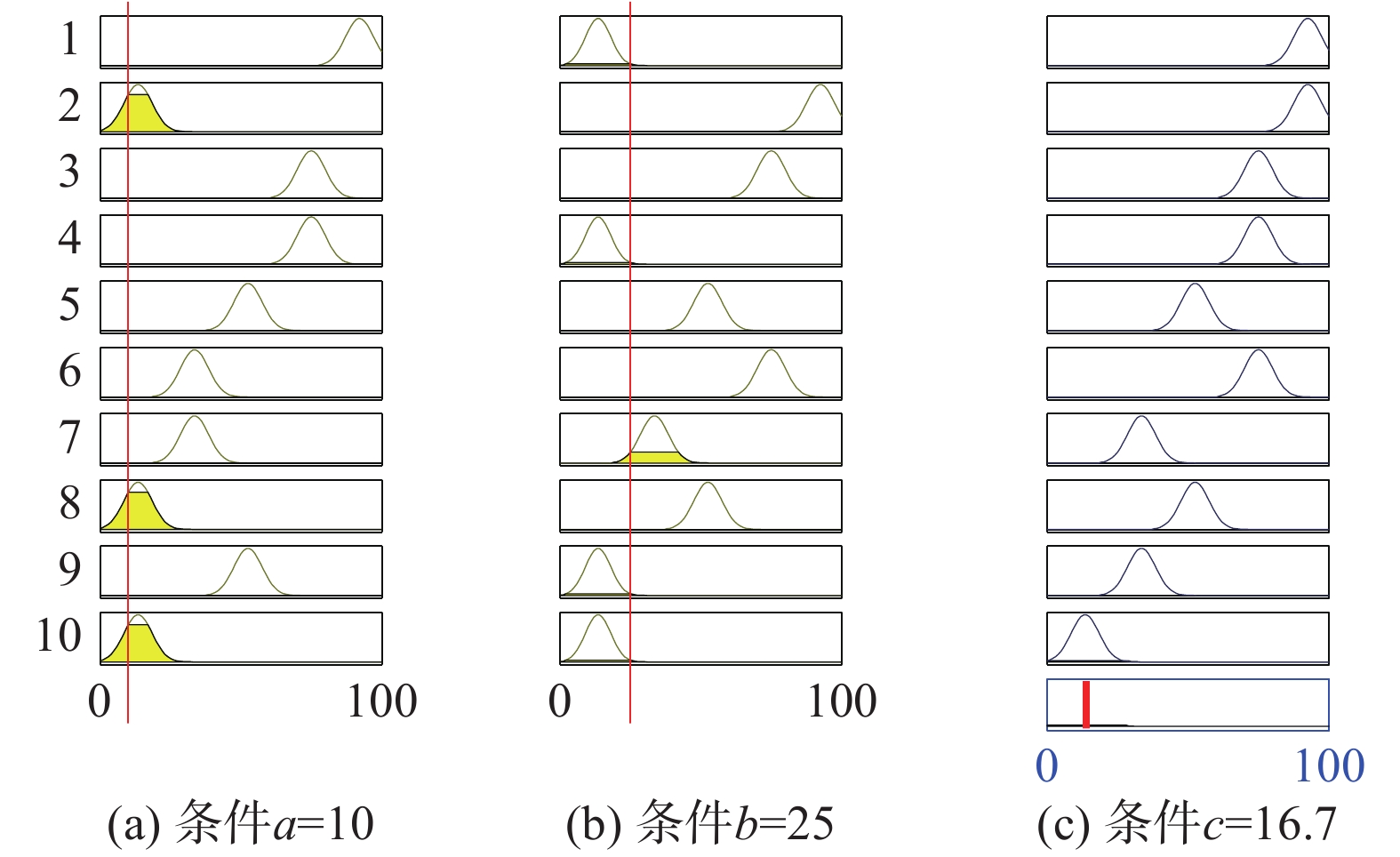
同样输入(10,25),隶属度函数法评价得到系统资源占用的情况如图10所示。
|
Download:
|
| 图 10 隶属度函数法推理出的资源占用 Fig. 10 FIS inference result | |
通过对比云模型和隶属度函数法对资源占用进行评价的两个实验,分析并得出以下结论:
1)云模型推理机进行了10次循环推理得出:第10条云规则为最大触发强度,第8条云规则为次最大触发强度。而隶属度函数法也用同样的输入经推导后得到的系统资源占用输出为16.7,其占用率很低。
2)对比云模型和隶属度函数法针对SCADA系统评价的数据,可以看出云模型得到的系统评价是一个正态分布的数据,有别于传统隶属度函数得到的确切数据,这体现出云模型算法的随机性。
3)隶属度函数法得到的结果是单纯按照训练样本规则来进行计算的,如果待测数据不相似于训练样本,隶属度函数法就不能很好地推理出结论,而通过云模型评价可以进行很好的评价,所以云模型评价得到的系统评价更为科学和可信。
5 结束语本文首先利用因素空间相关理论为SCADA系统构造了信息安全评价的模型,该数学框架描述了信息安全的油气SCADA系统,并创新性地提出云模型推理算法来处理模糊信息,接着构造二维多规则发生器,并在MATLAB上采用云模型对资源占用进行评价。本文将信息的随机性和模糊性特点结合,克服了传统隶属函数法数据不完整的缺点以及模糊推理评价法依赖专家和决策者偏好的主观性,比传统隶属度函数法在结果展现上更为客观,本文的工作对云模型的深入的研究具有重要意义。但是由于本文只针对事中因素的资源占用进行评价,考虑的评价因素不够完善,因此,今后的研究重点会考虑更多的因素,进一步形成系统的风险评价。
| [1] |
饶志宏, 兰昆, 蒲石. 工业SCADA系统信息安全技术[M]. 北京: 国防工业出版社, 2014: 83–120. RAO Zhihong, LAN Kun, PU Shi. Information security technologies on industrial SCADA systems[M]. Beijing: National Defense Industry Press, 2014: 83–120. (  0) 0)
|
| [2] |
陈冬青, 彭勇, 谢丰. 我国工业控制系统信息安全现状及风险[J]. 中国信息安全, 2012(10): 64-70. CHEN Dongqing, PENG Yong, XIE Feng. Information security status and risk of China's industrial control system[J]. China information security, 2012(10): 64-70. DOI:10.3969/j.issn.1674-7844.2012.10.034 (  0) 0)
|
| [3] |
杜湘瑜, 尹全军, 黄柯棣, 等. 基于云模型的定性定量转换方法及其应用[J]. 系统工程与电子技术, 2008, 30(4): 772-776. DU Xiangyu, YIN Quanjun, HUANG Kedi, et al. Transformation between qualitative variables and quantity based on cloud models and its application[J]. Systems engineering and electronics, 2008, 30(4): 772-776. (  0) 0)
|
| [4] |
COOK F S. Secure access point for scada devices[P]. US: 8176532, 2012-05-08.
( 0) 0)
|
| [5] |
KNAPP E D. 工业网络安全[M]. 北京: 国防工业出版社, 2014: 12–145. KNAPP E D. Industrial network security[M]. Beijing: National Defense Industry Press, 2014: 12–145. (  0) 0)
|
| [6] |
IEC. IEC 62443-1-1, Security for industrial automation and control systems. Part 1-1 terminology, concepts, and models[S]. IEC, 2013.
( 0) 0)
|
| [7] |
李静. 基于蜜罐日志分析的主动防御研究和实现[D]. 上海: 上海交通大学, 2009. LI Jing. The research and implementation of initiative defense based on analysis honeypot logs[D]. Shanghai: Shanghai Jiao Tong University, 2009. (  0) 0)
|
| [8] |
刘增良, 刘有才. 因素神经网络理论及其应用[M]. 贵阳: 贵州科技出版社, 1994. Liu Zengliang, LIU Youcai. Factor neural networks and its application[M]. Guiyang: Guizhou Science and Technology Press, 1994. (  0) 0)
|
| [9] |
刘增良, 刘有才. 因素神经网络理论及实现策略研究[M]. 北京: 北京师范大学出版社, 1992. LIU Zengliang, LIU Youcai. Research on the theory of factor neural nerwork and its realization[M]. Beijing: Research on the throry of factor neural network and its realization, 1992. (  0) 0)
|
| [10] |
杨朝晖, 李德毅. 二维云模型及其在预测中的应用[J]. 计算机学报, 1998, 21(11): 961-969. YANG Zhaohui, LI Deyi. Planar model and its application in prediction[J]. Chinese journal of computers, 1998, 21(11): 961-969. DOI:10.3321/j.issn:0254-4164.1998.11.001 (  0) 0)
|
| [11] |
李静. 基于云模型的C2C卖家信任评价方法研究[D]. 天津: 南开大学, 2009. LI Jing. Study on the evaluation method of C2C sellers trust based on cloud model[D]. Tianjin: Nankai University, 2009. (  0) 0)
|
| [12] |
王国胤, 李德毅. 云模型与粒计算[M]. 北京: 科学出版社, 2012: 3–90. WANG Guoyin, LI Deyi. Cloud model and granular computing [M]. Beijing: Science Press, 2012: 3–90. (  0) 0)
|
| [13] |
温景容, 武穆清, 宿景芳. 信息物理融合系统[J]. 自动化学报, 2012, 38(4): 507-517. WEN Jingrong, WU Muqing, SU Jingfang. Cyber-physical system[J]. Acta automatica sinica, 2012, 38(4): 507-517. (  0) 0)
|
| [14] |
FOVINO I N, MASERA M, GUIDI L, et al. An experimental platform for assessing SCADA vulnerabilities and countermeasures in power plants[C]//Proceedings of the 3rd Conference on Human System Interactions. Rzeszow, Poland, 2010: 679–686.
( 0) 0)
|
| [15] |
曹谢东. 模糊信息处理及应用[M]. 北京: 科学出社, 2003: 103–104. CAO Xiedong. Fuzzy information processing and application[M]. Beijing: Science Press, 2003: 103–104. (  0) 0)
|
 2018, Vol. 13
2018, Vol. 13


