2. 计算智能与智能系统北京市重点实验室,北京 100124
2. Beijing Key Laboratory of Computation Intelligence and Intelligence System, Beijing 100124, China
径向基函数(RBF)神经网络由于其准确的局部感知特性和强大的非线性逼近能力,已被广泛应用于时间序列预测、非线性系统在线建模与控制等领域[1]。神经网络的研究和应用对于复杂工业过程建模提供了新的方法;与此同时,神经网络的设计成为非线性动态过程建模的重点和难点。RBF神经网络的性能严重依赖于网络的结构和参数,包括隐含层节点的数量、中心和宽度、隐含层到输出层的连接权值等参数[2]。事实上,如果网络结构越大,系统动力学错综复杂,表现良好的性能,但是会增大计算量和计算时间,容易导致“过拟合”;反之,规模过小,内部动力学过于简单,学习能力不足,不能高精度地逼近非线性映射,而且网络的参数优化算法能够保证网络达到较好的性能,能够较快收敛,因此,RBF网络的结构和参数学习算法研究对于实际应用和理论研究具有重要的实际意义。
为使RBF神经网络能够根据实际被控过程自适应的动态调整,近年来不少学者进行研究。Platt[3]首先提出资源分配网络算法(resource allocation network,RAN),根据实际对象能够动态增加RBF网络隐含层节点,但是该算法只增加隐节点不能删减,对于处理复杂问题时网络结构会出现冗余。在此基础上,为解决这一问题,Lu等[4]提出一种最小资源分配算法(minimal resource allocation network, MRAN),该算法能够在学习过程中增加和删减神经元动态调整去适应被控过程,该方法受到广泛应用,但是却忽略了神经元结构调整之后的参数学习,导致网络收敛速度较慢[5]。Huang[6]提出一种在线调整的RBF结构设计方法;随后出现广义增长修剪算法(generalized growing and pruning RBF,GGAP-RBF),根据隐含层神经元的重要性判断是否增删,但仅仅考虑对新增加或者删减的神经元进行参数调整,有效提高算法的运算速度,但是网络初始值的设定需要依据整体样本数据,因而不适合在线学习。Gonzales[7]采用进化计算的思想,利用其良好的鲁棒性和全局搜索能力对网络的结构和参数进行调整学习,取得较好的效果。文献[8-9]提出用粒子群(particle swarm optimization,PSO)算法自动调整每个RBF网络的中心,宽度和权值,能够获得不错的建模性能,但是该算法由于训练过程中需要全局搜索,需要较长的训练时间而且算法计算复杂,不利于实时在线建模。Lian[10]提出自组织RBF网络(self-organizing RBF, SORBF),设计仅仅采用训练误差作为结构调整判断条件,没有考虑隐含层和输出层之间的相关性以及网络调整后参数设置问题,训练时间较长。Yu等[11]提出基于误差修正的思想,每次采用误差最大的点对应的输入数据作为新增加神经元的中心,采用改进的LM算法优化所有隐节点的参数,训练时间快,能够采用精简的结构去逼近非线性函数,但是该自组织机制只能增加隐节点不能删减,而且对于多输入的输入数据如何判断中心不能很好地确定。要想使RBF网络具有更好的非线性建模性能,完成结构设计之后,寻找快速的参数学习算法对网络的性能也是至关重要的。常见的参数训练算法有BP算法、高斯–牛顿算法和LM算法等。其中,最常用的是BP算法,但是该算法由于搜索空间限制容易陷入局部极小,收敛速度慢等。近年来,具有快速收敛速度和强有力搜索空间的二阶LM算法被引入到训练RBF网络,取得了很好的效果,获得了广泛应用[12-13]。但是该算法由于雅可比矩阵的计算会增加计算量和存储空间,影响算法的训练速度,因此,本文采用一种改进的LM算法对参数进行训练。
针对RBF网络的结构和参数设计问题,首先,利用隐含层和输出层之间的回归关系,采用相对贡献指标结合训练误差信息处理能力,最大程度地挖掘隐含层和输出层之间的隐含信息,解决了RBF网络结构动态调整的问题;同时,采用改进的LM算法,将整个雅可比矩阵的计算转化为向量相乘的形式,避免整个雅可比矩阵的存储,加速算法的训练时间和收敛速度;最终保证RBF网络能够根据实际处理对象的动态过程快速准确地自适应调整结构和参数,达到满意的非线性逼近能力和预测精度,验证了算法的有效性。
1 RBF网络RBF网络是一个包括输入层、隐含层和输出层的3层前馈神经网络,其拓扑结构如图1所示。

|
Download:
|
| 图 1 RBF网络拓扑结构图 Fig. 1 The topology structure of RBF network | |
图1中网络的输入向量为
M为输入向量的维数,隐含层激活函数采用高斯函数,隐含层第j个神经元的输出表达式如式(1)所示。
| ${{\varPhi} _j}(t) = \exp( - \frac{{{{\left\| {{x}(t) - {{c}_j}(t)} \right\|}^2}}}{{\sigma _j^2(t)}})$ | (1) |
式中:Φj(t)为隐含层第j个神经元的输出;‖·‖为欧几里得范数;
| ${y_1}(t) = \sum\limits_{j = 1}^H {{{ w}_{j1}}{{\varPhi} _j}\left( t \right)} $ | (2) |
式中:wi1为第j个隐含层神经元与输出层的连接权值向量,y1(t)为输出层神经元的输出。
2 自组织RBF网络的设计 2.1 相对贡献指标网络结构调整的设计思想是采用回归的思想,分别对隐含层和输出层矩阵进行成分提取为ti和vi,要求提取的成分对于原变量信息具有最大的解释能力,而且具有最大的相关性,得到隐含层神经元和输出层神经元的相对贡献指标,用来表示此神经元对输出神经元的贡献程度;同时结合网络的误差信息处理能力,作为判断结构是否调整的依据。
相对贡献指标:RBF神经网络隐节点j在样本数为P个的相对贡献指标定义为
| ${ RC}\left( j \right) = \frac{{\sum\limits_{i = 1}^r {({{\varUpsilon}_{ij}}{{{\beta}} _i}} )}}{{\sum\limits_{h = 1}^H {(\sum\limits_{i = 1}^r {{{\varUpsilon}_{ih}}{{{\beta}} _i}} } )}}$ | (3) |
式中:
| ${{t}_i} = {{\varPhi} _{i - 1}}{{\varUpsilon}_i},0 \leqslant i \leqslant r$ | (4) |
| ${{\varPhi} _{i - 1}} = {t_i}{{{\alpha}} _i}^{{T}} + {{\varPhi} _i}$ | (5) |
| ${{v}_i} = {{y}_{i - 1}}{{u}_i}$ | (6) |
| ${{y}_{i - 1}} = {{v}_i}{{\beta}_i}^{{T}} + {{y}_i}$ | (7) |
| ${{\beta}_i} = \frac{{{{y}_i}^{{T}}{{t}_i}}}{{{{\left\| {{{t}_i}} \right\|}^2}}}\;\;{{{\alpha}} _i} = \frac{{{{\varPhi }_i}^{{T}}{{t}_i}}}{{{{\left\| {{{t}_i}} \right\|}^2}}}$ | (8) |
式中:ti和vi是第i对成分的得分向量;αi和βi为成分的负荷量;Φi和yi为第i次迭代产生的残差矩阵,不断迭代直到得到r个成分, 并且r=rank(Φ0);Φ0是隐含层矩阵和输出矩阵对P个样本的标准化矩阵。另外要求提取的成分具有最大的相关性,通过拉格朗日法转化为求权重向量ϒi和ui。进而求出相对贡献指标。
2.2 结构调整机制 2.2.1 神经元增加机制结合上述相对贡献指标RC和网络误差信息处理能力作为神经元增加机制的判定条件,当算法迭代t次的误差比t–n大时,代表此时网络对于动态过程的信息处理能力不足,需要增加新的隐节点,分裂当前隐含层神经元和输出神经元之间具有最大相对贡献的隐含层神经元j,此神经元表示和输出神经元之间具有最大的贡献度,即满足式(9):
| $\left\{ {\begin{array}{*{20}{c}} {E(t) - E\left( {t - n} \right) > 0} \\ {j = { arg} \mathop { max}\limits_{1 \leqslant j \leqslant H} ({{RC}}(j))} \end{array}} \right.$ | (9) |
式中:E(t)和E(t–n)分别为迭代步数t和t–n时的训练误差,n是样本间隔,j是隐含层神经元和输出神经元相对贡献RC最大的神经元,H是在t时刻存在的隐含层神经元数量。对新增加的神经元参数设置为
| ${{c}_{ new}}(t) = \frac{1}{2}\left( {{{c}_j}(t) + {x}(t)} \right)$ | (10) |
| ${\sigma _{ new}}(t) = {\sigma _j}(t)$ | (11) |
| ${{w}_{ new}}(t) = {{e}_j}(t){({{\varPhi} _{ new}}(t))^{ - 1}}$ | (12) |
式中:cj(t)、σj(t)分别代表第j个神经元分裂前的中心和宽度;cnew、σnew代表新增加神经元的中心和宽度;wnew为新增加神经元的输出连接权值;ej(t)为t时刻神经网络的误差;Φnew(t)为新增加神经元的隐含层输出值。
2.2.2 神经元删减机制如果当前第k个隐含层神经元和输出层的RC小于设定的阈值ε,说明此神经元对输出的相对贡献较小,可以认为此神经元对输出的贡献很小甚至可以忽略,所以删掉第k个神经元,则满足:
| $\left\{ {\begin{array}{*{20}{c}} {{ min}({{RC}}(j)) < \varepsilon } \\ {k = { arg} \mathop { min}\limits_{1 \leqslant j \leqslant H} ({ RC}(j))} \end{array}} \right.$ | (13) |
式中:k是隐含层神经元和输出神经元相对贡献最小的神经元,ε为设定的删减阈值。
| ${c}_{_{i - 1}}'(t) = {{c}_k}(t)$ | (14) |
| $\sigma _{i - 1}'(t) = {\sigma _k}(t)$ | (15) |
| $w_{i - 1}^{''}(t) = w_{i - 1}'(t) + \frac{{{{{\varPhi }}_k}(t)}}{{{{\varPhi }}_{i - 1}'(t)}}{w_k}(t)$ | (16) |
式中:
采用改进的LM算法(improved LM algorithm, ILM)去优化RBF网络的中心、宽度和权值。不同于之前算法的矩阵运算方式,文中采用一种将矩阵运算转化为向量相乘的方式,不需要存储整个雅可比矩阵,这样避免整个雅可比矩阵的计算,适用于输入数量比较多。其中,拟海森矩阵和梯度向量的计算通过子矩阵及其子向量叠加和的方式来得到的[15]。同时,在训练过程中算法引入自适应学习率,这样能够加快网络的收敛速度,提高算法的预测精度。具体更新规则如式(17)所示:
| ${{\varOmega }}\left( {t + 1} \right) = {{\varOmega }}\left( t \right) - {\left( {{{Q}}\left( t \right) + {{\lambda }}(t){{I}}} \right)^{ - 1}}{{\varTheta }}(t)$ | (17) |
式中:Ω(t)为更新规则包含参数向量,Θ(t) 为梯度向量,Ԛ(t)为拟海森矩阵,I是为了避免拟海森矩阵奇异设置的单位矩阵,根据文献[16],自适应学习率λ(t)被定义为
| $\lambda \left( t \right) = \alpha \left\| {{e}\left( t \right)} \right\| + \left( {1 - \alpha } \right)\left\| {{ j}{{\left( t \right)}^{{T}}}{e}\left( t \right)} \right\|$ | (18) |
式中:α为正实数,α∈(0, 1)。参数向量Ω(t)包括更新网络的所有参数:连接权值w,中心向量c,宽度向量σ。
| $\begin{array}{c}{{\varOmega }}(t) = \left[ {{w_{^1}}(t) \cdots {w_{^h}}(t) \cdots {w_{^H}}(t)}\;{c_1}_1(t) \cdots {c_{1,j}}(t) \cdots {c_{h,P}}(t)\;{{\sigma _1}(t) \cdots {\sigma _h}(t) \cdots {\sigma _H}(t)} \right]\end{array}$ | (19) |
拟海森矩阵Ԛ(t)和梯度向量Θ(t)的计算分别是对应的子矩阵与子向量的累加求和得到的,计算公式为
| ${Q}(t) = \sum\limits_{p = 1}^P {{{q}_p}(t)} ,p = 1,2 \cdots \!,P$ | (20) |
| ${{\varTheta }}(t) = \sum\limits_{p = 1}^P {{{\varphi} _p}(t)} ,p = 1,2 \cdots \!, P$ | (21) |
式中:P是样本总数,子矩阵qp(t)与子向量φp(t)的计算公式分别为
| ${{q}_p}(t) = {{{j}}_p}{(t)^{{T}}}{{{j}}_p}(t)$ | (22) |
| ${{\varphi} _p}\left( t \right) = {{{j}}_p}{\left( t \right)^{{T}}}{{ e}_p}\left( t \right)$ | (23) |
第p个样本的训练误差定义为
| ${{e}_p}\left( t \right) = {{y}_p}\left( t \right) - {{o}_p}\left( t \right)$ | (24) |
式中:P为样本数,ep(t)为训练误差,yp(t)与op(t)是分别为第p个输入样本对应的网络输出与实际输出,雅克比矩阵行向量jp(t)如式(25)所示:
| $\begin{array}{c}{{j}_p}\left( t \right) = \left[ {\displaystyle\frac{{ {{e}_p}\left( {t} \right)}}{{ {{w}_1}\left( {t} \right)}} \cdots \frac{{ {{e}_p}\left( {t} \right)}}{{ {{w}_H}\left( {t} \right)}}\;\frac{{ {{e}_p}\left( {t} \right)}}{{ {\sigma _1}\left( {t} \right)}} \cdots \frac{{ {{e}_p}\left( {t} \right)}}{{ {\sigma _H}\left( {t} \right)}}}\; \displaystyle\frac{{ {{e}_p}\left( {t} \right)}}{{ {{c}_{1,1}}\left( {t} \right)}} \cdots \frac{{ {{e}_p}\left( {t} \right)}}{{ {{c}_{h,i}}\left( {t} \right)}} \cdots \frac{{ {{e}_p}\left( {t} \right)}}{{ {{c}_{H,I}}\left( {t} \right)}} \right]\end{array}$ | (25) |
根据文献[17]式(25)中误差对权值的导数,误差对宽度的导数,误差对中心的导数计算公式分别为
| $\frac{{ {{e}_p}}}{{ {{w}_h}}} = - \frac{{ {{o}_p}}}{{ {{w}_h}}} = - {{\varphi }_h}\left( {{{x}_P}} \right)$ | (26) |
| $\begin{array}{c}\displaystyle\frac{{ {{e}_p}}}{{ {\sigma _h}}} = - \frac{{ {{o}_{p,1}}}}{{ {\sigma _h}}} = - \frac{{ {o_p}}}{{ {\varphi _h}\left( {{{x}_P}} \right)}}\frac{{ {\varphi _h}\left( {{{x}_P}} \right)}}{{ {\sigma _h}}}{{ = }}\\ - \displaystyle\frac{{2{{w}_{h,1}}{\varphi _h}({{x}_p}){{\left\| {{{x}_{p,i}} - {{c}_h}_{,i}} \right\|}^2}}}{{\sigma _h^3}}\end{array}$ | (27) |
| $\begin{array}{c}\displaystyle\frac{{ {{e}_p}}}{{ {{c}_{h,i}}}} = - \frac{{ {{o}_p}}}{{ {{c}_{h,i}}}} = - \frac{{ {{o}_p}}}{{ {\varphi _h}\left( {{{x}_P}} \right)}}\frac{{ {\varphi _h}\left( {{{x}_P}} \right)}}{{ {{c}_{h,i}}}}{{ = }}\\[10pt] - \displaystyle\frac{{2{{w}_{h,m}}{\varphi _h}({{x}_p})({{x}_{p,i}} - {{c}_{h,i}})}}{{\sigma _h^2}}\end{array}$ | (28) |
雅可比矩阵行向量jp(t)的计算由式(26)~(28)计算得到,对于所有输入模式,拟海森矩阵和梯度向量分别由式(20)和(21)得到,然后应用更新规则(17)对3个参数同时进行更新。采用上述ILM算法去优化RBF网络参数,加快算法的收敛速度并且提高网络的预测准确度。
RC-RBF 网络的设计算法的步骤如下:
1) 初始随机给定一个RBF神经网络,输入节点与输出节点个数根据具体实验设置,隐节点个数随机设定,所有的参数随机产生在一个小范围内。
2) 对于输入样本x(t),隐含层到输出层之间的权值、宽度、中心分别通过式(26)~(28)进行调整,采用固定样本个数的在线形式,然后,判断神经网络是否满足结构调整条件,满足条件则转向3),否则转向6)。
3) 根据式(3)计算当前存在的隐含层神经元与网络输出计算相对贡献指标RC,如果第t步的训练RMSE比第t-n步大时:e(t)-e(t-n)>0时,则转向4);转向5),判断是否满足删减条件,否则转向6)。
4) 此时,说明神经网络信息处理能力不足,需要增加神经元,按照式(9),选出相对贡献指标最大的神经元进行分裂,根据式(10)~(12)对新增加神经元的设定初始化参数。
5) 如果满足删减条件(13),则删除相对指标贡献值小于阈值ε的隐含层神经元,删除与此神经元的连接权值、中心和宽度,并利用式(14)~(16)对其临近的神经元的相应参数进行调整。
6) 利用改进的LM算法对神经网络的参数进行更新。
7) 满足停止条件或达到计算次数时停止计算,否则转向2)(网络结构还需调整)进行重新训练。
3 收敛性分析网络是否收敛决定了算法的性能,因为网络在结构调整之后对其收敛性往往不能保证,以下给出结构调整阶段的收敛性证明,主要分为3部分:1)隐节点增加阶段;2)隐节点删减阶段;3)隐节点数目不变的阶段。
假设:当前网络存在J个隐含层神经元,当前时刻的误差为eJ(t)。
1)当满足神经元增加条件时,分裂神经元,此时神经元数目变为J+1个,此时网络的误差变为
| $\begin{array}{c}{{{e}'}_{J + 1}}(t) = {y_p}(t) - \displaystyle\sum\limits_{j = 1}^{J + 1} {{w_j}} (t){{\varPhi }_j}(t) = \\{y_p}(t) - (\displaystyle\sum\limits_{j = 1}^J {{w_j}} (t){{\varPhi }_j}(t) + {w_{ new}}(t){{\varPhi }_{ new}}(t)) = \\{e_j}(t) - \displaystyle\frac{{{e_j}(t)}}{{{{\varPhi }_{ new}}(t)}}{{\varPhi }_{ new}}(t) = 0\end{array}$ | (29) |
可以看出,隐含层新增加神经元之后,其参数设置对网络的输出误差进行了补偿,调整后误差为0,一定程度上加快算法的学习速度。
2)当满足删减条件时,删除第k个神经元,此时神经元的数量变为J-1,神经网络的输出误差为
可以看出,删掉神经元与输出之间的连接权值,中心,宽度等参数,对其邻近的神经元进行参数更新,神经元调整前后,神经网络的输出误差相等,可见结构删减对网络的误差没有产生影响。
| $\begin{array}{c}{e}{'_{J - 1}}(t) = {y_p}(t) - \displaystyle\sum\limits_{j = 1}^{J - 1} {{w_j}} (t){{\varPhi }_j}(t) = \\{y_p}(t) - (\displaystyle\sum\limits_{j = 1,j \ne k,j \ne i - 1}^J {{w_j}} (t){{\varPhi }_j}(t) + {w_{i - 1}}(t){{\varPhi }_{i - 1}}(t)) = \\{y_d}(t) - (\displaystyle\sum\limits_{j = 1,j \ne k,j \ne i - 1}^J {{w_j}} (t){{\Phi }_j}(t) + \\\left( {w_{_{i - 1}}'(t) + \displaystyle\frac{{{{\varPhi }_k}(t)}}{{{\varPhi }_{i - 1}'(t)}}{w_k}(t)} \right){\varPhi }_{_{i - 1}}'(t)) = \\{y_d}(t) -\displaystyle \sum\limits_{j = 1,j \ne i - 1}^J {{w_j}} (t){{\varPhi }_j}(t) - w_{_{i - 1}}'(t){{\varPhi }_{i - 1}}(t) {e_J}(t)\end{array}$ | (30) |
3) 隐节点数目不变的阶段
为了证明算法在固定神经元时算法的收敛性,定义一个Lyapunov函数:
| $F({\varOmega} (t)) = \frac{1}{2}{{{e}}^{{T}}}(t){{e}}(t)$ | (31) |
根据泰勒展开式可以得到,Lyapunov函数F(Ω(t))的变化量:
| $\begin{array}{c} \Delta F({{\varOmega }}(t)) = F({{\varOmega }}(t + 1)) - F({{\varOmega }}(t)) = \\ - \nabla {E^{{T}}}({{\varOmega }}(t))\Delta {{\varOmega }}(t) + \\ \displaystyle\frac{1}{2}\Delta {{{\varOmega }}^{{T}}}(t){\nabla ^2}{E}({{\varOmega }}(t))\Delta {{\varOmega }}(t) \\ \end{array} $ | (32) |
| $\nabla E({{\varOmega }}(t)) = {{\varTheta }}({{\varOmega }}(t))$ | (33) |
| ${\nabla ^2}{E}({{\varOmega }}(t)) = {Q}({{\varOmega }}(t)) + \lambda (t){{I}}$ | (34) |
式中:
| $\Delta {{\varOmega }}(t) = {({Q}({{\varOmega }}(t)) + \lambda (t){{I}})^{ - 1}}{{\varTheta }}(t)$ | (35) |
现在有以下收敛定理:
假设RC-RBF神经网络中的隐含层神经元数为固定J,同时网络参数根据式(17)中的规则进行更新,如果满足以下假设:
| $\left\| {\Delta {{\varOmega }}(t)} \right\| \leqslant { min}\left\{ \left\| {\Delta {{\varOmega }}(t - 1)} \right\|,\frac{{{{\varTheta }}({{\varOmega }}(t - 1))}}{{{{Q}}({{\varOmega }}(t - 1))}}\right\} $ | (36) |
那么,结合等式(32)~(34)可以得到
| $\Delta {{F}}({{\varOmega }}(t)) = - \frac{1}{2}\Delta {{{\varOmega }}^{{T}}}(t){\nabla ^2}{{E}}({{\varOmega }}(t))\Delta {{\varOmega }}(t)$ | (37) |
| $\Delta {{F}}({{\varOmega }}(t)) < 0$ | (38) |
由此可以得出Lyapunov函数F(Ω(t))不是增加的,进一步得出当e(t)→0,网络收敛
| $\mathop {\lim }\limits_{t \to \infty } e(t) = {0}$ | (39) |
综上所述,通过网路误差补偿更新神经元的参数,对神经元增长和删减两阶段的收敛性证明;同时也对结构固定阶段的RBF网络的收敛性也进行证明,因此提出设计方法的收敛性得以验证。
4 仿真实验RC-RBF神经网络能够根据研究对象的复杂动态变化在线调整隐含层神经元的个数,提高网络的预测能力,为验证算法的有效性和可行性,对Mackey-class时间序列和污水处理关键出水参数氨氮预测进行预测实验,对其算法进行验证。
利用均方根误差函数作为衡量网路的性能指标函数,计算公式如式(40)所示。
| ${ RMSE}(t) = \sqrt {\frac{1}{{2P}}\sum\limits_{p = 1}^P {{{({y_p}(t) - {o_p}(t))}^2}} } $ | (40) |
式中:P为样本总数,yp(t)为第p个样本t时刻对应的网络输出,op(t)为第p个样本t时刻对应的期望输出。
1) Mackey-Glass时间序列预测
Mackey-Glass时间序列预测是一个典型的验证自组织网络性能的基准函数[18]。其微分方程表达式如式(41)所示:
| $x(t + 1) = (1 - a)x(t) + \frac{{bx(t - \tau )}}{{1 + {x^{10}}(t - \tau )}}$ | (41) |
式中:a=0.1,b=0.2,τ=17,并且初始条件为x(0)=1.2, p=6, Δt=6。过去的4个值{x(t), x(t–Δt), x(t–2Δt), x(t–3Δt)}去预测x(t+p)的值,预测模型如式(42)所示:
| $x\left( {t + p} \right) = f\left[ {x\left( t \right),x\left( {t - \Delta t} \right),x\left( {t - 2\Delta t} \right),x\left( {t - 3\Delta t} \right)} \right]$ | (42) |
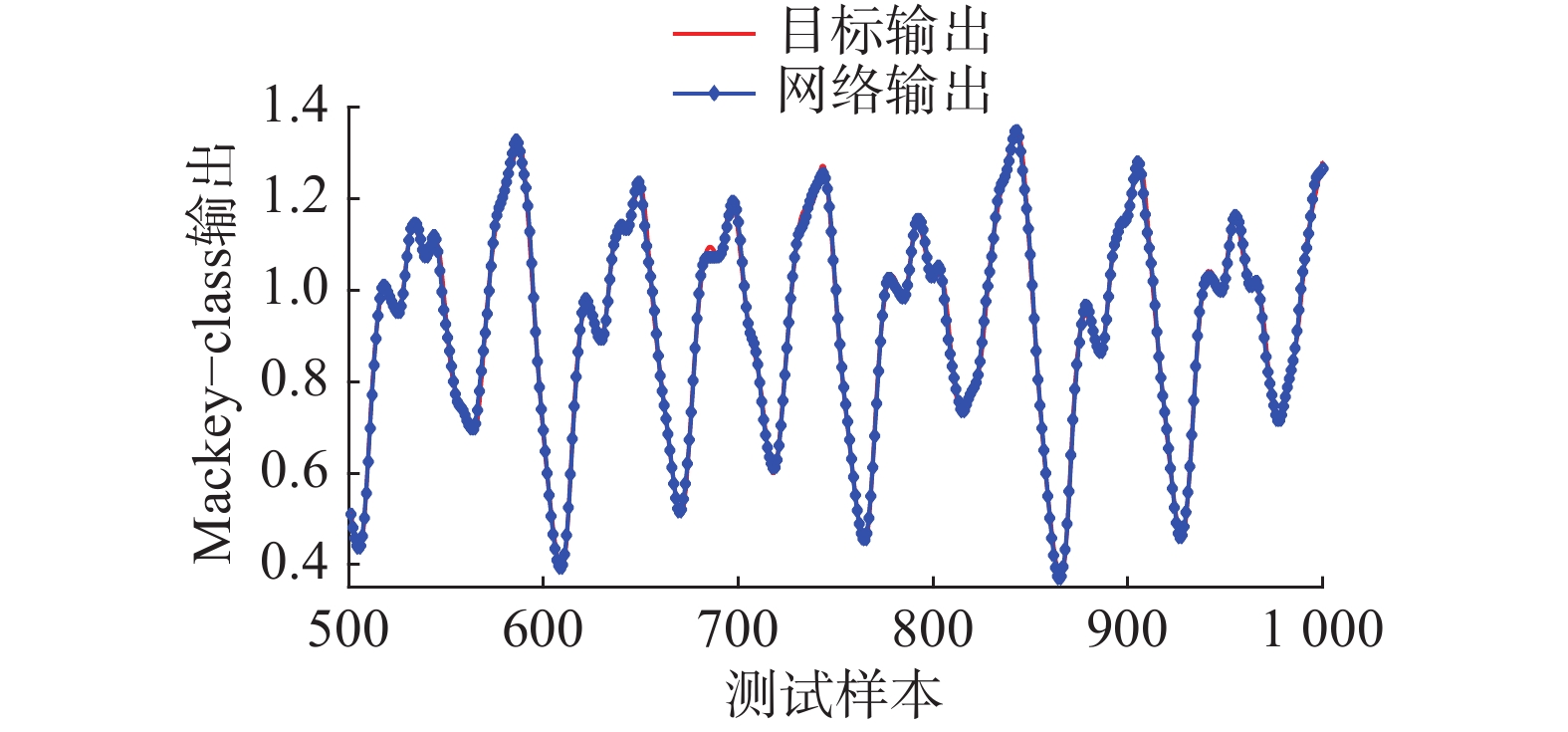
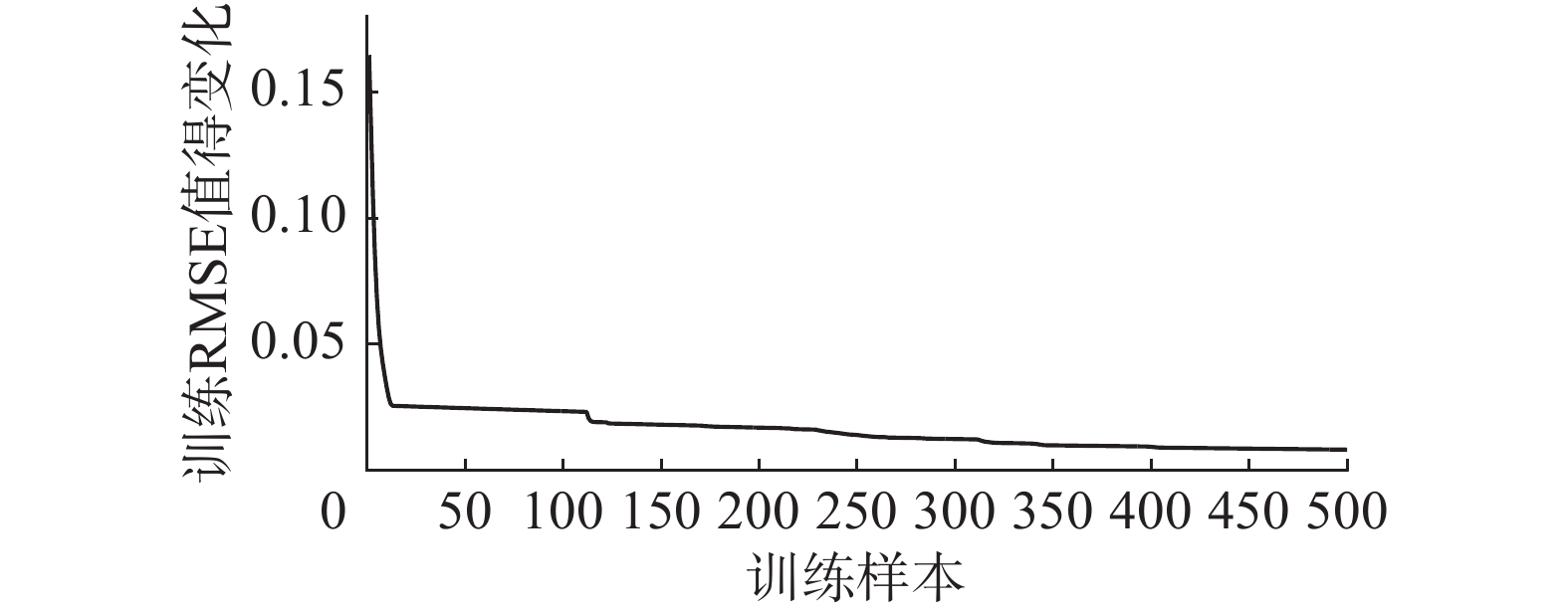
根据式(42)产生1 000个数据,其中,t∈[136, 535]产生500组作为训练数据,t∈[636, 1 135]产生的500组用作测试数据。网络的初始结构为4-3-1,阈值ε为0.1。图2~5的仿真结果分别为训练过程中隐节点数目的变化,网络测试输出和实际输出曲线,Mackey-class测试误差曲线,训练RMSE变化曲线。
|
Download:
|
| 图 2 Mackey-class测试输出和实际输出 Fig. 2 The curve of Mackey-class test output and actual output | |

|
Download:
|
| 图 3 Mackey-class测试误差曲线 Fig. 3 The curve of Mackey-class testing error | |
|
Download:
|
| 图 4 训练RMSE值的变化曲线 Fig. 4 The curve of training RMSE value | |

|
Download:
|
| 图 5 训练过程中隐节点的数目变化 Fig. 5 The number of hidden layer numbers | |
从图2可以看出,网络的测试输出与实际输出曲线基本吻合,说明该方法能够较好地逼近非线性时间序列。图3中显示网络的测试误差曲线,误差值范围保持在[-0.04, 0.04]较小的范围内,表现出良好的泛化性能。图4显示的网络训练RMSE变化曲线,误差随着训练过程一直保持下降趋势,证明表2算法能够快速收敛到满意的性能。
为了验证算法的有效性,该方法与其他自组织神经网络进行对比,NFN-FOESA[19],自组织RBF神经网络(self-organizing RBF neural networks, SORBF)[20],增长–修剪RBF神经网络(growing and pruning RBF neural networks, GAP-RBF)[21]、RBF-AFSII[22]、SOFMLS[23]。表1展现了不同算法的性能指标,从表中可以看出,和其他方法相比,该方法能够采用较精简的结构很好地逼近非线性时间序列。
| 表 1 不同算法的性能对比 Tab.1 The performance of different algorithms |
| 表 2 不同算法的性能对比 Tab.2 The performance of different algorithms |
2) 污水处理关键水质参数氨氮预测
出水水质参数预测模型的建立对于污水处理中减少微生物风险和过程的优化控制提供了一定的管理决策支持依据。由于污水处理过程中影响硝化和反硝化的因素众多,动力学反应及其复杂,导致影响氨氮的参数很多,而且各参数之间相互作用,具有强烈的耦合和非线性特性,因此很难精确建立其机理模型;而且,氨氮的检测,现在大多采用实验室取样离线分析,操作繁琐,需要很长的时间才能检测出等原因,不利于实时准确获得水质参数。因此,采用数据驱动的方式,利用上述方法根据污水处理厂实际输入输出数据对氨氮这一出水参数建立准确快速的软测量模型。
实验过程中,数据取自北京市某污水处理厂2014年的真实测量数据,剔除异常数据并进行数据归一化之后,140组数据作为训练数据,50组数据作为测试数据。为消除输入数据间的高度相关性通过主元分析的方法,选出对氨氮影响较大的输入变量,依次为温度T (Temperature),好氧前段DO (Dissolved Oxygen),好氧末端总固体悬浮物TSS (Total suspended solids concentration),出水PH (Acidity and basicity),厌氧末端ORP (Oxidation-reduction potential),泥龄。输出变量为出水氨氮。网络的初始结构为6-2-1,删减阈值设为0.1。预测性能通过预测精度pa(prediction accuracy)来衡量。
| ${ pa} = \frac{{\sum\limits_{t = 1}^N {(1 - |{y_p}(t) - o(t)|/o(t))} }}{N}$ | (43) |
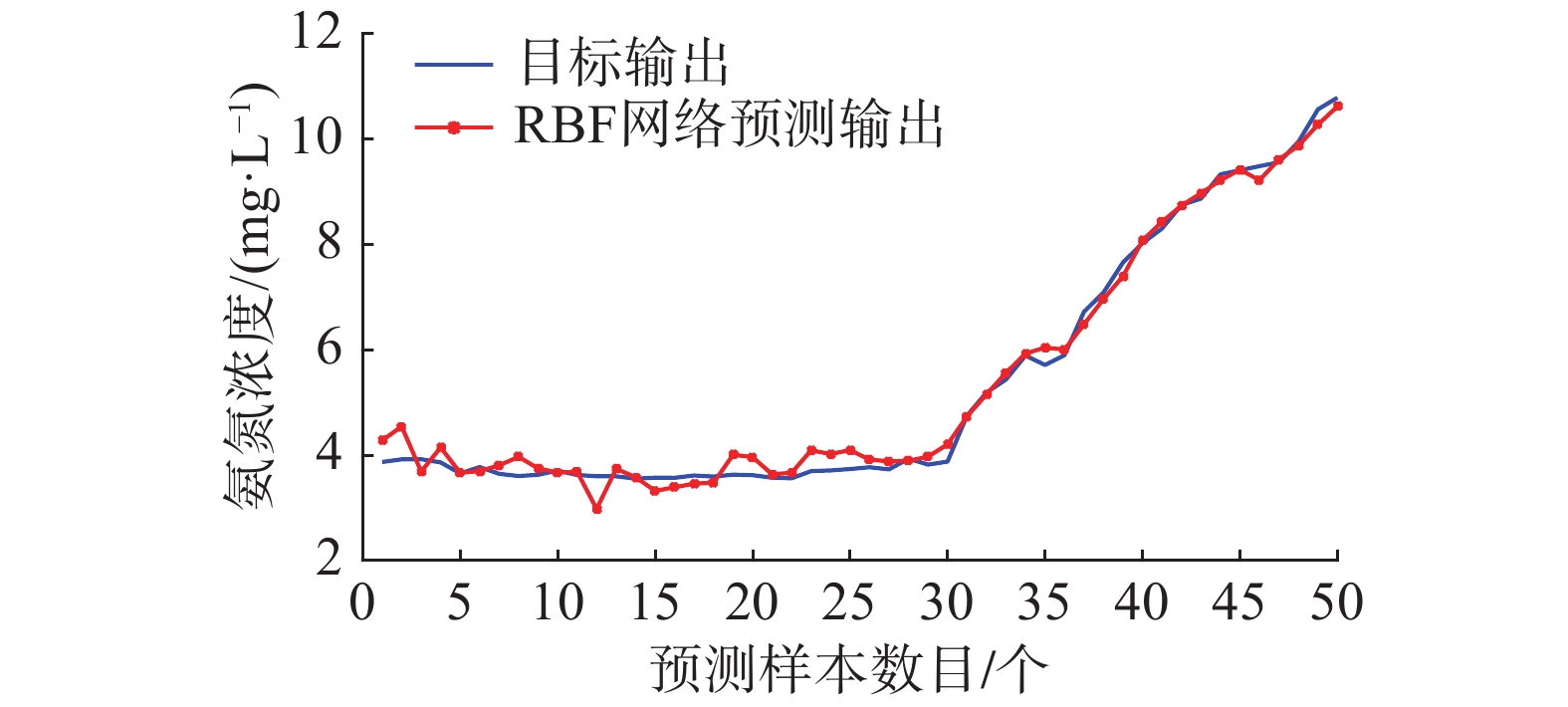
预测精度pa越大,说明基于RC-RBF神经网络的氨氮预测模型性能越好。实验仿真结果如图6~10。

|
Download:
|
| 图 6 网络训练输出和实际输出曲线 Fig. 6 Network training output and Actual output | |
|
Download:
|
| 图 7 训练RMSE值变化 Fig. 7 The curve of tranining RMSE value | |

|
Download:
|
| 图 8 训练过程中隐节点的数目变化 Fig. 8 The number of hidden layer number | |
|
Download:
|
| 图 9 网络测试输出和实际输出 Fig. 9 The curve of test the actual output | |
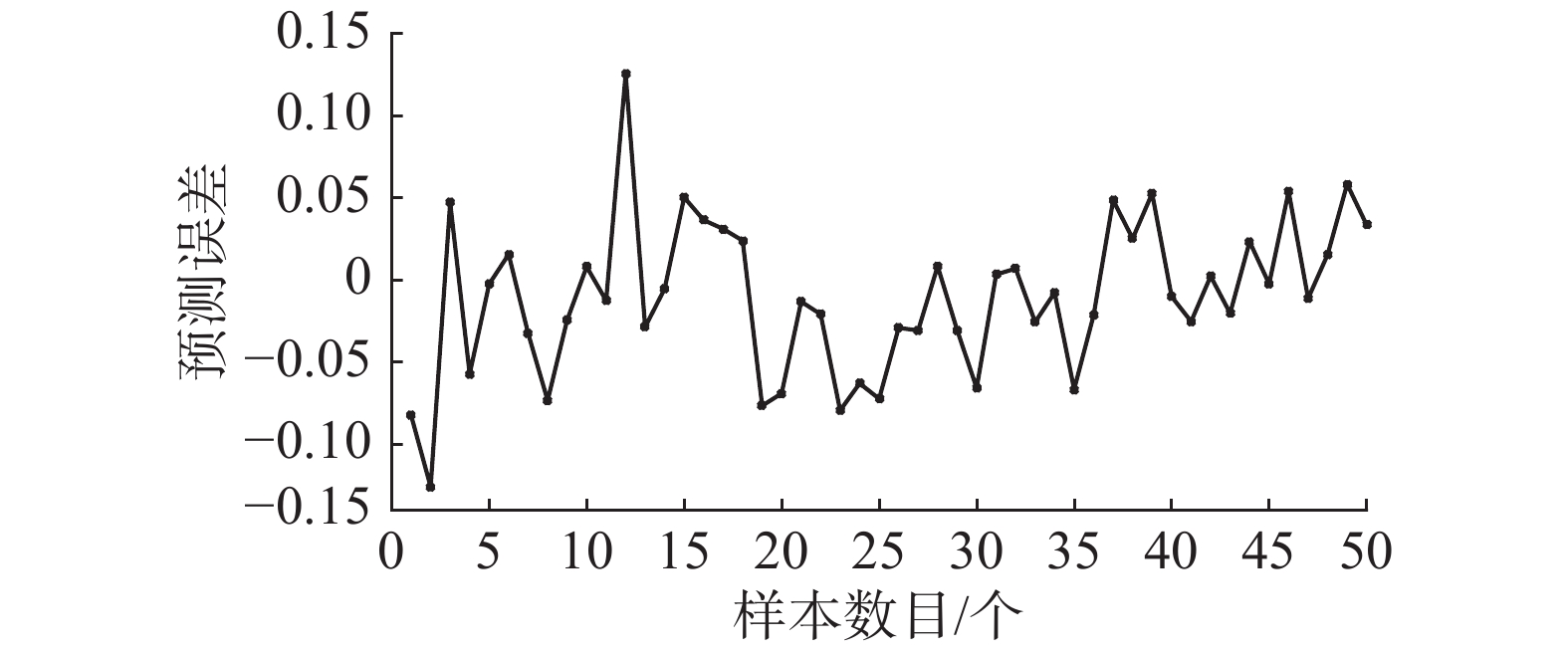
从仿真结果可以看出,图6显示的RBF网络训练输出和氨氮实际输出曲线,曲线基本重合,可以看出算法对污水处理动态过程具有较好的学习能力。图7表明算法在训练过程中RMSE的值呈现下降趋势,训练时间为仅为1.24 s,快速收敛到较小的期望误差。图9显示RBF网络测试输出和实际输出变化曲线,测试输出值和氨氮实际值基本吻合。从图10网络测试误差曲线看出,测试误差较小,说明对于实际非线性动态变化过程,RC-RBF神经网络表现出良好的泛化能力。为了说明该方法针对氨氮预测的有效性,还和其他方法进行对比,采用固定神经元的改进LM算法(Improved LM algorithm, ILM)优化的RBF网络(ILM-RBF),RBF神经网络,BP网络3个对比实验。表2显示了算法的性能对比。从中可以看出,和其他方法相比,该方法对于氨氮的预测精度更高,训练和测试误差都较小。
|
Download:
|
| 图 10 网络测试误差曲线 Fig. 10 The curve of network testing error | |
基于以上仿真结果,可以得出基于改进的自适应LM算法的自组织RBF神经网络能够很好地对污水处理氨氮指标快速准确地在线预测,并且具有较小的测试误差和较高的预测精度,对于污水处理出水参数的实时监测和控制具有重要的意义,有利于污水处理厂的正常运行。
5 结束语文中通过采用相对贡献指标来设计网络结构;同时,采用改进的LM算法训练RBF神经网络的参数,使得网络能够根据非线性系统准确快速地在线结构调整和参数优化,并表现出良好的泛化能力和预测精度,一定程度上提高了RBF神经网络的非线性系统的建模性能和算法的鲁棒性。
1) 提出基于相对贡献指标结合误差信息处理能力来最大程度的挖掘隐含层神经元对输出神经元的相对贡献,作为判断网络结构是否删减的条件,并且对增加和删减阶段的神经元参数进行更新补偿;同时,证明网络结构删减和增加阶段,神经元固定3个阶段的收敛性,证明结构动态变化过程是收敛的。
2) 采用改进的LM算法,将矩阵运算转化为向量相乘的方式,避免整个雅可比矩阵的存储,有效地减少了训练时间和矩阵的存储空间,自适应学习率的引入加快算法的收敛速度,并且提高了算法的预测性能。
3) 采用改进LM算法的RC-RBF神经网络通过对Mackey-class时间序列预测和污水处理过程的出水参数氨氮进行建模预测,仿真实验可以看出网络对于解决实际问题和非线性函数逼近实验都具有较好的泛化能力和预测精度。
综上所述,本文提出的相对贡献指标结合网络信息处理能力能够有效解决RBF网络的结构调整问题;同时采用具有快速收敛特性的改进LM算法对网络参数优化,非线性时间序列仿真实验和污水处理氨氮预测实验都证明算法具有较好的预测精度,对于实际非线性系统的建模与应用有一定的理论意义和可行性。
| [1] |
QIAO J F, ZHANG Z Z, BO Y C. An online self-adaptive modular neural network for time-varying systems[J]. Neurocomputing, 2014, 125: 7-16. DOI:10.1016/j.neucom.2012.09.038 ( 0) 0)
|
| [2] |
韩红桂, 李淼, 乔俊飞. 基于模型输出敏感度分析的动态神经网络结构设计[J]. 电子学报, 2010, 38(3): 731-736. HAN Honggui, LI Miao, QIAO Junfei. Design of dynamic neural network based on the sensitivity analysis of model output[J]. Acta electronica sinica, 2010, 38(3): 731-736. (  0) 0)
|
| [3] |
PLATT J. A resource-allocating network for function interpolation[J]. Neural computation, 1991, 3(2): 213-225. DOI:10.1162/neco.1991.3.2.213 ( 0) 0)
|
| [4] |
LU Y G, SUNDARARAJAN N, SARATCHANDRAN P. A sequential learning scheme for function approximation using minimal radial basis function neural networks[J]. Neural computation, 1997, 9(2): 461-478. DOI:10.1162/neco.1997.9.2.461 ( 0) 0)
|
| [5] |
PANCHAPAKESAN C, PALANISWAMI M, RALPH D, et al. Effects of moving the center's in an RBF network[J]. IEEE transactions on neural networks, 2002, 13(6): 1299-1307. DOI:10.1109/TNN.2002.804286 ( 0) 0)
|
| [6] |
HUANG G B, SARATCHANDRAN P, SUNDARARAJAN N. A generalized growing and pruning RBF (GGAP-RBF) neural network for function approximation[J]. IEEE transactions on neural networks, 2005, 16(1): 57-67. DOI:10.1109/TNN.2004.836241 ( 0) 0)
|
| [7] |
GONZALEZ J, ROJAS I, ORTEGA J, et al. Multi-objective evolutionary optimization of the size, shape, and position parameters of radial basis function networks for function approximation[J]. IEEE transactions on neural networks, 2003, 14(6): 1478-1495. DOI:10.1109/TNN.2003.820657 ( 0) 0)
|
| [8] |
FENG H M. Self-generation RBFNs using evolutional PSO learning[J]. Neurocomputing, 2006, 70(1): 241-251. ( 0) 0)
|
| [9] |
HAO C, YU G, XIA H. Online modeling with tunable RBF network[J]. IEEE transactions on cybernetics, 2013, 43(3): 935-947. DOI:10.1109/TSMCB.2012.2218804 ( 0) 0)
|
| [10] |
LIAN J M, LEE Y G, SCOTT D, et al. Self-organizing radial basis function network for real-time approximation of continuous-time dynamical systems[J]. IEEE transactions on neural networks, 2008, 19(3): 460-474. DOI:10.1109/TNN.2007.909842 ( 0) 0)
|
| [11] |
YU H, REINER P D, XIE T T, et al. An incremental design of radial basis function networks[J]. IEEe transactions on neural networks and learning systems, 2014, 25(10): 1793-1803. DOI:10.1109/TNNLS.2013.2295813 ( 0) 0)
|
| [12] |
CONSTANTINOPOULO C, LIIKAS A. An incremental training method for the probabilistic RBF network[J]. IEEE transactions on neural networks, 2006, 17(4): 966-974. DOI:10.1109/TNN.2006.875982 ( 0) 0)
|
| [13] |
CHEN S, HANZO L, TAN S. Symmetric complex-valued RBF receiver for multiple-antenna-aided wireless systems[J]. IEEe transactions on neural networks, 2008, 19(9): 1659-1665. DOI:10.1109/TNN.2008.2000582 ( 0) 0)
|
| [14] |
王晓丽, 黄蕾, 杨鹏, 等. 动态RBF神经网络在浮选过程模型失配中的应用[J]. 化工学报, 2016, 3(67): 897-902. WANG Xiaoli, HUANG Lei, YANG Peng, et al. Dynamic RBF neural networks for model mismatch problem and its application in flotation process[J]. CIESC journal, 2016, 3(67): 897-902. (  0) 0)
|
| [15] |
WILAMOWSKI B M, YU H. Improved computation for Levenberg–Marquardt training[J]. IEEE transactions on neural networks, 2010, 21(6): 930-937. DOI:10.1109/TNN.2010.2045657 ( 0) 0)
|
| [16] |
MA C, JIANG L. Some research on Levenberg–Marquardt method for the nonlinear equations[J]. Applied mathematics and computation, 2007, 184(2): 1032-1040. DOI:10.1016/j.amc.2006.07.004 ( 0) 0)
|
| [17] |
XIE T T, YU H, HEWLETT J, et al. Fast and efficient second-order method for training radial basis function networks[J]. IEEE transactions on neural networks and learning systems, 2012, 23(4): 609-619. DOI:10.1109/TNNLS.2012.2185059 ( 0) 0)
|
| [18] |
QIAO J F, HAN H G. Identification and modeling of nonlinear dynamical systems using a novel self-organizing RBF-based approach[J]. Automatica, 2012, 48(8): 1729-1734. DOI:10.1016/j.automatica.2012.05.034 ( 0) 0)
|
| [19] |
CHEN C, WANG F Y. A self-organizing neuro-fuzzy network based on first order effect sensitivity analysis[J]. Neurocomputing, 2013, 118: 21-32. DOI:10.1016/j.neucom.2013.02.009 ( 0) 0)
|
| [20] |
HAN H G, CHEN Q L, QIAO J F. An efficient self-organizing RBF neural network for water quality prediction[J]. Neural networks the official journal of the international neural network society, 2011, 24(7): 717-25. DOI:10.1016/j.neunet.2011.04.006 ( 0) 0)
|
| [21] |
HUANG G B, SARATCHANDRAN P, SUNDARARAJAN N. An efficient sequential learning algorithm for growing and pruning RBF (GAP-RBF) networks[J]. IEEE transactions on systems, man, and cybernetics, Part B: (Cybernetics), 2004, 34(6): 2284-2292. DOI:10.1109/TSMCB.2004.834428 ( 0) 0)
|
| [22] |
CHO K B, WANG B Y. Radial basis function based adaptive fuzzy systems and their applications to system identification and prediction[J]. Fuzzy sets and systems, 1996, 83(3): 325-339. DOI:10.1016/0165-0114(95)00322-3 ( 0) 0)
|
| [23] |
EBADZADEH M M, SALIMI-BADR A. CFNN: correlated fuzzy neural network[J]. Neurocomputing, 2015, 148: 430-444. DOI:10.1016/j.neucom.2014.07.021 ( 0) 0)
|
| [24] |
An R, Li W J, Han H G, et al. An improved Levenberg-Marquardt algorithm with adaptive learning rate for RBF neural network[C]//IEEE Control Conference, [s.l.], 2016: 3630-3635.
( 0) 0)
|
 2018, Vol. 13
2018, Vol. 13


