在计算机视觉和模式识别领域,数据降维和特征提取一直是比较重要的研究方向。主成分分析(principal component analysis,PCA)[1]和线性鉴别分析(linear discriminant analysis, LDA)[2]是最经典的两种线性特征提取算法,其中主成分分析是无监督特征提取算法的代表,线性鉴别分析是监督特征提取算法的代表。而单特征提取算法只能从一个角度或一个通道来处理信号数据[3]。在通常的分类任务中,数据经常有多种表示方式。传统的单特征提取算法主要针对单表示数据的维数约减[4],不适合多表示数据的维数约减。
典型相关分析(canonical correlation analysis,CCA)是一种经典的多元统计分析方法。于1936年由H.Hotelling[5]首次提出,现已被成功应用于字符与人脸等图像识别任务中[6-7],并取得了良好的效果。但是,在处理含噪声数据情况时,CCA的特征表示能力却有限。在通常的模式识别分类任务中,数据会包含很多由于设备故障或者自然环境产生的噪声,这在一定程度上限制了CCA的应用范围。
近年来,许多学者[8-10]提出了低秩表示(low-rank representation,LRR)理论。Wright等[9]也基于低秩分解提出了针对噪声数据的鲁棒主成分分析(robust principal component analysis,RPCA)。通过对原始噪声数据进行低秩处理,RPCA可以有效地抽取出高维数据中的低维子空间结构。
为了提升CCA在噪声情况下抽取线性相关性的能力,受低秩理论的启发,提出了鲁棒典型相关分析(robust canonical correlation analysis, RbCCA)。RbCCA首先对抽取出的特征集运用RPCA进行低秩分解,提取出原始特征的低秩主分量和噪声稀疏分量。基于这两种分量分别构建对应的协方差矩阵。通过最大化低秩分量的相关性,同时最小化噪声分量的相关性来建立判别准则函数,进而求取鉴别投影矢量。在MFEAT手写体数据库以及ORL和Yale人脸数据库中的实验结果表明:在不同程度的噪声数据下,RbCCA算法的识别效果均优于现有CCA方法的识别效果。
1 典型相关分析基本原理假设两组随机矢量集x∈Rp与y∈Rq,并且E(x)=0,E(y)=0,典型相关分析就是寻找一对投影方向α∈Rp与β∈Rq,使得投影x*=αTx与y*=βTy之间具有最大的相关性,称这种相关为典型相关,对应的投影方向α和β通过最大化如下相关准则函数获得[11-12]:
| $ \begin{array}{*{20}{c}} {{\rho _{{\rm{CCA}}}}\left( {\mathit{\boldsymbol{\alpha }},\mathit{\boldsymbol{\beta }}} \right) = \frac{{\mathit{\boldsymbol{E}}\left( {{\mathit{\boldsymbol{\alpha }}^{\rm{T}}}\mathit{\boldsymbol{x}}{\mathit{\boldsymbol{y}}^{\rm{T}}}\mathit{\boldsymbol{\beta }}} \right)}}{{\sqrt {\mathit{\boldsymbol{E}}\left( {{\mathit{\boldsymbol{\alpha }}^{\rm{T}}}\mathit{\boldsymbol{x}}{\mathit{\boldsymbol{x}}^{\rm{T}}}\mathit{\boldsymbol{\alpha }}} \right) \cdot \mathit{\boldsymbol{E}}\left( {{\mathit{\boldsymbol{\beta }}^{\rm{T}}}\mathit{\boldsymbol{y}}{\mathit{\boldsymbol{y}}^{\rm{T}}}\mathit{\boldsymbol{\beta }}} \right)} }} = }\\ {\frac{{{\mathit{\boldsymbol{\alpha }}^{\rm{T}}}{\mathit{\boldsymbol{S}}_{xy}}\mathit{\boldsymbol{\beta }}}}{{\sqrt {{\mathit{\boldsymbol{\alpha }}^{\rm{T}}}{\mathit{\boldsymbol{S}}_{xx}}\mathit{\boldsymbol{\alpha }} \times {\mathit{\boldsymbol{\alpha }}^{\rm{T}}}{\mathit{\boldsymbol{S}}_{yy}}\mathit{\boldsymbol{\beta }}} }}} \end{array} $ | (1) |
式中:E(·)表示随机变量的期望,Sxx和Syy分别表示随机矢量x和y的组内协方差矩阵,Sxy表示随机矢量x与y的互协方差矩阵,在这里,假设Sxx和Syy是非奇异矩阵。
在实际求解中ρCCA(α、β)的极值与α、β的大小无关,只与α、β的方向有关。为了确保解的唯一性,可令:
| $ {\mathit{\boldsymbol{\alpha }}^{\rm{T}}}{\mathit{\boldsymbol{S}}_{xx}}\mathit{\boldsymbol{\alpha }} = {\mathit{\boldsymbol{\beta }}^{\rm{T}}}{\mathit{\boldsymbol{S}}_{yy}}\mathit{\boldsymbol{\beta }} = 1 $ | (2) |
在式(2) 的约束下,式(1) 可等价的表示为
| $ \begin{array}{l} \mathop {\max }\limits_{\mathit{\boldsymbol{\alpha }},\mathit{\boldsymbol{\beta }}} {\mathit{\boldsymbol{\rho }}_{{\rm{CCA}}}}\left( {\mathit{\boldsymbol{\alpha }},\mathit{\boldsymbol{\beta }}} \right) = {\mathit{\boldsymbol{\alpha }}^{\rm{T}}}{\mathit{\boldsymbol{S}}_{xy}}\mathit{\boldsymbol{\beta }}\\ {\rm{s}}{\rm{.t}}{\rm{.}}\;\;\;\;{\mathit{\boldsymbol{\alpha }}^{\rm{T}}}{\mathit{\boldsymbol{S}}_{xx}}\mathit{\boldsymbol{\alpha = }}{\mathit{\boldsymbol{\beta }}^{\rm{T}}}{\mathit{\boldsymbol{S}}_{yy}}\mathit{\boldsymbol{\beta = }}1 \end{array} $ | (3) |
运用奇异值分解对式(3) 进行求解,得到投影矢量集α和β。
2 基于低秩分解的鲁棒典型相关分析典型相关分析作为一种经典的多元统计分析方法,已被成功应用于字符与人脸等图像识别任务中[6-7],并取得了良好的效果。但是,在处理含噪声数据时,CCA的特征表示能力却有限。为了提升CCA在噪声情况下的特征表示能力,引入低秩理论处理噪声,提出了新的CCA模型——鲁棒典型相关分析。
鲁棒典型相关分析(RbCCA)是针对含噪声数据而提出的一种典型相关分析(CCA)改进算法。RbCCA通过将含噪声数据进行低秩分解,得到低秩分量和噪声分量。基于这两种分量,RbCCA构建出新的协方差矩阵。提出的优化准则函数能够在最大化本质特征的相关性的同时最小化噪声的相关性,从而尽可能地降低噪声对典型投影矢量的影响。提升了传统CCA在含噪声数据下的特征表示能力。
2.1 RbCCA协方差矩阵的构建在模式识别任务中,为了避免噪声影响分类结果,许多已有的方法通常直接利用通过低秩分解得到的低秩分量进行特征降维和模式分类。但是,一般情况下噪声分量中也包含了一些对分类有利的信息[13],不能直接遗弃。因此,基于低秩分量和噪声分量,建立新的互协方差矩阵,改进CCA的目标优化方程,提出了鲁棒典型相关分析。
为了获得给定含噪声观察矩阵W∈Rm×n中对应的低秩分量Z∈Rm×n和噪声分量E∈Rm×n,Wright等[9, 14]提出了秩最小化方程:
| $ \begin{array}{*{20}{c}} {\mathop {\min }\limits_{Z,E} {{\left\| Z \right\|}_ * } + \lambda {{\left\| E \right\|}_{{l_1}}}}\\ {{\rm{s}}{\rm{.t}}{\rm{.}}\;\;\;\mathit{\boldsymbol{W}} = \mathit{\boldsymbol{Z}} + \mathit{\boldsymbol{E}}} \end{array} $ | (4) |
式中:λ>0是一个和噪声有关的参数,‖·‖l为不同的矩阵范数,代表了不同的正则化方法。根据文献[8, 15]选取l1范数作为正则化方法对噪声数据进行低秩分解。
给定含噪声样本随机矢量xN∈RP、yN∈Rq。通过式(4) 可以求解出对应的低秩分量xZN、yZN和噪声分量xZE、yZE。
对于求解得到的低秩主分量和噪声稀疏分量,分别计算对应的组内协方差矩阵和互协方差矩阵。其中SxxZ、SxxE和SxyZ、SxyE的计算公式如下:
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{S}}_{xx}^Z = E\left[ {{{\left( {\mathit{\boldsymbol{x}}_Z^N - E\left( {\mathit{\boldsymbol{x}}_Z^N} \right)} \right)}^{\rm{T}}}\left( {\mathit{\boldsymbol{x}}_Z^N - E\left( {\mathit{\boldsymbol{x}}_Z^N} \right)} \right)} \right]\\ \mathit{\boldsymbol{S}}_{xx}^E = E\left[ {{{\left( {\mathit{\boldsymbol{x}}_E^N - E\left( {\mathit{\boldsymbol{x}}_E^N} \right)} \right)}^{\rm{T}}}\left( {\mathit{\boldsymbol{x}}_E^N - E\left( {\mathit{\boldsymbol{x}}_E^N} \right)} \right)} \right]\\ \mathit{\boldsymbol{S}}_{xy}^Z = E\left[ {{{\left( {\mathit{\boldsymbol{x}}_Z^N - E\left( {\mathit{\boldsymbol{x}}_Z^N} \right)} \right)}^{\rm{T}}}\left( {\mathit{\boldsymbol{y}}_Z^N - E\left( {\mathit{\boldsymbol{y}}_Z^N} \right)} \right)} \right]\\ \mathit{\boldsymbol{S}}_{xy}^E = E\left[ {{{\left( {\mathit{\boldsymbol{x}}_E^N - E\left( {\mathit{\boldsymbol{x}}_E^N} \right)} \right)}^{\rm{T}}}\left( {\mathit{\boldsymbol{y}}_E^N - E\left( {\mathit{\boldsymbol{x}}_E^N} \right)} \right)} \right] \end{array} \right. $ |
类似,也可以得出SyyZ、SyyE和SyxZ、SyxE的计算公式。
2.2 算法原理与模型构建RbCCA将xN和yN的低秩分量,噪声分量区别对待,即求一对投影方向α和β,使得αTSxyZβ尽可能大的同时αTSxyEβ尽可能小。于是得到改进后的典型相关准则函数为
| $ \left\{ \begin{array}{l} \mathop {\max }\limits_{\alpha ,\beta } \mathit{\boldsymbol{\rho }}_{{\rm{CCA}}}^Z\left( {\mathit{\boldsymbol{\alpha }},\mathit{\boldsymbol{\beta }}} \right) = {\mathit{\boldsymbol{\alpha }}^{\rm{T}}}\mathit{\boldsymbol{S}}_{xy}^Z\mathit{\boldsymbol{\beta }}\\ \mathop {\min }\limits_{\alpha ,\beta } \mathit{\boldsymbol{\rho }}_{{\rm{CCA}}}^E\left( {\mathit{\boldsymbol{\alpha }},\mathit{\boldsymbol{\beta }}} \right) = {\mathit{\boldsymbol{\alpha }}^{\rm{T}}}\mathit{\boldsymbol{S}}_{xy}^E\mathit{\boldsymbol{\beta }} \end{array} \right. $ | (5) |
式中:ρCCAZ(ρCCAE)为低秩(噪声)分量的相关性,SxyZ(SxyE)为低秩(噪声)分量的协方差矩阵。
式(5) 是一个多目标方程优化问题,很难直接求解。通过最大化公式(5) 中两个准则函数的差值进行求解[16],即
| $ \begin{array}{*{20}{c}} {\mathop {\max }\limits_{\alpha ,\beta } \left\{ {\mathit{\boldsymbol{\rho }}_{{\rm{CCA}}}^Z\left( {\mathit{\boldsymbol{\alpha }},\mathit{\boldsymbol{\beta }}} \right) - \mathit{\boldsymbol{\rho }}_{{\rm{CCA}}}^E\left( {\mathit{\boldsymbol{\alpha }},\mathit{\boldsymbol{\beta }}} \right)} \right\} = }\\ {{\mathit{\boldsymbol{\alpha }}^{\rm{T}}}\mathit{\boldsymbol{S}}_{xy}^Z\mathit{\boldsymbol{\beta }} - {\mathit{\boldsymbol{\alpha }}^{\rm{T}}}\mathit{\boldsymbol{S}}_{xy}^E\mathit{\boldsymbol{\beta }} = }\\ {{\mathit{\boldsymbol{\alpha }}^{\rm{T}}}\left( {{\mathit{\boldsymbol{\alpha }}^{\rm{T}}}\mathit{\boldsymbol{S}}_{xy}^Z\mathit{\boldsymbol{\beta }} - \mathit{\boldsymbol{S}}_{xy}^E} \right)\mathit{\boldsymbol{\beta }}} \end{array} $ | (6) |
式(6) 满足在最大化本质特征的相关性的同时最小化噪声的相关性的要求,保证了求解得出的投影矢量的鉴别能力。相应地,能够得到式(7) 约束:
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{\alpha }}^{\rm{T}}}\left( {\mathit{\boldsymbol{S}}_{xx}^Z - \mathit{\boldsymbol{S}}_{xx}^E} \right)\mathit{\boldsymbol{\alpha = }}1\\ {\mathit{\boldsymbol{\beta }}^{\rm{T}}}\left( {\mathit{\boldsymbol{S}}_{yy}^Z - \mathit{\boldsymbol{S}}_{yy}^E} \right)\mathit{\boldsymbol{\beta = }}1 \end{array} \right. $ | (7) |
令Sxy*替代式(7) 中的SxyZ-SxyE,Sxx*、Syy*分别替代式(7) 中的SxxZ-SxxE和SyyZ-SyyE,综合式(6)、(7),得到转换后的RbCCA的准则函数:
| $ \begin{array}{*{20}{c}} {\mathop {\max }\limits_{\mathit{\boldsymbol{\alpha }},\mathit{\boldsymbol{\beta }}} \mathit{\boldsymbol{\rho }}_{{\rm{CCA}}}^ * \left( {\mathit{\boldsymbol{\alpha }},\mathit{\boldsymbol{\beta }}} \right) = {\mathit{\boldsymbol{\alpha }}^{\rm{T}}}\mathit{\boldsymbol{S}}_{xy}^ * \mathit{\boldsymbol{\beta }}}\\ {{\rm{s}}{\rm{.t}}{\rm{.}}\;\;{\mathit{\boldsymbol{\alpha }}^{\rm{T}}}\mathit{\boldsymbol{S}}_{xx}^ * \mathit{\boldsymbol{\alpha }} = 1,{\mathit{\boldsymbol{\beta }}^{\rm{T}}}\mathit{\boldsymbol{S}}_{yy}^ * \mathit{\boldsymbol{\beta }} = 1} \end{array} $ | (8) |
式(8) 满足了在最大化本质特征的相关性的同时最小化噪声成分的相关性的要求。最大程度上降低了噪声对典型投影矢量的影响,增强了投影矢量的鉴别能力。
2.3 RbCCA模型求解式(8) 的求解方法同CCA算法的求解。利用Lagrange乘数法,可以将问题转化为求解如下两个广义特征方程的问题:
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{S}}_{xy}^ * {\left( {\mathit{\boldsymbol{S}}_{yy}^ * } \right)^{ - 1}}\mathit{\boldsymbol{S}}_{yx}^ * \mathit{\boldsymbol{\alpha = }}{\zeta ^2}\mathit{\boldsymbol{S}}_{xx}^ * \mathit{\boldsymbol{\alpha }}\\ \mathit{\boldsymbol{S}}_{yx}^ * {\left( {\mathit{\boldsymbol{S}}_{xx}^ * } \right)^{ - 1}}\mathit{\boldsymbol{S}}_{xy}^ * \mathit{\boldsymbol{\beta = }}{\zeta ^2}\mathit{\boldsymbol{S}}_{yy}^ * \mathit{\boldsymbol{\beta }} \end{array} \right. $ | (9) |
于是求解式(9) 就等同于求解矩阵(Syy*)-1Syx*(Sxx*)-1Sxy*或(Sxx*)-1Sxy*(Syy*)-1Syx*的特征值和特征矢量问题。选取前d个最大特征值对应的特征矢量(α1*, α2*, …, αd*)和(β1*, β2*, …, βd*)作为RbCCA的投影方向。则α*=(α1*, α2*, …, αd*)和(β*=β1*, β2*, …, βd*)为最终求得的投影矢量集。
对于给定的样本矢量x和y,对原始特征进行投影后得到变换后的特征分量(α*)Tx和(β*)Ty。为了方便后续的模式分类,采用式(10) 的串行特征融合策略对特征进行融合:
| $ P = \left[ {\begin{array}{*{20}{c}} {{{\left( {{\mathit{\boldsymbol{\alpha }}^ * }} \right)}^{\rm{T}}}\mathit{\boldsymbol{x}}}&{{{\left( {{\mathit{\boldsymbol{\beta }}^ * }} \right)}^{\rm{T}}}\mathit{\boldsymbol{y}}} \end{array}} \right] $ | (10) |
式(10) 计算对应投影后的特征矢量及其特征组合,将组合后的特征用于模式分类。
RbCCA既满足了多表示数据的维数约减要求,保持了较好的识别率,又填补了传统CCA在噪声数据下特征表示能力差的缺陷,提升了CCA处理噪声数据的能力。
3 实验结果与分析本实验的目的是验证本文所提算法RbCCA在噪声数据下特征提取的有效性,分别在多特征手写体数据集MFEAT和ORL以及Yale两个人脸数据库上进行了识别实验。其中λ的取值需根据噪声强度的大小进行调整。实验中均采取串行融合的策略进行特征融合,并选取最近邻分类器进行模式分类。
3.1 MFEAT手写体数据库MFEAT手写体数据库一共包含fac、fou、kar、mor、pix、zer 6组特征,每组特征包含0~9共10个数字,每个数字类别包含200个样本。6组特征,每两组特征进行组合共15种组合,随机挑选其中的10种组合做10次随机实验,每次实验从每种组合中随机选择100个作为训练样本,100个作为测试样本。训练样本总数和测试样本总数均为1 000。实验开始前,在原始MFEAT数据库上,分别在6组特征加入10%的椒盐噪声来模拟实际应用中的噪声。
表 1随机抽取MFEAT数据库中10种特征组合,分别将CCA、PLS、LPCCA、RCCA以及RbCCA等算法做了对比实验。实验数据表明,RbCCA在这10种特征组合的识别率平均比CCA的识别率高出10%。在fac_fou、fou_zer以及mor_pix 3种组合里,RbCCA的识别更是高出CCA识别结果的15%以上。表 1初步证实了RbCCA对噪声数据特征提取的有效性。
| 表 1 MFEAT不同特征组合下识别算法识别率 Tab.1 Different characteristics of the combination identify the algorithm recognition rate in MFEAT |
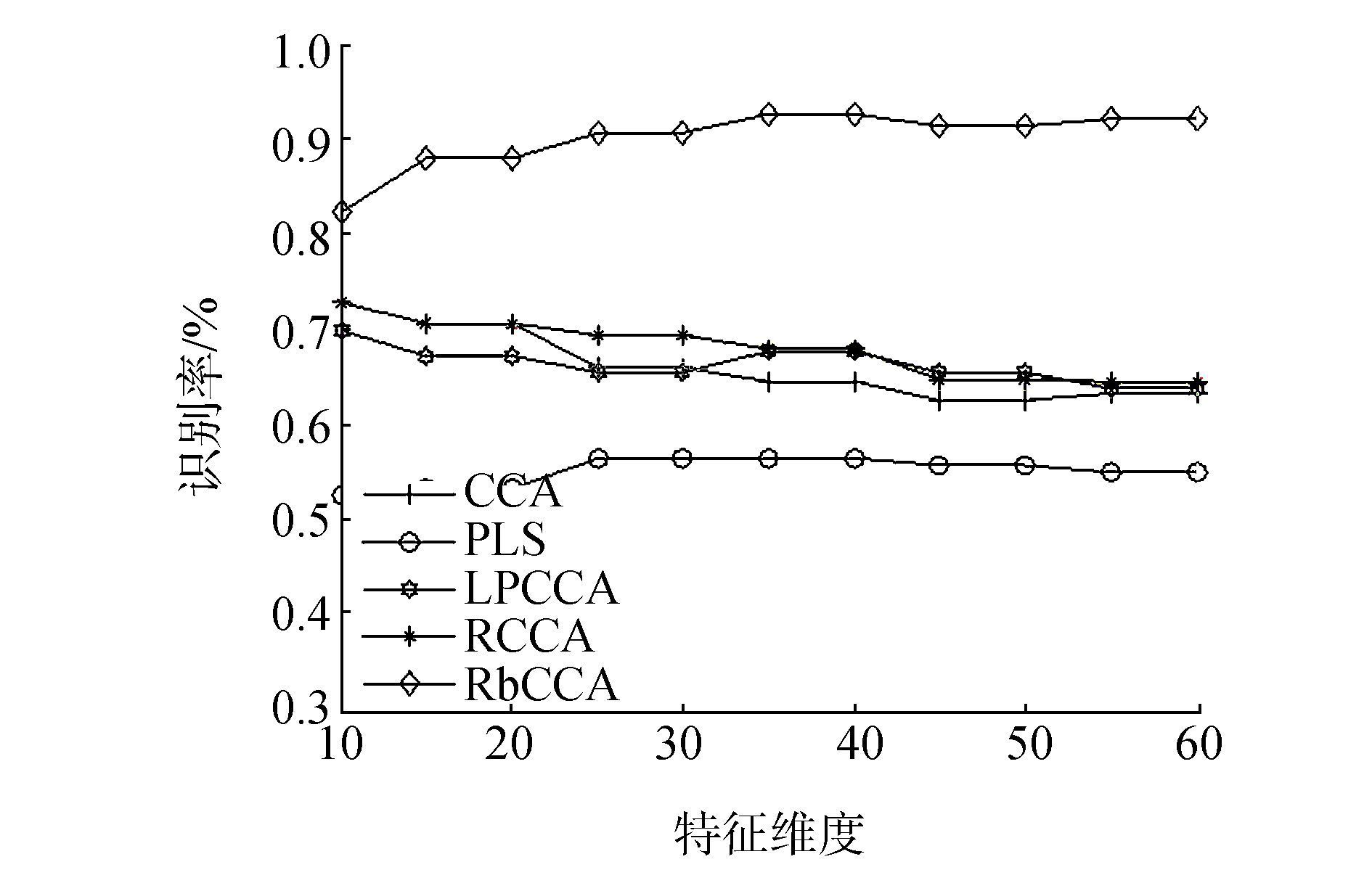
图 1列出了添加噪声后的MFEAT数据中的fac_fou特征组合上CCA、PLS、LPCCA、RCCA以及RbCCA等算法的对比实验结果曲线图。通过图 1可以很明显看出,RbCCA的识别率远远高于其他算法。随着特征维度的增加,RCCA、LPCCA、CCA算法的识别率在逐渐下降,而RbCCA的识别率却呈上升趋势。这是由于随着特征维度增加,特征中包含的噪声也在增加,影响了RCCA、LPCCA、CCA的分类正确率。图 1表明RbCCA能够较好地提取噪声数据中图像的原始信息,针对噪声图像的分类识别效果优于其他4种算法。
|
图 1 识别方法识别结果随着特征维度增加的识别曲线图 Fig.1 The recognition curve of the recognition method with the increase of the feature dimension |
ORL人脸数据库[17]由剑桥大学AT & T实验室创建,包含40人共400张面部图像,每幅图像大小92×112像素,部分图像包括了姿态,表情和面部饰物的变化。图 2给出了ORL人脸库中某人的10张图像。

|
图 2 ORL人脸数据库中某人的10张图像 Fig.2 10 images of a person in the ORL face database |
实验预处理阶段,每幅图像分别加入10%椒盐噪声模拟噪声分量。实验中,对于每一类,若无特别说明,均是随机选择5幅作为训练样本,其余5幅作为测试样本。
表 2、图 3分别列出了在选择不同训练样本数目和变化不同特征维度时,6组对比算法的识别效果。算法中RPCA+CCA是直接利用低秩分量来计算典型相关分析投影矢量的算法简称。
| 表 2 ORL人脸库不同的训练样本数下识别算法的识别率 Tab.2 ORL face database under different training samples identify the recognition rate of the algorithm |
|
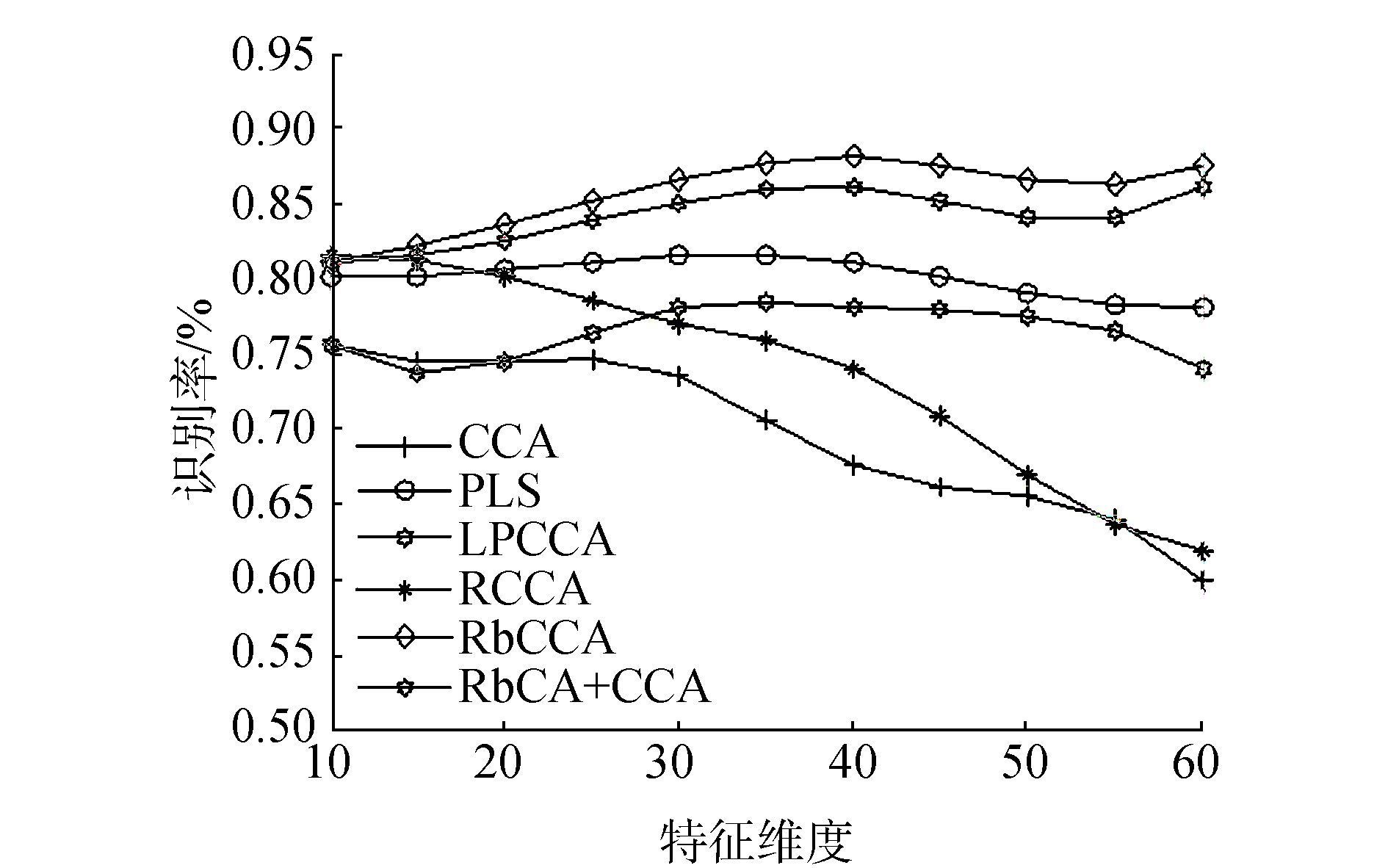
图 3 识别方法识别结果随特征维度增加的变化曲线图 Fig.3 The recognition curve of the recognition method with the increase of the feature dimension |
表 2的实验数据表明,随着训练样本数目的增加,几种算法的识别率均有不同程度的提升。对比RPCA+CCA和CCA的识别率,可以看出RPCA+CCA的识别效果优于CCA。这也从侧面说明了RPCA对于噪声的鲁棒性。
通过图 3可以看出,随着特征维度的增加,除RPCA+CCA和RbCCA之外的其余4种算法的识别率均呈下降趋势,这是由于随着特征维度的增加,抽取的特征中所包含的噪声成分也在增加,对识别效果产生了较大的影响。随着特征维度的增加,RPCA+CCA和RbPCCA的识别正确率均呈上升趋势,并且由于RbCCA模型利用到了噪声成分的信息,所以它的识别效果始终优于只利用低秩分量的RPCA+CCA的模型的识别效果。
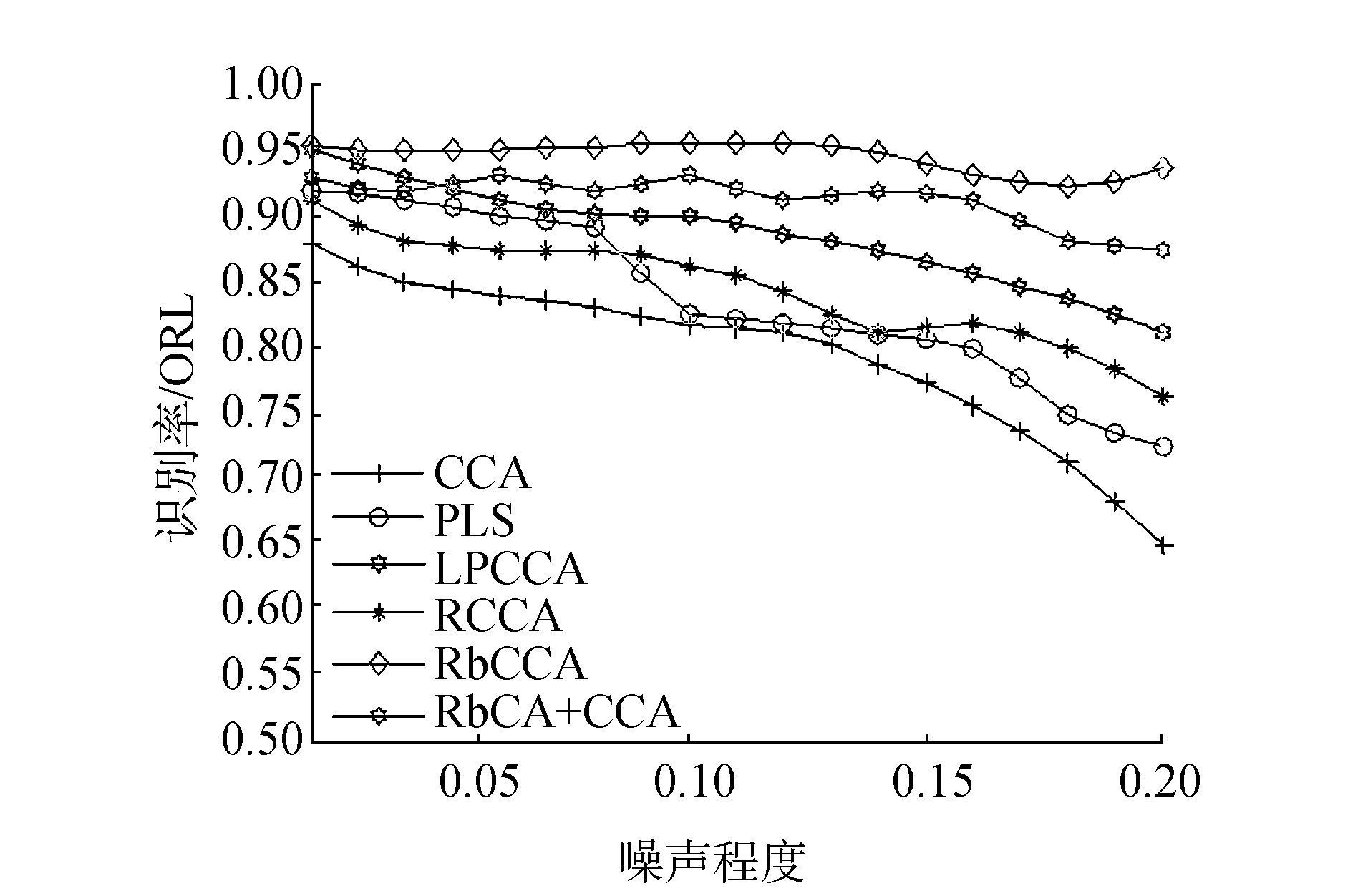
图 4显示了随着数据样本所含噪声强度的增加,6种算法的识别率变化曲线图。在本次实验中,选取每类6个样本作为训练样本,其余4个样本作为测试样本。从图 4中可以看出,随着噪声强度的增加,6种算法的识别正确率均有不同程度的下降趋势。相对于其他算法,RbCCA识别率下降趋势较为平缓,并且噪声强度在2%~20%时,它的识别率始终保持在了92%以上。进一步证实了RbCCA对噪声具有很好的鲁棒性,能够很好地提取噪声数据的有效特征。
|
图 4 识别方法识别结果随着噪声强度增加的变化曲线图 Fig.4 The result of the recognition method with the increase of the noise intensity |
Yale人脸数据库[18-21]包含15个人的165幅灰度图像,每人11幅,包括光照方向(左、右和正面)、眼睛、表情变化(正常、愉快、悲伤、困乏、惊讶和眨眼)。图像大小为100像素×100像素。图 5是Yale人脸库中某人的11幅图像。

|
图 5 Yale数据库中某人的11幅图像 Fig.5 11 images of one person in Yale database |
实验预处理阶段,对每幅图像分别加入10%椒盐噪声,实验中,对于每一类,若无特别说明,均是随机选择6幅作为训练样本,其余5幅作为测试样本。
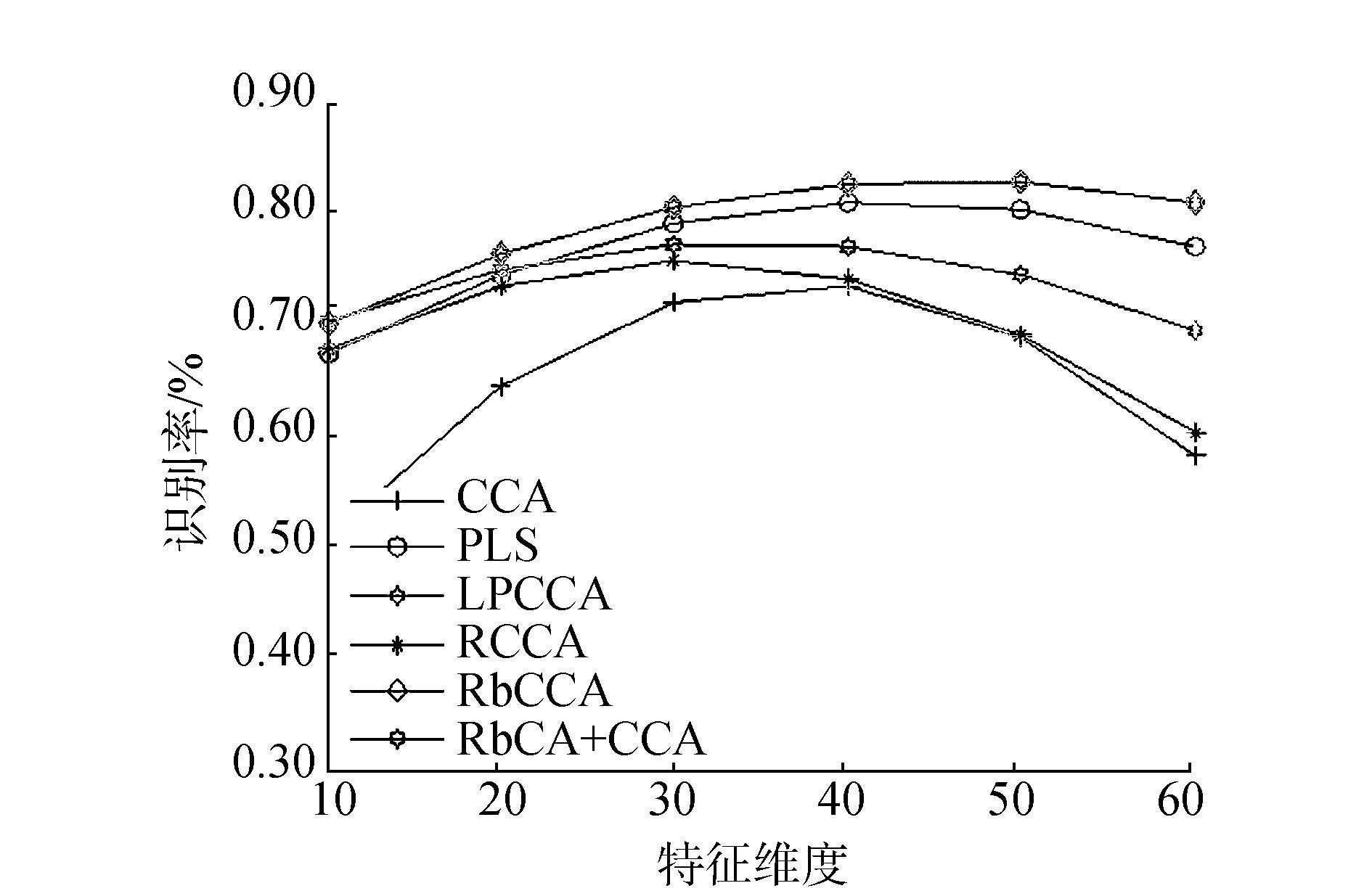
表 3、图 6分别表示了在选择不同训练样本数目和变换不同特征维度时,6组对比算法的识别效果。表 3的实验数据进一步表明RbCCA对于噪声数据特征提取的有效性。
| 表 3 Yale人脸库不同的训练样本数下,CCA、PLS、LPCCA、RCCA、RPCA+CCA、RbCCA算法的识别率 Tab.3 Recognition rates for CCA, PLS, LPCCA, RCCA, RPCA + CCA, RbCCA algorithms for different training samples in the Yale face database |
|
图 6 识别方法识别结果随着特征维度增加的变化曲线图 Fig.6 The recognition curve of the recognition method with the increase of the feature dimension |
通过图 6可以看出,特征维数在10~40之间,随着特征维数的增加,6种算法的识别正确率均有不同程度的提升。从总体上看,RbCCA算法的识别率始终高于其他5种算法。特征维度大于40维之后,随着特征维度的增加,除RPCA+CCA和RbCCA之外的其余4种算法的识别率均呈下降趋势。RbCCA模型因为利用到了噪声成分的信息,所以它的识别效果始终优于只利用低秩成分的RPCA+CCA模型的识别效果。
图 7是针对不同噪声强度每种算法的识别率变化曲线图。本次实验中随机选取每一类的7个样本作为训练样本,其余4个作为测试样本。变化曲线表明,随着噪声强度的增加,6种算法的识别率均有不同程度的下降。从图中可以看出,随着噪声强度的增加,CCA识别率下降得最快,相比较来看,RPCA+CCA以及RbCCA的下降趋势相对平缓。虽然随着噪声强度的增加,RbCCA识别率稍有降低。但是噪声强度从2%~20%之间,它的识别率均在91%以上,远远优于其他5种算法的识别率。这也进一步表明了RbCCA对于噪声数据处理的有效性。

|
图 7 识别方法识别结果随着噪声强度增加的变化曲线图 Fig.7 The result of the recognition method with the increase of the noise intensity |
为了提升CCA噪声数据的处理能力,本文提出鲁棒典型相关分析算法(RbCCA)。RbCCA首先对两组特征进行低秩分解,从而分解得到低秩以及噪声分量。基于这两种分量,RbCCA构建出新的协方差矩阵。提出的准则函数能够最大化本质特征的相关性,同时最小化噪声的相关性,从而尽可能少地降低噪声对典型投影矢量的影响,增强投影矢量的鉴别能力。在MFEAT手写体、ORL和Yale人脸数据上的实验表明,相比于现有的CCA方法,RbCCA对噪声数据具有较强的鲁棒性,在模式分类任务中可以达到较好的识别率。
在实际应用方面,RbCCA中存在一些问题值得进一步研究。在低秩分解时参数λ的值对噪声强度大小以及特征维度的大小很敏感,需要调整参数λ的值才能达到较好的识别效果。如何建立一个参数选择标准或者函数关系,以适应不同范围的噪声强度以及特征维度还有待进一步研究论证。
| [1] |
FUKUNAGA K. Introduction to statistical pattern recognition[M]. Academic press, 2013.
( 0) 0)
|
| [2] |
FISHER R A. The use of multiple measurements in axonomic problems[J]. Annals of eugenics, 1936, 7(2): 179-188. DOI:10.1111/j.1469-1809.1936.tb02137.x ( 0) 0)
|
| [3] |
杨勇, 蔡舒博. 一种基于两步降维和并行特征融合的表情识别方法[J]. 重庆邮电大学学报:自然科学版, 2015, 27(3): 377-387. YANG Yong, CAI Shubo. Facial expression recognition method based on two-steps dimensionality reduction and parallel feature fusion[J]. Journal of chongqing university of posts and telecommunications:natural science edition, 2015, 27(3): 377-387. (  0) 0)
|
| [4] |
HOU C, ZHANG C, WU Y, et al. Multiple view semi-supervised dimensionality reduction[J]. Pattern recognition, 2010, 43(3): 720-730. DOI:10.1016/j.patcog.2009.07.015 ( 0) 0)
|
| [5] |
HOTELLING H. Relations between two sets of variates[J]. Biometrika, 1936, 28(3/4): 321-377. DOI:10.2307/2333955 ( 0) 0)
|
| [6] |
孙权森, 基于相关投影分析的特征抽取与图像识别研究[D]. 南京: 南京理工大学, 2006. SUN Quansen. Research on feature extraction and image recognition based on correlation projection analysis[D]. Nanjing:Nanjing University of Science and Technology, 2006. http://cdmd.cnki.com.cn/Article/CDMD-10288-2006183401.htm (  0) 0)
|
| [7] |
HOUShudong, 孙权森. 稀疏保持典型相关分析及在特征融合中的应用[J]. 自动化学报, 2012, 38(4): 659-665. HOU Shudong, SUN Quansen. Sparse maintaining canonical correlation analysis and its application in feature fusion[J]. Journal of automation, 2012, 38(4): 659-665. (  0) 0)
|
| [8] |
LIU G, LIN Z, YAN S, et al. Robust recovery of subspace structures by low-rank representation[J]. IEEE transactions on pattern analysis and machine intelligence, 2013, 35(1): 171-184. DOI:10.1109/TPAMI.2012.88 ( 0) 0)
|
| [9] |
WRIGHT J, GANESH A, RAO S, et al. Robust principal component analysis:Exact recovery of corrupted low-rank matrices via convex optimization[C]//Advances in neural information processing systems. Vancouver, BC, Canada, 2009:2080-2088.
( 0) 0)
|
| [10] |
LIU G, LIN Z, YU Y. Robust subspace segmentation by low-rank representation[C]//Proceedings of the 27th international conference on machine learning (ICML-10). Haifa, Israel. 2010:663-670.
( 0) 0)
|
| [11] |
袁运浩. 多重集典型相关分析理论及在高维多表示数据中的应用[D]. 南京: 南京理工大学, 2013. YUAN Yunhao. Canonical correlation analysis theory of multiple sets and its application in multi-representation data[D]. Nanjing:Nanjing University of Science and Technology, 2013. (  0) 0)
|
| [12] |
孙权森, 曾生根, 王平安, 等. 典型相关分析的理论及其在特征融合中的应用[J]. 计算机学报, 2005, 28(9): 1524-1533. SUN Quansen, ZENG Shenggen, WANG Pingan, et al. The theory of canonical correlation analysis and its application in feature fusion[J]. Chinese journal of computers, 2005, 28(9): 1524-1533. (  0) 0)
|
| [13] |
张凡龙. 基于核范数的低秩理论与方法研究[D]. 南京: 南京理工大学, 2015. ZHANG Fanlong. Research on low rank theory and method based on kernel norm[D]. Nanjing:Nanjing University of Science and Technology, 2015. (  0) 0)
|
| [14] |
CANDÈS E J, LI X, MA Y, et al. Robust principal component analysis[J]. Journal of the ACM (JACM), 2011, 58(3): 11. ( 0) 0)
|
| [15] |
BAO B K, LIU G, XU C, et al. Inductive robust principal component analysis[J]. IEEE transactions on image processing, 2012, 21(8): 3794-3800. DOI:10.1109/TIP.2012.2192742 ( 0) 0)
|
| [16] |
SHEN X B, SUN Q S, YUAN Y H. A unified multiset canonical correlation analysis framework based on graph embedding for multiple feature extraction[J]. Neurocomputing, 2015, 148: 397-408. DOI:10.1016/j.neucom.2014.06.015 ( 0) 0)
|
| [17] |
FERDINANDO S, ANDY H. Parameterisation of a stochastic model for human face identification[C]//Proceedings of 2nd IEEE Workshop on Applications of Computer Vision. Sarasota FL, 1994.
( 0) 0)
|
| [18] |
BELHUMEUR P, HEPANHA J, KRIEGMAN D. Eigenfaces vs. Fisherfaces:recognition using class specific linear projection[J]. IEEE transactions on pattern analysis and machine intelligence, 1997, 19(7): 711-720. DOI:10.1109/34.598228 ( 0) 0)
|
| [19] |
袁宝华, 王欢, 任明武. 基于完整LBP特征的人脸识别[J]. 计算机应用研究, 2012, 29(4): 1557-1559. YUAN Baohua, WANG Huan, REN Mingwu. Face recognition based on complete lbp feature[J]. Journal of computer applications, 2012, 29(4): 1557-1559. (  0) 0)
|
| [20] |
何国辉, 甘俊英. 二维主元分析在人脸识别中的应用研究[J]. 计算机工程与设计, 2006, 27(24): 4667-4669. HE Guohui, GAN Junying. Application of two-dimensional principal component analysis in face recognition[J]. Computer engineering and design, 2006, 27(24): 4667-4669. DOI:10.3969/j.issn.1000-7024.2006.24.018 (  0) 0)
|
| [21] |
赵军, 赵艳, 杨勇, 等. 基于降维的堆积降噪自动编码机的表情识别方法[J]. 重庆邮电大学学报:自然科学版, 2016, 28(6): 844-848. ZHAO Jun, ZHAO Yan, YANG Yong, et al. Facial expression recognition method based on stacked denoisingauto-encoders and feature reduction[J]. Journal of chongqing university of posts and telecommunications:natural science edition, 2016, 28(6): 844-848. (  0) 0)
|
 2017, Vol. 12
2017, Vol. 12


