阿尔茨海默病(Alzheimer’s disease,AD),即老年痴呆症,是发生在老年期及老年前期的一种原发性退行性脑疾病,其临床表现为认知和记忆功能减退。Brookmeyer等研究结果显示,全球约有2 660万人患有老年痴呆症,到2050年平均每85人中有1人会受到老年痴呆症的影响[1-2]。轻度认知障碍(mild cognitive impairment,MCI)是正常人转化为阿尔茨海默病的一个中间过程,每年有高达15%的轻度认知障碍患者会转化为AD[3-4]。因此准确地诊断AD和MCI,对尽早治疗和减缓疾病的恶化是非常重要的。医学上的诊断主要依靠NINCDS-ADRDA、DSM-IV等临床诊断标准,这些方法无法自动地诊断病人的病情发展状态,因此需要可以识别出细微生物标志的算法。
近些年来,神经影像技术迅速发展,主要包括结构核磁共振成像(structural magnetic resonance imaging, SMRI),弥散张量成像(diffusion tensor imaging, DTI),功能核磁共振成像(functional MRI, fMRI),脑电图(electro-encephalogram, EEG)和脑磁图(magnetoencephalography, MEG)。在fMRI、EEG和MEG图像中,人们可以获取功能连接网络,用于反映不同脑区的解剖连接模式。
最近出现的研究认为,临床变量值可以用于评估AD的阶段以及预测病情的发展。在现有的研究中,Cheng等[5]提出了一种新的半监督多模态向量回归法预测临床评分;Zhang等[6]提出了一种多模态多任务的方法同时解决脑疾病的回归和分类问题;Zhu等[7]提出了一种基于损失函数的相似性度量矩阵,充分利用高阶信息解决脑疾病的回归和分类问题。然而,上述的方法都是基于脑影像的研究,而目前大多数有关功能连接网络的研究[8-9]主要关注于诊断受试人员是否患有该疾病,并不能很好地判断出受试人员目前所处的状态,以及受试人员是否有潜在患AD的隐患。基于功能网络的研究已经成功地应用于AD/MCI的分类诊断[10-11],说明AD/MCI引起了功能网络的变化,这为功能网络用于预测临床得分提供了理论保证。
为解决已有研究所存在的不足,本文提出了一种基于脑连接网络的阿尔茨海默病临床变量值预测的方法,用于对AD/MCI病人的临床评分进行回归分析。具体来说,首先对获取到的fMRI图像做预处理,获得对应的功能连接网络。其次,从功能网络中提取两种特征,一种是节点的聚类系数,整个网络的聚类系数定义为各个节点的聚类系数的均值,它可以描述网络中节点之间的连接紧密程度;另一种是边的权重,对边的权重使用LASSO算法选择出具有判别性的边。最后,将上一步中经过提取、选择后的特征合并成一个向量,用支持向量回归机(support vector regression machine, SVRM)进行回归预测。
1 数据集本文所分析的数据集来源于阿尔茨海默病神经影像学ADNI(http://adni.loni.usc.edu/),ADNI由国际老年研究所,生物医学成像和生物工程研究所,美国食品和药物管理局,民营医药企业和非营利组织于2003年启动。ADNI是许多学术机构和私营机构共同努力的结果,被招募被试者来自于美国和加拿大中超过50个以上的地区。ADNI的最初目标是招募800名成人,年龄55~90岁之间,其中大约有200个认知能力正常的老年人,400个轻度认知障碍(MCI)患者,200个阿尔茨海默病(AD)患者。认知正常人和MCI数据是连续3年跟踪测试得到的,而AD数据是连续2年跟踪测试得到的。
在本文的研究中使用了包含临床变量值简易精神状态检查(Mini mental state examination,MMSE)值的fMRI模态数据(总共139个样本),其中40个正常人(normal control,NC),79个MCI病人(45个EMCI(early MCI)病人和34个LMCI(late MCI)病人),20个AD病人。表 1给出了这些受试者的详细信息。
| 表 1 受试者信息统计表 Tab.1 Demographic information of the subjects |
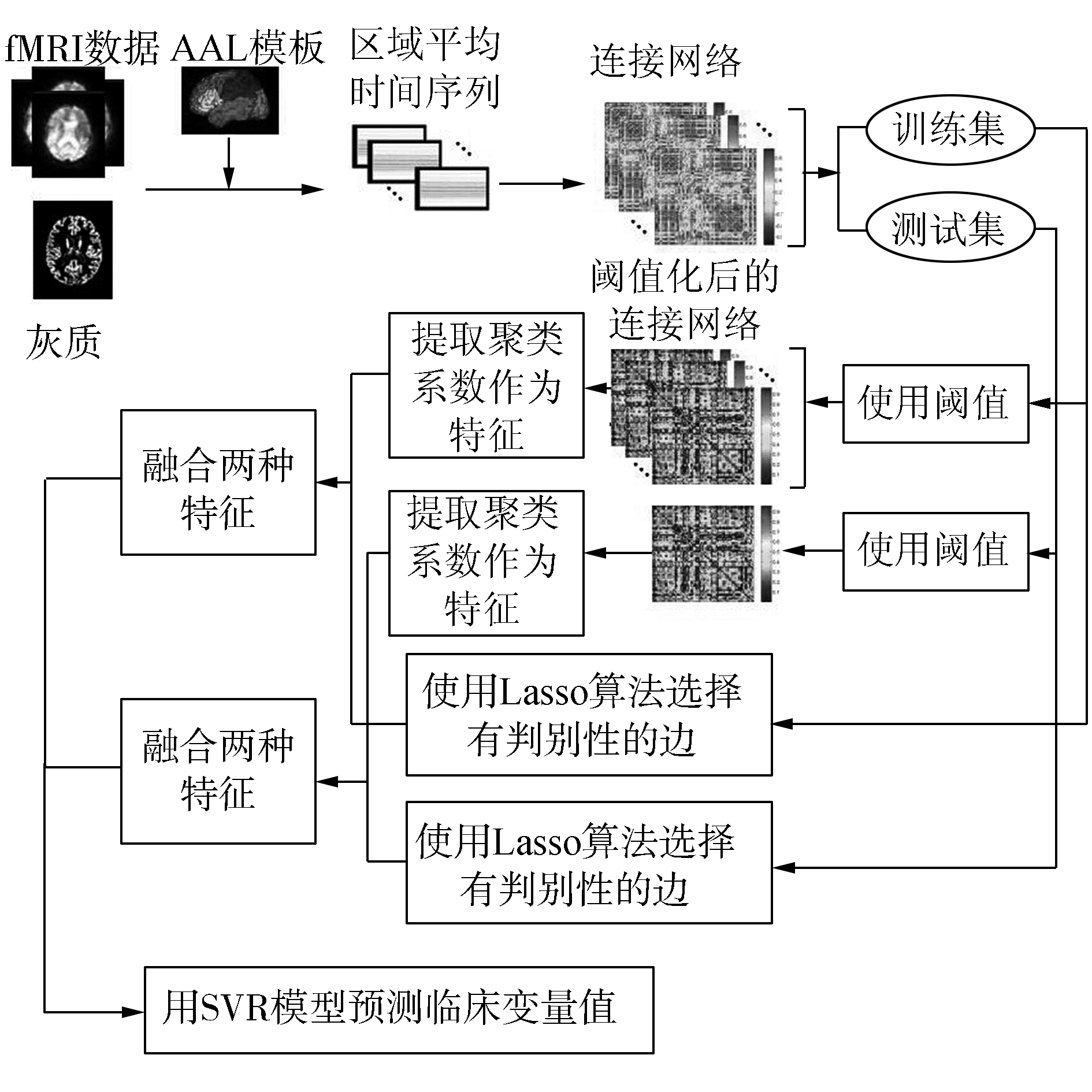
AD/MCI回归预测主要分为5个步骤:1) 预处理,通过处理原始的fMRI图像来构建功能连接网络;2) 网络节点特征提取;3) 网络边权重特征的选择;4) 特征融合;5) 使用SVR进行回归预测。图 1给出了本文的方法框架。
|
图 1 提出方法的框架 Fig.1 The framework of the proposed method |
对采集到的原始数据,我们使用Data Processing Assistant for Resting-State fMRI (DPARSF)[12]进行切片时间校正(slice timing)、头动校正(motion correlation)和空间正则化(spatial normalization)等标准预处理流程。接着每个对象的fMRI图像所对应的脑空间根据AAL (automated anatomical labeling)模板被分割为90个脑区(每个脑区对应图中的一个顶点),计算每个脑区的平均时间序列以及脑区间的Pearson相关系数作为脑区间的连接强度, 从而获得了大脑的功能性连接网络。这里,得到了一个90 ×90维的加权全连接脑网络,且该网络是一个对角线上为1的对称矩阵。
2.2 网络节点特征提取聚类系数常被用来作为网络的特征[13-14],整个网络的聚类系数定义为各个节点的聚类系数的均值,它可以描述网络中节点之间的连接紧密程度。聚类系数含义清晰,定义简单,计算量小,因此成为了功能网络研究中首选的特征之一。值得注意的是,聚类系数一般定义在无权网络中,而我们构建的功能网络是有权网络。因此本文使用阈值化的方法,将有权的功能网络转化为无权网络,然后计算无权网络中每个节点的聚类系数。这里,阈值的设置是0和1之间的任意值。
定义1(阈值化方法) 给定有权图G= [w(i, j)]∈Rn×n和阈值T,使用下面公式阈值化连接网络:
| $ \boldsymbol{w}\left( i, j \right)=\left\{ \begin{align} & 0, \ \ \ \ \ \ \boldsymbol{w}\left( i, j \right)<\boldsymbol{T} \\ & 1, \ \ \ \ \ \ \ 其他 \\ \end{align} \right. $ | (1) |
式中n表示感兴趣区域ROI(region of interest)的个数。
定义2(聚类系数) 给定一个无权无向图G,G中的第i个节点的聚类系数计算公式为
| $ {{C}_{i}}=\frac{2\times {{E}_{i}}}{{{k}_{i}}\times \left( {{k}_{i}}-1 \right)} $ | (2) |
式中:ki表示第i个节点的邻接点的个数,Ei可由式(3) 计算得到
| $ {{E}_{i}}=\sum\limits_{j, h\in n}{{{a}_{ij}}\times {{a}_{ih}}\times {{a}_{jh}}} $ | (3) |
式中:n表示ROI的个数;aij代表第i个节点和第j个节点之间的连接强度,经过阈值化后,连接强度值为0或者1。
从式(2) 可以看出,当一个点的邻接点之间的连接越紧密,聚类系数的值就越高。在脑疾病患者的功能网络中,聚类系数可以很好地反映单个感兴趣区域的异常。
我们首先使用式(1) 将有权网络转化为无权网络,接着使用式(2) 计算节点的聚类系数,得到一个节点的特征矩阵A∈ Rn×c,其中n表示样本个数,c表示节点特征个数。
2.3 网络边权重特征选择边是构成整个功能网络的重要数据,反映了不同脑区之间的连接强度,可以有效地区别不同类型患者之间的差异。对预处理得到的加权全连接脑网络,将网络中的边权值取出拉成一个向量。对单个样本,其脑网络维度为90×90维,可以拉成一个90×(90-1)/2=4 005维的向量。
然而,并不是所有的边都具有判别性,本文使用Lasso算法[15]选择出具有判别性的边作为特征。
Lasso是一种基于一范式的特征选择方法,与已有的特征选择方法相比,Lasso不仅能够准确地选择出与类相关的变量,同时还具有特征选择的稳定性。并且经验数据表明,当有大量不相关的特征而却只有少量样本时Lasso方法非常有效[16]。
Lasso回归估计稀疏表示系数w可描述为
| $ \boldsymbol{\hat{w}}=\text{argmin}\left\| \boldsymbol{y}-\boldsymbol{Aw} \right\|_{2}^{2}+\boldsymbol{\lambda} {{\left\| \boldsymbol{w} \right\|}_{1}} $ |
将求得的系数矩阵w中值为0所对应的原始数据中的特征值去掉。得到了一个经过特征选择后的较低维的特征矩阵B∈Rn×e,其中n表示样本个数,e表示具有判别性的边的特征个数。
2.4 特征融合研究人员发现数据的不同特征可互为补充,以提高分类预测性能。可以同时利用数据的不同特征来提高分类准确率。这种融合的方法对于有限的训练样本尤为有效。可以看出,融合思想是一种综合分析的思想,因此,对于同一模态的数据的多种特征进行综合分析、评判和决策处理也是某种意义上的融合方式。对于脑功能网络的研究,其所需要的数据信息可以从以上提取到的各种特征中,通过融合得出一种贡献最大、最具有判别性的综合特征。
在本文的实验中,将前面提取到的两种数据特征进行线性融合。具体计算如下,设节点的特征矩阵为
| $ \boldsymbol{A}=\left[\begin{matrix} {{a}_{11}} & \cdots & {{a}_{1c}} \\ \vdots & {} & \vdots \\ {{a}_{n1}} & \cdots & {{a}_{nc}} \\ \end{matrix} \right] $ |
边特征矩阵为
| $ \boldsymbol{B}=\left[\begin{matrix} {{b}_{11}} & \cdots & {{b}_{1e}} \\ \vdots & {} & \vdots \\ {{b}_{n1}} & \cdots & {{b}_{ne}} \\ \end{matrix} \right] $ |
则融合后的特征矩阵为
| $ \boldsymbol{C}=\left[\begin{matrix} {{a}_{11}} & \cdots & {{a}_{1c}} \\ \vdots & {} & \vdots \\ {{a}_{n1}} & \cdots & {{a}_{nc}} \\ \end{matrix}\begin{matrix} {{b}_{11}} & \cdots & {{b}_{1e}} \\ \vdots & {} & \vdots \\ {{b}_{n1}} & \cdots & {{b}_{ne}} \\ \end{matrix} \right] $ |
式中:n表示样本个数; c表示节点特征个数; e表示边特征个数。
2.5 模型训练对于融合后的特征,使用支持向量回归机SVR对阿尔茨海默病的临床变量值MMSE进行回归预测。
3 实验结果与分析 3.1 实验设置本文的实验考虑4种回归问题:AD vs. NC、AD vs. MCI、MCI vs. NC以及EMCI vs. LMCI。为了评估所有比较方法的性能,计算了预测临床评分和真实的临床评分之间的相关系数(correlation coefficient,CC)和均方根误差(root mean squared error,RMSE)。相关系数越大说明预测值和真实值这两组数据之间相关性越强。均方根误差越小说明预测模型越能更好地描述实验数据。
本文比较的所有方法均采用留一法进行交叉验证。具体而言,在每次的实验中,选取一个样本作为测试样本,其余样本作为训练样本。计算出的预测值组成的预测向量和原始标签向量做相关分析,来衡量该模型的性能。
在使用Lasso做特征选择的过程中,本文使用稳定性特征选择算法[17]来避免过拟合。稳定性选择是一种基于二次抽样和选择算法相结合较新的方法,它的主要思想是在不同的数据子集和特征子集上运行特征选择算法,不断地重复,最终汇总特征选择结果。
在本文的实验中,采用网格搜索的方法来确定最优的聚类系数阈值和Lasso模型中的一范数参数。
3.2 比较方法本文选取如下的方法进行比较。
基于原始特征的方法:使用没有经过任何特征选择的脑网络数据,作为基线方法。
基于边特征的方法:只使用脑网络中的边权重,选择出具有判别性的特征,本文的实验中使用Lasso算法做特征选择。
基于节点特征的方法:只使用脑网络中节点的聚类系数。
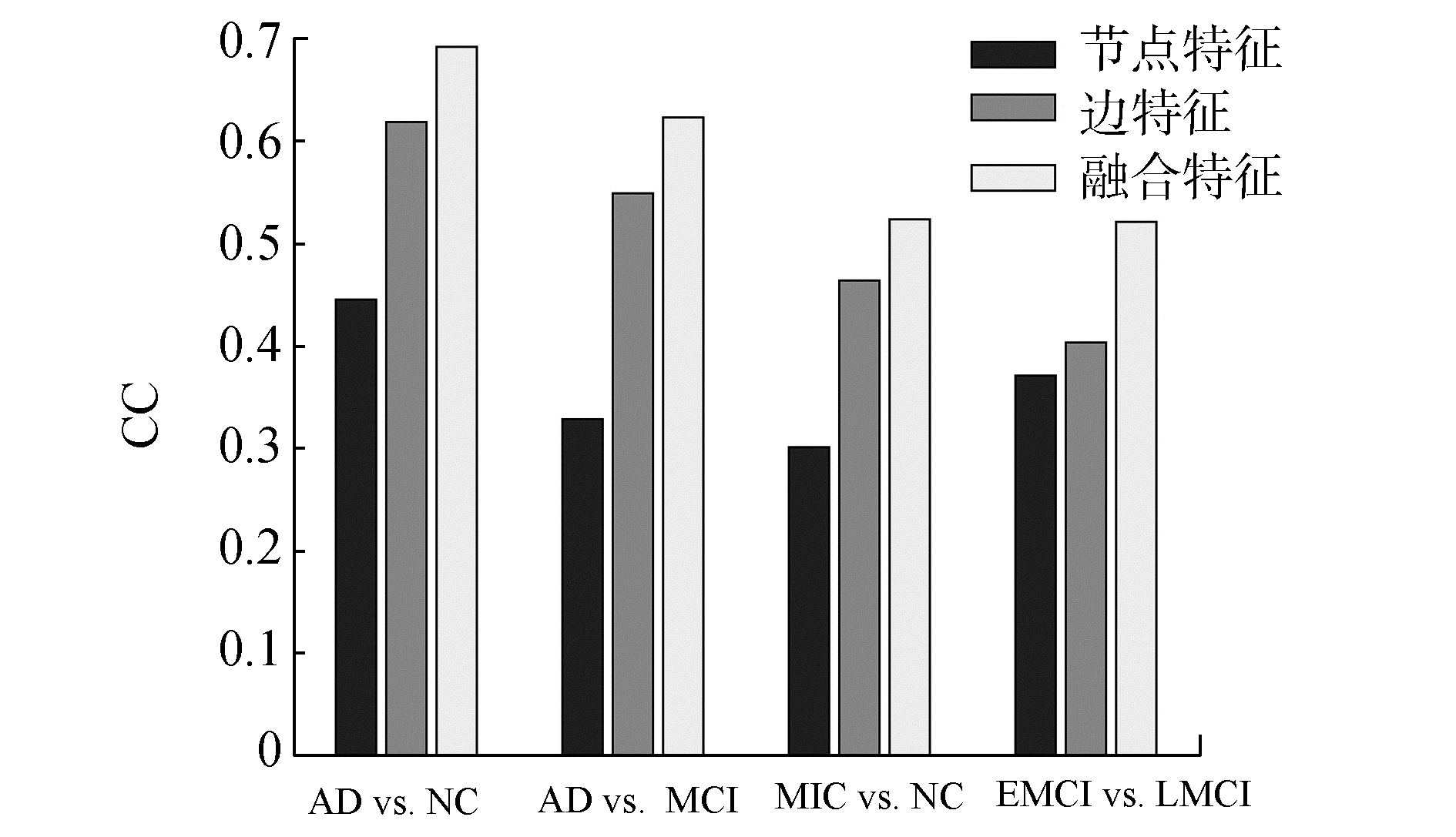
3.3 实验结果本文通过对临床变量值MMSE的估计来评估回归性能。在表 2、图 2、图 3中显示了比较方法计算得到的CC和RMSE的值。从表 2中可以看到没有经过特征选择、特征提取的原始数据的回归性能最不好,这说明特征的选择和提取对于之后的模式识别有着至关重要的影响。此外,本文所提出的融合多特征的方法在任意一组对照实验中均优于单一特征的方法。可以看到各个方法对于MMSE这一临床评分的预测性能,在AD vs. NC中,使用本文方法,计算得到的CC达到了0.692 2,RMSE为3.097 2。而单一特征CC值最高达到了0.618 9,RMSE最小的为3.378 0。在AD vs. MCI中,本文方法计算得到的CC值达到了0.623 3,RMSE值为2.776 7。而单一特征CC值最高达到了0.549 3,RMSE最小的为3.024 1。本文提出的方法在MCI vs. NC和EMCI vs. LMCI实验中同样获得了好的预测结果。
|
图 2 不同方法的相关系数 Fig.2 The correlation coefficient of |
|
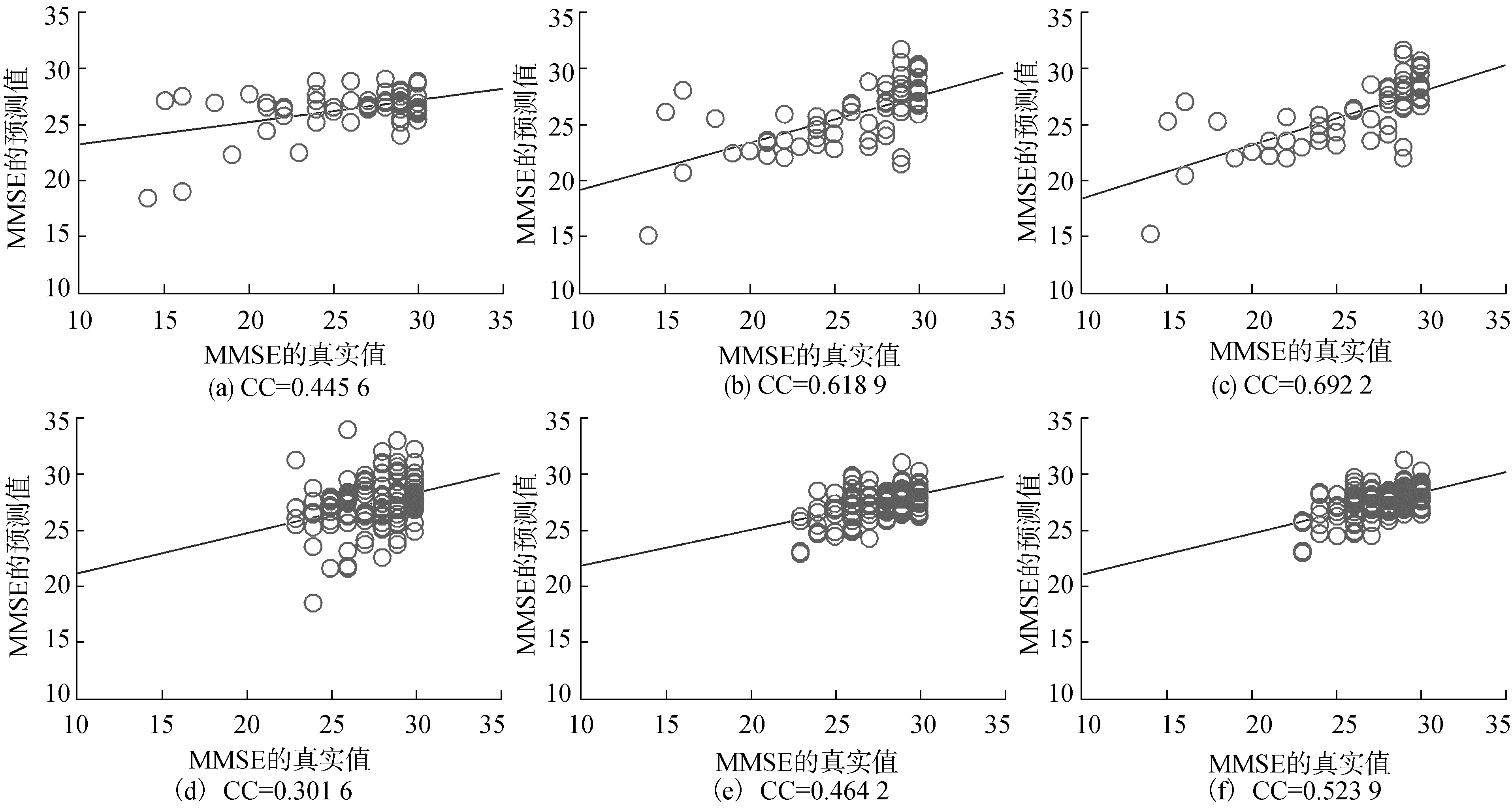
注:每幅图上面的为AD vs. NC, 下面的为MCI vs. NC 图 3 使用不同方法获得的散点图和相关系数 Fig.3 Scatter plots and the respective correlation coefficients obtained by the competing methods |
| 表 2 不同特征方法的回归性能 Tab.2 Regression performances of the competing methods |
图 2的柱状图更加直观地显示了所提出的融合多特征的方法优于单一特征的方法。图 3绘制的散点图显示了不同特征在不同的回归问题上所表现出的不同性能。
表 2、图 2、图 3还表明,本文方法在AD和NC这一对照实验中,有着更好的回归性能。这种情况说明患者和正常人的脑功能网络特征存在明显的差异,这使得模式识别过程更加容易。同时也说明了该类脑疾病的发作会影响其脑连接网络的结构,与前人的研究结果相符合。
3.4 最具判别性的脑区本文还研究了所使用的特征选择方法挑选出的最具判别性的脑区。因为在每次进行交叉验证时,所用的训练集不同导致选择出的边也不完全相同。因此,我们选择在所有交叉验证中出现频率最高的特征作为最具有判别力的特征。表 3给出了在MCI vs. NC实验中出现频率最高的10个脑区。图 4在一个大脑模板空间中画出了在MCI vs. NC实验中的10个最具有判别性的脑区。从表 3中可以看出,大部分选择脑区和以前研究人员使用组分析方法研究的结果是一致的。特别是一些脑如杏仁核(Amygdala)、海马旁回(ParaHippocampus)和颞前叶(Precuneus)等已被广泛认为可能与AD是相关的[18-23]。本文结果和前人研究结果是一致的,这也表明提出的方法能够发现与疾病相关的大脑区域从而辅助治疗。
| 表 3 MCI vs. NC实验中出现频率最高的10个脑区名称 Tab.3 The name of top 10 selected brain regions in MCI vs. NC |

|
图 4 MCI vs. NC实验中出现频率最高的10个脑区 Fig.4 Top 10 selected brain regions in MCI vs. NC |
本文提出了一种基于脑连接网络的方法,用于预测AD临床变量值,其中选择点的聚类系数和边的权重作为特征。通过对不同类型特征的融合,大大提高了预测的性能。从本文的实验中可以发现,在脑疾病的回归问题上,脑功能连接网络模态也有较好的回归性能;多个特征融合的使用优于单一特征的使用。
然而本文更多的是为了证明脑功能连接网络的数据信息能够用来预测临床评分这一问题。在特征提取和特征选择上运用了研究中较为普遍的算法。今后的工作中将尝试对现有的特征选择、特征提取算法有针对性地加以改进,使得模型能够更好地挖掘脑网络信息,增强模型的预测能力,从而辅助医生的诊断。
| [1] |
BROOKMEYER R, JOHNSON E, ZIEGLER-GRAHAM K, et al. Forecasting the global burden of Alzheimer's disease[J]. Alzheimers and dementia, 2007, 3(3): 186-91. DOI:10.1016/j.jalz.2007.04.381 ( 0) 0)
|
| [2] |
FAN Yong, RAO Hengyi, HURT H, et al. Multivariate examination of brain abnormality using both structural and functional MRI[J]. NeuroImage, 2007, 36(4): 1189-1199. DOI:10.1016/j.neuroimage.2007.04.009 ( 0) 0)
|
| [3] |
PETERSEN R C, DOODY R, KURZ A, et al. Current concepts in mild cognitive impairment[J]. Archives of neurology, 2001, 58(12): 1985-1992. DOI:10.1001/archneur.58.12.1985 ( 0) 0)
|
| [4] |
PETERSEN R C, SMITH G E, WARING S C, et al. Mild cognitive impairment: clinical characterization and outcome[J]. Archives of neurology, 1999, 56(3): 303-308. DOI:10.1001/archneur.56.3.303 ( 0) 0)
|
| [5] |
CHENG Bo, ZHANG Daoqiang, CHEN Songcan, et al. Semi-supervised multimodal relevance vector regression improves cognitive performance estimation from imaging and biological biomarkers[J]. Neuroinformatics, 2013, 11(3): 339-353. DOI:10.1007/s12021-013-9180-7 ( 0) 0)
|
| [6] |
ZHANG Daoqiang, SHEN Dinggang, Alzheimer's Disease Neuroimaging Initiative. Multi-modal multi-task learning for joint prediction of multiple regression and classification variables in alzheimer's disease[J]. NeuroImage, 2012, 59(2): 895-907. DOI:10.1016/j.neuroimage.2011.09.069 ( 0) 0)
|
| [7] |
ZHU Xiaofeng, SUK H I, SHEN Dinggang. A novel matrix-similarity based loss function for joint regression and classification in AD diagnosis[J]. NeuroImage, 2014, 100: 91-105. DOI:10.1016/j.neuroimage.2014.05.078 ( 0) 0)
|
| [8] |
Wee C Y, Yap P T, Li Wenbin, et al. Enriched white matter connectivity networks for accurate identification of MCI patients[J]. NeuroImage, 2011, 54(3): 1812-1822. DOI:10.1016/j.neuroimage.2010.10.026 ( 0) 0)
|
| [9] |
CHEN Gang, WARD B D, XIE Chunming, et al. Classification of Alzheimer disease, mild cognitive impairment, and normal cognitive status with large-scale network analysis based on resting-state functional MR imaging[J]. Radiology, 2011, 259(1): 213-221. DOI:10.1148/radiol.10100734 ( 0) 0)
|
| [10] |
WANG Jinhui, ZUO Xinian, DAI Zhengrui, et al. Disrupted functional brain connectome in individuals at risk for Alzheimer's disease[J]. Biological psychiatry, 2013, 73(5): 472-481. DOI:10.1016/j.biopsych.2012.03.026 ( 0) 0)
|
| [11] |
JIE Biao, ZHANG Daoqiang, WEE C Y, et al. Topological graph kernel on multiple thresholded functional connectivity networks for mild cognitive impairment classification[J]. Human brain mapping, 2014, 35(7): 2876-2897. DOI:10.1002/hbm.22353 ( 0) 0)
|
| [12] |
WEE C Y, YAP P T, ZHANG Daoqiang, et al. Identification of MCI individuals using structural and functional connectivity networks[J]. NeuroImage, 2012, 59(3): 2045-2056. DOI:10.1016/j.neuroimage.2011.10.015 ( 0) 0)
|
| [13] |
YAN Chaogan, FENG Yufeng. DPARSF: a MATLAB toolbox for "pipeline" data analysis of resting-state fMRI[J]. Frontiers in systems neuroscience, 2010, 4: 13. ( 0) 0)
|
| [14] |
ZANIN M, SOUSA P, PAPO D, et al. Optimizing functional network representation of multivariate time series[J]. Scientific reports, 2012, 2: 630. ( 0) 0)
|
| [15] |
TIBSHIRANI R. Regression shrinkage and selection via the lasso[J]. Journal of the royal statistical society, 1996, 58(1): 267-288. ( 0) 0)
|
| [16] |
NG A Y. Feature selection, L1, vs. L2, regularization, and rotational invariance[C]//Proceedings of the twenty-first International Conference on Machine Learning. New York, NY: ACM, 2004.
( 0) 0)
|
| [17] |
MEINSHAUSEN N, BüHLMANN P. Stability selection[J]. Journal of the royal statistical society, 2010, 72(4): 417-473. DOI:10.1111/rssb.2010.72.issue-4 ( 0) 0)
|
| [18] |
WOLF H, JELIC V, GERTZ H J, et al. A critical discussion of the role of neuroimaging in mild cognitive impairment[J]. Acta neurologica scandinavica supplementum, 2003, 107(S179): 52-76. DOI:10.1034/j.1600-0404.107.s179.10.x ( 0) 0)
|
| [19] |
POULIN S P, DAUTOFF R, MORRIS J C, et al. Amygdala atrophy is prominent in early Alzheimer's disease and relates to symptom severity[J]. Psychiatry research: neuroimaging, 2011, 194(1): 7-13. DOI:10.1016/j.pscychresns.2011.06.014 ( 0) 0)
|
| [20] |
SOLODKIN A, CHEN E E, VAN HOESEN G W, et al. In vivo parahippocampal white matter pathology as a biomarker of disease progression to Alzheimer's disease[J]. Journal of comparative neurology, 2013, 521(18): 4300-4317. DOI:10.1002/cne.23418 ( 0) 0)
|
| [21] |
DERFLINGER S, SORG C, GASER C, et al. Grey-matter atrophy in Alzheimer's disease is asymmetric but not lateralized[J]. Journal of Alzheimer's disease: JAD, 2011, 25(2): 347-357. ( 0) 0)
|
| [22] |
DAI Zhengjia, YAN Chaogan, LI Kuncheng, et al. Identifying and mapping connectivity patterns of brain network hubs in Alzheimer's disease[J]. Cerebral cortex, 2015, 25(10): 3723-3742. DOI:10.1093/cercor/bhu246 ( 0) 0)
|
| [23] |
HU Chenghui, JU Ronghui, SHEN Yusong, et al. Clinical decision support for Alzheimer's disease based on deep learning and brain network[C]//Proceedings of 2016 IEEE International Conference on Communications. Kuala Lumpur: IEEE, 2016: 1-6.
( 0) 0)
|
 2017, Vol. 12
2017, Vol. 12


