聚类分析作为一种重要的数据处理技术已经被广泛地应用到各种领域,如模式识别、数据挖掘等。在聚类分析中,需要根据数据点之间的相似或相异程度,对数据点进行区分和分类。因此对于不同的数据集,选择合适的距离度量方式对算法的聚类性能有重要的影响[1]。欧式距离是较为常用的距离度量方式,但其具有以下不足:1) 采用欧式距离的方法通常是假设所有变量都是不相关的,并且数据所有维度的方差都为1,所有变量的协方差为0[2];2) 欧式距离仅仅适用于特征空间中的超球结构,对于其他结构的数据集不太理想;3) 欧式距离对噪声比较敏感,聚类结果容易受到噪声的干扰[3]。因此,欧式距离在实际应用中受到了限制。
针对这些问题,近年来提出了多种距离学习的方法,根据在距离学习过程中是否有先验的训练样本,距离学习可以分为有监督距离学习[4-6]和无监督距离学习[7-8]。在有监督距离学习的方法中,需要借助数据集的辅助信息进行距离学习,其中辅助信息通常以约束对的形式来表示[9]。由数据集辅助信息学习得到的距离函数,可以有效地反映数据集的自身特点,对数据集具有很好的适用性。
在之前的研究中,人们提出了许多利用辅助信息进行距离学习的算法。比如,将距离学习转化为凸优化问题的方法[4]、相关成分分析法[5]、区分成分分析法等[10]。然而这些方法大多数将目标函数假设在马氏距离的框架下,本质上来说,针对马氏距离学习得到的新距离是欧式距离的线性变换,仍然有欧式距离的缺点。在含有辅助信息的数据集中,欧式距离的聚类性能和鲁棒性不理想。
因此,本文提出了一种基于混合距离学习的鲁棒模糊C均值聚类算法(HR-FCM)。在此算法中,数据集的未知距离被表示成若干候选距离的线性组合,在候选的距离度量中加入了非线性的距离度量。与其他有监督的聚类算法[11-12]不同的是,HR-FCM利用数据集本身含有的少数的辅助信息进行混合距离的学习,相对于欧式距离没有考虑到数据集本身的特征,利用数据集的辅助信息学习得到的混合距离融合了数据集的一些特征,提高了提高算法的聚类性能和鲁棒性。
1 混合距离学习 1.1 混合距离由于数据集结构特征不同,为了合理地计算不同数据集之间的距离,在距离学习中引入权重已经成为一种常用的方法。本文定义数据集中的混合距离度量的线性组合如下:
| $ \begin{array}{*{20}{c}} {D\left( {\mathit{\boldsymbol{x}},\mathit{\boldsymbol{y}}} \right) = \sum\limits_{i = 1}^p {{\omega _i}{d_i}\left( {\mathit{\boldsymbol{x}},\mathit{\boldsymbol{y}}} \right)} }\\ {{\rm{s}}{\rm{.t}}{\rm{.}}\;\sum\limits_{i = 1}^p {{\omega _i} = 1} ,0 \le {\omega _i} \le 1,i = 1,2, \cdots ,p} \end{array} $ | (1) |
由文献[13]可证式(1) 中D(x, y)是一个距离函数。下面将介绍距离学习的过程。
本文的数据集分为两个部分:1) 训练集,它是以约束对形式存在的辅助信息;2) 用来聚类的数据集。本文将所有的训练样本集合表示为D={(xak, xbk, yk), k=1, 2, …, np}, 其中np为成对约束的对数。每一对约束对都是一个包含3个元素的元组(xak, xbk, yk),其中xak和xbk为d维向量的样本点,yk是点对xak和xbk之间关系的类标。当xak和xbk属于同一类样本时,yk为正;相反,yk为负。使用X={x1, x2, …, xN}来表示D中所有的训练样本点,其中N表示样本点的个数。
在距离学习中,借鉴文献[2]的思想,利用最大边界的框架,优化目标函数:
| $ \begin{array}{*{20}{c}} {\mathop {\min }\limits_{{\omega _i},\beta } J = \frac{1}{2}\sum\limits_{i = 1}^p {\omega _i^2} - C\sum\limits_{k = 1}^n {{y_k}\left( {\sum\limits_{i = 1}^p {{\omega _i}{d_i}\left( {\mathit{\boldsymbol{x}}_a^k,\mathit{\boldsymbol{x}}_b^k} \right)} - \beta } \right)} }\\ {{\rm{s}}{\rm{.t}}{\rm{.}}\;\;{y_k}\left( {\sum\limits_{i = 1}^p {{\omega _i}{d_i}\left( {\mathit{\boldsymbol{x}}_a^k,\mathit{\boldsymbol{x}}_b^k} \right)} - \beta } \right) > 0}\\ {\sum\limits_{i = 1}^p {{\omega _i} = 1} ,0 \le {\omega _i} \le 1,i = 1,2, \cdots ,p} \end{array} $ | (2) |
式中:di(xak, xbk)表示第k对约束对的第i个距离分量,为了便于表示,在之后的介绍中用dik来代替di(xak, xbk)。yk为该对样本点的对应类标,C为惩罚因子,β为阈值。
使用拉格朗日乘子法优化式(2),其拉格朗日函数为
| $ \begin{array}{*{20}{c}} {L = \frac{1}{2}\sum\limits_{i = 1}^p {\omega _i^2} - C\sum\limits_{k = 1}^{{n_p}} {{y_k}\left( {\sum\limits_{i = 1}^p {{\omega _i}{d_i}\left( {\mathit{\boldsymbol{x}}_a^k,\mathit{\boldsymbol{x}}_b^k} \right)} - \beta } \right)} + }\\ {\lambda \left( {1 - \sum\limits_{i = 1}^p {{\omega _i}} } \right) + \sum\limits_{i = 1}^p {{\varphi _i}{\omega _i}} } \end{array} $ | (3) |
式中:φi和λ为拉格朗日乘子。则式(3) 的KKT条件为
| $ \left\{ \begin{array}{l} \frac{{\partial L}}{{\partial {\omega _i}}} = 0\\ {\varphi _i} \ge 0\\ {\varphi _i}{\omega _i} = 0 \end{array} \right. $ | (4) |
显然由式(4) 无法求得ωi,因此先舍弃ωi非负的条件,则可重新构建新的拉格朗日函数,如式(5) 所示:
| $ \begin{array}{*{20}{c}} {L = \frac{1}{2}\sum\limits_{i = 1}^p {\omega _i^2} - C\sum\limits_{k = 1}^{{n_p}} {{y_k}\left( {\sum\limits_{i = 1}^p {{\omega _i}{d_i}\left( {\mathit{\boldsymbol{x}}_a^k,\mathit{\boldsymbol{x}}_b^k} \right)} - \beta } \right)} + }\\ {\lambda \left( {1 - \sum\limits_{i = 1}^p {{\omega _i}} } \right)} \end{array} $ | (5) |
可以求得
| $ {\omega _i} = \frac{1}{p} + C\sum\limits_{k = 1}^{{n_p}} {{y_k}d_i^k} - \frac{C}{p}\sum\limits_{j = 1}^p {\sum\limits_{k = 1}^{{n_p}} {{y_k}d_j^k} } $ | (6) |
由式(6) 可以看出,即使在成功的优化过程下ωi也可能出现负值,由前文看出,在考虑ωi为负的条件下,无法用拉格朗日函数求解。因此,在受到加权中心模糊聚类算法[14]的启发,可以将ωi改写为式(7) 的形式:
| $ {\omega _i} = \left\{ \begin{array}{l} 0,\;\;\;\;\;i \in {p^ - }\\ \frac{1}{{\left| {{p^ + }} \right|}} + C\sum\limits_{k = 1}^{{n_p}} {{y_k}d_i^k} - \frac{C}{{\left| {{p^ + }} \right|}}\sum\limits_{j = 1}^p {\sum\limits_{k = 1}^{{n_p}} {{y_k}d_j^k} } ,\;\;\;i \in {p^ + } \end{array} \right. $ | (7) |
式中:p+表示所有使ωi取正值的i的集合,p-表示无法使ωi取正值的i的集合,使用|p+|和|p-|来分别表示集合p+和p-的大小。
对于阈值β,使用梯度下降的方法进行求解,通过求偏导,得到β的梯度如下:
| $ {\nabla _\beta }J = C\sum\limits_{k = 1}^{{n_p}} {{y_k}} $ | (8) |
为了满足约束条件:
| $ {\nabla _\beta }J = C\sum\limits_{k = 1}^{\left| {n_p^ + } \right|} {{y_k}} $ | (9) |
式中:|np+|表示集合np+的大小。使用梯度下降的方法,求解β′=β-γ∇βJ,其中,γ表示为梯度下降的学习速率,设置
由于集合np+不断改变,则等式进一步修改为如下形式:
| $ {\omega _i} = \left\{ \begin{array}{l} 0,\;\;\;\;\;i \in {p^ - }\\ \frac{1}{{\left| {{p^ + }} \right|}} + C{E_i},\;\;\;i \in {p^ + } \end{array} \right. $ | (10) |
式中:
| $ {E_i} = \sum\limits_{k = 1}^{{n_p}} {{y_k}d_i^k} - \frac{1}{{\left| {{p^ + }} \right|}}\sum\limits_{j = {p^ + }} {\sum\limits_{k = n_p^ + }^{{n_p}} {{y_k}d_j^k} } $ | (11) |
具体的算法描述如下:
求解集合p+和p-的算法,算法1如下:
1) 初始化p+=∅, p0-={1, 2, …, p}, h=0;
2)h=h+1, ph+=ph-1++{i}, ph-=ph-1--{i}, 其中
3) 通过式(10) 计算ωg并判断其是否大于0。其中
求解ω具体算法,算法2步骤如下:
输入 数据矩阵X∈Rd×N,惩罚因子C,成对约束(xak, xbk, yk),其中yk={+1, -1};
输出 距离权值ω,阈值β。
步骤:
1) 初始化:
2) 计算距离矩阵:D(i, k),
3) 设置迭代步数:t=1,
4) 循环,直至收敛:
① 更新学习率:γ=1/t, t=t+1
② 更新训练子集:
| $ n_p^ + = \left\{ {{y_k} \in D:{y_k}\left( {\sum\limits_{i = 1}^p {{\omega _i}{d_i}\left( {x_a^k,x_b^k} \right) - \beta } > 0} \right)} \right\} $ |
③ 计算梯度:
| $ {\nabla _\beta }J = C\sum\limits_{k \in n_p^ + } {{y_k}} $ |
④ 更新阈值:β′=β-γ∇βJ;
⑤ 更新集合p+和p-,使用算法1;
⑥ 更新ω。
至此,通过对训练集的距离学习,得到的权值ωi,从而得到新的距离函数。通过数据集本身构成的辅助信息学习得到的混合距离,对数据集自身的适应性更高,更有利于聚类效果的改善。
1.2 时间复杂度分析这个部分主要讨论所提算法的时间复杂度,HR-FCM算法的时间复杂度主要讨论的是混合距离学习的时间复杂度。总的来说,混合距离学习的最大时间复杂度为O(N2dp),其中N表示训练数据集中样本的个数,d表示样本的维度,p表示候选距离的个数。算法的主要时间消耗在求解距离矩阵D中,时间复杂度为O(Ndp)。在迭代循环中,每一步都有一个线性的时间复杂度,为O(max(N, np))。
2 基于混合距离学习的鲁棒的FCM算法模糊C均值聚类算法(FCM),它是一种基于目标函数的聚类算法,是迄今为止应用最广泛、理论最为完善的聚类算法。传统的FCM聚类算法使用欧式距离作为距离度量函数导致其聚类性能和鲁棒性较差。
针对传统FCM算法的缺点,近年来研究者们提出了一些改进的FCM算法,例如:基于改进的模糊划分的模糊C均值聚类算法(IFP-FCM)[15]和基于改进的模糊划分的泛化的模糊C均值聚类算法(GIFP-FCM)[16]。IFP-FCM算法是由Höppner和Klawonn提出的一种改进的FCM聚类算法。IFP-FCM算法通过对每个数据增加一个隶属约束函数,以降低算法对噪声的敏感性,增加了算法的鲁棒性。但是此算法仍然沿用的是传统的欧式距离作为距离度量,受到IFP-FCM算法的启发,朱林等提出了GIFP-FCM算法。
在此启发下,本文提出了一种基于混合距离学习的鲁棒的FCM聚类算法,算法描述如下:
假设给定一个样本集合X={x1, x2, …, xn},其中n是样本的个数,每一个样本是d维,预设聚类中心的集合为V={vi, 1≤i≤c}, 其中c表示类别数。令uij表示第j个样本隶属于第i类的程度。则隶属矩阵为U={uij|1≤i≤c, 1≤j≤n}。对于每一个样本xj,通过构造一个新的隶属约束函数
| $ \begin{array}{*{20}{c}} {J = \sum\limits_{i = 1}^c {\sum\limits_{j = 1}^n {u_{ij}^md_p^2\left( {{\mathit{\boldsymbol{x}}_j},{\mathit{\boldsymbol{v}}_i}} \right)} } + \sum\limits_{j = 1}^n {{a_j}} \sum\limits_{i = 1}^c {{u_{ij}}\left( {1 - u_{ij}^{m - 1}} \right)} \;{\rm{s}}{\rm{.t}}{\rm{.}}\;\;\;m > 1}\\ {\sum\limits_{i = 1}^c {{u_{ij}} = 1} ,\;\;\;\;0 \le {u_{ij}} \le 1,\;\;\;1 \le i \le c,1 \le j \le n} \end{array} $ | (12) |
式中:
使用拉格朗日乘数法对式(12) 进行优化,得到新的聚类中心和隶属函数如式(13) 和式(14):
| $ {\mathit{\boldsymbol{v}}_i} = \frac{{\sum\nolimits_{j = 1}^n {u_{ij}^m{\mathit{\boldsymbol{x}}_j}} }}{{\sum\nolimits_{j = 1}^n {u_{ij}^m} }} $ | (13) |
| $ {u_{ij}} = \frac{1}{{\sum\nolimits_{k = 1}^c {{{\left( {\frac{{d_p^2\left( {{\mathit{\boldsymbol{x}}_j},{\mathit{\boldsymbol{v}}_i}} \right) - \alpha \times \mathop {\min }\limits_{1 \le s \le c} d_p^2\left( {{\mathit{\boldsymbol{x}}_j},{\mathit{\boldsymbol{v}}_s}} \right)}}{{d_p^2\left( {{\mathit{\boldsymbol{x}}_j},{\mathit{\boldsymbol{v}}_k}} \right) - \alpha \times \mathop {\min }\limits_{1 \le s \le c} d_p^2\left( {{\mathit{\boldsymbol{x}}_j},{\mathit{\boldsymbol{v}}_s}} \right)}}} \right)}^{\frac{1}{{m - 1}}}}} }} $ | (14) |
| $ {d_p}\left( {{\mathit{\boldsymbol{x}}_j},{\mathit{\boldsymbol{v}}_i}} \right) = \left( {\sum\limits_{k = 1}^n {{{\left| {{\mathit{\boldsymbol{x}}_j} - {\mathit{\boldsymbol{v}}_i}} \right|}^p}} } \right)\frac{1}{p}\;\;\;\;{\rm{s}}{\rm{.t}}{\rm{.}}\;\;\;\;1 < p < 2 $ | (15) |
式(15) 是表示样本与类中心的距离度量公式,当p=2时,式(15) 就是传统的欧氏距离。
本文提出的HR-FCM算法,加入了距离学习的过程,通过距离学习出来的距离度量比传统的欧式距离更佳适合具有辅助信息的数据集,增加了算法的聚类性能和鲁棒性。因此,用新的混合距离D替换式(13) 和式(14) 中的距离度量dp,得到新的聚类中心公式(16) 和隶属度计算公式(17);
| $ {v_i} = \frac{{\sum\nolimits_{j = 1}^n {u_{ij}^m{\mathit{\boldsymbol{x}}_j}} }}{{\sum\nolimits_{j = 1}^n {u_{ij}^m} }} $ | (16) |
| $ {u_{ij}} = \frac{1}{{\sum\nolimits_{k = 1}^c {{{\left( {\frac{{{\mathit{\boldsymbol{D}}^2}\left( {{\mathit{\boldsymbol{x}}_j},{\mathit{\boldsymbol{v}}_i}} \right) - \alpha \times \mathop {\min }\limits_{1 \le s \le c} {\mathit{\boldsymbol{D}}^2}\left( {{\mathit{\boldsymbol{x}}_j},{\mathit{\boldsymbol{v}}_s}} \right)}}{{{\mathit{\boldsymbol{D}}^2}\left( {{\mathit{\boldsymbol{x}}_j},{\mathit{\boldsymbol{v}}_k}} \right) - \alpha \times \mathop {\min }\limits_{1 \le s \le c} {\mathit{\boldsymbol{D}}^2}\left( {{\mathit{\boldsymbol{x}}_j},{\mathit{\boldsymbol{v}}_s}} \right)}}} \right)}^{\frac{1}{{m - 1}}}}} }} $ | (17) |
式中距离度量D的定义如式(18):
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{D}}\left( {\mathit{\boldsymbol{x}},\mathit{\boldsymbol{y}}} \right) = \sum\limits_{i = 1}^p {{\omega _i}{d_i}\left( {\mathit{\boldsymbol{x}},\mathit{\boldsymbol{y}}} \right)} }\\ {{\rm{s}}{\rm{.t}}{\rm{.}}\;\;\;\sum\limits_{i = 1}^p {{\omega _i} = 1} ,0 \le {\omega _i} \le 1} \end{array} $ | (18) |
式中:ωi是通过距离学习得到的权值。
算法3 HR-FCM算法
输入 数据矩阵X∈Rd×N,权值向量ω,聚类数目c,阈值ε,模糊指数m,抗噪参数α,最大迭代次数T;
输出 最终的隶属矩阵U。
步骤:
1) 初始化:uij=uij1, t=1;
2) 使用式(16) 计算新的聚类中心vit+1;
3) 使用式(17) 计算新的隶属矩阵uijt+1;
4) 如果‖Ut+1-Ut‖<ε或者t>T, 输出最终的隶属矩阵,否则t=t+1返回2)。
HR-FCM算法通过使用距离学习得到的新的混合距离代替传统FCM算法中的欧式距离,进一步增加了算法的抗噪性能。再者,通过数据集本身的辅助信息进行距离的学习的得到的混合距离,比原有的欧式距离更加适合数据集,提高了算法的适用性。HR-FCM算法与传统的FCM算法相比,具有更佳的聚类性能和鲁棒性。
3 实验研究和分析本章通过实验检测本文提出的HR-FCM算法的聚类性能和鲁棒性能。本章的实验主要分为两个部分:1) 将本文提出的HR-FCM算法与现有的基于欧氏距离的聚类算法作比较,如:FCM、K-means和K-medoids, 检测算法的聚类性能;2) 主要是检测算法的鲁棒性能,通过对实验数据加入不同程度的随机噪声,并与FCM算法和GIFP-FCM算法作比较。
3.1 实验设置和实验数据本文的实验参数设置如下:阈值ε=10-5,最大迭代次数T=300,模糊指数T=300,m∈{1.5, 2, 3, 4}, α∈{0.5, 0.7, 0.9, 0.99}。为了实验结果的公平,重复每次聚类过程20,实验结果取均值。
实验中对于候选距离的选取,选择了基于欧式距离的含有方差的距离分量d1(x, y),非线性的距离分量d3(x, y), 曼哈顿距离分量d2(x, y)。由这3种距离分量线性组合后的混合距离D(x, y)是一个非线性的距离函数。本文预设的3个距离度量如式(19) 所示:
| $ \left\{ \begin{array}{l} {d_1}\left( {\mathit{\boldsymbol{x}},\mathit{\boldsymbol{y}}} \right) = {\left( {\mathit{\boldsymbol{x}} - \mathit{\boldsymbol{y}}} \right)^{\rm{T}}}\frac{1}{{{\sigma ^2}}}\left( {\mathit{\boldsymbol{x}} - \mathit{\boldsymbol{y}}} \right)\\ {d_2}\left( {\mathit{\boldsymbol{x}},\mathit{\boldsymbol{y}}} \right) = \sum\limits_{i = 1}^d {\frac{{\left| {{\mathit{\boldsymbol{x}}_i} - {\mathit{\boldsymbol{y}}_i}} \right|}}{{{\sigma ^2}}}} \\ {d_3}\left( {\mathit{\boldsymbol{x}},\mathit{\boldsymbol{y}}} \right) = 1 - \exp \left( { - \frac{{ - 3{{\left\| {\mathit{\boldsymbol{x}} - \mathit{\boldsymbol{y}}} \right\|}^2}}}{{{\sigma ^2}}}} \right) \end{array} \right. $ | (19) |
本文选取的实验数据集均来自UCI数据集,数据集细节如表 1。由于UCI数据集中没有约束对形式的辅助信息,需要选取数据集中的一部分带标签的数据集构成约束对作为训练集。其中,拥有相同的类标的样本点构成正约束对,不同的类标的构成负约束对,选取相同数目的正负约束对进行距离学习。对于本文中的数据集,前6个取10%的数据集构成训练集,最后两个取1%的数据集。
| 表 1 数据集信息 Tab.1 Description of data sets |
在抗噪声实验中,在数据集中随机加入10%和20%的高斯白噪声(SNR=40 db或者30 db),分别计算本文提出的HR-FCM算法、传统FCM聚类算法和GIFP-FCM算法的聚类性能。
3.2 评价方法为了评估算法的聚类效果,本文采用了一些标准的评价方法,包括归一化互信息(NMI)[17]和芮氏指数(RI)[18-19], 这些将用来评价HR-FCM算法与FCM的聚类效果。
| $ {\rm{NMI}}\left( {X,Y} \right) = \frac{{I\left( {X,Y} \right)}}{{\sqrt {H\left( X \right) \cdot H\left( Y \right)} }} $ | (20) |
| $ {\rm{RI}}\left( {X,Y} \right) = \frac{{a + b}}{{n \times \left( {n - 1} \right)/2}} $ | (21) |
式中:X定义了已知标签的原始数据,Y定义了对未知标签的原始数据的聚类结果,I(X, Y)定义了X和Y之间的互信息,H(X)和H(Y)分别代表了X和Y的熵,a定义了X和Y中任意两个具有相同类标签并且属于同一个样本的数目,b定义了X和Y中任意两个具有不同标签并且属于不同类的样本的个数,n表示原始样本的个数。显而易见,NMI和RI的值都是介于0~1的,NMI和RI的值越大,表示X和Y之间的相似度就越高,即算法的效果越好。
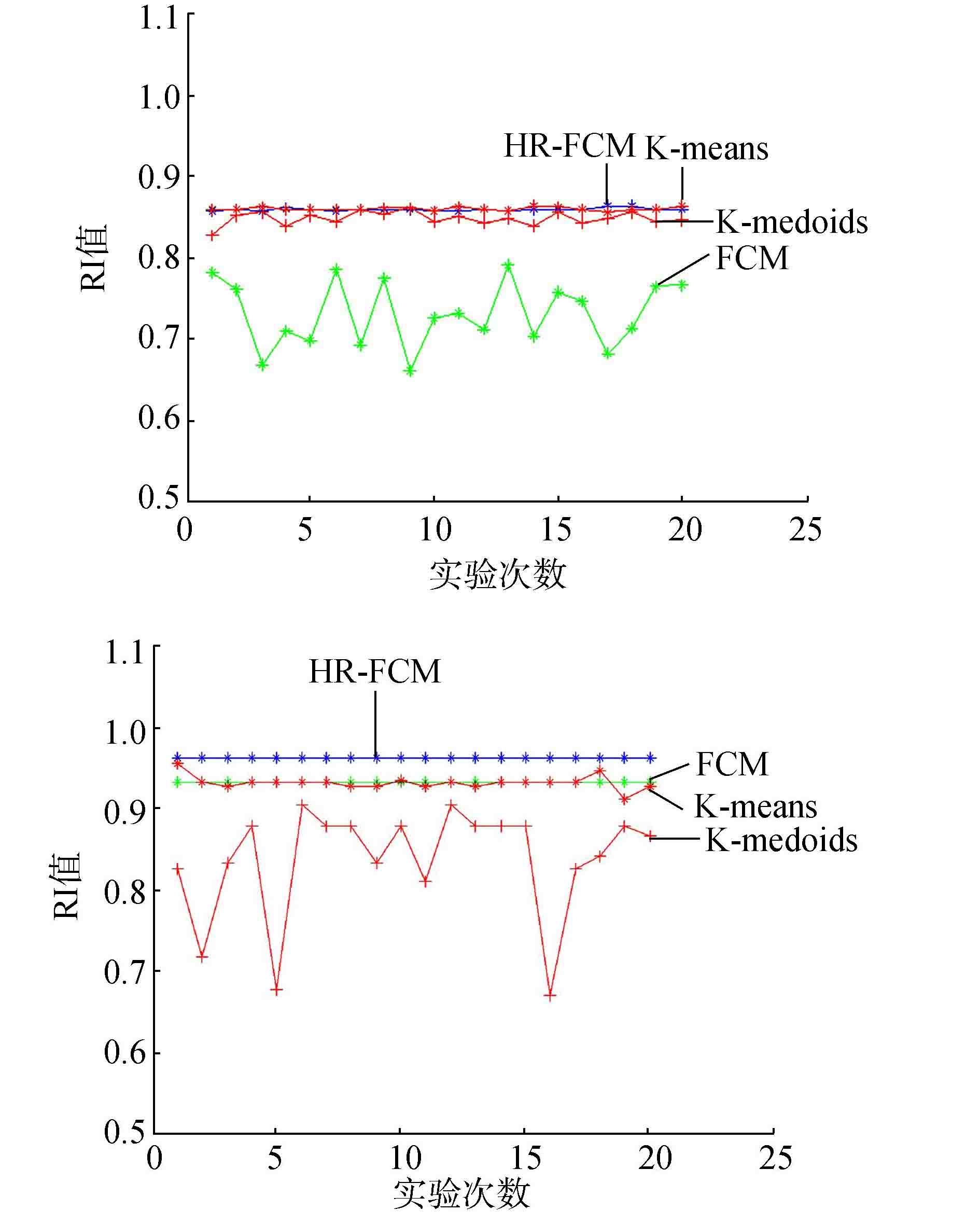
3.3 实验结果和分析在第1部分的实验中,为了检测算法的聚类性能,设置HR-FCM算法中的抗噪参数α=0,比较使用了混合距离的HR-FCM算法与使用欧氏距离的FCM算法和其他常用的基于欧氏距离的聚类算法,检测混合距离对聚类性能的影响。选取上述7个数据集作为本次实验的实验数据集,每组数据集运行20次,实验结果选取RI和NMI值的均值,实验结果如图 1和图 2所示。
|
图 1 各数据集的RI值 Fig.1 The RI on the different data sets |
|
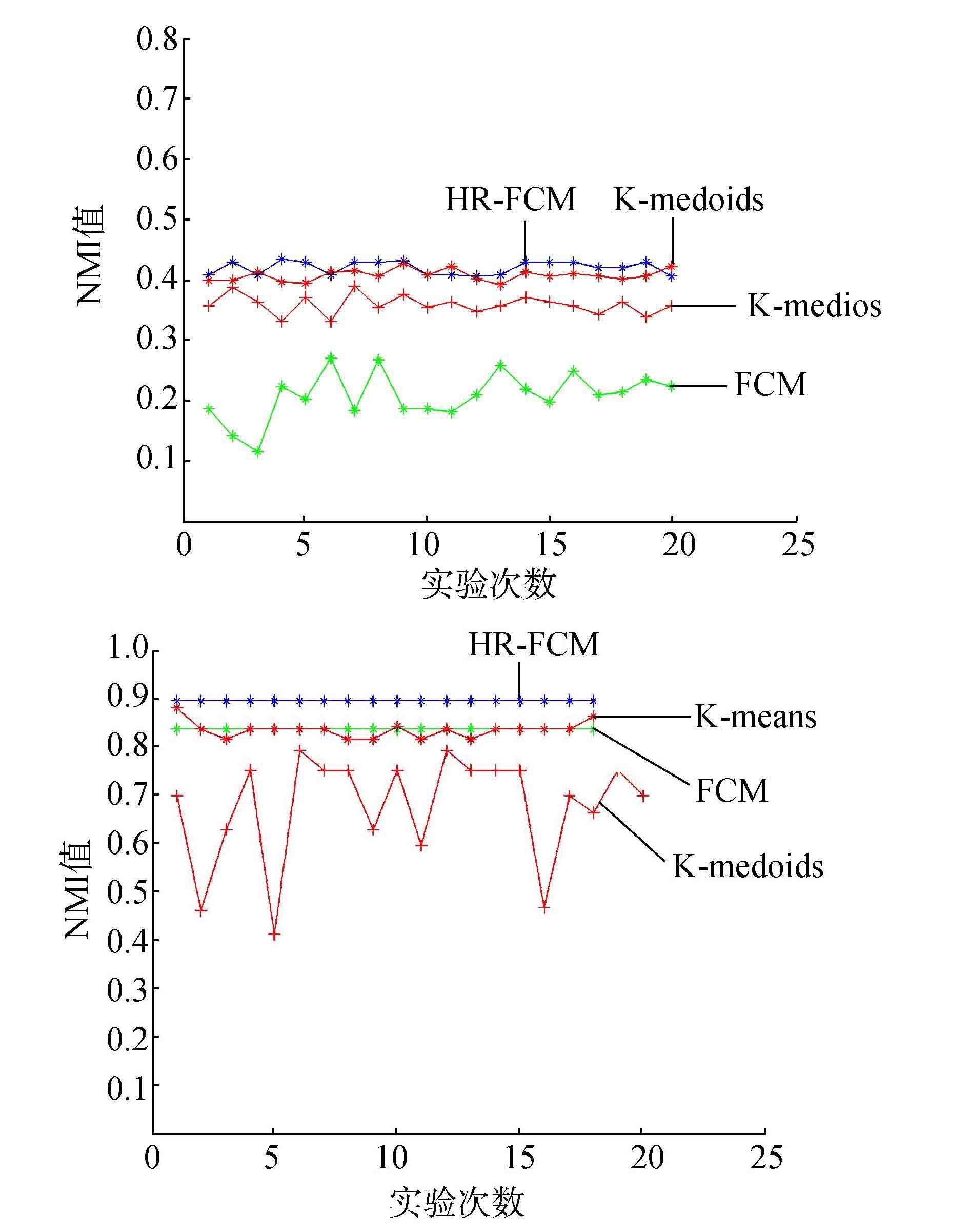
图 2 各数据集的NMI值 Fig.2 The NMI on the different data sets |
第1部分的实验结果表明:对于小数据集,HR-FCM算法的聚类性能不仅比传统的基于欧氏距离的FCM聚类算法要好,也比基于欧氏距离的K-mean和K-medoids的聚类算法性能好。对于大样本数据集,由于样本数对于FCM聚类算法的影响比K-means和K-medoids的大,此时,距离度量对于聚类性能的影响力下降,因此,K-means和K-medoids算法的聚类性能较佳,但是与传统的FCM聚类算法相比,本文提出的基于混合聚类的HR-FCM算法具有较好的聚类性能,如waveform数据集。
从表 2的实验中还可以得到,对于高维的数据集,4种算法聚类性能都有一定的下降。由于数据维度的增加,单个样本的信息增加,在这些信息中存在着不同类型的信息,本文提出的混合距离度量函数相比传统的欧氏距离能够充分地度量出样本之间的距离,学习出样本之间的有效信息,提高算法的聚类性能。对于数据集wdbc和sonar, 表 2的实验结果显示了混合距离的有效性。
| 表 2 聚类算法性能 Tab.2 The performance of clustering algorithm |
为了检测算法在多类样本数据集中的聚类性能,实验中也使用了多类样本数据集vowel。由于多类样本中,随着类别的增加,对于样本之间的距离度量的难度增加,因此算法的聚类性能受到一定的影响,如图 1和图 2中,对于少类别数据集wine, 各个算法的RI和NMI值较高,对于多类别数据集vowel,各个算法的指标出现较大幅度的下降。图 1和图 2的实验结果也表明,对于多样本数据集,本文提出的HR-FCM算法的聚类性能与其他3种算法的聚类性能都出现了一定的下降,但是本文提出的算法较之其他3种算法的稳定性较高。
在第2部分的实验中,为了检测本文算法的鲁棒性能,设置了在两个多类别样本数据集上的对比实验,这两个数据集分别是小样本量的低维数据集vowel和大样本量的高维数据集led。本次实验主要是为了检测HR-FCM算法与传统的FCM算法和GIFP-FCM算法在聚类性能和鲁棒性能上面的差别,因此本次实验,比较了3种算法在不同模糊指数的情况下的聚类性能,通过改变噪声的添加比例,比较算法的鲁棒性能。为了进一步检测HR-FCM算法受抗噪参数的影响,本次实验设置不同的参数取值,通过比较聚类指标的变化显示算法的鲁棒性的变化。
从表 3和表 4的结果中容易看出在相同的模糊指数的情况下,HR-FCM算法的聚类性能和鲁棒性大多强于传统的FCM算法。在模糊指数一定的情况下,随着抗噪参数α的增加,HR-FCM算法的鲁棒性越来越强。在加入噪声后,算法的聚类性能收到了一定的影响,算法的聚类性能下降,FCM聚类算法的聚类性能下降较多。从表 4的实验结果中容易看出,在实验数据集为大数据集的情况下,本文提出的HR-FCM算法的聚类性能和鲁棒性强于传统的FCM算法。由表 3和表 4的结果也可以看出本文提出的HR-FCM算法的聚类结果要优于GIFP-FCM算法。由于本文使用混合距离代替传统的欧氏距离,因此本文的HR-FCM算法的鲁棒性能强于GIFP-FCM算法。
| 表 3 噪声实验结果 Tab.3 The results on the data sets with or without random noises |
| 表 4 噪声实验结果 Tab.4 The results on the data sets with or without random noises |
综上所述,对于含有辅助信息的数据集,本文提出的HR-FCM算法由于采用混合距离,使得算法具有较好的适应性,比传统的使用欧氏距离作为距离度量的FCM算法和GIFP-FCM算法具有更好的聚类性能和鲁棒性。
4 结束语在聚类的实际应用中,大多数数据集都含有一定量的辅助信息,这些辅助信息中含有重要的数据特征,但是这些辅助信息在聚类过程中常常被忽略。本文提出了一种利用数据集的辅助信息进行距离学习的方法,进而提出了一种改进的FCM算法HR-FCM。用数据集的辅助信息进行距离学习得到的混合函数,不仅能够反映出数据集本身的特征,而且比欧式距离更加契合数据集,更加适合于实际应用。在含有辅助信息的数据集中,本文提出的HR-FCM算法具有较好的聚类性能和鲁棒性。实验结果证明了结论。
| [1] |
王骏, 王士同. 基于混合距离学习的双指数模糊C均值算法[J]. 软件学报, 2010, 21(8): 1878-1888. WANG Jun, WANG Shitong. Double indices FCM algorithm based on hybrid distance metric learning[J]. Journal of software, 2010, 21(8): 1878-1888. (  0) 0)
|
| [2] |
WU L, HOI S C H, JIN R, et al. Learning bregman distance functions for semi-supervised clustering[J]. IEEE transactions on knowledge and data engineering, 2012, 24(3): 478-491. DOI:10.1109/TKDE.2010.215 ( 0) 0)
|
| [3] |
WU K L, YANG M S. Alternative c-means clustering algorithms[J]. Pattern recognition, 2002, 35(10): 2267-2278. DOI:10.1016/S0031-3203(01)00197-2 ( 0) 0)
|
| [4] |
XING E P, NG A Y, JORDAN M I, et al. Distance metric learning, with application to clustering with side-information[J]. Advances in neural information processing systems, 2003, 15: 505-512. ( 0) 0)
|
| [5] |
BAR-Hillel A, HERTZ T, SHENTAL N, et al. Learning a mahalanobis metric from equivalence constraints[J]. Journal of machine learning research, 2005, 6(6): 937-965. ( 0) 0)
|
| [6] |
郭瑛洁, 王士同, 许小龙. 基于最大间隔理论的组合距离学习算法[J]. 智能系统学报, 2015, 10(6): 843-850. ( 0) 0)
|
| [7] |
YE J, ZHAO Z, LIU H. Adaptive distance metric learning for clustering[C]//IEEE Conference on Computer Vision and Pattern Recognition. Minneapolis, USA, 2007:1-7.
( 0) 0)
|
| [8] |
WANG X, WANG Y, WANG L. Improving fuzzy c-means clustering based on feature-weight learning[J]. Pattern recognition letters, 2004, 25(10): 1123-1132. DOI:10.1016/j.patrec.2004.03.008 ( 0) 0)
|
| [9] |
HE P, XU X, HU K, et al. Semi-supervised clustering via multi-level random walk[J]. Pattern recognition, 2014, 47(2): 820-832. DOI:10.1016/j.patcog.2013.07.023 ( 0) 0)
|
| [10] |
HOI S C H, LIU W, LYU M R, et al. Learning distance metrics with contextual constraints for image retrieval[C]//IEEE Conference on Computer Vision and Pattern Recognition. New York, USA, 2006:2072-2078.
( 0) 0)
|
| [11] |
曾令伟, 伍振兴, 杜文才. 基于改进自监督学习群体智能(ISLCI)的高性能聚类算法[J]. 重庆邮电大学学报:自然科学版, 2016, 28(1): 131-137. ZENG Lingwei, WU Zhenxing, DU Wencai. Improved self supervised learning collection intelligence based high performance data clustering approach[J]. Journal of Chongqing university of posts and telecommunications:natural science edition, 2016, 28(1): 131-137. (  0) 0)
|
| [12] |
程旸, 王士同. 基于局部保留投影的多可选聚类发掘算法[J]. 智能系统学报, 2016, 11(5): 600-607. CHENG Yang, WANG Shitong. A multiple alternative clusterings mining algorithm using locality preserving projections[J]. CAAI transactions on intelligent systems, 2016, 11(5): 600-607. (  0) 0)
|
| [13] |
DUDA R O, HART P E, STORK D G. Pattern classification[M]//Pattern classification. Wiley, 2001:119-131.
( 0) 0)
|
| [14] |
MEI J P, CHEN L. Fuzzy clustering with weighted medoids for relational data[J]. Pattern recognition, 2010, 43(5): 1964-1974. DOI:10.1016/j.patcog.2009.12.007 ( 0) 0)
|
| [15] |
HOPPNER F, KLAWONN F. Improved fuzzy partitions for fuzzy regression models[J]. International journal of approximate reasoning, 2003, 32(2/3): 85-102. ( 0) 0)
|
| [16] |
ZHU L, CHUNG F L, WANG S. Generalized fuzzy C-means clustering algorithm with improved fuzzy partitions[J]. IEEE transactions on systems man and cybernetics part B, 2009, 39(3): 578-591. DOI:10.1109/TSMCB.2008.2004818 ( 0) 0)
|
| [17] |
STREHL A, GHOSH J. Cluster ensembles-a knowledge reuse framework for combining multiple partitions[J]. Journal of machine learning research, 2002, 3(3): 583-617. ( 0) 0)
|
| [18] |
IWAYAMA M, TOKUNAGA T. Hierarchical Bayesian clustering for automatic text classification[J]. IJCAI, 1996: 1322-1327. ( 0) 0)
|
| [19] |
RAND W M. Objective criteria for the evaluation of clustering methods[J]. Journal of the american statistical association, 1971, 66(336): 846-850. DOI:10.1080/01621459.1971.10482356 ( 0) 0)
|
 2017, Vol. 12
2017, Vol. 12


