船舶的横摇是一个不规则的非线性运动,在非线性横摇运动中,混沌现象对船舶的航行有非常大的影响,混沌运动是导致船舶倾覆的主要原因之一[1-4]。近年来,人们对船舶横摇混沌现象的形成以及预测做了深入研究,并针对混沌特性设计了不同的控制方法。R.F.Mohammad和N. Mehdi等[1]基于混沌嵌入式PSO算法设计分数阶PID控制器,实现了对船舶横摇混沌运动的有效控制;黄谦等[6]将滑膜变结构控制与自适应控制方法相结合,同时提出单输入自适应变结构控制法对船舶混沌运动进行控制并收到良好效果;胡开业等[7],采用随机Melnikov方法分析了在随机横浪中的船舶全局稳定性,并得出船舶横摇出现混沌运动的条件[5-7]。然而,对于已经配备了减摇鳍和减摇水舱的船舶的横摇混沌运动的控制,目前还没有可供遵循的方法。
本文运用混沌理论对综合减摇系统(配备减摇鳍和被动式减摇水舱的船舶系统)动力学方程进行混沌行为分析,并采用非线性反馈控制法对系统实现混沌控制,最后利用混沌蚁群算法对PID控制参数实现寻优。
1 综合减摇系统横摇混沌行为分析 1.1 综合减摇系统微分方程模型当船舶同时装备减摇鳍和被动式减摇水舱时,减摇鳍产生扶正力矩
| $ \left\{ \begin{array}{l} \left( {{I_1} + {J_{\rm{t}}} + C} \right)\ddot \phi + \left( {2{N_\phi } + B} \right)\dot \phi + \\ \left( {Dh' + A} \right)\phi - {\rho _{\rm{t}}}{S_0}{b^2}\ddot z - 2{\rho _{\rm{t}}}g{S_0}Rz = {K_\omega }\\ 2{\rho _{\rm{t}}}{S_0}{\lambda _{\rm{t}}}\ddot z + 2{N_{\rm{t}}}\dot z + 2{\rho _{\rm{t}}}g{S_0}z - \\ {\rho _{\rm{t}}}{S_0}{b^2}\ddot \phi - 2{\rho _{\rm{t}}}g{S_0}R\phi = 0 \end{array} \right. $ | (1) |
| $ \left\{ \begin{array}{l} A = {l_{\rm{f}}}{\rho _{\rm{t}}}{V^2}{A_{\rm{F}}}{K_{\rm{h}}}{K_{\rm{I}}}\left( {\partial Cy/\partial \alpha } \right)\\ B = {l_{\rm{f}}}{\rho _{\rm{t}}}{V^2}{A_{\rm{F}}}{K_{\rm{h}}}{K_{\rm{P}}}\left( {\partial Cy/\partial \alpha } \right)\\ C = {l_{\rm{f}}}{\rho _{\rm{t}}}{V^2}{A_{\rm{F}}}{K_{\rm{h}}}{K_{\rm{D}}}\left( {\partial Cy/\partial \alpha } \right) \end{array} \right. $ | (2) |
式中:lf为自减摇鳍上水动力压力中心到船舶重心的作用力臂;ρt为海水密度;V为航速;AF为减摇鳍的投影面积;(∂Cy/∂α)为升力系数斜率;ϕ为横摇角;
| $ \left\{ \begin{array}{l} {K_{\rm{P}}} = \frac{{2{N_\phi }F}}{{{l_{\rm{f}}}{\rho _{\rm{t}}}{A_{\rm{F}}}{V^2}\left( {\partial Cy/\partial \alpha } \right)}}\\ {K_{\rm{I}}} = \frac{{DhF}}{{{l_{\rm{f}}}{\rho _{\rm{t}}}{A_{\rm{F}}}{V^2}\left( {\partial Cy/\partial \alpha } \right)}}\\ {K_{\rm{D}}} = \frac{{{I_1}F}}{{{l_{\rm{f}}}{\rho _{\rm{t}}}{A_{\rm{F}}}{V^2}\left( {\partial Cy/\partial \alpha } \right)}} \end{array} \right. $ | (3) |
将式(1) 进行无量纲化得
| $ \left\{ \begin{array}{l} \ddot \phi + 2{v_\phi }\dot \phi + \omega _\phi ^2\phi - \beta \ddot z - {a_{\rm{t}}}z = {K_\omega }\\ \ddot z + 2{v_{\rm{t}}}\dot z + \omega _{\rm{t}}^2z - {b_{\rm{t}}}\ddot \phi - R\omega _{\rm{t}}^2\phi = 0 \end{array} \right. $ | (4) |
式中:
令
| $ \left\{ \begin{array}{l} {{\dot x}_1} = {x_2}\\ {{\dot x}_2} = \left[{{K_\omega } + \left( {{a_{\rm{t}}}-\beta \omega _{\rm{t}}^2} \right){x_3}-2{v_\phi }{x_2} + } \right.\\ \;\;\;\;\;\;\;\left. {\left( {\beta R\omega _{\rm{t}}^2-\omega _\phi ^2} \right){x_1} - 2\beta {v_{\rm{t}}}{x_4}} \right] \times {\left( {1 - \beta {b_{\rm{t}}}} \right)^{ - 1}}\\ {{\dot x}_3} = {x_4}\\ {{\dot x}_4} = \left[{{b_{\rm{t}}}{K_\omega } + \left( {{a_{\rm{t}}}{b_{\rm{t}}}-\omega _{\rm{t}}^2} \right){x_3}-2{v_{\rm{t}}}{x_4} + } \right.\\ \;\;\;\;\;\;\;\left. {\left( {R\omega _{\rm{t}}^2-\omega _\phi ^2{b_{\rm{t}}}} \right){x_1} - 2{v_\phi }{b_{\rm{t}}}{x_2}} \right] \times {\left( {1 - \beta {b_{\rm{t}}}} \right)^{ - 1}} \end{array} \right. $ | (5) |
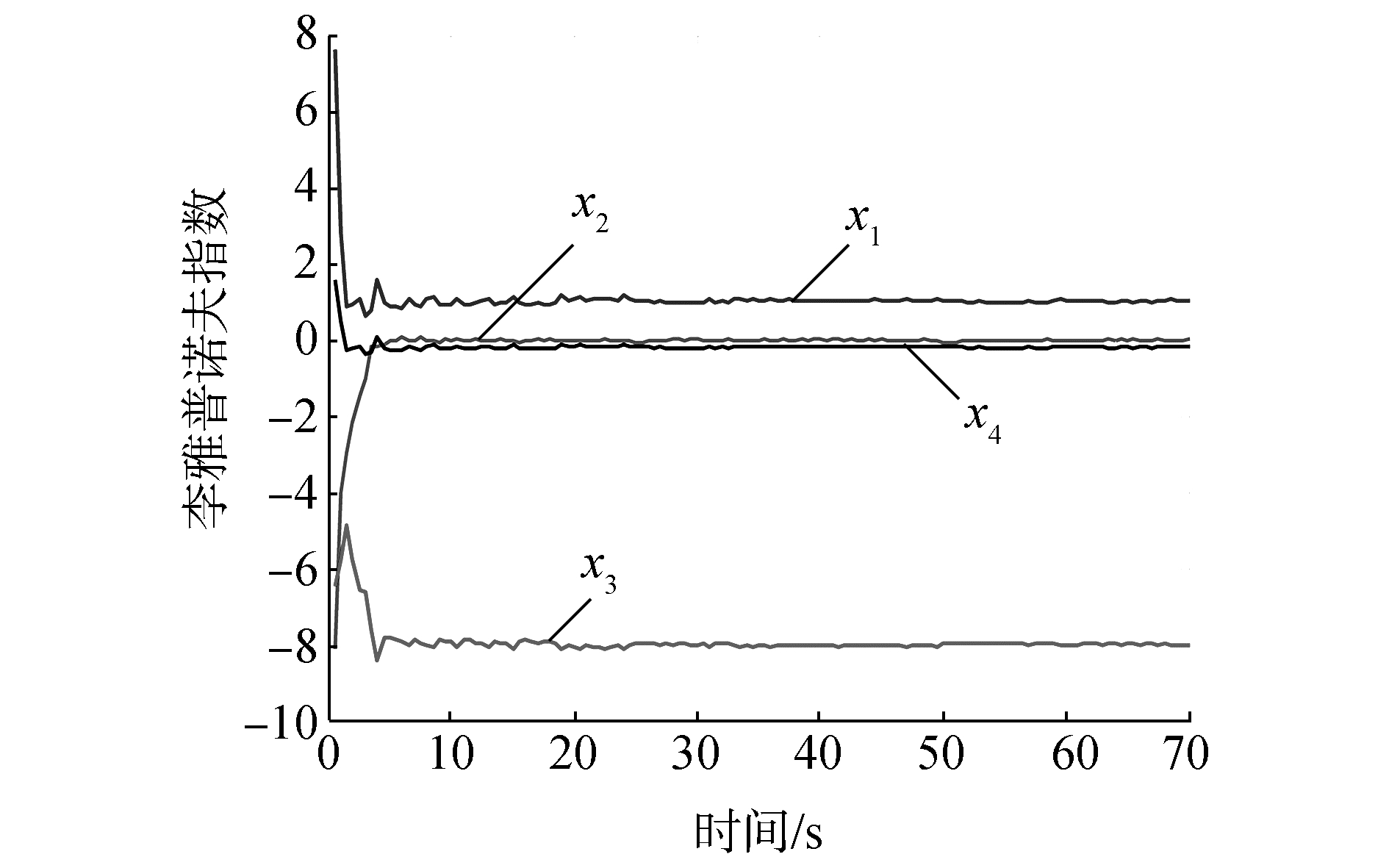
当系统参数Kω=20 000,at=0.013 1,β=0.004 9,ωt2=0.704 4,R=3.621 0,ωϕ2=0.704 4,2vt=0.187 4,2vϕ=0.059 6,bt=0.941 4时,利用wolf数值模拟方法求得系统随时间变化动态Lyapunov指数[12], 谱图如图 1所示,它直观地反映出非线性动力学系统随参数变化的动态特性。
|
图 1 综合减摇系统混沌的Lyapunov指数动态变化图 Fig.1 Dynamic change figure of Lyapunov index of the integrated stabilization chaotic system |
由图 1可知系统在该组参数条件下处于混沌状态。从平衡点及稳定性方面分析,令
| $ \mathit{\boldsymbol{J}} = \left[{\begin{array}{*{20}{c}} 0&1&0&0\\ {1.6953}&{-0.0599}&{0.0097}&{0.00092}\\ 0&0&0&1\\ {1.8955}&{-0.564}&{-0.6954}&{ - 3.883} \end{array}} \right] $ | (6) |
其特征值方程为:λ4+3.823λ3-1.232 6λ2-6.619 02λ-1.197 1=0。由微分方程理论知该系统平衡点为不稳定的鞍点,从理论上说明了该系统可能存在超混沌状态[13-14]。
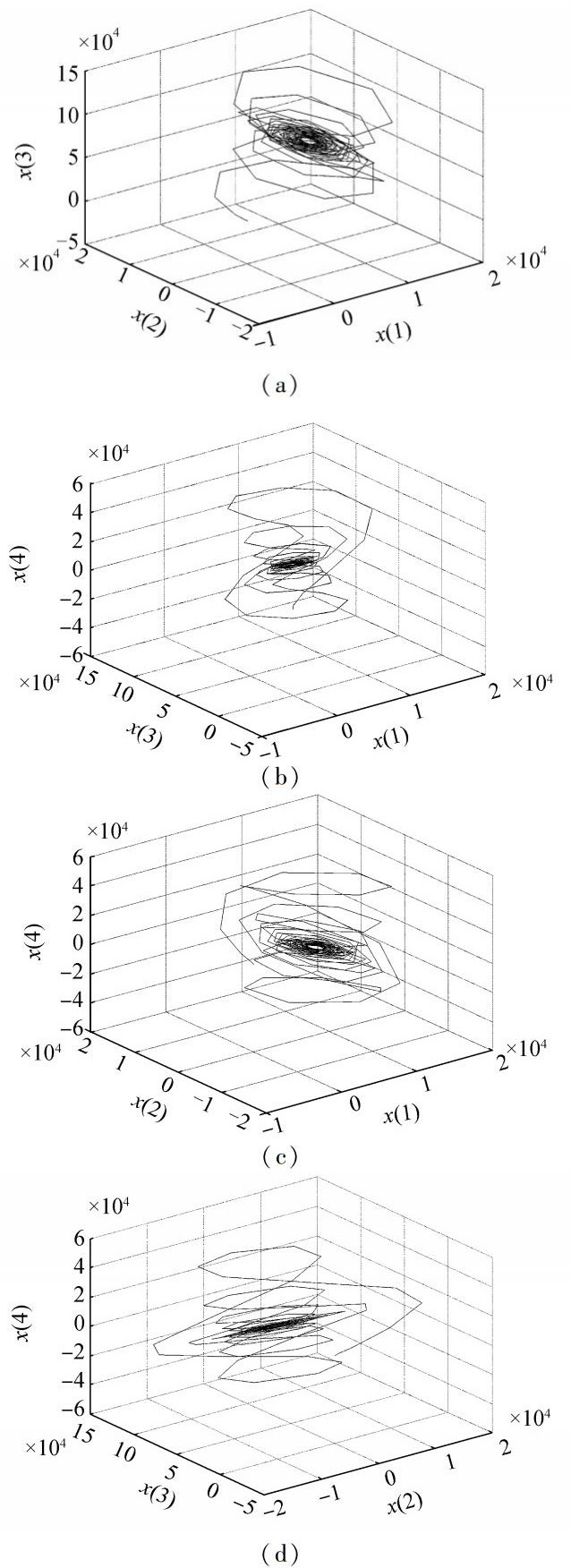
综合减摇混沌系统的三维混沌吸引子相图如图 2所示。
|
图 2 综合减摇混沌系统的三维混沌吸引子相图 Fig.2 Three-dimensional chaotic attractor phase diagram of integrated stabilization chaotic system |
利用分段二次函数x|x|作为产生混沌的发生器,选择合适分岔K参数作该混沌系统非线性反馈控制器,并应用于非线性系统中进行反馈操作,使系统寻找不稳定周期轨道同时实现混沌系统的有效控制[15-17]。对系统式(5) 进行混沌控制,把反馈控制器代入式(5) 得到系统方程(7),系统参数不变,则综合减摇混沌系统的混沌子相图如图 3所示。
|
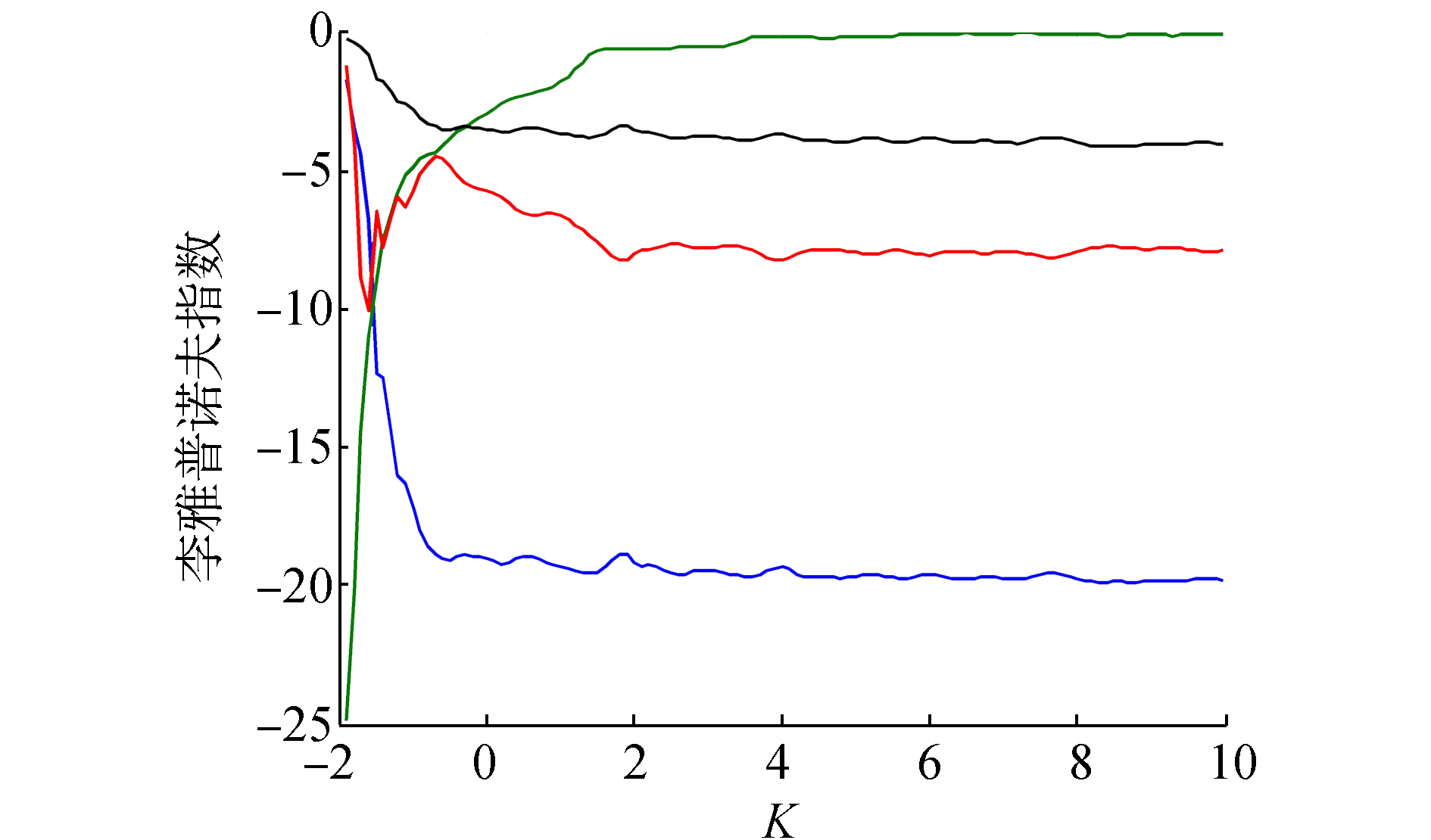
图 3 Lyapunov指数随K变化曲线 Fig.3 Graph of the Lyapunov index with the change of K |
| $ \left\{ \begin{array}{l} {{\dot x}_1} = {x_2}\\ {{\dot x}_2} = \left[{{K_\omega } + \left( {{a_{\rm{t}}}-\beta \omega _{\rm{t}}^2} \right){x_3}-2\beta {v_{\rm{t}}}{x_4} + } \right.\\ \;\;\;\;\;\;\;\left. {\left( {\beta R\omega _{\rm{t}}^2-\omega _\phi ^2} \right){x_1} - 2{v_\phi }{v_2}} \right] \times {\left( {1 -\beta {b_{\rm{t}}}} \right)^{ -1}} + K{x_2}\left| {{x_2}} \right|\\ {{\dot x}_3} = {x_4}\\ {{\dot x}_4} = \left( {{b_{\rm{t}}}{K_\omega } + \left( {{a_{\rm{t}}}{b_{\rm{t}}} -\omega _{\rm{t}}^2} \right){x_3} - 2{v_{\rm{t}}}{x_4} + } \right.\\ \;\;\;\;\;\;\;\left. {\left( {R\omega _{\rm{t}}^2 - \omega _\phi ^2{b_{\rm{t}}}} \right){x_1} - 2{v_\phi }{b_{\rm{t}}}{x_2}} \right] \times {\left( {1 - \beta {b_{\rm{t}}}} \right)^{ - 1}} \end{array} \right. $ | (7) |
式中K为系统的分岔参数。图 4是受控系统在参数K下的Lyapunov指数图。
|
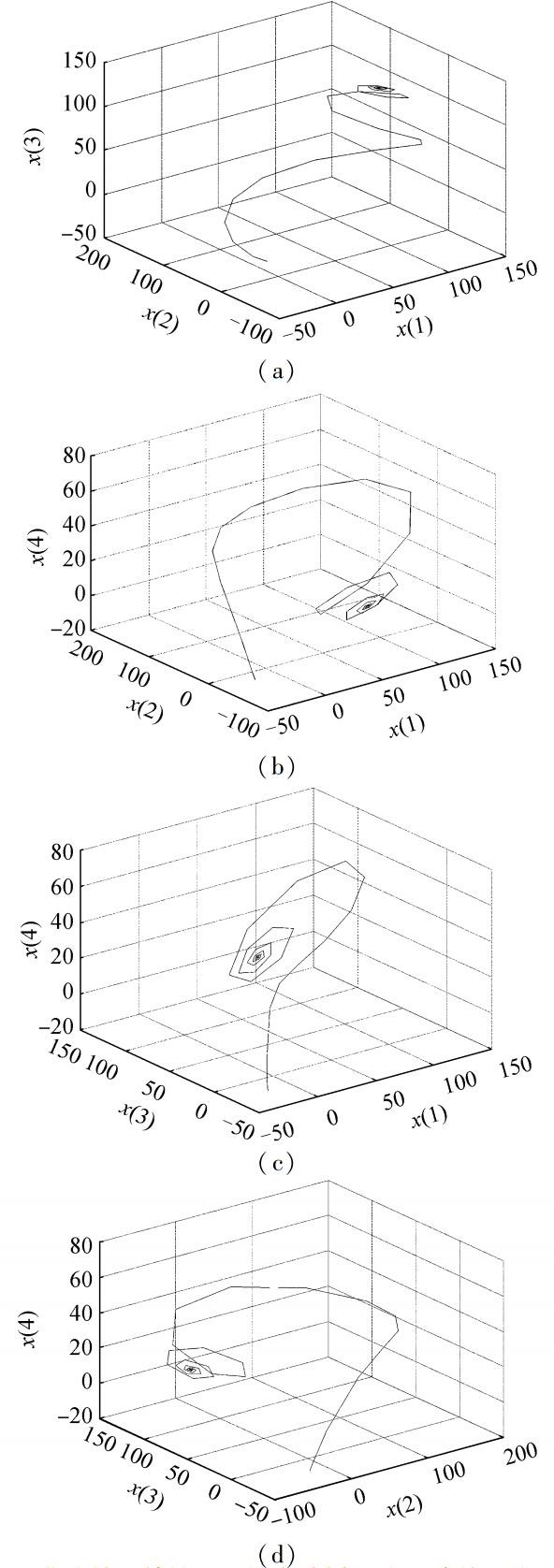
图 4 非线性反馈控制后综合减摇混沌系统的三维混沌子相图 Fig.4 Three-dimensional chaotic attractor phasediagram after nonlinear feedback control |
由图 4可知,当K∈[-2 4]时,系统的Lyapunov指数都非正,系统一直处于周期态;当K>4时,系统进入混沌态。图 3给出了系统在分岔参数K=2值下的三维相图。从图 3可得:系统处于周期态,而非混沌运动,故选择当Lyapunov指数为负时所对应的K值可有效控制系统的混沌行为。
2 混沌蚁群算法的综合减摇系统PID控制参数寻优 2.1 混沌蚁群优化算法利用网格划分策略将离散优化蚁群算法思想应用到连续函数优化的问题,有很多不足之处。例如:搜索时间和范围与遗传算法相比,该算法搜索时间较长,易出现局部最优,发生停滞,其对最优解的寻找不易实现[18-20]。本文将蚁群算法与混沌优化算法有机结合,应用于PID控制参数寻优问题,不仅可以避免搜素过程中停滞现象,同时还可以解决搜索效率低的问题。具有混沌特性蚁群算法搜索过程可分为两个步骤:首先,利用混沌搜索算法初步确定最优解所在范围的大小;然后,在确定最优蚂蚁基础上再利用混沌算法进行寻优,若满足终止条件,则获得最优解。混沌蚁群算法流程如图 5所示。

|
图 5 混沌蚁群算法流程图 Fig.5 Flow chart of chaos ant colony algorithm |
将混沌蚁群优化算法应用于综合减摇系统PID控制器[21]的优化原理方框图如图 6所示。

|
图 6 混沌蚁群算法优化原理图 Fig.6 Optimization schematic of chaos ant colony algorithm |
利用混沌蚁群算法优化控制器PID参数的主要步骤依次为:
1) PID控制参数优化问题转化为蚁群算法适用的组合优化问题
首先把控制器的控制参数KP、KI、KD转换为一个组合寻优的问题,在满足控制精度要求情况下,可将控制参数值视为5位有效数字,所以待寻参数(KP、KI、KD)组成15位的数字序列记为{ci, i=1, 2, …, 15},每个ci取值为yj{j=1, 2, …, 9},因此每次序列可以在{(ci, yj)∣i=1, 2,…,15;j=1, 2,…,9}组成区域中表示,即这个序列就是人工蚂蚁的一条路径。
2) 目标函数的建立
为保证控制器具有良好的性能,必须选择合适的目标函数,因此采用改进ITAE性能指标作为
| $ {\rm{ITAE}} = \left\{ \begin{array}{l} \int_0^{{t_i}} {\left| {y\left( t \right) - {y_{ * p}}\left( t \right)} \right|{\rm{d}}t}, \;\;\;\;\;y\left( t \right) \ge {y_{ * p}}\left( t \right)\\ \int_0^{{t_i}} {\left| {y\left( t \right) - {y_{ * p}}\left( t \right)} \right|{\rm{d}}t}, \;\;\;\;\;y\left( t \right) < {y_{ * p}}\left( t \right) \end{array} \right. $ | (8) |
式中p为调节因子,一般p大于1,可根据实际问题适当调整。
3) 路径的构建
路径的构建是蚁群算法研究中的关键环节,当蚂蚁从(ci-1, yj)爬行到下一个(ci, yj)节点按照随机比例概率进行选择,当所有蚂蚁到达(15, yj)即实现一次循环。在此过程中,假设蚂蚁此过程中爬行相邻节点所用时间是相等的,与路径无关。则蚂蚁从(ci-1, yj)爬行到下一个(ci, yj)节点按式(9) 计算选择路径的概率:
| $ {P_k}\left( {{c_i}, {y_j}, t} \right) = \frac{{{\tau ^a}\left( {{c_i}, {y_j}, t} \right){\eta ^\beta }\left( {{c_i}, {y_j}, t} \right)}}{{\sum\limits_{j = 0}^9 {{\tau ^a}\left( {{c_i}, {y_j}, t} \right){\eta ^\beta }\left( {{c_i}, {y_j}, t} \right)} }} $ | (9) |
式中:Pk(ci, yj, t)表示t时刻蚂蚁从(ci-1, yj)爬行到下一个(ci, yj)节点的概率;τa(ci, yj, t)为t时刻(ci, yj)节点上的信息量;ηβ(ci, yj, t)为t时刻(ci, yj)节点上的能见度。
4) 信息素的更新
当全部蚂蚁从原点出发,15个单位时间过后,每只蚂蚁都爬到终点,即完成一次参数寻优。每经过1个单位时间,节点(ci, yj)信息素强度都会改变,即
| $ \tau \left( {{c_i}, {y_j}, t + 15} \right) = \rho \tau \left( {{c_i}, {y_j}, t} \right) + \Delta \tau \left( {{c_i}, {y_j}} \right) $ | (10) |
| $ \Delta \tau \left( {{c_i}, {y_j}} \right) = \sum\limits_k^m {\Delta {\tau _k}\left( {{c_i}, {y_j}} \right)} $ | (11) |
| $ \Delta {\tau _k}\left( {{c_i}, {y_j}} \right) = \left\{ \begin{array}{l} Q/{F_k}\\ 0 \end{array} \right. $ | (12) |
式中:ρ为信息素挥发系数;m为蚂蚁的数量;Q为信息素增强系数,由经验取值;Fk表示第k只蚂蚁在本次循环中的目标函数值。
2.3 仿真及结果分析用文献[22]中船舶模型作为控制模型,当分岔参数K=2时的混沌系统转化为式(4) 形式的传递函数为被控函数,采样周期为1 ms,输入信号为阶跃信号。
混沌蚁群优化算法方案选取如下:迭代次数N=50,蚂蚁总数m=30,信息素挥发系数ρ=0.85,信息素增强系数Q=1,蚂蚁爬行速度v=0.3,经过50次迭代后,寻到最优控制参数KP=16.563,KI=2.013,KD=0.237,表 1给出了基于混沌蚁群算法的PID参数优化算法与基于遗传算法的PID参数优化算法的优化值比较结果。
| 表 1 PID参数优化算法比较 Tab.1 Comparison of PID parameter optimization algorithm |
由表 1可知:选择合理参数后,基于混沌蚁群算法的PID控制参数寻优算法获得的最优解优于基于遗传算法的PID参数优化算法获得的最优解。
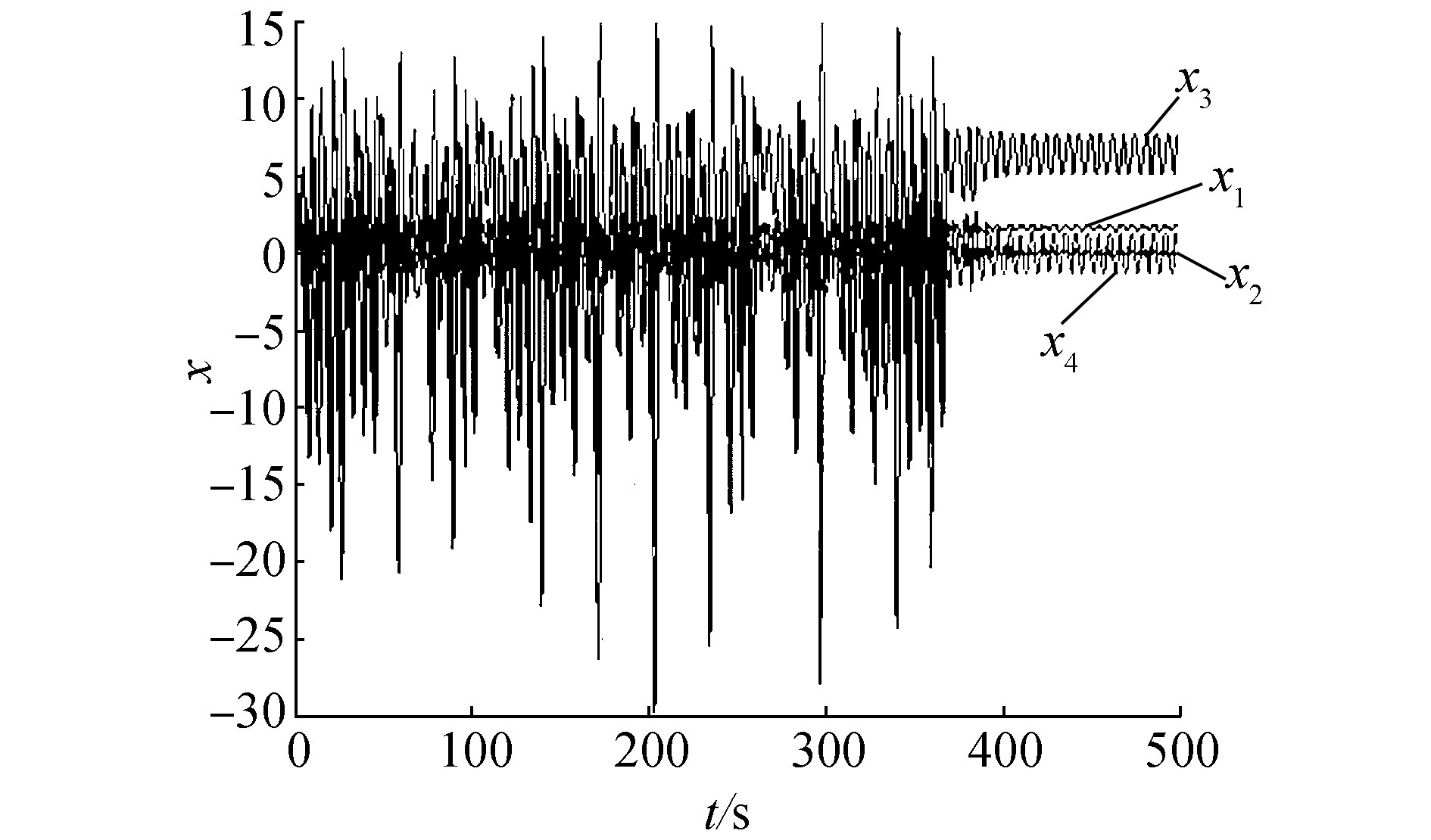
图 7为基于遗传算法的PID参数优化算法的系统响应图,图 8为基于混沌蚁群算法的PID参数优化算法的系统响应图。由图 7和图 8的对比可以看出,基于混沌蚁群算法的PID参数优化算法能够快速抑制系统混沌现象,在反映时间上,较遗传算法减少50%以上。
|
图 7 基于遗传算法的PID控制系统的响应 Fig.7 Responses of PID control system based on genetic algorithm |

|
图 8 基于混沌蚁群算法的PID控制系统的响应 Fig.8 Responses of PID control system based on chaos ant colony optimization |
为验证算法对船舶综合减摇系统控制的有效性,分别采用基于混沌蚁群优化算法和遗传优化算法在不同海情下得到的PID控制参数最优值如表 2和表 3所示。
| 表 2 基于混沌蚁群算法的PID控制参数最优值 Tab.2 The optimal value of PID control parameters based on chaos ant colony algorithm |
| 表 3 基于遗传算法的PID控制参数最优值 Tab.3 The optimal value of PID control parameters based on genetic algorithm |
由表 2和表 3可得:在不同海情下,基于混沌蚁群算法PID控制系统的减摇效率均能达80%左右,无论寻优效率还是减摇效率方面均明显优于基于遗传算法的PID控制器控制效果。
3 结束语运用数值模拟方法对综合减摇系统在特定参数条件下的超混沌特性进行分析,证明了系统存在混沌行为。采用二次函数作为非线性反馈控制,实现了对船舶减摇混沌系统的控制。利用某船模型进行仿真验证,结果表明,基于混沌蚁群算法的PID参数寻优不但搜索参数范围扩大了,解决了陷入局部最优值缺点,同时还提高了搜索精度及效率。
| [1] |
李天伟, 刘晓光, 彭伟骅, 等. 船舶航向保持中的混沌运动控制[J]. 计算机应用, 2013, 33(1): 234-238. LI Tianwei, LIU Xiaoguang, PENG Weihua, et al. Chaotic ship maneuvering control in course-keeping[J]. Journal of computer applications, 2013, 33(1): 234-238. (  0) 0)
|
| [2] |
于立君, 陈佳, 刘繁明, 等. 改进粒子群算法的PID神经网络解耦控制[J]. 智能系统学报, 2015, 10(5): 699-704. YU Lijun, CHEN Jia, LIU Fanming, et al. An improved particle swarm optimization for PID neural network decoupling control[J]. CAAI transactions on intelligent systems, 2015, 10(5): 699-704. (  0) 0)
|
| [3] |
YU Lijun, LIU Shaoying, LIU Fanming, et al. Energy optimization of the fin/rudder roll stabilization system based on the multi-objective genetic algorithm(MOGA)[J]. Journal of marine science and application, 2015, 14(2): 202-207. DOI:10.1007/s11804-015-1292-z ( 0) 0)
|
| [4] |
刘胜, 孔琳. 基于工控机的船舶航向/横摇控制信息处理系统[J]. 智能系统学报, 2011, 6(3): 268-271. LIU Sheng, KONG Lin. An information processing system of ship course/roll control based on an industrial computer[J]. CAAI transactions on intelligent systems, 2011, 6(3): 268-271. (  0) 0)
|
| [5] |
FAIEGHI M R, NADERI M, JALALI A A. Design of fractional-order PID for ship roll motion control using chaos embedded PSO algorithm[C]//Proceedings of 2011 2nd International Conference on Control, Instrumentation and Automation (ICCIA). Shiraz: IEEE, 2011: 606-610. http://ieeexplore.ieee.org/document/6356727/
( 0) 0)
|
| [6] |
黄谦, 李天伟, 王书晓, 等. 舰船混沌运动的单输入自适应变结构控制[J]. 动力学与控制学报, 2015, 13(6): 443-448. HUANG Qian, LI Tianwei, WANG Shuxiao, et al. Chaos control of ship steering via single input adaptive sliding mode control method[J]. Journal of dynamics and control, 2015, 13(6): 443-448. (  0) 0)
|
| [7] |
胡开业, 丁勇, 王宏伟, 等. 船舶在随机横浪中的全局稳定性[J]. 哈尔滨工程大学学报, 2011, 32(6): 719-723. HU Kaiye, DING Yong, WANG Hongwei, et al. Global stability of ship motion in stochastic beam seas[J]. Journal of Harbin engineering university, 2011, 32(6): 719-723. (  0) 0)
|
| [8] |
金鸿章, 赵卫平, 綦志刚, 等. 大型船舶综合减摇系统的研究[J]. 中国造船, 2005, 46(1): 29-35. JIN Hongzhang, ZHAO Weiping, QI Zhigang, et al. Research on integrated roll stabilization system for large ships[J]. Shipbuilding of China, 2005, 46(1): 29-35. (  0) 0)
|
| [9] |
于立君, 孙经广, 刘繁明, 等. 广义预测算法在综合减摇系统控制器设计中的应用[J]. 船舶工程, 2013, 35(6): 76-79. YU Lijun, SUN Jingguang, LIU Fanming, et al. Application of generalized prediction algorithm in designing integrated stabilization system controller[J]. Ship engineering, 2013, 35(6): 76-79. (  0) 0)
|
| [10] |
MATOUK A E. Stability conditions, hyperchaos and control in a novel fractional order hyperchaotic system[J]. Physics letters A, 2009, 373(25): 2166-2173. DOI:10.1016/j.physleta.2009.04.032 ( 0) 0)
|
| [11] |
LI C W, DU Yichun, WU Jianxing, et al. Synchronizing chaotification with support vector machine and wolf pack search algorithm for estimation of peripheral vascular occlusion in diabetes mellitus[J]. Biomedical signal processing and control, 2014, 9: 45-55. DOI:10.1016/j.bspc.2013.10.001 ( 0) 0)
|
| [12] |
WALDNER F, KLAGES R. Symmetric jacobian for local Lyapunov exponents and Lyapunov stability analysis revisited[J]. Chaos, solitons and fractals, 2012, 45(3): 325-340. DOI:10.1016/j.chaos.2011.12.014 ( 0) 0)
|
| [13] |
BARRIO R, MARTÍNEZ M A, SERRANO S, et al. When chaos meets hyperchaos: 4D Rössler model[J]. Physics letters A, 2015, 379(38): 2300-2305. DOI:10.1016/j.physleta.2015.07.035 ( 0) 0)
|
| [14] |
WANG Junwei, XIONG Xiaohua, ZHAO Meichun, et al. Fuzzy stability and synchronization of hyperchaos systems[J]. Chaos, solitons and fractals, 2008, 35(5): 922-930. DOI:10.1016/j.chaos.2006.05.087 ( 0) 0)
|
| [15] |
KAKMENI F M M, BOWONG S, TCHAWOUA C, et al. Strange attractors and chaos control in a Duffing-Van der Pol oscillator with two external periodic forces[J]. Journal of sound and vibration, 2004, 277(4/5): 783-799. ( 0) 0)
|
| [16] |
张文娟, 俞建宁, 张建刚, 等. 利用非线性反馈控制一类振动系统的振动[J]. 重庆理工大学学报:自然科学, 2013, 27(1): 27-31. ZHANG Wenjuan, YU Jianning, YANG Jiangang, et al. Using nonlinear feedback control for the vibration of a nonlinear vibration system[J]. Journal of Chongqing university of technology: natural science, 2013, 27(1): 27-31. (  0) 0)
|
| [17] |
LIU Yajuan, LEE S M. Synchronization criteria of chaotic Lur'e systems with delayed feedback PD control[J]. Neurocomputing, 2016, 189: 66-71. DOI:10.1016/j.neucom.2015.12.058 ( 0) 0)
|
| [18] |
陈烨. 变尺度混沌蚁群优化算法[J]. 计算机工程与应用, 2007, 43(3): 68-70. CHEN Ye. Scaleable chaotic ant colony optimization[J]. Computer engineer and applications, 2007, 43(3): 68-70. (  0) 0)
|
| [19] |
朱洪华, 黄永华. 基于遗传算法的减摇鳍PID控制器优化[J]. 电脑知识与技术, 2011, 7(11): 2642-2644. ZHU Honghua, HUANG Yonghua. Optimization the PID controller of fin stabilizer based on genetic algorithm[J]. Computer knowledge and technology, 2011, 7(11): 2642-2644. DOI:10.3969/j.issn.1009-3044.2011.11.067 (  0) 0)
|
| [20] |
李士勇, 柏继云. 连续函数寻优的改进量子扩展蚁群算法[J]. 哈尔滨工程大学学报, 2012, 33(1): 80-84. LI Shiyong, BAI Jiyun. Extended quantum ant colony algorithm for continuous function optimization[J]. Journal of Harbin engineering university, 2012, 33(1): 80-84. (  0) 0)
|
| [21] |
王辉, 王科俊, 于立君. 减摇鳍模糊免疫自适应PID控制器设计及仿真研究[J]. 海军工程大学学报, 2007, 19(4): 17-21, 29. WANG Hui, WANG Kejun, YU Lijun. Design and simulation of fuzzy immune self-adaptation PID controller of fin stabilizer[J]. Journal of naval university of engineering, 2007, 19(4): 17-21, 29. (  0) 0)
|
| [22] |
冯铁城, 陶尧森. 可控被动水舱研究[J]. 中国造船, 1997(1): 8-14. FENG Tiecheng, TAO Yaosen. A study on passive controlled antiroll tank[J]. Ship building of China, 1997(1): 8-14. (  0) 0)
|
 2017, Vol. 12
2017, Vol. 12


