跨摄像头目标再确认是目前多摄像机智能监控领域的一个重点研究方向^[1]，如何在不同的光照条件、不同的行人姿态以及不同尺度甚至遮挡等复杂环境下实现不同监控摄像头下的同一目标的再确认，是现在智能监控领域研究的热点。能否在复杂的环境中快速地匹配到同一目标的关键点在于能否找到目标在时间、空间上的不变特性以及选择合适的匹配算法。

目前最先进的算法对VIPeR(viewpoint invariant pedestrian recognition)数据库的视频目标进行再确认的正确率为40%，处于比较低的水平^[2]。根据上文所述，目标再确认主要的研究方法分为两类：目标外观特征类和度量算法类。而目标外观特征类的研究又可以归纳为3类：1)依据目标本身的整体特征进行描述，如文献[3-9]通过建立整体相关特征颜色直方图进行目标再确认；2)基于目标本身的局部特征进行目标匹配，如文献[10-13]通过训练大量样本得出的数据作为匹配函数，依据目标本身的颜色特征、纹理特征进行目标的再确认；3)通过整体和局部多特征融合来匹配目标，如文献[14-18]通过人体本身的局部LBP(local binary patterns)特征、SIFT(scale-invariant feature transform)特征以及整体的颜色特征进行描述，来完成目标再确认。度量算法类的研究方向相对特征类方法而言，对目标外观特征的要求较低，更多地依赖选择和训练优秀的度量函数。比如，ERSVM方法^[19]采用基于相对距离排序的SVM分类器集成多个特征向量权重；文献[20]采用多核SVM学习的方法融合颜色和视觉单词直方图；文献[21]采用直方图交叉核；文献[22]采用夹角余弦法等相似度量函数进行目标匹配。

以上两类方法在目标再确认过程中，度量算法类对特征的选择要求较低，通常能取得更好的再确认效果。但其训练的时间和空间复杂度较高，且场景和图库变化时需要重新训练。目标外观特征类方法则需要人为地寻找和设计较好的特征，该方法的性能依赖于特征的优劣程度。本文受两类方法优点的启发，在特征类方法的思路下设计和构造优秀的特征；同时在度量算法类方法的思路下，引入物理学科中的热扩散原理作为度量函数^[23]，并最终建立基于优化的扩散距离的度量函数完成目标再确认。

基于上文所述，引入度量算法的基础来源于扩散距离。扩散距离是物理学中用于描述热力场中存在的一种扩散现象的，国外学者Ling等^[23]曾提出了一种非线性基于扩散现象和距离判断方式二者结合的扩散距离，它是模拟热扩散和记录随机扩散遍历的时间计算两点之间的距离。这使得扩散距离具有可以很好地描述目标间相似性的特性，同时，传统度量算法存在诸多缺点，比如：对图像形变比较敏感；缺少考虑像素间的空间关系；较小的形变就能使距离计算变化较大，从而产生误匹配等，而扩散距离的引入克服了以上不足。基于扩散距离的众多优点，因此本文引入扩散距离，并对其进行优化，构造出优秀的相似性度量函数，以完成对行人目标的再确认。

1 多特征描述

目标再确认过程中，描述每个目标的外观相当于从目标身上找到可辨识性的特征。在描述目标特征时，直方图是目前应用最广泛的的外观描述器。但是，大部分基于直方图的方法，其不足之处是缺少特征分布的空间信息。比如，基于直方图的方法不能分辨出一个穿着白色衬衫和黑色裤子的行人与另一个穿着黑色衬衫和白色裤子的行人是否是不同的。

因此，文中提出了一个新颖而简单的方法：基于两级区域的直方图提取方法。首先，提出的第一级区域为：行人整个身体区域(H_global)颜色直方图；提出的二级区域为：行人的上半身区域(H_tor)和腿部区域(H_leg)如图1所示。图中(a)、(d)为一级区域身体直方图，图(b)、(e)为二级区域身躯直方图，图(c)、(f)为二级区域腿部直方图。

图1(a)、(d) 一级所提取的H_global直方图，(d)直方图中的3个峰值在(a)直方图中可以找到相似的对应，因此单纯靠全局直方图很难发现目标是两个不同的人；通过对图1中的两个原始图像分别提取身躯段和腿部段的H_tor和H_leg直方图，对应于二级，如图1左图中的(b)、(c)和图1右图中的(e)、(f)所示，对比图1(b)和图1(e)，可发现两者身躯直方图明显不同，同时对比图1(c)和图1(f)也能发现两者的腿部直方图也是明显不同的，可以通过局部直方图的差异，发现两目标并不是同一个人。通过上述方法可以有效地提取颜色的空间信息，并区分出图1两个行人的不同。

人体目标本身具有很多稳定不变的特征，这些不变特征在应对因光照变化或细微的肢体动作变化时具有很好的鲁棒性。因此，为了更好利用这些优势特征来克服由于光照变化或其他因素所带来的干扰，本文在下文中会从整体特征和局部特征两方面来介绍本文所提取的这些优势多特征，实验表明，使用这些多特征中的任何一类进行匹配时，识别率都不太理想，但结合下文中的多特征进行目标再确认时，可以很大程度上提高目标的识别率。

1.1 整体特征

整体特征使用基于一级区域(图1中Level 1)的RGB颜色直方图进行粗识别。在提取RGB颜色直方图时，本文将R、G、B 这3个通道分别进行量化。而量化过程中存在两个极端问题：粗量化会造成大量的可辩别性信息被放弃，细量化会生成稀疏直方图。本文在3个通道使用相同的量化级数32bins。通过大量实验验证了本文所使用的32bins具有较好的可辨别性和准确性。通过图1可以很清楚地体现出来。

1.2 局部特征

局部特征相对整体特征而言更加注重局部小范围特征的不变性，采用更细腻的特征描述子或者具有较强鲁棒性的特征来进行匹配。观察大部分行人目标的H_tor和H_leg特征发现：最显著的局部差异特征仍是颜色特征，实验过程中发现使用颜色特征应对摄像机镜头旋转变化所造成的差异具有很好的辨别性。所以在下文中的局部特征表述过程中，基于上文中二级区域H_tor和H_leg的基础上，为了使人体目标取得更佳的匹配效果使用GrabCut^[24]背景去除法，将干扰背景(头部也当作背景)进行去除，同时将RGB颜色通道模型和加权HSV颜色通道模型作为主要的局部特征；而另一方面考虑到局部人体目标的表象和形状能够被梯度或边缘的方向密度分布很好地描述，方向梯度直方图(histogram of oriented gradient，HOG)特征可以通过计算和统计图像局部区域的梯度方向直方图来构成特征，并且能够对图像的几何和光学形变都能保持很好的不变性，所以，将结构性HOG描述子作为次要的局部特征。

1.2.1 局部RGB颜色特征

观察数据库中行人目标发现：去除头部的影响后，由于目标行人上身所穿的衣服和下身所穿的裤子在颜色上往往会表现出明显的差异，所以本文在二级区域H_tor和H_leg基础上使用局部RGB颜色直方图匹配。通过观察图2(b)：掩膜背景图(图中干扰背景和头部已经去除)和测试样本库里的图片(国际通用标准库VIPeR中的样本图片大小：48×128)分析得到：头部和身躯段的平均分界线在第20行，身躯段和腿部段的平均分界线在62行。为了减少背景对匹配结果的干扰，如图2(c)所示，将身躯段去除左右边界各4列，即使用整张图像的第20~60行，第6~44列作为身躯段窗口；同时，在腿部段部分去除最下面的8行，以及左右各14列，使用整张图像的第66~122行，第14~36列，作为腿部段窗口。在量化过程中，同整体特征量化数相同，提取每个通道对其量化后的直方图统计如图2。

图2中，分段处理和图1中的两级区域一致，将图像中的人物按照不对称原则分为头部、身躯和腿部3个水平段，并将图像中的人物的身躯和腿部按照对称原则分为两个垂直段，并且去掉权重比较小的头部像素点，得到的实际效果如图2(c)所示。图2(d)代表实验过程中所绘制的图2(b)被去除头部和背景干扰之后，身躯和腿部的R、G、B分量直方图。其中，图2(d)中的横轴，0~31代表身躯段和腿部段上的R颜色通道统计直方图(其中0~15代表身躯段，16~31代表腿部段)；32~63代表身躯段和腿部段上的G颜色通道统计直方图；64~95代表身躯段和腿部段上的B颜色通道统计直方图。

局部RGB颜色直方图充分利用了空间分布信息，可以有效区分出上文所提到的上身下身穿衣颜色的不同。在局部特征描述方面的应用中，可以较好地实现应对图像旋转和平移的改变所带来的影响，并且还可借助归一化技术，来达到不受图像尺度的改变所带来的影响，充分利用了局部颜色特征的优势。

1.2.2 加权HSV特征

根据人眼视觉特性, 颜色信息中HSV特征相比较RGB特征，在应对光照变化方面，可以很大程度上忽略图像亮度变化所带来的影响；在二级区域中对HSV模型使用高斯分布的加权处理，可以在提取空间信息基础上更好地对特征权重化处理，所以本文选择HSV颜色模型作为局部特征之一来使用。

考虑到由于人体目标特征分布比例的差异性，有些显著特征在人体身上的某些部位所占比例很重，而有些特征则在人体身上的某些部位所占比例很小。通过观察图3(b)发现：身躯和腿部中间部分的颜色特征比较明显，对图像匹配时的影响会比较重，所以相应地给予较大的权重分配，越远离垂直坐标的颜色特征对匹配性能的提高影响较小，甚至会降低匹配性能，所以相应地给予远离垂直坐标的点以较小的权重分配。根据人体不同部位所对应的分段坐标对HSV直方图进行高斯分布的加权^[16]处理。

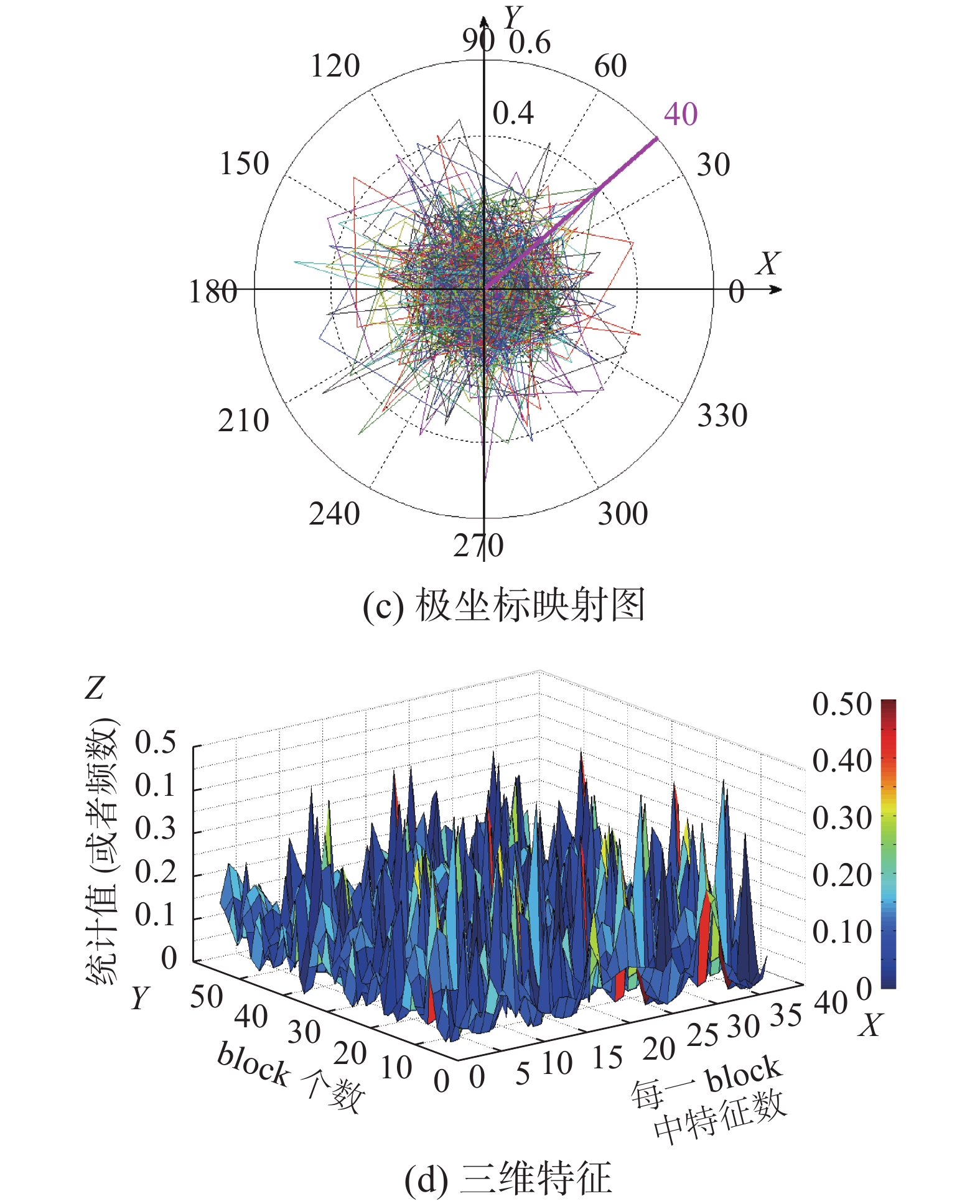
如图3所示，为了更形象地表现人体身上特征权重的分布，文中提取人体不同位置对应的高斯分布图谱3(b)和三维空间中的核能量图谱3(c)。考虑到光照的影响会对匹配精度造成很大的影响，因而为了抑制光照变化，将HSV中的亮度值(V)分配较小区间段。文中的H、S、V通道分别分成16、16、4段，进而得到一个加权的108段(其中0~31段为头部段，已被忽略计算；32~71段为身躯段；72~107为腿部段)HSV直方图，其相应的实验效果如图3(d)。

1.2.3 HOG特征

HOG是目标检测常用的特征描述子。目标局部的表象和形状能够被梯度或边缘的方向的密度分布很好地描述^[24]。具体的实现方法是：首先将图像分成小的连通区域，我们把它叫细胞单元^[25]。然后采集细胞单元中各像素点梯度或边缘的方向直方图。最后把这些直方图组合起来就可以构成特征描述器。为了提高性能，还可以把这些局部直方图在图像的更大的范围内(也可称为区间或block)进行对比度归一化，所采用的方法是：先计算各直方图在这个区间(block)中的密度，然后根据这个密度对区间中的各个细胞单元做归一化。本文在实际操作中使用的参数为：窗口大小统一为48×128，block块大小为16×16，每个block划分为4个cell，并且block每次滑动8个像素(即一个cell的宽)，以及梯度方向划分为9个区间，最后在0~360^o范围内统计，将cell的梯度方向360^o分成9个方向块，也就是每360^o/9=40^o分到一个方向，方向大小按像素边缘强度加权，对cell内每个像素用梯度方向在直方图中进行加权投影(映射到固定的角度范围)，其相应的实验效果如图4(c)所示。实验过程中，根据上文相应参数对图4(a)进行HOG特征提取，提取过程中的实验效果如图4所示。

从图中可以清晰的看出：本文将cell的梯度方向以40^o为一个单位，分成一个方向；图4(d)代表实验过程中提取的归一化后HOG 3维特征曲面图。由于HOG方法是在图像的局部细胞单元上操作的，所以它对图像几何和光学的形变能够保持很好的不变性，归一化后能对光照变化和阴影获得更好的效果。它的优点不仅包括对图像几何和光学形变方面能保持良好的不变性，还包括归一化后允许行人有细微的肢体动作，且不影响检测效果，多特征融合HOG特征描述可以很好地提高匹配率。

2 相似性度量函数

在相似性度量函数的建立方面，传统度量算法大多基于欧氏距离或者余弦距离等进行优化。然而，欧式距离和余弦距离本身存在诸多缺点，比如：欧式距离不能从高维特征向量恢复到具有低维的几何机构，对图像的形变比较敏感和缺少像素间的空间关系；余弦距离存在位置判定上差异性太大以及对数值的不敏感导致结果的众多误差等缺点。考虑到传统相似性度量算法的不足，本文引进物理学温度场扩散距离^[26]的概念来建立相似性度量函数。扩散距离的本质来源于物理学中的温度场，它不同于欧式距离中的距离长短决定相似度大小的标准。扩散距离中的相似度取决于温度扩散路径的多少以及热扩散的快慢。本文所使用的基于优化扩散距离相似性度量函数用于衡量个体在空间上存在的距离，距离越远，说明个体间的差异越大，反之，差异越小。优化扩散距离在一定程度上弥补了欧式和余弦距离的不足的同时，在匹配性能上显示了较优的表现^[26]。其原理如下：

首先，假设 ${ his}{{ t}_{{1}}}(x)$ 和 ${ his}{{ t}_{{2}}}(x)$ 为两个一维分布，其差异可以表示成：

$d(x) = { his}{{ t}_1}(x) - { his}{{ t}_2}(x)$

(1)

如果存在一个独立的温度场 $T(x,t)$ 中，在时间t=0时，有 $T(x,0) = d(x)$ 。那么温度场 $T(x,t)$ 的计算公式为

$\left\{ \begin{array}{l}T(x,t) = {T_0}(x) \cdot \phi (x)\\{T_0}(x) = T(x,0) = d(x)\\\phi (x,t) = \displaystyle\frac{1}{{\sqrt {2{\text{π}}} t}}{ ex}{{ p}^{ - {x^2}/2{t^2}}}\end{array} \right.$

(2)

那么一维分布 ${ his}{{ t}_{{1}}}(x)$ 和 ${ his}{{ t}_{{2}}}(x)$ 的扩散距离定义为

$\hat K({ his}{{ t}_1},{ his}{{ t}_2}) = \int_0^{\bar t} {k(|T(x,t)|)} { d}t$

(3)

式中： $\bar t$ 是一个正常数，且 $k(|T(x,t)|) = \int_{ - \infty }^{ + \infty } {|T(x,t)|{ d}x} $ 。

由于一维扩散距离的应用没有多大实际意义，所以推广到高维且引入高斯金字塔对扩散距离进行优化，进一步提高了相似性度量函数的计算效率。

假设有两个p维直方图 ${ His}{{ t}_1}(X)$ 和 ${ His}{{ t}_{{2}}}(X)$ ，其中X为p维的实矩阵，由于高斯金字塔中图像的平滑子采样不会产生混淆现象，能有效的描述温度场 $T(x,t)$ 的离散化连续性扩散过程，所以本文使用基于成熟的高斯金字塔的交替距离定义高维扩散距离，即

$K({ His}{{ t}_1},{ His}{{ t}_2}) = \sum\limits_{l = 0}^L {k(|{d_l}(x)|)} $

(4)

式中：

${d_0}( X) = { His}{{ t}_1}( X) - { His}{{ t}_2}( X),l = 0$

(5)

${d_l}({ X}) = [{d_{l - 1}}( X) * \phi ({ X},\sigma )]{ \downarrow _{2/3}}\;,\;l = 1,2,\cdots, L$

(6)

$\phi ({ X},\sigma ) = \frac{1}{{{{(2{\text{π}} )}^{p/2}}\sigma }}{ ex}{{ p}^{ - {{ X}^{{T}}}{ X}/2{\sigma ^2}}}$

(7)

式(6)中的 $ \downarrow $ 代表降采样，如果采样值偏小，有效信息会缺失；如果采样值偏大，会带来计算效率降低的问题，综合以上考虑，本文采样值大小设定为经验值 ${ \downarrow _{2/3}}$ ，即取采样值的2/3。L是高斯金字塔的层数，σ是高斯函数 $\phi ({ X},\sigma )$ 的标准差，式(7)中p代表直方图的维数。然后，使用L₁范数标准对式(4)进行简化^[26]：

$K({ His}{{ t}_1},{ His}{{ t}_2}) = \sum\limits_{l = 1}^L {{d_l}({ X})} $

(8)

从式(6)可以看出，d_l中的向下采样操作在运算量上呈指数减少，同时使用采样值的2/3，又能够最大限度保留样本值的信息；其次，高斯滤波卷积操作是线性运算，在计算效率上明显有优势。但是，优化后的扩散距离虽然在计算效率上提高不少，但是由式(4)和(5)可以知道，优化扩散距离在表示空间向量直方图 ${ His}{{ t}_1}( X)$ 和 ${ His}{{ t}_{{2}}}( X)$ 之间的累积差时，缺少对内部单个元素之间差异的表示。虽然使用式(8)可以直接应用到相似距离度量中，但其忽略了空间向量对应元素之间的相似性的影响，因而其精确度会存在误差。由于不同 ${ Hist}( X)$ 中的每个元素代表不同的特征属性，比如wHSV(weighted HSV, 加权HSV)直方图中的第z个元素代表第z个区域内的像素点的总个数或者代表图像中的颜色值为z。所以，进行相似性距离度量时，既要考虑累积差异的影响，也要考虑对应元素间相似性的影响。假设： ${ His}{{ t}_1}( X) = \left[ {3,7,10} \right]$ ， ${ His}{{ t}_{{2}}}( X) = \left[ {1,1,5} \right]$ ， ${ His}{{ t}_3}( X) = \left[ {3,6,2} \right]$ ，为简化计算，令 $\phi ({ X},\sigma ) = 1$ ，不使用降采样，相应的 $K({ His}{{ t}_1},{{His}}{ t_2}) = \sqrt {{{65}}} =\! K({ His}{{ t}_1},{ His}{{ t}_{{3}}})$ ，无法区分哪两个直方图更相似。通过观察 ${ His}{{ t}_1}( X)$ 、 ${ His}{{ t}_{{2}}}( X)$ 和 ${ His}{{ t}_3}( X)$ 发现， ${ His}{{ t}_{13}}( X)$ 相比 ${ His}{{ t}_{12}}( X)$ 拥有更多相同或者相近的元素个数。从直观上，只能定性的认为 ${ His}{{ t}_1}( X)$ 与 ${ His}{{ t}_3}( X)$ 应该比 ${ His}{{ t}_1}( X)$ 与 ${ His}{{ t}_2}( X)$ 更相似。

通过以上分析，在计算空间向量直方图之间距离时，不应该将内部元素归置一样的权值，而应该对那些元素值间对应相同或者相近的给予更大的权值。所以，本文在优化扩散距离基础上进行二次优化，提出加权式扩散距离，相应表达式为

首先，将式(5)改写成

${d_0}( X) = \sqrt {\sum\limits_{i = 0}^n {{{({ His}{{ t}_{1i}}( X) - { His}{{ t}_{2i}}( X))}^2}} } $

(9)

式中：1i和2i分别代表直方图1中第i个元素和直方图2中第i个元素， $i \in {{\{ 0 , }}n{{\} }}$ ；式(5)和(9)代表类似的含义，即两个直方图差异的距离等同于两个直方图中每一个对应元素差异的累积。那么计算时使用的公式即为式(9)。

其次，将式(9)改写成

$\left\{ \begin{array}{l}{d_0}( X) = \displaystyle\sqrt {\sum\limits_{i = 0}^n {\frac{{{r_i}}}{R}{{({ His}{{ t}_{1i}}( X) - { His}{{ t}_{2i}}( X))}^2}} } \\{r_i} = { ex}{{ p}^{ - |{ His}{{ t}_{1i}} - { His}{{ t}_{2i}}|/\sigma }},\sigma = 1\end{array} \right.$

(10)

式中：R为归一化因子， $R = \sum {{r_i}} $ ；r_i为权值；σ为调节因子。根据式(10)计算，同样按照 $K({ His}{{ t}_1},{ His}{{ t}_2}) \!\!=\!\! {{2}}{{.337}}$ ， $K({ His}{{ t}_1},{ His}{{ t}_2}) = {{1}}{{.025}}$ ，因而能从直观上，定量的得出 ${ His}{{ t}_1}( X)$ 与 ${ His}{{ t}_3}( X)$ 应该比 ${ His}{{ t}_1}( X)$ 与 ${ His}{{ t}_2}( X)$ 更相似。由此可以看出，本文提出的对优化扩散距离的二次优化，对计算匹配距离时拥有更好的区分性，精度进一步提高。

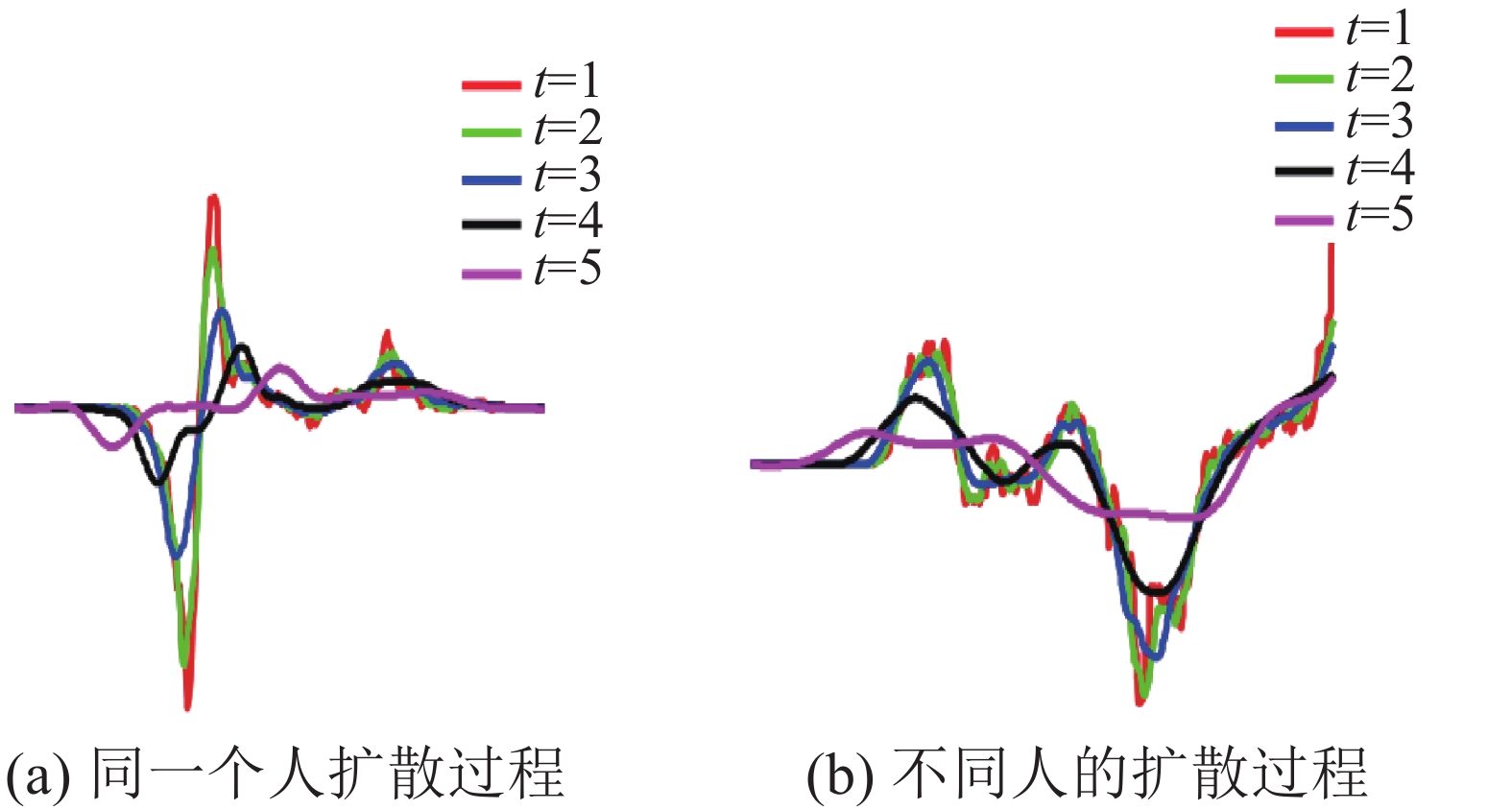
图5显示了不同时间段扩散距离的状态。图5(a)中显示同一个人在不同视角下的直方图差异的扩散过程；图5(b)中显示不同的人在不同视角下的直方图差异的扩散过程。通过两幅图的对比我们可以看到，(a)图相比(b)图衰减更快，即同类人直方图的扩散距离小于不同类人的。

3 目标再确认 3.1 归一化处理

单独使用上述3种特征描述中任何一种所建立的相似性度量函数都不能达到较好的匹配效果，所以本文使用多特征融合进而建立起的相似性度量函数进行目标再确认，对上述3种特征提取相应特征直方图，然后分别计算相应的优化扩散距离，为防止由于不同特征算出的扩散距离有较大差异而影响目标再确认结果，对每类特征描述计算所得到的扩散距离都做归一化处理。

3.2 总体相似性度量函数的建立

目标再确认中，通常会有两组图像数据：待识别目标I_A和候选目标I_B。本文利用两组图像数据库，对上述3类特征得到的扩散距离都做相应的归一化处理之后，使用式(8)结合式(10)来计算不同图像库I_A和I_B中的图像之间的匹配距离 $d({I_A},{I_B})$ 。

$\begin{array}{c}d({I_A},{I_B}) = \alpha \cdot {d_g}({{{RGB}}_g}({I_A}),{{{RGB}}_g}({I_B})) + \\\beta \cdot {d_{ lca}}({{{RGB}}_{ lca}}({I_A}),{{{RGB}}_{ lca}}({I_B})) + \\\lambda \cdot {d_{ lca}}(w{{{HSV}}_{ lca}}({I_A}),w{{{HSV}}_{ lca}}({I_B})) + \\\mu \cdot {d_{ lca}}({{{HOG}}_{ lca}}({I_A}),{{{HOG}}_{ lca}}({I_B}))\end{array}$

(11)

式中：g代表一级区域；lca代表二级区域；α、β、λ、μ分别代表不同特征直方图的权重， $\alpha {{ + }}\beta + \lambda + \mu = 1$ 。本文对于粗识别过程中的整体RGB特征直方图分配经验值为α=0.2影响因素较大的局部RGB直方图给予较大的权值，选择目前最佳的经验值β=0.4；对于影响因素较弱的加权HSV直方图给予目前最佳的经验值λ=0.3；对于影响因素最小的局部HOG直方图给予相对较弱的经验值μ=0.1。总的评价准则函数即总的相似性度量函数为式(11) 。

4 实验验证

上文所述理论相比传统再确认算法在特征选择和度量算法上都进行了优化，同时，本文进行多组实验验证了本文所提出优化算法的可行性，下文会分别从实验运行效果和实验数据统计来阐述本文的有效性。

4.1 实验运行效果

从实验运行结果来看应用本文原理编程实现的匹配成功率较为理想，能够很好地实现目标再确认的功能，如图6(a)、图7所示。下面显示的效果图中图6(a)和图7是目标再确认中显示正确的效果图，图6(a)图显示了实验过程中成功再确认的案列，而图7是实验完成后所有再确认成功的部分汇总。尽管本文算法可以很好地实现目标再确认，但是，仍存在少数失败的案列，比如图6(b)所示。

图6(a)是实验中匹配正确的效果图，从图中可以看出两个摄像头中所呈现的目标的颜色特征有很大相似性，在图6(a)中行人身上的局部颜色特征，如上身身躯和下身身躯的颜色差异性很明显，其他特征的干扰比较小，因而在特征表达更具体，更有辨别性。所以在算法中可以比较容易地将目标进行再确认。相比之下，图6(b)中两个行人在进行躯体分割，特征提取等过程后，由于用于提取特征而分割出来的部分特征较为接近(左右两图上身衣服和下身裤子的颜色分别比较接近)，因而导致出现了错误的再确认结果。

本文通过随机选取图片库中45对图片进行目标再确认实验，将部分匹配成功对在MATLAB画布中显示在一起(图7)，可以更加直观地看出本文的算法达到了良好的再确认效果。具体性能指标可以通过下文中实验数据统计评估结果进行说明。

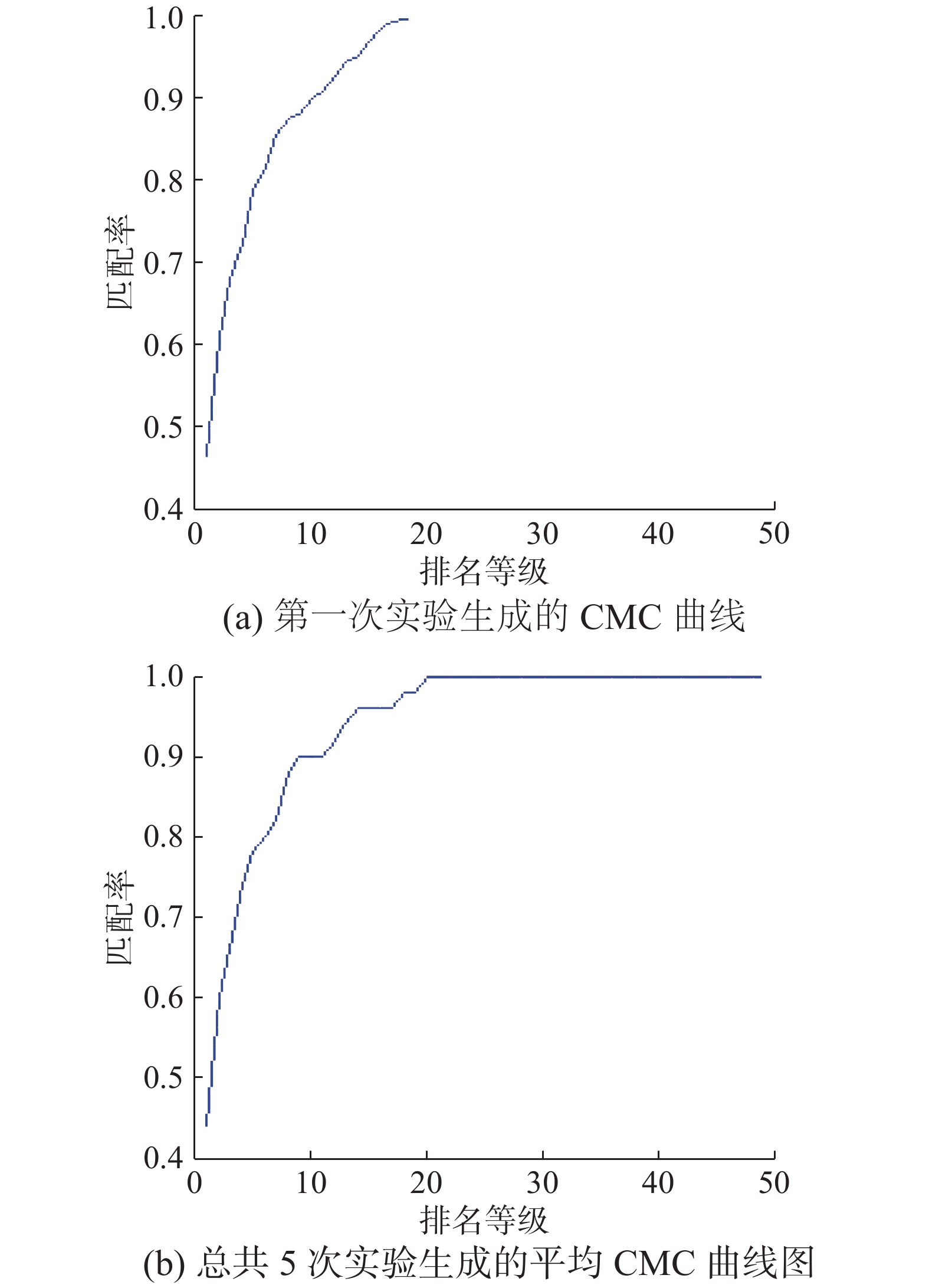
4.2 实验数据统计评估

评价目标再确认的性能是否优良并没有统一的标准，但目前在评估行人再确认性能方面主要采用的是累积匹配特性曲线CMC^[27](cumulative match characteristic)。CMC曲线反映的是在目标图库前n个最相似候选目标内找到正确匹配图片的概率^[27]。实验中随机抽取50对行人目标进行测试，实验的总次数是5次。最后给出平均CMC曲线(横坐标为排名，纵坐标为识别率)。假设曲线上有一点(m, n)，代表排名前m个的匹配目标中能够命中的概论是n，当然其中的m可以理解成所有匹配数目中具有最大相似度的前m个目标，n自然是这m个目标中包含正确匹配结果的比率)^[27]，实验运行第1次和5次实验运行之后生成CMC平均曲线效果图如图8中的(a)和(b)图所示。

图8(a)图中显示的是第1次实验完成后生成的CMC性能曲线，其中图中的横轴代表排名等级，竖轴是识别率，从曲线上可以看出第1次实验至少前20位匹配的效率才能达到100%，此处的识别率也代表：达到最高效率所需要匹配的数量越少，说明该算法越好。图8(b)图中显示的5次实验完成后生成的平均CMC性能曲线，从曲线上可以看出5次实验完成后求平均值生成的CMC曲线图中显示，至少前19位匹配的效率才能达到100%，当然这里达到最高效率所需要匹配数量越少，也说明该算法越好。图中第一次实验获得了44%的匹配率，5次平均实验后获得的匹配率为46%，相比现有提出的参考算法，本文算法的匹配率是比较理想的。

4.3 不同数据集实验对比分析 4.3.1 基于VIPeR数据库实验结果

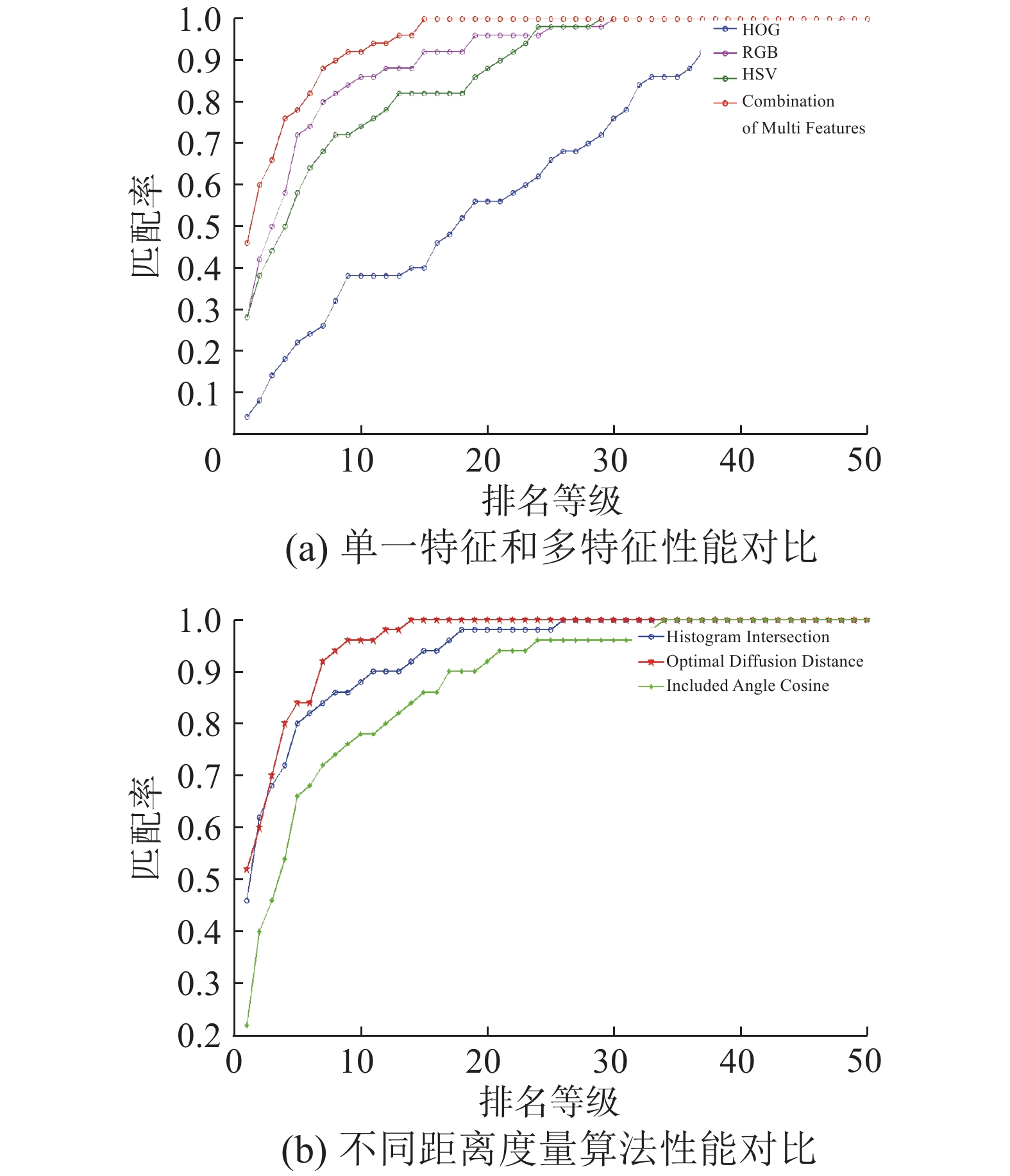
本文在实现基于优化扩散距离算法的基础上使用多特征融合的方式进行目标再确认，实验过程中，本文为了突出多特征组合的优势，相应的做了多组实验：单一特征和多特征在同样距离度量算法的软硬件环境下进行了识别率对比，其相应实验效果如图9(a)所示；同时将本文算法和传统的目标再确认的其他优秀算法(夹角余弦度量算法和直方图交叉核度量算法)进行了性能方面上的对比，其相应实验效果图如图9(b)所示。如图9(a)所示，通过CMC曲线图可以看出，使用本文中的多特征来识别时匹配率更高。从图中统计出Rank=1, 3, 6, 8, 10排名时所对应单一特征和多特征组合的识别率，可以从数据中观察出，本文中使用多特征组合所得识别率为46.2%；仅使用RGB特征所得识别率为28.2%；仅使用HSV特征所得识别率为27.5%；仅使用HOG特征所得识别率为4.5%；无论在哪个排名阶段，总体上，本文使用的多特征组合相对使用单一特征来进行识别时，多特征组合的识别率更高，更有优势。

如图9(b)所示，通过3种算法的CMC曲线对比图可以很明确地看出，本文算法在相同条件下识别率更高。从图中统计出Rank=1, 3, 6, 8, 10排名时所对应不同算法的识别率，可以从数据中观察出，本文的识别率已经达到了50.5%，而其他优秀算法中的直方图交叉核和夹角余弦算法的识别率分别为47.3%和22.5%；无论在哪个排名阶段，总体上，优化扩散距离算法相比其他两种优秀算法在识别率方面都比较高。

为了体现本文算法在识别率上的优势，实验中，同时进行了不同优秀算法和本文算法的性能对比，对应性能表如下表1所示。

通过表1特征类算法的对比：SDALF (symmetry-driven accumulation of local features)方法在提取前景后分割人体目标为头部、躯干和腿部3部分的基础上进行wHSV、最大稳定颜色区域和重复纹理块组合识别，最后使用欧式距离进行测距，实验中的匹配率达到了19.77%，这个应用广泛的算法的优势在于较好特征的建立，但是在距离度量上还是使用传统的欧式距离，相比而言，本文在距离度量上的优势是显而易见的；CPS(custom pictorial structures)方法的优势在于能够根据人体结构检测出人体的各个部位进行识别，能够更好地提取前景特征，匹配率达到了20.32%；eLDFV(encoded local descriptors fisher vectors)方法结合SDALF使用Fisher向量编码图像的亮度和梯度信息，匹配率达到了21.42%，但是对于度量算法仍然需要改进；SCEFA(structural constraints enhanced feature accumulation)方法虽然使用基于Gabor纹理模式的关键点检测和双向匹配颜色区域特征的方法，匹配率达到了25.36%，其多特征的构建是最大的优点；eSDC(effectiveness salience and dense correspondence)方法也是结合SDALF以及非监督的学习方式去寻找个体更好的特征，匹配率达到了很高的26.77%，但是欠缺考虑距离度量算法的改进；特征类中的HSCD(hybrid spatiogram and covariance descriptor)方法结合了空间直方图和区域协方差两种优秀的统计描述，并且从多个层次的统计区域提取多类互补性较好的统计向量，这个方法和同类相比是最好的，得到了29.32%的识别率。通过表2所展现的度量算法来看：ELF(ensemble of localized features)方法虽然AdaBoost分类器选取颜色和纹理特征，这种方法充分利用了分类器的选优特性，识别率仅仅为11.36%；ERSVM(Ensemble RankSVM)方法和PRDC(relative distance comparison)相类似，利用相对距离排序的SVM分类器集成多个特征向量权重，此方法在度量算法方面优势很明显，但是在特征方面仍需要改进；LMNN-R(large margin nearest neighbor with rejection)方法也使用相对距离比较的PRDC方法，使用了大边近邻分类器，在特征设计方面同样需要改进。

度量算法类中，性能表现最好的是HI(histogram intersection)，直方图交叉核，该算法是一种基于隐式对应关系的内核函数，解决了无序、可变长度的矢量集合的判别分类的问题，而且是正定的，由于该算法的优势，应用到目标再确认领域，匹配率高达47.38%，因此，通过上文所述，同等条件下，度量算法类相比特征类在匹配率方面具有一定的优势。而查看表格，本文算法无论在特征类还是距离度量类对比中，其50.5%的匹配率仍然具有一定的优势。通过以上优秀算法和本文算法在数据上对比可以看出，本文在基于VIPeR图像库的基础上，识别率方面性能相对比较好，这是因为本文特征设计上的优势和优秀度量算法引入的原因。

4.3.2 基于ETHZ数据库实验结果

ETHZ数据库是从运动的摄像机中获取的图像，ETHZ1包含83个目标的4 857幅图像；ETHZ2包含35个目标的1 936幅图像；ETHZ3包含28个行人的1 762幅图像。本文使用这类数据库作为测试样本库，用来验证本文算法和余弦、直方图正交算法的性能对比。在数据库中，光照的改变和行人的遮挡相对严重，人体姿态方面变化比较小。根据获得的目标的帧数，可以将目标再确认分为以下3类：

1) 单帧对单帧(single vs single, SvsS)

2) 多帧对单帧(multiple vs single, MvsS)

3) 多帧对多帧(multiple vs multiple, MvsM)

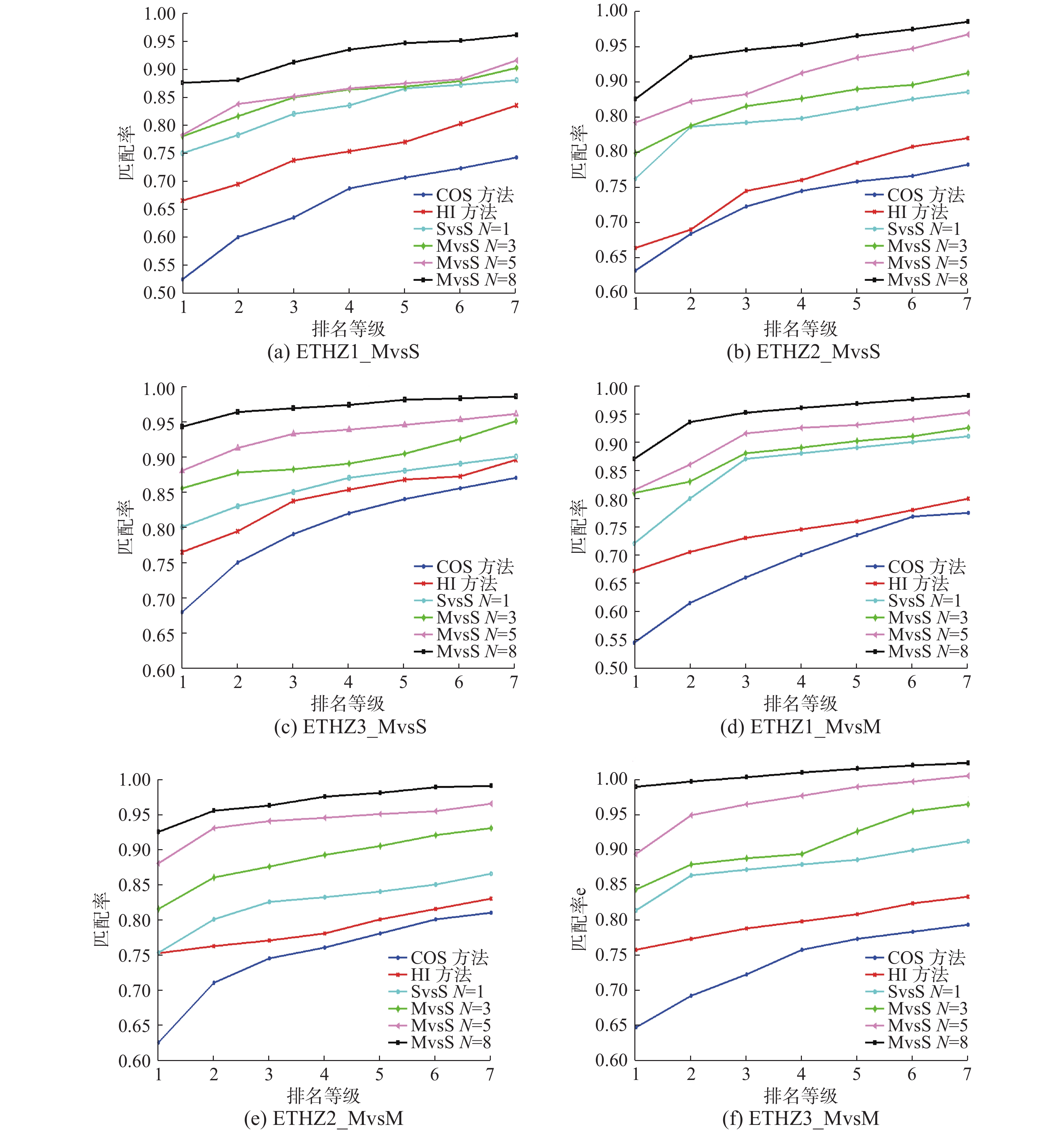
本文分别测试了SvsS、MvsS、MvsM模式下的不同算法的目标再确认的性能，相应的CMC曲线图如图10所示。

在图10中，(a)、(d)分别代表ETHZ1数据集下MvsS和MvsM的性能表现；(b)、(e)分别代表ETHZ2数据集下MvsS和MvsM的性能表现；(c)、(f)分别代表ETHZ3数据集下MvsS和MvsM的性能表现。通过测试ETHZ数据库中的实验图像可以发现，在不同ETHZ集下，本文算法在匹配精度方面，一直保持领先。ETHZ1中，在MvsS和MvsM帧下，本文算法在Rank=1时都达到了87%左右；ETHZ2中，在MvsS和MvsM帧下，本文算法在Rank=1时分别达到了87.5%和93%左右；ETHZ3中，在MvsS和MvsM帧下，本文算法在Rank=1时分别达到了94%和96%左右。相比余弦算法和直方图正交算法，本文算法能够得到更好的表现，其原因在于：由于多特征的使用，可以应对摄像机镜头的不同、遮挡所造成的差异；更重要的是在距离匹配过程中所应用的优化扩散距离，可以有效应对光亮、阴影等造成的差异，并且利用直方图的空间信息更加精确其对应距离，从而准确的进行目标再确认。这也是本文适合更多场景且无需监督的原因，通过在ETHZ数据集上的表现，可以看出本文算法的性能还是不错的，观察匹配出的效果图发现，本文所提出算法在应对姿态、视角、和光照变化等方面具有较好的鲁棒性。

5 结束语

通过上文中的理论分析和实验验证，本文最大的创新点在于引入物理学温度场的扩散距离的概念并进行优化，来建立相似性度量函数。并为了提高优化扩散距离的计算效率，进行了二次加权性优化，进而提高了计算的准确性。特征提取方面，定义了两级区域直方图提取方案，这种简易而有效的方法可以在特征基础上实现空间信息的添加，从而提高了识别率。在两级区域方案基础上，通过高斯加权HSV直方图，整体、局部RGB直方图，以及HOG特征描述子3类特征的综合使用，并辅以适当的加权处理，较好地实现了行人目标再确认。最后，本文优化算法与同类别的其他优秀算法以及传统目标再确认过程中所使用的有监督的训练学习型度量算法进行了对比。相比其他算法，本文的优点是：目标再确认准确率明显提高，同时不需要大量的训练样本、节省了训练时间、可以适应大部分的场景变化、节省内存开支等，在一定程度上体现了本文算法的优越性。但本文仍然还有许多需要改进的地方，比如如何在更加复杂的环境中可以更高效率的进行目标再确认，这也是本文下一步研究的重点。