2. 复杂工程系统测量与控制教育部重点实验室, 江苏 南京 210096
2. Key Laboratory of Measurement and Control of Complex Systems of Engineering, Ministry of Education, Nanjing 210096, China
服务机器人长期工作在与人共处的环境中,针对采用车载激光、视觉等各种传感器实现的机器人自定位,人的运动会对其定位的准确性造成影响,甚至导致定位失败。
以往解决方法大多从改进算法本身入手,由于经典粒子滤波算法无法补偿动态环境中未建模障碍物对机器人定位产生的干扰,R.Valencia等[1]在经典的蒙特卡罗定位的基础上利用已知的静态地图和在感知更新阶段建立的短期地图进行基于正态分布变换[2]的蒙特卡罗定位,以补偿环境发生短期变化时对定位精度产生的干扰,该算法满足实时性并具有一定的鲁棒性,但是没有考虑静态地图发生永久性变化的情况。J.Röwekämper等[3]将蒙特卡罗定位[4]、KLD采样和使用扫描配准[5]的精细定位结合起来,在不改变环境条件的情况下实现机器人移动作业。这种方法虽然精度高但是实现起来复杂而且实时性难以保证。文献[6]通过对观测模型可定位性和基于里程计的预测模型协方差两个指标的在线估计,动态调节两者在粒子集[7]位姿修正中的比重。这种方法满足一定的实时性,但是对于动态障碍物影响因子的计算需要离线获得,并没有利用传感器数据来实时地更新未建模目标的分布信息。
以上算法都是单一地利用激光传感器,仅通过算法改进提高动态环境下的定位精度。近年来,更多的研究者倾向于使用多传感器的信息融合技术[8]。尤其是随着机器视觉的发展,将视觉与激光传感器结合使用为动态环境下机器人定位提供了新思路,如段鹏等[9]采用分布式激光雷达和视觉摄像机,将基于自然特征的场景识别技术与Monte Carlo方法有机结合,提出了一种实时的服务机器人位姿估计方法。本文考虑到当环境中未建模动态障碍物主要为人时,从激光传感器读数中检测人腿存在一定困难,而RGB-D传感器相比普通视觉摄像机,不仅提供场景的颜色信息,还提供深度信息,因此利用RGB-D传感器能够快速检测人体躯干的位置及区域[10-11],并利用投影后的人体躯干点云估算激光数据受人腿干扰的范围。但Kinect传感器的精度却比激光传感器低,因此如何发挥两者各自优势、研究一种更易于实现的动态环境下可靠、快速地机器人自定位方法,是问题的关键。
为此,本文考虑环境中的人为主要未建模动态障碍物,提出一种基于多传感器的可定位性在线估计方法,并用于解决机器人可靠自定位问题。利用RGB-D传感器对人体的实时检测结果,估算激光数据是由人腿干扰引起的范围,并使用高斯模型估计该范围内每一束激光上的存在未建模动态障碍物的先验概率。解决了动态障碍物影响因子和动态可定位性矩阵在线估计问题,使动态可定位性矩阵更加真实可靠地反映环境中的未建模动态障碍物。
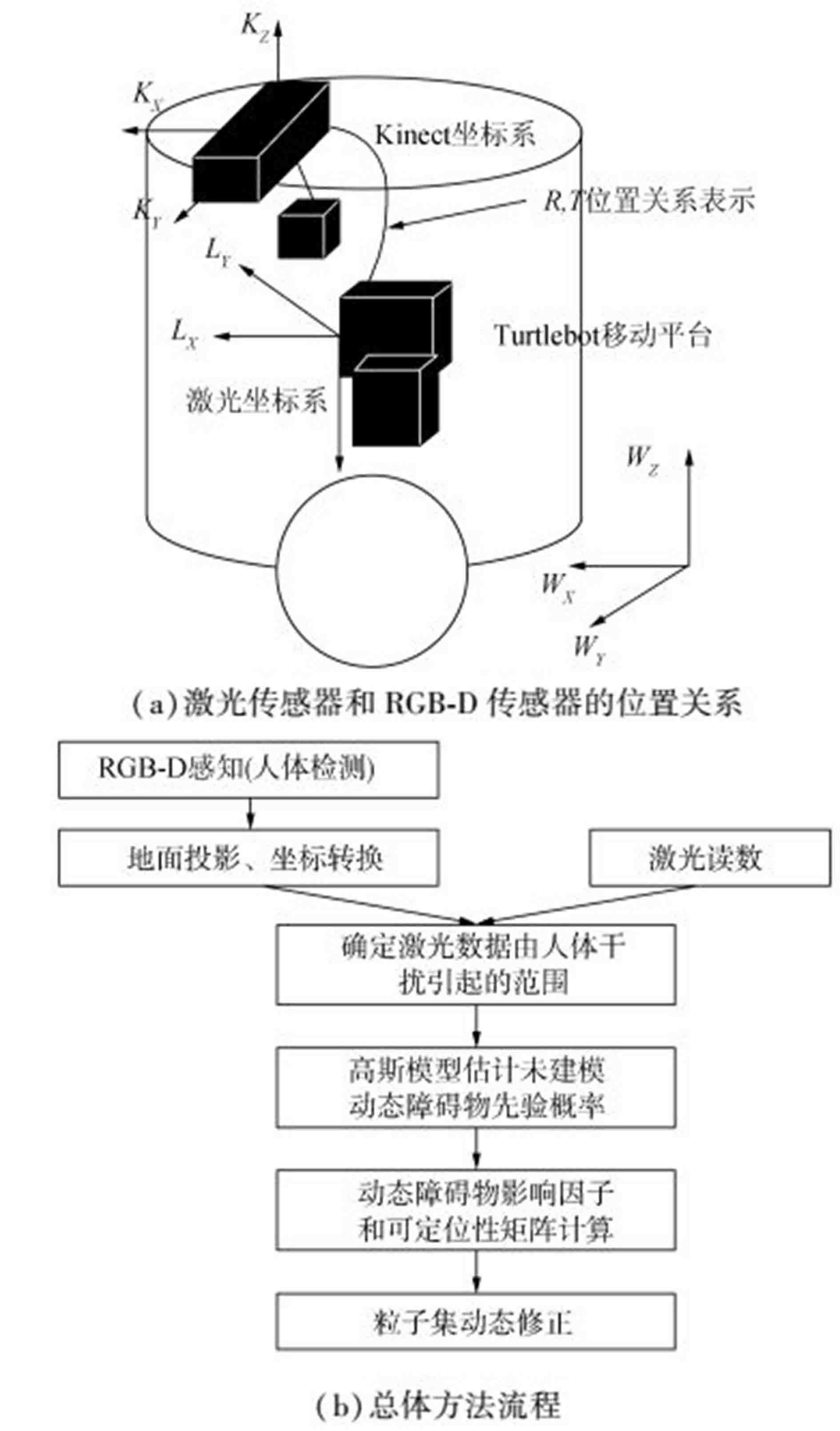
1 总体方法由于RGB-D传感器与激光传感器精度存在较大差异,本文并不是将两者数据直接融合,而是在可定位性理论框架下利用RGB-D传感器信息辅助激光传感器下的动态可定位性在线估计,从而既不丢失激光传感器定位精度,又能避免较为困难地从激光读数中检测人腿。即利用RGB-D传感器对人体的检测结果估计每一束激光读数中存在未建模动态障碍物的概率,利用动态可定位性估计和预测模型协方差对粒子集进行校正[12]。两种传感器之间的位置关系和总体方法如图 1所示。
|
图 1 两种传感器的位置关系和总体方法 Fig.1 Positional relationship of two sensors and method outline |
激光传感器和RGB-D传感器之间的位置关系用旋转矩阵R和平移矩阵T表示,图 1(a)描述了本文实验平台中两种传感器之间的位置关系,其中:
| $ \mathit{\boldsymbol{R}} = \left[ {\begin{array}{*{20}{c}} 1&0&0&0\\ 0&{ - 1}&0&0\\ 0&0&{ - 1}&0\\ 0&0&0&1 \end{array}} \right],\mathit{\boldsymbol{T}} = \left[ {\begin{array}{*{20}{c}} 1&0&0&{0.113}\\ 0&1&0&{0.012}\\ 0&0&1&{ - 0.13}\\ 0&0&0&1 \end{array}} \right] $ | (1) |
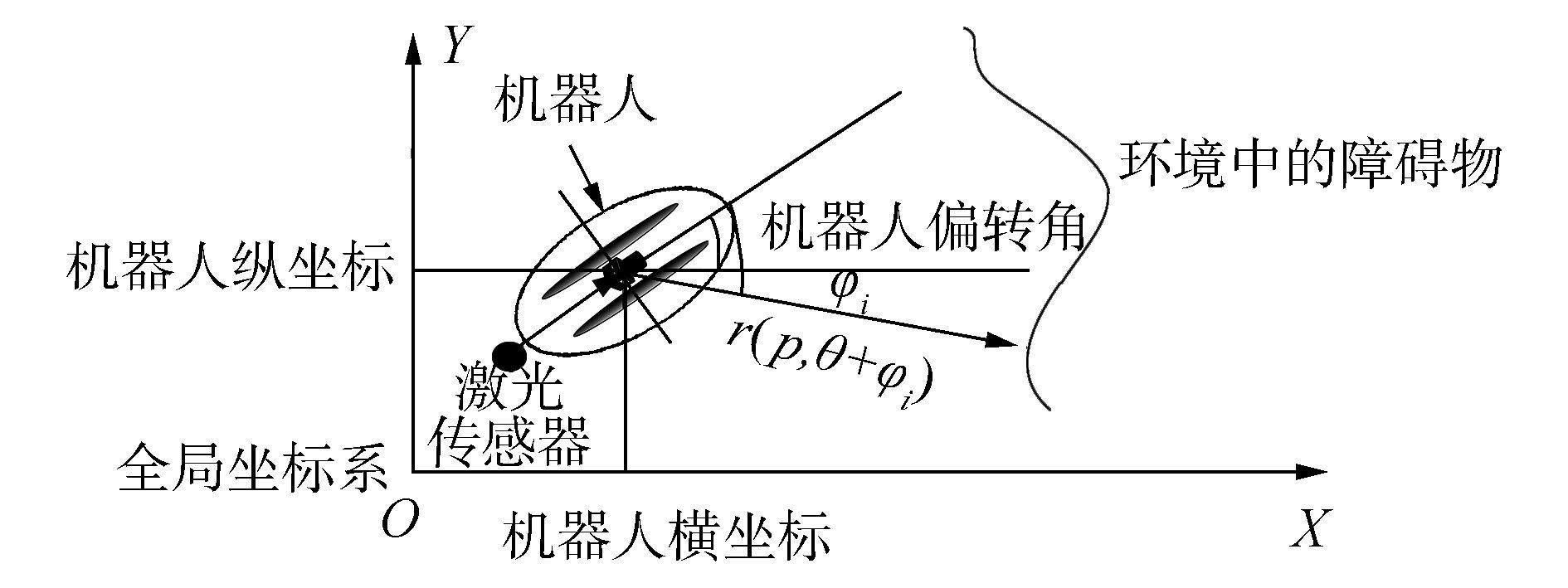
静态可定位性矩阵是基于统计学理论中的Fisher信息矩阵提出的,Fisher信息提供了观测信息中蕴含关于待估参数信息量大小的度量。针对服务机器人依靠激光数据和先验地图进行位姿估计,A. Censi[13]依据图 2的机器人模型将Fisher信息矩阵定义为式(2) 所示的激光扫描到环境表面斜率的函数。
|
图 2 机器人在全局地图中的模型 Fig.2 Robot model in global map |
| $ \mathit{\boldsymbol{\tau }}\left( \mathit{\boldsymbol{p}} \right) = \sum\limits_i^n {\frac{1}{{{\sigma ^2}}}\left[ {\frac{{\partial \mathit{\boldsymbol{r}}_i^{\rm{T}}}}{{\partial \mathit{\boldsymbol{p}}}}\frac{{\partial {\mathit{\boldsymbol{r}}_i}}}{{\partial \mathit{\boldsymbol{p}}}}} \right]} $ | (2) |
式中:p=(x, y, θ)为机器人的位姿,ri为机器人在当前位姿下第i个激光束的长度,σ2为激光数据的噪声方差。王炜[6]根据概率栅格地图的特点对Fisher信息矩阵τ(p)离散化,用ΔriE/Δp近似$\partial {r_{iE}}/\partial p$,得到静态可定位性矩阵$\mathit{\boldsymbol{\hat \tau }}\left(\mathit{\boldsymbol{p}} \right)$。
$\mathit{\boldsymbol{\hat \tau }}\left(\mathit{\boldsymbol{p}} \right)$仅考虑到已知静态概率栅格地图,未考虑局部动态信息对机器人可定位性的影响。而在实际环境中,未知障碍物会导致激光数据匹配度降低甚至失效,无法反映其可定位性。因此在$\mathit{\boldsymbol{\hat \tau }}\left(\mathit{\boldsymbol{p}} \right)$的基础上,考虑局部激光扫描数据,引入动态障碍物影响因子si以度量动态障碍物对激光扫描数据的影响。
如图 2所示,机器人在参考位置P0=[x0, y0, θ0]已知的前提下,设激光测距仪实际获取的第i个激光束的长度为ri,扫描到已知栅格为事件A,扫描到未知障碍物为事件B,则根据贝叶斯公式,该激光点扫描到已知栅格的概率为
| $ p\left( {A\left| {{r_i}} \right.} \right) = \frac{{p\left( {{r_i}\left| A \right.} \right)p\left( A \right)}}{{p\left( {{r_i}\left| A \right.} \right)p\left( A \right) + p\left( {{r_i}\left| B \right.} \right)p\left( B \right)}} $ | (3) |
设第i个激光束的全局坐标位置(xi, yi)为
| $ \left\{ \begin{array}{l} {x_i} = {x_0} + {r_i}\cos \left( {{\varphi _i} + {\theta _0} - {\rm{ \mathsf{ π} /2}}} \right)\\ {y_i} = {y_0} + {r_i}\sin \left( {{\varphi _i} + {\theta _0} - {\rm{ \mathsf{ π} /2}}} \right) \end{array} \right. $ | (4) |
则p(ri|A)=μxiyi。μxiyi为原始地图中(xi, yi)处的栅格概率值,将1-p(A|ri)定义为未知障碍物影响因子si,si值越大该激光数据对机器人可定位性的提高越小。
2.2 利用RGB-D感知的未建模动态障碍物概率估计由于激光传感器与Kinect传感器的数据已通过坐标转换进行了对齐,本文采用Kinect传感器实现视野中的快速人体检测。在RGB-D数据中使用HOG+SVM[14]方法实现移动机器人作业场景中人体的检测并得到关于人体的点云数据。
每一簇关于人体的点云经过点云投影和坐标变换到激光坐标系下后,利用其中的三维信息确定激光数据是由人体干扰引起的角度范围:对于每一簇对齐后的人体点云数据{pi|pi=(xi, yi),i=1, 2, …, n},计算每一个点云对应的角度θi,即
| $ {\theta _i} = \arctan 2\left( {{\rm{point}}\left[ i \right].y,{\rm{point}}\left[ i \right].x} \right) $ | (5) |
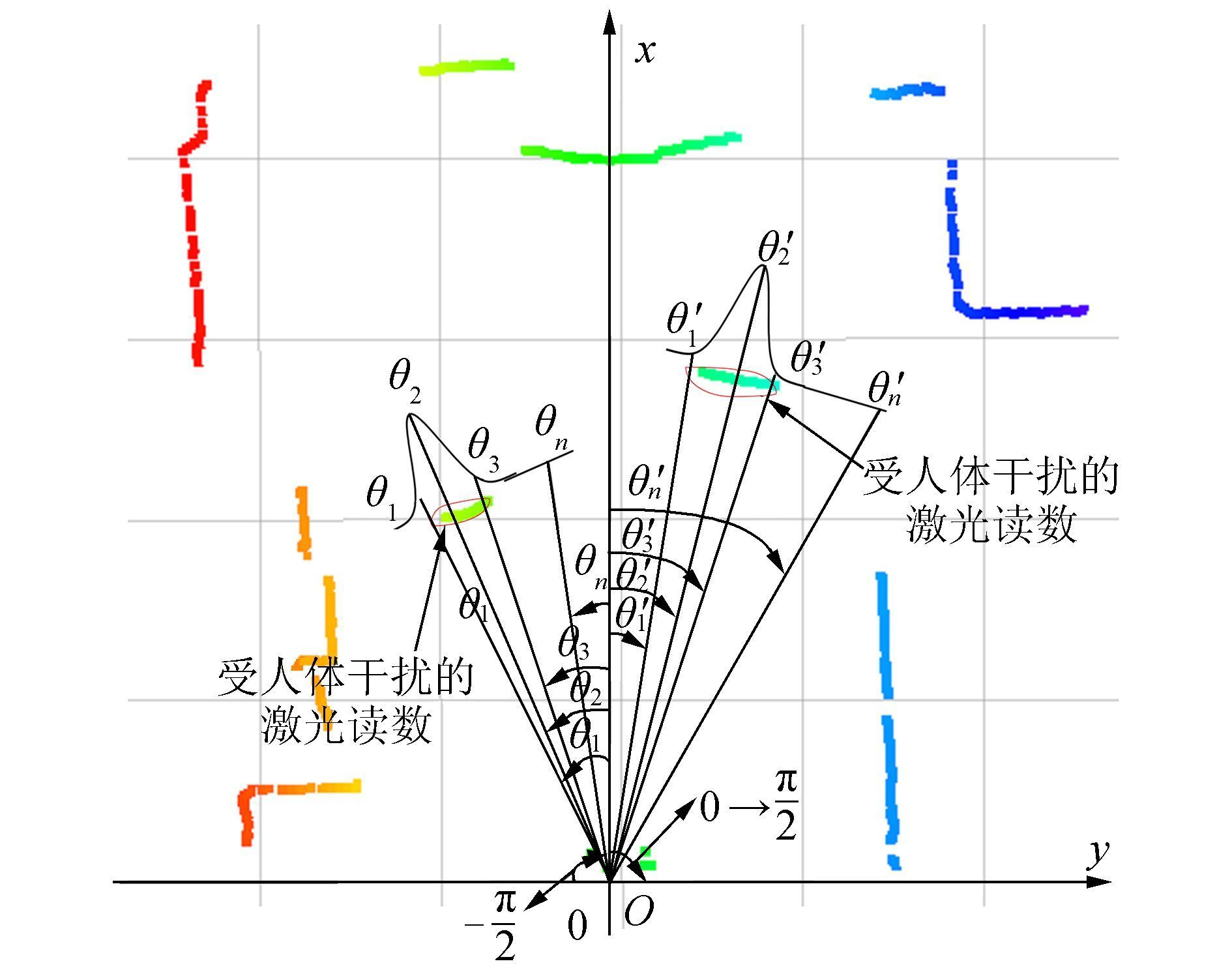
并得到每一簇人体点云的统计信息,即角度θi, i=1, 2, …, n的最大和最小值θmax和θmin。当使用RGB-D传感器检测到场景中存在n个人时,用同样的方法确定n对θmax和θmin,记做(θkmin, θkmax),k=1, 2, …, n。对于一个特定范围本文用高斯模型确定该范围内每一束激光上的未建模动态障碍物概率并记为εi(i表示第i束激光),如图 3所示。
|
图 3 未建模动态障碍物概率估计 Fig.3 Estimating the probability of unmodeled obstacles |
则整个视场中激光束的未建模动态障碍物的概率估计为εi, 可以用式(6) 计算:
| $ {\varepsilon _i} = \left\{ \begin{array}{l} \frac{1}{{\sqrt {2{\rm{\pi }}} {\sigma _k}}}\exp \left( { - \frac{{{{\left( {{\varphi _i} - {\mu _k}} \right)}^2}}}{{2\sigma _k^2}}} \right),\;\;{\varphi _i} \in \left( {{\theta _{k\min }},{\theta _{k\max }}} \right)\\ 0,\;\;\;\;其他 \end{array} \right. $ | (6) |
式中:φi为第i束激光的角度,μk和σk可用pmax、pmin、θkmax、θkmin唯一确定。若场景中出现提取出来的两簇点云有重叠的情形(图 4)。

|
图 4 点云数据有重叠情形 Fig.4 Cases where point clouds are overlapped |
重叠区域中的每一束激光在两个高斯模型中对应两个不同的概率值,分别为εi1和εi2。
| $ {\varepsilon _{i1}} = \left( {\frac{1}{{\sqrt {2{\rm{ \mathsf{ π} }}} {\sigma _1}}}} \right)\exp \left( { - \frac{{{{\left( {{\varphi _i} - {\mu _1}} \right)}^2}}}{{2\sigma _1^2}}} \right) $ | (7) |
| $ {\varepsilon _{i2}} = \left( {\frac{1}{{\sqrt {2{\rm{ \mathsf{ π} }}} {\sigma _2}}}} \right)\exp \left( { - \frac{{{{\left( {{\varphi _i} - {\mu _2}} \right)}^2}}}{{2\sigma _2^2}}} \right) $ | (8) |
μk和σk可以用pmax、pmin、θkmax、θkmin唯一确定(k=1, 2),则该激光束对应的未建模动态障碍物概率估计为
| $ {\varepsilon _i} = \alpha {\varepsilon _{i1}} + \beta {\varepsilon _{i2}},\;{\rm{s}}{\rm{.t}}{\rm{.}}\;\alpha {\rm{ + }}\beta {\rm{ = 1}} $ | (9) |
由于p(B)表示激光扫描到未建模动态障碍物的概率,与εi的物理含义相同,则式(3) 可重写为
| $ p\left( {A\left| {{r_i}} \right.} \right) = \frac{{{\mu _{{x_i}{y_i}}}p\left( A \right)}}{{{\mu _{{x_i}{y_i}}}p\left( A \right) + \frac{{\Delta {r_B}}}{{{r_{iE}}}}{\varepsilon _i}\sum {p\left( {{r_i}\left| {{r_B}} \right.} \right)} }} $ | (10) |
式中:p(A)=1-p(B),p(B)为环境中存在未知障碍物的先验概率。本文中p(B)通过RGB-D传感器对人体的实时检测来获取,进而解决动态障碍物影响因子的在线计算问题,使si更加可靠的反映环境中未建模的动态障碍物。在得到动态障碍物影响因子后,结合静态可定位性矩阵可得到动态可定位性矩阵D(P)(式(11)),D(P)兼顾原始地图和局部动态信息的影响,反映机器人在P处的可定位性。
| $ \mathit{\boldsymbol{D}}\left( \mathit{\boldsymbol{P}} \right) = \sum\limits_i^n {\frac{{1 - {s_i}}}{{{\sigma ^2}}}\left[ {\begin{array}{*{20}{c}} {\frac{{\Delta r_{iE}^2}}{{\Delta {x^2}}}}&{\frac{{\Delta r_{iE}^2}}{{\Delta x\Delta y}}}&{\frac{{\Delta r_{iE}^2}}{{\Delta x\Delta \theta }}}\\ {\frac{{\Delta r_{iE}^2}}{{\Delta x\Delta y}}}&{\frac{{\Delta r_{iE}^2}}{{\Delta {y^2}}}}&{\frac{{\Delta r_{iE}^2}}{{\Delta y\Delta \theta }}}\\ {\frac{{\Delta r_{iE}^2}}{{\Delta x\Delta y}}}&{\frac{{\Delta r_{iE}^2}}{{\Delta y\Delta \theta }}}&{\frac{{\Delta r_{iE}^2}}{{\Delta {\theta ^2}}}} \end{array}} \right]} $ | (11) |
经典粒子滤波定位算法依赖里程计数据进行预测更新,依赖激光数据进行感知更新。当环境中存在动态障碍物时,粒子集权重更新依据丢失;而里程计信息由于累积误差也不能单独用于机器人定位。为此本文估计机器人的观测模型可定位性矩阵以及文献[6]中详细介绍的预测模型协方差codo, t,并使用其修正方法将两者作为权重指标,调节粒子集依据观测模型对预测位姿的修正值:设t时刻粒子滤波通过预测模型得到的机器人位姿为
| $ {P_{{\rm{odo,}}t}} = {P_{t - 1}} + {f_{{\rm{odo}}}}\left( {\Delta {u_t}} \right) $ | (12) |
式中:Pt-1为上一时刻定位结果,Δut为里程计在该周期的输入量,fodo为运动模型。在预测模型基础上,通过观测信息对粒子权重进行更新,得到新的粒子集{pPF, t, wt}, pPF, t为粒子的位姿,wt为粒子权重。新的表示机器人位姿的粒子集为
| $ {P_{{\rm{PF}},t}} = \sum\limits_i {{w_i}\left( {{z_i},M} \right)p_{{\rm{PF,}}t}^i} $ | (13) |
式中:zi为激光测距仪的观测值,M为地图信息。粒子集根据观测信息对预测位姿的修正值为ΔPobs, t=PPF, t-Podo, t。t时刻的观测模型可定位性矩阵为DPF, t,当观测模型可定位性矩阵DPF, t的行列式较大时,粒子集可以较精确反映机器人位姿概率分布,然而当观测模型可定位性较低时,粒子集权重分配干扰严重,定位可靠性降低。
利用预测模型协方差和观测模型可定位性指标动态调节基于观测信息对预测位姿的修正值:
| $ {P_t} = {\mathit{\boldsymbol{P}}_{{\rm{odo}},t}} + {\left( {{\mathit{\boldsymbol{D}}_{{\rm{PF,}}t}} + {k_1}\mathit{\boldsymbol{C}}_{{\rm{odo}},t}^{ - 1}} \right)^{ - 1}}{\mathit{\boldsymbol{D}}_{{\rm{PF,}}t}}\Delta {\mathit{\boldsymbol{P}}_{{\rm{ods}},t}} $ | (14) |
式中:k1为比例系数,调节观测模型可定位性矩阵与预测模型协方差的权重比例关系。由此可知,在动态环境中,观测模型可定位性较低,机器人位姿主要依赖里程计信息减小观测噪声对定位精度产生的影响;动态环境中未知障碍物较少时,机器人观测模型可定位性较高,粒子集根据观测信息修正预测位姿,消除里程计的累积误差,保证全局定位稳定性。
4 实验结果本文实验所采用的硬件平台如图 5所示。

|
图 5 Turtlebot移动平台 Fig.5 Turtlebot mobile platform |
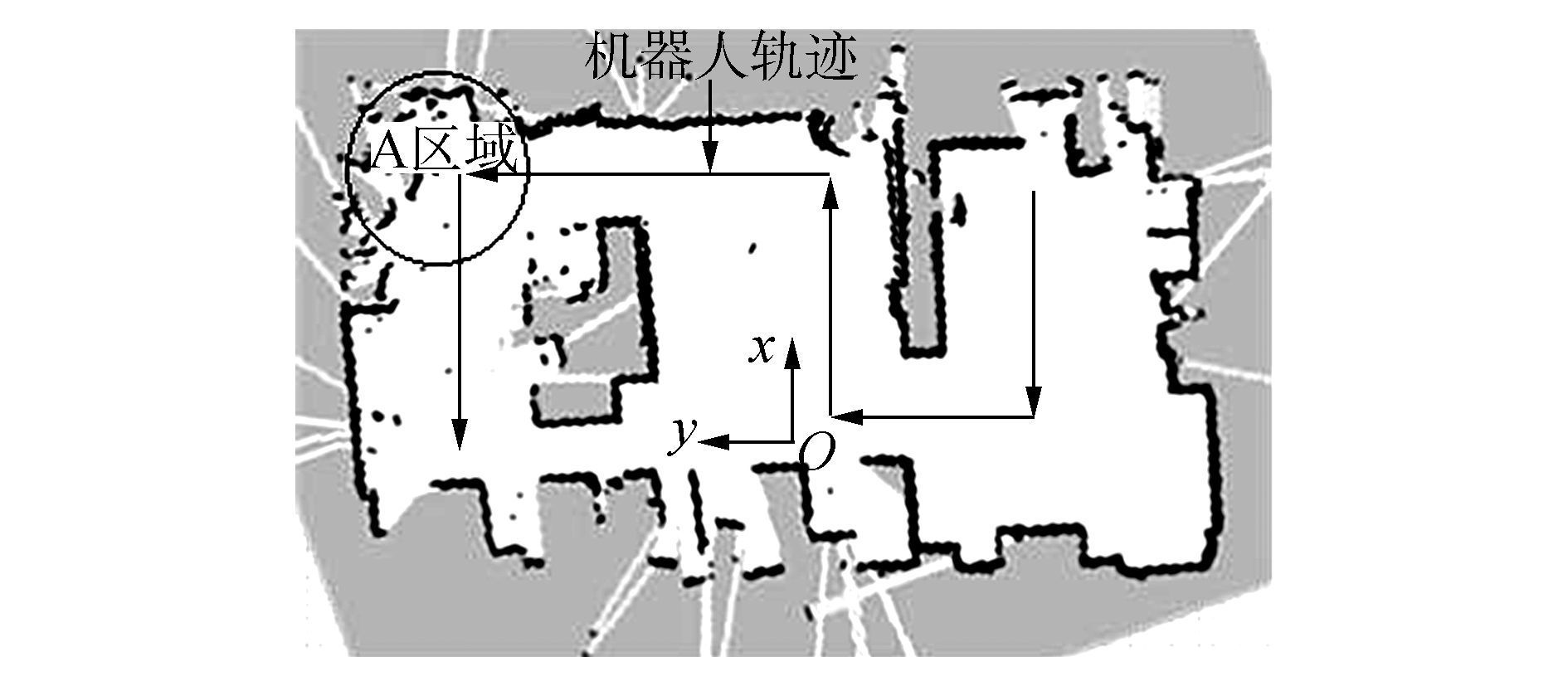
激光测距仪为Hokuyo的URG-04LX-UG01,其距离为0.02~5.60 m。采用ROS[15](Robot operating system)中间件对移动平台内置里程计数据、激光数据、点云数据等进行封装,利用OpenNi中间件控制Kinect传感器获取场景的三维视觉信息,并通过PCL(point cloud library)[16-17]实现人体检测,进而辅助激光测距仪进行机器人自定位。采用gmapping功能包[18]创建实验环境的栅格地图(图 6)。
|
图 6 环境模型和机器人行走轨迹 Fig.6 Environment model and robot trajectory |
为得到对比实验结果,控制机器人从初始状态运动到固定轨迹的起始点完成最初的位姿估计,位姿均方差的收敛过程如图 7所示,然后在结构化环境和动态环境中控制机器人沿着固定轨迹行走(图 6),并分别采用经典的蒙卡罗定位和本文提出的改进方法得到位姿跟踪过程中的误差,最后以跟踪结果的均方差为标准对这4种定位结果进行比较。

|
图 7 定位均方差收敛过程 Fig.7 Convergence process of localization error |
首先在结构化环境中(没有人体干扰的情况下)控制机器人沿着设定好的轨迹行走(如图 6),使机器人尽可能遍历整个环境,分别使用经典定位算法和本文提出的改进算法得出机器人在行走过程中x方向和y方向的定位均方差,如图 8所示。

|
图 8 x和y方向定位均方差对比 Fig.8 Comparison of localization error in x and y-axis |
通过对图(8) 的观察可知:两种定位方法在结构化环境中整体定位效果相差不多,x方向和y方向的定位均方差在3~5 cm之间;改进的定位算法源于经典的粒子滤波算法,当环境整体的可定位性较好时,其修正方法决定了改进的方法与经典的算法功能等效;但是当移动机器人的定位周期在200~300之间时,经典定位算法的两个方向的定位均方差都出现了变大的趋势,而改进的方法没有出现这种现象。这是因为当定位周期在200~300之间时,机器人运动到图 6中的A区域,该区域环境结构杂乱而地图创建效果差,影响机器人的定位精度使其定位均方差增大但是改进的定位方法中的可定位性矩阵会对地图的创建效果进行评估,在这个区域中的可定位性较小,主要依靠里程计进行定位,使定位均方差不会出现较大的变动。
4.2 动态环境中的对比实验在有人干扰的动态环境中控制机器人沿着上述的固定路线行走,分别采用经典算法和本文提出的改进方法进行评估,真实场景如图 9所示,图 10为定位过程中两帧激光和点云数据,图 9图 10均包含人体相互重叠和没有人体相互重叠两种情况。对于检测出的人体点云有相互重叠的情形按照式(9) 所示计算动态障碍物影响因子并用于机器人定位。

|
图 9 移动机器人定位的动态场景 Fig.9 Robot localization in dynamic environment |

|
图 10 含人体点云坐标转换后数据的激光扫描实例 Fig.10 Example of laser scan data containing point clouds after coordinate transform |
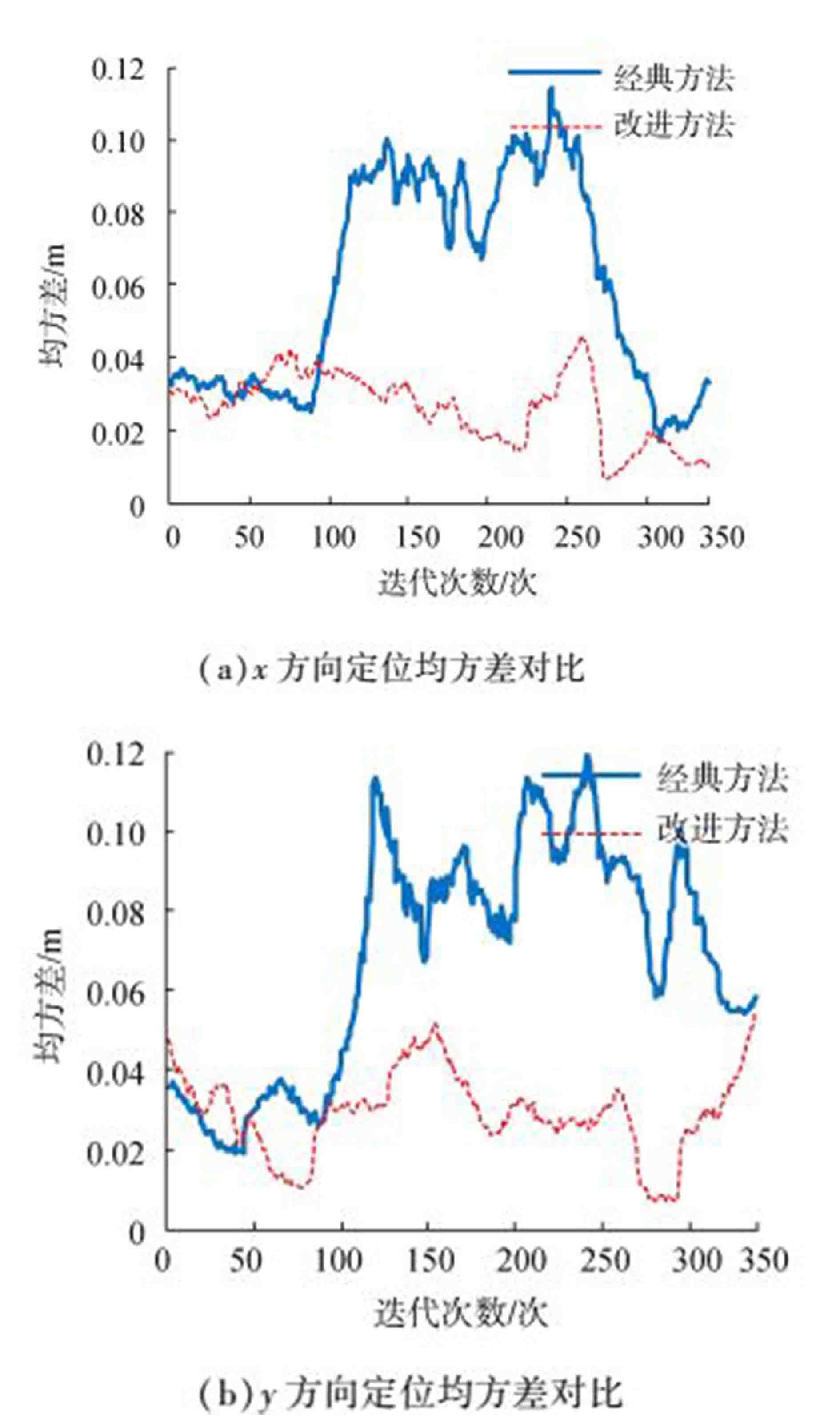
经典定位算法和本文改进算法的对比效果如Fig. 11。
|
图 11 x和y方向定位均方差对比 Fig.11 Comparison of localization error in x and y-axis |
从图 11中可以发现,当机器人在前100个运行周期中经典的粒子滤波算法以典型的性能进行定位,两个方向上的定位均方差在4 cm左右。而在100~200个运行周期中经典算法定位均方差出现增大的趋势:在机器人的定位场景中有人出现,干扰了机器人的激光传感器读数,进而影响感知更新使其粒子更加发散。在第200~300个运行周期中,还是由于地图创建效果的原因使粒子在原来的基础上继续发散。由图 11中的统计数据可以看到, 在这两个阶段,两个方向的定位均方差最大已经达到10 cm以上,而最小的也在4 cm以上,定位性能严重下降。观察本文提出的改进算法的定位结果,发现虽然部分均方差在5 cm以上不及经典算法在静态环境中的性能,但在相同环境中比经典方法更具鲁棒性:可定位性矩阵不仅对静态的结构化环境进行评价,还对环境中的未知障碍物(人)进行检测和评估,当环境中未知障碍物增多而影响激光数据时,通过粒子集的动态修正减少感知更新对粒子集的影响,使机器人主要依靠预测更新进行定位,以保证改进定位算法在动态环境中的鲁棒性。
5 结束语针对动态环境下移动机器人定位性能下降甚至失效的问题,提出了一种利用RGB-D传感器辅助激光传感器的动态可定位性在线估计方法,并用于移动机器人可靠自定位。本算法一方面通过RGB-D传感器对人体的检测并利用可定位性矩阵估计人体对激光数据的影响;另一方面通过预测模型的协方差矩阵估计里程计数据的可信度,进而融合这两个矩阵对机器人位姿进行修正。在结构化环境和动态环境中分别使用这两种方法进行测试评估,实验结果表明了本文所提出的算法对提高动态环境下移动机器人定位性能的有效性,同时结果也表明改进的算法保证了定位系统在多人运动干扰情况下的鲁棒性。
| [1] |
SAARINEN J, ANDREASSON H, STOYANOV T, et al. Normal distributions transform Monte-Carlo localization(NDT-MCL)[C]//2013 IEEE/RSJ International Conference on Intelligent Robots and Systems. Tokyo, Japan, 2013:382-389.
( 0) 0)
|
| [2] |
VALENCIA R, SAARINEN J, ANDREASSON H, et al. Localization in highly dynamic environments using dual-timescale NDT-MCL[C]//2014 IEEE International Conference on Robotics and Automation (ICRA). Hong Kong, China, 2014:3956-3962.
( 0) 0)
|
| [3] |
RÖWEKÄMPER J, SPRUNK C, TIPALDI G D, et al. On the position accuracy of mobile robot localization based on particle filters combined with scan matching[C]//2012 IEEE/RSJ International Conference on Intelligent Robots and Systems. Vilamoura, Portugal, 2012:3158-3164.
( 0) 0)
|
| [4] |
DELLAERT F, FOX D, BURGARD W, et al. Monte Carlo localization for mobile robots[C]//Proceedings of the 1999 IEEE International Conference on Robotics and Automation. Detroit, USA, 1999:1322-1328.
( 0) 0)
|
| [5] |
CENSI A. An ICP variant using a point-to-line metric[C]//2008 IEEE International Conference on Robotics and Automation. Pasadena, USA, 2008:19-25.
( 0) 0)
|
| [6] |
王炜. 移动机器人的可定位估计及其应用[D]. 上海: 上海交通大学, 2012: 21-43. WANG Wei. Localizability estimation for mobile robot and its application[D]. Shanghai:Shanghai JiaoTong University, 2012:21-43. (  0) 0)
|
| [7] |
苗少帅, 周峰. IMM迭代无迹Kalman粒子滤波目标跟踪算法[J]. 重庆邮电大学学报:自然科学版, 2015, 27(01): 44-48. MIAO Shaoshuai, ZHOU Feng. IMM iterated unscented Kalman particle filter algorithm for target tracking[J]. Journal of Chongqing university of posts and telecommunications:natural science edition, 2015, 27(01): 44-48. (  0) 0)
|
| [8] |
张闯, 郭晨. 二阶自适应权值粒子滤波的多传感器信息融合[J]. 哈尔滨工程大学学报, 2016, 37(10): 1347-1352. ZHANG Chuang, GUO Chen. Multi-sensor information fusion of a particle filter on the basis of a two-stage adaptive weight[J]. Journal of Harbin engineering university, 2016, 37(10): 1347-1352. (  0) 0)
|
| [9] |
段鹏. 与人共融的家庭服务机器人定位与导航[D]. 济南: 山东大学, 2015: 39-58. DUAN Peng. Localization and navigation of home service robot in considering of human-robot harmony[D]. Ji'nan, China:Shandong University, 2015:39-58. http://cdmd.cnki.com.cn/Article/CDMD-10422-1015368638.htm (  0) 0)
|
| [10] |
CHOI W, PANTOFARU C, SAVARESE S. Detecting and tracking people using an RGB-D camera via multiple detector fusion[C]//2011 IEEE International Conference on Computer Vision Workshops. Barcelona, Spain, 2011:1076-1083.
( 0) 0)
|
| [11] |
SPINELLO L, ARRAS K O. People detection in RGB-D data[C]//2011 IEEE/RSJ International Conference on Intelligent Robots and Systems. San Francisco, USA, 2011:3838-3843.
( 0) 0)
|
| [12] |
王勇, 陈卫东, 王景川, 等. 面向拥挤环境的移动机器人改进粒子滤波定位[J]. 机器人, 2012, 34(5): 596-603. WANG Yong, CHEN Weidong, WANG Jingchuan, et al. Improved particle filter localization in crowded environments for mobile Robots[J]. Robot, 2012, 34(5): 596-603. (  0) 0)
|
| [13] |
CENSI A. On achievable accuracy for range-finder localization[C]//2007IEEE International conference on Robotics and Automation. Roma, Italy, 2007:4170-4175.
( 0) 0)
|
| [14] |
DALAL N, TRIGGS B. Histograms of oriented gradients for human detection[C]//2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. San Diego, USA, 2005:886-893.
( 0) 0)
|
| [15] |
ROS[EB/OL].[2016-05-14].http://wiki.ros.org/.
( 0) 0)
|
| [16] |
RUSU R B, COUSINS S. 3D is here:Point Cloud Library (PCL)[C]//2011 IEEE International Conference on Robotics and Automation (ICRA). Shanghai, China, 2011:1-4.
( 0) 0)
|
| [17] |
MUNARO M, et al. News articles[EB/OL].[2016-04-26]. http://www.pointclouds.org/news/.
( 0) 0)
|
| [18] |
GERKEY B. Gmapping[EB/OL].[2016-06-18]. wiki.ros.org/gmapping.
( 0) 0)
|
 2017, Vol. 12
2017, Vol. 12


