2. 宿迁学院 信息工程学院,江苏 宿迁 223800;
3. 西华大学 制造与自动化省高校重点实验室,四川 成都 610039;
4. 华中科技大学 数字制造装备与技术国家重点实验室,湖北 武汉 430074;
5. 安徽理工大学 煤矿安全高效开采省部共建教育部重点实验室,安徽 淮南232001
2. School of Information Engineering, Suqian College, Suqian 223800, China;
3. Key Laboratory of Manufacturing & Automation, Xihua University, Chengdu 610039, China;
4. State Key Laboratory of Digital Manufacturing Equipment & Technology, Huazhong University of Science and Technology, Wuhan 430074, China;
5. Key Laboratory of Safety and High-efficiency Coal Mining, Ministry of Education, Anhui University of Science and Technology, Huainan, 232001, China
阈值分割[1-4]因为简单有效且快速实用,可广泛应用于刀具磨损、火焰、工业CT等一系列机器视觉检测领域。其关键是依据目标和背景在图像中的不同灰度信息,快速确定最佳阈值,将图像中感兴趣的目标从背景中提取出来,从而得到清晰的边缘。其中以熵为准则的方法是国内外众多学者的研究热点之一[5-9],Kapur等最早将熵的定义引入阈值选取,提出了一维最大Shannon熵法,后续学者们又提出以Arimoto熵[10]、Tsallis熵[11-13] 、Renyi熵[14-17]为准则的阈值分割方法。文献[14-15]利用基于灰度级和邻域平均灰度级的二维直方图,只考虑在对角线上其他区域的目标和背景的有用信息,获得的最佳阈值存在误差,会产生目标点和背景点的错分,最终影响图像的分割效果。文献[14-17]所述的4种方法均是基于二维Renyi熵法,只利用图像灰度级出现的概率信息,而忽略了图像类内灰度均匀性,必然会造成某些图像的分割质量欠佳。与一维Renyi熵法相比,分割精度有所提高,但运行时间增加。为了降低运行时间,引入了快速递推公式[14, 17],使总运算量由
基于上述分析,本文提出了一种基于混沌布谷鸟优化(chaotic cuckoo search optimization,CCSO)的二维Renyi灰度熵图像阈值选取方法。该方法全面利用像素的灰度信息和邻域梯度信息,构建了图像的二维直方图,推导出二维Renyi灰度熵阈值选取公式,与上述的二维Renyi熵法相比,避免因直方图的近似假设而造成分割结果不准确。然后,在计算适应度函数时引入快速递推算法,以降低适应度函数的运算时间。最后,利用Tent映射产生的混沌序列对布谷鸟算法进行优化,用改进后的布谷鸟算法来搜索二维Renyi灰度熵的最佳阈值,大大提高搜索速度。本文方法与二维Arimoto熵法[10]、基于粒子群优化(PSO)的二维Renyi熵法[15]、基于混沌粒子群优化(chaotic particle swarm optimization,CPSO)的二维Tsallis灰度熵法[12]、基于布谷鸟算法(CS)的二维Renyi灰度熵法相比,在分割结果和运算时间上均具有明显的优势。
1 一维Renyi灰度熵阈值选取方法现有大小为
令
| ${p_{x,y}} = \left\{ {\begin{array}{*{20}{c}}{\displaystyle\frac{{f\left( {x,y} \right)}}{{\displaystyle\sum\limits_{\left( {m,n} \right) \in {D_{\rm{o}}}} {f\left( {m,n} \right)} }}\begin{array}{*{20}{c}},&{\left( {x,y} \right) \in {D_{\rm{o}}}}\end{array}}\\[23pt]{\displaystyle\frac{{f\left( {x,y} \right)}}{{\displaystyle\sum\limits_{\left( {m,n} \right) \in {D_{\rm{b}}}} {f\left( {m,n} \right)} }}\begin{array}{*{20}{c}},&{\left( {x,y} \right) \in {D_{\rm{b}}}}\end{array}}\end{array}} \right.$ |
则目标类的Renyi灰度熵
| $\begin{array}{c}H_{\rm{o}}^\alpha \left( t \right) =\displaystyle \frac{1}{{1 - \alpha }}\ln \sum\limits_{\left( {x,y} \right) \in {D_{\rm{o}}}} {{{\left( {{p_{x,y}}} \right)}^\alpha }} = \\[15pt]\displaystyle\frac{1}{{1 - \alpha }}\ln \sum\limits_{i = 0}^t {h\left( i \right){{\left( {\frac{i}{{\displaystyle\sum\limits_{i' = 0}^t {h\left( {i'} \right)i'} }}} \right)}^\alpha }} \end{array}$ | (1) |
同理,可以得到背景类的Renyi灰度熵
| $H_{\rm{b}}^\alpha \left( t \right) = \frac{1}{{1 - \alpha }}\ln \sum\limits_{i = t + 1}^{L - 1} {h\left( i \right){{\left( {\displaystyle\frac{i}{{\displaystyle\sum\limits_{i' = t + 1}^{L - 1} {h\left( {i'} \right)i'} }}} \right)}^\alpha }} $ | (2) |
由此可得目标类和背景类的总Renyi灰度熵为
| $\begin{array}{c}{H^\alpha }\left( t \right) = H_{\rm{o}}^\alpha \left( t \right) + H_{\rm{b}}^\alpha \left( t \right) = \\[7pt]\displaystyle\frac{1}{{1 - \alpha }}\ln \displaystyle\sum\limits_{i = 0}^t {h\left( i \right){{\left( {\displaystyle\frac{i}{{\displaystyle\sum\limits_{i' = 0}^t {h\left( {i'} \right)i'} }}} \right)}^\alpha }} {\rm{ + }}\\[30pt]\displaystyle\frac{1}{{1 - \alpha }}\ln \displaystyle\sum\limits_{i = t + 1}^{L - 1} {h\left( i \right){{\left( {\displaystyle\frac{i}{{\displaystyle\sum\limits_{i' = t + 1}^{L - 1} {h\left( {i'} \right)i'} }}} \right)}^\alpha }} \end{array}$ | (3) |
当图像的总Renyi灰度熵越大,目标和背景的类内灰度越趋于均匀,因此最佳阈值
| ${t^*} = \arg \mathop {\max }\limits_{0 \leqslant t \leqslant L - 1} \left\{ {{H^\alpha }\left( t \right)} \right\}$ | (4) |
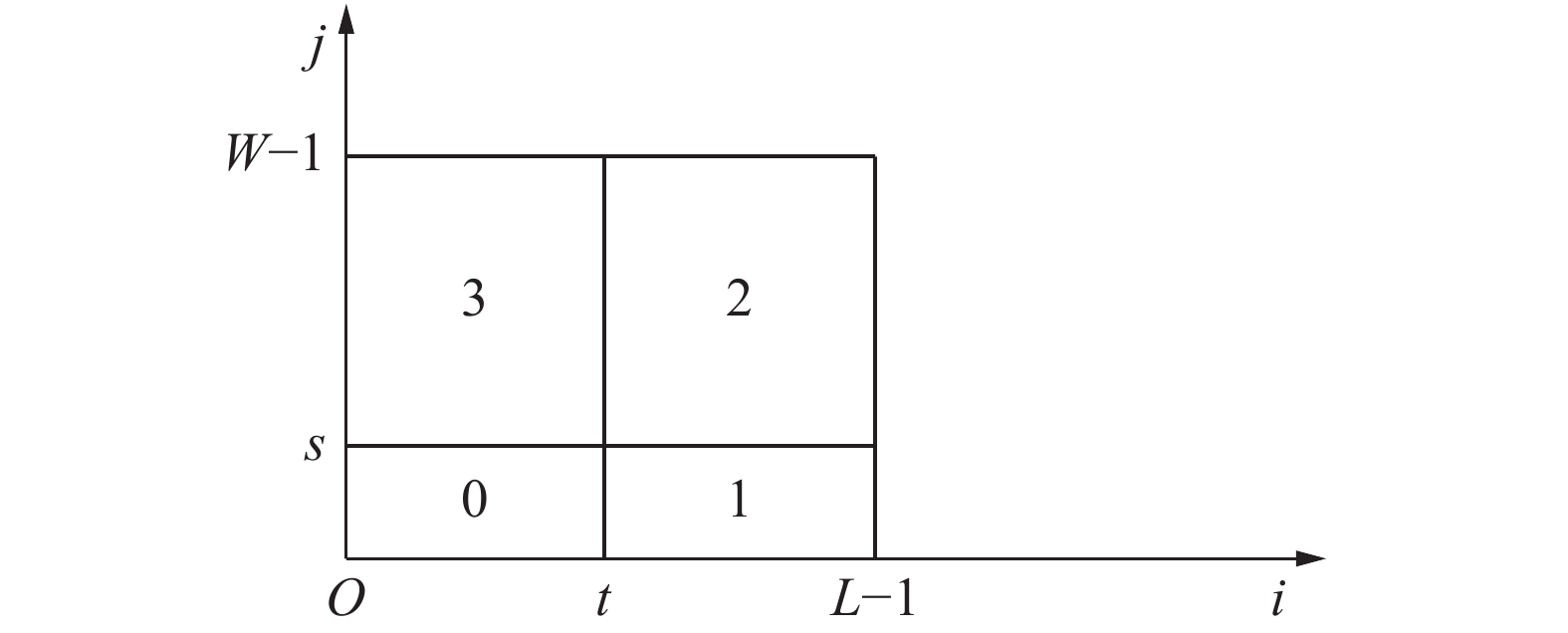
一幅
式中:
| ${D_{\rm{o}}} = \left\{ {\left( {i,j} \right)\left| {i = 0,1, \cdots \! ,t;} \right.} \right.\left. {j = 0,1, \cdots \! ,W - 1} \right\}$ |
背景类为
| ${D_{\rm{b}}} = \left\{ {\left( {i,j} \right)} \right.\left| {i = t + 1,} \right.t{\rm{ + }}2, \cdots \! ,L - 1;j = 0,1, \cdots \! ,\left. {W - 1} \right\}$ |
|
Download:
|
| 图 1 灰度-梯度二维直方图 Fig. 1 Gray-gradient two-dimensional histogram | |
将式(2)和式(3)推广到二维,则目标类和背景类的二维Renyi灰度熵
| ${{\mathit{\boldsymbol{H}}}_{\rm{o}}^\alpha \left( {t,s} \right) = {{\left[ {{\mathit{\boldsymbol{H}}}_{{\rm{o}}i}^\alpha \left( {t,s} \right)\,\,{\mathit{\boldsymbol{H}}}_{{\rm{o}}j}^\alpha \left( {t,s} \right)} \right]}^{\rm{T}}} = }\\[8pt]{\left[ {\displaystyle\frac{1}{{1 - \alpha }}\ln \sum\limits_{j = 0}^s {\sum\limits_{i = 0}^t {h\left( {i,j} \right){{\left( {\displaystyle\frac{i}{{\displaystyle\sum\limits_{j' = 0}^s {\displaystyle\sum\limits_{i' = 0}^t {h\left( {i',j'} \right)i'} } }}} \right)}^\alpha }} } } \right.}{{{\left. {\displaystyle\frac{1}{{1 - \alpha }}\ln \sum\limits_{j = 0}^s {\sum\limits_{i = 0}^t {h\left( {i,j} \right){{\left( {\frac{j}{{\displaystyle\sum\limits_{j' = 0}^s {\sum\limits_{i' = 0}^t {h\left( {i',j'} \right)j'} } }}} \right)}^\alpha }} } } \right]}^{\rm{T}}}}$ | (5) |
| ${{\mathit{\boldsymbol{H}}}_{\rm{b}}^\alpha \left( {t,s} \right) = {{\left[ {{\mathit{\boldsymbol{H}}}_{{\rm{b}}i}^\alpha \left( {t,s} \right)\,\,{\mathit{\boldsymbol{H}}}_{{\rm{b}}j}^\alpha \left( {t,s} \right)} \right]}^{\rm{T}}} = }\\[8pt]{\left[ {\displaystyle\frac{1}{{1 - \alpha }}\ln \sum\limits_{j = 0}^s {\sum\limits_{i = t + 1}^{L - 1} {h\left( {i,j} \right){{\left( {\frac{i}{{\displaystyle\sum\limits_{j' = 0}^s {\sum\limits_{i' = t + 1}^{L - 1} {h\left( {i',j'} \right)i'} } }}} \right)}^\alpha }} } } \right.}{{{\left. {\displaystyle\frac{1}{{1 - \alpha }}\ln \displaystyle\sum\limits_{j = 0}^s {\sum\limits_{i = t + 1}^{L - 1} {h\left( {i,j} \right){{\left( {\frac{j}{{\displaystyle\sum\limits_{j' = 0}^s {\sum\limits_{i' = t + 1}^{L - 1} {h\left( {i',j'} \right)j'} } }}} \right)}^\alpha }} } } \right]}^{\rm{T}}}}$ | (6) |
则基于灰度-梯度的二维Renyi灰度熵的图像阈值选取准则函数为
| $\begin{array}{c}\varphi \left( {t,s} \right) = {\mathit{\boldsymbol{H}}}_{\rm{o}}^\alpha \left( {t,s} \right) + {\mathit{\boldsymbol{H}}}_{\rm{b}}^\alpha \left( {t,s} \right) = \\[8pt]\displaystyle\frac{1}{{1 - \alpha }}\ln \frac{{\displaystyle\sum\limits_{j = 0}^s {\sum\limits_{i = 0}^t {h\left( {i,j} \right){i^\alpha }} } }}{{{{\left[ {\displaystyle\sum\limits_{j' = 0}^s {\displaystyle\sum\limits_{i' = 0}^t {h\left( {i',j'} \right)i'} } } \right]}^\alpha }}} + \\[42pt]\displaystyle\frac{1}{{1 - \alpha }}\ln \frac{{\displaystyle\sum\limits_{j = 0}^s {\displaystyle\sum\limits_{i = 0}^t {h\left( {i,j} \right){j^\alpha }} } }}{{{{\left[ {\displaystyle\sum\limits_{j' = 0}^s {\sum\limits_{i' = 0}^t {h\left( {i',j'} \right)j'} } } \right]}^\alpha }}} + \\[42pt]\displaystyle\frac{1}{{1 - \alpha }}\ln \frac{{\displaystyle\sum\limits_{j = 0}^s {\displaystyle\sum\limits_{i = t + 1}^{L - 1} {h\left( {i,j} \right){i^\alpha }} } }}{{{{\left[ {\displaystyle\sum\limits_{j' = 0}^s {\displaystyle\sum\limits_{i' = t + 1}^{L - 1} {h\left( {i',j'} \right)i'} } } \right]}^\alpha }}} + \\[42pt]\displaystyle\frac{1}{{1 - \alpha }}\ln \frac{{\displaystyle\sum\limits_{j = 0}^s {\sum\limits_{i = t + 1}^{L - 1} {h\left( {i,j} \right){j^\alpha }} } }}{{{{\left[ {\displaystyle\sum\limits_{j' = 0}^s {\sum\limits_{i' = t + 1}^{L - 1} {h\left( {i',j'} \right)j'} } } \right]}^\alpha }}}\end{array}$ | (7) |
令
| $\begin{array}{c}{u_{{\rm{o}}i}}\left( {t,s} \right) = \displaystyle\sum\limits_{j = 0}^s {\sum\limits_{i = 0}^t {h\left( {i,j} \right){i^\alpha }} } \\[25pt]{u_{{\rm{o}}j}}\left( {t,s} \right) = \displaystyle\sum\limits_{j = 0}^s {\sum\limits_{i = 0}^t {h\left( {i,j} \right){j^\alpha }} } \\[25pt]{u_{{\rm{b}}i}}\left( {t,s} \right) = \displaystyle\sum\limits_{j = 0}^s {\sum\limits_{i = t + 1}^{L - 1} {h\left( {i,j} \right){i^\alpha }} } \\[25pt]{u_{{\rm{b}}j}}\left( {t,s} \right) = \displaystyle\sum\limits_{j = 0}^s {\sum\limits_{i = t + 1}^{L - 1} {h\left( {i,j} \right){j^\alpha }} } \\[25pt]{v_{{\rm{o}}i}}\left( {t,s} \right) = \displaystyle\sum\limits_{j' = 0}^s {\sum\limits_{i' = 0}^t {h\left( {i',j'} \right)i'} } \\[25pt]{v_{{\rm{o}}j}}\left( {t,s} \right) = \displaystyle\sum\limits_{j' = 0}^s {\sum\limits_{i' = 0}^t {h\left( {i',j'} \right)j'} } \\[25pt]{v_{{\rm{b}}i}}\left( {t,s} \right) = \displaystyle\sum\limits_{j' = 0}^s {\sum\limits_{i' = t + 1}^{L - 1} {h\left( {i',j'} \right)i'} } \\[25pt]{v_{{\rm{b}}j}}\left( {t,s} \right) = \displaystyle\sum\limits_{j' = 0}^s {\sum\limits_{i' = t + 1}^{L - 1} {h\left( {i',j'} \right)j'} } \end{array}$ |
那么有
| $\begin{array}{c}\varphi \left( {t,s} \right) = \displaystyle\frac{1}{{1 - \alpha }}\left( {\ln \displaystyle\frac{{{u_{{\rm{o}}i}}\left( {t,s} \right)}}{{v_{{\rm{o}}i}^\alpha \left( {t,s} \right)}}} \right. + \ln \displaystyle\frac{{{u_{{\rm{o}}j}}\left( {t,s} \right)}}{{v_{{\rm{o}}j}^\alpha \left( {t,s} \right)}} + \\[10pt]\left. {\ln \displaystyle\frac{{{u_{{\rm{b}}i}}\left( {t,s} \right)}}{{v_{{\rm{b}}i}^\alpha \left( {t,s} \right)}} + \ln \displaystyle\frac{{{u_{{\rm{b}}j}}\left( {t,s} \right)}}{{v_{{\rm{b}}j}^\alpha \left( {t,s} \right)}}} \right)\end{array}$ | (8) |
当函数
| $\left( {{t^{\rm{*}}},{s^*}} \right) = \arg \mathop {\max }\limits_{0 \leqslant t \leqslant L - 1,\,0 \leqslant s \leqslant L - 1} \left\{ {\varphi \left( {t,s} \right)} \right\}$ | (9) |
为进一步提高二维Renyi灰度熵法的运算效率,可采用快速递推方法计算式(9)的中间参量
| $\begin{array}{l}\left\{ {\begin{array}{*{20}{c}}\!\!\!\!\!\!\! {{u_{{\rm{o}}i}}\left( {0,0} \right) = 0\begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{}&{}\end{array}}&{}\end{array}}&{}\end{array}}&{}&{}&{}\end{array}\begin{array}{*{20}{c}}{}\end{array}}\\{{u_{{\rm{o}}i}}\left( {t,0} \right) = {u_{{\rm{o}}i}}\left( {t - 1,0} \right) + h\left( {t,0} \right){t^\alpha }\begin{array}{*{20}{c}}{}\end{array}\begin{array}{*{20}{c}}{}\end{array}\begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{}\end{array}}\end{array}}\\\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! {{u_{{\rm{o}}i}}\left( {0,s} \right) = {u_{{\rm{o}}i}}\left( {0,s - 1} \right) + h\left( {0,s} \right) \times 0\begin{array}{*{20}{c}}{}\end{array}}\\\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! {{u_{{\rm{o}}i}}\left( {t,s} \right) = {u_{{\rm{o}}i}}\left( {t,s - 1} \right) + {u_{{\rm{o}}i}}\left( {t - 1,s} \right) - }\end{array}} \right.\\\begin{array}{*{20}{c}}{}&{}&{}&{}\end{array}{u_{{\rm{o}}i}}\left( {t - 1,s - 1} \right) + h\left( {t,s} \right)t\end{array}$ | (10) |
其他7个中间参量,即
布谷鸟算法是模拟布谷鸟通过寻找寄生巢来确定最佳寄生巢的智能算法。为了方便操作,Yang等将布谷鸟的巢寄生过程假设为以下的3种理想状态:
1) 1只布谷鸟1次只能产1枚蛋,并随机选择寄生巢来放置鸟蛋;
2) 在选择寄生巢的过程中,只有最佳的寄生巢被保留到下一代;
3) 可用来放蛋的寄生巢数量是固定的,寄生巢主人发现外来蛋的概率是p0。
在假设的3种理想状态下,布谷鸟算法利用式(12)完成对寄生巢位置的迭代更新。
| $X_i^{t + 1} = X_i^t + \beta \oplus L\left( \lambda \right),1 \leqslant i \leqslant n$ | (12) |
式中:
设搜索空间的维数为d,需要求解的目标函数为
1) 设置算法的相关参数:种群大小、维数、最大发生概率p0和最大迭代次数等;种群初始化,随机产生n个d维寄生巢位置
2) 利用适应度函数计算每个鸟巢的适应度值,得到当前整个鸟巢的最优解。
3) 记录上一代的最佳鸟巢位置,利用式(12)完成其他鸟巢的位置更新。
4) 将新的鸟巢位置与上一代最佳鸟巢位置进行比较,若更优,则作为当前最佳鸟巢位置。
5) 经过位置更新后,将随机产生数
6) 若达到最大迭代次数,则执行7);否则,返回执行2)。
7) 输出全局最佳鸟巢位置。
3.2 二维Renyi灰度熵阈值选取的混沌布谷鸟优化算法步骤将混沌扰动的理念引入布谷鸟优化算法,借助混沌序列的遍历性和随机性完成最佳阈值搜寻,可提高算法的精度和收敛速度。由于Tent映射的遍历性和寻优效果相对较高,本文将基于Tent映射的混沌迭代扰动和布谷鸟算法相结合应用于二维Renyi灰度熵阈值选取。
Tent映射方程为
| ${x_n} = \left\{ {\begin{array}{*{20}{c}}{\displaystyle\frac{{{x_n}}}{{0.7}}\begin{array}{*{20}{c}},&{0 < {x_n} \leqslant 0.7}\end{array}}\\[8pt]{\displaystyle\frac{{1 - {x_n}}}{{0.3}}\begin{array}{*{20}{c}},&{0.7 < {x_n} \leqslant 1}\end{array}}\end{array}} \right.$ | (13) |
为了提升搜索精度,对位置最优的寄生巢采用混沌扰动算子进行变异,用混沌扰动后产生较优的位置代替原位置,即
| $\left\{ {\begin{array}{*{20}{c}}{{R_d} = \beta \left| {\displaystyle\frac{1}{n}\sum\limits_{j = 0}^n {\mathit{\boldsymbol{x}}_{j,d}^k - \mathit{\boldsymbol{x}}_{{\rm{hb}},d}^k} } \right|\begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{}&{}\end{array}}&{}\end{array}}\\[10pt]{\begin{array}{*{20}{c}}\!\!\!\!\!\!\!\!\!\!{\mathit{\boldsymbol{x}}_{{\rm{nb}},d}^k = \mathit{\boldsymbol{x}}_{{\rm{hb}},d}^k + {R_d}\left( {2{{\mathit{\boldsymbol{x}}}_d}\left( i \right) - 1} \right)}&{}\end{array}}\end{array}} \right.$ | (14) |
式中:
混沌布谷鸟优化算法的具体步骤如下:
1)种群参数设置。最大迭代次数
2)利用式(6)~(11)计算各寄生巢的适应度函数值,确定当前寄生巢最优位置及其适应度函数值。
3)寄生巢的位置按式(12)完成更新,得到新的寄生巢位置,计算各寄生巢位置的适应度函数值,并进行比较,更新寄生巢的历史最优位置。
4)比较随机产生数
5)按式(13)、式(14)对最优位置寄生巢执行混沌扰动,与扰动之前的寄生巢位置比较,记录最优寄生巢位置。
6)对迭代次数t做出判断,当
7)输出Renyi灰度熵的最优阈值
运用提出的基于CCSO的二维Renyi灰度熵阈值法对各种图像进行实验,并与二维Arimoto熵法[10]、PSO的二维Renyi熵法[15]、CPSO的二维Tsallis灰度熵法[12]、基于CS的二维Renyi灰度熵法在分割结果和运行时间上进行比较。图2~5以刀具磨损图像(327×156)、狒狒图像(512×512)、工业CT图像(371×300)、模糊火焰图像(468×369)为例,给出5种阈值选取方法的分割结果。基于PSO的二维Renyi熵法和基于CPSO的二维Tsallis灰度熵法的粒子群数均为20,最大迭代次数为50;基于CS的二维Renyi灰度熵法的最大迭代次数为50,种群规模为30个,概率
如图2所示,二维Arimoto熵法无法将刀具磨损区域从正常区域中分割出来,故没有得到磨损区域的边缘;基于PSO的二维Renyi熵法、基于CPSO的二维Tsallis灰度熵法、基于CS的二维Renyi灰度熵法虽然能检测出磨损区域,但仍存在大量正常区域的边界;本文方法较好地分割出磨损区域,轮廓清晰,并分割出了较小的磨损区域。

|
Download:
|
| 图 2 刀具图像及分割结果 Fig. 2 Tool wear image and segmentation results | |
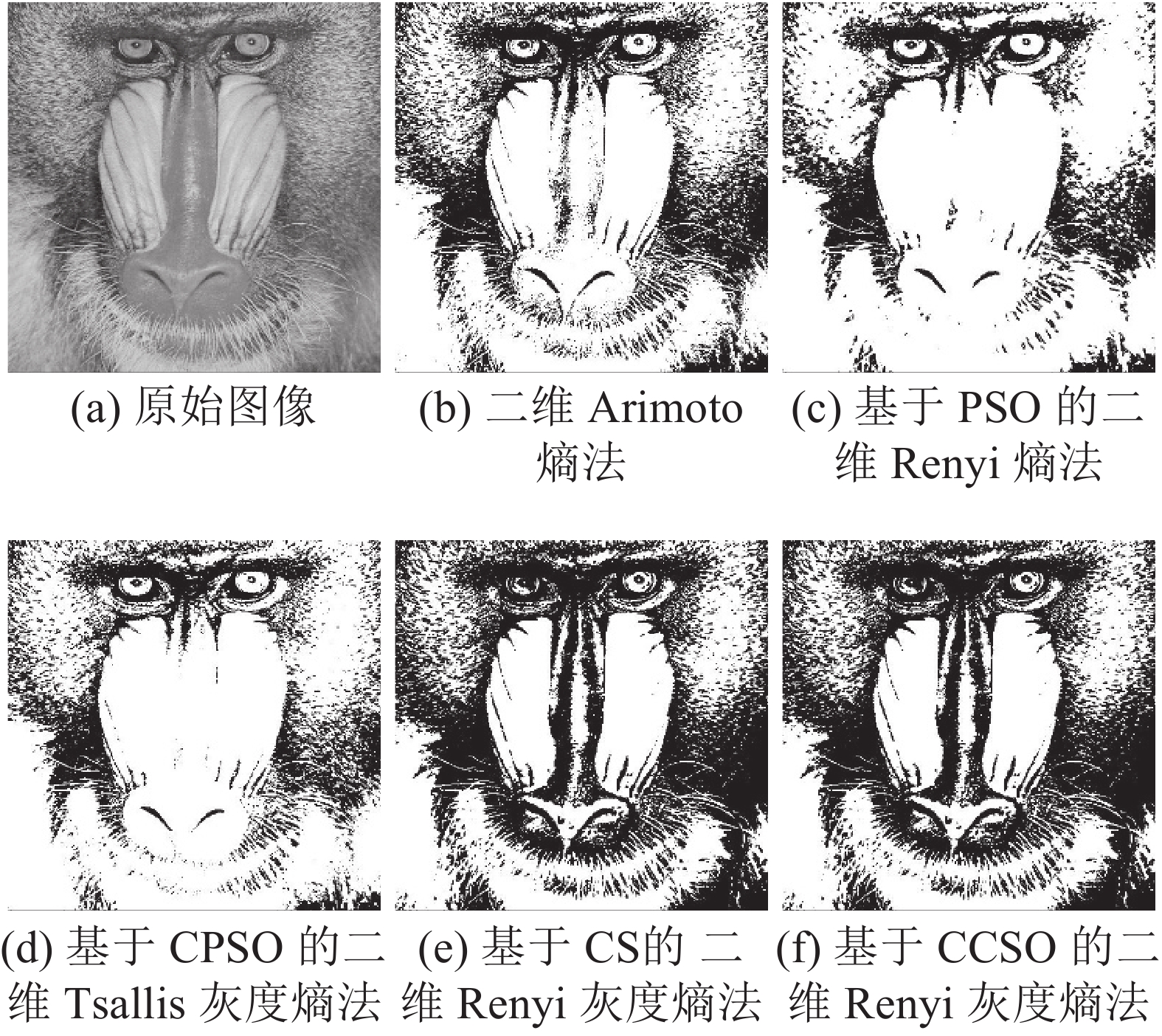
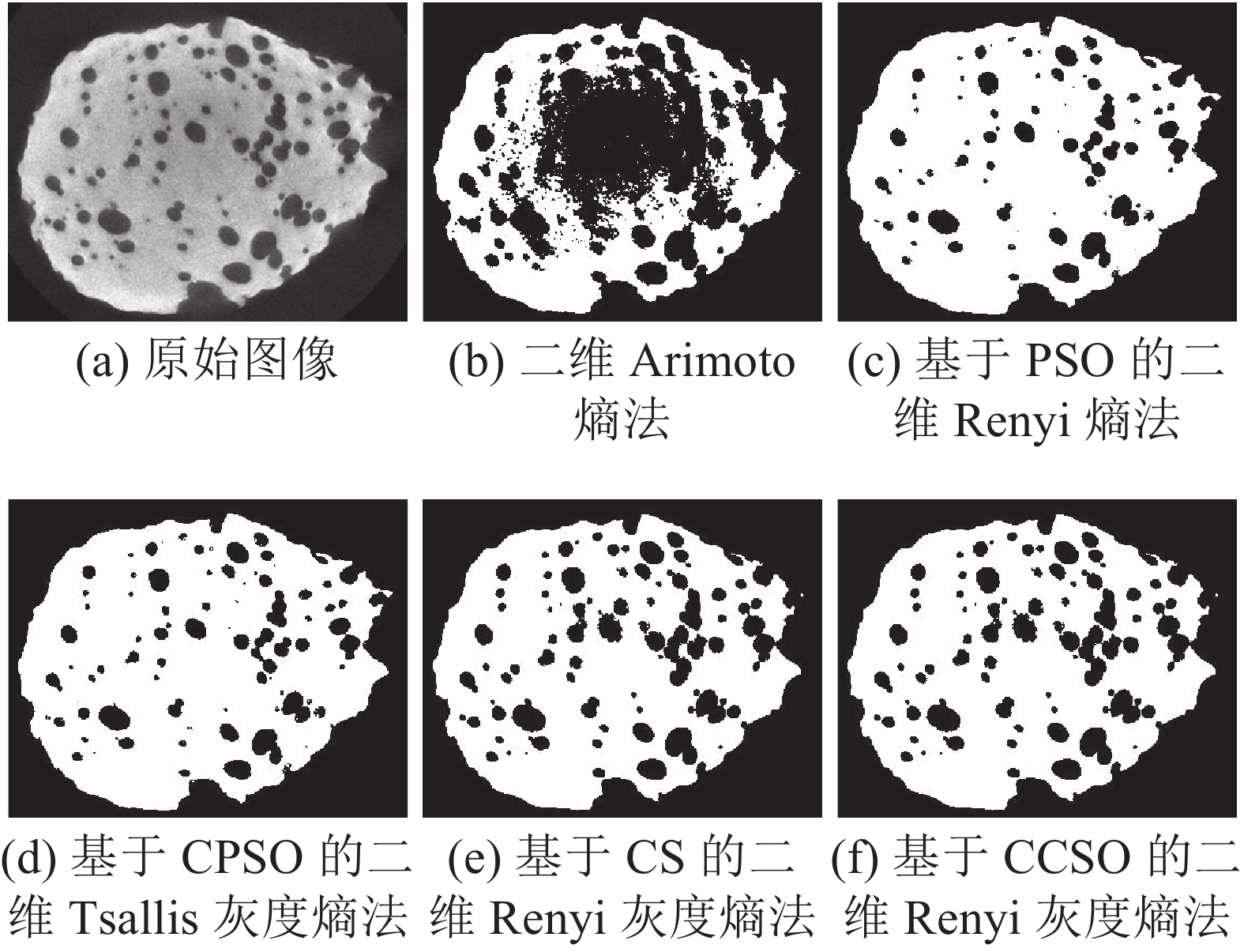
图3所示狒狒图像,Renyi灰度熵提取的狒狒鼻子和胡须清晰可见,细节信息丰富;而其他3种方法均在不同程度上丢失了部分信息。如图4所示,二维Arimoto熵法的分割结果中存在大量虚警目标,图4(b)中部有大量阴影,覆盖CT图像的部分信息。基于PSO的二维Renyi熵法和基于CPSO的二维Tsallis灰度熵法降低了虚警率,但物体的外边界和内部空洞轮廓不够清晰,如图4(c)、(e),空洞边界不清晰且尺寸变小,部分孔洞未被分割出来,不利于后续的检测和识别。基于CS的二维Renyi灰度熵法和本文方法在减少虚警目标的同时准确地分割出物体的外围轮廓及内部空洞的边界。由图5可以看出,基于PSO的二维Renyi熵法和二维Arimoto熵法分割出的火焰轮廓均不够准确,而二维Arimoto熵法还丢失了左上方的火焰目标;基于CPSO的二维Tsallis灰度熵法、基于CS的二维Renyi灰度熵法、本文提出的方法分割得到的火焰边界清晰准确。
|
Download:
|
| 图 3 狒狒图像及分割结果 Fig. 3 Baboon image and segmentation results | |
|
Download:
|
| 图 4 工业CT图像及分割结果 Fig. 4 Industrial CT image and segmentation results | |

|
Download:
|
| 图 5 火焰图像及分割结果 Fig. 5 Flame image and segmentation results | |
图像分割的好坏运用区域内部均匀性测度来做定量评价。均匀性测度的大小决定阈值分割方法的优劣,得到均匀测度值越大,分割质量越高。表1列出了上述5种分割算法相应的均匀测度值的比较。由表可见,本文方法的测度值高于其他方法,其分割质量相对更高。综合上述分析,本文提出的基于CCSO的二维Renyi灰度熵图像阈值选取方法具有较强的普适性,分割后的目标边缘准确,细节丰富。对于磨损细节丰富的刀具图像、边缘模糊的火焰图像和孔洞大小不均的工业CT图像,均得到很好的分割效果,对后续的刀具磨损检测、火焰的识别和工业CT的无损检测具有很大的积极意义。
| 表 1 5种阈值分割方法的均匀测度值对比 Tab.1 Uniformity comparisons of five thresholding methods |
表2给出了5种阈值分割方法的最佳阈值和运行时间。由表2可见,本文提出的基于CCSO的二维Renyi灰度熵图像阈值选取方法运行时间明显缩短,比二维Arimoto熵法、基于CPSO的二维Tsallis灰度熵法、基于CS的二维Renyi灰度熵法的运行时间平均节省30%左右,比基于PSO的二维Renyi熵法的运行时间节省80%左右。
| 表 2 5种阈值分割方法的最佳阈值及运行时间 Tab.2 Optimal thresholds and running times of five thresholding methods |
本文提出了混沌布谷鸟优化的二维Renyi灰度熵阈值选取方法。Renyi灰度熵考虑了图像类内灰度均匀性,使得图像目标和背景总的Renyi灰度熵变大,从而改善图像的分割效果。采用灰度-梯度直方图完成目标和背景区域划分,根据Renyi灰度熵的定义导出二维Renyi灰度熵阈值选取方法,避免了图像噪声点和边界点对分割的干扰,有效地提高了抗噪性能。同时引入Tent映射的混沌序列对布谷鸟算法进行优化,在计算适应度函数值时采用快速递推算法,具有较快的收敛速度。与其他方法相比,本文方法提取的图像边界完整,纹理细节清晰,运算时间明显减少。
| [1] |
MEHMET S, BULENT S. Survey over image thresholding techniques and quantitative performance evaluation[J]. Journal of electronic imaging, 2004, 13(1): 146-165. DOI:10.1117/1.1631315 ( 0) 0)
|
| [2] |
吴一全, 孟天亮, 吴诗婳. 图像阈值分割方法研究进展20年(1994—2014)[J]. 数据采集与处理, 2015, 30(01): 1-23. WU Yiquan, MENG Tianliang, WU Shihua. Research progress of image thresholding methods in recent 20 years (1994-2014)[J]. Journal of data acquisition and processing, 2015, 30(01): 1-23. (  0) 0)
|
| [3] |
吴一全, 孟天亮, 王凯. 基于斜分倒数交叉熵和蜂群优化的火焰图像阈值选取[J]. 光学精密工程, 2014, 22(1): 235-243. WU Yiquan, MENG Tianliang, WANG Kai. Threshold selection of flame image based on reciprocal cross entropy and bee colony optimization[J]. Optics and precision engineering, 2014, 22(1): 235-243. (  0) 0)
|
| [4] |
吴一全, 张金矿. 二维直方图θ-划分最大平均离差阈值分割算法
[J]. 自动化学报, 2010, 36(5): 634-643. WU Yiquan, ZHANG Jinkuang. Image thresholding based on two-dimensional histogram θ-division and maximum between-cluster deviation criterion [J]. Acta automatica sinica, 2010, 36(5): 634-643. (  0) 0)
|
| [5] |
YIN Jun, WU Yiquan, ZHU Li. Multi-thresholding based on symmetric Tsallis-cross entropy and particle swarm optimization[J]. Advanced materials research, 2013, 760-762: 1457-1461. DOI:10.4028/www.scientific.net/AMR.760-762 ( 0) 0)
|
| [6] |
LIU Yaoyong, LI Shuguang. Two-dimensional arimoto entropy image thresholding based on ellipsoid region search strategy[C]//Proceedings of 2010 International Conference on Multimedia Technology. Ningbo, China, 2010: 1–4.
( 0) 0)
|
| [7] |
MAHMOUDI L, ZAART A E. A survey of entropy image thresholding techniques[C]//Proceedings of the 2nd International Conference on Advances in Computational Tools for Engineering Applications. Beirut, Lebanon, 2012: 204–209.
( 0) 0)
|
| [8] |
朱磊. 自适应阈值分割技术及在工业视觉检测中的应用[D]. 无锡: 江南大学, 2014. ZHU Lei. Adaptive threshold segmentation technology and its application in industrial visual inspection[D]. Wuxi: Jiangnan University, 2014. (  0) 0)
|
| [9] |
曹建农. 图像分割的熵方法综述[J]. 模式识别与人工智能, 2012, 25(6): 958-971. CAO Jiannong. Review on image segmentation based on entropy[J]. Pattern recognition and artificial intelligence, 2012, 25(6): 958-971. (  0) 0)
|
| [10] |
张弘, 范九伦. 二维Arimoto熵直线型阈值分割法[J]. 光子学报, 2013, 42(2): 234-240. ZHANG Hong, FAN Jiulun. Two-dimensional Arimoto entropy linear-type threshold segmentation method[J]. Acta photonica sinica, 2013, 42(2): 234-240. (  0) 0)
|
| [11] |
吴一全, 王凯, 曹鹏祥. 蜂群优化的二维非对称Tsallis交叉熵图像阈值选取[J]. 智能系统学报, 2015, 10(1): 103-112. WU Yiquan, WANG Kai, CAO Pengxiang. Two-dimensional asymmetric Tsallis cross entropy image threshold selection using bee colony optimization[J]. CAAI transactions on intelligent systems, 2015, 10(1): 103-112. (  0) 0)
|
| [12] |
吴一全, 吴诗婳, 张晓杰. 利用混沌PSO或分解的2维Tsallis灰度熵阈值分割[J]. 中国图象图形学报, 2012, 17(8): 902-910. WU Yiquan, WU Shihua, ZHANG Xiaojie. Two-dimensional Tsallis gray entropy image thresholding using chaotic particle swarm optimization or decomposition[J]. Journal of image and graphics, 2012, 17(8): 902-910. DOI:10.11834/jig.20120802 (  0) 0)
|
| [13] |
SARKAR S, DAS S. Multilevel image thresholding based on 2D histogram and maximum tsallis entropy—a differential evolution approach[J]. IEEE transactions on image processing, 2013, 22(12): 4788-4797. DOI:10.1109/TIP.2013.2277832 ( 0) 0)
|
| [14] |
潘喆, 吴一全. 二维Renyi熵图像阈值选取快速递推算法[J]. 中国体视学与图像分析, 2007, 12(2): 93-97. PAN Zhe, WU Yiquan. Fast recurring algorithms of image thresholding based on two-dimensional Renyi’s entropy[J]. Chinese journal of stereology and image analysis, 2007, 12(2): 93-97. (  0) 0)
|
| [15] |
顾晓清, 孙玉强, 侯振杰. 鲁棒的二维Renyi熵图像阈值分割快速算法[J]. 计算机科学, 2012, 39(9): 284-288. GU Xiaoqing, SUN Yuqiang, HOU Zhenjie. Fast robust thresholding method based on two-dimensional Renyi’s entropy[J]. Computer science, 2012, 39(9): 284-288. (  0) 0)
|
| [16] |
TEIXEIRA A, MATOS A, ANTUNES L. Conditional rényi entropies[J]. IEEE transactions on information theory, 2012, 58(7): 4273-4277. DOI:10.1109/TIT.2012.2192713 ( 0) 0)
|
| [17] |
雷博. 二维直线型Renyi熵阈值分割方法[J]. 西安邮电学院学报, 2010, 15(3): 19-22. LEI Bo. Two-dimensional thresholding method based on linear-type Renyi entropy[J]. Journal of Xi’an university of posts and telecommunications, 2010, 15(3): 19-22. (  0) 0)
|
| [18] |
YANG X S, DEB S. Cuckoo search via Lévy flights[C]//Proceedings of 2009 World Congress on Nature and Biologically Inspired Computing. Coimbatore, India, 2009: 210–214.
( 0) 0)
|
| [19] |
周欢, 李煜. 具有动态惯性权重的布谷鸟搜索算法[J]. 智能系统学报, 2015, 10(4): 645-651. ZHOU Huan, LI Yu. Cuckoo search algorithm with dynamic inertia weight[J]. CAAI transactions on intelligent systems, 2015, 10(4): 645-651. (  0) 0)
|
| [20] |
YANG X S, DEB S. Engineering optimisation by cuckoo search[J]. International journal of mathematical modelling and numerical optimisation, 2010, 1(4): 330-343. DOI:10.1504/IJMMNO.2010.035430 ( 0) 0)
|
 2018, Vol. 13
2018, Vol. 13

