2. 中国科学院 脑科学与智能技术卓越创新中心, 上海 200031
2. Center for Excellence in Brain Science and Intelligence Technology, Chinese Academy of Sciences, Shanghai 200031, China
心电信号是心脏电活动在体表的综合表现,心电信号诊断因可靠、简便、对患者无创等优点,临床应用十分广泛。然而心电信号在测量时不可避免地存在一些强干扰和噪声,如基线漂移、工频噪声、肌电噪声和环境噪声等[1]。如何有效排除各种噪声,准确提取出有用的心电信号波形,是临床心脏病智能诊断的重要基础。
心电信号的频率在0.05~100 Hz之间,其中90%的能量集中在0.25~35 Hz之间。而心电信号噪声主要有50 Hz/60 Hz及其谐波组成的工频干扰、5~2k Hz的肌电干扰以及频率小于0.5 Hz的基线漂移等[2]。目前常用的方法主要有形态学滤波法[3]、EMD分解法[4]、基于小波理论的小波阈值法[5-7]、小波熵阈值去噪法[8]以及相关方法的结合[9-10]等。形态学滤波法处理基线漂移效果完美,但处理高频噪声会产生阶段误差。基于EMD分解法能够对信号自适应地从高频到低频分解为固有模态函数,根据噪声一般分布的频段,直接舍弃某些高频分量和低频分量,在去掉噪声的同时也会去掉一部分原始信号。小波变换是一种信号的时间-频率分析方法,具有多分辨率的特征,去除心电噪声效果显著。小波阈值去噪法在计算噪声方差时,通常将最高一层高频小波系数看作噪声,求取其作为噪声方差,具有一定误差。文献[8]中的基于小波熵的去噪法,对高频小波系数进行处理,高频噪声去除效果良好,但忽略了低频近似系数的影响,基线漂移去除效果不理想。
针对以上问题,本文提出一种基于相关性的小波熵心电信号去噪方法。首先对信号进行小波分解,对基线漂移,通过置零近似系数去除;对肌电噪声和工频噪声,需要在高频小波系数中对信号和噪声进行区分,利用各尺度间有效信号和噪声相关性不同的特性,对高频小波系数进行相关性处理,将有效信号和噪声分离,从而利用噪声计算小波熵阈值。最后将置零的近似系数和各尺度阈值处理后的高频系数进行重构,得到去噪信号。算法充分利用不同类型的噪声特性,能够在一次小波分解、重构的过程中同时滤除心电信号的3种主要噪声,且根据信号能量自适应地选取阈值的方式,能够在提高信噪比的同时更好地保护有效信号。本文最后利用MIT-BIH标准心电数据库等检验了所提算法,仿真实验结果表明,算法复杂度低,且去噪效果显著优于目前典型的心电去噪算法。
1 小波阈值去噪算法假设含噪信号由式(1)表示:
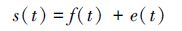 |
(1) |
式中:t为时间序列,t=1,2,…,N,s(t)为含噪信号;f(t)为原始信号,e(t)为噪声。
小波变换是一种信号的多尺度分析方法,离散小波分解通过Mallet算法[11]实现,如式(2)。
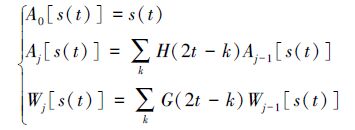 |
(2) |
式中:s(t)为原始信号;j为分解层数;H、G为小波分解滤波器系数;Aj为信号在层的近似部分(即低频部分)的近似系数;Wj为信号s(t)在第j层的细节系数(即高频部分)的小波系数。
小波去噪的根本任务是在小波域将信号的小波变换与噪声的小波变换有效地分离。由于有效信号分解后的小波系数绝对值比较大,而噪声信号的能量相对分散,表现为小波分解后的小波系数绝对值较小,因此可以通过阈值处理方法进行去噪。当小波变换系数小于阈值时,认为主要由噪声引起,予以舍弃;当小波系数大于阈值时,认为主要由信号引起,予以保留;然后用新的近似系数和小波系数进行重构得到去噪后的信号。
信号与噪声的分离关键在于阈值的选择,Donoho提出的阈值计算公式如式(3)所示:
 |
(3) |
式中:σ=median(|Wj,k|)/0.674 5,Wj,k为尺度上点的小波系数。通常直接对最高一层高频小波系数取中值作为噪声方差,认为这一层高频小波系数都是由噪声引起的,而忽略了高频小波系数中除了噪声以外仍可能含有的有效信号。如何选取阈值是关键,因此本文提出了一种基于小波熵和相关性的阈值选取方法。
2 基于相关性的小波熵阈值去噪算法 2.1 算法的基本思想对含噪信号进行小波分解后得到低频近似系数和高频小波系数。一般将低于0.5 Hz的低频分量看作基线漂移,为去除基线漂移,算法根据基线漂移的低频特性来确定小波分解的层数,使分解得到的最低频的近似系数的频率范围接近基线漂移的频率范围,再将最低频的近似系数置零即去掉基线漂移。
工频和肌电噪声和心电信号频谱有重叠,需要在高频小波系数中进行处理。根据有效信号的小波系数在各尺度间具有较强的相关性,而噪声的小波系数在各尺度间无明显的相关性,可以区分有效信号和噪声。对高频小波系数进行相关性分析,确定噪声夹杂的有效信号的位置,并将这些有效信号置零;设置噪声能量阈值,循环多次剔除有效信号从而得到各尺度新的高频小波系数。如果忽略对高频小波系数的相关性处理工作,在去噪过程中会因为未有效区分噪声,导致有效信号损失。小波熵作为小波变换与信息熵的结合,可以在时频域上对信息的能量做出度量[12]。将经过相关性分析的高频小波系数等分为若干区间,计算各区间的小波熵值,选取最大小波熵值子区间的高频小波系数平均值的绝对值作为噪声方差。这种方法在一定程度上减少了阈值选取的盲目性。
2.2 相关性计算相关系数计算公式如式(4)所示:
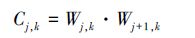 |
(4) |
式中:Cj,k为分解尺度j上k点的相关系数,Wj,k和Wj+1,k分别为尺度j和尺度j+1上k点的小波系数。
为使相关系数与小波系数具有可比性,需要定义规范化相关系数[13],定义(5)为Cj,k的规范化相关系数:
 |
(5) |
式中:Ncj,k为尺度j上k点的规范化系数,并且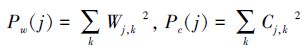
显然,在尺度j下,小波系数Wj,k与规范化相关系数具有相同的能量,这为它们之间提供了可比性。记录各尺度规范化相关系数大于高频小波系数的位置,该位置即为各尺度高频小波系数中有效信号的位置,并将该位置的高频小波系数置零,得到新的高频小波系数,认为其全部是由噪声引起的,由这些系数计算噪声方差。
2.3 小波熵对信号进行l尺度分解,设尺度j上的小波系数为Wj=(Wj,1,Wj,2,…,Wj,N)。若小波基函数为正交基,尺度j的小波变换满足能量守恒原则。因此,尺度j的小波能量Ej等于该尺度小波系数的平方和,如式(6)所示 :
 |
(6) |
式中N为采样点数。信号的总能量计算公式如式(7)所示:
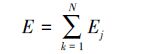 |
(7) |
由式(6)和式(7)可以确定第j层小波系数的信号能量在总能量中存在的概率为
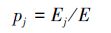 |
(8) |
已知概率,可以确定信号小波熵S[15]为
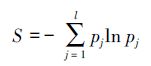 |
(9) |
本文提出的噪声方差计算公式如式(10):
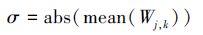 |
(10) |
采用的阈值处理函数如式(11):
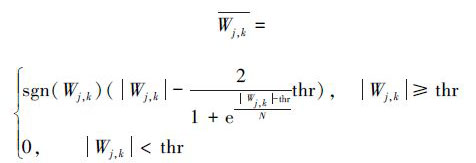 |
(11) |
式中:Wj,k为小波系数;
1) 根据基线漂移的低频特性设置小波分解层数,对含噪信号进行多尺度分解,得到最低频的近似系数和各尺度高频小波系数。
2) 将低频近似系数置零,去除基线漂移。
3) 选取有限个样本的方差作为初始噪声的方差[14],这里采用最高频小波系数的前80个点估计初始噪声,计算方差sigma1,设置阈值k。
4) 将相邻尺度的高频小波系数进行相关性计算,将系数大于规范化系数的位置上的小波系数置零,剩下的为噪声产生的系数,从而估计噪声方差sigma2。
5) 若sigma2>k·sigma1,返回4),否则,利用sigma2和小波熵计算全局阈值。
6) 对每一层的高频小波系数利用全局阈值进行处理。并将新低频近似系数和新高频小波系数进行重构,得到去噪后的信号。
3 数据仿真与实验结果本文在Intel Core i5-3470 CPU+4G内存的计算机平台上,使MATLAB软件编程实现对信号的仿真实验,选取的小波函数为bior3.7小波。
3.1 数据来源和评价标准实验针对心电信号进行定性和定量仿真实验。定性实验数据采用来自MIT-BIH[16]心律失常数据库(Arrhythmia Database)和MIT-BIH噪声数据库(即Nstdb Database)中真实的心电数据。定量实验为方便计算,利用MATLAB模拟干净的心电信号。
本文的方法是在分析小波系数相邻尺度相关性和小波熵的基础上提出来的,为了验证所提算法的优越性,使用信噪比(SNR)、均方根误差(MSE)和运行时间T 3个指标来进行衡量和比较。信噪比和均方根误差公式如式(12)、(13):
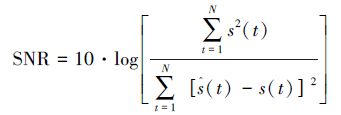 |
(12) |
 |
(13) |
式中:
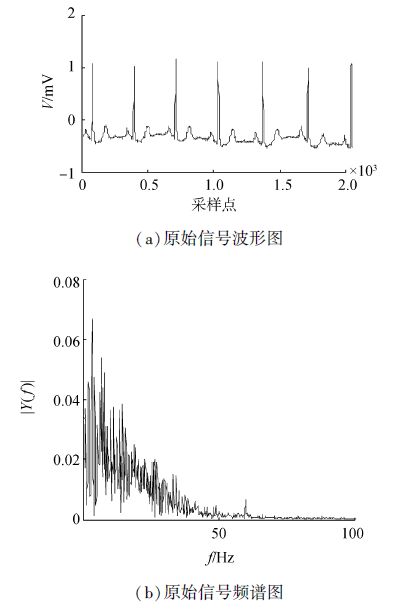
MIT-BIH心律失常数据库(Arrhythmia Database)中的心电数据含噪声较少,选取其100号数据的前2 048个数据作为本次研究的信号,人为加入工频干扰、基线漂移和高频噪声(包括肌电干扰)3种噪声。基线漂移、工频干扰和高频噪声分别来自MIT-BIH噪声数据库(Nstdb Database)中的bw、em和ma数据。本文算法与改进的小波阈值算法[1]和小波熵去噪算法[8]对比,以输入信噪比为-2.6 dB、均方误差为0.253 9为例,去噪效果如图 1~5所示,为方便观察基线漂移,显示前6个周期。
|
| 图 1 原始信号波形及频谱图 Fig. 1 The waveform and spectrum of original signals |
|
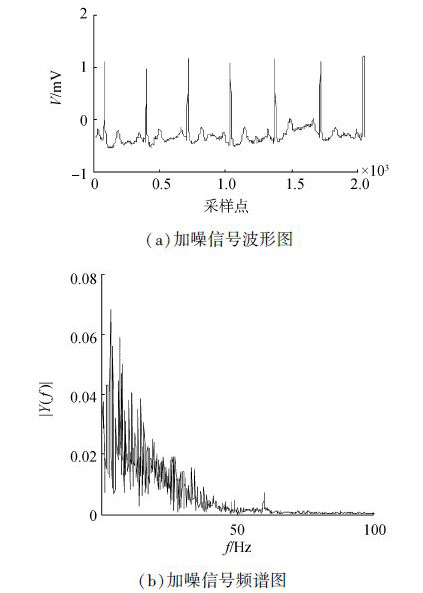
| 图 2 加噪信号波形及频谱图 Fig. 2 The waveform and spectrum of noisy signals |
|
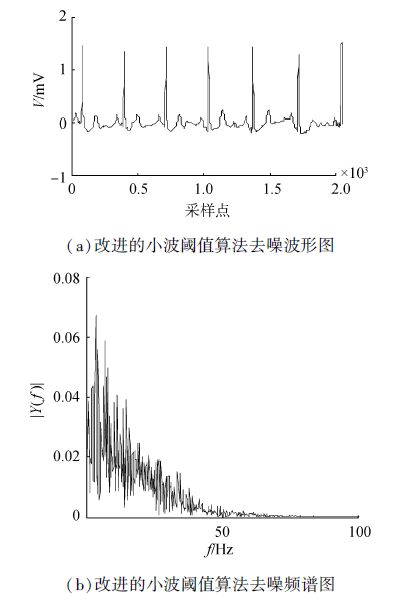
| 图 3 改进的小波阈值算法去噪波形及频谱图 Fig. 3 The waveform and spectrum of de-nosing signals of improved wavelet threshold algorithm |

|
| 图 4 小波熵算法去噪波形及频谱图 Fig. 4 The waveform and spectrum of de-nosing signals of wavelet entropy algorithm |

|
| 图 5 本文算法去噪波形及频谱图 Fig. 5 The waveform and spectrum of de-nosing signals of proposed algorithm |
该数据库中工频噪声主要集中在60 Hz左右。可以看出,本文提出的基于相关性的小波熵去噪算法与目前两种典型的心电信号去噪算法相比,基线漂移、60 Hz工频干扰被很好地去除;波形连续性强,无震荡现象,波形清晰完整,去除肌电噪声效果显著。即可以在一次小波分解、重构的过程中同时去除3种主要的心电信号噪声。
3.3 对噪声数据库信号去噪MIT-BIH噪声数据库(Nstdb Database)是真实的带噪声的信号,对该数据库中118e06信号的前2 048个数据分别用3种去噪算进行去噪,结果如图 6~9所示,为方便观察波形,对比去噪效果,波形只显示3个周期。

|
| 图 6 含噪信号波形及频谱图 Fig. 6 The waveform and spectrum of noisy signals |

|
| 图 7 改进的小波阈值算法去噪波形及频谱图 Fig. 7 The waveform and spectrum of de-nosing signals of developed wavelet threshold algorithm |
|
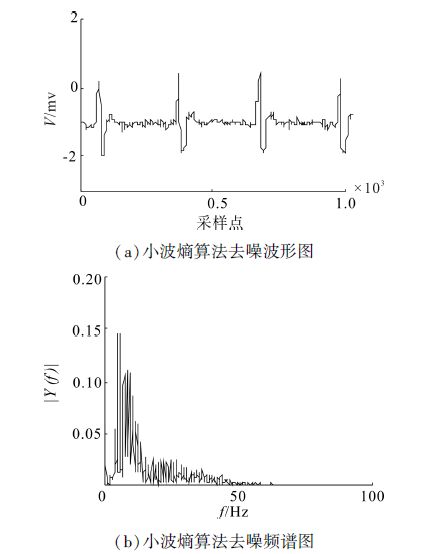
| 图 8 小波熵算法去噪波形及频谱图 Fig. 8 The waveform and spectrum of de-nosing signals of wavelet entropy algorithm |
|
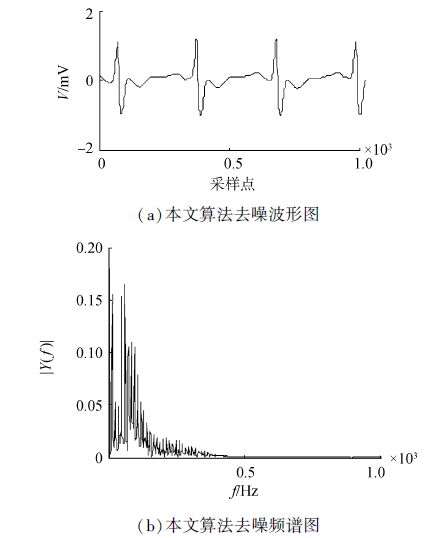
| 图 9 本文算法去噪波形及频谱图 Fig. 9 The waveform and spectrum of de-nosing signals of proposed algorithm |
由图 6~9可以看出,该数据中工频干扰不明显,本文提出的算法去噪的波形含噪声较少,波形无震荡现象。说明对基线漂移和肌电噪声去除效果要优于其他两种算法。
3.4 定量分析去噪性能为定量评价去噪效果,分别运用改进的小波阈值算法、小波熵去噪算法和本文提出的基于相关性的小波熵阈值去噪算法对含噪信号进行去噪。由于MIT-BIH数据库中的数据原本就受多种噪声干扰,不能得到理想“纯净”的信号,不便于计算SNR。因此采用MATLAB的心电模拟函数(ecg)模拟一段干净的心电信号,通过叠加噪声bw、em和ma,构造含噪信号。各算法去噪性能通过SNR、MSE和运行时间T来评价。去噪后的信号信噪比越高,则说明去噪效果越好;去噪后信号均方误差越小,说明去噪后信号与原始信号重合度越高;运行时间越小,算法复杂度越小。分别如表 1、表 2和图 10所示。
| 输入 SNR/dB |
改进小波 阈值去噪 算法[1]/dB |
小波熵阈 值去噪算 法[8]/dB |
本文算法/dB |
| -5.611 8 | 2.871 7 | -5.405 6 | 3.476 5 |
| -3.806 8 | 4.030 0 | -3.585 8 | 4.675 8 |
| -2.101 8 | 4.454 3 | -1.810 9 | 4.933 6 |
| -0.101 9 | 5.747 1 | -0.085 5 | 6.219 2 |
| 0.437 4 | 5.726 9 | 0.668 1 | 5.934 8 |
| 1.205 3 | 5.702 0 | 1.369 1 | 5.965 6 |
| 2.138 9 | 7.111 3 | 2.182 9 | 7.368 2 |
| 3.665 3 | 7.794 4 | 3.548 1 | 7.920 1 |
| 5.177 2 | 7.743 4 | 5.002 6 | 7.956 5 |
| 6.561 9 | 9.020 9 | 5.421 8 | 9.067 4 |
| 8.359 3 | 8.989 7 | 5.002 6 | 9.089 7 |
| 9.065 2 | 9.027 3 | 7.897 0 | 9.106 7 |
| 10.332 4 | 9.087 5 | 8.790 1 | 9.150 4 |
| 输入 SNR/dB |
改进小波 阈值去噪 算法[1]/dB |
小波熵阈 值去噪算 法[8]/dB |
本文算法/dB |
| -5.611 8 | 0.052 8 | 0.355 0 | 0.045 9 |
| -3.806 8 | 0.040 0 | 0.233 5 | 0.034 2 |
| -2.101 8 | 0.036 7 | 0.155 1 | 0.032 8 |
| -0.101 9 | 0.027 2 | 0.104 3 | 0.024 4 |
| 0.437 4 | 0.027 3 | 0.087 7 | 0.026 1 |
| 1.205 3 | 0.027 3 | 0.072 8 | 0.025 9 |
| 2.138 9 | 0.019 9 | 0.016 8 | 0.018 7 |
| 3.665 3 | 0.017 0 | 0.045 2 | 0.016 2 |
| 5.177 2 | 0.017 5 | 0.032 3 | 0.016 3 |
| 6.561 9 | 0.012 8 | 0.029 3 | 0.012 2 |
| 8.359 3 | 0.012 7 | 0.032 3 | 0.012 4 |
| 9.065 2 | 0.012 5 | 0.066 6 | 0.012 0 |
| 10.332 4 | 0.012 9 | 0.013 5 | 0.012 3 |
|
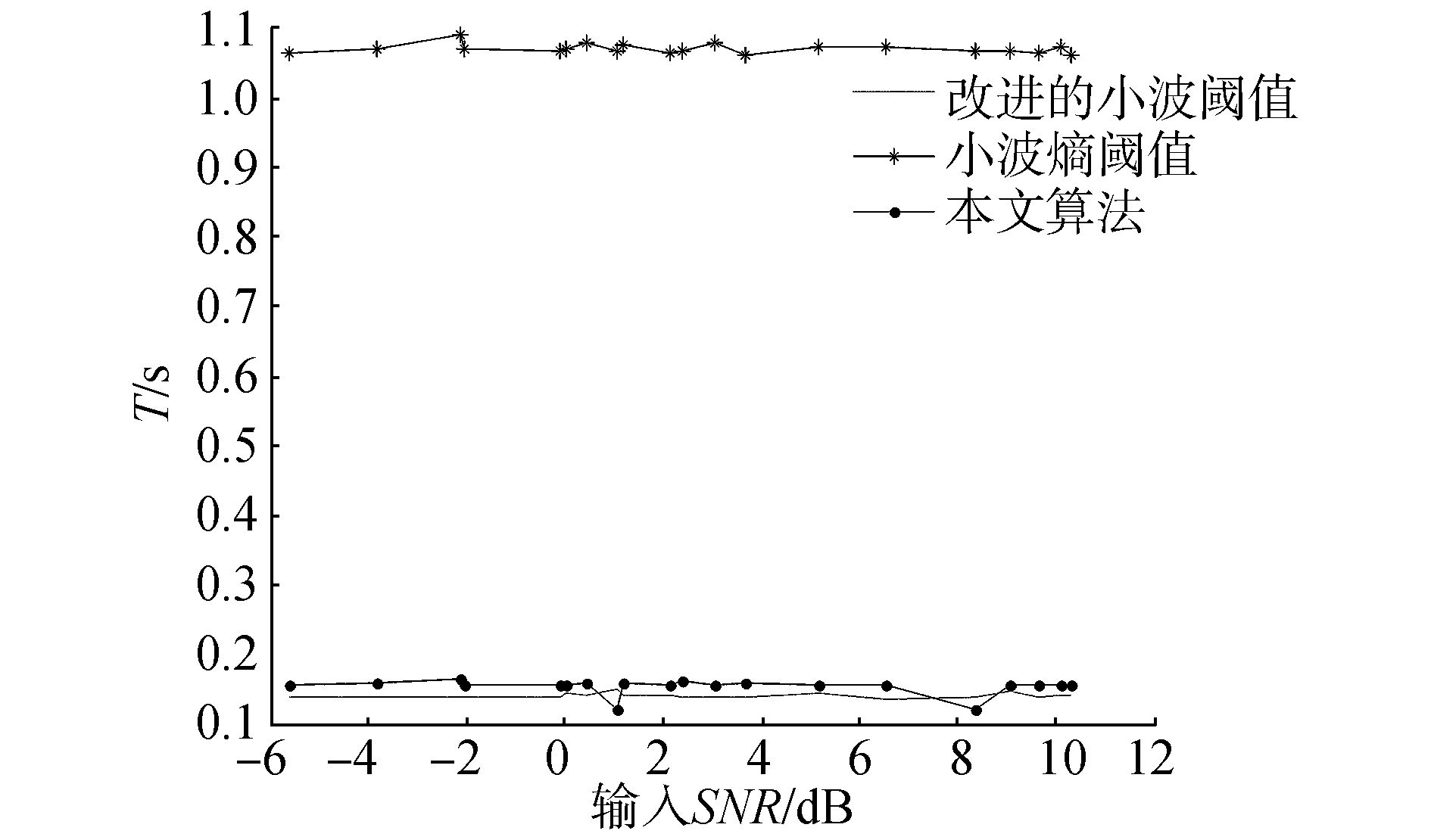
| 图 10 不同信噪比下3种算法去噪过程的运行时间 Fig. 10 The run time of three algorithms in different SNR |
从表 1和表 2可以看出,当输入信号的信噪比范围从-5 dB~10 dB时,经过本文提出的算法去噪后在SNR和MSE上的结果都要优于改进的小波去噪法以及小波熵阈值去噪法,尤其在输入信号信噪比较低时,优势更明显。输入的3种噪声比例不同,去噪结果稍有不同,小波熵阈值法基线漂移去除效果较差,在基线漂移占比大时,信噪比较低。
从图 10可以看出,本文算法的运行时间与改进的小波阈值算法相当,远远小于小波熵阈值算法。原因在于,小波分解、重构的过程复杂,算法复杂度较高相较计算阈值、相关性处理,运行时间较长。本文算法和改进的小波阈值去噪算法都只需要一次小波分解、重构;而小波熵阈值去噪需要两重小波分解、重构,所以算法复杂度高。综上可以看出,本文提出的去噪算法的去噪效果要优于其他两种算法。
4 结束语本文针对心电信号3种主要噪声的特性,提出了一种基于相关性的小波熵心电信号去噪算法。算法可以在一次小波分解、重构的过程中,同时去除掉基线漂移、工频干扰、肌电噪声3种噪声;利用各尺度间高频小波系数的相关处理多次剔除有用信号,利用噪声计算小波熵阈值具有自适应性;并选择合适的阈值函数,避免波形震荡。与其他去噪算法对比,复杂度较小,但去噪效果明显提高。另外,实验中发现在输入噪声信噪比特别小的情况下,去噪算法会对原始信号产生一定的损失,在以后的工作中将深入研究此问题。
| [1] |
赵艳娜, 魏珑, 徐舫舟, 等. 基于小波变换的心电信号去噪综合算法[J].
现代生物医学进展, 2009, 9 (16) : 3128-3130.
ZHAO Yanna, WEI Long, XU Fangzhou, et al. ECG signal denoising algorithm based on wavelet transform[J]. Progress in modern biomedicine, 2009, 9(16) : 3128-3130. |
| [2] | HARITHA C, GANESAN M, SUMESH E P. A survey on modern trends in ECG noise removal techniques[C]//Proceedings of 2016 International Conference on Circuit, Power and Computing Technologies (ICCPCT). Nagercoil:IEEE, 2016:1-7. |
| [3] |
赵志华, 许爱华. 基于形态学的ECG小波自适应去噪算法[J].
计算机工程与设计, 2008, 29 (8) : 2140-2142.
ZHAO Zhihua, XU Aihua. ECG adaptive wavelet transform of denoising algorithm based on morphology[J]. Computer engineering and design, 2008, 29(8) : 2140-2142. |
| [4] | TAI Shenchuan, SUN C C, YAN W C. A 2-D ECG compression method based on wavelet transform and modified SPIHT[J]. IEEE transactions on biomedical engineering, 2005, 52(6) : 999-1008DOI:10.1109/TBME.2005.846727. |
| [5] |
杨思军, 郝继飞, 闫文杰, 等. 小波滤波与QRS波检测[J].
计算机工程与应用, 2011, 47 (12) : 239-241.
YANG Sijun, HAO Jifei, YAN Wenjie, et al. Wave filtering and QRS detection[J]. Computer engineering and applications, 2011, 47(12) : 239-241. |
| [6] | DONOHO D L. denoising by soft-thresholding[J]. IEEE transactions on information theory, 1995, 41(3) : 613-627DOI:10.1109/18.382009. |
| [7] | AGANTE P M, DE SA J P M. ECG noise filtering using wavelets with soft-thresholding methods[C]//Proceedings of 1999 Computers in Cardiology. Hannover:IEEE, 1999, 26:523-538. |
| [8] |
侯宏花, 桂志国. 基于小波熵的心电信号去噪处理[J].
中国生物医学工程学报, 2010, 29 (1) : 22-28.
HOU Honghua, GUI Zhiguo. Denosing processing of ECG signal based on wavelet entropy[J]. Chinese journal of biomedical engineering, 2010, 29(1) : 22-28. |
| [9] |
欧阳波, 程栋, 王玲. 改进小波阈值算法在心电信号去噪中的应用[J].
计算机工程与应用, 2015, 51 (4) : 213-217.
OUYANG Bo, CHENG Dong, WANG Ling. Improved wavelet threshold algorithm in application of ECG signal de-noising[J]. Computer engineering and applications, 2015, 51(4) : 213-217. |
| [10] | LI Nianqiang, LI Ping. An improved algorithm based on EMD-wavelet for ECG signal de-nosing[C]//Proceedings of 2009 International Joint Conference on Computational Sciences and Optimization. Sanya, China:IEEE, 2009, 1:825-827. |
| [11] | MALLAT S. 信号处理的小波导引[M]. 北京: 机械工业出版社, 2003. |
| [12] |
刘霞, 黄阳, 黄敬, 等. 基于经验模态分解(EMD)的小波熵阈值地震信号去噪[J].
吉林大学学报:地球科学, 2016, 46 (1) : 262-269.
LIU Xia, HUANG Yang, HUANG Jing, et al. Wavelet entropy threshold seismic signal denoising based on empirical mode decomposition (EMD)[J]. Journal of Jilin university:earth science edition, 2016, 46(1) : 262-269. |
| [13] |
李文, 刘霞, 段玉波, 等. 基于小波熵与相关性相结合的小波模极大值地震信号去噪[J].
地震学报, 2012, 34 (6) : 841-850.
LI Wen, LIU Xia, DUAN Yubo, et al. Wavelet modulus maxima denoising of seismic signals based on combined wavelet entropy and correlation[J]. Acta seismologica sinica, 2012, 34(6) : 841-850. |
| [14] | ROSSO O A, BLANCO S, YORDANOVA J, et al. Wavelet entropy:a new tool for analysis of short duration brain electrical signals[J]. Journal of neuroscience methods, 2001, 105(1) : 65-75DOI:10.1016/S0165-0270(00)00356-3. |
| [15] | 朱泽煌, 胡广书, 郭恒, 等. MIT-BIH心电数据库的开发及用作检测标准[J]. 中国生物医学工程学报, 1993, 12 (4) : 244-249. |
| [16] |
徐效文, 曾超, 崔松野, 等. MIT-BIH数据库心电数据重采样研究[J].
计算机工程与应用, 2011, 47 (8) : 245-248.
XU Xiaowen, ZENG Chao, CUI Songye, et al. Research on resampling of ECG data from MIT-BIH database[J]. Computer engineering and applications, 2011, 47(8) : 245-248. |



