针对空间失控失效航天器进行在轨营救与维修是当前航天领域的一个重要发展方向[1-2]。失控目标在空间中处于自由运行的状态,其对接端口随本体一起在空间中运动,位置时刻都在发生变化,使得传统的姿态轨道独立控制不能适应快速姿轨机动的要求[3-4]。为此,国内外学者开展了大量航天器姿轨联合控制问题的研究,如Segal[5]研究了航天器姿态动态对轨道运动的影响,指出建立耦合的动力学模型可以提高基于视觉的相对位姿控制精度;Liao[6]研究了追踪器本体坐标系下航天器姿轨一体化控制律设计问题,建立了考虑推进器配置的姿轨动力学模型,并设计了非线性鲁棒一体化控制律;Shan[7]设计了一种自适应同步控制策略,提出了基于交叉耦合概念的六自由度航天器编队飞行控制方法;Zhang[8]建立了追踪航天器本体坐标系下六自由度模型,采用自适应反步法设计了姿轨联合控制器等。
航天器的控制系统需要具有高可靠性和高精度,为了降低任务风险,顺利完成航天任务,航天器控制技术必须在地面得到充分的实验验证[9-11]。依托数学模型解算与物理反馈结合,驱动模拟器在地面试验环境中再现航天器空间运动控制过程的验证仿真方法,是置信水平较高的一种仿真方法,相关的试验系统有德国宇航局的EPOS交会对接仿真系统[12]和中国空间技术研究院的九自由度验证系统[13]等。但是由于实验场地大小、机构速度、运行时间等方面的约束,文献[5-8]中给出的各类控制方法无法在地面实验环境中进行验证。
相似理论是解决航天器姿轨系统先进控制方法与实验验证在场地大小、机构速度、运行时间等方面矛盾的一个有力工具。通过相似三定理[14]建立仿真模型系统与航天器姿轨原型系统间的相似性准则,得到不同比例约束下的航天器姿轨相似动力学模型,并以此设计控制器,可以解决复杂姿轨控制策略地面验证的问题。国内外学者对此也开展了部分研究工作,如意大利都灵理工大学[15]为设计开发交会对接的GNC系统算法,运用尺度缩比方法通过地面气浮试验台仿真了从近程导引到最后对接过程的运动情况;何兆伟等[16]针对水浮仿真系统验证航天器二体运动控制过程提出了相似性分析方法;孙施浩等[17]基于相似理论、长度量纲分解和绝对运动等效代换方法提出了一种可实现空间合作目标运动再现的相似性试验设计方法。然而针对航天器绕飞逼近翻滚目标运动再现的姿轨控制问题,应用相似理论设计相应控制器的应用和研究工作至今还未见到。
本文首先介绍适用于绕飞逼近翻滚目标运动再现的地面仿真验证系统,然后在追踪器本体坐标系下建立了航天器交会对接相对运动的六自由度姿轨联合模型,并应用相似理论将其转换为可适用于实验验证的缩比相似动力学模型,在此基础上,设计反步控制器,使其跟踪用多项式函数设计的参考轨迹,在有限时间内对翻滚目标实现绕飞逼近对接。
1 运动再现系统为了在地面实验室空间内验证航天器姿轨控制方案、星载计算机性能以及测量敏感器量测可信度等任务,需要在地面再现航天器在空间中的轨道姿态真实运动。采用动力学计算与运动学等效思想[18]设计的仿真实验,是通过实时计算航天器的姿轨动力学模型得到航天器空间中的轨道姿态运动,然后由模拟器运动机构跟踪计算出的轨迹,再现航天器空间的运动。
图 1是文献[20]中提出的航天器全方位交会地面验证系统,具有9个运动自由度,包含2个三轴转台,以及垂向、周向、径向运动模块。其中,中心固定的三轴转台模拟目标航天器在轨三轴绝对姿态运动,另外六自由度的运动机构模拟服务航天器在轨三轴绝对姿态运动和服务航天器与目标航天器在轨三轴相对位置运动。

|
| 图 1 地面模拟器样机示意图 Fig. 1 Schematic diagram of ground motion simulator |
在这个九自由度运动模拟器中,径向运动范围为0~10 m,垂向运动范围为-2~2 m。而对应服务航天绕飞逼近翻滚目标任务,启动时两航天器相对距离一般需要在100 m之外,且速度不易太大,任务时间较长,因此,地面实验验证中需要应用相似理论方法,对距离和时间进行缩比处理以满足地面试验需求。
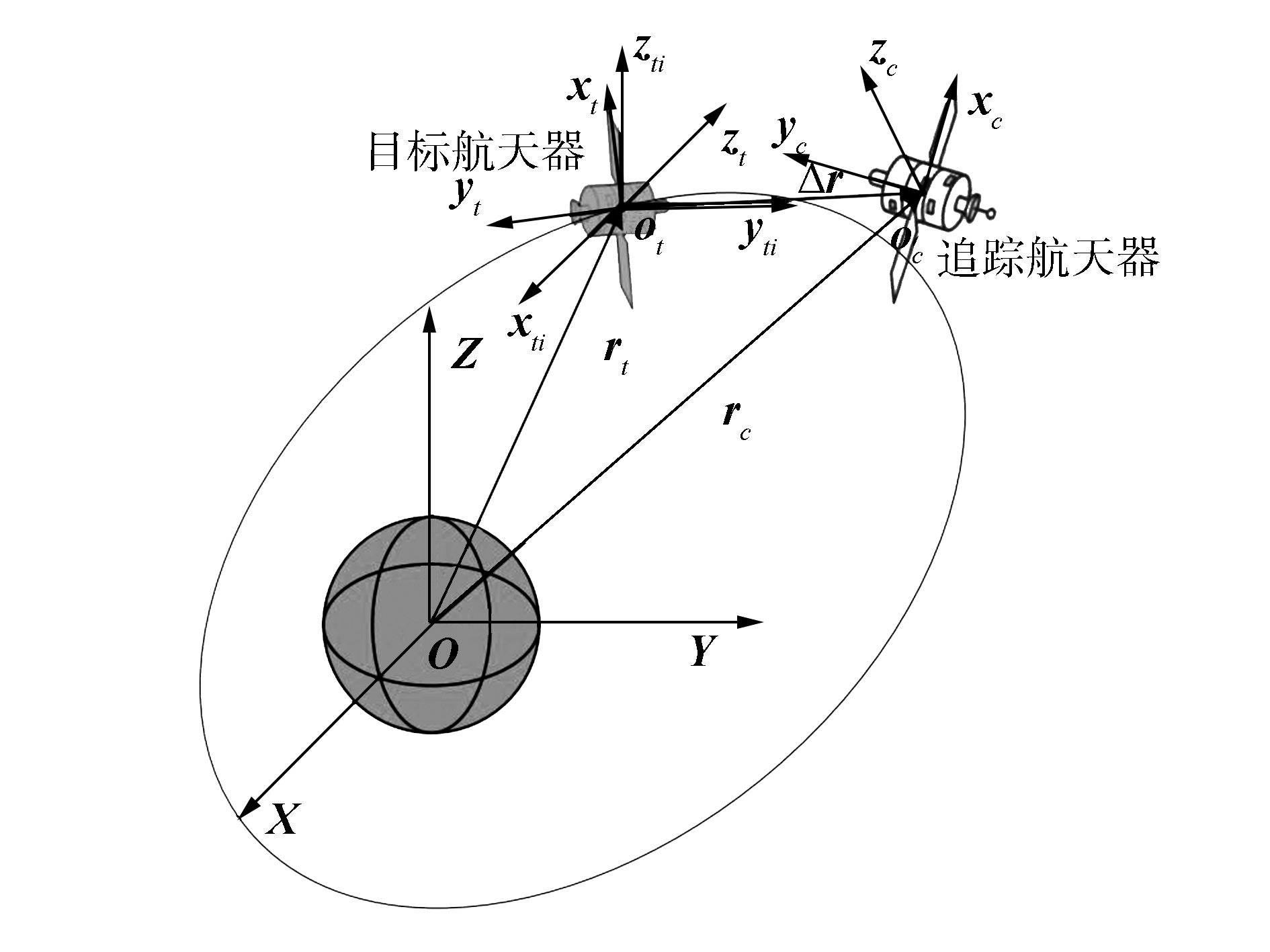
2 相似动力学模型建立针对与椭圆轨道上失控翻滚目标航天器的交会对接任务,在追踪器本体坐标系下建立六自由度姿轨联合模型,并经相似变换得到姿轨联合相似动力学模型,以满足同时高精度控制航天器相对位置姿态,实现目标逼近。定义3个坐标系,如图 2所示。
|
| 图 2 坐标系示意图 Fig. 2 Several coordinate frames |
赤道惯性坐标系为OXYZ,其中OXY是赤道面,OX从地心指向春分点,OZ垂直于赤道平面指向北;追踪器本体坐标系为ocxcyczc,其中oc是追踪航天器质心,坐标轴ocxc、ocyc和oczc与航天器惯量主轴重合;目标器平动坐标系otixtiytizti,oti是目标器质心,otixti、otiyti和otizti与坐标系OXYZ各轴平行。(在仿真试验中,地面惯性坐标系与坐标系otixtiytizti相对应。)
定义在OXYZ下追踪器的位置矢量rc,目标器的位置矢量rt,追踪器相对目标器的位置矢量Δr;追踪器本体坐标系相对惯性系姿态四元数qc、角速度ωc;目标器本体坐标系相对惯性系姿态四元数qt、角速度ωt。追踪标器本体坐标系相对目标器本体坐标系的姿态四元数为qct=qt-1°qc,qo、qv分别为qct的标量和矢量部分。()c、()t分别表示矢量在追踪器本体和目标器本体坐标系下的分量列阵。
2.1 追踪器本体坐标系下航天器相对姿轨模型[19]航天器相对轨道动力学方程:
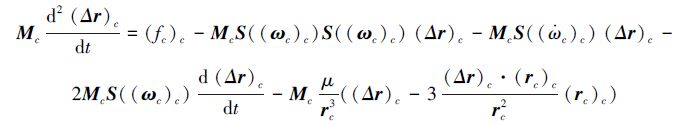 |
(1) |
式中:S(·)表示叉乘矩阵。
航天器相对姿态动力学方程:
 |
(2) |
式中:Lct(qct)=(q02-qvTqv)I+qvqvT-2q0S(qv)是目标航天器本体坐标系到追踪航天器的旋转矩阵。
航天器相对姿态运动学方程为
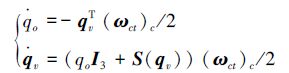 |
(3) |
下文为符号简单,追踪器本体坐标系下的分量列阵均省略()c。
记x1=[Δr qv]T和x2=[dΔr/dt ωct]T,则联立方程(1)、(2)和(3)有姿轨联合方程:
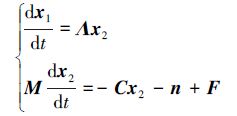 |
(4) |
初始条件:x1(0)=[Δr(0) qv(0)]T,
x2(0)=[dΔr(0)/dt ωct(0)]T。
其中:
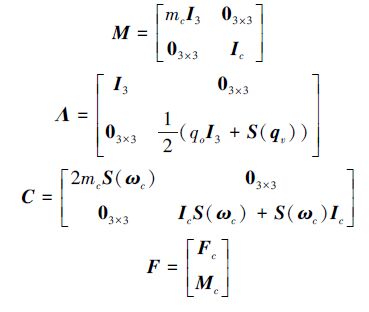 |
 |
记λi表示系统变量i的缩比系数,即λi=im/ip,给定交会对接再现任务的长度、时间、质量3个基本量纲缩比系数λL、λT、λM,则根据相似理论的量纲分析法[17],可得姿轨联合相似动力学模型为
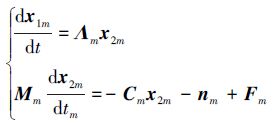 |
(5) |
初始条件满足:
 |
式中:tm=λTt,
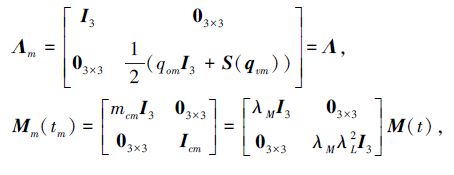 |
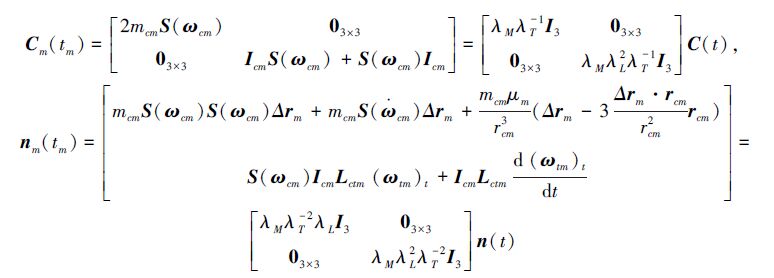 |
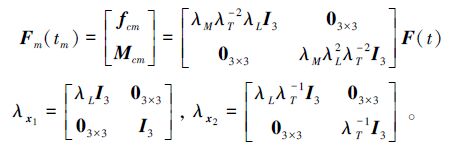 |
式中下标m表示相似动力学模型系统量。
3 控制器设计首先,针对给定的初始状态和期望完成时间,设计一条有限时间收敛且动态性能良好的参考轨迹。然后,将方程(5)转化为误差动态方程,利用反步法设计跟踪控制器实现有限时间交会对接。
3.1 参考轨迹设计假定交会对接初始条件:
 |
姿态同步时间为Tq,对接完成时间为Tr。
则根据相似理论,相似过程的初始条件:
 |
模拟器完成姿态同步时间Tqm=λTTq,对接完成时间为Trm=λTTr。
针对给定的初始条件和终端收敛条件,利用多项式向量函数设计相对位置(Δrm)r(tm)、相对速度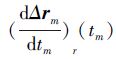
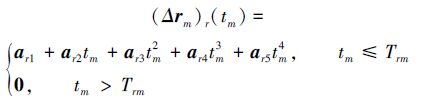 |
(6) |
满足:
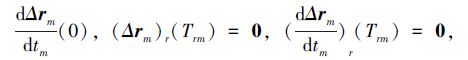

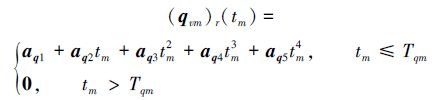 |
(7) |
满足: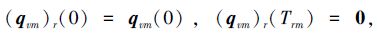

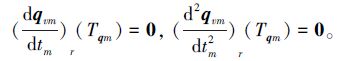
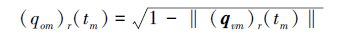 |
(8) |
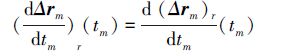 |
(9) |
 |
(10) |
定义与参考轨迹的位置、速度误差、姿态和角速度误差:
 |
(11) |
式中eqctm=[eqom eqvm]是姿态误差四元数。记:
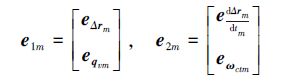 |
容易验证,根据式(6)~(10)所设计的参考轨迹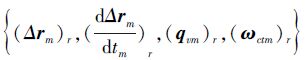
1) e1m(0)=0,e2m(0)=0;
2) 参考轨迹(Δrm)r(tm)、(qvm)r(tm)二次可微;
3) 参考轨迹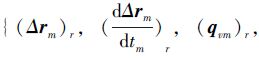
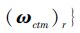
基于此性质,定义系统参考状态:
 |
如果设计的控制器能够保证
 |
(12) |
那么根据误差定义(11),系统状态一定能够满足:
 |
由于已经验证参考状态可以在有限时间内收敛到零,所以系统状态x1m、x2m也一定可以在有限时间内收敛到零,由此接下来的工作就是设计合适的控制器保证式(12)成立。
根据上述误差定义以及方程(5)可得误差动态方程:
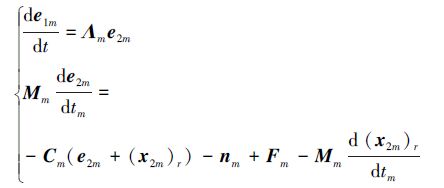 |
(13) |
用反步法设计虚拟控制器:
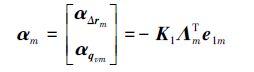 |
(14) |
定义
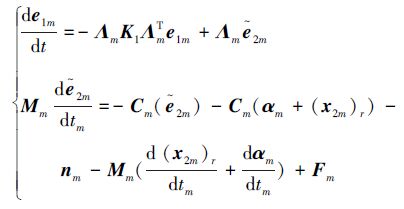 |
(15) |
定理 1 考虑误差动态系统(15),任意给定正定矩阵K1、K2,则设计如下跟踪控制器:
 |
(16) |
可保证相似模型(5)的系统状态始终跟踪多项式向量函数设计的参考轨迹,即x1m(tm)≡(x1m)r(tm)、x2m(tm)≡(x2m)r(tm),对tm≥0。
证明 考虑如下Lyapunov函数:
 |
(17) |
对时间tm求导,代入方程(15)可得:
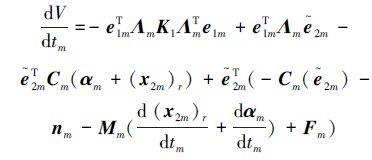 |
(18) |
将控制器(16)代入式(18),并注意到Cm是反对称阵,可得:
 |
(19) |
根据参考轨迹的设计要求,可以保证:
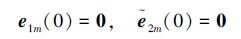 |
则根据Lyapunov稳定性理论,有:
 |
即e1m(tm)≡0,
进一步,根据虚拟控制器设计式(14)可得:
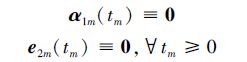 |
因此,在控制器(16)作用下,相似系统(5)的状态x1m、x2m能够完全跟踪设计的有限时间收敛参考轨迹(x1m)r、(x2m)r。
与文献[5-8]相比,本文研究的航天器绕飞逼近翻滚目标的姿轨联合控制问题,是在追踪航天器本体系下建立的航天器姿轨耦合的相似动力学模型,通过设计相似系数,可与实验系统在场地大小、机构速度、运行时间等方面的约束相匹配。
当基本量刚相似比为1时,控制器(16)即可应用于航天器交会对接的姿轨联合控制。
4 数值实验 4.1 仿真条件目标航天器参数:轨道参数如表 1所示,航天器质量mt=8 000 kg,转动惯量矩阵:
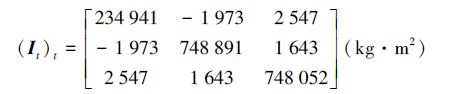 |
初始姿态四元数和姿态角速度分别为
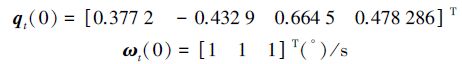 |
目标航天器无轨道和姿态机动。
| 参数 | 数值 |
| 偏心率 | 0.73 |
| 半长轴/km | 24 371 |
| 升交点赤经/(°) | 98 |
| 轨道倾斜角/(°) | 0 |
| 近地点幅角/(°) | 0 |
| 初始真近点角/(°) | 10 |
追踪航天器参数:轨道倾斜角为(10-5)°,初始真近点角为(10-1.5×10-5)°,其他轨道参数均与目标航天相同。航天器质量mc=6 000 kg,转动惯量矩阵:
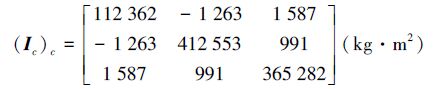 |
初始姿态四元数和姿态角速度分别为
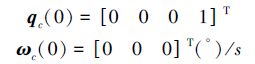 |
绕飞逼近任务过程:首先完成姿态同步,并到达对接口后方2 m的位置,其中姿态同步时间为Tq=2 000 s,到达对接口后方时间Tr1=10 000 s,然后保持当前状态Tr2=7 200 s,最终直线逼近完成对接时间为Tr3=2 000 s。
基本量纲相似比系数:
λL=1/10,λT=1/10,λm=1/1 000
在运动再现仿真中,采用的是动力学仿真与运动学等效思想,上述姿态轨道动力学模型仅在计算机内进行数值解算,因此涉及的动力学参数,如航天器的惯量阵I,航天器质量m,均是数值量,与运动模拟器机构真实惯量和质量无关,质量量纲缩比系数λm可任意选取,在这里为了控制量数值显示方便取为数值1/1 000。
控制器参数:
K1=diag(60,60,60),K2=diag(50,50,50)
仿真系统总体结构框图如图 3。其中相似变换模块:
 |
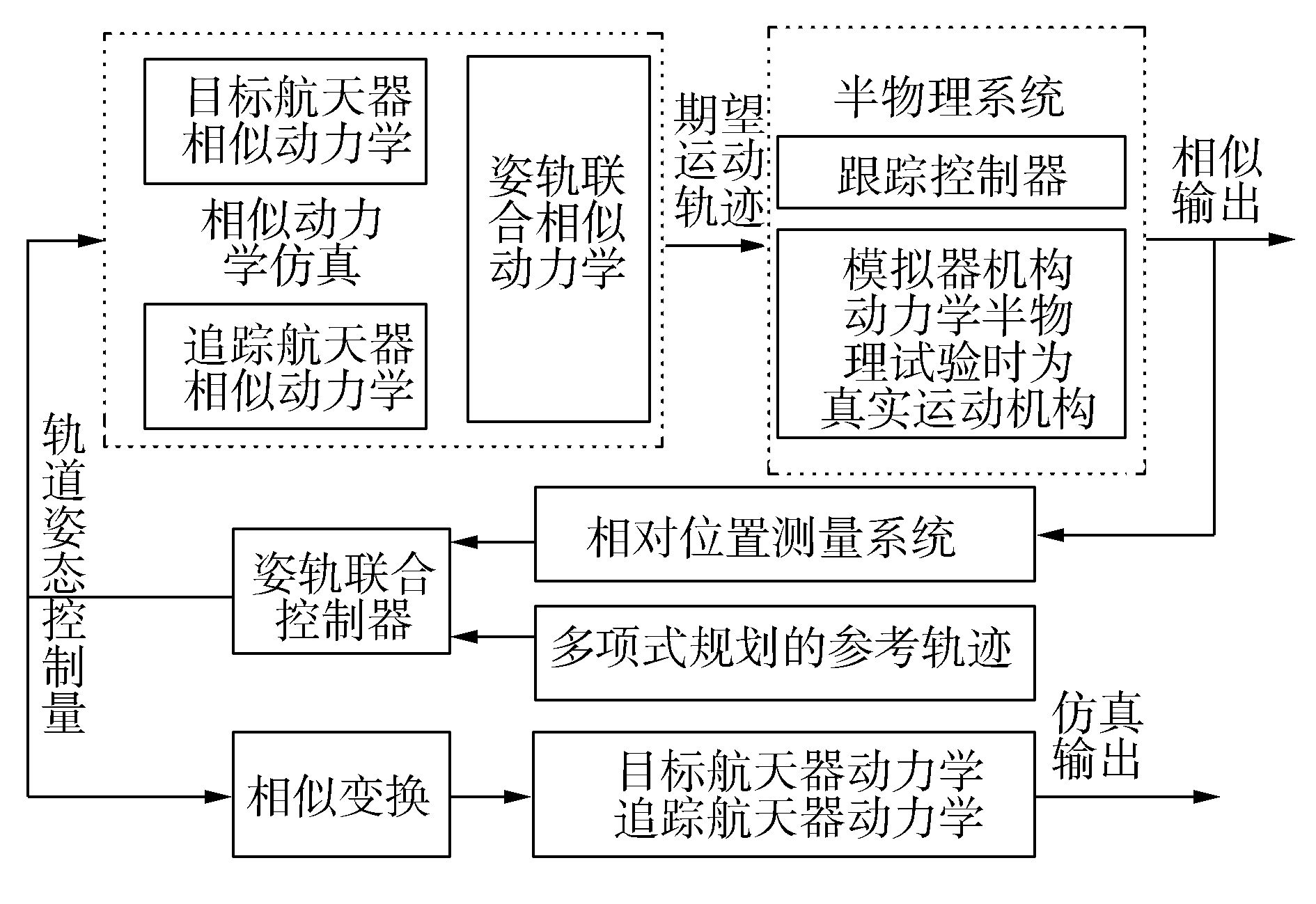
|
| 图 3 仿真结构框图 Fig. 3 Block diagram of simulation |
仿真输出为航天器空间运动状态的输出,相似输出为地面运动再现系统的输出。仿真结果如图 4~11所示。
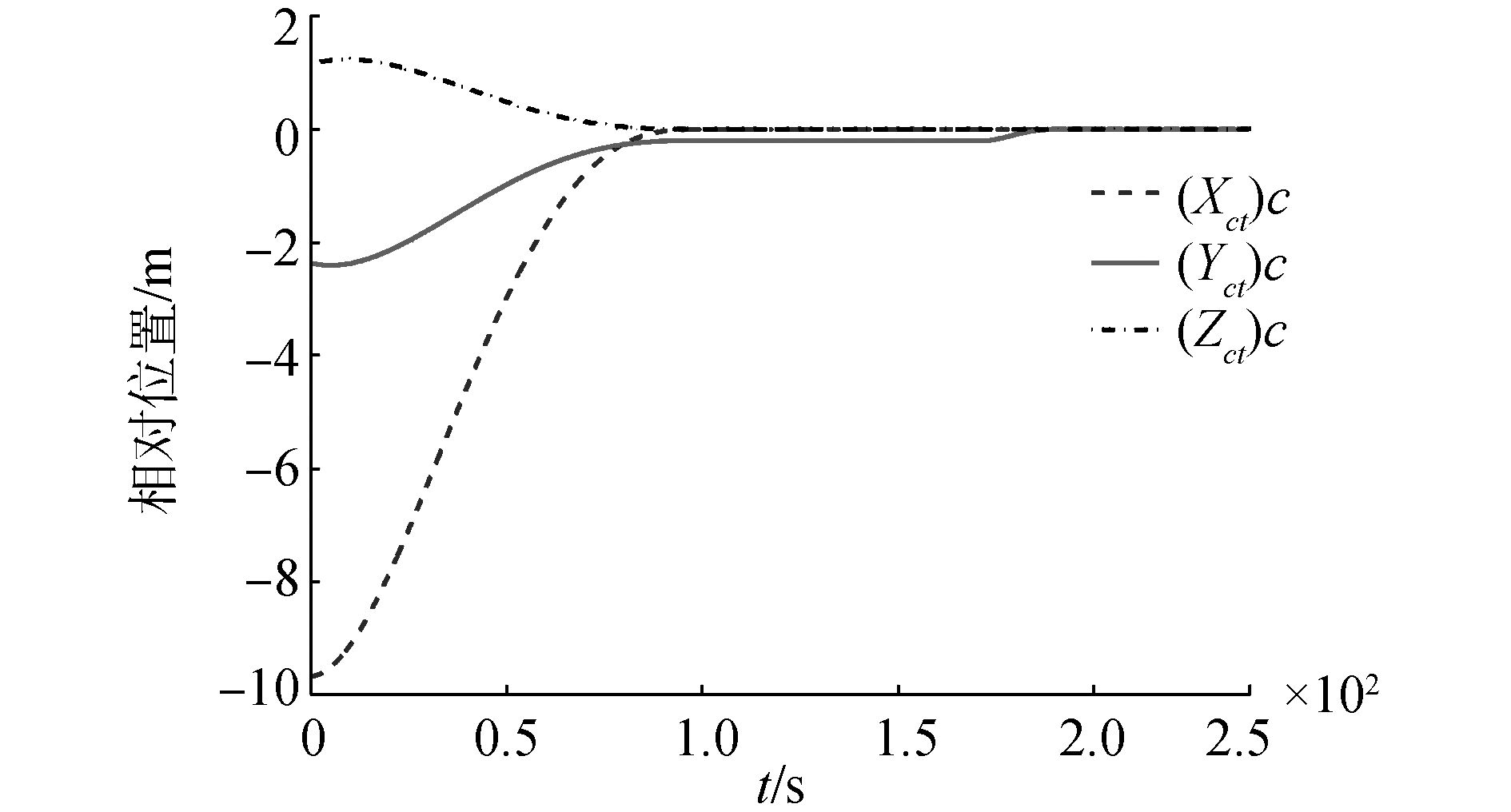
|
| 图 4 位置参考轨迹 Fig. 4 Reference trajectory of position |
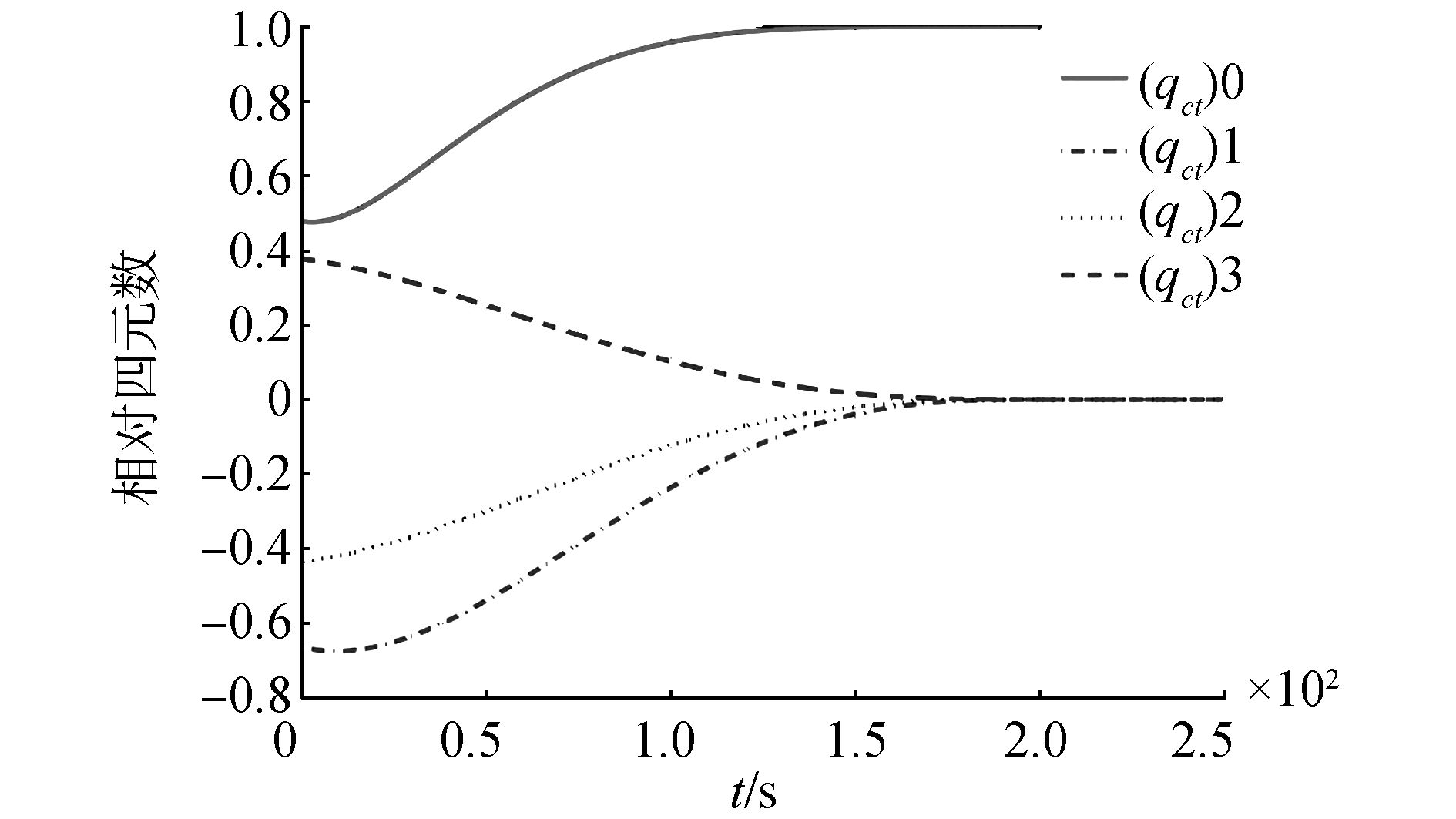
|
| 图 5 姿态参考轨迹 Fig. 5 Reference trajectory of attitude |

|
| 图 6 控制器控制力和力矩 Fig. 6 The force and moment of visual controller |

|
| 图 7 跟踪误差曲线 Fig. 7 Block diagram of simulation |
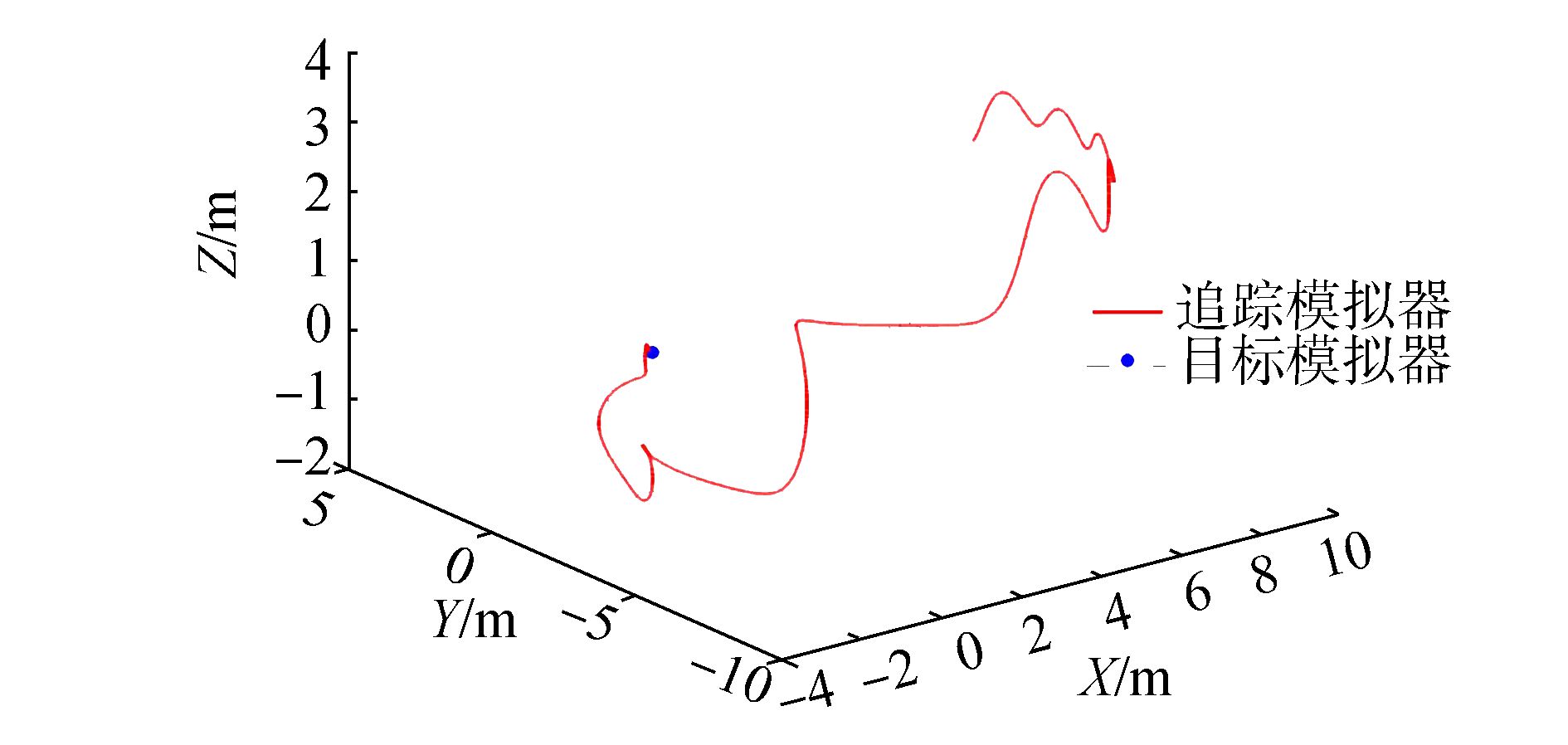
|
| 图 8 0~1 000 s坐标系otixtiytizti下的运动轨迹 Fig. 8 Trajectory in otixtiytizti at time 0~1 000 s |

|
| 图 9 1 000~2 400 s坐标系otixtiytizti下的运动轨迹 Fig. 9 Trajectory in otixtiytizti at time 1 000~2 400 s |

|
| 图 10 坐标系ocxcyczc下的航天器相对轨道运动 Fig. 10 Relative orbit trajectory in ocxcyczcframe |
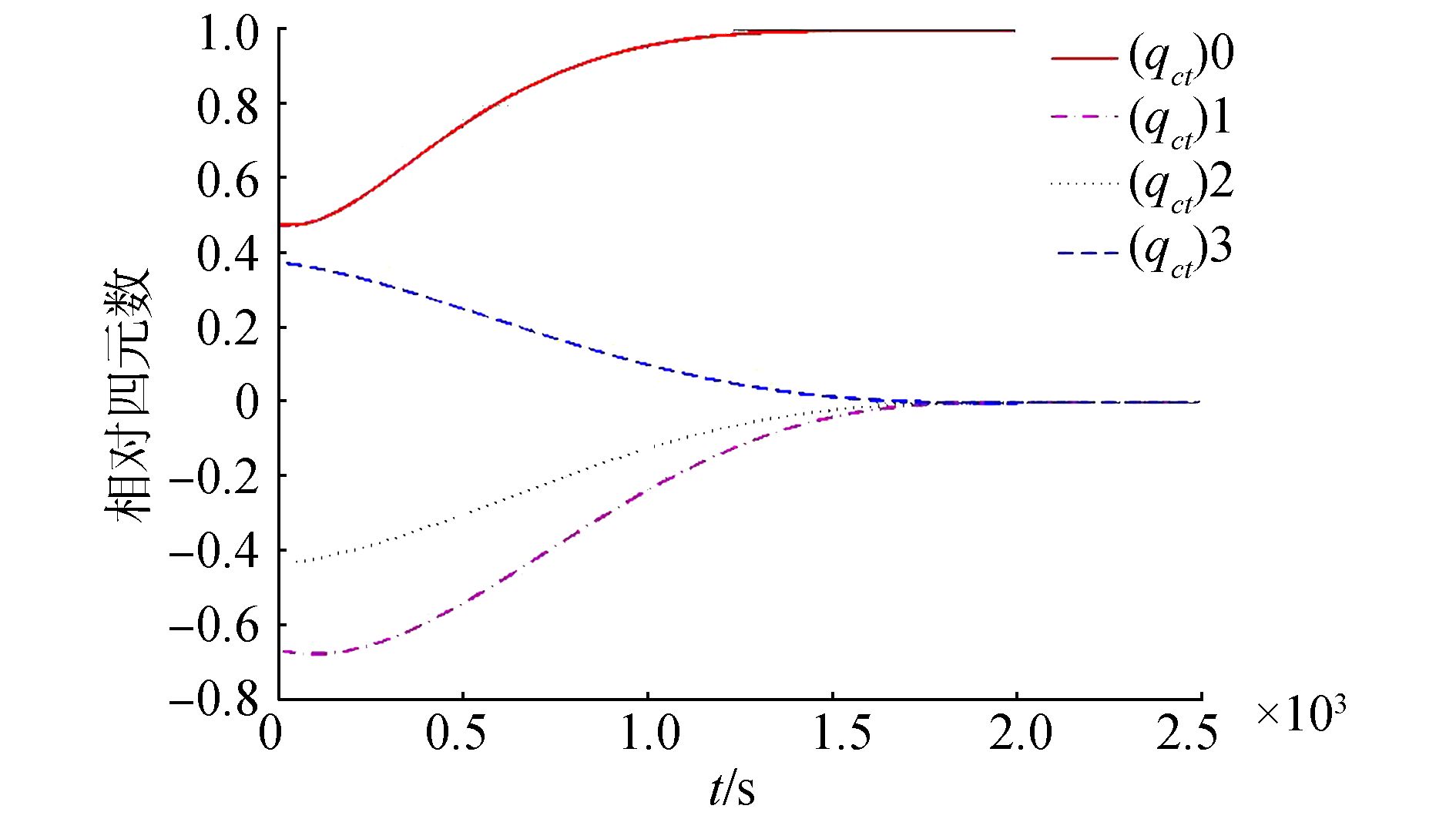
|
| 图 11 航天器相对姿态四元数 Fig. 11 Relative attitude quaternion |
根据设定的交会对接任务过程、初始条件及相似比例系数,求得多项式拟合的相似系统姿轨的参考轨迹如图 4、5所示,满足给定时间收敛且动态性能良好。由反步法设计的姿轨联合控制器控制量及跟踪误差如图 6、7所示,由于设计的参考轨迹初始值与系统状态初始值相同,且仿真未考虑系统模型不确定性及干扰,因此全程控制误差几乎为零,控制量平滑且能量消耗较小。
图 8、9是在坐标系otixtiytizti下两航天器的相对轨道运动轨迹,分别对应0~1 000 s和1 000~2 400 s。从图中可以看到追踪航天器逼近目标,最终实现对接的过程。由于目标处于翻滚状态,因此接近轨迹不再是沿单一方向的直线逼近。
图 10和11为追踪航天器在坐标系ocxcyczc下的姿轨运动曲线,对比图 4、5,运动距离相差λL=1/10,运动时间相差λT=1/10,姿态角度数量相同λqc=1,符合预期的相似比结果。
本文主要为了说明姿轨联合控制器设计方法,未考虑系统不确定性和干扰。当考虑航天器姿轨动力学和模拟器动力学存在不确定性和干扰时,可以应用鲁棒控制、滑模控制[20-21]等方法重新设计控制器(16),但是相似性条件和仿真框架、过程均不变。
5 结束语本文考虑了地面试验环境中服务航天器与翻滚目标绕飞逼近运动再现的姿轨联合控制问题,以相似理论为基础建立了姿轨联合相似动力学模型,给出姿轨联合控制器的设计方法。通过数值仿真实例说明了基于运动再现的姿轨控制方法理论上的有效性。进一步的工作是考虑实际系统中模型不确定性以及干扰存在的情况下,在试验样机上开展验证,以提高本文提出方法的可信度。
| [1] | FLORES-ABAD A, MA O, PHAM K, et al. A review of space robotics technologies for on-orbit servicing[J]. Progress in aerospace sciences, 2014, 68 : 1-26DOI:10.1016/j.paerosci.2014.03.002. |
| [2] | NOLET S. Development of a guidance, navigation and control architecture and validation process enabling autonomous docking to a tumbling satellite[D]. Boston, USA:Massachusetts Institute of Technology, 2007:34-36. |
| [3] |
李鹏, 岳晓奎, 袁建平. 基于θ-D方法的在轨操作相对姿轨耦合控制[J].
中国空间科学技术, 2012, 32 (4) : 8-14.
LI Peng, YUE Xiaokui, YUAN Jianping. Coupled control of relative position and attitude based on θ-D technique for on-orbit operations[J]. Chinese space science and technology, 2012, 32(4) : 8-14. |
| [4] | PAN Haizhou, KAPILA V. Adaptive nonlinear control for spacecraft formation flying with coupled translational and attitude dynamics[C]//Proceedings of the 40th IEEE Conference on Decision and Control. Orlando, Florida, USA:IEEE, 2001:2057-2062. |
| [5] | SEGAL S, GURFIL P. Effect of kinematic rotation-translation coupling on relative spacecraft translational dynamics[J]. Journal of guidance, control, and dynamics, 2009, 32(3) : 1045-1050DOI:10.2514/1.39320. |
| [6] |
廖飞, 季海波, 解永春. 追踪器本体坐标系下航天器姿轨一体化控制律设计[J].
控制与决策, 2015, 30 (9) : 1679-1684.
LIAO Fei, JI Haibo, XIE Yongchun. Integrated orbit and attitude control for spacecraft in body fixed coordinate of chaser[J]. Control and decision, 2015, 30(9) : 1679-1684. |
| [7] | SHAN J. Synchronized attitude and translational motion control for spacecraft formation flying[J]. Proceedings of the institution of mechanical engineers, part G:journal of aerospace engineering, 2009, 223(6) : 749-768DOI:10.1243/09544100JAERO448. |
| [8] | ZHANG Feng, DUAN Guangren. Robust adaptive integrated translation and rotation finite-time control of a rigid spacecraft with actuator misalignment and unknown mass property[J]. International journal of systems science, 2014, 45(5) : 1007-1034DOI:10.1080/00207721.2012.743618. |
| [9] |
李智斌, 吴宏鑫, 解永春, 等. 航天器智能控制实验平台[J].
自动化学报, 2001, 27 (5) : 695-699.
LI Zhibin, WU Hongxin, XIE Yongchun, et al. Experimental platform for spacecraft intelligent control[J]. Acta automatica sinica, 2001, 27(5) : 695-699. |
| [10] |
林来兴. 空间交会对接的仿真技术[J].
航天控制, 1990, 8 (4) : 66-71.
LIN Laixing. Simulation technology for rendezvous and docking in space[J]. Aerospace control, 1990, 8(4) : 66-71. |
| [11] |
刘良栋.
卫星控制系统仿真技术[M]. 北京: 中国宇航出版社, 2003: 15-21.
LIU Liangdong. Simulation technology for satellite control system[M]. Beijing: China Astronautic Publishing Press, 2003: 15-21. |
| [12] | BENNINGHOFF H, REMS F, BOGE T. Development and hardware-in-the-loop test of a guidance, navigation and control system for on-orbit servicing[J]. Acta astronautica, 2014, 102 : 67-80DOI:10.1016/j.actaastro.2014.05.023. |
| [13] |
石磊, 管乐鑫, 王京海, 等. 交会对接地面验证技术[J].
中国科学:技术科学, 2014, 44 (1) : 27-33.
SHI Lei, GUAN Yuexin, WANG Jinghai, et al. Ground test technology of rendezvous and docking[J]. Scientia sinica techologica, 2014, 44(1) : 27-33. |
| [14] | KLINE S J. Similitude and approximation theory[M]. New York: Springer, 1986: 76-103. |
| [15] | PERSSON S, BODIN P, GILL E, et al. PRISMA-an autonomous formation flying mission[C]//Proceedings of the ESA Small Satellite Systems and Services Symposium. Sardinia, Italy:ESA, 2006:25-29. |
| [16] |
何兆伟, 师鹏, 葛冰, 等. 航天器地面实验的相似性分析方法[J].
北京航空航天大学学报, 2012, 38 (4) : 502-508.
HE Zhaowei, SHI Peng, GE Bing, et al. Similitude investigation for ground experiment of spacecraft[J]. Journal of Beijing university of aeronautics and astronautics, 2012, 38(4) : 502-508. |
| [17] |
孙施浩, 赵林, 贾英民. 空间合作目标运动再现的相似设计方法研究[J].
宇航学报, 2014, 35 (7) : 802-810.
SUN Shihao, ZHAO Lin, JIA Yingmin. Similitude design method for motion reconstruction of space cooperative vehicles[J]. Journal of astronautics, 2014, 35(7) : 802-810. |
| [18] | XU Wenfu, LIANG Bin, XU Yangsheng, et al. A ground experiment system of free-floating robot for capturing space target[J]. Journal of intelligent and robotic systems, 2007, 48(2) : 187-208DOI:10.1007/s10846-006-9087-8. |
| [19] | FEHSE W. Automated rendezvous and docking of spacecraft[M]. Cambridge: Cambridge University Press, 2005: 362-417. |
| [20] | SUN Shihao, LI Hao, JIA Yingmin, et al. Development of a simulation platform for spacecraft Omni-directional rendezvous[C]//Proceedings of 2016 Chinese Intelligent Systems Conference. Xiamen, China, 2016:77-88. |



