计算机博弈,也称之为机器博弈,是人工智能领域的挑战性课题。它从模仿人脑智能的角度出发,以计算机下棋为研究载体,通过模拟人类棋手的思维过程,构建一种更接近人类智能的博弈信息处理系统,并可以拓展到其他相关领域,解决实际工程和科学研究领域中与博弈相关的难以解决的复杂问题[1-2]。作为人工智能研究的一个重要分支,它是检验计算机技术及人工智能发展水平的一个重要方向,为人工智能带来了很多重要的方法和理论,极大地推动了科研进步,并产生了广泛的社会影响和学术影响[3-5]。
计算机博弈是知识工程演绎的平台,是研究人工智能科学的“果蝇”[1]。如何提高机器智能,是计算机博弈研究的精髓所在。针对该领域技术进行研究,有助于更好地理解人类的智能,更好地推动人工智能技术和相关产业的融合与发展。
1 计算机博弈发展 1.1 起步阶段20世纪50年代开始,许多世界上著名的学者都曾经涉足计算机博弈领域的研究工作,为机器博弈的研究与开发奠定了良好的基础。阿兰·图灵(Alan Turing)先生最早写下了能够让机器下棋的指令,计算机之父冯·诺依曼(John von Neumann)提出了用于博弈的极大极小定理,信息论创始人科劳德·香农[6](Claude E. Shannon)首次提出了国际象棋的解决方案,人工智能的创始人麦卡锡(John McCarthy)首次提出“人工智能”(artificial intelligence)这一概念。1958年阿伯恩斯坦(Alex Bernstein)等[7]在IBM704机上开发了第1个成熟的达到孩童博弈水平的国际象棋程序。1959年,人工智能的创始人之一塞缪[8](A.L. Samuel)编了一个能够战胜设计者本人的西洋跳棋程序,1962年该程序击败了美国的一个州冠军。
研究机器博弈的学者们发现,博弈程序的智能水平与搜索深度有很大关系。他们研究的内容主要涉及:如何建立有效、快速的评价函数和评价方法,使评价的效率更高,花费的时间和空间的代价更小;如何在生成的博弈树上更准确有效地找到最优解,并由此发展出来各种搜索算法[9-11]。
1.2 发展阶段20世纪80年代末,随着计算机硬件和软件技术不断发展,计算机博弈理论日趋完善,学者们开始对电脑能否战胜人脑这个话题产生了浓厚的兴趣,并提出了以棋类对弈的方式,向人类发起挑战,计算机博弈研究进入了快速发展的阶段。
在国外,1986年7月,Hinton等[12]在自然杂志(Nature)上发表论文,首次系统简洁地阐述了反向传播算法在神经网络模型上的应用,给机器学习带来了希望,掀起了基于统计模型的机器学习热潮。1989年IBM公司研制的“深思”在与世界棋王卡斯帕罗夫进行的“人机大战”中,以0∶2败北。1995年IBM更新了“深蓝”程序,并使用新的集成电路将思考速度提高到每秒300万步,在1996年与卡斯帕罗夫的挑战赛中以2∶4败北。1997年“超级深蓝”融入了更深的开发,以3.5∶2.5击败了卡斯帕罗夫,这场胜利引起了世界范围内的轰动,它表明“计算机智能战胜了人类天才”。
在国内,南开大学黄云龙教授和他的学生在20世纪80年代,开发了一系列中国象棋程序。中山大学化学系教授陈志行先生在90年代初开发了围棋程序“手谈”,曾经获得世界冠军。
1.3 成熟阶段20世纪末期,国内外有许多科研机构和学者在计算机博弈领域进行深入探讨和实质性的研究。随着极大极小算法(minimax algorithm)[11]、α-β剪枝[9, 11]、上限置信区间算法(upper confidence bound apply to tree,UCT)[13]、并行搜索算法[14]、遗传算法[15]、人工神经网络[16]等技术日趋成熟,人工神经网络、类脑思维等科学也不断取得突破性进展,各种机器学习模型,例如支持向量机、 Boosting算法、最大熵方法等相继被提出,计算机博弈研究进入了一个前所未有的阶段。
2006年,Hinton和他的学生在Science上发表了一篇关于用神经网络降低数据维数的论文[16],开启了深度学习在学术界的浪潮。2007年科学杂志评出的人类10大科学突破中,包括了加拿大阿尔波特大学研究人员历时18年破解了国际跳棋(64)的研究成果,这是整个机器博弈发展史上的一个里程碑[5]。
2003年,台湾交通大学吴毅成教授发明了六子棋 (connect 6)[17],目前被认为是最公平的棋类。之后,东北大学徐心和教授[18]和他的团队[19-21]研究开发了中国象棋软件“棋天大圣”,具有挑战国内中国象棋顶级高手的实力;北邮刘知青[22-23]带领学生开发的“本手(LINGO)”围棋程序,能够战胜高水平业余围棋选手;哈工大王轩[24-26]、南航夏正友[27-28]分别带领学生开发了四国军棋博弈系统,这些程序都表现出较高的智能水平。
1.4 飞跃阶段最近几年,基于人工神经网络[3]取得了突破性的进展。运用该技术,成功地解决了计算机博弈领域中许多实际问题。
2012年6月,谷歌公司的Google Brain项目用并行计算平台训练一种称为“深度神经网络”(deep neural networks,DNN)的机器学习模型。2013年1月,百度宣布成立“深度学习研究所”(institue of deep learning,IDL)。在2015年10月5∶0击败了欧洲围棋冠军樊麾后,2016年1月,谷歌DeepMind团队在自然杂志(Nature)上发表封面论文称,他们研发出基于神经网络进行深度学习的人工智能围棋程序AlphaGo,能够在极其复杂的围棋游戏中战胜专家级人类选手[3]。2016年3月,AlphaGo又以4∶1战胜世界围棋冠军李世石,在学术界产生了空前的影响,这标志着计算机博弈技术取得重大成功,是计算机博弈发展史上新的跃迁。
2 赛事与学术交流由国际机器博弈协会(International Computer Games Association,ICGA)组织的国际计算机博弈比赛(Computer Olympiad,CO)每年一届,已经有了30多年的历史。比赛项目包括中国象棋、六子棋、亚马逊棋、围棋等,通过竞赛促进了世界范围内的计算机博弈技术的发展。同时,ICGA还每年组织学术研讨会,并出版ICGA季刊[27, 30-32]。
从1969年开始,国际人工智能联合会议(International Joint Conference on Artificial Intelligence,IJCAI)每两年举行一次,IJCAI是人工智能研究人员最主要国际会议之一。通过学术交流,发表计算机博弈的最新研究成果[33-35]。
2006年8月,由中国人工智能学会首次主办中国计算机博弈锦标赛,至今已举办10届。从2011年开始,由中国人工智能学会与教育部高等学校计算机类专业教学指导委员会共同主办全国大学生计算机博弈大赛暨全国锦标赛[36-37] ,目前已举办6届。这项赛事所设定的各项比赛,涉及计算机博弈相关的知识库、博弈平台[38]、搜索引擎、神经网络、机器学习与局面评估[39-40]等多种技术,吸引了越来越多的专家、学者与计算机博弈爱好者参与到计算机博弈相关研究中,为计算机博弈技术的交流与验证提供了一个公平、开放的平台。目前,竞赛项目涵盖了多种类型的博弈:
1) 按参与人数划分,包括双人博弈[41](如中国象棋、围棋)和多人博弈(如二打一扑克[42]);
2) 按参与人对他人了解程度划分,包括完备信息博弈[43](如中国象棋、围棋、六子棋、亚马逊棋、苏拉卡尔塔棋等)和非完全信息博弈[24, 44](如幻影围棋、军棋、二打一扑克);
3) 按参与人之间有无合作划分,包括合作博弈(如桥牌[45])与非合作博弈(如中国象棋)。
除了以上竞赛,还有各种世界范围内的人机大战活动,这些竞赛活动极大地激发了人们的挑战热情和创新精神,为社会培养了大量的科技精英,在促进了人工智能技术快速发展的同时,还产生了新的科研成果。
3 计算机博弈系统设计计算机博弈系统是指在特定规则下具有博弈能力的智能系统。在设计系统时,需要考虑知识表示、着法产生、搜索与评估几个方面。
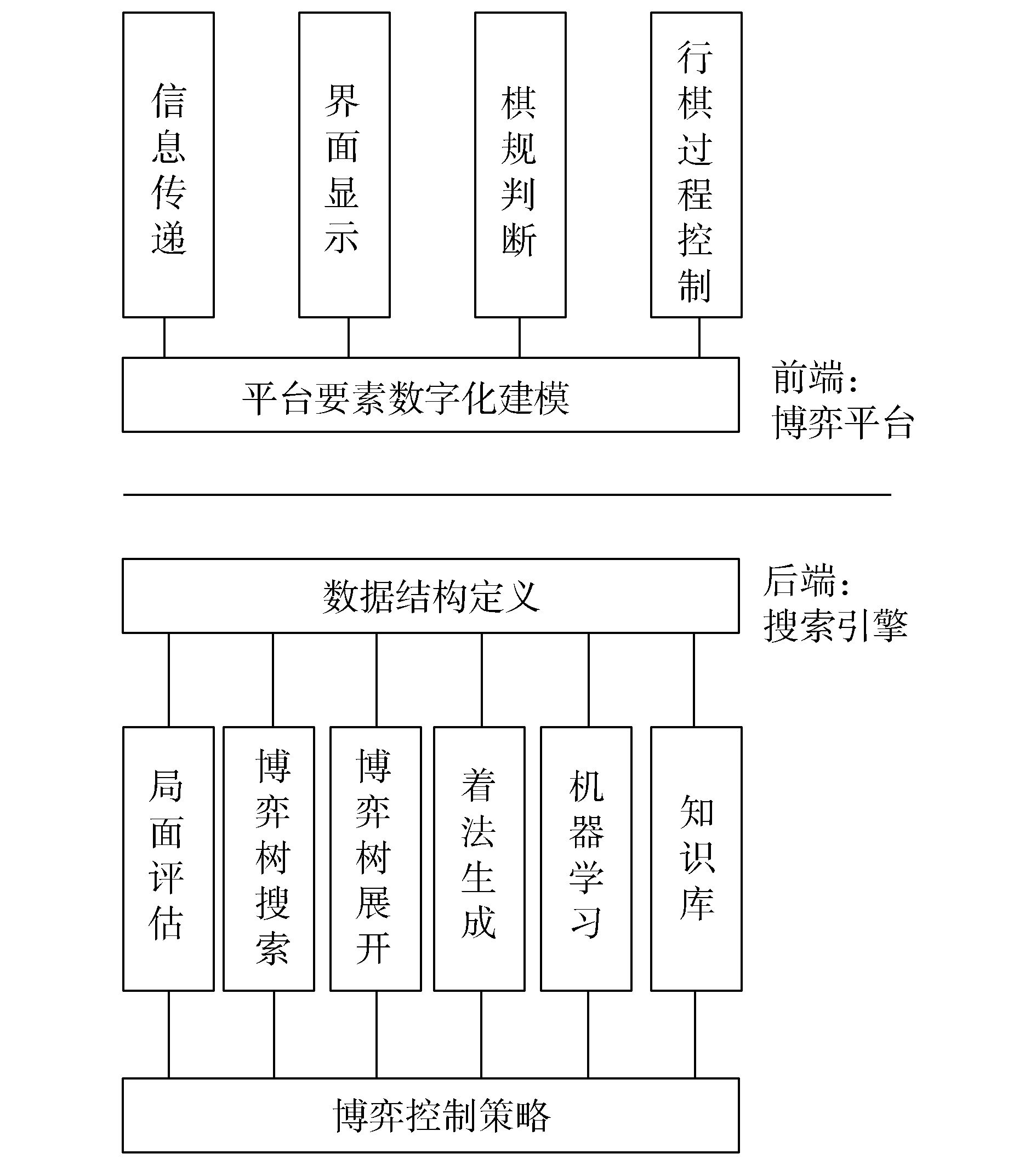
典型的计算机博弈系统的核心架构设计如图 1所示,可以划分为博弈平台和搜索引擎两大模块。其中,博弈平台主要负责界面显示、棋规判断、行棋过程控制、信息传递等[38],在其设计过程中,通常考虑通用性、易用性、健壮性、艺术性;博弈引擎主要负责知识学习、开(或残)局库设计[20, 46]、棋局评估、博弈树搜索、着法生成等。
|
| 图 1 计算机博弈系统典型架构 Fig. 1 Typical architecture of computer game system |
相对整个计算机博弈系统而言,后端搜索引擎是整个系统的核心部分,它是决定博弈胜负的关键,在搜索引擎的开发过程中,除了考虑与博弈平台的接口外,还要根据各个棋种的特点,选择合适的搜索算法和评估函数[47-48]。
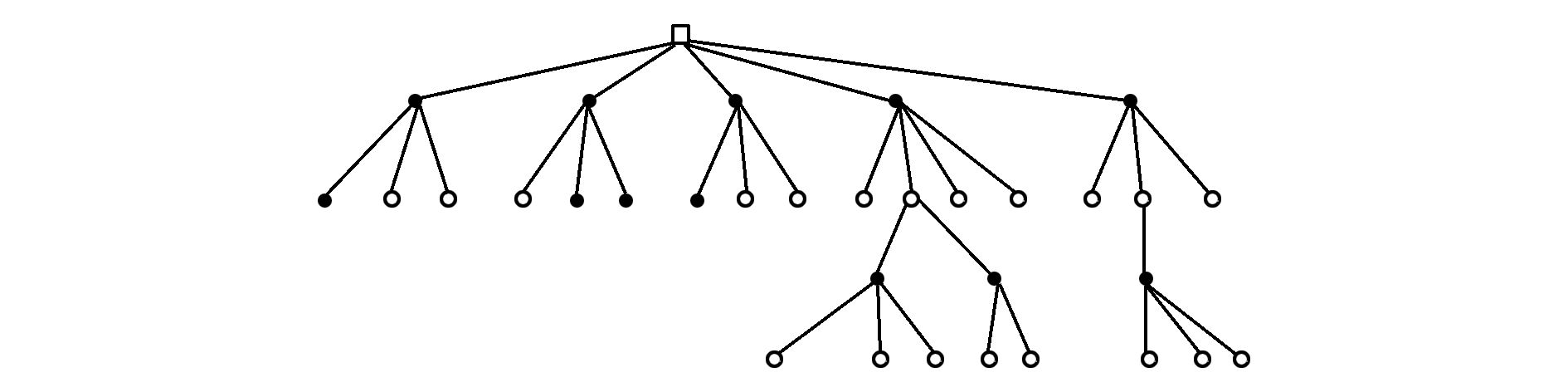
4 博弈树搜索技术 4.1 博弈树复杂度博弈树是由树枝和节点构成单向无环图,如图 2所示。博弈树的节点对应于某一个棋局,其分支表示走一步棋;根部对应于开始位置,其叶表示对弈到此结束。生成博弈着法的过程,对应博弈树的搜索与展开[49]。计算机博弈的过程是双方轮流给出着法,使棋局向着对本方有利的方向发展,直至最后的胜利。
|
| 图 2 博弈树示意图 Fig. 2 Schematic diagram of game tree |
搜索博弈树的目的就是在假设双方的走法都是最佳的情况下,找到从根节点到叶子节点的最佳路径,找出当前的最佳着法。
博弈树中的每个叶节点,都可以用评估函数来对其优劣进行评分,该值对于博弈双方都是最优的。博弈树的子树在搜索完成之后会返回一个博弈值,该值对于该子树是局部最优解,但是对整个博弈树来说并不一定是全局最优解。
在计算机博弈研究中,求解过程中计算复杂性是个难以逾越的难题。对于NP-complete、PSPACE-complete及EXPTIME-complete等难解的问题,不必将大量的精力花费在寻找问题的解析解上,而只能去寻求某种近似解。国内外学者对计算机博弈的计算复杂性[50-51]进行研究,证明了国际象棋和西洋跳棋属于EXPTIME-complete问题,围棋属于PSPACE-hard问题,中国象棋属于EXPTIME-complete问题[52]。
对于许多棋种而言,一棵完整博弈树的规模非常庞大,可以达到相当可观的天文数字,表 1中列出几种知名棋种的复杂度[53]。
| 棋种 | 状态空间复杂度 (10为底数) |
博弈树复杂度 (10为底数) |
| 国际跳棋(100格) | 30 | 54 |
| 海克斯 (11×11) | 57 | 98 |
| 国际象棋 | 46 | 123 |
| 中国象棋 | 48 | 150 |
| 亚马逊(10×10) | 40 | 212 |
| 将棋 | 71 | 226 |
| 六子棋 | 172 | 140 |
| 19路围棋 | 172 | 360 |
显然,把搜索树修整到合理范围内,减少其搜索空间,能够有效地进行展开和遍历搜索。
4.2 博弈树搜索以中国象棋、国际跳棋为代表的二人零和完备信息博弈,其搜索理论已经很系统。其中极大极小算法[53]是最基本的搜索算法,它奠定了计算机博弈的理论基础。以极大极小算法为基础的博弈树搜索算法,从搜索方向考虑,可以分为深度优先搜索和宽度优先搜索;从控制策略考虑,可以分为盲目搜索和启发搜索;从搜索范围考虑,可以分为穷尽搜索、裁剪搜索。
相对而言,宽度优先搜索、穷尽搜索和盲目搜索算法时间和空间开销巨大,难以做到很深的搜索。因此,在计算机博弈的实际应用中,很少直接使用此类算法解决问题。
4.2.1 穷尽搜索极大极小算法[54]是典型的穷尽搜索方法,通过它可以找到对于博弈双方都是最优的博弈值,但该算法对博弈树的搜索是一种变性搜索,算法实现相对麻烦。
负极大值算法在极大极小算法基础上进行了改进,把极小节点值(返回给搜索引擎的局面估值)取绝对值,这样每次递归都选取最大值。
4.2.2 裁剪搜索裁剪算法也称剪枝算法,是计算机博弈中最常用的主流算法,它包括深度优先的Alpha-Beta剪枝搜索[9]和以此为基础改进与增强的算法,如渴望窗口搜索(aspiration search)[55]、MTD(f)(memory-enhanced test driver with f and n)搜索[56]等。在具体应用中,合理地交叉使用各种搜索方法,可以具有更高的效率[56]。
Alpha-Beta剪枝是在极大极小算法基础上的改进算法,是其他剪枝算法的基础。目前,多数博弈程序都采用负极大值形式的Alpha-Beta搜索算法。为保证Alpha-Beta搜索算法的效率,需要调整树的结构,即对搜索节点排序,确保尽早剪枝。
渴望搜索是在Alpha-Beta搜索算法基础上,缩小搜索范围的改进算法。渴望搜索从一开始就使用小的窗口,从而在搜索之初,就可以进行大量的剪枝。通常,渴望搜索与遍历深化技术结合使用,以提高搜索性能。
3) MTD(f)搜索[56]
MTD(f)搜索实际上就是不断应用零窗口的Alpha-Beta搜索,缩小上界和下界,并移动初始值使其接近最优着法。MTD(f)算法简单高效,在国际象棋、国际跳棋等博弈程序里,MTD(f) 算法平均表现出色。
此外,还有各种在Alpha-Beta搜索基础上优化的算法,例如,有学者提出在博弈树同层结点中,用广度优先搜索,接力式空窗探测,平均搜索效率高于MTD(f)搜索[57]。通常,裁剪算法需要与置换表技术相结合,以减少博弈树的规模,提高搜索效率。
4.2.3 置换表[58]技术置换表是一个大的直接访问表,用来存储已经搜索过结点(或者子树)的结果,下次搜索遇到时直接运用。置换表的构造,一般使用 Hash 表和ZobristHash 技术来实现。
合理使用置换表,可以提高搜索效率,当博弈树的深度很大时,置换表对内存空间要求巨大。通常的对策是对置换表分配有限大小,并采用散列方式管理存取。具体应用到各个棋种中时,还要根据实际局面的节点类型,进行处理。
4.2.4 启发式算法“启发”(Heuristic)是指通过排序让Alpha-Beta剪枝的搜索树尽可能地接近最小树,优先搜索好的着法。启发通常有置换表启发、历史启发和杀手启发等常用的算法。
置换表启发是置换表与Alpha-Beta剪枝算法相结合的产物。在中国象棋等棋种中,通过引进置换表启发技术来增强搜索效率。
2) 历史启发[60]
历史启发也是迎合alpha-beta搜索对节点排列顺序敏感的特点来提高剪枝效率的。它通过维护着法历史,每当遇到好的着法,就给其历史得分一个相应的增量,使其具有更高的优先被搜索的权利。
历史启发是一种基于经验的择序标准,它克服了基于知识择序存在的知识不足的缺点,使得算法的择序具有很强的动态适应性。
3) 杀手启发[61]
杀手启发可以看作是历史启发的特例。它把同层中引发剪枝最多的节点称为杀手,当下次搜索到同一层时,如果杀手移动是合法的话,就优先搜索杀手。杀手启发可以对着法进行动态重排序,且提高了置换表的使用效率。
4.2.5 迭代深化[62]迭代深化也称为遍历深化,是一种常用的蛮力搜索机制,经常使用在深度优先搜索中。迭代深化最初是作为控制时间的机制而提出的,通过对博弈树进行多次遍历,并逐渐提高搜索深度,一直到指定的时间停止。
迭代深化利用Alpha-Beta剪枝算法对子节点排序敏感的特点,使用上次迭代后得到的博弈值,作为当前迭代的搜索窗口估值,以此为启发式信息计算当前迭代的博弈值。另外,它利用时间控制遍历次数,只要时间一到,搜索立即停止。在关键的开局和残局,由于分支较少,可以进行较深层次的搜索。Alpha-Beta剪枝经过一系列技术如置换表、历史启发、迭代深化等增强后,其性能可大幅提高。
4.2.6 最佳优先算法最佳优先的搜索算法,不受节点排序的影响,其搜索空间小于深度优先的最小树,理论上应该优于深度优先。实际上,最佳优先算法仍处于理论研究阶段。最佳优先算法分为两类:采用极大极小算法取值的SSS*[63-64]算法和DUAL*算法,不采用极大极小方法取值的B*[65]和PB*[66]算法。
SSS*和DUAL*算法都属于状态空间搜索(State Space Search),把极大极小树看成状态图,在不同的分支上展开多条路径,并且维护一个关于状态图的全局信息表。这两种算法是两个操作相反的过程,前者在搜索深度为偶数的极大极小搜索中表现较佳,后者则在深度为奇数搜索中较佳。
SSS*和DUAL*算法都过于复杂,难于理解,且时间和空间开销较大,在计算机博弈中实际应用较少。
B*算法用一个乐观值和一个悲观值来评价节点。当根节点的一个孩子的悲观值不比所有其他节点的乐观值差的时候,B*算法就结束了。算法搜索控制的关键是尽快找到终止条件。由于它对局面估值的依赖性太强,估值的可信度将直接影响最终结果。
PB*算法就是基于概率的B*算法,这个算法对概率的准确估计比较敏感,实现困难。
4.2.7 随机搜索随机搜索有两种算法:拉斯维加斯算法和蒙特卡罗算法。采样越多,前者越有机会找到最优解,后者则越接近最优解。
通常,要根据问题的约束条件来确定随机算法,如果对采样没有限制,但必须给出最优解,则采用拉斯维加斯算法。反之,如果要求在有限采样内求解,但不要求是最优解,则采用蒙特卡罗算法。
计算机博弈中,每步着法的运算时间、堆栈空间都是有限的,且仅要求局部优解,适合采用蒙特卡罗算法。由于非完备信息博弈也具有不确定性博弈的一些特征,所以蒙特卡罗算法也适用于非完备信息博弈。
1) 蒙特卡罗搜索(MCTS,Monte Carlo Tree Search)[67-70]
在人工智能的问题中,蒙特卡罗搜索是一种最优决策方法,它结合了随机模拟的一般性和树搜索的准确性。由于海量搜索空间、评估棋局和落子行为的难度,围棋长期以来被视为人工智能领域最具挑战的经典游戏。近年来,MCTS在类似计算机围棋等完备信息博弈、多人博弈以及其他随机类博弈难题上的成功应用而受到快速关注[71]。理论上,MCTS可以被用在以{状态,行动}定义并用模拟预测输出结果的任何领域。
基本的 MCTS 算法根据模拟的输出结果,按照节点构造博弈树,其过程如图 3所示,包括路径选择(Selection)、节点扩展(Expansion)、模拟实验(Simulation)、反向传播(Backpropagation)4个步骤。

|
| 图 3 构造MCTS博弈树的过程 Fig. 3 Process of constructing the MCTS game tree |
MCTS算法适用于有较大分支因子的博弈程序,如AlphaGo就是采用MCTS算法进行搜索[3]。
UCT算法,即上限置信区间算法,是一种基于MCTS发展的博弈树搜索算法,该算法通过扩展 UCB(upper confidence bound)到极大极小树搜索,将MCTS方法与UCB公式结合。
UCB计算方法如公式1所示,在向下遍历博弈树时,通过选择最大化该值来实现节点的选择。
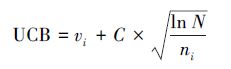 |
(1) |
式中:vi是节点i估计的值,ni是节点i被访问的次数,而N是其父节点已被访问的总次数,C 是可调参数。相对于传统的搜索算法,UCT时间可控,具有更好的鲁棒性,可以非对称动态扩展博弈树,在超大规模博弈树的搜索过程中,表现出时间和空间方面的优势。目前,UCT在搜索规模较大的完备信息博弈、复杂的多人博弈、非完备信息博弈以及随机类博弈项目中,表现出色[71]。
5 局面评估在计算机博弈系统中,对博弈局面评估得越全面、越准确,获胜的机率就会越高。但是,博弈有个很重要的约束条件就是时间。评估中考虑的问题越全面细致,则耗费的时间就越多,搜索的深度和速度必然受到影响。另外,随着搜索深度加深,信息处理量也会大幅提升。
设计评估函数需要考虑诸多因素,在完全信息博弈中双方的子力、领地、位置、空间、机动性、拍节、威胁、形状、图案都可以作为评估参数,非完备信息博弈中除了己方已知参数外,还要猜测对手的情况,并通过量化后加权组合而成。
国内外有不少学者在计算机博弈评估方面做了大量深入研究[72]。针对不同棋种的特点,学者们提出了各种不同的方式进行评估与优化:通过博弈记录来评估博弈树搜索[73];针对六子棋应用遗传算法进行寻优处理,优化机器博弈评估函数[40];在中国象棋里,把自适应遗传算法引入评估函数中,通过锦标赛算法对评估函数中的参数组合进行自动调整和优化[19];根据棋子的数量、移动范围、攻击范围、子力攻击力、盘面分值和占弧价值等对苏拉卡尔塔棋局面评估函数进行了研究[40];根据亚马逊棋领地、位置和机动性等特征在不同阶段的重要程度及权重值,给出一个分阶段的评估函数[47, 74]。
提高计算机博弈能力不能单纯依靠加大搜索深度,还需要将必要的相关博弈知识引入到相应的博弈搜索中,只有协调搜索算法与评估函数,博弈系统才能发挥有效作用。
6 综合优化技术计算机博弈中,目前应用较多的综合优化技术主要有并行计算、遗传算法和基于神经网络的深度学习。
6.1 并行计算并行计算[14, 75] 是为了提高计算速度,把博弈树动态分开,发挥计算机多CPU强大的并行处理能力,同时执行多个指令的算法。它不裁剪和缩小博弈树的规模,通过提高搜索速度,而进行优化系统。
并行计算有两种体系,单机体系SMP(Symmetric Multiprocessor)和分布式体系Cluster(计算机集群),对应多线程并行和多机并行。两者最大的区别是,前者可以共享存储器(并且共享同一地址的存储单元),后者则必须通过网络来交换数据。由于博弈搜索通常需要用到置换表,所以适合以SMP的方式多线程并行处理,但随着大数据、云计算等技术的成熟与完善,计算机集群技术将被越来越多地运用到计算机博弈中。
6.2 遗传算法遗传算法[15]是人工智能领域的关键技术,它是一种非数值、并行、随机优化、搜索启发式的算法,通过模拟自然进化过程随机化搜索最优解。它采用概率化的寻优方法,能自动获取和指导优化的搜索空间,自适应地调整搜索方向,不需要确定的规则,同时具有内在的隐并行性和更好的全局寻优能力。
遗传算法是解决搜索问题的一种通用算法,在计算机博弈中,遗传算法通常被用于搜索、自适应调整和优化局面评估参数。它的基本思想是将博弈树看作遗传操作的种群,博弈树中由根节点到叶子节点组成的所有子树为种群中的个体。根据优化目标设计评估函数,计算种群中每个个体的适应度函数值,依据适应度函数值的大小确定初始种群,让适应性强(适应度函数值大)的个体获得较多的交叉、遗传机会,生成新的子代个体,通过反复迭代,可得到满意解。
采用遗传算法优化局面估值时,可根据博弈程序与其他程序对弈的结果,检验某一组参数获胜的机率。经过多次试验,通常可以找到较好的估值参数。传统的算法一般只能维护一组最优解,遗传算法可以同时维护多组最优解。在实践中,遗传算法被引入了中国象棋、国际象棋、亚马逊等棋搜索与评估优化中,效果还是很明显的[19]。
6.3 深度学习深度学习是基于多层网络结构的一种机器学习方法,它逐层提取抽象特征,通过多层非线性传输,完成复杂的目标函数系统逼近。深度学习领域典型的网络模型包括卷积神经网络(convolutional neural networks,CNN)、深层玻尔兹曼机(deep boltzmann machine,DBM)和堆叠自动编码器(stacked auto-encoder,SAE)等[76]。
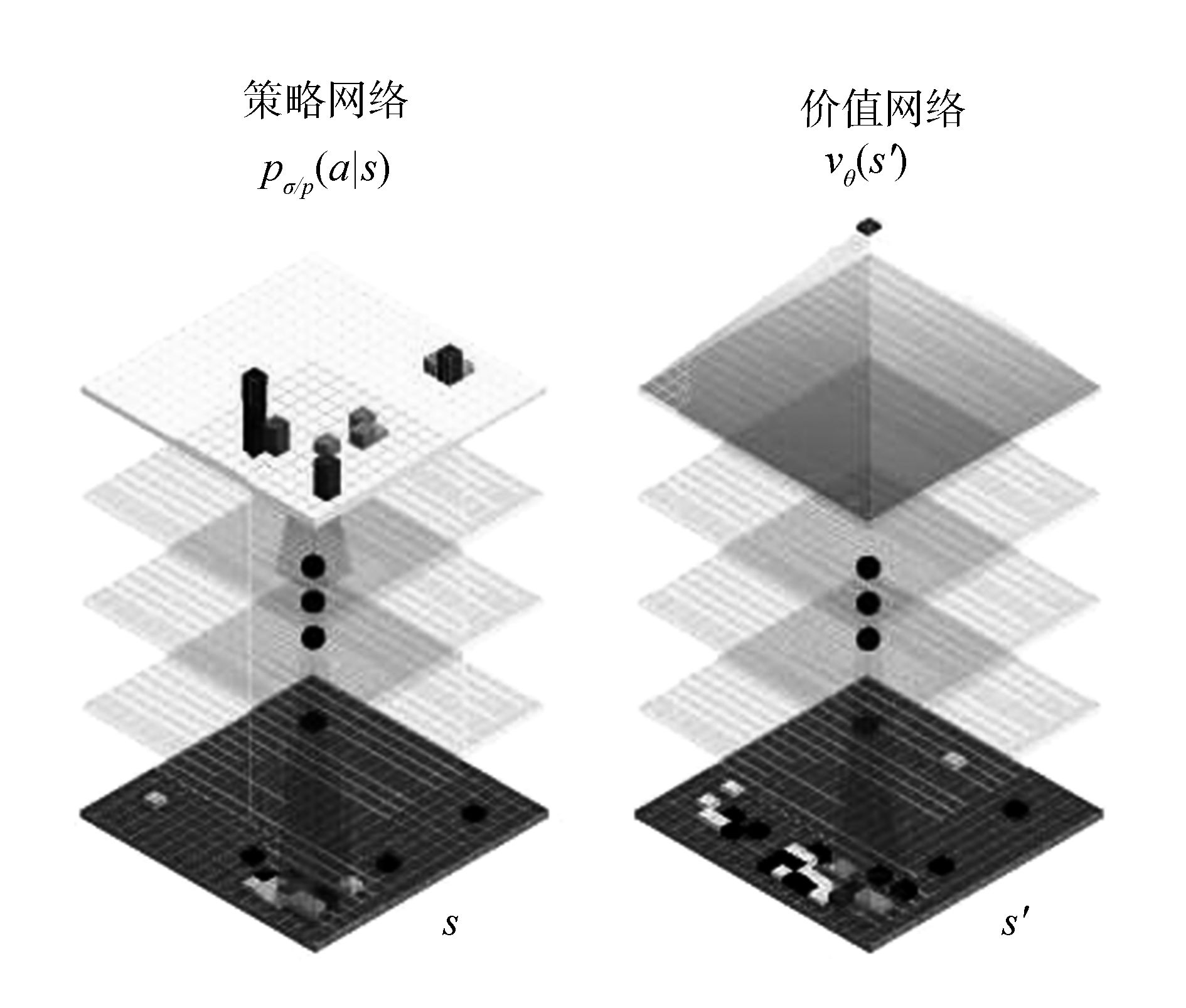
近几年,基于人工神经网络的深度学习技术逐渐被应用于计算机博弈中[3, 29],人工智能围棋程序AlphaGo是其典型代表[3]。AlphaGo成功的关键在于拥有两个大脑——落子选择器(move picker)和棋局评估器(position evaluator)。分别基于两种不同的深度神经网络——策略网络(policy network)和价值网络(value network),如图 4所示。前者用于学习高水平棋手的棋谱,获得如何在盘面落子的棋感;后者通过机器的增强型学习,获得形势判断的棋感。这两个棋感通过蒙特卡罗搜索的技术进行验证,使AlphaGo实现了技术突破。
尽管深度学习技术在围棋方面取得了前所未有的成功,但在拓展应用方面,如何合理利用深度学习方法来增强传统学习算法的性能,提升计算机博弈水平,仍是今后研究的重点。
|
| 图 4 AlphaGo神经网络体系结构原理图 Fig. 4 Schematic representation of the neural network architecture used in AlphaGo |
近年来,计算机博弈给人工智能带来了很多重要的方法和理论,在二人零和完备信息博弈研究方面,其知识结构系统层次清晰,已经取得了许多惊人的成果,其中,关于基于神经网络深度学习技术的研究与运用,已经达到新的高度。在中国象棋、围棋等完全信息的计算机博弈中,尽管状态空间和搜索树复杂度都较大,但经过大量学习与训练,结合大规模搜索算法,计算机占尽优势[78]。
另一个方面,对于军棋、麻将、桥牌、扑克等非完备信息博弈,以及具有模糊性和随机性的不确定性博弈,虽然在基于案例的策略研究方面有了一定进展,但因其相关理论研究还不成熟,相应的程序智力有限,仍难以战胜人类真正的高手。因此,在非完备信息和不确定性机器博弈方面,具有高效学习与抽象思维能力的博弈技术还有待进一步研究。另外,在计算机博弈平台方面的研究投入相对较少,对计算机博弈技术的发展也有所制约。
可以预见,在不远的将来,计算机博弈技术将融入各个领域的应用中,具体体现在如下几点:
1) 计算机博弈研究的内容将不断拓宽,处理的问题复杂程度越来越高,信息量将越来越大。为解决某类特定问题,技术方法将集成化,计算机博弈技术将与并行计算、大数据技术等相关技术结合。
2) 计算机博弈软件与硬件的结合越来越密切,固化博弈系统的智能硬件产品将越来越多地出现在人们的生活中,典型的应用包括:有博弈思维能力机器人、智能决策控制系统的无人驾驶汽车和无人机。
3) 计算机博弈技术将与其他学科进一步融合,越来越紧密地应用经济、生活、军事等领域,注重实际工程应用,解决实际问题。在虚拟现实仿真方面,特别是游戏与教育方面拥有广阔的应用前景。
4) 计算机博弈技术将呈现高度智能化趋势,通过与遗传算法、人工神经网络、类脑思维等人工智能技术进一步融合,类似基于神经网络深度学习的智能技术将大量涌现,使得计算机博弈程序的类脑智能越来越高。
5) 合理拓展现有的博弈技术,深入研究更加智能的普适算法,构建一个通用的计算机博弈系统,也将成为未来计算机博弈研究的重点。
8 结束语伴随着人工智能科学发展的60周年,计算机博弈也经历了起步、发展、成熟、飞跃4个阶段。依托各种形式的竞赛,极大地促进了学术交流,检验了新技术,推动了博弈的研究与发展。当前完备信息博弈技术相对比较成熟,非完备信息博弈和随机类博弈技术还需进一步发展。深度学习算法在AlphaGo围棋计算机博弈中的成功应用,引发了世界范围内对人工智能技术的高度关注,调动了更多的专家学者开展深入研究的积极性。尽管在计算机博弈领域还存在着各种各样的问题,许多工作还需要向更广领域和更深层次推进,但是随着研究人员的不断增加以及计算机博弈技术在各个领域的广泛应用,将会产生越来越多的研究成果。计算机博弈是一个颇有发展前途的研究领域。
| [1] |
徐心和, 邓志立, 王骄, 等. 机器博弈研究面临的各种挑战[J].
智能系统学报, 2008, 3 (4) : 288-293.
XU Xinhe, DENG Zhili, WANG Jiao, et al. Challenging issues facing computer game research[J]. CAAI transactions on intelligent systems, 2008, 3(4) : 288-293. |
| [2] | 徐心和. 计算机博弈--对于人类思维的挑战[J]. 中国科技博览, 2009 (34) : 194-195. |
| [3] | SILVER D, HUANG Ajia, MADDISON C J, et al. Mastering the game of Go with deep neural networks and tree search[J]. Nature, 2016, 529(7587) : 484-489DOI:10.1038/nature16961. |
| [4] | BENCH-CAPON T J M, DUNNE P E. Argumentation in artificial intelligence[J]. Artificial intelligence, 2007, 171(10/15) : 619-641. |
| [5] | PENNISI E. Breakthrough of the year:human genetic variation[J]. Science, 2007, 318(5858) : 1842-1843DOI:10.1126/science.318.5858.1842. |
| [6] | SHANNON C E. Programming a computer for playing chess[J]. Philosophical magazine, 1950, 41(314) : 2562275. |
| [7] | BERNSTEIN A, ARBUCKLE T, DE V ROBERTS M, et al. A chess playing program for the IBM 704[C]//Proceedings of the May 6-8, 1958, Western Joint Computer Conference:Contrasts in Computers. New York, NY, USA:ACM, 1958:157-159. |
| [8] | SAMUEL A L. Some studies in machine learning using the game of checkers. II:recent progress[J]. IBM journal of research and development, 1967, 11(6) : 601-617DOI:10.1147/rd.116.0601. |
| [9] | FULLER S H, GASCHNIG J G, GILLOGLY J J. Analysis of the alpha-beta pruning algorithm[R]. Carnegie:Carnegie Mellon University, 1973. |
| [10] | KORF R E. Depth-first iterative-deepening:an optimal admissible tree search[J]. Artificial intelligence, 1985, 27(1) : 97-109DOI:10.1016/0004-3702(85)90084-0. |
| [11] | ROIZEN I, PEARL J. A minimax algorithm better than alpha-beta? Yes and No[J]. Artificial intelligence, 1983, 21(1/2) : 199-220. |
| [12] | RUMELHART D E, HINTON G E, WILLIAMS R J. Learning representations by back-propagating errors[J]. Nature, 1986, 323(6088) : 533-536DOI:10.1038/323533a0. |
| [13] | GELLY S, SILVER D. Combining online and offline knowledge in UCT[C]//Proceedings of the 24th International Conference on Machine Learning. New York, USA:ACM, 2007:273-280. |
| [14] |
李之棠, 陈华民. 博弈树并行搜索算法[J].
小型微型计算机系统, 1998, 19 (10) : 53-56.
LI Zhitang, CHEN Huamin. Parallel game-tree search[J]. Mini-micro systems, 1998, 19(10) : 53-56. |
| [15] | DAVID-TABIBI O, KOPPEL M, NETANYAHU N S. Genetic algorithms for automatic search tuning[J]. ICGA journal, 2010, 33(2) : 67-79DOI:10.3233/ICG-2010-33202. |
| [16] | HINTON G E, SALAKHUTDINOV R R. Reducing the dimensionality of data with neural networks[J]. Science, 2006, 313(5786) : 504-507DOI:10.1126/science.1127647. |
| [17] | WU I C, CHANG H C. Threat-based proof search for Connect 6[R]. Taiwan, China:National Chiao Tung University, 2006. |
| [18] |
徐心和, 王骄. 中国象棋计算机博弈关键技术分析[J].
小型微型计算机系统, 2006, 27 (6) : 961-969.
XU Xinhe, WANG Jiao. Key technologies analysis of Chinese chess computer game[J]. Mini-micro systems, 2006, 27(6) : 961-969. |
| [19] |
王骄, 王涛, 罗艳红, 等. 中国象棋计算机博弈系统评估函数的自适应遗传算法实现[J].
东北大学学报:自然科学版, 2005, 26 (10) : 949-952.
WANG Jiao, WANG Tao, LUO Yanhong, et al. Implementation of adaptive genetic algorithm of evaluation function in Chinese chess computer game system[J]. Journal of northeastern university:natural science, 2005, 26(10) : 949-952. |
| [20] |
魏钦刚, 王骄, 徐心和, 等. 中国象棋计算机博弈开局库研究与设计[J].
智能系统学报, 2007, 2 (1) : 85-89.
WEI Qingang, WANG Jiao, XU Xinhe, et al. A study and design of opening-book of computer Chinese Chess[J]. CAAI transactions on intelligent systems, 2007, 2(1) : 85-89. |
| [21] |
徐长明, 南晓斐, 王骄, 等. 中国象棋机器博弈的时间自适应分配策略研究[J].
智能系统学报, 2006, 1 (2) : 39-43.
XU Changming, NAN Xiaofei, WANG Jiao, et al. Adaptive time allocation strategy in computer game of Chinese Chess[J]. CAAI transactions on intelligent systems, 2006, 1(2) : 39-43. |
| [22] | LIU Zhiqing, DOU Qing. Automatic pattern acquisition from game records in GO[J]. The journal of China universities of posts and telecommunications, 2007, 14(1) : 100-105DOI:10.1016/S1005-8885(07)60065-X. |
| [23] | LIU Zhiqing, DOU Qing, LI Wenhong, et al. Automatic acquisition of pattern collocations in GO[J]. The journal of China universities of posts and telecommunications, 2008, 15(1) : 61-67DOI:10.1016/S1005-8885(08)60063-1. |
| [24] |
马骁, 王轩, 王晓龙. 一类非完备信息博弈的信息模型[J].
计算机研究与发展, 2010, 47 (12) : 2100-2109.
MA Xiao, WANG Xuan, WANG Xiaolong. The information model for a class of imperfect information game[J]. Journal of computer research and development, 2010, 47(12) : 2100-2109. |
| [25] | ZHANG Jiajia, WANG Xuan, LIN Jing, et al. UCT algorithm in imperfect information multi-player military chess game[C]//Proceedings of the 11th Joint Conference on Information Sciences. Atlantis Press, 2008:1-9. |
| [26] | WANG X, XU Zhaoyang, MA X. TD (Λ) optimization of imperfect information game's evaluation function[R]. Japan:WCCGC, 2007. |
| [27] | XIA Zhengyou, ZHU Yongping, LU Hui. Using the loopy belief propagation in Siguo[J]. ICGA journal, 2007, 30(4) : 209-220. |
| [28] | XIA Zhengyou, ZHU Yongping, LU Hui. Evaluation function for siguo game based on two attitudes[C]//Proceedings of the Third International Conference on Fuzzy Systems and Knowledge Discovery. Berlin Heidelberg:Springer, 2006:1322-1331. |
| [29] | BENGIO Y, LAMBLIN P, POPOVICI D, et al. Greedy layer-wise training of deep networks[M]//SCHÖLKOPF B, PLATT J, HOFMANN T. Advances in Neural Information Processing Systems, vol 19. Cambridge:MIT Press, 2007:153-160. |
| [30] | COULOM R. Computing "Elo ratings" of move patterns in the game of go[J]. ICGA journal, 2007, 30(4) : 198-208. |
| [31] | FERREIRA D R. Determining the strength of chess players based on actual play[J]. ICGA journal, 2012, 35(1) : 3-19DOI:10.3233/ICG-2012-35102. |
| [32] | NIJSSEN J A M, WINANDS M H M. Search policies in multi-player games1[J]. ICGA journal, 2013, 36(1) : 3-21DOI:10.3233/ICG-2013-36102. |
| [33] | LEIFKER D B, KANAL L N. A hybrid SSS*/Alpha-Beta algorithm for parallel search of game trees[C]//Proceedings of the 9th International Joint Conference on Artificial Intelligence. San Francisco, CA, USA:ACM, 1985, 2:1044-1046. |
| [34] | PLAAT A, SCHAEFFER J, PIJLS W, et al. Best-first fixed-depth game-tree search in practice[C]//Proceedings of the 14th International Joint Conference on Artificial Intelligence. San Francisco, CA, USA:ACM, 1995, 1:273-279. |
| [35] | BURNS E, LEMONS S, ZHOU Rong, et al. Best-first heuristic search for multi-core machines[C]//Proceedings of the 21st International Jont Conference on Artifical Intelligence. San Francisco, CA, USA:ACM, 2009:449-455. |
| [36] | 王骄, 徐心和. 计算机博弈:人工智能的前沿领域--全国大学生计算机博弈大赛[J]. 计算机教育, 2012 (7) : 14-18. |
| [37] | 邱虹坤. 全国计算机博弈大赛网站[EB/OL].[2016-04-22]. 2013. http://www.caaigames.net. |
| [38] |
张利群. 实现苏拉卡尔塔棋网络博弈平台的吃子算法[J].
计算机工程与应用, 2016, 52 (7) : 62-66.
ZHANG Liqun. Realization of capture algorithm about Surakarta chess network battle platform in computer game[J]. Computer engineering and applications, 2016, 52(7) : 62-66. |
| [39] |
张小川, 陈光年, 张世强, 等. 六子棋博弈的评估函数[J].
重庆理工大学学报:自然科学版, 2010, 24 (2) : 64-68.
ZHANG Xiaochuan, CHEN Guangnian, ZHANG Shiqiang, et al. Research on evaluation functions for computer game of connect 6[J]. Journal of Chongqing university of technology:natural science, 2010, 24(2) : 64-68. |
| [40] |
李淑琴, 李静波, 韩裕华, 等. 苏拉卡尔塔博弈系统中评估函数的研究[J].
北京信息科技大学学报, 2012, 27 (6) : 42-45.
LI Shuqin, LI Jingbo, HAN Yuhua, et al. The assessment function in the Surakarta game system[J]. Journal of Beijing information science and technology university, 2012, 27(6) : 42-45. |
| [41] | TANG Pingzhong, LIN Fangzhen. Discovering theorems in game theory:two-person games with unique pure Nash equilibrium payoffs[J]. Artificial intelligence, 2011, 175(14/15) : 2010-2020. |
| [42] | RUBIN J, WATSON I. Case-based strategies in computer poker[J]. AI communications, 2012, 25(1) : 19-48. |
| [43] | FLESCH J, KUIPERS J, SCHOENMAKERS G, et al. Subgame-perfection in free transition games[J]. European journal of operational research, 2013, 228(1) : 201-207DOI:10.1016/j.ejor.2013.01.034. |
| [44] | GILPIN A, SANDHOLM T. Lossless abstraction of imperfect information games[J]. Journal of the ACM, 2007, 54(5) : 25DOI:10.1145/1284320. |
| [45] |
何大华, 陈传波. 关于桥牌的取胜策略[J].
华中科技大学学报:自然科学版, 2004, 32 (7) : 13-15.
HE Dahua, CHEN Chuanbo. The strategy for winning bridge game[J]. Journal of Huazhong university of science & technology:nature science edition, 2004, 32(7) : 13-15. |
| [46] | CHEN Bonian, LIU Pangfeng, HSU S C, et al. Aggregating consistent endgame knowledge in Chinese Chess[J]. Knowledge-based systems, 2012, 34 : 34-42DOI:10.1016/j.knosys.2011.11.020. |
| [47] |
郭琴琴, 李淑琴, 包华. 亚马逊棋机器博弈系统中评估函数的研究[J].
计算机工程与应用, 2012, 48 (34) : 50-54.
GUO Qinqin, LI Shuqin, BAO Hua. Research on evaluation function computer game of Amazon[J]. Computer engineering and applications, 2012, 48(34) : 50-54. |
| [48] | SCHADD M P D, WINANDS M H M. Best reply search for multiplayer games[J]. IEEE transactions on computational intelligence and AI in games, 2011, 3(1) : 57-66DOI:10.1109/TCIAIG.2011.2107323. |
| [49] |
李学俊, 王小龙, 吴蕾, 等. 六子棋中基于局部"路"扫描方式的博弈树生成算法[J].
智能系统学报, 2015, 10 (2) : 267-272.
LI Xuejun, WANG Xiaolong, WU Lei, et al. Game tree generation algorithm based on local-road scanning method for connect 6[J]. CAAI transactions on intelligent systems, 2015, 10(2) : 267-272. |
| [50] | ETESSAMI K, LOCHBIHLER A. The computational complexity of evolutionarily stable strategies[J]. International journal of game theory, 2008, 37(1) : 93-113DOI:10.1007/s00182-007-0095-0. |
| [51] |
高强, 徐心和. 时间复杂性和空间复杂性研究[J].
智能系统学报, 2014, 9 (5) : 529-535.
GAO Qiang, XU Xinhe. Research on time complexity and space complexity[J]. CAAI transactions on intelligent systems, 2014, 9(5) : 529-535. |
| [52] | GAO Qiang, XU Xinhe. Research on the computational complexity of n x n Chinese chess[J]. ICGA journal, 2015, 38(1) : 47-53DOI:10.3233/ICG-2015-38106. |
| [53] | VAN DER HERIK H J, UITERWIJK J W H M, VAN RIJSWIJCK J. Games solved:now and in the future[J]. Artificial intelligence, 2002, 134(1/2) : 277-311. |
| [54] | KAINDL H, SHAMS R, HORACEK H. Minimax search algorithms with and without aspiration windows[J]. IEEE transactions on pattern analysis and machine intelligence, 1991, 13(12) : 1225-1235DOI:10.1109/34.106996. |
| [55] | LU Hui, XIA Zhengyou. AWT:aspiration with timer search algorithm in Siguo[C]//Proceedings of the 6th International Conference on Computers and Games. Berlin Heidelberg:Springer-Verlag, 2008:264-274. |
| [56] |
邹竞. 基于MTD(f)的中国象棋人机博弈算法的设计与优化[J].
计算机与数字工程, 2008, 36 (9) : 38-43.
ZOU Jing. Chinese chess algorithm design and optimize based on MTD(f)[J]. Computer & digital engineering, 2008, 36(9) : 38-43. |
| [57] |
张明亮, 李凡长. 一种新的博弈树搜索方法[J].
山东大学学报:工学版, 2009, 39 (6) : 1-8.
ZHANG Mingliang, LI Fanzhang. A new search method for a game tree[J]. Journal of Shandong university:engineering science, 2009, 39(6) : 1-8. |
| [58] |
焦尚彬, 刘丁. 博弈树置换表启发式算法研究[J].
计算机工程与应用, 2010, 46 (6) : 42-45.
JIAO Shangbin, LIU Ding. Research on translation table heuristic algorithm[J]. Computer engineering and applications, 2010, 46(6) : 42-45. |
| [59] | DONKERS H H L M, UITERWIJK J W H M, VAN DER HERIK H J. Probabilistic opponent-model search[J]. Information sciences, 2001, 135(3/4) : 123-149. |
| [60] | SCHAEFFER J. The History heuristic and alpha-beta search enhancements in practice[J]. IEEE transactions on pattern analysis and machine intelligence, 1989, 11(11) : 1203-1212DOI:10.1109/34.42858. |
| [61] | SAKUTA M, HASHIMOTO T, NAGASHIMA J, et al. Application of the killer-tree heuristic and the lambda-search method to lines of action[J]. Information sciences, 2003, 154(3/4) : 141-155. |
| [62] | REINEFELD A, MARSLAND T A. Enhanced iterative-deepening search[J]. IEEE transactions on pattern analysis and machine intelligence, 1994, 16(7) : 701-710DOI:10.1109/34.297950. |
| [63] | MARSLAND T A, REINEFELD A, SCHAEFFER J. Low overhead alternatives to SSS[J]. Artificial intelligence, 1987, 31(2) : 185-199DOI:10.1016/0004-3702(87)90019-1. |
| [64] | PLAAT A, SCHAEFFER J, PIJLS W, et al. SSS*=alpha-beta + TT[J]. Computer Science, 2014, 8(1) : 25. |
| [65] | BERLINER H. The B* tree search algorithm:a best-first proof procedure[J]. Artificial intelligence, 1979, 12(1) : 23-40DOI:10.1016/0004-3702(79)90003-1. |
| [66] | BERLINER H J, MCCONNELL C. B * probability based search[J]. Artificial intelligence, 1996, 86(1) : 97-156DOI:10.1016/0004-3702(95)00092-5. |
| [67] | LORENTZ R. Using evaluation functions in Monte-Carlo tree search[J]. Theoretical computer science, 2016, 644 : 106-113DOI:10.1016/j.tcs.2016.06.026. |
| [68] | GUEZ A, SILVER D, DAYAN P. Scalable and efficient Bayes-adaptive reinforcement learning based on Monte-Carlo tree search[J]. Journal of artificial intelligence research, 2013, 48(1) : 841-883. |
| [69] | BROWNE C B, POWLEY E, WHITEHOUSE D, et al. A survey of Monte Carlo tree search methods[J]. IEEE transactions on computational intelligence and AI in games, 2012, 4(1) : 1-43DOI:10.1109/TCIAIG.2012.2186810. |
| [70] | BAIER H, WINANDS M H M. Time management for Monte Carlo tree search[J]. IEEE transactions on computational intelligence and AI in games, 2016, 8(3) : 301-314DOI:10.1109/TCIAIG.2015.2443123. |
| [71] | RAIKO T, PELTONEN J. Application of UCT search to the connection games of Hex, Y, * Star, and Renkula[C]//Proceedings of the Finnish AI Conference. Espoo, Finland, 2008. |
| [72] |
吕艳辉, 宫瑞敏. 计算机博弈中估值算法与博弈训练的研究[J].
计算机工程, 2012, 38 (11) : 163-166.
LV Yanhui, GONG Ruimin. Study on valuation algorithm and game training in computer game[J]. Computer engineering, 2012, 38(11) : 163-166. |
| [73] | TAKEUCHI S, KANEKO T, YAMAGUCHI K. Evaluation of game Tree search methods by game records[J]. IEEE transactions on computational intelligence and AI in games, 2010, 2(4) : 288-302DOI:10.1109/TCIAIG.2010.2102022. |
| [74] | LIEBERUM J. An evaluation function for the game of amazons[J]. Theoretical computer science, 2005, 349(2) : 230-244DOI:10.1016/j.tcs.2005.09.048. |
| [75] | MARSLAND T A, CAMPBELL M. Parallel search of strongly ordered game trees[J]. ACM computing surveys, 1982, 14(4) : 533-551DOI:10.1145/356893.356895. |
| [76] |
刘建伟, 刘媛, 罗雄麟. 深度学习研究进展[J].
计算机应用研究, 2014, 31 (7) : 1921-1930.
LIU Jianwei, LIU Yuan, LUO Xionglin. Research and development on deep learning[J]. Application research of computers, 2014, 31(7) : 1921-1930. |
| [77] | XIE Fan, LIU Zhiqing, WANG Yu, et al. Systematic Improvement of Monte-Carlo Tree Search with Self-generated Neural-Networks Controllers[M]//BLUM C, BATTITI R. Learning and Intelligent Optimization:Lecture Notes in Computer Science. Berlin Heidelberg:Springer, 2010:228-231. |
| [78] |
张小川, 唐艳, 梁宁宁. 采用时间差分算法的九路围棋机器博弈系统[J].
智能系统学报, 2012, 7 (3) : 278-282.
ZHANG Xiaochuan, TANG Yan, LIANG Ningning. A 9×9 go computer game system using temporal difference[J]. CAAI transactions on intelligent systems, 2012, 7(3) : 278-282. |



