2. 济南大学 数学科学学院, 山东 济南 250022;
3. 计算智能与智能系统北京市重点实验室, 北京 100124
2. School of Mathematical Science, University of Jinan, Jinan 250022, China;
3. Beijing Key Laboratory of Computational Intelligence and Intelligent System, Beijing 100124, China
人工神经网络是通过模仿大脑神经系统的组织结构及活动机理进行信息处理的新型网络系统,具有从环境中学习的能力,并引起诸多领域的广泛关注,比如信号处理、智能控制、模式识别、图像处理、非线性系统建模与优化、大数据处理、知识处理等领域[1-6]。迄今为止,应用最为广泛的神经网络学习方法是梯度类算法。然而,传统的梯度类算法本身存在一些难以解决的瓶颈问题,如收敛速度慢、易陷入局部极小点、对初始参数的设定依赖性较强等[7]。特别是对于深层神经网络及递归神经网络,梯度类算法存在梯度消失及梯度爆炸等问题,难以充分发挥神经网络强大的学习能力[8]。
另一方面,人们通过对大脑的解剖重构发现,随机连接存在于部分脑区域,并在神经表征过程中具有重要作用[9-10]。基于此生物学基础,部分学者提出了神经网络随机学习算法,通过求解简单线性回归问题计算与输出层节点连接的网络权值,而其他网络权值及阈值则根据给定概率分布,在特定的区间上随机生成,且不再进行调整[11]。该类算法无需性能函数的梯度信息,无需反复迭代,在一定程度上克服了传统梯度类算法遇到的瓶颈问题[12]。
近年来,众多学者将随机学习思想应用于训练不同结构的神经网络,并提出了多种类型的随机权神经网络模型,如单隐含层前馈神经网络[13-15],多隐含层前馈神经网络[16-18],级联神经网络[19-20],递归神经网络[21-23]。与传统的神经网络相比,随机权神经网络在保证相当的逼近和泛化能力的基础上,拥有极快的学习速度,降低了陷入局部极小点的概率,代码执行简单,易于理解与实现,无需性能函数的导数信息,适用范围更加广泛。因此随机权神经网络一经提出便成为神经网络领域的研究热点,并已成功应用于模式识别、信号处理、时间序列预测等领域[24-26]。然而,随机权神经网络研究才刚刚起步,在理论、技术及应用层面上还有很大的提升空间。
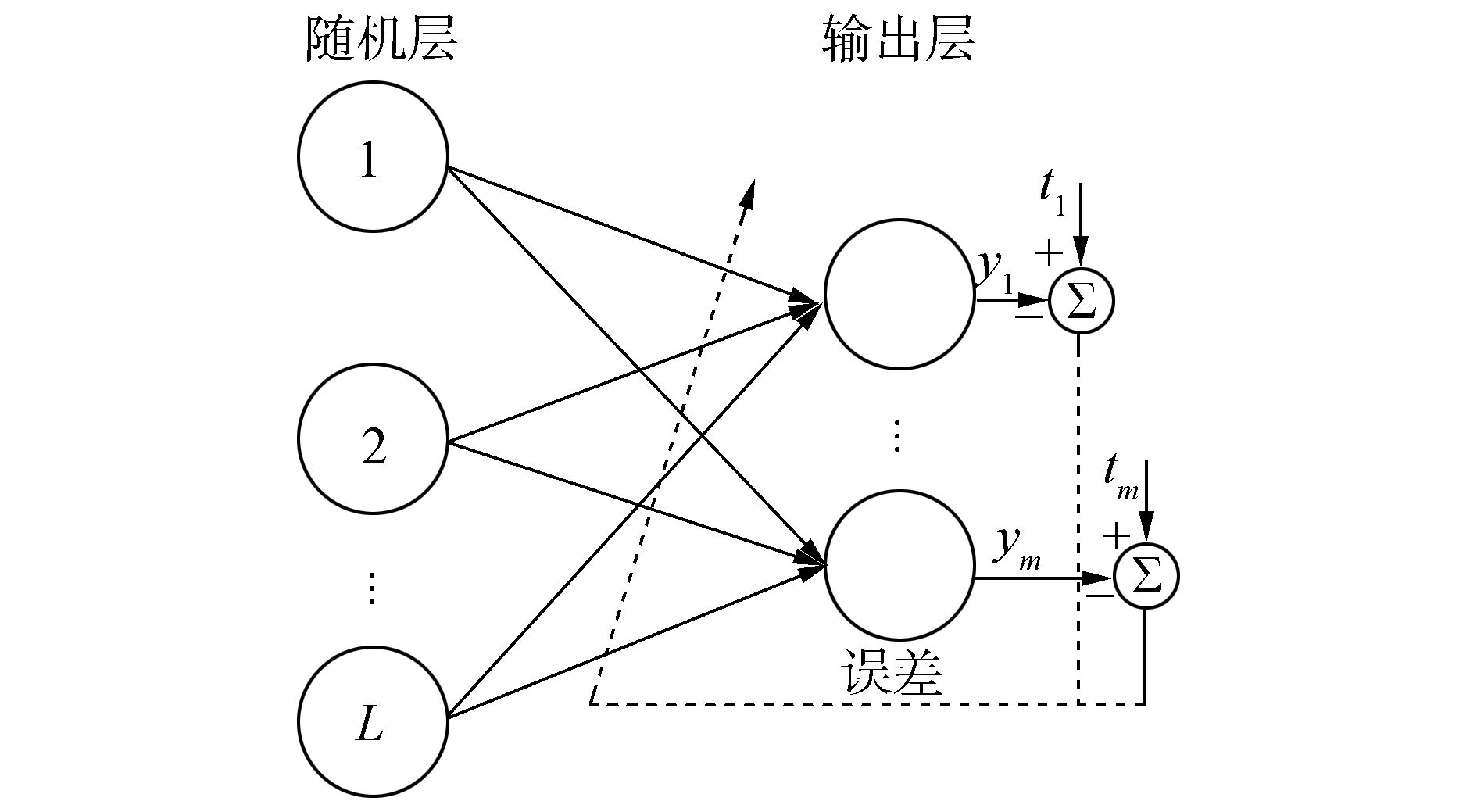
1 随机权神经网络简化模型给定任意N个不同的训练样本(xi,ti)|(xi,ti)∈Rn×Rm,1≤i≤N},假设与网络输出层相连的节点个数为L,则随机权神经网络可以简化为两层感知器结构,如图 1,其中与输出层相连的L个节点组成随机层。随机层中每个节点可能是一个输入节点,也可能是由输入节点及隐节点组成的复合节点。
|
| 图 1 随机权神经网络简化模型 Fig. 1 Simplified model of NNs with random weights |
如图 1所示,随机权神经网络的计算模型可概括为
 |
(1) |
式中:βj为随机层第j个节点与输出层之间的连接权值向量,θj为随机层第j个节点的随机权向量,gj为随机层第j个节点的映射函数。假设模型预测误差为ε,则式(1)可以等价地表示为
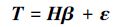 |
(2) |
式中:H为随机层输出矩阵,β为随机层与输出层间的连接矩阵,T为目标输出矩阵,分别表示为
 |
(3) |
在随机权神经网络模型(1)中,随机层节点的参数θj按照采用某种随机的方法进行初始化,并在随后的学习过程中保持不变,而权值βj则可以通过最小二乘求解式(2)获得,即
 |
(4) |
或通过岭回归算法,得
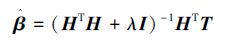 |
(5) |
式中λ为正则化系数。
神经网络随机学习算法步骤可概括如下:
1) 随机初始化随机层第j个隐节点的参数向量θj,j=1,2,…,L;
2) 由式(1)和式(3)计算网络随机层的输出矩阵H;
3) 由式(4)或式(5)计算网络的输出层权值矩阵;
4) 对训练好的网络进行测试。
根据随机层节点的连接方式,随机权神经网络可分为随机权单隐含层前馈神经网络、随机权多隐含层前馈神经网络、随机权级联神经网络及随机权递归神经网络,不同网络结构对应不同的映射函数及网络性能,下面对随机权神经网络的结构、映射函数以及网络性能进行具体分析。
2 随机权神经网络结构及性能分析 2.1 随机权单隐含层前馈神经网络前馈单隐含层神经网络(single hidden layer feedforward neural network,SLFN)是目前研究及应用最为广泛的前馈神经网络。在文献[27]中,作者将随机学习的思想应用于训练SLFN,分别研究网络的输入权值与输出权值对于网络性能的影响。仿真结果表明,输出权值对网络性能影响更加明显,而输入权值恰当初始化后可不必进行优化调节。但该文献并没有将随机学习算法作为一种可供选择的神经网络学习算法进行推广。Pao及Huang等分别对神经网络随机学习算法进行了深入地研究,各自提出了相应的随机权神经网络模型[28-29]。Rahimi等也提出了类似结构的随机权神经网络模型,并对网络的分类能力及测试误差边界给出了相应的理论分析[15]。
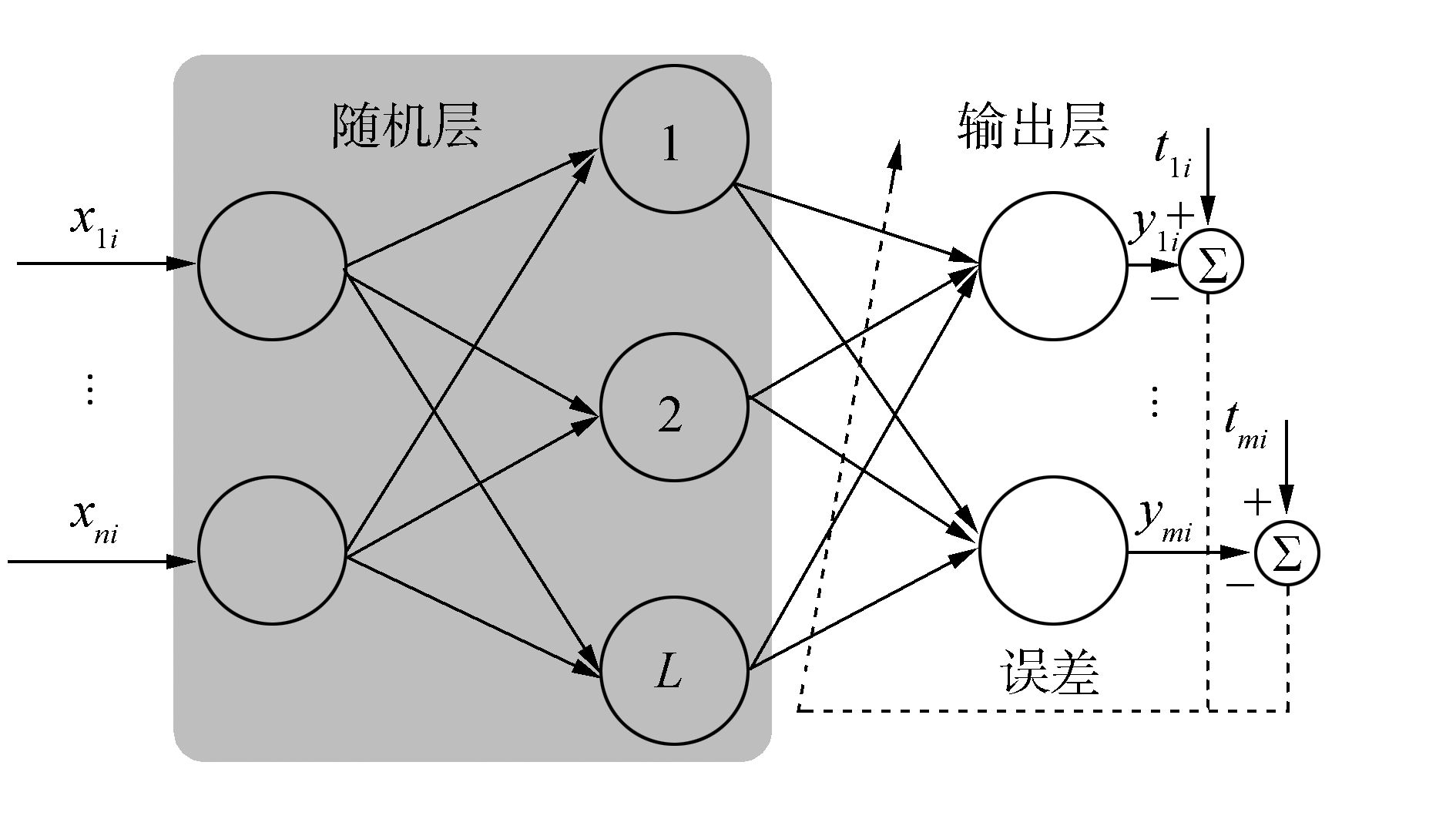
Huang等将随机学习算法应用于SLFN训练,提出了标准的随机权单隐含层神经网络模型(Extreme learning machine,ELM)[30],如图 2所示,其中随机层节点由输入层节点及隐含层节点复合而成。ELM网络随机层节点的映射函数为
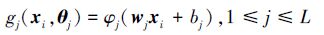 |
(6) |
式中:wj=(wj1,wj2,…,wjn),bj分别为第j个隐含层节点的输入权值及阈值,θj=(wj1,wj2,…,wjn,bj)为网络的随机权向量,取值于任意实数区间,xi(i=1,2,…,N)为网络输入。在文献[31]中,Huang等证明了该类网络以概率1任意精度逼近连续函数。Liu等从理论上严格证明,在选择恰当的激活函数的条件下,该类随机权单隐含层前馈神经网络可以获得与权值可调神经网络相当的泛化性能[32]。
|
| 图 2 随机权单隐含层前馈神经网络 Fig. 2 SLFN with random weights |
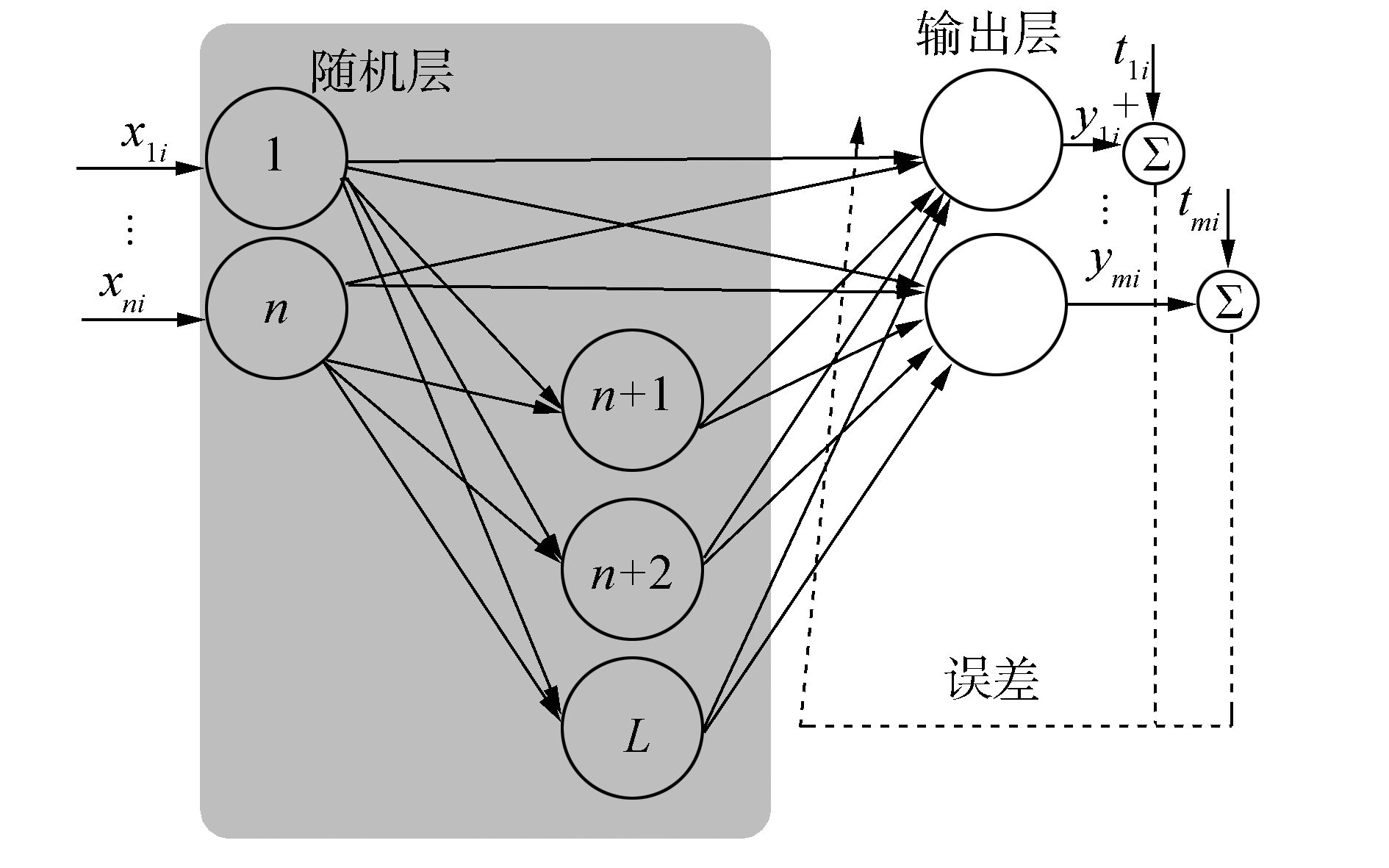
功能连接网络(functional-link neural network,FLNN)是一类特殊的SLFN[33],包括输入层、增强层(隐含层)及输出层,如图 3所示。与标准的SLFN不同,FLNN的输入节点同时连接隐含层节点及输出层节点。Pao等将神经网络随机学习算法用于FLNN网络训练,提出了随机权功能连接网络(random vector functional-link neural network,RVFL)[13, 28],其随机层输出包括输入节点输出以及输入节点与隐节点的复合节点输出。RVFL网络的随机层节点映射函数为
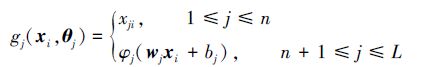 |
(7) |
式中:当j>n时,wj=(wj1,wj2,…,wjn),bj分别为第j个随机层节点的输入权值及阈值,θj=(wj1,wj2,…,wjn,bj)为网络的随机权向量,取值于某给定区间[-Ω,Ω,]xji(i=1,2,…,N;j=1,2,…,n)为网络输入。在文献[28]中,作者从理论上严格证明了RVFL对连续函数的任意逼近特性。Zhang等研究发现,输入层节点与输出层节点的直接连接对于RVFL的性能具有重要的影响[34]。
|
| 图 3 随机权功能连接网络 Fig. 3 FLNN with random weights |
近年来,随机权单隐含层神经网络研究取得了许多优秀的成果,比如在线算法[35]、分布式算法[36]、集成算法[37]、结构设计算法[38-42]、正则化算法[43-44]、聚类算法[45-46]等。但随机权单隐含层神经网络在大数据及知识处理方面的研究还需要进一步加强。
2.2 随机权多隐含层前馈神经网络与SLFN相比,多隐含层前馈神经网络(multiple hidden layer feedforward neural network,MLFN)在处理某些问题时展现出了更好的信息处理能力[47]。然而,由于纵深的网络结构,梯度类算法在训练MLFN时存在梯度消失及梯度爆炸问题,不能有效发挥MLFN的全部性能。深度学习方法能够有效地训练MLFN网络,并在模式识别等问题上取得很好的效果,但其整个训练过程是冗长的[48]。而基于随机学习算法的多隐含层前馈神经网络,称为随机权多隐含层前馈神经网络,仅网络的输出权值进行训练,而隐含层节点的网络权值随机设置且固定不变,从而极大地提高了网络的训练效率[49]。
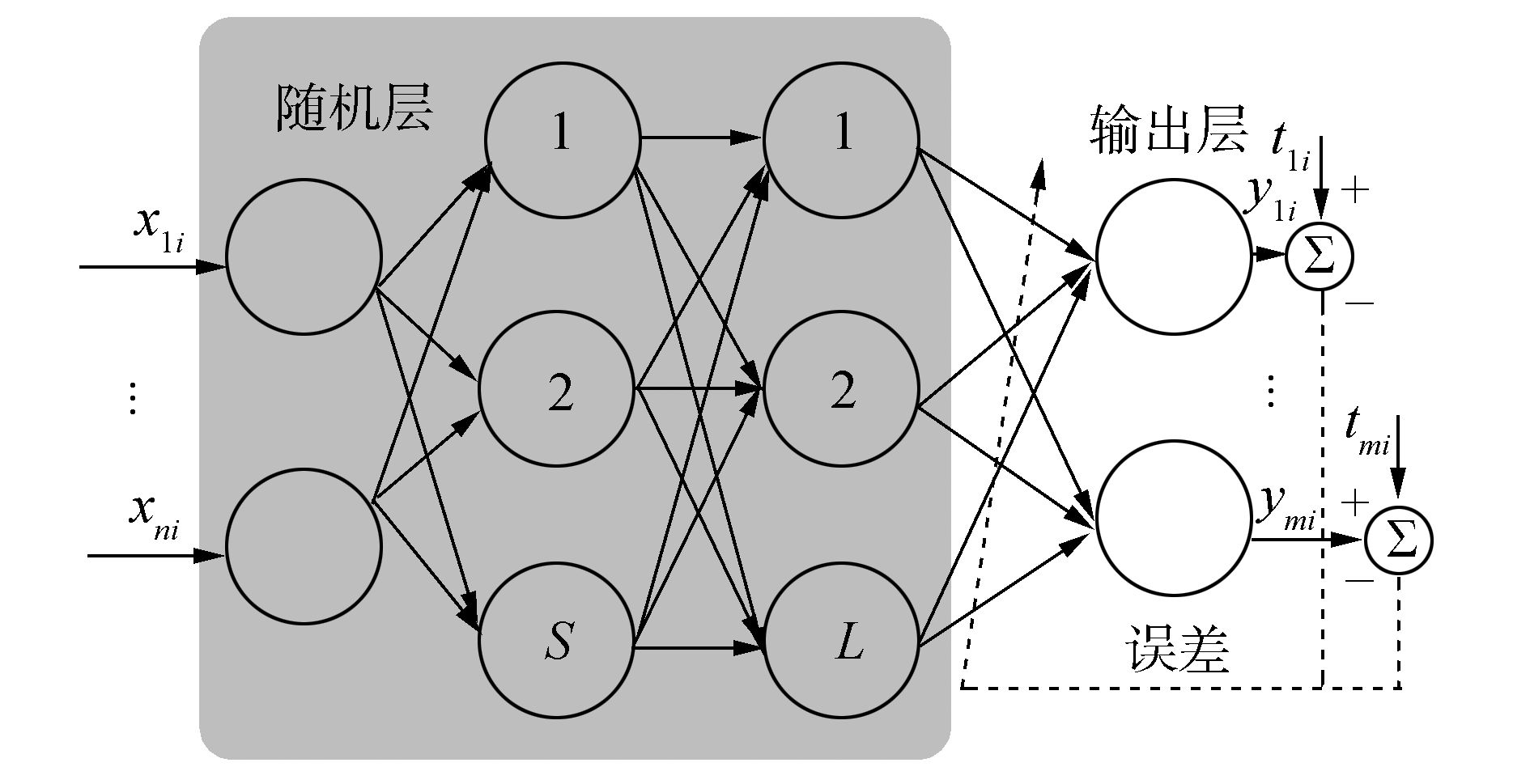
随机权多隐含层前馈神经网络中,随机层节点由输入节点及隐含层节点逐层复合而成,如图 4所示,其映射函数为
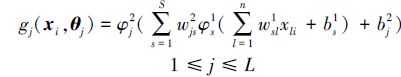 |
(8) |
式中:wsl1为连接第一隐含层第s个节点及输入层第l个节点的权值,wjs2为连接第二隐含层第j个节点及第一隐含层第s个节点的权值,bs1与bj2分别为第一隐含层第s个节点及第二隐含层第j个节点的阈值,θj=(w111,…,w1n1,b11,w211,…,wSn1,bS1,wj12,wj22,…,wjL2,bj2)为网络的随机权向量。
|
| 图 4 随机权多隐含层前馈神经网络 Fig. 4 MLNN with random weights |
基于随机学习的思想,文献[16]提出了无传播(no-propagation)算法用于训练MLFN网络。该算法利用LMS(least mean square)方法训练网络的输出权值,其他权值随机生成且固定不变。实验证明该算法构造的神经网络可以得到与权值可调网络相当的泛化能力。在文献[50]中,作者提出了双隐含层随机权前馈神经网络模型,该模型第一隐含层的输入权值随机生成,而第二隐含层的输入权值分析获取。在文献[51]中,作者将神经网络随机学习与深度信念网结合,设计了增量式随机权多隐含层前馈神经网络模型。在文献[17]中,Kasun等基于逐层随机初始化方法设计了随机权多隐含层前馈神经网络自动编码器。其将网络输入信号分解为多个隐含层,上一层的输出作为当前隐含层的目标输出。然而,该模型仅是简单的分层堆积,其最后一个隐含层的编码输出直接输送给了输出层,中间没有经过随机映射,不能保证模型的任意逼近特性[18]。因此,为了保证该自动编码器的任意逼近特性,Tang等在编码器最后一个隐含层与输出层之间增加了一个随机映射层,将MLFN的训练分为两个层次,即无监督的分层特征表示及有监督的特征分类[18]。
目前随机权多隐含层前馈神经网络已成功应用于人脸识别、图像处理及多分类学习[52-53]等领域,但对其研究才刚刚起步,理论研究不足,应用领域有待进一步扩大。
2.3 随机权级联神经网络近期研究成果表明,与多层感知结构相比较,级联神经网络(cascade neural network,CNN)结构具有更强的信息处理能力,因为其具有丰富的跨层链接及纵深的网络结构[54]。比如,Wilamowski 等研究证明级联神经网络用8个隐含层节点就可以解决255位的奇偶校验问题,而三层感知网络用8个隐含层节点只能解决7位的奇偶校验问题[55]。但是级联网络每一个隐含层节点就是一层,随着网络节点增加,网络深度不断增加,传统梯度类算法难以实现网络权值的优化。Wilamowski等提出的NBN(neuron by neuron)算法,可以沿着网络节点的连接次序逐一优化节点权值,虽然适用于CNN网络的权值优化,但对于较大规模(权值数大于500)的网络训练耗时太长[56]。而随机权级联神经网络,只有与输出节点连接的权值需要进行训练,其他权值随机设置且固定不变,从而极大地减少了级联网络的训练时间。
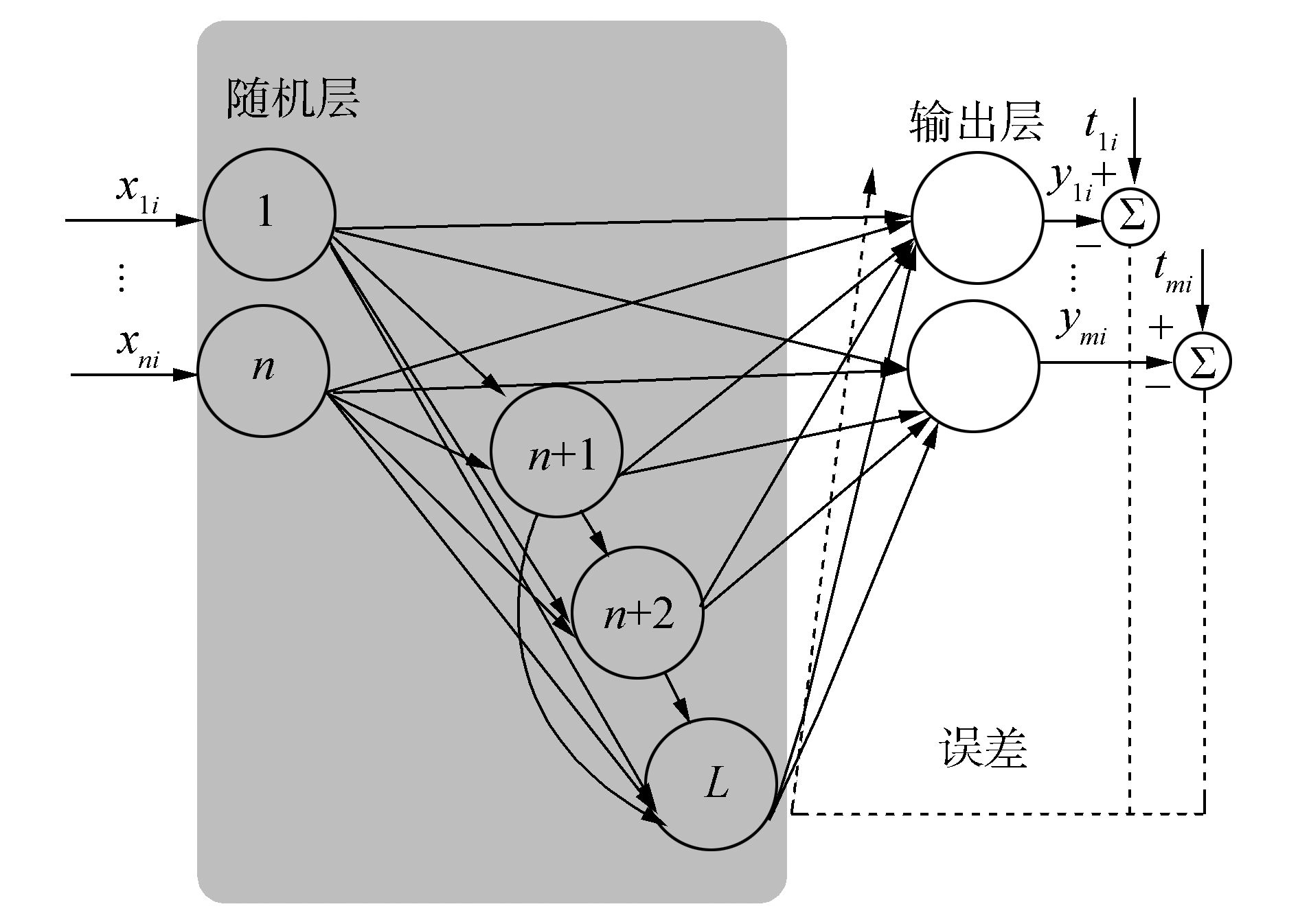
随机权级联神经网络的随机层节点由两部分组成,一部分为输入节点,另一部分由输入节点及隐含层节点逐层复合而成,如图 5所示。
|
| 图 5 随机权级联神经网络 Fig. 5 CNN with random weights |
其中随机层节点的映射函数为
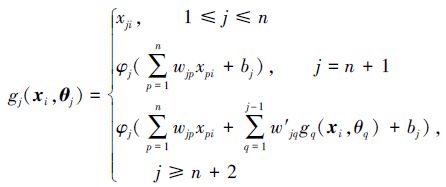 |
(9) |
式中:φj为第j个隐含层节点的激活函数,xpi(1≤p≤n)为第i个输入样本的第p个分量,wjp(1≤p≤n)第p个输入节点与隐节点j间的连接权值,w′jq(1≤q<j)为隐节点q与隐节点j间的连接权值,随机参数向量θj表示为
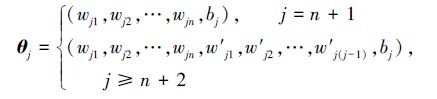 |
(10) |
在文献[19]中,作者基于随机学习的思想设计了随机权级联神经网络,并给出了网络的收敛性证明。在文献[20]中,作者基于正交最小二乘算法设计了类似的随机权级联神经网络。在文献[57]中,作者结合CNN网络及ELM算法,提出了具有级联结构的随机权神经网络,能够以较少的隐含层节点得到与ELM网络相当的信息处理能力。而在文献[58]中,作者证明了随机权级联神经网络的逼近特性。然而,与随机权单隐含层前馈神经网络相比,在具有相同数量网络权值的条件下,随机权级联神经网络并没有表现出更好的信息处理能力[57]。因此,进一步提高随机权级联神经网络的信息处理能力是当前该领域研究的重点之一。
2.4 随机权递归神经网络与前馈神经网络相比,递归神经网络(recurrent neural network,RNN)含有丰富的动力学特性,理论上能够解决具有时序特性的机器学习问题。然而在实际应用过程中,往往难以达到预期的目的,其原因在于传统的梯度类算法存在梯度消失及梯度爆炸等问题,难以快速有效地训练递归神经网络[8]。随机权递归神经网络仅仅训练网络的输出权值,而其他权值和阈值按照特定的规则随机设置且固定不变,极大地提高了递归神经网络的训练效率。
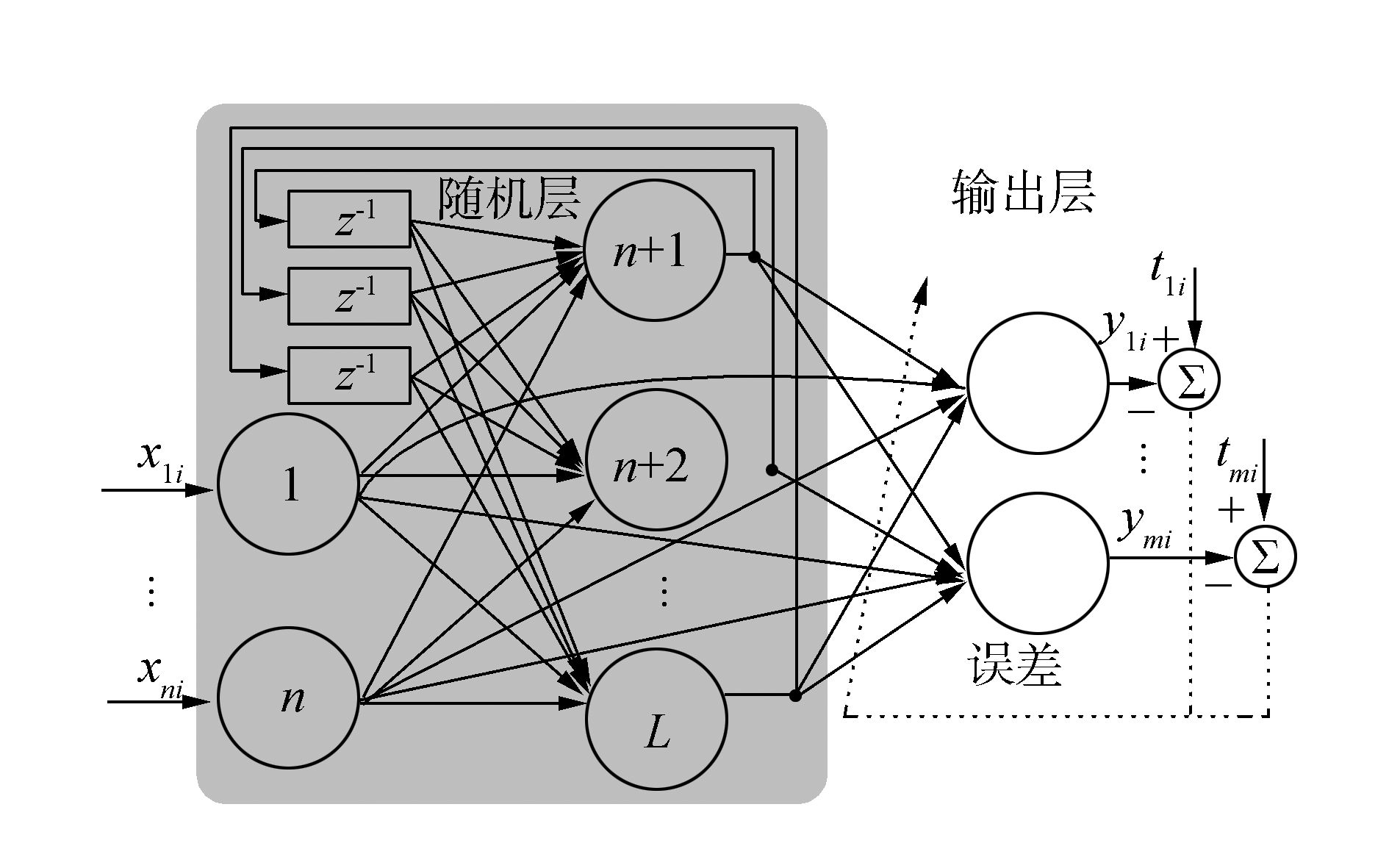
随机权递归神经网络随机层比较复杂,其节点包括两个组成部分:一部分为网络的输入节点,另一部分由输入节点及隐含层节点按时间顺序多重复合而成,如图 6。
|
| 图 6 随机权递归神经网络 Fig. 6 RNN with random weights |
其随机层节点的映射函数为
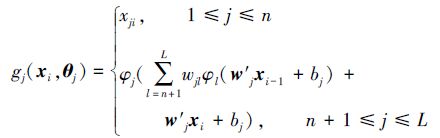 |
(11) |
式中:w′j=w′1j,w′2j,…,w′nj(j≥n+1)为输入层与第j个随机层节点间的连接权值向量,wjl(j≥n+1,l≥n+1)为连接第l个随机层节点与第j个随机层节点的权值,bj(j≥n+1)为第j个随机层节点的阈值,xi-1与xi分别为网络第i-1时刻及i时刻的网络输入。随机参数向量θj表示为
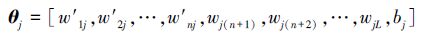 |
(12) |
目前,典型的随机权递归神经网络称为“储备池计算(reservoir computing)”模型,主要包括回声状态网络(echo state network,ESN)[22]、液体状态机(liquid state machine,LSM)[23]及BPDCBackpropagation decorrelation)学习规则[21]等。
ESN网络的随机层由大规模稀疏连接的递归模拟神经元构成,称为“动态储备池(dynamical reservoir)”。当动态储备池权值矩阵的最大奇异值小于1时,ESN网络动态储备池的输出状态由历史输入唯一确定,称为回声状态特性(eho state property,ESP)。H.Jaeger指出通过设置动态储备池权值矩阵的谱半径接近且小于1,使动态储备池可处于稳定边界,进而使ESN网络能够获得较好的信息处理能力[22]。与传统的递归神经网络相比,ESN网络处理时间序列预测问题的能力得到大幅提高[59],并成功应用于语音识别及非线性信号处理等领域[6-61]。然而针对具体问题,随机动态储备池并不是最优选择[62-63]。因此,ESN动态储备池结构和储备池权值矩阵设计仍然是该领域的开放课题,并出现了一些有意义的成果[64-70]。
LSM是一种在线网络模型,提出的动机是用于解决时序信号的实时计算问题,常用抽象的皮质微柱模型进行描述[71]。LSM的工作原理与ESN相近,但其随机层由LIF(leaky-integrate-and-fire)神经元构成,能够实时处理脉冲数据流,更具有生物相似性[72]。研究表明,当LSM的随机层的动态特性达到混沌边界时,模型可处于最佳状态[73]。目前,LSM模型已成功应用于时间序列预测及模式识别等领域[74-75]。
尽管各种储备池计算模型提出的动机及表现形式不同,但都选用大规模、随机连接的递归神经元,其映射函数如式(11)所示,是典型的随机权递归神经网络。目前,对于随机权递归神经网络随机层的动力学特性理解不够全面,其参数设置缺乏足够的理论指导,仍旧处于凑试阶段,在实际应用过程中设计更加困难,因此研究随机层的动力学特性,完善随机权递归神经网络的学习及稳定性理论,使其能够有更广泛的实际应用是该领域的热点问题之一。
3 随机权初始化方法随机权神经网络的核心思想是随机层神经元权值随机初始化且在后续学习过程中保持不变,所以随机权的初始化对于网络的性能具有重要的影响。而随机权前馈神经网络与随机权递归神经网络在随机权初始化方法上差别较大,本部分将分别进行分析总结。
3.1 前馈神经网络随机权初始化方法在文献[31]中,Huang等证明在任意区间上任意设置随机层权值,ELM网络以概率1任意精度逼近紧集上的连续函数。文献[28]中,Pao等研究指出,在特定区间[-Ω,Ω]上随机生成随机权,可使RVFL具有万能逼近特性,但没有给出Ω的具体确定办法。Zhang等研究发现,随机权的选取区间[-Ω,Ω]对网络的性能有较大影响,Ω过大或过小都将降低网络的性能[34]。目前,随机权神经网络的随机权初始化方法主要是在区间[-1, 1]上按照均匀分布或高斯分布随机设置。文献[14-16]皆应用完全随机的方法初始化相应网络的随机权。文献[39]基于随机初始化方法及激活函数的导函数构造了4层随机权神经网络,提高了ELM网络的学习和泛化能力。如此完全随机地设置随机权简单易行,但易于产生冗余或不良节点,致使随机层输出共线性,降低网络的泛化能力[76]。
为克服不良节点问题,选择性添加或删除随机节点是随机权初始化的重要方法。如文献[19]及[76]利用候选节点池初始化相应网络的随机权,首先生成多个随机节点构成候选节点池,然后根据给定的评价标准由池中选择最优节点添加至网络中。而文献[40]及[42]则首先生成规模较大的随机层,根据节点对网络性能的贡献度,删除贡献小的随机节点,以实现随机权的初始化。该类方法可以有效减少不良节点,降低网络的结构复杂度,从而提高网络的泛化性能。然而该方法也难以解决随机层输出共线性问题。Wang等基于矩阵的对角占优理论对随机权进行初始化,解决了一类ELM网络随机层输出共线性问题,但该方法对激活函数有特殊要求,不适用于sigmoid函数[77]。
3.2 递归神经网络随机权初始化方法递归神经网络具有复杂的动力学特性,网络权值的设定势必影响网络的稳定性及记忆能力,因此其随机权初始化更加重要。ESN网络是随机权神经网络的典型代表,因此本文仅以ESN网络为例分析随机权的初始化,即动态储备池结构设计。目前,主要动态储备池设计方法可分为无监督设计和有监督设计。
无监督设计可以分为两种情况:基于动态储备池本质特性随机生成或基于动态储备池激活状态优化设计。H.Jaeger以特定概率为储备池权值赋以几个简单的数值,然后通过比例因子对权值矩阵进行放缩,使动态储备池具有ESP特性[22]。文献[66]利用储备池权值矩阵的代数特性,基于奇异值分解设计动态储备池,使其具有特定的动态特性。文献[78]基于复杂网络理论,模仿生物神经网络中的小世界及无标度特性设计动态储备池,在保持ESN网络记忆能力的同时提高了网络的预测能力。文献[67]基于分块矩阵及侧抑制连接,设计模块化储备池结构,实现了动态储备池内部神经元的局部解耦。基于动态储备池本质特性随机生成权值的方法简单通用,但对于解决实际问题显然不是最优选则[63]。
文献[79]基于信息论与动态储备池激活状态,构建平均状态熵(average state entropy,ASE),评价动态储备池输出的多样性,然后通过最大化ASE设计动态储备池,增强了ESN网络的表征特性。文献[80]基于正交鸽子启发优化(orthogonal pigeon-inspired optimization,OPIO)方法设计动态储备池的随机权,并成功应用于图像处理,提高了图像的复原效果。文献[81]基于自组织算法及侧向互作用思想,提出动态储备池无监督优化设计方法,提高了ESN网络对关联信息过程的处理能力。基于动态储备池激活状态设计评价函数,通过优化评价函数设计储备池的方法,有效地利用了样本的输入信息,提高了ESN网络处理实际问题的能力,但该类方法没有考虑样本的输出信息,仍难以获得最优实用效果。
文献[82]通过平衡网络输出反馈与储备池内部反馈对储备池动态特性的影响设计了储备池权值矩阵,很好地解决了多个正弦波叠加的MSO(multiple superimposed oscillators)问题。文献[83]通过最大化储备池激活状态与样本期望输出间的平均互信息,优化环形储备池,提高了环形储备池ESN的信息处理能力。文献[84]基于先验数据及聚类算法设计具有小世界特性的动态储备池,提高了ESN网络的计算及预测能力。文献[85]基于梯度下降及ESN网络的线性输出层优化储备池,提高了网络信息处理能力。利用样本输入输出信息,有监督设计动态储备池的方法,可根据给定问题有针对性地优化设计动态储备池,提高了ESN网络的实用效率,但有监督设计难以实现知识的在线学习与推理。
4 结论及展望在随机权神经网络中,仅网络的输出权值需要训练,其他权值随机设置,整个训练过程无需网络的梯度信息,无需迭代,克服了传统神经网络收敛速度慢及局部极小问题。本文在给定随机权神经网络简化模型的基础上,分析了多个随机权神经网络的网络结构、映射函数、随机权设置方法及网络性能,回顾总结了随机权神经网络研究的现状。
尽管随机权神经网络研究取得了丰硕的成果,但从发展的角度看还有很长的路要走。结合研究现状,对随机权神经网络的研究提出以下展望。
1) 随机权神经网络结构设计研究。与传统的神经网络相比,随机权神经网络结构庞大,凑试法及单个神经元的增长修剪算法难以实现结构的快速有效设计,因此研究随机权神经网络的实时在线结构设计方法将是一个重要的研究方向。
2) 神经网络随机学习理论研究及生物学解释。人脑研究表明,大脑中存在大量随机现象,借鉴大脑的研究成果可进一步模拟大脑的随机特性,设计新的随机学习算法,实现大脑的部分功能;借用统计学及信息论的相关知识,研究随机权神经网络的统计学特性,可完善神经网络学习理论。
3) 研究随机权递归神经网络随机层参数设置及网络的稳定性问题。随机权递归神经网络是一个动态系统,其网络性能及稳定性依赖于随机层参数的选择,如随机层权值矩阵的谱半径、奇异值及稀疏性等。如何选择恰当的随机层参数使网络同时具有稳定性及高效的信息处理能仍然是该领域的开放课题。并出现了一些有意义的成果[63-67]。
4) 随机权神经网络在复杂流程工业过程中的应用研究,比如污水处理、水泥加工及石化生产行业。目前,随机权神经网络主要应用于模式分类问题,并取得较好的效果,而在流程工业过程中的应用研究较少。针对流程工业过程的时变、时滞、非线性、强耦合及不确定性等特点,设计恰当的随机权神经网络模型,实现流程工业过程的智能建模与控制,是随机权神经网络未来的应用研究方向之一。
| [1] | QI Min, ZHANG G P. Trend time series modeling and forecasting with neural networks[J]. IEEE transactions on neural networks, 2008, 19(5) : 808-816DOI:10.1109/TNN.2007.912308. |
| [2] |
赵洪伟, 谢永芳, 蒋朝辉, 等. 基于泡沫图像特征的浮选槽液位智能优化设定方法[J].
自动化学报, 2014, 40 (6) : 1086-1097.
ZHAO Hongwei, XIE Yongfang, JIANG Chaohui, et al. An intelligent optimal setting approach based on froth features for level of flotation cells[J]. Acta automatica sinica, 2014, 40(6) : 1086-1097. |
| [3] |
乔俊飞, 薄迎春, 韩广. 基于ESN的多指标DHP控制策略在污水处理过程中的应用[J].
自动化学报, 2013, 39 (7) : 1146-1151.
QIAO Junfei, BO Yingchun, HAN Guang. Application of esn-based multi indices dual heuristic dynamic programming on wastewater treatment process[J]. Acta automatica sinica, 2013, 39(7) : 1146-1151. |
| [4] | CHENG M H, HWANG K S, JENG J H, et al. Classification-based video super-resolution using artificial neural networks[J]. Signal processing, 2013, 93(9) : 2612-2625DOI:10.1016/j.sigpro.2013.02.013. |
| [5] | SCARDAPANE S, WANG Dianhui, PANELLA M. A decentralized training algorithm for echo state networks in distributed big data applications[J]. Neural networks, 2015, 78 : 65-74. |
| [6] | TENG T H, TAN A H, ZURADA J M. Self-organizing neural networks integrating domain knowledge and reinforcement learning[J]. IEEE transactions on neural networks & learning systems, 2015, 26(5) : 889-902. |
| [7] | ALHAMDOOSH M, WANG Dianhui. Fast decorrelated neural network ensembles with random weights[J]. Information sciences, 2014, 264 : 104-117DOI:10.1016/j.ins.2013.12.016. |
| [8] | GUSTAVSSON A, MAGNUSON A, BLOMBERG B, et al. On the difficulty of training recurrent neural networks[J]. Computer science, 2013, 52(3) : 337-345. |
| [9] | RIGOTTI M, BARAK O, WARDEN M R, et al. The importance of mixed selectivity in complex cognitive tasks[J]. Nature, 2013, 497(7451) : 585-590DOI:10.1038/nature12160. |
| [10] | BARAK O, RIGOTTI M, FUSI S. The sparseness of mixed selectivity neurons controls the generalization-discrimination trade-off[J]. The journal of neuroscience, 2013, 33(9) : 3844-3856DOI:10.1523/JNEUROSCI.2753-12.2013. |
| [11] | HUANG Gao, HUANG Guangbin, SONG Shiji, et al. Trends in extreme learning machines:a review[J]. Neural networks, 2015, 61 : 32-48DOI:10.1016/j.neunet.2014.10.001. |
| [12] | DENG Chenwei, HUANG Guangbin, XU Jia, et al. Extreme learning machines:new trends and applications[J]. Science China information sciences, 2015, 58(2) : 1-16. |
| [13] | PAO Y H, TAKEFUJI Y. Functional-link net computing:theory, system architecture, and functionalities[J]. Computer, 1992, 25(5) : 76-79DOI:10.1109/2.144401. |
| [14] | HUANG Guangbin, ZHU Qinyu, SIEW C K. Extreme learning machine:theory and applications[J]. Neurocomputing, 2006, 70 . |
| [15] | RAHIMI A, RECHT B. Weighted sums of random kitchen sinks:replacing minimization with randomization in learning[C]//Proceedings of the 21st International Conference on Neural Information Processing Systems. Vancouver, British Columbia, Canada:Curran Associates Inc., 2008:1313-1320. |
| [16] | WIDROW B, GREENBLATT A, KIM Y, et al. The No-Prop algorithm:A new learning algorithm for multilayer neural networks[J]. Neural networks, 2013, 37 : 182-188DOI:10.1016/j.neunet.2012.09.020. |
| [17] | KASUN L L C, ZHOU Hongming, HUANG Guangbin, et al. Representational learning with ELMs for big data[J]. IEEE intelligent systems, 2013, 28(6) : 31-34. |
| [18] | TANG Jiexiong, DENG Chenwei, HUANG Guangbin. Extreme learning machine for multilayer perceptron[J]. IEEE transactions on neural networks and learning systems, 2016, 27(4) : 809-821DOI:10.1109/TNNLS.2015.2424995. |
| [19] | QIAO Junfei, LI Fanjun, HAN Honggui, et al. Constructive algorithm for fully connected cascade feedforward neural networks[J]. Neurocomputing, 2016, 182 : 154-164DOI:10.1016/j.neucom.2015.12.003. |
| [20] | WAN Yihe, SONG Shiji, HUANG Gao. Incremental extreme learning machine based on cascade neural networks[C]//IEEE International Conference on Systems, Man, and Cybernetics. Kowloon:IEEE, 2015:1889-1894. |
| [21] | STEIL J J. Memory in backpropagation-decorrelation O(N) efficient online recurrent learning[C]//Proceedings of the 15th International Conference on Artificial Neural Networks:Formal Models and Their Applications. Berlin Heidelberg:Springer, 2005:750-750. |
| [22] | HERBERT J. The "echo state" approach to analyzing and training recurrent neural networks with an erratum note[R]. Bonn, Germany:German National Research Center for Information Technology, 2001. |
| [23] | MAASS W. Liquid state machines:motivation, theory, and applications[J]. Computability in context, 2010 : 275-296DOI:10.1142/9781848162778_0008. |
| [24] | LIANG Nanying, SARATCHANDRAN P, HUANG Guangbin, et al. Classification of mental tasks from EEG signals using extreme learning machine[J]. International journal of neural systems, 2006, 16(1) : 29-38DOI:10.1142/S0129065706000482. |
| [25] | SKOWRONSKI M D, HARRIS J G. Automatic speech recognition using a predictive echo state network classifier[J]. Neural networks, 2007, 20(3) : 414-423DOI:10.1016/j.neunet.2007.04.006. |
| [26] | LI Decai, HAN Min, WANG Jun. Chaotic time series prediction based on a novel robust echo state network[J]. IEEE transactions on neural networks and learning systems, 2012, 23(5) : 787-799DOI:10.1109/TNNLS.2012.2188414. |
| [27] | SCHMIDT W F, KRAAIJVELD M A, DUIN R P W. Feedforward neural networks with random weights[C]//Proceedings of 11th International Conference on Pattern Recognition Methodology and Systems. Hague, Holland:IEEE, 1992:1-4. |
| [28] | IGELNIK B, PAO Y H. Stochastic choice of basis functions in adaptive function approximation and the Functional-link neural net[J]. IEEE transactions on neural networks, 1995, 6(6) : 1320-1329DOI:10.1109/72.471375. |
| [29] | HUANG Guangbin. An insight into extreme learning machines:random neurons, random features and kernels[J]. Cognitive computation, 2014, 6(3) : 376-390DOI:10.1007/s12559-014-9255-2. |
| [30] | HUANG Guangbin, ZHU Qinyu, SIEW C K. Extreme learning machine:theory and applications[J]. Neurocomputing, 2006, 70(1/2/3) : 489-501. |
| [31] | HUANG G B, CHEN L, SIEW C K. Universal approximation using incremental constructive feedforward networks with random hidden nodes[J]. IEEE transactions on neural networks, 2006, 17(4) : 879-92DOI:10.1109/TNN.2006.875977. |
| [32] | LIU Xia, LIN Shaobo, FANG Jian, et al. Is extreme learning machine feasible? a theoretical assessment (Part I)[J]. IEEE transactions on neural networks and learning systems, 2014, 26(1) : 7-20. |
| [33] | DEHURI S, CHO S B. A comprehensive survey on functional link neural networks and an adaptive PSO-BP learning for CFLNN[J]. Neural computing and applications, 2010, 19(2) : 187-205DOI:10.1007/s00521-009-0288-5. |
| [34] | ZHANG Le, SUGANTHAN P N. A comprehensive evaluation of random vector functional link networks[J]. Information sciences, 2015, 367/368 : 1094-1105. |
| [35] | LIANG Nanying, HUANG Guangbin, SARATCHANDRAN P, et al. A fast and accurate online sequential learning algorithm for feedforward networks[J]. IEEE transactions on neural networks, 2006, 17(6) : 1411-1423DOI:10.1109/TNN.2006.880583. |
| [36] | SCARDAPANE S, WANG Dianhui, PANELLA M, et al. Distributed learning for random vector functional-link networks[J]. Information sciences, 2015, 301 : 271-284DOI:10.1016/j.ins.2015.01.007. |
| [37] | ALHAMDOOSH M, WANG Dianhui. Fast decorrelated neural network ensembles with random weights[J]. Information sciences, 2014, 264 : 104-117DOI:10.1016/j.ins.2013.12.016. |
| [38] | LI Ying. Orthogonal incremental extreme learning machine for regression and multiclass classification[J]. Neural computing and applications, 2014, 27(1) : 111-120. |
| [39] |
李凡军, 乔俊飞, 韩红桂. 网络结构增长的极端学习机算法[J].
控制理论与应用, 2014, 31 (5) : 638-643.
LI Fanjun, QIAO Junfei, HAN Honghui. Incremental constructive extreme learning machine[J]. Control theory & applications, 2014, 31(5) : 638-643. |
| [40] |
李凡军, 韩红桂, 乔俊飞. 基于灵敏度分析法的ELM剪枝算法[J].
控制与决策, 2014, 29 (6) : 1003-1008.
LI Fanjun, HAN Honghui, QIAO Junfei. Pruning algorithm for extreme learning machine based on sensitivity analysis[J]. Control and Decision, 2014, 29(6) : 1003-1008. |
| [41] | FENG Guorui, HUANG Guangbin, LIN Qingping, et al. Error minimized extreme learning machine with growth of hidden nodes and incremental learning[J]. IEEE transactions on neural networks, 2009, 20(8) : 1352-1357DOI:10.1109/TNN.2009.2024147. |
| [42] | MICHE Y, SORJAMAA A, BAS P, et al. OP-ELM:optimally pruned extreme learning machine[J]. IEEE transactions on neural networks, 2010, 21(1) : 158-162DOI:10.1109/TNN.2009.2036259. |
| [43] |
韩敏, 李德才. 基于替代函数及贝叶斯框架的1范数ELM算法[J].
自动化学报, 2011, 37 (11) : 1344-1350.
HAN Min, LI Decai. An norm 1 regularization term elm algorithm based on surrogate function and bayesian framework[J]. Acta automatica sinica, 2011, 37(11) : 1344-1350. |
| [44] | MICHE Y, VAN HEESWIJK M, BAS P, et al. TROP-ELM:a double-regularized ELM using LARS and Tikhonov regularization[J]. Neurocomputing, 2011, 74(16) : 2413-2421DOI:10.1016/j.neucom.2010.12.042. |
| [45] | MICHE Y, AKUSOK A, VEGANZONES D, et al. SOM-ELM-Self-organized clustering using ELM[J]. Neurocomputing, 2015, 165 : 238-254DOI:10.1016/j.neucom.2015.03.014. |
| [46] | HUANG Gao, LIU Tianchi, YANG Yan, et al. Discriminative clustering via extreme learning machine[J]. Neural networks, 2015, 70 : 1-8DOI:10.1016/j.neunet.2015.06.002. |
| [47] | ISLAM M M, SATTAR M A, AMIN M F, et al. A new constructive algorithm for architectural and functional adaptation of artificial neural networks[J]. IEEE transactions on systems, man, and cybernetics, part B (cybernetics), 2009, 39(6) : 1590-1605DOI:10.1109/TSMCB.2009.2021849. |
| [48] | SCHMIDHUBER J. Deep learning in neural networks:an overview[J]. Neural networks, 2014, 61 : 85-117. |
| [49] | HAN Honggui, WANG Lidan, QIAO Junfei. Hierarchical extreme learning machine for feedforward neural network[J]. Neurocomputing, 2014, 128 : 128-135DOI:10.1016/j.neucom.2013.01.057. |
| [50] | QU B Y, LANG B F, LIANG J J, et al. Two-hidden-layer extreme learning machine for regression and classification[J]. Neurocomputing, 2016, 175 : 826-834DOI:10.1016/j.neucom.2015.11.009. |
| [51] | ZHANG Jian, DING Shifei, ZHANG Nan, et al. Incremental extreme learning machine based on deep feature embedded[J]. International journal of machine learning and cybernetics, 2016, 7(1) : 111-120DOI:10.1007/s13042-015-0419-5. |
| [52] | QU B Y, LANG B F, LIANG J J, et al. Two-hidden-layer extreme learning machine for regression and classification[J]. Neurocomputing, 2016, 175 : 826-834DOI:10.1016/j.neucom.2015.11.009. |
| [53] | ZHANG Nan, DING Shifei, ZHANG Jian. Multi layer ELM-RBF for multi-label learning[J]. Applied soft computing, 2016, 43 : 535-545DOI:10.1016/j.asoc.2016.02.039. |
| [54] | HUNTER D, YU Hao, PUKISH M S, et al. Selection of proper neural network sizes and architectures-a comparative study[J]. IEEE transactions on industrial informatics, 2012, 8(2) : 228-240DOI:10.1109/TII.2012.2187914. |
| [55] | WILAMOWSKI B M. Challenges in applications of computational intelligence in industrial electronics[C]//Proceedings of 2010 IEEE International Symposium on Industrial Electronics. Bari:IEEE, 2010:15-22. |
| [56] | WILAMOWSKI B M, COTTON N J, KAYNAK O, et al. Computing gradient vector and jacobian matrix in arbitrarily connected neural networks[J]. IEEE transactions on industrial electronics, 2008, 55(10) : 3784-3790DOI:10.1109/TIE.2008.2003319. |
| [57] | OAKDEN A. Cascade networks and extreme learning machines[D]. Canberra:Australian National University, 2014. |
| [58] | LI Fanjun, QIAO Junfei, HAN Honggui, et al. A self-organizing cascade neural network with random weights for nonlinear system modeling[J]. Applied soft computing, 2016, 42 : 184-193DOI:10.1016/j.asoc.2016.01.028. |
| [59] | JAEGER H, HAAS H. Harnessing nonlinearity:predicting chaotic systems and saving energy in wireless communication[J]. Science, 2004, 304(5667) : 78-80DOI:10.1126/science.1091277. |
| [60] | SKOWRONSKI M D, HARRIS J G. Automatic speech recognition using a predictive echo state network classifier[J]. Neural networks, 2007, 20(3) : 414-423DOI:10.1016/j.neunet.2007.04.006. |
| [61] | XIA Yili, JELFS B, VAN HULLE M M, et al. An augmented echo state network for nonlinear adaptive filtering of complex noncircular signals[J]. IEEE transactions on neural networks, 2011, 22(1) : 74-83DOI:10.1109/TNN.2010.2085444. |
| [62] | LUKOSEVICIUS M, JAEGER H. Reservoir computing approaches to recurrent neural network training[J]. Computer science review, 2009, 3(3) : 127-149DOI:10.1016/j.cosrev.2009.03.005. |
| [63] |
彭宇, 王建民, 彭喜元. 储备池计算概述[J].
电子学报, 2011, 39 (10) : 2387-2396.
PENG Yu, WANG Jianmin, PENG Xiyuan. Survey on reservoir computing[J]. Acta electronica sinica, 2011, 39(10) : 2387-2396. |
| [64] | QIAO Junfei, LI Fanjun, HAN Honggui, et al. Growing echo-state network with multiple subreservoirs[J]. IEEE transactions on neural networks and learning systems, 2016, 99 : 1-14. |
| [65] | DENG Zhidong, ZHANG Yi. Collective behavior of a small-world recurrent neural system with scale-free distribution[J]. IEEE transactions on neural networks, 2007, 18(5) : 1364-1375DOI:10.1109/TNN.2007.894082. |
| [66] | STRAUSS T, WUSTLICH W, LABAHN R. Design strategies for weight matrices of echo state networks[J]. Neural computation, 2012, 24(12) : 3246-3276DOI:10.1162/NECO_a_00374. |
| [67] | XUE Yanbo, YANG Le, HAYKIN S. Decoupled echo state networks with lateral inhibition[J]. Neural networks, 2007, 20(3) : 365-376DOI:10.1016/j.neunet.2007.04.014. |
| [68] | NAJIBI E, ROSTAMI H. SCESN, SPESN, SWESN:three recurrent neural echo state networks with clustered reservoirs for prediction of nonlinear and chaotic time series[J]. Applied intelligence, 2015, 43(2) : 460-472DOI:10.1007/s10489-015-0652-3. |
| [69] |
薄迎春, 乔俊飞, 张昭昭. 一种具有small world特性的ESN结构分析与设计[J].
控制与决策, 2012, 27 (3) : 383-388.
BO Yingchun, QIAO Junfei, ZHANG Zhaozhao. Analysis and design on structure of small world property ESN[J]. Control and decision, 2012, 27(3) : 383-388. |
| [70] |
李凡军, 乔俊飞. 一种增量式模块化回声状态网络[J].
控制与决策, 2016, 31 (8) : 1481-1486.
LI Fanjun, QIAO Junfei. An incremental modular echo state network[J]. Control and decision, 2016, 31(8) : 1481-1486. |
| [71] | SCHRAUWEN B, VERSTRAETEN D, VAN CAMPENHOUT J M. An overview of reservoir computing:Theory, applications and implementations[C]//Proceedings of the 15th European Symposium on Artificial Neural Networks. Bruges, Belgium, 2007:471-482. |
| [72] | MAASS W, NATSCHLÃGER T, MARKRAM H. Real-time computing without stable states:a new framework for neural computation based on perturbations[J]. Neural computation, 2002, 14(11) : 2531-2560DOI:10.1162/089976602760407955. |
| [73] | LEGENSTEIN R, MAASS W. Edge of chaos and prediction of computational performance for neural circuit models[J]. Neural networks, 2007, 20(3) : 323-334DOI:10.1016/j.neunet.2007.04.017. |
| [74] | BURGSTEINER H, KRÖLL M, LEOPOLD A, et al. Movement prediction from real-world images using a liquid state machine[J]. Applied intelligence, 2007, 26(2) : 99-109DOI:10.1007/s10489-006-0007-1. |
| [75] |
张冠元, 王斌. 一种基于液体状态机的音乐和弦序列识别方法[J].
模式识别与人工智能, 2013, 26 (7) : 643-647.
ZHANG Guanyuan, WANG Bin. Liquid state machine based music chord sequence recognition algorithm[J]. Pattern recognition and artificial intelligence, 2013, 26(7) : 643-647. |
| [76] | HUANG Guangbin, CHEN Lei. Enhanced random search based incremental extreme learning machine[J]. Neurocomputing, 2008, 71(16/17/18) : 3460--3468. |
| [77] | WANG Yuguang, CAO Feilong, YUAN Yubo. A study on effectiveness of extreme learning machine[J]. Neurocomputing, 2011, 74(16) : 2483-2490DOI:10.1016/j.neucom.2010.11.030. |
| [78] | CUI H, LIU X, LI L. The architecture of dynamic reservoir in the echo state network[J]. Chaos, 2012, 22(3) : 033127DOI:10.1063/1.4746765. |
| [79] | OZTURK M C, XU Dongming. Analysis and design of echo state networks[J]. Neural computation, 2007, 19(1) : 111-138DOI:10.1162/neco.2007.19.1.111. |
| [80] | DUAN Haibin, WANG Xiaohua. Echo state networks with orthogonal pigeon-inspired optimization for image restoration[J]. IEEE transactions on neural networks and learning systems, 2015, 27(11) : 2413-2425. |
| [81] | BOCCATO L, ATTUX R, VON ZUBEN F J. Self-organization and lateral interaction in echo state network reservoirs[J]. Neurocomputing, 2014, 138 : 297-309DOI:10.1016/j.neucom.2014.01.036. |
| [82] | KORYAKIN D, LOHMANN J, BUTZ M V. Balanced echo state networks[J]. Neural networks the official journal of the international neural network, 2012, 36 : 35-45DOI:10.1016/j.neunet.2012.08.008. |
| [83] | YUENYONG S, NISHIHARA A. Evolutionary pre-training for CRJ-type reservoir of echo state networks[J]. Neurocomputing, 2015, 149 : 1324-1329DOI:10.1016/j.neucom.2014.08.065. |
| [84] | LI Xiumin, ZHONG Ling, XUE Fangzheng, et al. A priori data-driven multi-clustered reservoir generation algorithm for echo state network[J]. PLoS one, 2015, 10(4) : e0120750DOI:10.1371/journal.pone.0120750. |
| [85] | PALANGI H, DENG Li, WARD R K. Learning input and recurrent weight matrices in echo state networks[C]//Advances in Neural Information Processing Systems 22:Conference on Neural Information Processing Systems. Vancouver, British Columbia, Canada, 2009. |



