2. 重庆邮电大学 智能系统及机器人研究所, 重庆 400065;
3. 重庆邮电大学 先进制造学院, 重庆 400065
2. Research Center of Intelligent System and Robot, Chongqing University of Posts and Telecommunications, Chongqing 400065, China;
3. Advanced Manufacturing Engineering School, Chongqing University of Posts and Telecommunications, Chongqing 400065, China
路径规划是研究移动机器人的一个重要内容,按其规划范围,分为全局路径规划和局部路径规划。目前,针对这两种路径规划方式许多学者进行了深入研究,并提出了相应的解决方法。全局路径规划方法有栅格法、可视图法和神经网络法等;局部路径规划方法包括人工势场法、A*算法、人工蜂群算法等[1]。虽然这些算法得到广泛应用,但也存在一些缺点:栅格力度越小,栅格法对障碍物的描述越精确,但环境信息的存储会占据大量的存储空间,算法的搜索范围也将成指数增加[2];人工势场法由于斥力的作用,机器人很难准确到达目标点。A*算法对开放列表的维护是最耗时的,尤其是在地图过大的情况下。
移动机器人多目标点路径规划是指在复杂的环境下找到一条从起始点开始经过所有目标点的无碰撞的最优路径。在实际应用中,移动机器人多目标点路径规划多应用于电厂巡检、医院查房等。移动机器人多目标点路径规划的基本原则包括3个方面:1) 当前点或起始点以及目标点提前已知;2) 任意时刻机器人都可以决定移动路线;3) 机器人必须经过的所有目标点来完成路径规划。根据移动机器人多目标点路径规划的特点,移动机器人多目标点路径规划问题可以转化为旅行商(traveling saleman problem, TSP)问题。目前有很多算法用于解决TSP问题[3],但多目标点路径规划与TSP问题相比更复杂。因此本文提出了一种基于粒子群算法和蚁群算法相结合的混合算法用于解决移动机器人多目标点路径规划问题。
蚁群算法(ant colony optimization, ACO)是一种启发式进化算法,由蚂蚁觅食行为演化而来。在解决TSP问题上,蚁群算法表现出了较强的优越性。粒子群算法(particle swarm optimization, PSO)是一种群体智能算法,由鸟群觅食行为演化而来[4]。与一般的群体智能算法相比,PSO具有记忆特性,可以通过自我学习和向他人学习方式获得更多的信息。由于参数少,计算方便等优点,PSO广泛应用在优化问题上,并取得了很好的效果。随着移动机器人技术的发展,国内外学者对粒子群算法在移动机器人路径规划上做了大量的研究,如多机器人路径规划[5-6],自由浮动机器人轨迹规划[7]以及其他应用领域[8-9]。PSO在路径规划上应用广泛,ACO善于解决TSP问题,因此采用两者结合的方式非常适合移动机器人多目标点路径规划问题。
在一个包含障碍物的空间内,利用PSO算法对起始点到目标点及每个目标点与目标点之间进行路径规划。起始点、目标点以及障碍物位置已知,但是哪一条路线会被选择是未知的。为了确定哪一条路径会被选择,ACO被用于遍历起始点和所有目标点,以便得到一条经过所有点的最短路径。为了避免PSO出现早熟现象,提高算法的效率,提出了具有快速收敛性的粒子群算法。实验结果验证了混合算法的有效性以及改进的粒子群算法的优越性。
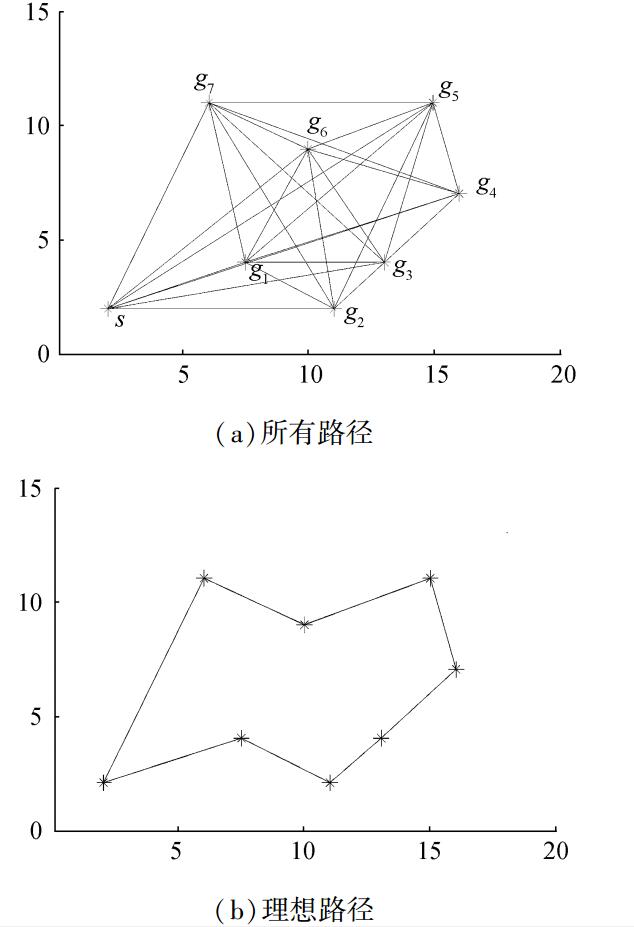
1 问题描述 1.1 多目标点路径规划假设在移动机器人多目标点路径规划中含有n个目标点,则移动机器人会产生n(n-1)/2条路径。为了满足移动机器人行走路径最短的要求,机器人需要从n(n-1)/2条路线中选择出一条经过所有点的最短路径。图 1描述了在起始点和目标点位置已知的情况下,移动机器人的运动轨迹。从图 1(a)中可知移动机器人的移动路线有很多条,且必须经过所有目标点才能完成路径规划;图 1(b)表示移动机器人运动的理想路线。
|
图 1 多点之间的路径轨迹 Fig.1 The path trajectory of multi-goal |
为了解决上述问题,我们将目标点的选择规划为TSP问题的一个分支。目前,求解TSP问题最有效的方法主要有郭涛算法、模拟退火算法、遗传算法、蚁群算法等[3]。由于这些算法都有优缺点,因此有些学者尝试结合两种或多种算法解决彼此算法上的缺点[10]。蚁群算法作为一种自组织正反馈算法,与其他算法相比,具有很强的鲁棒性。而且从本质上讲,蚁群算法的并行特性,强化了算法的可靠性。因此在解决多目标点选择的问题上,我们将采用蚁群算法搜索能够遍历所有目标点的方法。
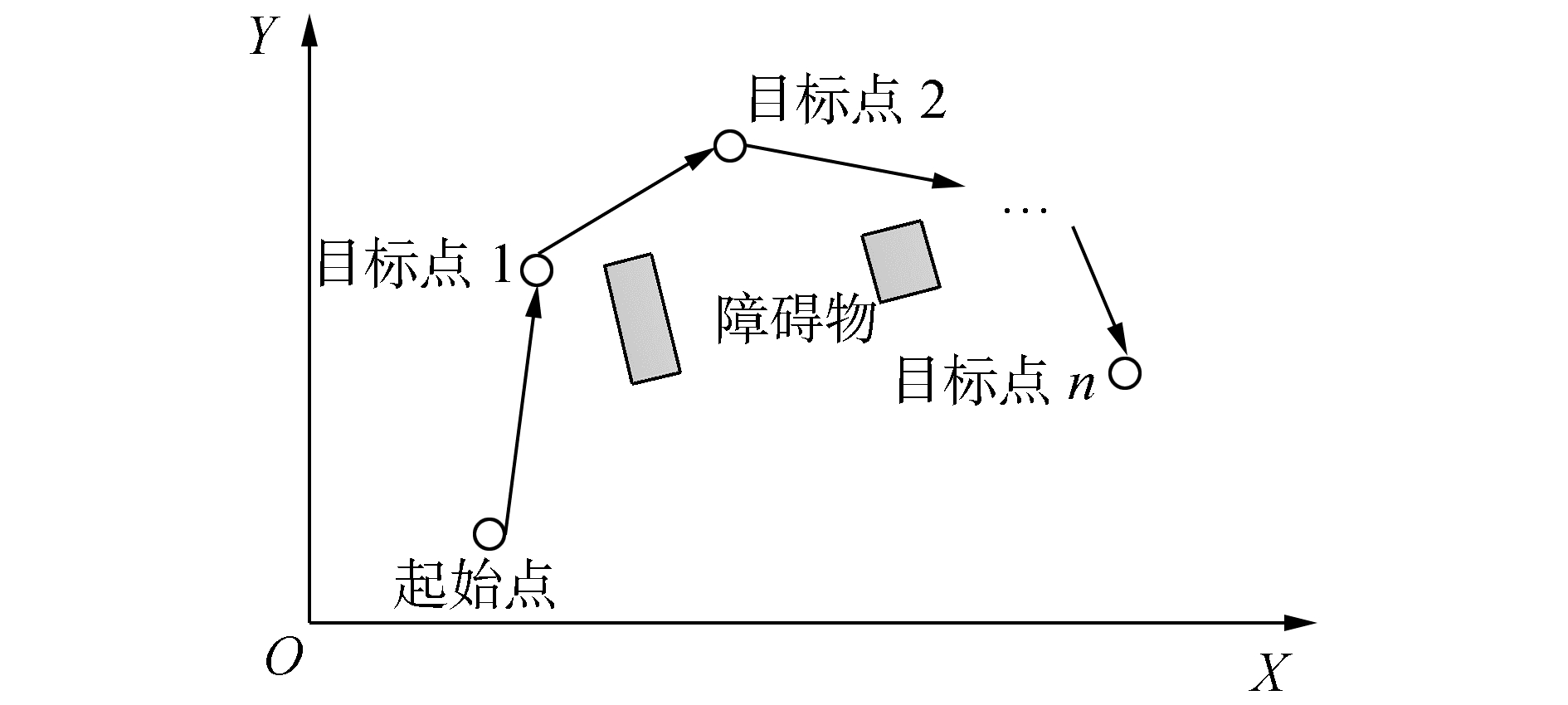
1.2 粒子的适应度函数粒子的适应度函数是检验粒子群算法收敛性的重要函数。在路径规划中,移动距离最短是机器人首要考虑的目标,其次是安全性。因此,将移动机器人运动距离作为粒子的首要适应度函数。移动机器人多目标点路径规划如图 2所示。由图 2可知,移动机器人从起始位置开始避开障碍物,经过一系列目标点到达目标点n。
|
图 2 移动机器人多目标点路径规划示意图 Fig.2 The diagram of mobile robot multi-goal path planning |
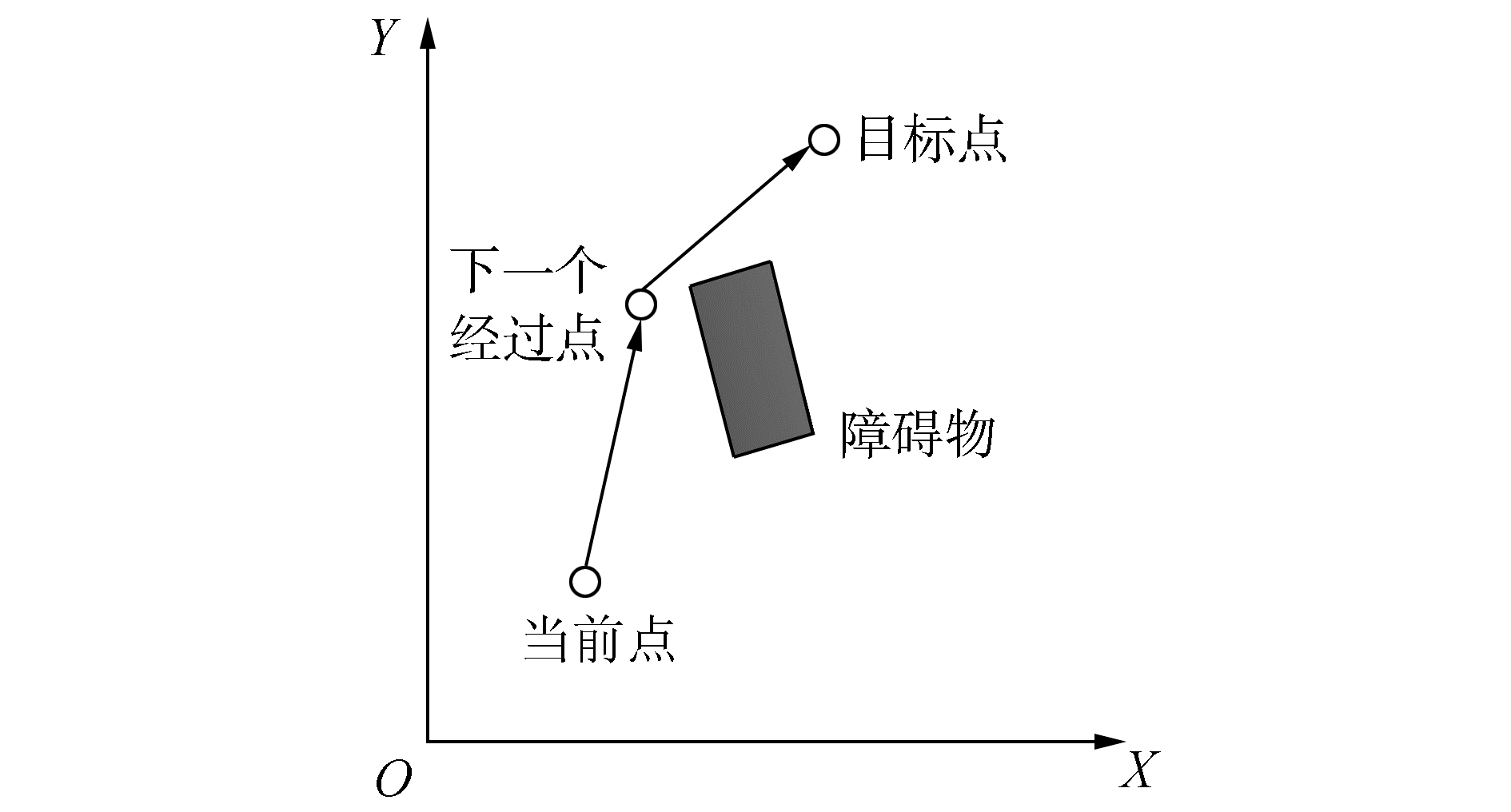
为了便于理解移动机器人多目标点路径规划,可将图 2中的多目标点路径规划分解为多个目标点中的两两目标点之间路径规划。机器人在保证两点之间路径规划最短的基础上才能保证多目标路径规划最短。分解后如图 3所示,机器人在当前点需要选择下一个所经过点,然后到达目标点,在此期间要避开障碍物。
|
图 3 当前点到目标点避障描述 Fig.3 The obstacle avoidance description of currentpoint to goal |
综上所述,为了保证路径规划的最短性,下一个移动点的选取是保证移动机器人运动轨迹最短的前提。因此,设立移动机器人路径规划目标函数F1,F1决定了移动机器人行走路径长度。本文中,F1定义为
| $ \begin{array}{l} {F_1} = \sum\limits_{j = 1}^g {\sum\limits_{i = 1}^S {\left[{\sqrt {{{\left( {x_{i, j}^{{\rm{current}}}-x_{i, j}^{{\rm{next}}}} \right)}^2} + {{\left( {y_{i, j}^{{\rm{current}}}-y_{i, j}^{{\rm{next}}}} \right)}^2}} + } \right.} } \\ \;\;\;\;\;\;\;\;\left. {\sqrt {{{\left( {x_{i, j}^{{\rm{next}}}-x_{i, j}^{{\rm{goal}}}} \right)}^2} + {{\left( {y_{i, j}^{{\rm{next}}} - y_{i, j}^{{\rm{goal}}}} \right)}^2}} } \right] \end{array} $ |
式中,g是目标点的个数,S是粒子个数。
移动机器人在向目标点移动过程中,除了要保证其最短性,安全性也是必须要考虑的。为此,将障碍物对目标点的斥力场函数作为安全性的惩罚函数。斥力场函数定义如下:
| $ {F_2} = \left\{ \begin{array}{l} {k_r} \times {\left( {\frac{1}{{d\left( {{x_R}, {x_O}} \right)}}-\frac{1}{{{d_m}}}} \right)^2}{d^2}\left( {{x_R}, {x_G}} \right), \;\;\;d\left( {{x_{R, }}{x_0}} \right) \le {d_m}\\ 0, \;\;\;\;\;\;\;d\left( {{x_{R, }}{x_0}} \right) > {d_m} \end{array} \right. $ |
式中:F2是障碍物对机器人的斥力;kr是斥力场系数;d(xR, xO)为机器人到障碍物的距离;d(xR, xG)是机器人到目标点的距离;dm是障碍物的影响范围。
移动机器人多目标点路径规划问题可以抽象为当前位置到目标点的最短距离的优化问题,而障碍物对机器人的斥力作用是保证最短路径安全性的前提。因此,针对路径规划的目标函数可以定义为
| $ F = \lambda {F_1} + \mu {F_2} $ |
式中λ和μ分别是最短路路径和约束条件的权重。
2 基本知识 2.1 标准粒子群算法在PSO算法中,每个粒子通过自我学习及向“他人”学习向问题空间中的最佳位置移动,进而找到最优解。N维空间内粒子的位置变量为xi=(xi1, xi2, …, xin),vi=(vi1, vi2, …, vin)为粒子的速度变量。粒子迭代时,通过向两个“极值”学习来更新自己:1) 局部最优值pbest;2) 全局最优值gbest。PSO充分利用局部最优值和全局最优值,可使优秀粒子的基因得到传承。粒子寻优的过程是粒子根据自我学习和向他人学习来更新自己的速度和位置,逐步获得最优解。粒子的速度和位置更新公式为
| $ \mathit{\boldsymbol{v}}_i^{t + 1} = \omega \mathit{\boldsymbol{v}}_i^t + {c_1}{r_1}\left( {{\mathit{\boldsymbol{p}}_{{\rm{best}}}}-\mathit{\boldsymbol{x}}_i^t} \right) + {c_2}{r_2}\left( {{\mathit{\boldsymbol{g}}_{{\rm{best}}}}-\mathit{\boldsymbol{x}}_i^t} \right) $ | (1) |
| $ \mathit{\boldsymbol{x}}_i^{t + 1} = \mathit{\boldsymbol{x}}_i^t + \mathit{\boldsymbol{v}}_i^t $ | (2) |
式中:ω是粒子的惯性权重;c1、c2是学习因子;r1、r2是[0, 1]的随机数;xit表示粒子t的位置且xit∈[xmin, xmax]; 速度vit∈[vmin, vmax]。当粒子的位置超出了[xmin, xmax]时,粒子被限制为xmin或xmax;若粒子的速度超出了vmax时,粒子的速度被限制为最大速度vmax。
2.2 反向学习策略Tizhoosh[11]在2005年基于相反数或对立点的概念提出了反向学习策略。在随后的发展中,该方法被应用于解决一些优化问题中[12-13]。反向坐标定义如下。
定义1[14] 假设x在一维空间中的坐标是-5,目标点的坐标为10。那么x反向点
| $ \tilde x = a + b-x $ |
式中x∈[a, b],且为实数。把上述定义应用到高维空间可表示成定义2。
定义2[14] 在N维空间中的一个点P可表示为P(x1, x2, …, xn),其中x1, x2, …, xn∈
R, 且xi∈[ai, bi], ∀i={1, 2, …, n}。则点P对应的反向点
| $ {{\tilde x}_i} = {a_i} + {b_i}-{x_i} $ |
将定义2应用到优化过程中,则反向机制的优化过程如定义3。
定义3[14] 根据定义1和定义2,反向学习可以描述为:假设f(x)是已知问题的函数方程,n维空间中的点Pi(x1, x2, …, xn)是函数方程f(x)的一个解,且xi∈[ai, bi], ∀i={1, 2, …, n}。则Pi的反向点为
基于反向学习策略的思想,本文提出一种改进的粒子群算法(opposition-based learning improved PSO, OBLIPSO)。本文采用反向学习策略时,将反向学习策略应用到单个粒子中,而不是粒子群体中,以便减小粒子迭代过程中的计算量。性能测试结果证明,改进的粒子群算法能抑制粒子早熟现象,提高收敛效率。下面介绍改进算法的主要机制和流程。
3.1 初始化种群粒子在问题空间中找到最优解的时间与粒子初始化时在空间中的分布存在正比关系,距离最佳位置近的粒子找到最优解的时间比距离最佳位置远的粒子要快。但是,粒子在问题空间中是随机分布的,每一个粒子相对于最优解的位置都是未知的。
基于以上分析,在改进的粒子群算法初始化时引入反向学习策略有助于粒子寻找最优解。在初始化时,首先,计算粒子的适应度值以及其反向粒子适应度值,并对两者进行比较,选择适应度值较好的粒子;其次,从种群中选择S个适应度值最好的粒子作为初始种群。
3.2 迭代进化过程在标准PSO算法中,粒子在问题空间中选择另一个粒子作为学习对象,根据式(1)、(2) 进行移动。但在粒子进化的过程中,粒子会发生早熟现象,导致算法无法得到最优解。由式(1) 可知,粒子的速度受到惯性权重和学习因子的影响:惯性权重影响着粒子的全局搜索和局部搜索能力,学习因子影响粒子获取信息的能力。为了找到问题最优解,粒子在进化的过程中,其全局搜索能力和局部搜索能力也应该随之发生变化,即从全局搜索渐变为局部搜索,保证粒子可以寻找到问题的最优解。同样,粒子也应该逐渐增强社交能力,由“自我”学习逐渐向“他人”学习过渡,以便获取更多有用的信息。
根据以上分析,粒子在寻优过程中,惯性权重应该保持动态变化。ω取值较大时,粒子的全局搜索能力较强;ω取值较小时,粒子的局部搜索能力较强。由于粒子在寻优的过程中,会逐渐靠近最优点,粒子的惯性权重应该随着寻优过程自适应变化。因此粒子的惯性权重更新公式为
| $ \omega = {\omega _{\max }}-\left( {{\omega _{\max }}-{\omega _{\min }}} \right)\left( {1-\frac{{{\rm{dis}}{{\rm{t}}_i}}}{{\max \_{\rm{dist}}}}} \right) $ |
式中:ωmax和ωmin分别是粒子惯性权重的最大值和最小值; disti是第i个粒子到全局最优粒子的欧几里德距离; max_dist是粒子到全局最优粒子的最大距离。disti和max_dist表达式分别为[15]
| $ \begin{array}{l} {\rm{dis}}{{\rm{t}}_i} = {\left( {\sum\limits_{d = 1}^D {{\mathit{\boldsymbol{g}}_{{\rm{bes}}{{\rm{t}}_d}}}-{\mathit{\boldsymbol{x}}_{i, d}}} } \right)^{\frac{1}{2}}}\\ \max \_{\rm{dist}} = \mathop {\arg \max \left( {{\rm{dis}}{{\rm{t}}_i}} \right)}\limits_i \end{array} $ |
学习因子c1和c2控制粒子本身记忆与同伴记忆之间的相对影响:c1的值较小时,表现为自我认知能力不足;c2的值较小时,表现为社交能力不足。为了保证在迭代过程中,粒子的自我认知和社交能力能够因时而异,因此,粒子的学习因子更新公式[16]如下:
| $ {c_1} = {c_{1\max }} \times {\left( {\frac{{{c_{1\min }}}}{{{c_{1\max }}}}} \right)^{\left( {\frac{t}{{{T_{\max }}}}} \right)}} $ |
| $ {c_2} = {c_{2\min }} \times {\left( {\frac{{{c_{2\max }}}}{{{c_{2\min }}}}} \right)^{\left( {\frac{t}{{{T_{\max }}}}} \right)}} $ |
式中:c1max和c2max以及c1min和c2min分别是学习因子c1和c2的最大值和最小值; t是当前的迭代次数;Tmax是最大迭代次数。
3.3 算法实现流程1) 首先初始化种群P(S),包括粒子的位置xi和速度vi,i=1, 2, …, S,S是种群的大小,初始化惯性权重ω以及学习因子c1和c2等参数。
2) 在速度和位置规定的范围内根据式(1)、(2) 更新第i个粒子的速度vi和位置xi。
3) 计算第i个粒子的适应度值fi。
4)ai=min(xi)。
5)bi=max(xi)。
6) 计算第i个粒子的位置和速度反向解:
7) 计算第i个粒子反向解的适应度值
8) 比较fi和
9) 从最优适应度值中选出S个适应度值最好的粒子组成初始化种群。
10) 接下来同粒子群算法基本流程。
11) 算法满足结束条件,结束算法过程。
4 实验结果与分析 4.1 OBLIPSO性能测试为了验证改进粒子群算法的性能是否得到改进,笔者将反向学习的粒子群算法与其他改进算法[15, 17-18]在4个适应度函数上进行对比。这4个适应度函数分别为Sphere函数、Rastrigin函数、Grewank函数、Schaffer函数,测试函数参数设置如表 1所示。
| 表 1 测试函数参数设置 Tab.1 The parameter setting of test function |
OBLIPSO算法参数设置为:粒子群大小为40,空间维度为2,ω=[0.4, 0.9],c1=[1.25, 2.75],c2=[0.5, 2.25],最大迭代次数为100。
在表 2中,OBLIPSO算法在四测试函数上的平均值均小于其他3种算法的值,尤其是在Sphere函数和Rastrigin函数中。从表 2中数据可知,OBLIPSO算法具有更好的收敛性,得到的解更优。表 3中的数据反映出改进算法的稳定性。OBLIPSO算法与IAPSO算法、IPSO算法和WPSO算法对比,在稳定性上表现得更好。
| 表 2 平均最优值结果对比 Tab.2 The comparison of average best values |
| 表 3 标准方差结果对比 Tab.3 The comparison of standard deviation |
由表 2和表 3数据可得:反向学习策略提高了种群的多样性,增加了粒子寻优成功概率,节省了粒子寻优时间;线性变化的惯性权重保障了粒子从全局搜索到局部搜索的线性转换,抑制了粒子早熟现象;学习因子的变化保证了粒子能够充分完成自我学习和社交行为,提高了粒子的收敛速度。
4.2 路径规划仿真实验为了验证新方法的实用性及有效性,笔者将该方法在仿真环境下进行实验。仿真实验环境设置在18×16的二维矩形空间内,并设置成简单环境和复杂环境。在环境中有不规则的障碍物,起始点位置使用方形表示,目标点处用五角形表示。
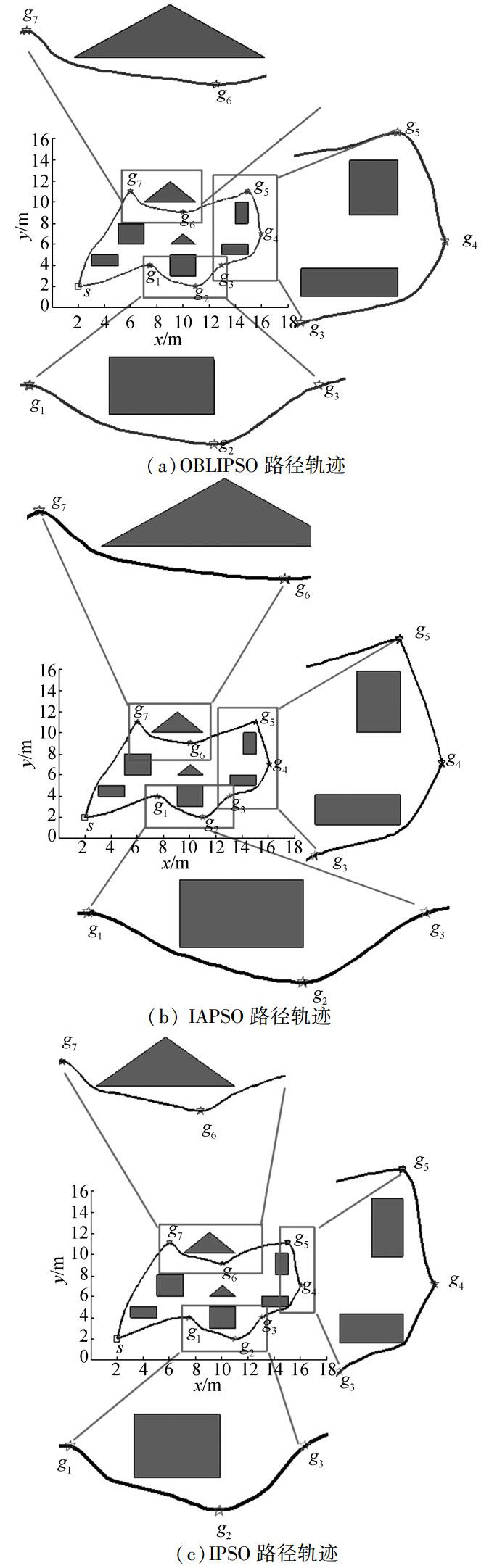
1) 第1次实验中,OBLIPSO算法的参数设置为:ωmax=0.9,ωmin=0.4,S=10,c1max=2.75,c2max=2.25, c1min=1.25, c2min=0.5,vmax=1.9,vmin=0,斥力场中的安全距离dm=2,kr=2.7,λ=0.25,μ=0.25,最大迭代次数为100。图 4(a)给出了在简单环境下的OBLIPSO作用的移动机器人多目标点移动轨迹。图 4(b)是IAPSO作用的运动轨迹。图 4(c)是IPSO作用的运动轨迹。
|
图 4 简单环境下的优化过程 Fig.4 The motion process in the first environment |
由图 4框中路径轨迹可知:在目标点3到目标点4和目标点6到目标点7之间,OBLIPSO和IAPSO的避障性能上优于IPSO,在经过目标点4和目标点5时,OBLIPSO的路径较为平滑。而且OBLIPSO在迭代72次左右时成功完成路径规划。
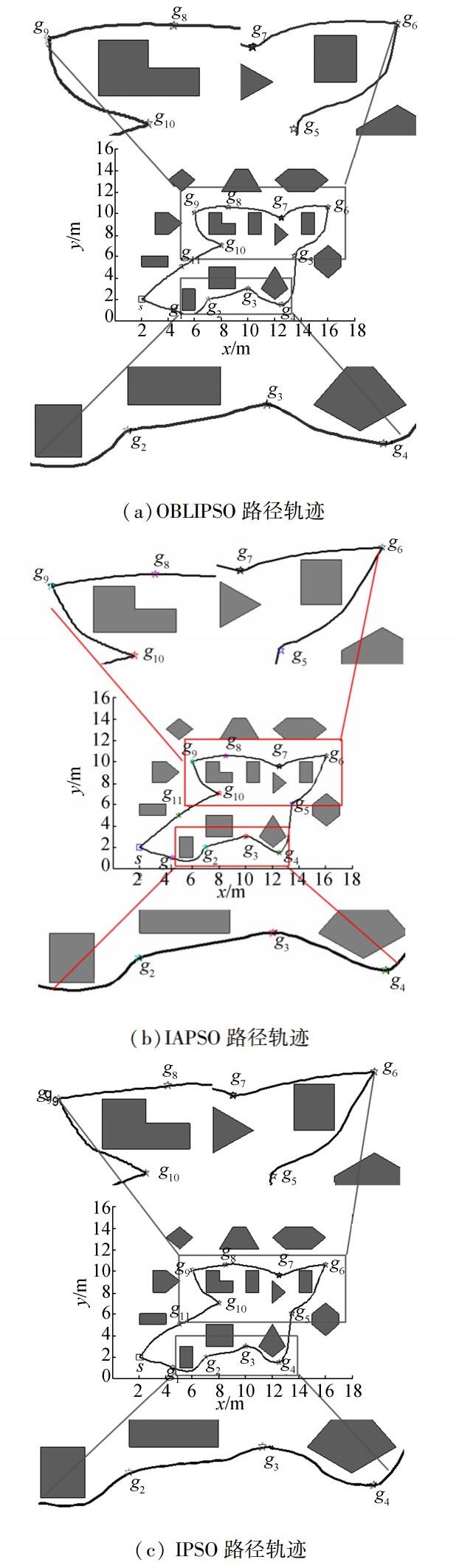
2) 在第2次实验中,实验环境相对第1次实验而言,增加了障碍物以及目标点的个数。实验参数设置如下:vmax=20,最大迭代次数为300,其余参数与第1次实验中参数相同。由于环境复杂度的增加,相对第1次实验而言,粒子收敛速度变慢。图 5(a)是在复杂环境下的OBLIPSO获得的移动机器人多目标点运动轨迹。图 5(b)是IAPSO获得的运动轨迹。图 5(c)是IPSO作用的运动轨迹。
|
图 5 复杂环境下迭代过程 Fig.5 The iteration process in complicated environment |
对比图 5中3条轨迹可知,随着障碍物和目标点增加,3种算法都满足了路径的可达性。根据图 5框中的路径轨迹可知,在经过目标点6和目标点9时,OBLIPSO算法规划的路径相比于IAPSO和IPSO算法规划的路径更为平滑。OBLIPSO算法规划的路径在目标点5与目标点10之间相比于IAPSO和IPSO算法规划的路径安全性更好,OBLIPSO移动距离较短(见表 4),而且其规划的路径安全性最好。
| 表 4 路径性能对比 Tab.4 The performance comparison of path |
3) 路径规划性能对比
重复10次上述两种任务的实验,取其平均值。移动机器人多目标点路径规划的时间消耗和移动距离性能对比如表 4所示。
从表 4数据中可以得出,随着任务复杂度的增加,OBLIPSO、IAPSO和IPSO在时间消耗上也在增加,任务越复杂,用时越多。但在进行相同任务时,OBLIPSO用时比IAPSO和IPSO少;在移动距离方面,简单任务时,OBLIPSO的移动距离比其他两种对比算法短,在复杂任务时,虽然OBLIPSO的移动距离长于IAPSO,但其比IPSO算法短;在路径安全性方面,OBLIPSO算法要优于其他两种对比算法。由于在设计路径规划目标函数时不仅考虑了路径最短性问题,也考虑到了其安全性的问题,因此综合两种环境下实验结果可以得出OBLIPSO算法综合性能强于IAPSO算法和IPSO算法。
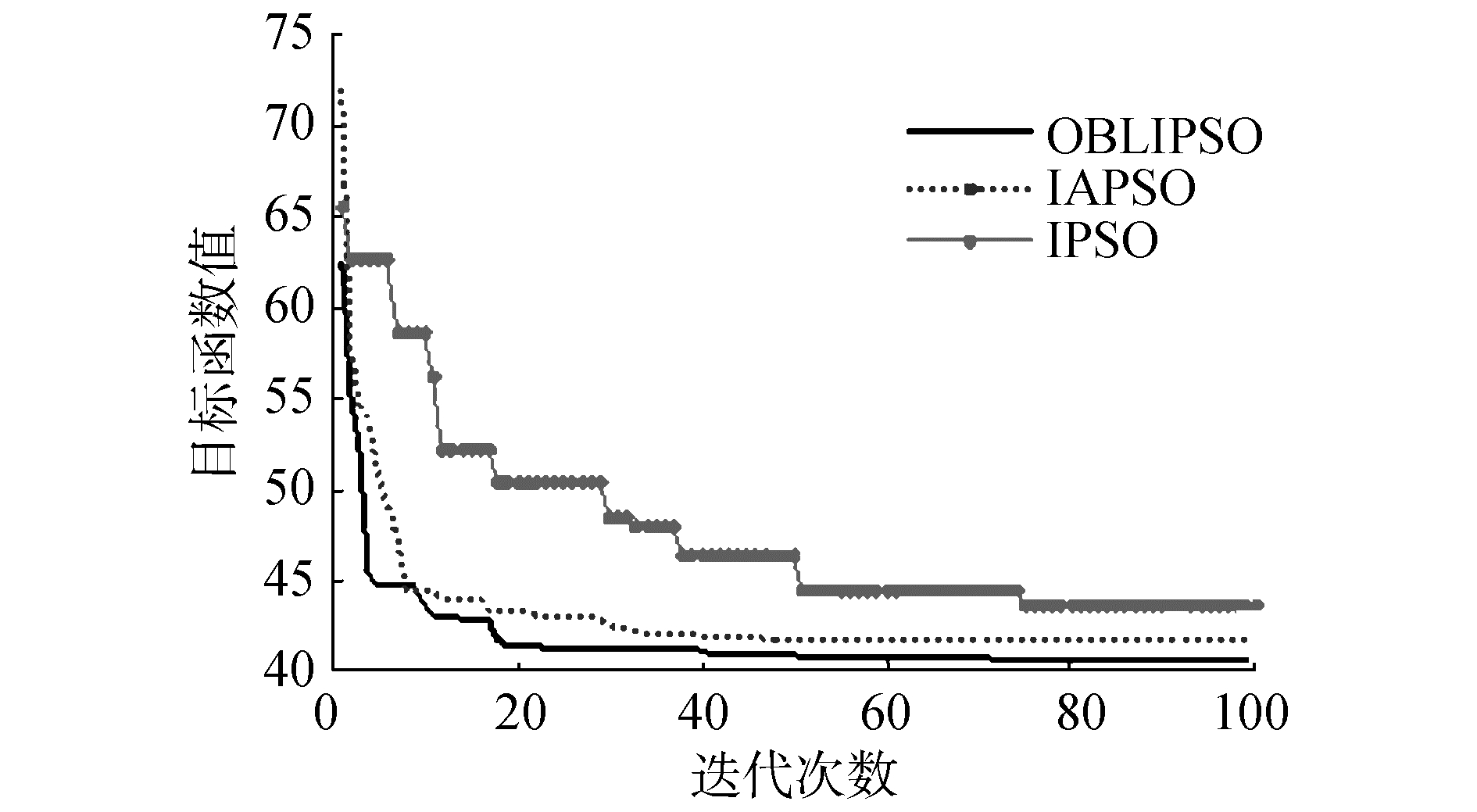
图 6给出的是简单环境下OBLIPSO算法、IAPSO算法和IPSO算法在目标函数上的收敛曲线对比。从图 6中曲线可以得出,在迭代72次左右时,OBLIPSO算法可在多目标点路径规划中寻到最优路径,而IAPSO算法和IPSO算法在迭代100次时仍未获得OBLIPSO算法的收敛值。
|
图 6 OBLIPSO与IAPSO和IPSO目标函数收敛曲线比较 Fig.6 The convergence comparison of OBLIPSO with IAPSO and IPSO |
综上所述,在相同任务下,OBLIPSO算法的综合性能优于IAPSO算法和IPSO算法。随着任务复杂度的变化,OBLIPSO算法能够有效且较好地完成移动距离和时间消耗以及安全性上表现得更好,表明了OBLIPSO算法能够有效且较好地完成移动机器人多目标点路径规划上有效性。
4.3 实际环境下路径规划为了验证OBLIPSO算法在实际应用中的有效性,笔者将在实际环境下对OBLIPSO算法进行实验验证。实验环境设置为重庆邮电大学自动化学院办公楼一楼。实验平台为先锋3机器人,软件背景为ROS(robot operation system)[19-21]。实验中设置了3个目标点,机器人从目标点1出发经过两个目标点,最后返回目标点1。
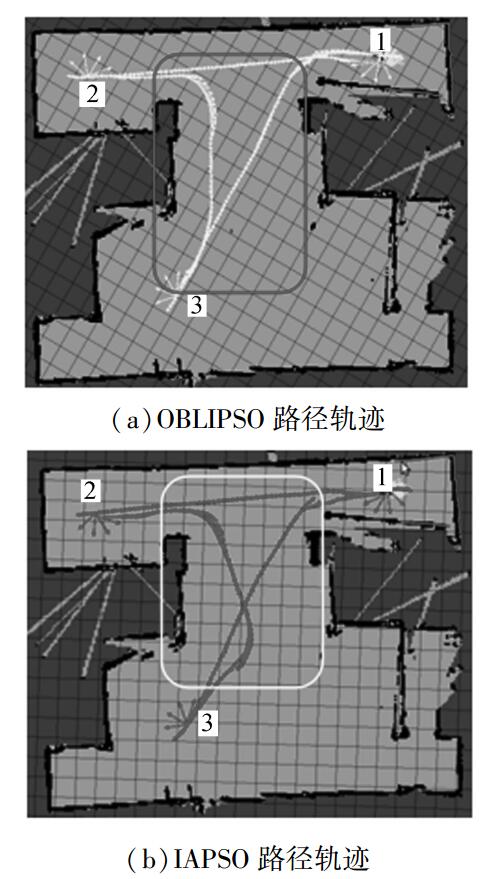
图 7中显示的是机器人在无障碍环境中完成的多目标点路径规划。图 7(a)为OBLIPSO算法规划的路径,图 7(b)为IAPSO算法规划的路径。由图 7可知:机器人从目标点2到目标点3的过程中,OBLIPSO算法能够保证机器人与墙体保持安全距离且路径平滑;IAPSO算法虽然保证了机器人与墙的安全距离,但由于机器人远离墙体移动造成了路径的交叉,如图 7中方框所示。
|
图 7 机器人在无障碍环境下的移动过程 Fig.7 The motion process of robot in barrier-freeenvironment |
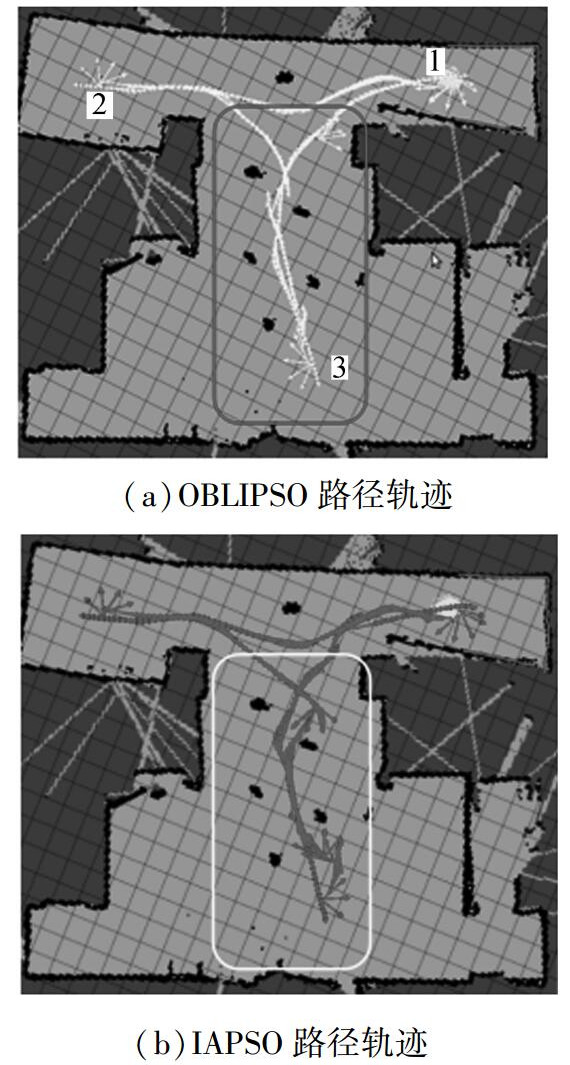
为了进一步验证OBLIPSO算法的有效性,环境中设置了障碍物,并改变了目标点3的位置,如图 8所示。图 8表示机器人在含有障碍物的环境下实现的多目标点路径规划。图 8(a)为OBLIPSO算法规划的路径,图 8(b)为IAPSO算法规划的路径。由图 8可知:在含有障碍物的环境中,机器人在两种算法下都能够避开障碍物完成路径规划,但是机器人从目标点2到目标点3的过程中,OBLIPSO算法能够保证机器人与障碍物保持安全距离并且路径平滑;IAPSO算法在移动过程中,虽然机器人与障碍物保持了安全的距离,但由于其路径的交叉导致移动轨迹较长,如图 8中方框所示。
|
图 8 机器人在障碍环境下的移动过程 Fig.8 The motion process of robot in the obstacle environment |
表 5为两次实验重复10次取得的时间和路径长度的平均值。由表 5可知:在障碍环境下,OBLIPSO算法可以实现机器人多目标点的路径规划,并且消耗的时间较少。
| 表 5 真实环境下路径性能对比 Tab.5 The performance comparison of path in real environment |
本文提出了一种结合ACO算法和OBLIPSO算法的移动机器人多目标点路径规划新方法,并通过实验验证了新方法的可行性。ACO算法在TSP问题上表现出较好的优越性,因此ACO算法适用于移动机器人的目标点选择问题。OBLIPSO算法不仅继承了PSO算法计算简单的特点,而且在初始化时引入反向学习策略,保证了粒子的多样性。在迭代过程中,OBLIPSO算法抑制了粒子的早熟,提高了收敛速度。采用4个适应度函数对OBLIPSO算法进行性能评估,取得了良好的测试结果。仿真实验与真实环境下实验结果表明提出的新方法是一种有效的多目标点路径规划方法。将本文提出的新方法应用到动态环境下的移动机器人的多目标点路径规划是下一步的研究内容。
| [1] |
杨兴, 张亚, 杨巍, 等. 室内移动机器人路径规划研究[J]. 科学技术与工程, 2016, 16(15): 234-238. YANG Xing, ZHANG Ya, YANG Wei, et al. Research on path planning of indoor mobile robot[J]. Science technology and engineering, 2016, 16(15): 234-238. DOI:10.3969/j.issn.1671-1815.2016.15.042 (  0) 0)
|
| [2] |
Ammar A, Bennaceur H, Châari I, et al. Relaxed Dijkstra and A* with linear complexity for robot path planning problems in large-scale grid environments[J]. Soft computing, 2016, 20(10): 4149-4171. DOI:10.1007/s00500-015-1750-1 ( 0) 0)
|
| [3] |
杜鹏桢, 唐振民, 孙研. 一种面向对象的多角色蚁群算法及其TSP问题求解[J]. 控制与决策, 2014(10): 1729-1736. DU Pengzhen, TANG Zhenmin, SUN Yan. An object-oriented multi-role ant colony optimization algorithm for solving TSP problem[J]. Control and decision, 2014(10): 1729-1736. (  0) 0)
|
| [4] |
AGRAWAL R K, BAWANE N G. Multiobjective PSO based adaption of neural network topology for pixel classification in satellite imagery[J]. Applied soft computing, 2015, 28(C): 217-225. ( 0) 0)
|
| [5] |
DAS P K, BEHERA H S, PANIGRAHI B K. Intelligent-based multi-robot path planning inspired by improved classical Q-learning and improved particle swarm optimization with perturbed velocity[J]. Engineering science and technology, an international journal, 2015, 19(1): 651-669. ( 0) 0)
|
| [6] |
YANG Mao, LI Chunzhe. Path planning and tracking for multi-robot system based on improved PSO algorithm[C]//Proceedings of 2011 International Conference on Mechatronic Science, Electric Engineering and Computer(MEC). Jilin: IEEE, 2011: 1667-1670. http://ieeexplore.ieee.org/document/6025799/
( 0) 0)
|
| [7] |
WANG Mingming, LUO Jianjun, WALTER U. Trajectory planning of free-floating space robot using particle swarm optimization(PSO)[J]. Acta astronautica, 2015, 112: 77-88. DOI:10.1016/j.actaastro.2015.03.008 ( 0) 0)
|
| [8] |
张万绪, 张向兰, 李莹. 基于改进粒子群算法的智能机器人路径规划[J]. 计算机应用, 2014, 34(2): 510-513. ZHANG Wanxu, ZHANG Xianglan, LI Ying. Path planning for intelligent robots based on improved particle swarm optimization algorithm[J]. Journal of computer applications, 2014, 34(2): 510-513. (  0) 0)
|
| [9] |
王娟, 吴宪祥, 郭宝龙. 基于改进粒子群优化算法的移动机器人路径规划[J]. 计算机工程与应用, 2012, 48(15): 240-244. WANG Juan, WU Xianxiang, GUO Baolong. Robot path planning using improved particle swarm optimization[J]. Computer engineering and applications, 2012, 48(15): 240-244. DOI:10.3778/j.issn.1002-8331.2012.15.049 (  0) 0)
|
| [10] |
张勇, 陈玲, 徐小龙, 等. 基于PSO-GA混合算法时间优化的旅行商问题研究[J]. 计算机应用研究, 2015, 32(12): 3613-3617. ZHANG Yong, CHEN Ling, XU Xiaolong, et al. Research on time optimal TSP based on hybrid PSO-GA[J]. Application research of computers, 2015, 32(12): 3613-3617. DOI:10.3969/j.issn.1001-3695.2015.12.019 (  0) 0)
|
| [11] |
TIZHOOSH H R. Opposition-based learning: a new scheme for machine intelligence[C]//Proceedings of 2005 and International Conference on Intelligent Agents, Web Technologies and Internet Commerce, International Conference on Computational Intelligence for Modelling, Control and Automation. Vienna: IEEE, 2005: 695-701. http://doi.ieeecomputersociety.org/10.1109/CIMCA.2005.1631345
( 0) 0)
|
| [12] |
MUÑOZ D M, LLANOS C H, COELHO L D S, et al. Hardware opposition-based PSO applied to mobile robot controllers[J]. Engineering applications of artificial intelligence, 2014, 28: 64-77. DOI:10.1016/j.engappai.2013.12.003 ( 0) 0)
|
| [13] |
汪慎文, 丁立新, 谢大同, 等. 应用反向学习策略的群搜索优化算法[J]. 计算机科学, 2012, 39(9): 183-187. WANG Shenwen, DING Lixin, XIE Datong, et al. Group search optimizer applying opposition-based learning[J]. Computer science, 2012, 39(9): 183-187. (  0) 0)
|
| [14] |
AL-QUNAIEER F S, TIZHOOSH H R, RAHNAMAYAN S. Opposition based computing-a survey[C]//Proceedings of the 2010 International Joint Conference on Neural Networks (IJCNN). Barcelona: IEEE, 2010. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=5596906
( 0) 0)
|
| [15] |
SURESH K, GHOSH S, KUNDU D, et al. Inertia-adaptive particle swarm optimizer for improved global search[C]//Proceedings of Eighth International Conference on Intelligent Systems Design and Applications. Kaohsiung: IEEE, 2008: 253-258. http://ieeexplore.ieee.org/xpls/icp.jsp?arnumber=4696340
( 0) 0)
|
| [16] |
姜建国, 叶华, 刘慧敏, 等. 融合快速信息交流和局部搜索的粒子群算法[J]. 哈尔滨工程大学学报, 2015, 36(5): 687-691. JIANG Jianguo, YE Hua, LIU Huimin, et al. Particle swarm optimization method with combination of rapid information communication and local search[J]. Journal of Harbin engineering university, 2015, 36(5): 687-691. (  0) 0)
|
| [17] |
GAO Bingkun, REN Xiuju, XU Mingzi. An improved particle swarm algorithm and its application[J]. Procedia engineering, 2011, 15: 2444-2448. DOI:10.1016/j.proeng.2011.08.459 ( 0) 0)
|
| [18] |
许少华, 李新幸. 一种自适应改变惯性权重的粒子群算法[J]. 科学技术与工程, 2012, 12(9): 2205-2208. XU Shaohua, LI Xinxing. An adaptive changed inertia weight particle swarm algorithm[J]. Science technology and engineering, 2012, 12(9): 2205-2208. (  0) 0)
|
| [19] |
张建伟, 张立伟, 胡颖, 等. 开源机器人操作系统: ROS[M]. 北京: 科学出版社, 2012.
( 0) 0)
|
| [20] |
COUSINS S, GERKEY B, CONLEY K, et al. Sharing Software with ROS[J]. IEEE robotics & automation magazine, 2010, 17(2): 12-14. ( 0) 0)
|
| [21] |
ZAMAN S, SLANY W, STEINBAUER G. ROS-based mapping, localization and autonomous navigation using a Pioneer 3-DX robot and their relevant issues[C]//Proceedings of 2011 Saudi International Electronics, Communications and Photonics Conference (SIECPC). Riyadh: IEEE, 2011: 1-5. http://ieeexplore.ieee.org/xpls/icp.jsp?arnumber=5876943
( 0) 0)
|
 2017, Vol. 12
2017, Vol. 12


