2. 重庆邮电大学 计算智能重庆市重点实验室, 重庆 400065;
3. 山西大学 计算智能与中文信息处理教育部重点实验室, 山西 太原 030006;
4. 浙江海洋大学 浙江省海洋大数据挖掘与应用重点实验室, 浙江 舟山 316022;
5. 南京大学 软件新技术国家重点实验室, 江苏 南京 210093
2. Key Laboratory of Computational Intelligence, Chongqing University of Posts and Telecommunications, Chongqing 400065, China;
3. Key Laboratory of Computational Intelligence and Chinese Information Processing of Ministry of Education, Shanxi University, Taiyuan 030006, China;
4. Key Laboratory of Oceanographic Big Data Mining and Application of Zhejiang Province, Zhejiang Ocean University, Zhoushan 316022, China;
5. State Key Laboratory for Novel Software Technology, Nanjing University, Nanjing 210093, China
自从1956年人工智能概念的提出,人工智能已经发展了整整60年。无论是最早的“推理期”、之后的“知识期”,还是目前蓬勃发展的“学习期”,这些历史时期都产生了极为璀璨的人工智能理论与技术,有力推动了信息技术的快速发展。目前,人工智能研究主要从两个方面展开:一类着重于感知机理的理解与模拟,包括视觉、触觉、嗅觉、听觉等动态输入的理解与建模;另一类着重于认知机理的理解与模拟,重点关注人类较高层次的认知机理与信息处理方法,包括人类的学习能力、求解能力、推理能力、决策能力等。
1 粒计算的发展及特点粒计算(granular computing)是当前人工智能领域中一种新的概念和计算范式,是研究基于多层次粒结构的思维方式、问题求解方法、信息处理模式及其相关理论、技术和工具的学科,属于人类较高层次认知机理研究的范畴。自1997年Zadeh[1]第1次提出粒计算的概念以来,涌现出许多关于粒计算研究的学术及应用成果。从研究水平来看,2016年国际期刊Journal of Granular Computing[2]在Springer创刊;国际学术会议有每年一次的IJCRS;国内会议有每年一次的CRSSC-CWI-CGrC;在近年来的国家自然科学基金申请中,粒计算理论及应用已经成为信息学部的申请和研究热点之一[3]。与此同时,Web-of-Science 检索结果显示,以粒计算为主题的文章除了计算机科学学科外,与多个学科具有关联(见表 1)。
| 研究领域 | 记录数 | 所占比例/% | 高引论文数 |
| 计算机科学 | 1 256 | 47.059 | 26 |
| 工程 | 919 | 34.432 | 2 |
| 物理 | 285 | 10.678 | 1 |
| 材料科学 | 193 | 7.231 | 1 |
| 机械 | 189 | 7.081 | 0 |
| 数学 | 165 | 6.182 | 0 |
| 地理科学 | 124 | 4.646 | 0 |
从研究内容看,早期粒计算的应用研究主要集中在数据粒化、多粒度分析、知识发现等方面。自2013年以来,有关粒计算的研究呈现出较强的应用价值。2015年在天津召开的 RSFDGrC 国际会议[4]上,发表的有关粒计算研究成果中,超过半数有关应用研究,如台湾省的Kao-Yi Shen和Gwo-Hshiung Tzeng将决策粗糙集和粒计算的方法应用于寿险公司营销模式分析。2017年SCI二区期刊信息科学专辑“大数据时代基于粒计算的机器学习”[5]明确指出,除了粒计算理论和模型的研究外,收稿范围扩展到所有与粒计算相关的工业界研究成果。专辑实际收录推荐系统、入侵检测等应用达一半之多。
当前,互联网和大数据催生了领域问题的大规模和复杂化。从人工智能角度来看,粒计算是模拟人类思考和解决大规模复杂问题的结构化求解模式,从实际问题的需要出发,用可行的满意近似解替代精确解。该理论改变了传统的计算观念,达到对问题的简化、提高问题求解效率等目的[6]。事实上,粒计算不仅是人类认知的一种天然特性,也是许多智能分析任务的内在需求。揭示和模拟人类的这种粒计算认知机理对人工智能发展具有重要作用。
正如张钹院士[7]所指出的“人类智能的一个公认特点,就是人们能从极不相同的粒度上观察和分析同一问题,并且很容易地从一个粒度世界转到另一个粒度世界”。这强有力地表现了人类问题求解过程中具备了在多个粒度空间之间进行通信和转换的能力。基于多粒度的数据建模就是通过获得的信息粒集和多个粒结构进行复杂数据分析,从中挖掘可用的知识并形成有效决策。若数据建模仅使用一个粒结构,则称其为基于单粒度的数据建模;若使用多个粒结构,则称其为基于多粒度的数据建模。“横看成岭侧成峰,远近高低各不同”,由于多粒度分析从多个角度、多个层次出发分析问题,可获得对于问题更加合理、更加满意的求解结果。总之,基于多粒度原理的模拟与实现对复杂问题的机器求解具有重要指导价值。
1.2 多粒度结构的普遍性许多数据具有多粒度、多层次特性。比如,对于广泛存在的生物网络数据,Nir Friedma等[8]在《Science》上发表的论文就认为在诸如复杂细胞网络、蛋白质互作用网络等生物数据中都广泛存在着多层次、多尺度特性。Clauset等[9]在《Nature》上发表的论文也指出,在复杂社会网络中也存在天然的层次结构,而社会网络面临的数据自身就是广泛存在的多模态数据。Ahn等[10]则专门研究了大规模复杂数据的多尺度复杂性特性。在军事、气象等领域,由卫星获得的多波段遥感数据也是典型的具有多层次、多尺度特性的多模态数据[11]。这些都暗示着反映复杂的模式发现与推理决策的多模态数据必然隐含着由这些数据所决定的局部与整体关系以及复杂的层次结构,即数据的多粒度/多层次特性。诸多数据异构变量之间往往具有天然的多粒度形态。不同于同构变量,它们可以自然地表达为一个线性空间。比如在多模态数据中,异构变量之间由于语义的不一致,它的知识表示和运算是挑战性问题。然而,这也正是人类的重要认知能力之一,人们可以从不同的传感器收集信息并进行有效融合以形成合理推理与决策。事实上,多模态数据既可以提供互补信息还可以提供协同信息,这是多模态数据分析的重要优势之一。互补信息是指多种传感器观测到的相互独立的特征信息,它可以扩展系统的性能;而协同信息则指的是单一传感器无法获得,需要依靠多种传感器协同作用才能获得的信息,它可以进一步扩大系统的控制范围。从粒计算的观点来看,在不同变量上对同一数据集获得的粒结构可能是不一样的,这为该数据的理解和认知提供了天然的具有互补性的多粒度结构。
1.3 认知结构的多粒度性近年来在人工智能领域最受关注的非深度学习莫属。自2006年Geoffrey Hinton等[12]在《Science》期刊发表“Reducing the dimensionality of data with neural networks”开始,深度学习的热潮从学术界席卷到了整个工业界。深度学习正是模拟人类大脑神经网络潜在地利用事物的底层特征到抽象特征的层次结构模型来认知事物的内在机制与原理,这是一种典型的多粒度结构。深度学习提供了一套丰富的、基于连接主义的建模框架,可以表达数据内在的丰富的粒度关系和结构。特别是,深度学习在图像、文字、语音等领域的识别方面取得了巨大成功,这些数据类型正是多粒度数据的重要组成部分。粒计算与深度学习有机结合[13]将是非常值得期待的研究方向。
1.4 任务处理的多粒度性在实际应用中,用户需求的多粒度特性决定了信息处理任务的多粒度特性。比如,在视频分析领域,数据挖掘任务可能是面向视频主题进行分类的,也可能是面向主角进行分类的,也可能是面向视频性质进行分类的。又如,在网络大数据领域,社团发现任务本身就是不同的粒度水平决定了发现社团的规模,不同的粒度水平观测到的网络动力学行为可能都是有所区别的。这些都使得挖掘任务可能同时面向不同层次、不同粒度,这个多粒度特性要求数据挖掘工具能够从多个粒度上同时探索数据隐含的模式,并进行有效融合,形成对事物的整体客观认识。
借鉴人类的这种粒计算认知机理,开展数据驱动的人工智能研究,有望诞生新的人工智能理论与方法,对数据挖掘、知识发现、机器学习等领域的发展具有重要的理论意义,同时对提高海量信息处理的效率具有实际的应用价值。需要指出的是,粒计算自然地具有多学科交叉的特性,粒计算的研究与发展有望推动信息科学、认知科学、数学等相关学科的深度融合,为人工智能各领域的共同繁荣、人工智能真正地成为类人智能做出贡献。
2 粒计算基本理论模型随着粒计算研究工作的不断深入,人们从不同的角度研究得到了不同的粒计算理论模型,主要有模糊集理论模型、粗糙集理论模型、商空间理论模型、云模型和三支决策理论模型等。粒计算理论模型大体分为两大类:一类是以信息的粒化为目标,如模糊集理论模型;另一类则以多粒度计算为目标,如粗糙集理论模型、商空间理论模型、云模型和三支决策理论模型。下面是它们的简单介绍。
2.1 模糊集理论模型模糊集理论[14]是Zadeh于1965年首先提出的,他认为元素总是以一定的程度属于某个集合,也可能以不同的程度属于几个集合。它是对经典集合理论的扩展,最主要的贡献在于引入了集合中元素对该集合的“隶属度”,从而将经典集合理论的特征函数取值范围由{0,1}推广到区间值[0, 1],将经典二值逻辑推广至多值逻辑,而集合中元素对集合本身的“隶属度”主要通过隶属函数来表示。“隶属度”的相关定义如下:
给定论域U上的一个模糊集F,对于任意x∈U都确定了一个μF(x),μF(x)称为x对F的隶属度[15]。映射:μF:U→0,1,称为F的隶属函数。隶属函数的值域为[0, 1],当μF(x)∈{0,1}时,模糊集F就是一个普通集合。一般地,用Fλ表示μF(x)≥λ的集合,称为λ截集或λ水平集:Fλ={xμF(x)≥λ,x∈U}
而λ强截集定义为
Fλ+={xμF(x)>λ,x∈U}
模糊集理论中,隶属函数扮演着基石的角色。王国胤教授[16]指出了模糊集是用不精确的方法来刻画不确定问题,其原因在于获取隶属度值是不确定的。在后续的研究中将精确唯一的隶属度值进行种种拓展,形成了许多新的理论体系,主要有直觉模糊集、二型模糊集、区间模糊集和Vague集等。
模糊集理论研究的是一种不确定性现象,主要针对于人类智能的研究,目的是使计算机能够模拟人的智能,具有能够在不精确以及部分精确的环境下给出合理决策的能力,而这一能力的基础就是对信息的模糊粒化。Zadeh在文献[17]中将粒定义为一个命题,定义并讨论了模糊粒的概率分布及概率的计算方法。随着模糊集理论的不断发展完善,使得以模糊逻辑和信息粒化为基础的模糊信息粒化理论[1, 17-18]得以更好地实现,它们为词计算的发展提供了前提条件。
2.2 粗糙集理论模型波兰学者Pawlak[19]在20世界80年代提出了粗糙集理论,它是一种处理不精确和不确定性知识的数学工具。粗糙集理论的本质是利用不可分辨关系(等价关系R)构成对象的等价类(X/R),而所有的等价类形成论域(U)的划分,从而建立一个近似空间。在近似空间中,通过下近似集(R(X))和上近似集(R(X))等概念刻画知识的不确定和不精确性。它们的定义为
R(X)={x∈U|[x]R⊆X}
R(X)={x∈U|[x]R∩X≠∅}
下近似集和上近似集把论域分成3个部分,分别为正区域(POSR(X))、负区域(NEGR(X))和边界域(BNDR(X)):
POSR(X)=R(X)
NEGR(X)=U-R(X)
BNDR(X)=R(X)-R(X)
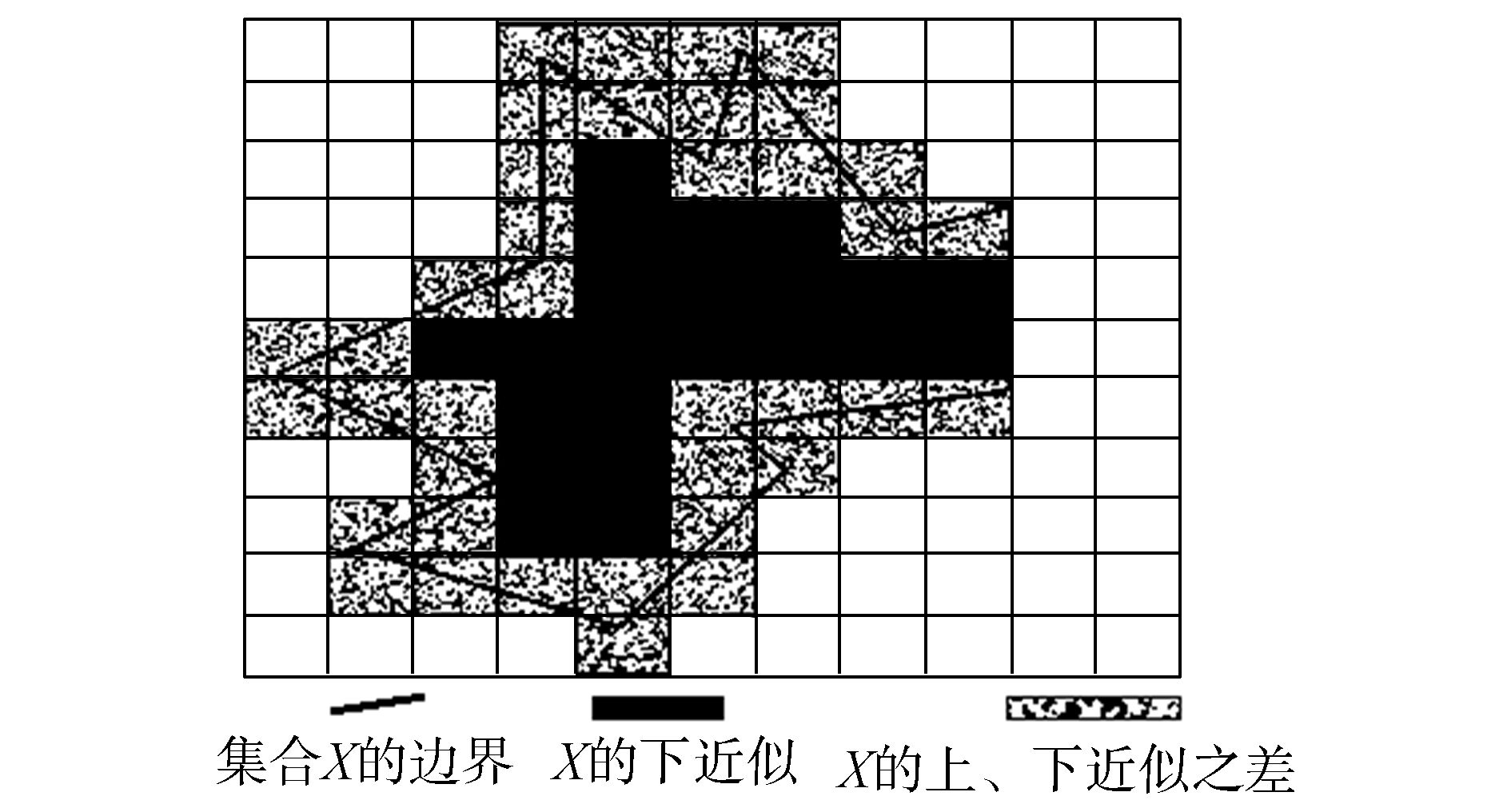
从图 1可知,在粒度一定的情况下,假设黑线勾勒出的知识表示概念X,那么概念X的下近似集就是由完全属于边界域范围内粒子组成,在图形中用黑体部分表示;概念X的上近似集包括灰色部分和黑色部分组成;概念X的边界域由是灰色部分组成。那么由此可以看出,当知识粒度越小,那么下近似集越大,边界越小。
|
| 图 1 粗糙集的上下近似集与边界域图 Fig. 1 Upper approximation,lower approximation and boundary region of rough set |
图 1表明,知识是有粒度的,且知识的不确定性与知识的粒度粗细存在正相关的关系:知识粒度越粗,它的不确定性越大(边界域越大)。在粗糙集理论中,知识被表示为对特定空间上的对象的划分能力,知识粒度被表示为对象的等价类,相同的知识称为不可分辨。以粗糙集理论为基础的粒计算研究,就是对知识空间上粒的表示、转换和相互依存等问题进行相关研究,以期得到更精确的知识表达。
2.3 商空间理论模型张钹院士和张铃教授[20]在研究问题求解时,开创性地提出了商空间理论。商空间理论模型可以用一个三元组(X,f,T)来表示:X表示问题论域,f表示论域的属性,T是表示论域的拓扑结构。对于一个给定的论域X的等价关系R,可以得到一个对应于R的商集[X],然后将[X]当成新的论域,必有一个对应的三元组([X],[f],[T]),称其为对应于R的商空间。商空间理论的推理模型主要依据两个重要的性质:一个是“保真原理”,指若一个命题在两个较细粒度的商空间中是真的,则(在一定条件下)在其合成的商空间中对应的问题也是真的;另一个是“保假原理”,指若一个命题在粗粒度空间中是假的,则该命题在比它细的商空间中也一定为假。
商空间理论的目的是研究不同商空间之间的关系、商空间的分解、合成和推理规律。它将复杂问题表示成不同粗细的粒度空间,然后构建多粒度的分层递阶商空间结构,并通过由粗到细或由细到粗的方式,利用“保真原理”和“保假原理”逐层在多粒度空间中进行多级逼近推理,最后将多粒度空间中粒的解组合成原始问题难题或整体粒的解,从而获得复杂问题的解。
2.4 云模型1995年李德毅院士在概率论和模糊数学的基础上提出隶属云和隶属云发生器[21],并进一步发展为云模型[22]。云的定义如下所示:
设U是一个用精确数值表示的定量论域,C是U上的定性概念,若定量值x∈U,且x是定性概念C的一次随机实现,x对C的确定度μ(x)∈[0, 1]是具有稳定倾向的随机数。
若μ:U→[0, 1],∀x∈U,x→μ(x)则x在论域U上的分布称为云,每一个x称为云滴。
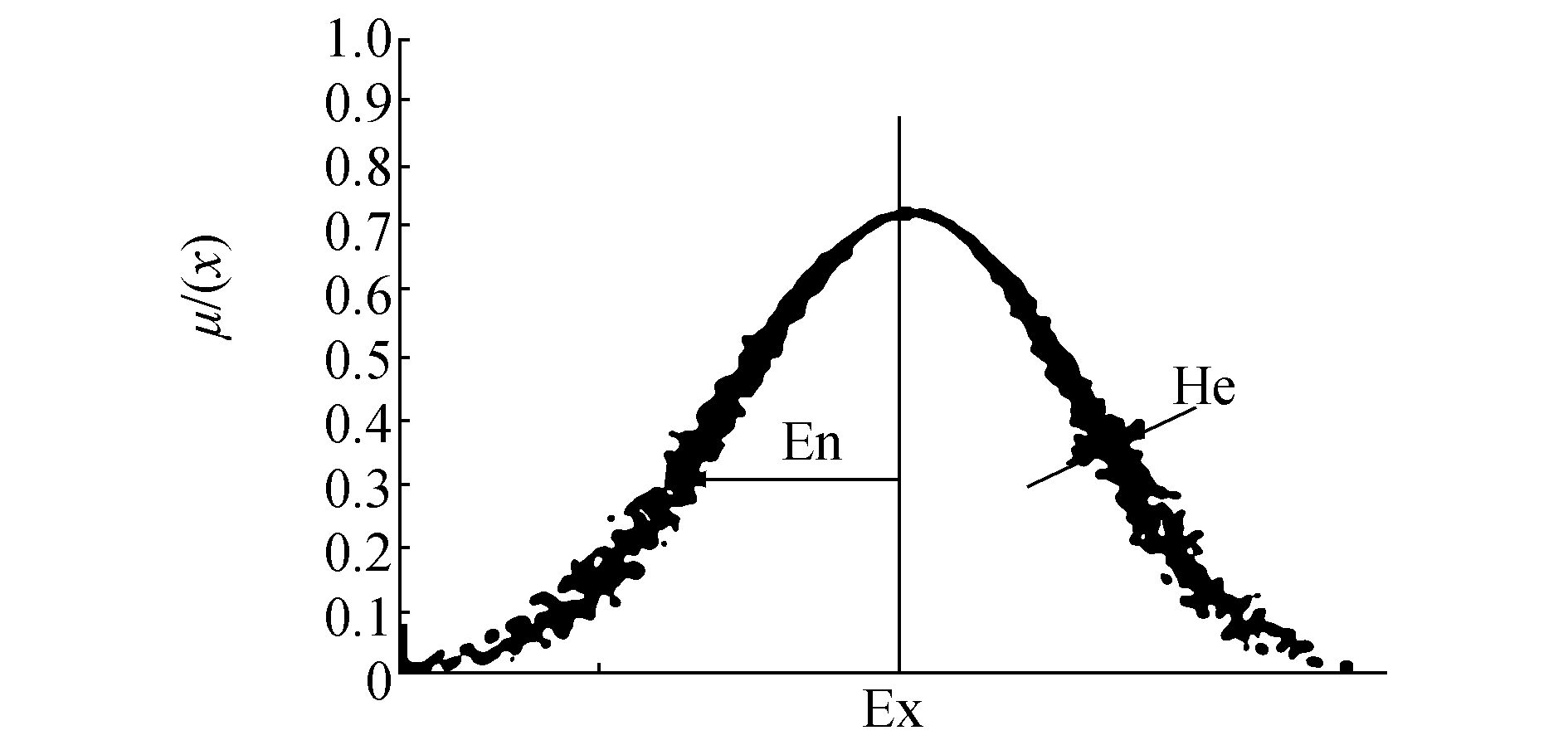
云由若干云滴组成,云滴是某个定性概念的一次随机实现,多次产生的云滴可以综合反映这个定性概念的整体特征。某个概念的整体特征可以用云的3个数字特征来表示,即期望Ex、熵En和超熵He。云和云的数字特征如图 2所示。
|
| 图 2 高斯云及其数字特征示意 Fig. 2 Gaussian cloud and its numerical characteristics |
云模型作为用语言值描述的某个定性概念与其数值表示之间的不确定性转换模型,可以刻画语言值中大量存在的随机性、模糊性以及两者之间的关联性。它主要基于高斯混合模型从原始数据中提取概念(粒化),以云滴的方式对概念进行表示(粒度表达),通过云的跃迁构建云模型的层次结构(粒的层次构建),利用云模型的3个数字特征进行云运算和云推理(粒计算)。作为粒计算的基本模型之一,云模型具有粒计算从不同的层次、不同的角度观察和分析问题的特点,具有粒计算将复杂问题分解成若干子问题分别求解,降低计算复杂度的特点。
2.5 三支决策理论模型三支决策理论[22-24]最初是由加拿大里贾纳大学的姚一豫在粒计算和粗糙集理论的研究基础上提出的。三支决策的主要思想就是将待求解问题通过映射f分解为3个部分:L-域、M-域和R-域,然后对不同的部分采用不同的处理方法进行分析求解,它为复杂问题求解提供了一种有效的策略与方法。根据映射f的不同,分为定性三支决策和定量三支决策。在定量三支决策模型中,通过映射函数,以及引入的一对阈值(α,β)(一般1≥α≥β≥0),在三支决策空间中进行3个区域的计算,如下所示[25]:
接受域:ACP(α,β)(E,A)={x∈U|E(A)(x)≥α}
拒绝域:REJ(α,β)(E,A)={x∈U|E(A)(x)≤β}
不确定域:UNC(α,β)(E,A)={x∈U|β<E(A)<α}
式中:E(A)为论域U上关于集合A⊆U的映射函数。一般情况下,不确定域与M-域相对应,接受域和拒绝域则根据实际情况与L-域和R-域相对应。
三支决策理论很好地模拟了人类解决实际问题的思维,首先确定了接受域(即明确接受的部分)和拒绝域(即明确拒绝的部分),然后重点研究不确定域的待确认部分。不确定域是不精确对象的集合,对不确定域求解的目的就是降低其不精确性,实际上就是对不确定域进行多粒度挖掘。不确定域的不精确性主要受对象的粒度过粗影响,当我们基于对象的属性进行粒度变换及多粒度运算后,使得不确定域对象的粒度由粗糙逐步细化,从而我们对不确定域对象逐步向接受域和拒绝域转换,使得不确定域的认知愈加清晰。
3 知识的多粒度表示基于单粒度的粒计算模型虽然具有粒计算的所有要素(粒化、粒层、粒算子、粒度),但是由于只能从某个角度近似求解,潜在地丢失了复杂问题中多角度信息对问题求解的贡献。构造以单粒度为基础的多粒度可以融合单粒度的信息,充分利用不同粒度之间的关系,具有更强的表示能力。因此,知识的多粒度表示与信息融合具有内在的一致性。
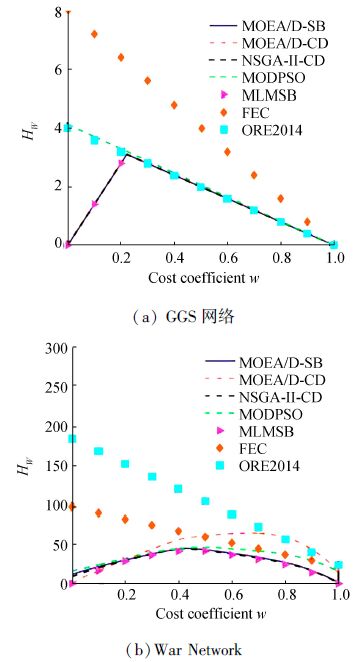
许多研究表明,多粒度表示下的求解在计算复杂度、求解性能等方面具有更好的效果。文献[26]研究了社会网络中的平衡转化与计算问题,实验证明通过结合不同社团内部和社团之间的结构化信息,提出的算法MOEA/D-SB具有最小的计算代价(Hw),如图 3所示。文献[27]从图像和连环画两个本体的结构化设计出发,实现了对纸质连环画结构的自动分析,如图 4所示。
|
| 图 3 不同权重参数下无向符号社会网络转换代价 Fig. 3 Transformation cost Hw with the parameter w for undirected signed network |

|
| 图 4 连环画结构的自动分析 Fig. 4 Automatic analysis of comic structure |
多粒度表示是使用多粒度方法计算复杂问题的前提,可以从多粒度的内涵、效果和表示形式3个层面分析。
1) 从内涵来看:多粒度的实质是通过多个单粒度的粒合成与分解,近似刻画对数据恰当表述的合理结构[28-29]。这种隐藏的结构通常难以直接根据数据特点确定。通常情况下,多粒度的粒层并不是由单个粒化准则决定,也不是由多个单粒度简单地通过粒度交运算得到,是单粒度意义下的超粒。
2) 从效果来看:多粒度下不同信息粒的合成,实际上是信息粒对问题求解效果的合成,最终目的是提高问题求解的质量。因此,多粒度计算的实质是对潜在影响求解的不同信息粒重要性加权,使得相对正向得益强化,相对负向得益弱化。
3) 从表示形式来看:与粒计算模型的选择相关。如基于粗糙集的多粒度研究合成的信息粒以集合[30]的形式表达,基于商空间的多粒度研究合成的信息粒以商空间三元组[31-32]的形式表达。针对不同的多粒度表示方式,王国胤等[33]给出了在大数据背景下模型选取和多粒度设计的框架性描述。
3.2 多粒度的主要模型由于多粒度本身是相对于单粒度而言,其语义解释方面并没有任何附加的约束,因而模型中关于多粒度的解释也不尽相同。本文将从信息系统角度出发,总结已有的5种主要的多粒度模型。
3.2.1 多粒度粗糙集钱宇华等[33]提出的多粒度粗糙集模型能有效模拟人类求解复杂问题时兼顾多个粒度综合评价的思维方式。不同于经典Pawlak粗糙集中从一个属性集的角度定义基于等价划分的信息粒,多粒度粗糙集的信息粒基于一个属性集序列建立。多个不可分辨关系确定论域的层次划分构造多粒度的粒空间,其中每个粒空间具有Pawlak意义下的上下近似。基于多粒度论域空间上对目标概念近似逼近。基于多粒度粗糙集可以有效处理单粒度粗糙集无法解决的以下3种情况:
1) 同一个对象在不同决策者下的分类情况存在矛盾或不一致,此时商集不能进行交运算,因而目标概念不能以交运算来近似;
2) 决策者的决策或观点相互独立,任何两个商集的交运算是冗余的;
3) 在特定背景下,如针对分布式信息系统的数据分析,没有必要进行交运算。
由于赋予了商集决策观点的语义,基于一组对同一个分类概念观点可以得到不同的概念近似,其中具有最小决策正域的称为多粒度乐观粗糙集,具有最大决策正域的称为多粒度悲观粗糙集。形象地讲,乐观粗糙集的上下近似具有求同存异的语义,悲观粗糙集的上下近似具有求同排异的语义。在此基础上,许多关于多粒度粗糙集的变种相继提出。具体包括:
1) 在二元关系的泛化方面:林国平[34]研究了多粒度1型和2型邻域粗糙集模型;徐伟华[35]提出了基于容差覆盖信息粒的乐观多粒度粗糙集和悲观多粒度粗糙集;Chen等[36]通过对乐观悲观算子的模糊化,定义了一种可调节的多粒度模糊粗糙集。
2) 在信息粒融合策略的泛化方面:吴伟志等[37]基于证据理论构造不完备信息系统下的悲观多粒度粗糙集;钱宇华等[38]通过将证据理论用于优化聚类集成,提出了一种新的信息融合方法。
3.2.2 多尺度粗糙集吴伟志等[11]提出的多尺度粗糙集是信息系统条件属性在偏序结构意义下的推广。不同于传统粗糙集中每个条件属性信息以单一形式表示,多尺度粗糙集的每个条件属性信息对应一个偏序结构,而偏序结构本身是由于属性具有多粒度造成的。通过映射到不同的层次,丰富了决策依据的同时,可以根据需要在某一粒度上综合不同层次的属性信息综合决策。
多尺度粗糙集属性粒度的选取是一个重要的问题。针对属性层次提升过程中决策一致性的变化,吴伟志等[39]从保持最大决策一致性角度出发,通过定义信息表决策一致性、上近似一致性、下近似一致性给出了最优粒度的评价标准。在此基础上,吴伟志等[40]等研究了决策一致多尺度粗糙集和决策不一致多尺度粗糙集的属性约简算法。
3.2.3 覆盖粗糙集覆盖意义下的上下近似语义要求对概念给出最大(最小)描述。由于满足这一描述的刻画方式与语义之间是多对一的关系,为了尽可能准确地基于覆盖描述概念而对已有覆盖近似算子的合成,自然地形成了多粒度研究前提。祝峰等[41]给出了拓扑视角下最大(最小)描述方式,总结出覆盖粗糙集下上下近似相互依赖关系。在此基础上,提出了3种不同的覆盖粗糙集及其相互近似转化关系[42]。祝峰等[43]指出,广义粗糙集模型邻域化在一定条件下可以构造覆盖粗糙集,但是由于覆盖粗糙集的多粒度性,两者并不等价。苗夺谦等[44]通过结合已有覆盖粗糙集研究的基础,提出了4种多粒度乐观覆盖粗糙集,并分析了多种粗糙集上下近似之间的包含关系。在此基础上,Pedrycz等[45]进一步研究了模糊近似空间下多粒度覆盖粗糙集。
3.2.4 层次粗糙集人类在复杂问题求解前具有与问题求解相关的、结构化的先验知识,先验知识本身由于个体的差异和对问题的认识,表现为属性层次的多样性。苗夺谦等[46]提出了层次粗糙集模型,使得不同属性扩展为不同的概念层次树,从而由一个决策表可以衍生出多个局部具有偏序关系的决策表,不仅有效提升了求解效率,还能在不同层次得到不同的决策知识。钱进等[47]基于MapReduce机制,提出了大数据下层次粗糙集属性约简算法。李天瑞等[48-49]进一步研究了在不完备动态环境下,由于属性层次的粗化/细化导致的粗糙近似的更新问题及相应算法。
3.2.5 双量化粗糙集粗糙集近似空间的本质是二维的,同时考虑概念的相对量化与绝对量化将有助于近似空间的完备化。张贤勇[50]提出了相对和绝对量化可以分别通过概率粗糙集和程度粗糙集构造,并提出了一系列基于逻辑运算的双量化粗糙集及其区域保持约简算法。此后,学者从双量化粗糙集的构造方式上开展了一系列研究。徐伟华[51]等提出基于精度程度近似组合的策略;胡宝清[52]等提出统一概率表示策略。随着研究的深入;张贤勇和苗夺谦[53]提出双量化粗糙集的关键在于定义一对具有相对、绝对语义的度量,在此基础上研究了基于重要性-精确度的定性、定量约简。
4 粒计算不确定性度量与推理当今世界处在一个信息时代。信息是人类认识世界和改造世界的知识源泉。人们接触到的各种各样的信息,有时候是确定的,更多时候是不确定的。进入21世纪以来,不确定性问题的研究工作受到越来越多的关注[54]。如何对不确定性信息和数据进行有效的处理,从而发现不确定性信息中蕴涵的知识和规律,是一个重要的研究课题[55]。度量自然现象的不确定性程度称为不确定性度量[56]。常见的方法有概率论、熵、证据理论等。
4.1 单粒度下不确定性度量与推理 4.1.1 单粒度下不确定性度量单粒度下的不确定性度量可以具有不同的语义,是传统度量在应用领域的具体实现。然而一般来说具有以下三点共同的性质。
1) 有界性:度量的最大值/最小值对应当前粒结构对问题最完美/最不完美的表达,多数度量的取值范围为[0, 1];
2) 单调性:如果结构A对问题的描述比结构B对问题的描述更完美,结构C对问题的描述比结构A对问题的描述更完美,则结构C对问题的描述比结构B对问题的描述更完美;
3) 对称性:如果结构A对问题的度量和结构B对问题的度量在某种程度范围内无差别,那么结构B对问题的度量和结构A对问题的度量在相同程度范围内无差别。
通常意义下,不确定性度量具有语义和计算视角两个层面。下面从概率论、信息熵、证据理论3种计算视角出发,简要回顾单粒度下不确定性度量研究现状。
1) 基于概率论的度量
1933年前苏联科学家Kolmogorov在提出的公理化的概率论[57]。下面介绍概率论有关的基本概念。
定义 1[57] 设Ω是非空集合,A是由Ω的一些子集(也称事件)构成的σ代数。若集函数Pr满足如下3条公理:
公理 1 Pr{Ω}=1;
公理 2 对任意事件A∈A都有Pr{A}≥0;
公理 3 对任意可列个不相交的事件
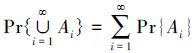
定义 2[57] 设Ω是非空集合,A是由Ω的一些子集构成的σ代数。而Pr为概率测度,则三元组(Ω,A,Pr)称为概率空间。
定义 3[57] 一个随机变量就是从概率空间(Ω,A,Pr)到实数集的可测函数。
定义 4[57] n维随机变量就是从概率空间(Ω,A,Pr)到n维实数向量空间的一个可测函数。
定义 5[57] 随机变量ξ的概率分布定义为Φ(x)=Pr{ω∈ξ|ξ(ω)≤x},也就是说,Φ(x)是随机变量ξ取值小于或等于x的概率。
定义 6[57] 设ξ为一随机变量,Φ是ξ的概率分布函数。如果对所有的x∈(-∞,+∞),函数φ:
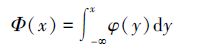 |
则称φ为随机变量ξ的概率密度函数。
定义 7[57] 设(ξ1,ξ2,…,ξn)是概率空间(Ω,A,Pr)上的随机向量,如果函数Φ:(-∞,+∞)n→[0, 1]满足Φ(x1,x2,…,xn)=
Pr{ω∈Ω|ξ1(ω)≤x1,ξ2(ω)≤x2,…,ξn(ω)≤xn},则称Φ为随机向量(ξ1,ξ2,…,ξn)的联合概率分布。
定义 8[57] 设(ξ1,ξ2,…,ξn)是概率空间(Ω,A,Pr)上的随机向量。如果对于所有(x1,x2,…,xn)∈(-∞,+∞)n,存在φ:
∫-∞x1∫-∞x2…∫-∞xnφ(y1,y2,…,yn)dy1dy2…dyn,
则称φ为随机向量(ξ1,ξ2,…,ξn)的联合概率密度函数。
2) 基于熵的度量
随着通信技术的发展,Shannon于1948年提出了信息熵的概念[58]。将粒化后的结构看成论域的不同划分,并与模糊集、粗糙集等模型相结合,人们先后提出了模糊熵、粗糙熵等概念。
定义 9[59] 设U是论域,P是U上的一个等价关系,P在U上导出的划分A={X1,X2,…,Xn},则P在U的子集组成的σ代数上定义的概率分布为
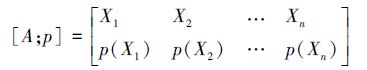 |
式中:
定义 10[59] 设U是论域,P、Q是U上的两个等价关系,P、Q在U上导出的划分分别为A、B,其中A={X1,X2,…,Xn},B={Y1,Y2,…,Ym},则P与Q的联合概率分布为
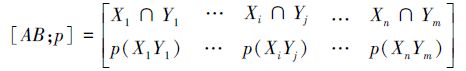 |
式中: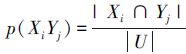
定义 11[59] 设U是论域,P是U上的一个等价关系,P在U上导出的划分A={X1,X2,…,Xn},则知识P的熵H(P)为
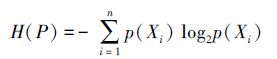 |
定义 12[59] 设U是论域,P、Q是U上的两个等价关系,P、Q在U上导出的划分分别为A、B,其中A={X1,X2,…,Xn},B={Y1,Y2,…,Ym},则知识Q相对于知识P的条件熵为
 |
定义 13[60] 知识P与Q的互信息为
I(P;Q)=H(Q)-H(Q|P)
定义 14[61] 设A是论域U上的一个模糊集,xi∈U,μA(xi)是xi的隶属度函数,值域为[0, 1]。则A的模糊熵为
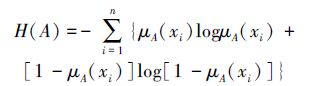 |
定义 15[61] 在信息系统(U,A)中,论域U={x1,x2…,xn},属性集A={a1,a2…,am},X⊆U, B⊆A,对象子集X关于B的近似精度、粗糙度分别定义为
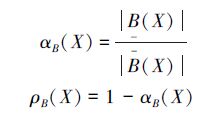 |
定义 16[62] 在信息系统(U,A)中,属性子集B⊆A对论域的划分U/B={X1,X2,…,Xm},属性集B的熵定义如下:
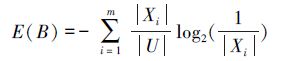 |
X⊆U在划分U/B上的粗糙熵定义为
 |
3) 基于证据理论的度量
证据理论是由Dempster首先提出的,后经他的学生Shafer发扬光大,所以也称D-S理论[63-64]。
定义 17 基本概率分配函数(又称为mass函数):对于任意一个属于U的子集A(命题),对应于一个数m∈[0, 1],且满足
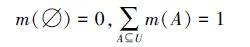 |
则称函数m为幂集2U上的基本概率分配函数,m(A)称为A基本概率数。
定义 18 信任函数:命题A的信任函数Bel:2U→[0, 1]为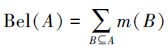
定义 19[66] 似然函数:命题A的似然函数Pl:2U→[0, 1]为:Pl(A)=1-Bel(~A)=
定义 20 证据的信任函数:对任何命题A⊆U的信任函数为
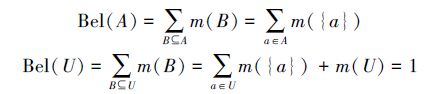 |
定义 21 证据的似然函数:对任何命题A⊆U的似然函数为
Pl(A)=1-Bel(~A)=m(U)+Bel(A)
根据以上定义,可以看出命题的信任函数和似然函数之间满足下列关系:
Pl(A)≥Bel(A)
Pl(A)-Bel(A)=m(U)
除了以A[Bel(A),Pl(A)]作为A的不确定性度量外,还可用类概率函数来度量。
定义 22 类概率函数:设U为有限域,对任何命题A⊆U,A的类概率函数为
 |
定义 23[65-66] 设K=(U,R)是一个知识库,R∈
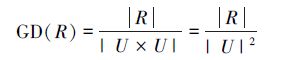 |
定义 24[65-66] 设K=(U,R)是一个知识库,知识R∈
Dis(R)=1-GD(R)
梁吉业和史忠植[62]给出了不完备信息系统中的信息熵的形式,其形式如下:
 |
为了区别于Shannon信息熵,梁吉业和史忠植[58]信息熵的另一种形式,即
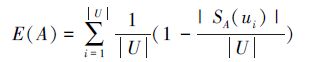 |
后来,钱宇华和梁吉业[68]将粗糙熵引入到不完备信息系统中,给出了不完备信息系统的粗糙熵:
 |
钱宇华和梁吉业[67]在不完备信息系统中给出了组合熵的定义:
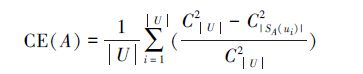 |
王俊红等[69]给出了不完备信息系统中知识粒度的定义:
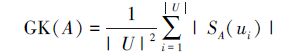 |
为了对不完备信息系统的知识粒度有更加直观的理解,钱宇华和梁吉业[68]在不完备信息系统中提出了组合粒度的概念:
 |
为了更好地理解不确定性度量的本质,梁吉业等[68]建立了信息熵、粗糙熵、组合熵、知识粒度和组合粒度之间的如下关系:
 |
1) 基于概率论的不确定性推理
贝叶斯决策论是不确定性推理的重要工具。在概率论下,对象信息的分布被认为服从一个概率分布。最小化错误率和最小化决策代价是两种典型的推理目标。为了便于表达,我们假定x、
① 当不确定性推理的目标是最小化错误率时:
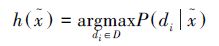 |
② 当不确定性推理的目标是最小化决策代价时:
 |
式中:P(di
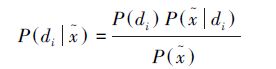 |
决策粗糙集模型是代价敏感下以最小化代价为目标的三支求解模型。根据属性条件独立性假设的强弱,可构造朴素贝叶斯分类器、半朴素贝叶斯分类器。此外,考虑到对象对粒结构隶属的不确定性,概率论可与其他策略(如集成学习)组合构成新的推理机制。
2) 基于证据理论的不确定性推理
证据理论是一种广义的概率论,天然地具有不同证据合成的推理方法,表述如下。
① 当条件部分为命题的逻辑组合时,整个条件部分的计算:
f1(A1∧A2)=min{f1(A1),f1(A2)}
f1(A1∨A2)=max{f1(A1),f1(A2)}
②结论部分的计算,即已知f1(A),A→B(c1,c2,…,ck),计算f1(B)。
首先计算基本分配函数m(B),然后计算结论部分命题B的信任函数Bel(B)、似然函数Pl(B),最后计算类概率函数和正确性。
③ 独立证据导出统一假设。
如果有n条规则支持同一命题时,根据Dempster组合规则,总的基本概率分配函数m为各规则结论得到的基本概率分配函数的正交和。
4.2 多粒度下不确定性度量与推理 4.2.1 多粒度不确定性度量多粒度不确定性度量可以评价多粒度的分类质量以及不同粒度的重要性,是多粒度精准决策的基础。多粒度不确定性度量方式有多种,目前多以数字特征的形式表示,是传统单粒度研究意义下的拓展。常见的度量包括以下几类:
1) 以近似分类精度为代表的概念近似刻画不确定性度量;
2) 以属性重要度为代表的决策知识不确定性度量;
3) 以粒度为代表的多粒度层次不确定性度量。
上述不确定性度量在多粒度研究中因粒计算模型选取、定义角度、多粒度构造策略的差异而有所不同。例如徐伟华[72]等研究了多粒度优势粗糙集下的近似分类精度度量;梁吉业[73]等研究了多粒度近似空间中不确定性度量的粒度单调性保持;王国胤[74]等分析了多粒度概率粗糙集的粒度变化导致区域不确定性。
不确定性度量的计算策略可以从不同角度展开。信息熵是一种有效度量不确定性的工具,刻画了信息粒度的关于问题求解的信息量。自从苗夺谦[75]等将信息熵引入度量粗糙集不确定性以来,被广泛用于度量信息系统、知识粒度的不确定性,其变种条件熵、互补熵、拓扑熵、组合熵等提供了不同的度量视角。代表性工作有:张清华[31]提出了用信息熵序列度量分层递阶商空间不确定性;米据生等[76]引入知识粒改进了已有融合熵中的非单调性问题;李华雄等[77]给出了多粒度直觉模糊粗糙集下的粗糙熵和信息熵。
4.2.2 多粒度下不确定性推理多粒度的推理是实现精准决策的重要方法,根据粒计算模型选择的不同,多粒度推理的内涵也有所不同。从粗糙集角度来看,多粒度推理的主要任务是在保持分类能力不变的前提下信息粒和粒空间的约简,而其关键问题在于对约简目标的定义。从商空间角度来看,推理的主要任务在于如何利用不同商空间之间的层次关系实现基于分层递阶模型的信息粒合成。
多粒度推理代表性工作如下:基于一组对原有信息表覆盖的子系统,梁吉业等[78]在多粒度视角下对大规模数据进行有效分解,在此基础上提出了一种针对大规模数据的高效的属性约简算法;李进金等[79]基于不同邻域半径的属性约简效果,提出了基于斯皮尔曼尺距离的约简排序算法;钱宇华等[80]通过定义多粒度空间中粒度重要性,提出了基于分布约简的悲观多粒度粗糙集粒度约简方法;折延宏等[81]提出了基于局部最优属性粒度的属性约简方法;邓大勇等[82]将信息表划分为多个相关联的子信息系统簇,提出了基于并行约简的概念漂移探测方法。
5 粒计算理论应用研究展望粒计算,作为人类对复杂问题求解的一种认知模式,已经在知识发现、数据挖掘、图像处理等方面取得了重要的进展,显现出重大的应用价值。下面将从大数据分析、计算生物学、社交网络分析、多粒度联合计算、认知计算以及粒计算形式化描述6个方面展望未来的研究方向。
5.1 大数据分析大数据的挑战带来了人工智能技术、存储技术以及下一代网络技术的发展机遇。大数据经常具有多层次或多粒度特性。粒计算已经成为目前发展迅速的海量信息处理模式[83]。在已有粒计算方法处理大规模数据的研究中,如Ruan等[84]使用模糊信息粒化方法先对时间序列进行粒化,然后使用SVMs对粒化了的时间序列进行回归分析和预测,提高了大规模时间序列分析的速度。
5.2 计算生物学计算生物学与生物信息学的研究内容往往交织在一起,都属于交叉学科。在对生物学中信息的采集、存储和分析处理基础上,计算生物学主要侧重于利用数学模型和计算仿真技术对生物学问题进行研究。已有研究工作中,如He等[85]在由聚类算法所智能分割的信息粒上建立各个SVM模型进行蛋白质预测,有效地解决了海量数据的多分类问题。
5.3 社交网络分析通过分析社交网络数据,建立模型,从而挖掘出有价值的信息。对主观性文档的分析和处理,一直是该领域研究的热点问题。已有工作将多粒度的思想应用于特征选择中,如文献[86]中提出了一种基于LDA的多粒度主题情感混合模型,它同时考虑两个粒度上的情感和主题分布——文档级和局部,局部分布的生成受到文档级分布的影响。该方法在情感分类准确率和稳定性方面都有不错的提升。苗夺谦[87]等在行人再识别问题上引入了多通道思想获取图片在多个不同粒度下的特征信息,并证明基于相互关联的多通道特征能更有效跟踪和识别行人。
5.4 多粒度联合计算多粒度联合计算[88, 89]是指将复杂问题的求解分配到数据表示的多个粒度层次上成为子任务,各个粒度层次上相对简单的功能协同起来,最终完成复杂问题的求解[67]。围绕该目标,既可以融合已有典型多粒度模型构造更全面的多粒度模型,也可以引入机器学习相关理论构建新的多粒度模型,而深度学习正是后一种方式的代表,其实质是多粒度联合计算,在诸多应用均取得了突破性进展。然而,无论是融合已有模型还是构建新模型,都必须结合具体领域背景和数据分析需求作相应的调整,以有效解决行业级应用问题。这种趋势和周志华教授在CNCC2016[90]会议上提出的学件(模型+规约)思想是一致的。
5.5 认知计算认知是人工智能研究的重要课题之一。以往对认知的研究往往从某个角度展开,缺乏结构化思维,而这个不足恰恰是粒计算的优势所在。张钹和张铃在20 世纪90年代初[13]在其专著《问题求解理论及应用》中特别指出“人类智能的一个公认特点,就是人们能从极不相同的粒度上观察和分析同一问题。人们不仅能在不同粒度世界上进行问题的求解,而且能够很快地从一个粒度世界跳到另一个粒度世界,往返自如,毫无困难”。多粒度空间的相互转化是认知模型的关键[91]。文献[92]中,支持人们已形成了一个关于世界的粒度观点,在此观点下,人类的观察、度量、概念化和推理都是在粒度意义下进行的。应用粒计算思想,可以分析语义特征以及形式概念系统模型,进行不确定性分析,建立与优化认知计算模型,从而更好地揭示各种相关领域成果对认知的协作原理。
5.6 粒计算形式化描述尽管目前粒计算研究无论在模型还是应用都得到了蓬勃发展,然而在统一语言描述方面还不够完备。一些基础性问题,如基于粒的思想比较不同粒之间的差异,仍然没有得到很好的解决。最近,刘清等[93]提出以非标准分析作为深入展开粒计算基础理论研究的思想,并在超实数意义下定义了不可区分关系。这对于深入认识粒计算的内在逻辑,丰富粒计算理论体系都具有深远的意义。
6 结束语粒计算理论是一种结构化求解模型,能够有效处理大数据中的不确定性,显著降低问题求解的复杂程度,其模型的可构造性使得在不同数据和领域背景下具有丰富的表达形式,与大数据研究高度契合,是一条极具发展潜力的新途径。本文回顾了自粒计算研究以来的主要数学模型,强调了多粒度研究的价值,总结了典型的不确定性度量,并展望了粒计算在大数据时代的重点突破方向。希望能够对高效大数据方法的提出以及人工智能领域基础性问题的研究提供借鉴和启发。
| [1] | ZADEH L A. Toward a theory of fuzzy information granulation and its centrality in human reasoning and fuzzy logic[J]. Fuzzy sets and systems, 1997, 90(2) : 111-127DOI:10.1016/S0165-0114(97)00077-8. |
| [2] | http://link.springer.com/journal/41066. |
| [3] | http://www.nsfc.gov.cn/nsfc/cen/xmzn/2016xmzn/04/06xx/004.html. |
| [4] | http://dblp.uni-trier.de/db/conf/rsfdgrc/. |
| [5] | HU Qinghua, MI Jusheng, CHEN Degang. Granular computing based machine learning in the era of big data[J]. Information Sciences, 2017, 378 : 242-243DOI:10.1016/j.ins.2016.10.048. |
| [6] |
梁吉业, 钱宇华, 李德玉, 等. 大数据挖掘的粒计算理论与方法[J].
中国科学:信息科学, 2015, 45 (11) : 1355-1369.
LIANG Jiye, QIAN Yuhua, LI Deyu, et al. Theory and method of granular computing for big data mining[J]. Scientia sinica informationis, 2015, 45(11) : 1355-1369DOI:10.1360/N112015-00092. |
| [7] | ZHANG Bo, ZHANG Ling. Theory and applications of problem solving[M]. New York: North Holland, 1992. |
| [8] | FRIEDMAN N. Inferring cellular networks using probabilistic graphical models[J]. Science, 2004, 303(5659) : 799-805DOI:10.1126/science.1094068. |
| [9] | CLAUSET A, MOORE C, NEWMAN M E J. Hierarchical structure and the prediction of missing links in networks[J]. Nature, 2008, 453(7191) : 98-101DOI:10.1038/nature06830. |
| [10] | AHN Y Y, BAGROW J P, LEHMANN S. Link communities reveal multiscale complexity in networks[J]. Nature, 2010, 466(7307) : 761-764DOI:10.1038/nature09182. |
| [11] | WU W Z, LEUNG Y. Theory and applications of granular labelled partitions in multi-scale decision tables[J]. Information sciences, 2011, 181(18) : 3878-3897DOI:10.1016/j.ins.2011.04.047. |
| [12] | GEOFFREY E, Ruslan R. Reducing the dimensionality of data with neural networks[J]. Science, 2006, 313(5786) : 504-507DOI:10.1126/science.1127647. |
| [13] | HU Hong, PANG Liang, SHI Zhongzhi. Image matting in the perception granular deep learning[J]. Knowledge-based systems, 2016, 102 : 51-63DOI:10.1016/j.knosys.2016.03.018. |
| [14] | ZADEH L A. Fuzzy sets[J]. Information and control, 1965, 8(3) : 338-353DOI:10.1016/S0019-9958(65)90241-X. |
| [15] | SHANNON C E. A mathematical theory of communication[J]. The bell system technical journal, 1948, 27(3) : 379-423DOI:10.1002/bltj.1948.27.issue-3. |
| [16] | WANG Guoyin, HU Jun, ZHANG Qinghua, et al. Granular computing based data mining in the views of rough set and fuzzy set[C]//Proceedings of 2008 IEEE International Conference on Granular Computing. Hangzhou, China:IEEE, 2008:67-78. |
| [17] | ZADEH L A. Fuzzy sets and information granularity[C]//GUPTA N, RAGADE R, YAGER R. Advances in Fuzzy Set Theory and Applications. Amsterdam:North-Holland, 1979:3-18. |
| [18] | ZADEH L A. Some reflections on soft computing, granular computing and their roles in the conception, design and utilization of information/intelligent systems[J]. Soft computing, 1998, 2(1) : 23-25DOI:10.1007/s005000050030. |
| [19] | PAWLAK Z. Rough sets[J]. International journal of computer & information sciences, 1982, 11(5) : 341-356. |
| [20] | 张钹, 张铃. 问题求解理论及应用[M]. 北京: 清华大学出版社, 1990. |
| [21] |
李德毅, 孟海军, 史雪梅. 隶属云和隶属云发生器[J].
计算机研究与发展, 1995, 32 (6) : 15-20.
LI Deyi, MENG Haijun, SHI Xuemei. Membership clouds and membership cloud generators[J]. Journal of computer research & development, 1995, 32(6) : 15-20. |
| [22] | 李德毅, 杜鹢. 不确定性人工智能[M]. 北京: 国防工业出版社, 2014. |
| [23] | YAO Yiyu. An outline of a theory of three-way decisions[C]//Proceedings of the 8th International RSCTC Conference. Chengdu, China:Springer, 2012, 7413:1-17. |
| [24] | 姚一豫. 三支决策研究的若干问题[M]//刘盾, 李天瑞, 苗夺谦, 等. 三支决策与粒计算[M]. 北京:科学出版社, 2013:1-13. |
| [25] | HU Baoqing. Three-way decisions space and three-way decisions[J]. Information sciences, 2014, 281 : 21-52DOI:10.1016/j.ins.2014.05.015. |
| [26] | MA Lijia, GONG Maoguo, YAN Jianan, et al. A decomposition-based multi-objective optimization for simultaneous balance computation and transformation in signed networks[J]. Information sciences, 2017, 378 : 144-160DOI:10.1016/j.ins.2016.10.035. |
| [27] | UERIN C, RIGAUD C, BERTET K., et al. An ontology-based framework for the automated analysis and interpretation of comic book's images[J]. Information sciences, 2017, 378 : 109-130DOI:10.1016/j.ins.2016.10.032. |
| [28] | YAO Yiyu, SHE Yanhong. Rough set models in multigranulation spaces[J]. Information sciences, 2016, 327 : 40-56DOI:10.1016/j.ins.2015.08.011. |
| [29] | ZHANG Xiaohong, MIAO Duoqian, LIU Caihui, et al. Constructive methods of rough approximation operators and multigranulation rough sets[J]. Knowledge-based systems, 2016, 91 : 114-125DOI:10.1016/j.knosys.2015.09.036. |
| [30] |
苗夺谦, 徐菲菲, 姚一豫, 等. 粒计算的集合论描述[J].
计算机学报, 2012, 35 (2) : 351-363.
MIAO Duoqian, XU Feifei, YAO Yiyu, et al. Set-theoretic formulation of granular computing[J]. Chinese journal of computers, 2012, 35(2) : 351-363DOI:10.3724/SP.J.1016.2012.00351. |
| [31] | ZHANG Qinghua, WANG Guoyin. The uncertainty measure of hierarchical quotient space structure[J]. Mathematical problems in engineering, 2011, 2011, 513195 . |
| [32] | WANG Guoyin, XU Ji, ZHANG Qinghua, et al. Multi-granularity intelligent information processing[C]//Proceedings of the 15th International Conference, RSFDGrC. Tianjin, China:Springer, 2015:36-48. |
| [33] | QIAN Yuhua, LIANG Jiye, Yao Yiyu, Dang Chuangyin. MGRS:A multi-granulation rough set[J]. Information sciences, 2010, 180 : 949-970DOI:10.1016/j.ins.2009.11.023. |
| [34] | LIN Guoping, QIAN Yuhua, LI Jinjin. NMGRS:neighborhood-based multigranulation rough sets[J]. International journal of approximate reasoning, 2012, 53(7) : 1080-1093DOI:10.1016/j.ijar.2012.05.004. |
| [35] | XU Weihua, WANG Qiaorong, ZHANG Xiantao. Multi-granulation rough sets based on tolerance relations[J]. Soft computing, 2013, 17(7) : 1241-1252DOI:10.1007/s00500-012-0979-1. |
| [36] | Chen Yan. An adjustable multigranulation fuzzy rough set[J]. International journal of machine learning and cybernetics, 2016, 7(2) : 267-274DOI:10.1007/s13042-015-0436-4. |
| [37] | TAN Anhui, WU Weizhi, LI Jinjin, et al. Evidence-theory-based numerical characterization of multigranulation rough sets in incomplete information systems[J]. Fuzzy sets and systems, 254(2016) : 18-35. |
| [38] | LI Feijiang, QIAN Yuhua, WANG Jieting, et al. Multigranulation information fusion:a dempster-shafer evidence theory-based clustering ensemble method[J]. Information sciences, 2017, 378 : 389-409DOI:10.1016/j.ins.2016.10.008. |
| [39] | WU Weizhi, LEUNG Y. Optimal scale selection for multi-scale decision tables[J]. International journal of approximate reasoning, 2013, 54(8) : 1107-1129DOI:10.1016/j.ijar.2013.03.017. |
| [40] | GU Shenming, WU Weizhi. On knowledge acquisition in multi-scale decision systems[J]. International journal of machine learning and cybernetics, 2013, 4(5) : 477-486DOI:10.1007/s13042-012-0115-7. |
| [41] | ZHU W. Topological approaches to covering rough sets[J]. Information sciences, 2007, 177(6) : 1499-1508DOI:10.1016/j.ins.2006.06.009. |
| [42] | ZHU W, WANG Feiyue. On three types of covering-based rough sets[J]. IEEE transactions on knowledge and data engineering, 2007, 19(8) : 1131-1144DOI:10.1109/TKDE.2007.1044. |
| [43] | ZHU W. Relationship between generalized rough sets based on binary relation and covering[J]. Information sciences, 2009, 179(3) : 210-225DOI:10.1016/j.ins.2008.09.015. |
| [44] | LIU Caihui, MIAO Duoqian, QIAN Jin. On multi-granulation covering rough sets[J]. International journal of approximate reasoning, 2014, 55(6) : 1404-1418DOI:10.1016/j.ijar.2014.01.002. |
| [45] | LIU Caihui, PEDRYCZ W. Covering-based multi-granulation fuzzy rough sets[J]. Journal of intelligent & fuzzy systems, 2016, 30(1) : 303-318. |
| [46] | FENG Qinrong, MIAO Duoqian, CHENG Yi. Hierarchical decision rules mining[J]. Expert systems with applications, 2010, 37(3) : 2081-2091DOI:10.1016/j.eswa.2009.06.065. |
| [47] | QIAN Jin, LV Ping, YUE Xiaodong, et al. Hierarchical attribute reduction algorithms for big data using MapReduce[J]. Knowledge-based systems, 2015, 73 : 18-31DOI:10.1016/j.knosys.2014.09.001. |
| [48] | CHEN Hongmei, LI Tianrui, RUAN Da. Maintenance of approximations in incomplete ordered decision systems while attribute values coarsening or refining[J]. Knowledge-based systems, 2012, 31 : 140-161DOI:10.1016/j.knosys.2012.03.001. |
| [49] | CHEN Hongmei, LI Tianrui, LUO Chuan, et al. A rough set-based method for updating decision rules on attribute values' coarsening and refining[J]. IEEE transactions on knowledge and data engineering, 2014, 26(12) : 2886-2899DOI:10.1109/TKDE.2014.2320740. |
| [50] | 张贤勇. 基于精度与程度逻辑组合的几类粗糙集模型及其算法研究[D]. 成都:四川师范大学, 2011. ZHANG Xianyong. Study on several rough set models and their algorithms based on logical combinations of precision and grade[D]. Chengdu:Sichuan Normal University, 2011. |
| [51] | XU Weihua, GUO Yanting. Generalized multigranulation double-quantitative decision-theoretic rough set[J]. Knowledge-based systems, 2016, 105 : 190-205DOI:10.1016/j.knosys.2016.05.021. |
| [52] | FANG Bowen, HU Baoqing. Probabilistic graded rough set and double relative quantitative decision-theoretic rough set[J]. International journal of approximate reasoning, 2016, 74 : 1-12DOI:10.1016/j.ijar.2016.03.004. |
| [53] | ZHANG Xianyong, MIAO Duoqian. Double-quantitative fusion of accuracy and importance:systematic measure mining, benign integration construction, hierarchical attribute reduction[J]. Knowledge-based systems, 2016, 91 : 219-240DOI:10.1016/j.knosys.2015.09.001. |
| [54] |
李德毅, 刘常昱, 杜鹢, 等. 不确定性人工智能[J].
软件学报, 2004, 15 (11) : 1583-1594.
LI Deyi, LIU Changyu, DU Yi, et al. Artificial intelligence with uncertainty[J]. Journal of software, 2004, 15(11) : 1583-1594. |
| [55] |
王国胤, 张清华. 不同知识粒度下粗糙集的不确定性研究[J].
计算机学报, 2008, 31 (9) : 1588-1598.
WANG Guoyin, ZHANG Qinghua. Uncertainty of rough sets in different knowledge granularities[J]. Chinese journal of computers, 2008, 31(9) : 1588-1598. |
| [56] |
张清华, 王国胤, 胡军.
多粒度知识获取与不确定性度量[M]. 北京: 科学出版社, 2013.
ZHANG Qinghua, WANG Guoyin, HU Jun. Knowledge acquisition of multi-granular and uncertainty measurements[M]. Beijing: Science Press, 2013. |
| [57] |
刘宝碇, 彭锦.
不确定理论教程[M]. 北京: 清华大学出版社, 2005.
LIU Baoding, PENG Jin. Tutorial of uncertainty theory[M]. Beijing: Tsinghua Press, 2005. |
| [58] |
苗夺谦, 李德毅, 姚一豫, 等.
不确定性与粒计算[M]. 北京: 科学出版社, 2011.
MIAO Duoqian, LI Deyi, YAO Yiyu, et al. Uncertainty and granular computing[M]. Beijing: Science Press, 2011. |
| [59] |
苗夺谦, 王珏. 粗糙集理论中知识粗糙性与信息熵关系的讨论[J].
模式识别与人工智能, 1998, 11 (1) : 34-40.
MIAO Duoqian, WANG Jue. On the relationships between information entropy and roughness of knowledge in rough set theory[J]. Pattern recognition & artificial intelligence, 1998, 11(1) : 34-40. |
| [60] | DE LUCA A, TERMINI S. A definition of a nonprobabilistic entropy in the setting of fuzzy sets theory[J]. Information and control, 1972, 20(4) : 301-312DOI:10.1016/S0019-9958(72)90199-4. |
| [61] |
张文修, 吴伟志, 梁吉业, 等.
粗糙集理论与方法[M]. 北京: 科学出版社, 2001.
ZHANG Wenxiu, WU Weizhi, LIANG Jiye, et al. Rough sets theory and method[M]. Beijing: Science Press, 2001. |
| [62] | LIANG Jiye, SHI Zhongzhi. The information entropy, rough entropy and knowledge granulation in rough set theory[J]. International journal of uncertainty, fuzziness and knowledge-based systems, 2004, 12(1) : 37-46DOI:10.1142/S0218488504002631. |
| [63] | DEMPSTER A P. Upper and lower probabilities induced by a multivalued mapping[J]. The annals of mathematical statistics, 1967, 38(2) : 325-339DOI:10.1214/aoms/1177698950. |
| [64] | SHAFER G. A mathematical theory of evidence[M]. Princeton: Princeton University Press, 1976. |
| [65] |
苗夺谦, 范世栋. 知识的粒度计算及其应用[J].
系统工程理论与实践, 2002, 22 (1) : 48-56.
MIAO Duoqian, FAN Shidong. The calculation of knowledge granulation and its application[J]. Systems engineering-theory & practice, 2002, 22(1) : 48-56. |
| [66] | 苗夺谦, 王国胤, 刘清, 等. 粒计算:过去、现在与展望[M]. 北京: 科学出版社, 2007. |
| [67] | QIAN Yuhua, LIANG Jiye. Combination entropy and combination granulation in incomplete information system[J]. Lecture notes in computer science, 2006, 4062(2) : 184-190. |
| [68] | WANG Junhong, LIANG Jiye, QIAN Yuhua, et al. Uncertainty measure of rough sets based on a knowledge granulation for incomplete information systems[J]. International journal of uncertainty, fuzziness and knowledge-based systems, 2008, 16(2) : 233-244DOI:10.1142/S0218488508005157. |
| [69] |
梁吉业, 钱宇华. 信息系统中的信息粒与熵理论[J].
中国科学E辑:信息科学, 2008, 51 (10) : 1427-1444.
LIANG Jiye, QIAN Yuhua. Information granules and entropy theory in information systems[J]. Science in China series F:information sciences, 2008, 51(10) : 1427-1444DOI:10.1007/s11432-008-0113-2. |
| [70] | BAYES T. An essay towards solving a problem in the doctrine of chances[J]. Philosophical transactions of the royal society, 53(1763) : 370-418. |
| [71] | YU Jianhang, ZHANG Xiaoyan, ZHAO Zhenhua, et al. Uncertainty measures in multigranulation with different grades rough set based on dominance relation[J]. Journal of intelligent & fuzzy systems, 2016, 31 : 1133-1144. |
| [72] | LIN Guoping, LIANG Jiye, QIAN Yuhua. Uncertainty measures for multigranulation approximation space[J]. International journal of uncertainty fuzziness and knowledge-based systems, 2015, 23(3) : 443-457DOI:10.1142/s0218488515500191. |
| [73] | ZHANG Qinghua, ZHANG Qiang, WANG Guoyin. The uncertainty of probabilistic rough sets in multi-granulation spaces[J]. International journal of approximate reasoning, 2016, 77 : 38-54DOI:10.1016/j.ijar.2016.06.001. |
| [74] | 苗夺谦. Rough Set理论及其在机器学习中的应用研究[D]. 1997, 北京,中国科学院自动化研究所. MIAO Duoqian. Rough set theory and its application in machine learning[D]. 1997, Beijing, Institute of Automation, Chinese Academy of Sciences. |
| [75] | MA Zhouming, MI Jusheng. A comparative study of MGRSs and their uncertainty measures[J]. Fundamenta informaticae, 2015, 142 : 161-181DOI:10.3233/FI-2015-1289. |
| [76] | HUANG Bing, GUO Chunxiang, LI Huaxiong, et al. Hierarhical structures and uncertainty measures for intuitionistic fuzzy approximate space[J]. Information Sciences, 2016, 336 : 92-114DOI:10.1016/j.ins.2015.12.005. |
| [77] | LIANG Jiye, WANG Feng, DANG Chuangyin, et al. An efficient rough feature selection algorithm with a multi-granulation view[J]. International journal of approximate reasoning, 2012, 53(6) : 912-926DOI:10.1016/j.ijar.2012.02.004. |
| [78] | LIN Yaojin, LI Jinjin, LI Peirong, et al. Feature selection via neighborhood multi-granulation fusion[J]. Knowledge-based systems, 2014, 67 : 162-168DOI:10.1016/j.knosys.2014.05.019. |
| [79] |
桑妍丽, 钱宇华. 一种悲观多粒度粗糙集中的粒度约简算法[J].
模式识别与人工智能, 2012, 25 (3) : 361-366.
SANG Yanli, QIAN Yuhua. A granular space reduction approach to pessimistic multi-granulation rough sets[J]. Pattern recognition and artificial intelligence, 2012, 25(3) : 361-366. |
| [80] | SHE Yanhong, LI Jinhai, YANG Hailong. A local approach to rule induction in multi-scale decision tables[J]. Knowledge-based systems, 2015, 89 : 398-410DOI:10.1016/j.knosys.2015.07.020. |
| [81] |
邓大勇, 徐小玉, 黄厚宽. 基于并行约简的概念漂移探测[J].
计算机研究与发展, 2015, 52 (5) : 1071-1079.
DENG Dayong, XU Xiaoyu, HUANG Houkuan. Concept drifting detection for categorical evolving data based on parallel reducts[J]. Journal of computer research and development, 2015, 52(5) : 1071-1079. |
| [82] |
徐计, 王国胤, 于洪. 基于粒计算的大数据处理[J].
计算机学报, 2015, 38 (8) : 1497-1517.
XU Ji, WANG Guoyin, YU Hong. Review of big data processing based on granular computing[J]. Chinese journal of computers, 2015, 38(8) : 1497-1517. |
| [83] | RUAN Junhu, WANG Xuping, SHI Yan. Developing fast predictors for large-scale time series using fuzzy granular support vector machines[J]. Applied soft computing, 2013, 13(6) : 3981-4000. |
| [84] | HE Jieyue, ZHONG Wei, HARRISON R, et al. Clustering support vector machines and its application to local protein tertiary structure prediction[C]//Proceedings of the 6th International Conference on Computational Science. Reading, UK:Springer-Verlag, 2006:710-717. |
| [85] |
欧阳继红, 刘燕辉, 李熙铭, 等. 基于LDA的多粒度主题情感混合模型[J].
电子学报, 2015, 43 (9) : 1875-1880.
OUYANG Jihong, LIU Yanhui, LI Ximing, et al. Multi-grain sentiment/topic model based on LDA[J]. Acta electronica sinica, 2015, 43(9) : 1875-1880. |
| [86] | WANG Xuekuan, ZHAO Cairong, MIAO Duoqian, et al. Fusion of multiple channel features for person re-identification[J]. Neurocomputing, 2016, 213 : 125-136DOI:10.1016/j.neucom.2015.12.140. |
| [87] | XU Weihua, YU Jianhang. A novel approach to information fusion in multi-source datasets:a granular computing viewpoint[J]. Information sciences, 2017, 378 : 410-423DOI:10.1016/j.ins.2016.04.009. |
| [88] | LIN Guoping, LIANG Jiye, QIAN Yuhua, et al. A fuzzy multigranulation decision-theoretic approach to multisource fuzzy information systems[J]. Knowledge-based systems, 2016, 91 : 102-113DOI:10.1016/j.knosys.2015.09.022. |
| [89] | http://cncc.ccf.org.cn/struct/7. |
| [90] | LI Jinhai, HUANG Chenchen, QI Jianjun, et al. Three-way cognitive concept learning via multi-granularity[J]. Information Sciences, 2017, 378 : 244-263DOI:10.1016/j.ins.2016.04.051. |
| [91] | YAO Yiyu. Three-way decisions and cognitive computing[J]. Cognitive Computation, 2016, 8(4) : 543-554DOI:10.1007/s12559-016-9397-5. |
| [92] |
刘清, 邱桃荣, 刘斓. 基于非标准分析的粒计算研究[J].
计算机学报, 2015, 38 (8) : 1618-1627.
LIU Qing, QIU Taorong, LIU Lan. The research of granular computing based on nonstandard analysis[J]. Chinese journal of computers, 2015, 38(8) : 1618-1627. |



