压缩感知(compressed sensing,CS)[1-3]通过利用信号的稀疏特性,在远小于Nyquist采样率的条件下,用随机采样获取信号的离散样本,然后通过非线性重建算法重建信号。由于压缩感知理论具有“轻编码、重解码”的特点,压缩感知理论应用到低功耗无线传输的硬件系统中是一个比较合理的选择。压缩感知主要解决的3个问题分别为信号的稀疏表示、观测矩阵的构造以及重构算法的设计[4]。观测矩阵性能的好坏直接关系到是否可以精确重构出原始的数据,因此观测矩阵在压缩感知过程中的数据采样和信号重构环节起着至关重要的作用。
目前,从观测矩阵元素构造分析,观测矩阵可分为两类:1) 随机观测矩阵,如高斯随机、伯努利等,元素都服从相互独立的同分布,与稀疏矩阵的非相干性较强,能够以较大的概率满足RIP[5]条件,但是计算量和时间复杂度较大,存储量大的缺点使其难以在硬件上实现;2) 确定性观测矩阵,如托普利兹矩阵、多项式矩阵等[6-7],它们元素确定且结构固定,适合硬件实现,但是重建效果一般。另外,还有一些针对特定信号的测量矩阵,例如部分哈达玛观测矩阵[8]、雷达信号的卷积观测矩阵[9]、语音信号的观测矩阵[10]等。虽然这些矩阵在特定条件下优于高斯随机观测矩阵,但是其普适性不高,比如部分哈达玛观测矩阵的观测数据必须是2的k次幂。目前,也有学者基于伪随机序列来构建观测矩阵[11-15],并验证了伪随机序列的性能要优于高斯随机矩阵,但是相关观测矩阵的构造方式较为烦琐。因此,需要研究易于硬件实现、构造简单且重构效果较好的观测矩阵,这种研究对于压缩感知理论能够应用于实际具有重要价值。
本文在深入研究确定性观测矩阵的基础上,对在硬件上容易实现且重构效果好的观测矩阵进行重点研究。首先,针对部分哈达玛观测矩阵提出一种改进的构造方式,即顺序选取行向量构造观测矩阵,经过仿真验证采用这种简单的构造方式,在相同的重构算法下信号重构效果更优。然后,依据伪随机序列的特点和循环思想,提出了构造简单的观测矩阵——循环m序列观测矩阵和循环gold序列观测矩阵。最后,经过仿真验证本文所提出的两种观测矩阵具有良好的适应性和实用性。
1 观测矩阵的改进与构造目前,嵌入式硬件系统面临的主要问题包括能源受限、计算能力较弱、存储有限。因此,设计易于硬件实现的观测矩阵需要遵循如下原则:
1) 观测矩阵的存储空间较少,元素简单;
2) 计算尽量只涉及加减法,元素必须是实数;
3) 观测矩阵与稀疏矩阵不相干性较强;
4) 能够快速采样和重建。
确定性观测矩阵如托普利兹、哈达玛等,它们的元素都是由±1或者0、1构成,矩阵的计算只涉及加减法运算,没有复杂的乘法运算,因此,确定性观测矩阵的这些优势可以作为构造易于硬件实现观测矩阵的出发点。
1.1 顺序部分哈达玛观测矩阵的构造部分哈达玛观测矩阵具有优良的观测性能,可以在更少的观测值下重构出原始信号,并且在同样采样率下,信号的重构效果明显优于其他观测矩阵。哈达玛矩阵的元素由1和-1构成,其构造过程如下:
| $ {{\mathit{\boldsymbol{H}}}_{1}}=\left[1 \right] $ | (1) |
| $ {\mathit{\boldsymbol{H}}_2} = \left[{\begin{array}{*{20}{c}} 1 & 1\\ 1 & {-1} \end{array}} \right] $ | (2) |
| $ {\mathit{\boldsymbol{H}}_4} = \left[{\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{H}}_2}} & {{\mathit{\boldsymbol{H}}_2}}\\ {{\mathit{\boldsymbol{H}}_2}} & {-{\mathit{\boldsymbol{H}}_2}} \end{array}} \right] = \left[{\begin{array}{*{20}{c}} 1 & 1 & 1 & 1\\ 1 & {-1} & 1 & {-1}\\ 1 & 1 & {-1} & { - 1}\\ 1 & { - 1} & { - 1} & 1 \end{array}} \right] $ | (3) |
| $ \begin{array}{l} {\mathit{\boldsymbol{H}}_N} = {\mathit{\boldsymbol{H}}_{{2^n}}} = {\mathit{\boldsymbol{H}}_2} \times {\mathit{\boldsymbol{H}}_{{2^{n- 1}}}} = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left[{\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{H}}_{{2^{n-1}}}}} & {{\mathit{\boldsymbol{H}}_{{2^{n-1}}}}}\\ {{\mathit{\boldsymbol{H}}_{{2^{n-1}}}}} & { - {\mathit{\boldsymbol{H}}_{{2^{n - 1}}}}} \end{array}} \right] = \left[{\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{H}}_{\frac{N}{2}}}} & {{\mathit{\boldsymbol{H}}_{\frac{N}{2}}}}\\ {{\mathit{\boldsymbol{H}}_{\frac{N}{2}}}} & {-{\mathit{\boldsymbol{H}}_{\frac{N}{2}}}} \end{array}} \right] \end{array} $ | (4) |
由上述构造过程可以发现,其构造方式是生成N·N大小的哈达玛正交矩阵,N=2k,k=1, 2, …,然后在随机选取M行后,形成M·N大小的部分哈达玛观测矩阵,但是通过此种方式所构成的观测矩阵与稀疏矩阵之间的非相干性会减弱。在重点分析哈达玛观测矩阵后,本文提出一种简化的构造方式,即在选取M行向量时,不是随机选取,而是连续顺序选取,比如可以选取1:M行或者N-M+1:N行向量形成观测矩阵,这样形成的观测矩阵更能保持哈达玛矩阵的正交性和不相干性,并且构造方式简单更加易于硬件实现,仿真结果表明这种构造方式能够达到更好的重构效果,仿真结果详见3.1节。本文将顺序选取行向量构造的部分哈达玛观测矩阵称为顺序部分哈达玛观测矩阵。
1.2 循环伪随机序列观测矩阵的构造部分哈达玛矩阵虽然能够在采样率较低的情况下精确重建原始信号,但是信号的长度必须是2的k次幂,应用范围受到了限制。有没有既可以突破信号长度限制又可以满足RIP条件和非相干性原则的确定性观测矩阵呢?
已有相关文献证明,当观测矩阵Φ的元素满足式(5) 和式(6) 平衡均匀分布时,能够满足RIP条件[16-20]。比如部分哈达玛矩阵就是满足式(5) 的特殊均匀分布的观测矩阵,其中元素±1各占1/2。
| $ {\varphi _{i, j}} = \left\{ \begin{array}{l} -1, \;\;p = \frac{1}{2}\\ 1, \;\;\;\;p = \frac{1}{2} \end{array} \right. $ | (5) |
| $ {\varphi _{i, j}} = \left\{ \begin{array}{l} \frac{{-1}}{{\sqrt 3 }}, \;\;p = \frac{1}{6}\\ 0, \;\;\;\;\;p = \frac{1}{3}\\ \frac{1}{{\sqrt 3 }}, \;\;p = \frac{1}{6} \end{array} \right. $ | (6) |
本文将伪随机序列m序列和gold序列作为压缩感知观测矩阵构造的突破点,提出一种由简单的m序列和gold序列构造观测矩阵的方式。
如果一个序列,一方面它是可以预先确定的,并且是可以重复地生产和复制的,另一方面它又具有某种随机序列的随机特性(即统计特性),这种序列即为伪随机序列。伪随机序列又称为伪噪声序列,即PN码,它具有3个特点:
1) 序列中各元素接近等概率出现,即元素0与1出现的个数相差不超过1个;
2) 序列中连续出现相同元素被称为游程,在同长度的游程中,“0”的游程数和“1”的游程数大致相等;
3) 具有类似白噪声的自相关特性。
m序列和gold序列同属于伪随机序列,满足上述序列的特点。m序列是最长线性移位寄存器序列,线性移位寄存器是由移位寄存器加上反馈系数后所产生的(见图 1),反馈系数ci一旦确定,产生的m序列就确定了。产生的m序列根据反馈系数不同而变化,序列的长度与线性移位寄存器(反馈系数)的级数有关,即长度len=2n-1。每一个级数n都有一个与之对应的多项式:
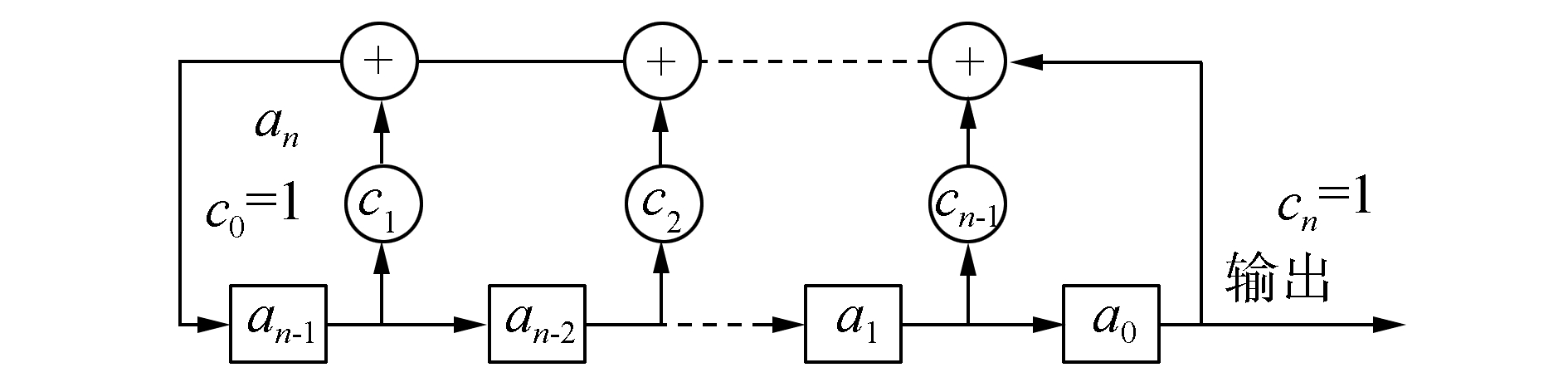
|
图 1 n位线性反馈移位寄存器结构 Fig.1 n-bit linear feedback shift register structure |
| $ f\left( x \right) = \sum\limits_i^n {{c_i}{x^i}} $ | (7) |
多项式(7) 为级数n的本原多项式,即反馈系数多项式。文中讨论的序列均由(0, 1) 或者(-1, 1) 组成,这两种序列所产生伪随机序列的相关性是相同的,本文构成的观测矩阵元素选用的是(-1, 1)。根据m序列的性质所生成序列1元素比-1元素多一个,可以认为各个元素都占1/2,因此可以推测m序列构成的观测矩阵能够精确重建原始信号。
如果把两个码长相等,码速相同的m序列发生器产生的优选对序列作模2加运算,生成的新的码序列即为gold序列。每改变两个m序列相对位移就可得到一个新的gold序列。因为总共有2n-1个不同的相对位移,加上原来的两个m序列本身,所以两个n级移位寄存器可以产生2n+1个Gold序列。该序列的自相关函数具有三值特性,虽然这三个值出现的概率不同,却仍然具有良好的自相关和互相关特性,生产的序列-1和1的次数相差不大,可以近似认为各占1/2,而且形成gold序列的数量要比m序列大很多,一对m序列优选对就能够生成2n+1条gold码,这也是gold序列的优点之一。
简单地介绍了上述两种序列的产生过程和性质,下面详细介绍用m序列和gold序列构造观测矩阵的具体方法。
m序列观测矩阵构造方法,主要利用循环矩阵的思想,将生成的m序列每次循环右移一位,构成N列,最后再顺序选取M行构成观测矩阵。
1) 首先生成周期L=2N-1的m序列(元素为±1),其中L>N(N为原始信号长度),作为观测矩阵的第一列;
2) 将m序列元素循环右移一位,产生新的序列,作为观测矩阵的第二列;
3) 依次将前一行的m序列右移一位,产生新的序列,作为观测矩阵的下一列;
4) 重复步骤3,直到生成N列,构成L×N的矩阵;
5) 顺序选取1:M行构成观测矩阵Mx。
生成的矩阵形式如式(8) 所示,可以看成循环m序列矩阵,本文称为循环m序列观测矩阵。
| $ {\mathit{\boldsymbol{M}}_x} = \left[{\begin{array}{*{20}{c}} {{m_1}} & {{m_n}} & \cdots & {{m_n}}\\ {{m_2}} & {{m_1}} & \cdots & {{m_{n-1}}}\\ \vdots & \vdots & {} & \vdots \\ {{m_n}} & {{m_{n-1}}} & \cdots & {{m_1}} \end{array}} \right] $ | (8) |
Gold序列观测矩阵的构造方法与循环m序列观测矩阵类似。利用循环矩阵的思想生成gold序列观测矩阵的步骤如下:
1) 首先生成周期L=2n-1的gold序列(元素为±1),gold序列是两个m序列优选对,其中L>N(原始信号长度),作为观测矩阵的第1列;
2) 将m序列元素循环右移一位,产生新的序列,作为观测矩阵的第2列;
3) 其他步骤参见循环m序列观测矩阵的构造方法。
生成的矩阵形式如式(9) 所示,同样可以看成循环gold序列矩阵,本文称为循环gold序列观测矩阵。
| $ {\mathit{\boldsymbol{G}}_x} = \left[{\begin{array}{*{20}{c}} {{g_1}} & {{g_n}} & \cdots & {{g_n}}\\ {{g_2}} & {{g_1}} & \cdots & {{g_{n-1}}}\\ \vdots & \vdots & {} & \vdots \\ {{g_n}} & {{g_{n-1}}} & \cdots & {{g_1}} \end{array}} \right] $ | (9) |
上述步骤中之所以要顺序选取M行向量构成观测矩阵,也是出于计算能力的考虑,毕竟嵌入式系统硬件计算能力较弱,随机选取会增加计算消耗。
2 伪随机观测矩阵相关证明m序列和gold序列都是伪随机序列,1与0出现的概率约为1/2,可以认为伪随机序列是二值序列,因此由伪随机序列构成的观测矩阵元素是服从均匀分布的。上一个章节已经说明,当观测矩阵Φ满足式(5) 分布时,将以极大的概率满足RIP条件。本文可以将按照式(5) 分布的观测矩阵划分为两个随机二进制矩阵:
| $ {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_s} = {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_a}-{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_b} $ | (10) |
压缩感知观测过程为
| $ \mathit{\boldsymbol{y = }}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_x} $ | (11) |
将其等价成如下形式:
| $ {y_i} = \left\langle {x, {\varphi _i}} \right\rangle, i = 1, 2, \cdots, n $ | (12) |
则对于每一个观测值有
| $ \begin{array}{l} {y_i}\left( {x, {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_s}} \right) = {y_i}\left( {x, {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_a}} \right)-\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{y_i}\left( {x, {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_b}} \right), \;\;\;\;\;1 \le i \le n \end{array} $ | (13) |
由式(13) 可以看出, 当Φs获取原始信号x的全部信息时,Φa只获取了一部分信息。假设Φs所获取的信息量为1,则当n足够大的时候,Φa获取的信息量将以(14) 式所示的概率变化:
| $ 1-{\left( {1/2} \right)^n} = 1-{2^{-n}} $ | (14) |
最终获得的信息量也接近1。根据文献[14-15]可以得出结论:Φa是一个服从随机二进制分布的大小为n×N的矩阵,给定n,N,δ∈(0,1) 和k≤cn/log2(N/k),存在c1,c2>0,则当存在一个相应的服从式(5) 的随机均匀分布矩阵Φs以概率p≥1-2exp(-nc2)满足RIP时,随机二进制矩阵Φa能使可压缩信号以概率p≥[1-2exp(-nc2)](1-2-n)精确重构。其中:
| $ {c_2} \le \frac{{\left( {3\delta- {\delta ^3}} \right)}}{{48}}- {c_1}\left[{1 + \frac{{{{\log }_2}\left( {12/\delta } \right)}}{{{{\log }_2}\left( {N/k} \right)}}} \right] $ | (15) |
式中k为信号的稀疏度。
从矩阵的构造方法来看,循环m序列和循环gold序列观测矩阵具有良好的互相关特性,与非相干性条件恰好吻合,由于构造的观测矩阵满足一定的线性独立随机性,符合观测传感对观测矩阵的要求。
3 仿真验证与分析本文通过改进部分哈达玛观测矩阵的构造方式,构造了顺序部分哈达玛观测矩阵;利用伪随机序列中的m序列和gold序列的特性构造了循环m序列和循环gold序列观测矩阵,并给出了简单的数学证明来说明伪随机序列可以作为观测矩阵。下面通过仿真来验证所构造的观测矩阵的性能。首先,将顺序部分哈达玛矩阵与部分哈达玛矩阵进行对比;然后,将所构造的循环伪随机序列的可用性与其他观测矩阵进行对比;最后,将所构造的观测矩阵在常用重构算法上进行对比分析。
本文仿真采用二维Lena标准图像进行分块压缩采样和重建,选取大小为8×8块,采用离散余弦变换(DCT)进行稀疏变换,采样率分别为0.25,0.5和0.75。
3.1 顺序部分哈达玛观测矩阵仿真分析对顺序部分哈达玛观测矩阵进行仿真实验分析,重建算法选用的是正交匹配追踪(OMP)算法,其仿真结果如表 1所示。
| 表 1 重构图像PSNR值 Tab.1 PSNR value of reconstructed image |
通过表 1可以看出,当采样率较低时,顺序部分哈达玛观测矩阵重建后图像的PSNR值要比随机选取的部分哈达玛矩阵明显高出近5 dB; 当采样率较高时,两者之间的差距就不大了。这种顺序选取的部分哈达玛矩阵,结构固定,无需多次测量,可以在采样率较低的情况下达到很好的重构效果。另外,哈达玛观测矩阵存在蝶型快速算法,非常适用于硬件系统,从而减少系统的能源消耗,为硬件实现压缩感知原理提供了较好的支持。
3.2 循环伪随机序列构造的观测矩阵可用性验证文中简单证明了循环伪随机可以作为观测矩阵的理论可能性,下面通过仿真来验证构造的观测矩阵的适应性和实用性。表 2列出了高斯随机观测矩阵、托普利兹观测矩阵、顺序部分哈达玛观测矩阵的对比结果,重建算法选用的是OMP算法;并且展示了这几种观测矩阵在不同采样率下,重建后的图像的PSNR值。
| 表 2 同观测矩阵重构时的PSNR值 Tab.2 PSNR value of different measurement matrix reconstruction |
图 2展示了采样率为0.25时,各观测矩阵采样时重建的图像仿真效果图。由表 2和图 2可知,当采样率较低时,顺序部分哈达玛的观测效果最佳,比高斯随机矩阵高出将近9 dB,其他确定性观测矩阵也比高斯随机矩阵高出4 dB;当采样率提升到0.50时,顺序部分哈达玛矩阵也要高出6 dB,而其他观测矩阵也高出1 dB;随着采样率提高到0.75时,各个观测矩阵的重建效果差距就较小了。通过仿真结果可以看出,在采样率较低时,确定性观测矩阵的重建效果较好,其中改进的顺序部分哈达玛矩阵采样效果最好,而构造的循环伪随机(循环m序列和循环gold序列)观测矩阵也表现出较好的采样效果。

|
图 2 采样率为0.25时仿真结果图 Fig.2 Simulation result at sampling rate 0.25 |
仿真实验依然沿用上文的条件,测试图像为256×256的Lena图像,重构算法选用的是求解最小l0-范数和l1-范数各类别中有代表性的BP算法、OMP算法以及OMP算法的改进算法分段正交匹配追踪算法(StOMP),对比的观测矩阵包括高斯随机矩阵、顺序部分哈达玛矩阵、循环m序列矩阵和循环gold序列矩阵,m序列采用7级反馈系数,选用的本原多项式为f(x)=x7+x6+x3+x1,即各寄存器的初始状态为[1 1 0 0 1 0 1]。
本次仿真与上文不同的是,稀疏基为小波变换,每次处理256个像素,采样率从0.2到0.8变化,步长为0.05。高斯随机观测矩阵、顺序部分哈达玛观测矩阵、循环m序列观测矩阵和循环gold序列观测矩阵在不同的重建算法下的PSNR仿真结果分别如图 3~6所示。
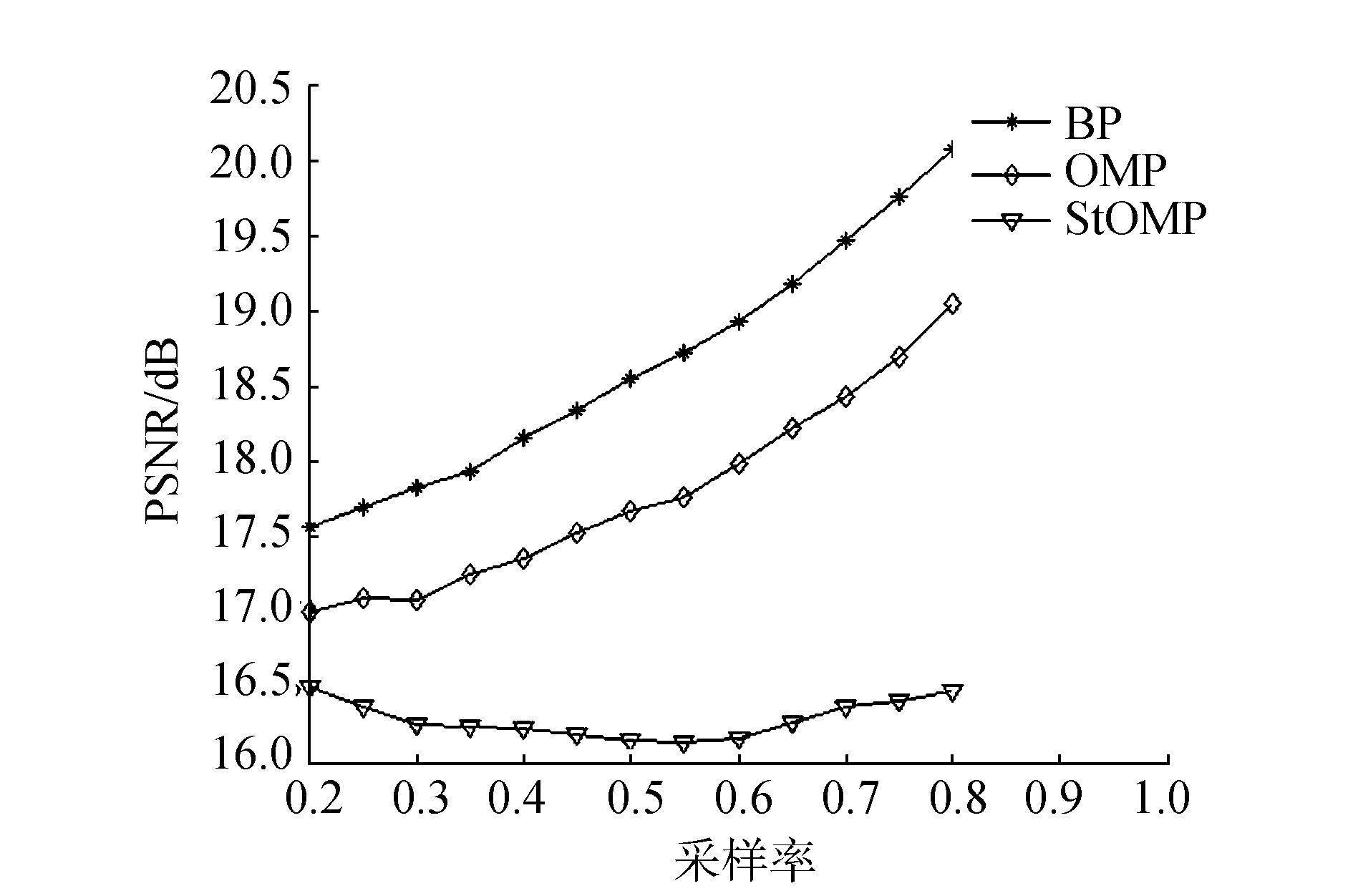
|
图 3 高斯随机矩阵在不同重建算法下的PSNR仿真结果 Fig.3 PSNR simulation result of Gaussian random matrix under different reconstruction algorithm |
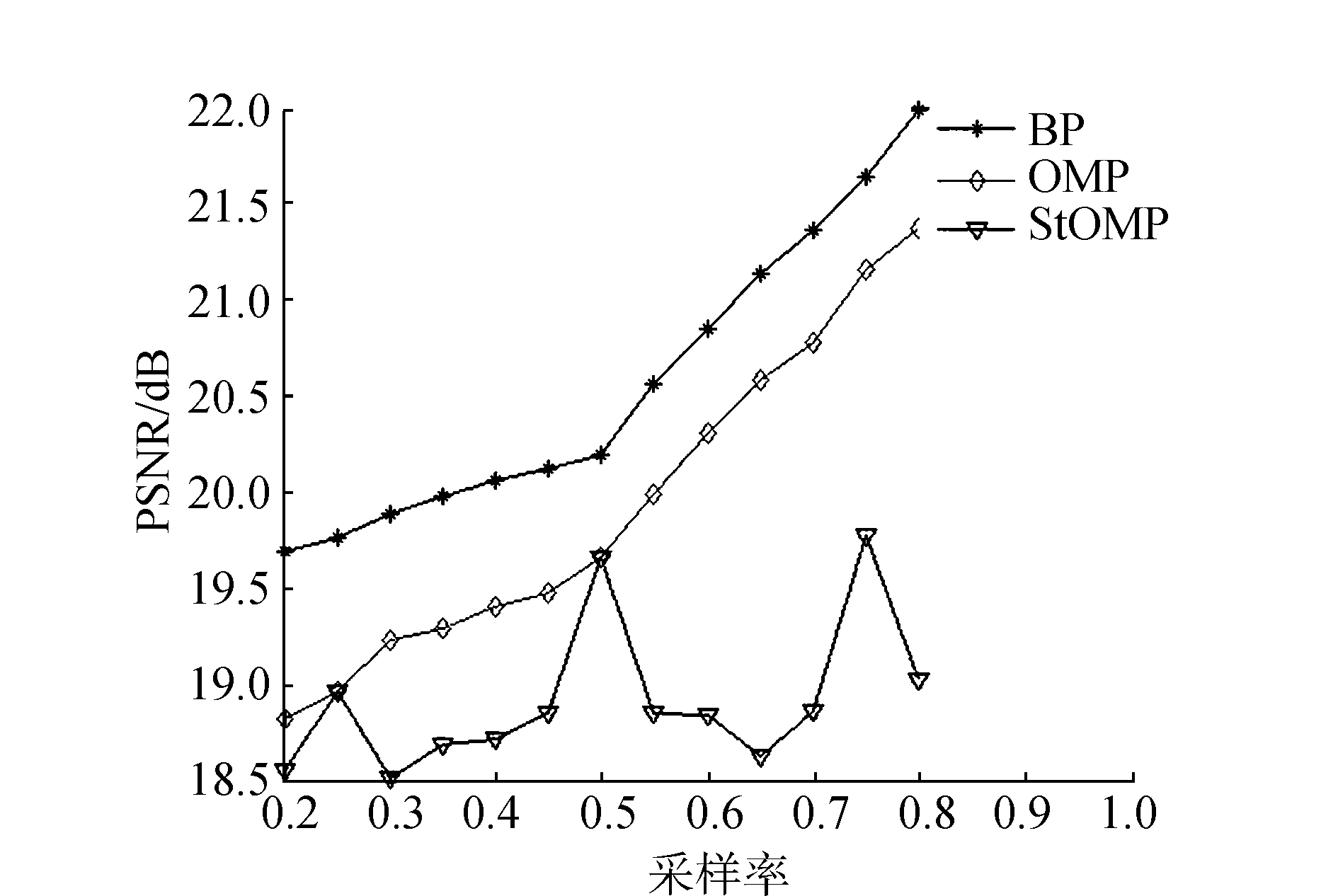
|
图 4 顺序部分哈达玛矩阵在不同重建算法下的PSNR仿真结果 Fig.4 PSNR simulation result of partial order Hadamard matrix under different reconstruction algorithm |
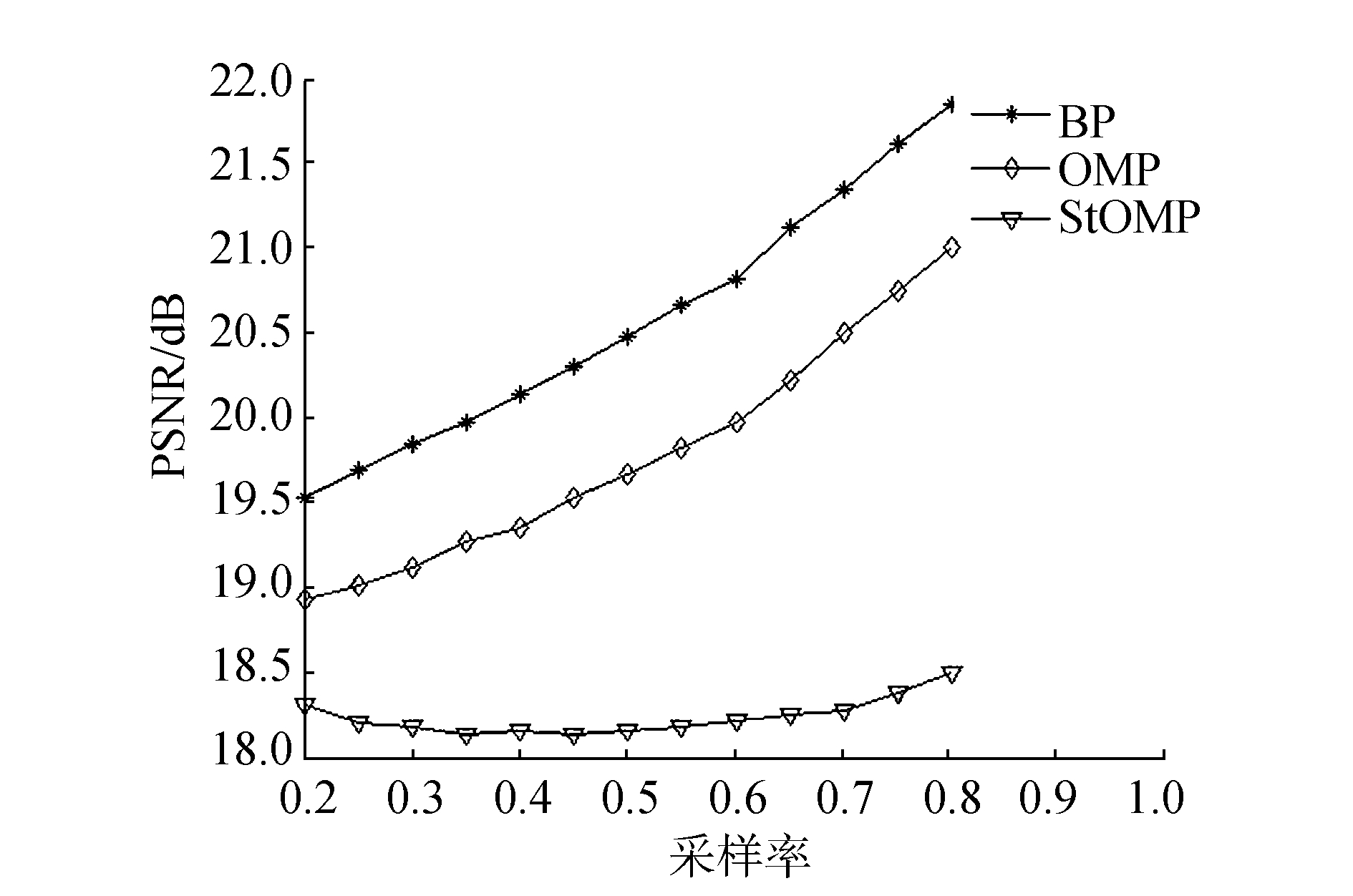
|
图 5 循环m序列矩阵的PSNR仿真结果 Fig.5 PSNR simulation result of recycled m sequence measurement matrix |

|
图 6 循环gold序列矩阵在不同重建算法下的PSNR仿真结果 Fig.6 PSNR simulation result of recycled gold sequence measurement matrix under different reconstruction algorithm |
由图 3~6可知,顺序部分哈达玛观测矩阵的重建效果最好,比高斯随机矩阵高出近2 dB,4种观测矩阵在BP算法和OMP算法上的重建效果总体趋势一样,都是随着采样率的提升而提升,在StOMP算法上顺序部分哈达玛观测矩阵重建效果成跳跃变化,而其他两种观测矩阵重建效果趋于稳定提高。循环伪随机观测矩阵的重建效果也要优于高斯随机矩阵。
本文对4种观测矩阵在重建算法重构时间上进行对比分析,如表 3所示。
| 表 3 观测矩阵重建耗时对比表 Tab.3 Construction consuming time comparison among diffetent measurement matrix |
表 3是在采样率为0.6条件下的记录,通过表 3对比分析,可以得出在同等条件下顺序部分哈达玛矩阵和循环伪随机序列矩阵的重建运行时间要比高斯随机矩阵少。由上述对比可以验证,顺序部分哈达玛矩阵和循环伪随机序列矩阵的性能要优于高斯随机观测矩阵。
4 结束语本文针对嵌入式硬件系统能源有限,存储较小,计算能力差的特点,提出了两种易于硬件实现,且占内存较小的观测矩阵,即顺序部分哈达玛观测矩阵和循环伪随机观测矩阵(循环m序列矩阵和循环gold序列矩阵)。经过仿真分析可知,这两类观测矩阵在重建效果上要比高斯随机矩阵优越。另外,这两类矩阵在构造上也比较简单,具有递推特性,易于硬件实现,避免了随机矩阵的不确定性且克服了随机矩阵浪费存储资源的缺陷,节省大量存储空间。其中,循环伪随机观测矩阵还克服了部分哈达玛矩阵对信号长度的限制,构造的观测矩阵不但具有一定的理论意义,还为硬件实现压缩感知观测矩阵提供了一种新的思路,具有良好的实际应用价值。
| [1] |
CANDES E, ROMBERG J. Robust signal recovery from incomplete observations[C]//Proceedings of International Conference on Image Processing. Atlanta, GA: IEEE, 2006: 1281-1284. http://ieeexplore.ieee.org/xpls/icp.jsp?arnumber=4106771
( 0) 0)
|
| [2] |
CANDES E J, TAO T. Decoding by linear programming[J]. IEEE transactions on information theory, 2005, 51(12): 4203-4215. DOI:10.1109/TIT.2005.858979 ( 0) 0)
|
| [3] |
DONOHO D L. Compressed sensing[J]. IEEE transactions on information theory, 2006, 52(4): 1289-1306. DOI:10.1109/TIT.2006.871582 ( 0) 0)
|
| [4] |
戴琼海, 付长军, 季向阳. 压缩感知研究[J]. 计算机学报, 2011, 34(3): 425-434. DAI Qionghai, FU Changjun, JI Xiangyang. Research on compressed sensing[J]. Chinese journal of computers, 2011, 34(3): 425-434. (  0) 0)
|
| [5] |
CANDES E J, TAO T. Near-optimal signal recovery from random projections: universal encoding strategies?[J]. IEEE transactions on information theory, 2007, 52(12): 5406-5425. ( 0) 0)
|
| [6] |
HAUPT J, BAJWA W U, RAZ G, et al. Toeplitz compressed sensing matrices with applications to sparse channel estimation[J]. IEEE transactions on information theory, 2010, 56(11): 5862-5875. DOI:10.1109/TIT.2010.2070191 ( 0) 0)
|
| [7] |
DEVORE R A. Deterministic constructions of compressed sensing matrices[J]. Journal of complexity, 2007, 23(4/5/6): 918-925. ( 0) 0)
|
| [8] |
蒋留兵, 黄韬, 沈翰宁, 等. 基于局部随机化哈达玛矩阵的正交多匹配追踪算法[J]. 系统工程与电子技术, 2013, 35(5): 914-919. JIANG Liubing, HUANG Tao, SHEN Hanning, et al. Orthogonal multi matching pursuit algorithm based on local randomized Hadamard matrix[J]. Systems engineering and electronics, 2013, 35(5): 914-919. (  0) 0)
|
| [9] |
刘记红, 徐少坤, 高勋章, 等. 基于随机卷积的压缩感知雷达成像[J]. 系统工程与电子技术, 2011, 33(7): 1485-1490. LIU Jihong, XU Shaokun, GAO Xunzhang, et al. Compressed sensing radar imaging based on random convolution[J]. Systems engineering and electronics, 2011, 33(7): 1485-1490. (  0) 0)
|
| [10] |
徐皓波, 于凤芹. 基于稀疏预处理和循环观测的语音压缩感知[J]. 计算机工程与应用, 2014, 50(23): 220-224. XU Haobo, YU Fengqin. Speech compressed sensing based on sparse pre-treatment and circulant measurement[J]. Computer engineering and applications, 2014, 50(23): 220-224. DOI:10.3778/j.issn.1002-8331.1304-0329 (  0) 0)
|
| [11] |
党骙, 马林华, 田雨, 等. M序列压缩感知测量矩阵构造[J]. 西安电子科技大学学报:自然科学版, 2015(2): 186-192. DANG Kui, MA Linhua, TIAN Yu, et al. Construction of the compressive sensing measurement matrix based on m sequences[J]. Journal of Xidian University: Natural Science, 2015(2): 186-192. (  0) 0)
|
| [12] |
王学伟, 崔广伟, 王琳, 等. 基于平衡GOLD序列的压缩感知测量矩阵的构造[J]. 仪器仪表学报, 2014, 35(1): 97-102. WANG Xuewei, CUI Guangwei, WANG Lin, et al. Construction of measurement matrix in compressed sensing based on balanced Gold sequence[J]. Chinese journal of scientific instrument, 2014, 35(1): 97-102. (  0) 0)
|
| [13] |
BARANIUK R, DAVENPORT M, DEVORE R, et al. A Simple proof of the restricted isometry property for random matrices[J]. Constructive approximation, 2008, 28(3): 253-263. DOI:10.1007/s00365-007-9003-x ( 0) 0)
|
| [14] |
ZHANG G S, JIAO S H, XU X L, et al. Compressed sensing and reconstruction with bernoulli matrices[C]//Proceedings of 2010 IEEE International Conference on Information and Automation (ICIA). Harbin: IEEE, 2010: 455-460. http://ieeexplore.ieee.org/document/5512379/
( 0) 0)
|
| [15] |
ZHANG G S, JIAO S H, XU X L. Compressed sensing and reconstruction with Semi-Hadamard matrices[C]//Proceedings of 2010 2nd International Conference on Signal Processing Systems (ICSPS). Dalian: IEEE, 2010: V1-194-V1-197. http://ieeexplore.ieee.org/document/5555570/
( 0) 0)
|
| [16] |
SO NG, YUN CAO Wei, SHEN Yanfei, et al. Compressed sensing image reconstruction using intra prediction[J]. Neurocomputing, 151(3): 1171-1179. ( 0) 0)
|
| [17] |
WU X, HUANG G, WANG J, et al. Image reconstruction method of electrical capacitance tomography based on compressed sensing principle[J]. Measurement science and technology, 2013, 24(7): 075-085. ( 0) 0)
|
| [18] |
LANGET H, RIDDELL C, TROUSSET Y, et al. Compressed sensing dynamic reconstruction in rotational angiography[J]. Med image comput comput assist interv, 2012, 7510(1): 223-230. ( 0) 0)
|
| [19] |
SHCHUCKINA A, KASPRZAK P, DASS R, et al. Pitfalls in compressed sensing reconstruction and how to avoid them[J]. Journal of biomolecular Nmr, 2016: 1-20. ( 0) 0)
|
| [20] |
PARK JY, YAP HL, ROZELL CJ, et al. Concentration of measure for block diagonal matrices with applications to compressive signal processing[J]. IEEE transactions on signal processing, 2011, 59(12): 5859-5875. DOI:10.1109/TSP.2011.2166546 ( 0) 0)
|
 2017, Vol. 12
2017, Vol. 12


