2. Mining Institute, Liaoning Technical University, Fuxin 123000, China
单隐藏层前馈神经网络由于其学习能力强、能够逼近复杂非线性函数、优异的信息分布式存储和并行协同处理能力以及鲁棒性好的特点,使得神经网络在很多领域得到了广泛的应用。由于神经网络监督学习的本质,在神经网络训练过程中,随机初始权值后,输入信号通过网络正向传递,得到模拟输出信号,之后依据输出信号和数据标签之间的误差反向传播的方式调整网络权值,使均方误差最小,从而使网络映射输出更好地“拟合逼近”数据标签,以达到学习的目的。
在神经网络的分类应用中,神经网络分类器训练过程是一个调整分类超曲面的过程,在训练初始阶段通过随机产生一个超曲面,然后依据误差来调整超曲面的位置,直到数据集中属于不同类的点正好位于超曲面的不同侧面。这种处理机制决定了神经网络进行数据分类最终获得的分类超曲面有可能相当靠近训练集中的点[1],不仅导致网络训练时间长,而且使网络分类边界过于靠近样本集中点,导致较差的分类泛化能力,所以数据样本对于网络训练时间、网络性能有重要的影响。
一个数据集可以用数据特征、数据量、数据分布来描述。数据约简的目的主要是减少信息量,将一些无关紧要的信息去掉后,不影响系统原有的功能表达。目前,针对数据约简的研究主要集中在两个方面:基于特征选择约简和基于实例选择约简。
基于特征选择的数据约简是指在所有特征中选择某些重要的、有代表性的特征,去除对处理结果影响小甚至无影响的特征,以达到提取主要特征的目的。常见的特征选择方法主要有粗糙集法[2]、主成分分析法[3]、基于流行学习的Autoencoder[4]等。
基于实例选择的数据约简是从原始数据集中选择具有代表性的实例,去除冗余的和相似性较大的数据,得到相对较小的约简数据集,以达到减少数据量和改变数据分布的目的。目前针对实例选择的数据约简方法主要有基于聚类、基于样本距离、基于分类边界的数据约简方法。聚类约简方法首先通过模糊聚类[5]、K邻近聚类[6]等聚类方法对训练数据进行聚类分析,选择目标样本,剔除冗余样本,以达到数据约简的目的,然后用约简后的数据作为新的训练数据进行分类器训练。整个分类系统分为数据约简和分类训练两个阶段,第1阶段的数据筛选结果对于最终分类器的性能起着关键性的作用,此外每个阶段需要调整相应的模型参数,整个分类系统过于复杂。基于样本距离的约简方法[7],通过构建样本间距离度量 (通常为欧氏距离),保留边界样本,剔除非边界样本。该方法同聚类的概念类似,仍属于两阶段的分类系统。基于分类边界数据约简方法主要为支持向量机算法 (SVM)[8],SVM算法基于最优分类边界的概念,从训练集中选择支持向量,使得对支持向量的划分等价于对整个数据集的划分。
此外,文献[9]利用HMM模型,通过模型的预测概率将训练样本分为好样本、差样本和边界样本,然后分析了选择不同的训练样本对于分类器的影响。文献[10]的Adaboosting算法依据分类错误率,通过增加错分类样本权重,减小正确分类样本权重的方法,改变样本的权重分布,以达到重点关注错分类样本的目的,然后通过多个弱分类器加权综合获得强分类器,Adaboosting方法没有约简训练数据,只是更改样本分布权重,达到了重点关注错分类样本的目的。
当数据量大和数据过于集中时,神经网络分类器训练时间长,泛化能力差;结合数据约简和样本权值的思想,本文提出了一种基于动态数据约简 (dynamic data reduction,DDR) 的神经网络训练方法。该方法依据神经网络迭代训练过程中的训练样本的分类错误率,动态更新训练样本的权重,然后依据权重对训练数据进行动态约简,从而达到缩短网络训练时间、增强网络泛化能力的目的。该方法将数据约简和分类器训练融合为一个阶段,比文献[5-7]的方法具有快速的特点,比文献[8]具有简单的优势。
1 DDR训练方法 1.1 BP神经网络BP (back propagation) 神经网络是一种单向传播的多层前馈网络,采用误差反向传播权值学习算法 (BP算法),是目前应用较多的一种模型。BP神经网络的基本单元是神经元,按照神经元的功能不同将其分成若干层,通常最左侧的为输入层,最右侧的为输出层,而中间的为隐层,只有相邻层神经元之间存在权值连接,每层内部神经元无连接,其结构如图 1所示。
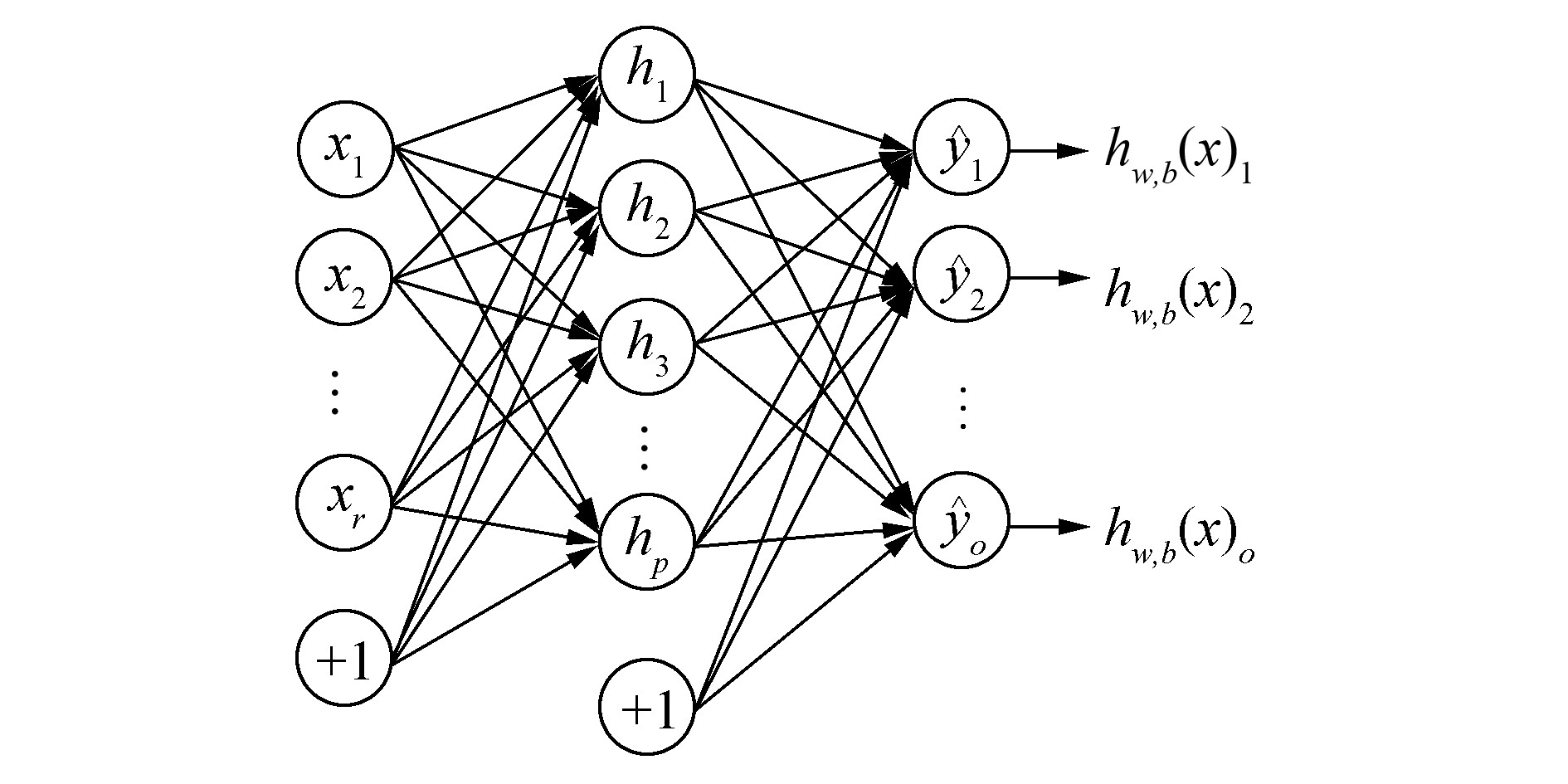
|
| 图 1 BP神经网络结构 Fig. 1 BP neural network structure |
BP神经网络的信息传递过程主要分为两个阶段:信息前馈传递阶段和误差反馈阶段。信息前馈阶段,每层的输入信息,首先通过连接权值进行融合计算,再通过相应类型的激活函数进行激活变换得到输出信号,然后将输出信号作为输入传入下一层进行相似的信息变换,最终传递到输出层得到网络最终输出。误差反馈阶段,由于神经网络是一种监督学习算法,将信号的前馈输出和真实标签之间的误差,通过连接权值从输出层反向传播至输入层,并依据梯度值来更新连接权值,从而达到学习的目的。
1.2 DDR训练方法设计思想从分类的角度来说,分类的任务在于寻找分类面,将分类空间划分为不同的类区域,训练的作用在于分类超曲面的生成,从这个方面来说,边界样本就是位于理想分类超曲面附近的样本。神经网络在训练过程中可以理解为依据训练数据调整分类超曲面的过程,训练样本中,如果某种类别的数据量越多, 它在训练出的模型中所起的作用就越大,分类超曲面越靠近该分类。所以训练样本的分布主要影响分类超曲面的位置,训练样本的个数则主要影响网络的训练时间。
依据文献[5, 7, 9]通过聚类或样本距离,依据数据样本位置分布将数据分为核样本和边界样本,核样本数据一般位于数据类别聚类中心或远离类别边界的位置,边界样本位于相邻类别的临近或重叠位置。从聚类分析的观点来看,位于类中心的核样本更具代表性,所表达信息量更大,核样本可以使得训练出的模式类区域更加紧凑,不同模式类区域间隔更大,但核样本数目太多,不仅增加网络训练时间,还容易使得分类超曲面过于靠近核样本,使得分类区域过小,从而使得边界样本被划分到超曲面以外,使得网络分类错误率增加,泛化能力降低。文献[11]指出,基于神经网络的模式识别中,训练样本的总数目对于神经网络训练的影响不是十分重要,重要的是其中边界样本的数目;有了足够多的边界样本,就可以训练出好的分类超曲面。但由于网络中边界样本个数相对较少,较少的训练数据很容易导致网络发生过拟合现象,同样会导致网络泛化能力下降。所以在神经网络分类器训练过程中,在利用全部边界样本的基础上,为了防止由于数据较少引起的过拟合问题,实验还应选择相应数量的核样本来协同训练。
由于神经网络训练过程可以理解为分类超曲面移动的过程,训练样本中,核样本个数多,且分布在边界样本内部,所以在网络迭代训练过程中,核样本一般位于分类超曲面内部,其分类错误率较低,而边界样本随着分类超曲面的移动,其分类错误率也随之波动。所以在网络训练过程中应该减少核样本的作用,增加边界样本的比重。
基于上述思想,本文提出了一种基于训练分类错误率的动态数据约简方法 (DDR):在网络训练过程中,首先赋给每个训练样本一个权重值xwi (i=1, 2, …,m,m为原始训练样本总数) 作为样本的重要性度量,则样本构成权重向量XW={xw1, …, xwi, …,xwm};然后再依据每次迭代所有原始训练样本的分类错误率动态更新每个训练样本的权重值,更新规则为:降低正确分类样本的权重值,增加错误分类样本的权重值,以达到重点关注易错分类的边界样本,弱化易正确分类的核样本的目的;最后依据数据约简规则对训练样本进行挑选。数据约简选择规则为:对于正确分类的训练样本,在[0, 1]随机选择一个数值rand,若rand小于样本的权重值,则选择该样本为新的训练样本;否则剔除该样本。这样在迭代过程中一直迭代分类正确的核样本,由于其权值持续降低,被选择的概率较小;而边界样本由于其分类准确性随着分类超曲面的移动而波动,所以其权重值较大,被选择的概率较大;对于错误分类的样本则全部选择。然后将全部错分类样本和随机选择的部分正确分类样本作为新的训练样本集,进行下一次迭代训练。由于神经网络训练过程中迭代收敛较慢,训练过程往往需要较长的迭代次数,这样会使核样本的权重值持续降低,一些错误分类边界样本的权重值则持续增加,导致训练样本的权值差异较大,不利于正确分类样本的选择。为了避免上述问题,在权重值更新后通过权重值上下限约束,对权重值进行规范化处理,权重下限值为xwb,xwb>0,权重上限值为xwt,xwt≤1,即权重xwi∈[xwb, xwt],i=1, 2, …,m,通过权值的规范化约束,使得迭代过程中选择边界样本的同时,也选择部分核样本进行协同训练,以避免由于样本过少而引起的过拟合现象。
1.3 DDR训练方法算法描述设训练集为X={(x1, y1), …, (xi, yi), …, (xm, ym)}, xi∈Rr,训练样本批量为s,样本总均值误差为E,批量均值误差为e,连接权值为w,学习率为α,迭代次数为k,样本权重集为XW,正确分类样本权重集为XWright,权重增量为xwd,权重标识集为XS,错分类样本集为Xwrong,正确分类样本集为Xright,从Xright中选择的样本集Xselect,约简后训练样本集为Xreduction,则动态数据约简的神经网络分类器训练方法算法如下:
算法1 动态数据约简的神经网络分类器训练
输入 X, xwd, xwb, xwt=1, XW(1, i)=0.5, i=1, 2,…,m;
输出 神经网络分类器f(x)。
1) 初始化网络结构,随机初始化网络权值;
2) 训练样本规则化预处理;
3) 对当前训练样本Xreduction进行随机乱序操作,重新排列样本的顺序;
4) 按照训练样本排列序号,依次提取批量s个样本,样本分成n个批次,n=round (m/s)。
5) 计算网络各批量的均值误差
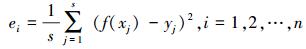 |
6) 子批量内均值修正网络的权值:
 |
7) 计算所有样本的均值误差:
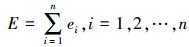 |
8) 依据分类错误率更新样本权重值:
 |
9) 样本权重约束
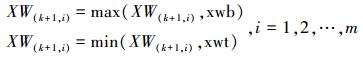 |
10) 样本约简选择
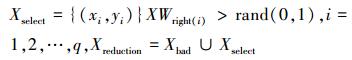 |
11) 根据迭代次数进行判断是否达到收敛要求,若达到要求则网络完成训练,否则循环3)~11)。
算法补充说明:round () 函数表示对小数进行舍入取整操作;神经网络更新规则当s=m时,即为全批量权值更新规则;当s=1时,即为增量权值更新规则;当1 < s < m时,即为子批量权值更新规则。
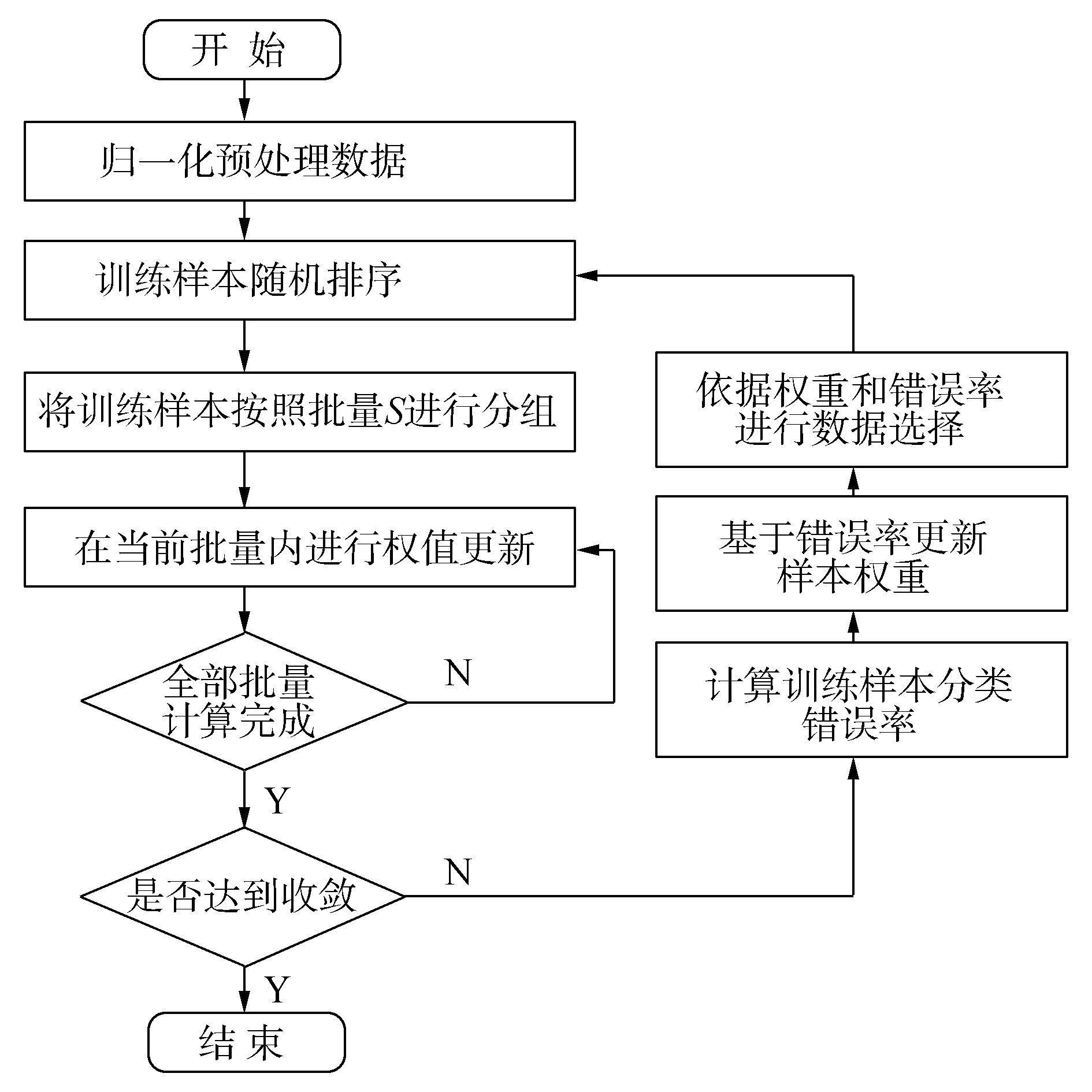
动态数据约简的神经网络训练方法如图 2。
|
| 图 2 动态数据约简神经网络训练方法流程图 Fig. 2 Flow chart of neural network training method for dynamic data reduction |
实验网络神经元激励函数均采用单级S型 (Sigmoid) 激励函数,训练中采用动量项梯度下降算法作为网络训练算法,为了加速网络收敛,选用子批量网络权值更新规则,同时为了避免过拟合现象,实验输入数据经过预处理后再输入到网络中,并且在训练过程中加入权值惩罚项。
为了使算法稳定收敛到最小,采用学习率缩减的方式来调节学习率,设学习率改变次数比例参数为scaleIndex,学习率改变程度参数为scaleLr,学习率改变总次数为ChangeTimes,学习率调整策略见算法2。
算法2 学习率调整算法
输入 T,scaleIndex,scaleLr,ChangeTimes;
输出 学习率curLr。
ChangeIndex =T*scaleIndex
FOR k=1:K
IF k>ChangeIndex&&curTimes < ChangeTimes
ChangeIndex =k+scaleIndex*(K-k)
curLr =curLr*scaleLr
curTimes =curTimes+1
为了全面公平地对比标准神经网络训练方法 (STD) 和本文提出的数据约简神经网络训练方法 (DDR),将两种神经网络在相同的网络结构、初始权值和学习参数配置下进行训练。
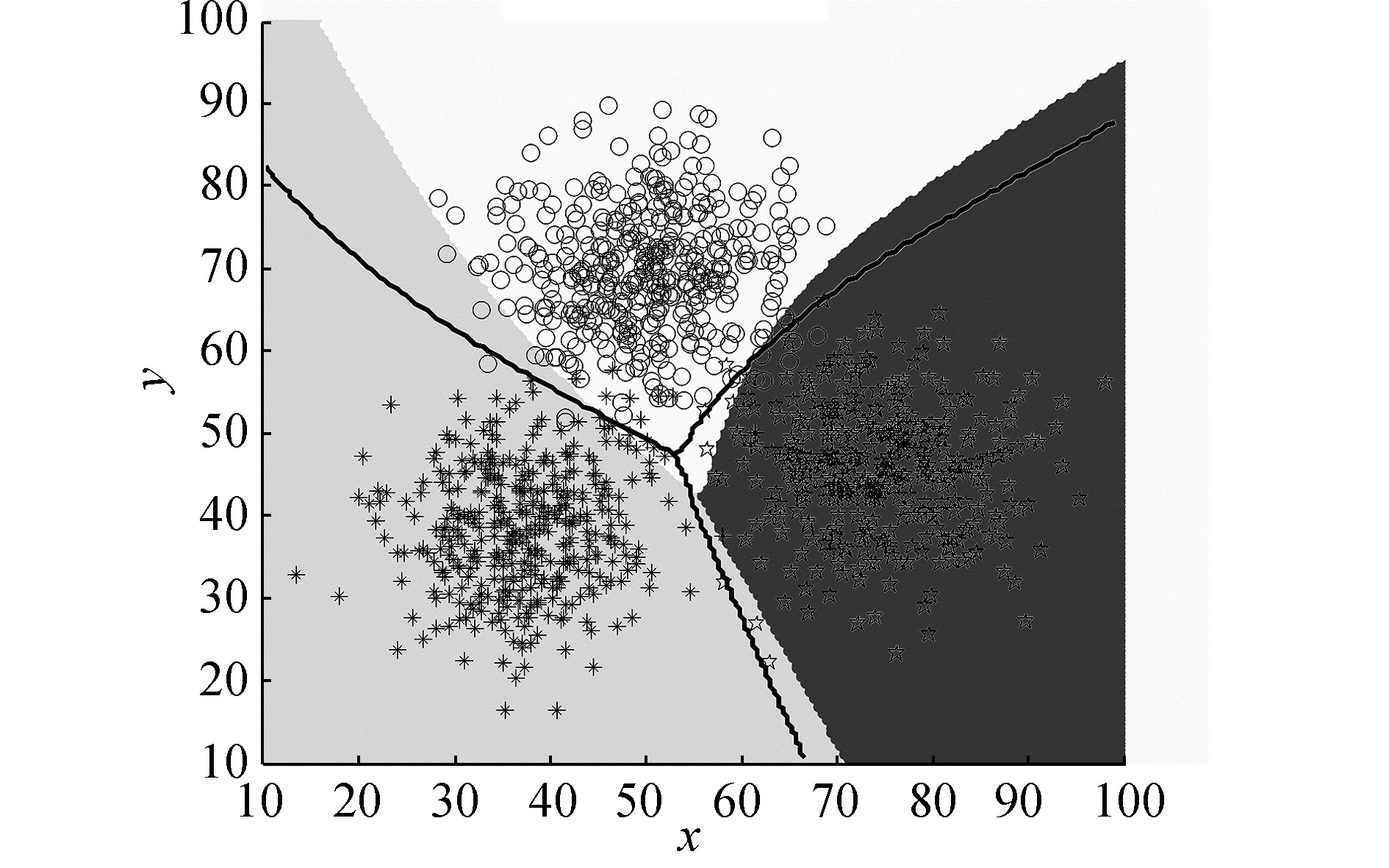
2.2 人工数据可视化分析为了可视化验证动态数据约简神经网络训练方法在训练过程中数据约简过程,实验采用正态分布生成3分类的2维点数据集,各类点的坐标均值分别为 (38, 38),(50, 70),(75, 45),每个维度的方差为55,每个类别400个样本,总计1 200个样本。生成的数据集如图 5所示,星号为类别A,五角星为类别B,圆圈为类别C,数据集中每个类的中心点数据密集,边界点相对稀疏,且边界别点之间存在重叠。
|
| 图 5 神经网络分类器边界图 Fig. 5 Neural network classifier boundary map |
实验参数设置:训练样本个数为600,测试样本个数为600,网络结构为2-3-3,迭代次数为500,学习率为0.2,动量项为0.9,权值惩罚系数为10-5,学习改变参数scaleIndex和scaleLr均为2/3,ChangeTimes为8,初始训练样本权重为0.5,权重增量系数为0.005,权值上限为1,权值下限为0.1。
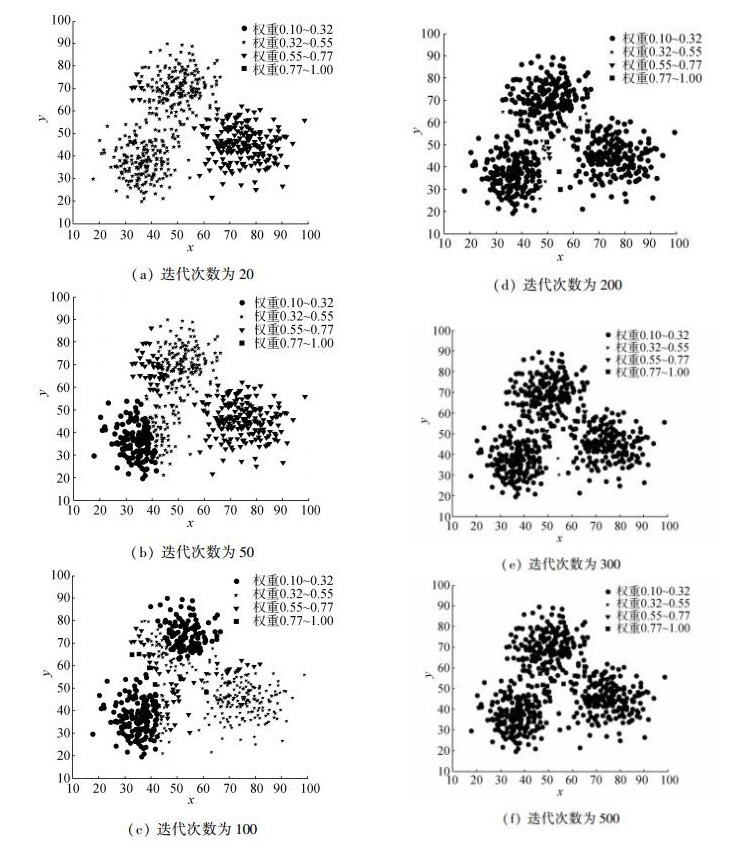
依据实验参数设置可知,训练样本权重xwi∈[0.1, 1], i=1, 2, …,m。为了可视化实验过程的训练样本权重分布,实验将权重取值范围分成[0.1, 0.32]、[0.32, 0.55]、[0.55, 0.77]、[0.77, 1]4个区间,依次使用圆圈、五角星、倒三角、正方形4种图形来标记每个区间内的训练样本, 训练样本权重分布如图 3所示。
|
| 图 3 训练样本权重分布图 Fig. 3 Training sample weight distribution graph |
分析图 3可知,随着迭代次数的增加,在变化趋势上,样本点的形状呈现两极化的趋势,处于权重中段的五角星和倒三角的样本点个数逐渐减少,处于权重两端的圆圈和正方形的样本点个数逐渐增多;在分布趋势上,远离类别边界的点最先变为圆圈,临近类别边界的点缓慢变化为圆圈,而一些位于边界附近容易错分的样本点最终变化为正方形。这说明远离类别边界或位于类别中心的核样本数据更容易被正确分类,而临近或位于类别边界的样本较难被正确分类,从而也证明基于训练错误率的样本权值能够反映样本是否为边界样本,即可以从权值上区分核样本和边界样本。
相应迭代次数下,训练数据集中通过随机数和权重比较选择的训练样本如图 4所示,图中五角星、倒三角、圆圈标记点为原始的训练样本,正方形框标记点为当前迭代次数下,选择的训练样本。

|
| 图 4 选择的训练样本分布图 Fig. 4 Selected training sample distribution map |
分析图 4可知,随着迭代次数的增加,在变化趋势上,约简后的训练样本 (正方形框样本) 逐渐减少;在分布上,约简后的正方形框样本中核样本的比重逐渐减少,边界样本的比重逐渐增大。这说明基于样本权重的数据约简方法能够筛选掉大部分核样本,保留部分核样本,弱化了核样本的作用,增加了边界样本的比重,约简数据的同时,通过保留部分核样本进行协同训练,避免了仅选择少数边界样本会造成的过拟合问题。
标准训练方法STD和动态数据约简方法DDR训练的神经网络分类器,最终形成的分类边界如图 5所示。图中白色、灰色和深灰色区域为STD方法每个类别对应的区域,区域边界即为标准训练方法训练的神经网络对应的分类边界。黑色实线为DDR方法训练的神经网络的分类边界。
对比图 5中两个神经网络分类器边界可知,DDR方法训练的神经网络分类器边界在一个更加恰当的分类位置区分各个类别,比STD方法具有更少的错分类样本,这也说明通过增加边界样本的比重,削弱核样本作用训练的神经网络分类器具有更强的分类泛化能力。
基于以上分析可知,基于样本权重的动态数据约简方法能够区分并挑选边界样本和核样本,并随着网络的迭代训练,逐渐增加边界样本比重,弱化核样本作用,从而训练出泛化能力更好的神经网络分类器。
2.3 标准数据集实验分析为了验证基于动态数据约简的神经网络训练方法在标准分类数据集上的效果,选取10组标准数据集进行数值实验,其中Forest等9组来自UCI分类数据集,Mnist标准数据集来自官方网站。各组数据集属性以及训练集,测试集样本个数信息见表 1。10组数据集中Forest、IS、SL、Mnist具有固定的分类训练集个数和测试集个数,剩余的非固定数据集,训练集和测试集个数比例基本保持1:1。
| 名称 | 样本个数 | 训练样本 | 属性个数 | 类别数 |
| Forest | 523 | 198 | 27 | 4 |
| Glass | 214 | 100 | 9 | 6 |
| IP | 180 | 90 | 34 | 2 |
| Iris | 150 | 75 | 4 | 3 |
| IS | 2 310 | 210 | 19 | 7 |
| LIR | 20 000 | 10 000 | 61 | 10 |
| Seeds | 210 | 105 | 7 | 3 |
| SL | 6 435 | 4 000 | 36 | 6 |
| Wine | 178 | 90 | 13 | 3 |
| Mnist | 60 000 | 10 000 | 784 | 10 |
在相同的实验条件下,标准训练算法 (STD) 和动态数据约简训练方法 (DDR) 训练的神经网络分类器,最终训练集均方误差loss,训练集分类错误率train-Avg,测试集分类错误率test-Avg和训练时间time,30次实验的平均结果如表 2所示。对比STD和DDR两种训练方法的最终均方误差,除Seeds数据集外,STD训练方法的均方误差均大于DDR训练方法的均方误差,说明DDR训练方法在整个训练上更加关注边界样本,弱化了对于训练样本整体的“逼近拟合”。
| 数据集名称 | Method | loss | train-Avg | test-Avg | time |
| Forest | STD | 0.007 5 | 0.07 | 15.66 | 5.34 |
| DDR | 0.011 6 | 0.00 | 15.79 | 2.11 | |
| Glass | STD | 0.036 6 | 4.47 | 35.37 | 7.70 |
| DDR | 0.050 4 | 1.63 | 33.48 | 3.29 | |
| IP | STD | 0.004 4 | 0.30 | 30.04 | 1.24 |
| DDR | 0.010 8 | 0.00 | 29.96 | 0.41 | |
| Iris | STD | 0.025 8 | 3.07 | 4.22 | 0.67 |
| DDR | 0.058 5 | 1.87 | 3.69 | 0.36 | |
| IS | STD | 0.027 4 | 3.51 | 10.14 | 2.52 |
| DDR | 0.032 6 | 1.14 | 8.72 | 1.53 | |
| LIR | STD | 0.114 1 | 12.92 | 14.41 | 122.33 |
| DDR | 0.144 6 | 8.05 | 11.01 | 77.80 | |
| SL | STD | 0.058 2 | 7.06 | 9.62 | 78.14 |
| DDR | 0.065 2 | 5.80 | 9.78 | 34.15 | |
| Seeds | STD | 0.034 0 | 3.40 | 6.44 | 1.42 |
| DDR | 0.013 2 | 0.13 | 4.98 | 3.73 | |
| Wine | STD | 0.001 0 | 0.04 | 2.65 | 0.71 |
| DDR | 0.001 7 | 0.00 | 2.50 | 0.49 | |
| Mnist | STD | 0.004 5 | 0.10 | 1.51 | 2 104.83 |
| DDR | 0.004 7 | 0.03 | 1.61 | 1 129.18 |
对比分类错误率,DDR训练方法比STD训练方法在较高的均方误差下具有更低的训练分类错误率,除Forest、SL和Mnist 3个数据集外取得相近的预测分类错误率外,DDR训练方法在其余数据集上均具有更低的测试分类错误率。综合对比均方误差和错分类错误率可知,DDR训练方法在较大的均方误差下取得了较小的训练和测试分类错误率,说明DDR训练方法更加注重边界样本的作用,具有防止过拟合的能力,能够训练分类泛化能力更好的神经网络。
对比网络训练时间,DDR训练方法具有更短的训练时间。由于每个数据集的训练样本个数,迭代次数、批量值、权重下限值等训练参数不同,所以相对STD训练方法,DDR训练方法时间缩短程度有所不同,总体上选择的权重下限值和学习批量越小,DDR训练方法所需的训练时间越短,但过小的权重下限值和学习批量,容易引起网络波动,使得网络的分类泛化能力较差。
基于以上对比分析可知,相对标准的神经网络训练方法STD,动态数据约简的神经网络训练方法DDR是一种收敛速度更快、分类泛化能力更好的神经网络训练方法。
3 结论与展望动态数据约简神经网络训练方法 (DDR) 利用神经网络迭代训练的特性,借助训练样本权值,实现了单阶段动态地约简训练样本。通过奖励错分类样本的权值,惩罚正确分类样本权值的权值更新规则,依据权值来约简训练样本,在减少训练样本的同时,增加了对于分类影响较大的边界样本的作用,弱化了冗余核样本的作用。通过人工数据集实验可视化分析可知:基于分类错误率的权值更新方式,能够利用权值有效地区分训练集中的边界样本和核样本,基于权值的数据约简规则,可以剔除冗余核样本,增加边界样本的比重。通过标准数据集实验可知:基于动态数据约简的神经网络训练方法是一种收敛速度更快、分类泛化能力更强的神经网络训练方法。但动态约简神经网络训练方法相对于标准神经网络训练方法需要调节权重下限值,权重增量值等参数,增加了网络训练的复杂性,后续研究可围绕约简参数的自适应调节展开,以简化动态约简神经网络训练方法参数。
| [1] | 毛勇. 基于支持向量机的特征选择方法的研究与应用[D]. 杭州: 浙江大学, 2006. MAO Yong. A study on feature selection algorithms based on support vector machine and its application[D]. Hangzhou: Zhejiang University, 2006. |
| [2] |
覃政仁, 吴渝, 王国胤. 一种基于Rough Set的海量数据分割算法[J].
模式识别与人工智能, 2006, 19(2): 249-256.
QIN Zhengren, WU Yu, WANG Guoyin. A partition algorithm for huge data sets based on rough set[J]. Pattern recognition and artificial intelligence, 2006, 19(2): 249-256. |
| [3] | ABDI H, WILLIAMS L J. Principal component analysis[J]. Wiley interdisciplinary reviews: computational statistics, 2010, 2(4): 433-459. DOI:10.1002/wics.v2:4. |
| [4] | RIFAI S, VINCENT P, MULLER X, et al. Contractive auto-encoders: explicit invariance during feature extraction[C]//Proceedings of the 28th International Conference on Machine Learning. Bellevue, WA, USA: ICML, 2011. |
| [5] |
周玉, 朱安福, 周林, 等. 一种神经网络分类器样本数据选择方法[J].
华中科技大学学报:自然科学版, 2012, 40(6): 39-43.
ZHOU Yu, ZHU Anfu, ZHOU Lin, et al. Sample data selection method for neural network classifier[J]. Journal of Huazhong university of science and technology: natural science edition, 2012, 40(6): 39-43. |
| [6] |
郝红卫, 蒋蓉蓉. 基于最近邻规则的神经网络训练样本选择方法[J].
自动化学报, 2007, 33(12): 1247-1251.
HAO Hongwei, JIANG Rongrong. Training sample selection method for neural networks based on nearest neighbor rule[J]. Acta automatica sinica, 2007, 33(12): 1247-1251. |
| [7] | HARA K, NAKAYAMA K. A training method with small computation for classification[C]//Proceedings of the IEEE-INNS-ENNS International Joint Conference on Neural Networks. Como, Italy: IEEE, 2000: 543-548. |
| [8] | 邓乃扬, 田英杰. 数据挖掘中的新方法——支持向量机[M]. 北京: 科学出版社, 2004. |
| [9] |
刘刚, 张洪刚, 郭军. 不同训练样本对识别系统的影响[J].
计算机学报, 2005, 28(11): 1923-1928. .
LIU Gang, ZHANG Honggang, GUO Jun. The influence of different training samples to recognition system[J]. Chinese journal of computers, 2005, 28(11): 1923-1928. DOI:10.3321/j.issn:0254-4164.2005.11.020. |
| [10] | SCHAPIRE R E, SINGER Y. Improved boosting algorithms using confidence-rated predictions[J]. Machine learning, 1999, 37(3): 297-336. DOI:10.1023/A:1007614523901. |
| [11] | 韦岗, 贺前华. 神经网络模型学习及应用[M]. 北京: 电子工业出版社, 1994. |



