2. 上海大学 微电子研究与开发中心,上海 200010
2. Microelectronic Research and Development Center, Shanghai University, Shanghai 200010, China
自主机器人和无人驾驶车成为近几年来人工智能领域研究的新热点,该技术在服务业、交通运输、工业、环境勘探、国防以及生活各个方面都有着广阔的应用前景。同时德国工业4.0及中国制造2025也把焦点聚集在无人化和智能化,智能产业正在迎来前所未有的发展机遇,将催生庞大的市场。SLAM(同时定位和地图创建,simultaneous localization and mapping, )是自主机器人和无人驾驶车领域的关键技术。当前SLAM的实现方案可以分为基于概率的方案[1-3]和基于非概率的方案[4-5]。ICP(最近邻点迭代,iterative closest point)-SLAM作为基于非概率的方案之一,由于其具有原理简单、成本较低等优点而得到了广泛关注[6-8]。并且相比于传统的导航技术,如蓝牙定位、惯性导航系统等[9-11],ICP-SLAM不仅能实现定位,还能实现地图创建。但随着自主机器人和无人驾驶车的速度越来越快,所处环境变得越来越复杂,这对SLAM实时性提出了更高要求。由于传统ICP-SLAM实时性差,同时建模精度和鲁棒性也不高,显然不能再满足这方面的要求。造成传统ICP-SLAM实时性差的原因:一方面,因为传统ICP算法不能提供初始姿态矩阵进行粗匹配,从而导致达到收敛条件的迭代次数大量增加; 另一方面,由于缺少粗匹配,必须通过全局搜索才能完成匹配点搜索,这也大大增加了计算开销,降低了传统ICP-SLAM实时性。因此,为了提高ICP-SLAM的实时性,必须对传统ICP-SLAM进行优化。
当前,对传统ICP-SLAM的优化大都是选取ICP算法的某个步骤进行优化。ICP算法最早由Besl和Mckay为解决3-D物体对准问题而提出的[12]。根据Rusinkiewicz和Levoy的理论[13],ICP算法可以分成下面6个步骤:选择控制点,匹配点搜索,计算匹配点权重,设定一个匹配点误差方程,通过最小化匹配点误差方程求出旋转矩阵和平移矩阵,同时定位和地图创建。当前ICP算法的研究主要集中在优化匹配点搜索策略上。主流的匹配点搜索策略可以大致分为下面几种。基于特征的匹配点搜索方法[14-16]包括如基于直线特征、基于曲率特征和基于斜率特征等, 该方法在提取几何特征时增加了额外的计算开销,降低了ICP-SLAM实时性。并且几何特征的提取容易受测量噪声和移动物体的影响,降低了ICP-SLAM的鲁棒性。另外, 基于几何划分的匹配点搜索也被广泛引用,如Delaunay划分[17]和K-D树划分[18]。几何划分可以提高匹配点搜索的质量和效率。但当相邻两帧的重叠区域很小时,该方法则不再适用。除此之外,考虑到激光雷达作为ICP-SLAM的主要传感器,所以为了能更好地利用激光雷达特殊的数据结构,提出了基于Polar-Cartesian Hybrid Transforms的Polar Point Matching Rule方法[19]。该方法通过在极坐标系下,寻找相近的旋转角度,实现了快速的匹配点搜索。但该方法并不能提供初始姿态矩阵实现粗匹配,所以仍然采用全局搜索实现匹配点搜索。综上,可以看出大多数ICP算法都采用了全局搜索。但随着全局地图的扩大,全局搜索会导致计算消耗量的累计效应。虽然局部ICP-SLAM[20-21]某种程度上可以解决这个问题,但是局部ICP-SLAM首先把全局地图划分成多个局部地图,然后对每个局部地图进行局部ICP-SLAM。所以,局部ICP-SLAM的本质上还是采用了全局搜索。并且局部ICP-SLAM还要保存各个局部地图的相对位置,增加了额外内存开销。
综上所述,为了有效提高ICP-SLAM的实时性,本文提出基于粗匹配和局部尺度压缩搜索的快速ICP-SLAM。该快速ICP-SLAM在激光雷达的基础上增加了MEMS磁力计,这个MEMS磁力计能直接输出当前航向角。并且引入全局地标,通过激光雷达扫描并测量全局地标,计算出机器人当前的位置信息。最后由航向角和机器人当前的位置信息共同构成完整的初值姿态矩阵。当得到了初值姿态矩阵后,首先通过该初值姿态矩阵实现当前帧和全局地图的粗匹配。其次,在ICP算法的每次迭代中,采用局部尺度压缩搜索完成匹配点搜索,从而避免了由全局搜索带来的巨大计算开销。同时,每次迭代完成之后,匹配点的搜索范围通过动态阈值被缩小,加快匹配点搜索的速度,这将进一步提高ICP-SLAM实时性。实验结果显示,本文提出的快速ICP-SLAM相比于传统ICP-SLAM,迭代次数减少了92.34%,ICP算法运行时间减少了98.86%。同时,ICP-SLAM的系统负载也被控制在稳定状态,其整体性能得到较大的改善。
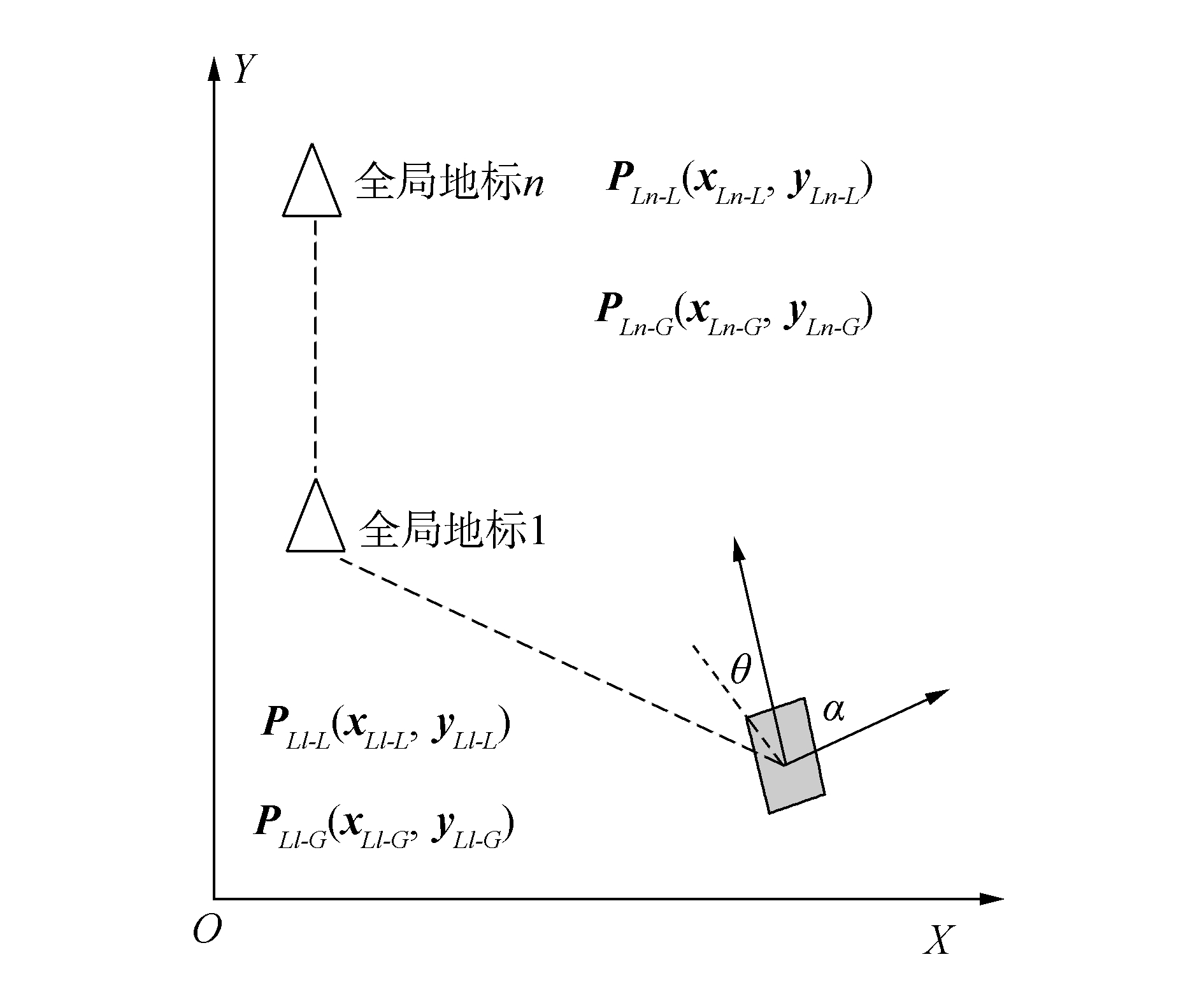
1 基于初始位姿矩阵的粗匹配从上述分析可以看出,粗匹配是实现快速ICP-SLAM的首要步骤。粗匹配的过程为:通过旋转和平移变换,使得两个形状类似但处于不同空间位置的物体大致重合。这是因为,当形状相同的两个物体处于二维平面的不同位置时,必然能找到一个平移矩阵和旋转角使得这两个物体完全重合。而机器人的初始位姿矩阵就包含了这样一个平移矩阵和旋转角。其中,机器人当前的坐标(xt, yt)可以看作平移矩阵,机器人的航向角θt可以看作旋转角。那么机器人t时刻的姿态矩阵可以表示成一个1×3矩阵Poset(xt, yt, θt)。Poset(xt, yt, θt)可以通过MEMS磁力计和全局地标计算得到。这样在ICP算法开始前,可以通过矩阵Poset(xt, yt, θt)完成当前帧和全局地图的粗匹配。全局地标在全局坐标系中的坐标为已知信息,设图 1中的第n个全局地标在全局坐标系中的坐标为PLn-G(xLn-G, yLn-G)。同时设第n个全局地标在机器人局部坐标系的坐标为PLn-L(xLn-L, yLn-L),则(xt, yt)可以通过式(1) 计算得到:
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{x}}_t} = {\mathit{\boldsymbol{x}}_{Ln - G}} - {\mathit{\boldsymbol{x}}_{Ln - L}}\cos {\mathit{\boldsymbol{\theta }}_t} - {\mathit{\boldsymbol{y}}_{Ln - L}}\sin {\mathit{\boldsymbol{\theta }}_t}\\ {\mathit{\boldsymbol{y}}_t} = {\mathit{\boldsymbol{y}}_{Ln - G}} + {\mathit{\boldsymbol{y}}_{Ln - L}}\sin {\theta _t} - {\mathit{\boldsymbol{y}}_{Ln - L}}\cos {\theta _t} \end{array} \right. $ | (1) |
|
图 1 计算姿态矩阵 Fig.1 Initial pose matrix |
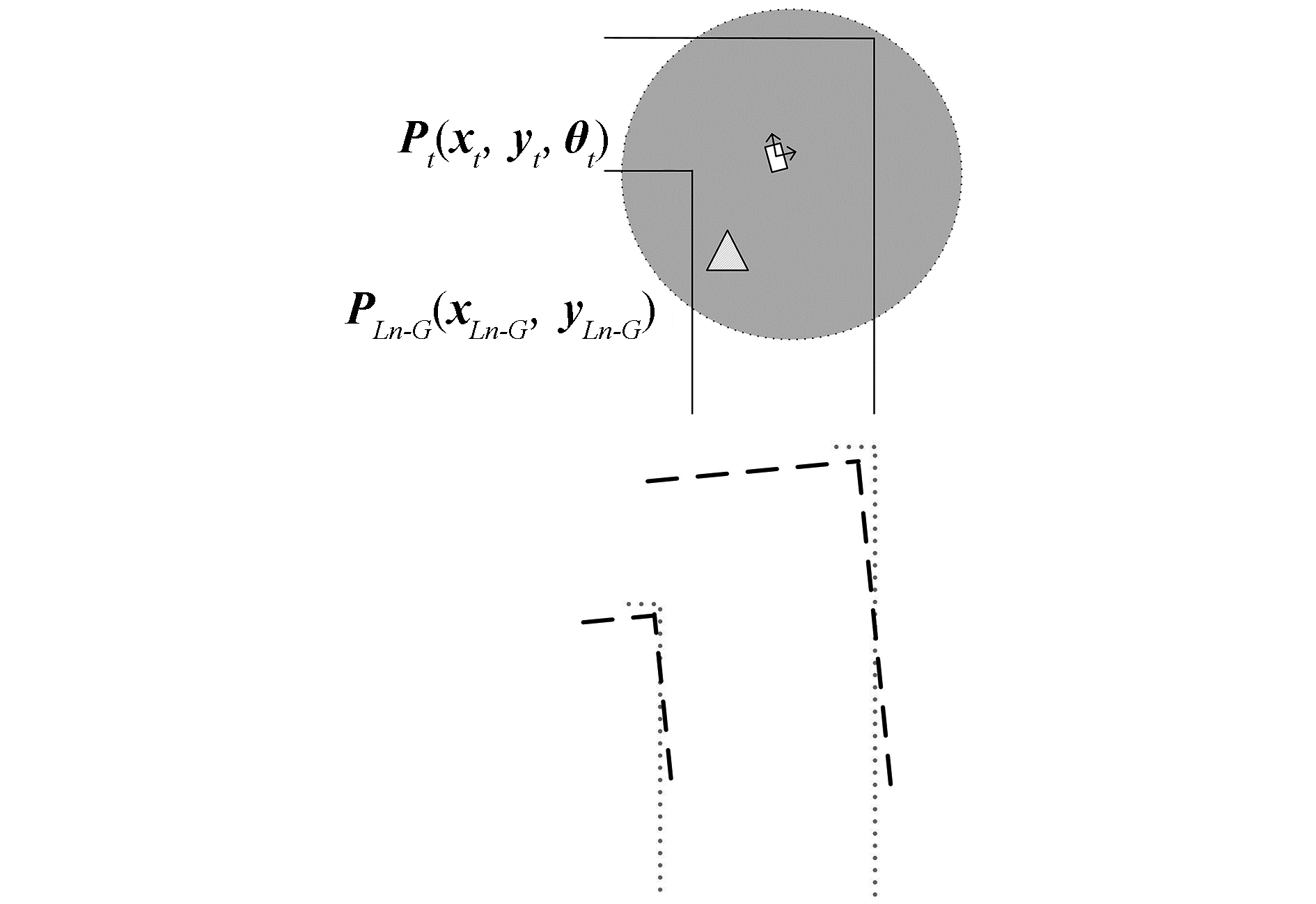
当机器人移动到图 2中的(xt, yt)位置时,设其姿态矩阵为Poset(xt, yt, θt)。激光雷达获取当前扫描帧并记为Ft′(图 2中的灰色圆部分),并测出第n个全局地标在机器人局部坐标系下的坐标PLn-L(xLn-L, yLn-L)。假设激光雷达的角度分辨率为ρ,则Ft′中的点数N可通过式(2) 得到
|
图 2 粗匹配示意图 Fig.2 Rough align |
| $ N = \varphi /\rho $ | (2) |
式中φ为激光雷达的可视角(例如360°)。根据(1) 式可计算出(xt, yt),如式(3) 所示:
| $ \left[ \begin{array}{l} {\mathit{\boldsymbol{x}}_t}\\ {\mathit{\boldsymbol{y}}_t} \end{array} \right] = \mathit{\boldsymbol{T}}{\mathit{\boldsymbol{P}}_{Ln - L}} + {\mathit{\boldsymbol{P}}_{Ln - G}} $ | (3) |
式中T如公式(4) 所示:
| $ \mathit{\boldsymbol{T}} = \left[ {\begin{array}{*{20}{c}} { - \cos {\mathit{\boldsymbol{\theta }}_t}}&{ - \sin {\mathit{\boldsymbol{\theta }}_t}}\\ {\sin {\mathit{\boldsymbol{\theta }}_t}}&{ - \cos {\mathit{\boldsymbol{\theta }}_t}} \end{array}} \right] $ | (4) |
因为全局地标为全局的静态参照物,所以通过该方法计算得到的Poset(xt, yt, θt)不存在累计误差。
同样在图 2中记全局地图为Mglobal(图 2中的点线),并记Ft′和Mglobal粗匹配的结果为Ft(图 2中的虚线),结合式(5),则Ft可以通过式(6) 得到,其中Ft′和Ft都是一个N×2矩阵,如式(7) 和式(8) 所示:
| $ {\mathit{\boldsymbol{T}}_{{\rm{rotate}}}} = \left[ {\begin{array}{*{20}{c}} {\cos {\mathit{\boldsymbol{\theta }}_t}}&{\sin {\mathit{\boldsymbol{\theta }}_t}}\\ { - \sin {\mathit{\boldsymbol{\theta }}_t}}&{\cos {\mathit{\boldsymbol{\theta }}_t}} \end{array}} \right] $ | (5) |
| $ {\mathit{\boldsymbol{F}}_t} = {\mathit{\boldsymbol{F}}_t}^\prime {\mathit{\boldsymbol{T}}_{{\rm{rotate}}}} + {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{x}}_t}}&{{\mathit{\boldsymbol{y}}_t}}\\ {{\mathit{\boldsymbol{x}}_t}}&{{\mathit{\boldsymbol{y}}_t}}\\ \vdots & \vdots \\ {{\mathit{\boldsymbol{x}}_t}}&{{\mathit{\boldsymbol{y}}_t}} \end{array}} \right]_{N \times 2}} $ | (6) |
| $ {\mathit{\boldsymbol{F}}_t}^\prime = \left[ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{x'}}}_1}}&{{{\mathit{\boldsymbol{y'}}}_1}}\\ {{{\mathit{\boldsymbol{x'}}}_2}}&{{{\mathit{\boldsymbol{y'}}}_2}}\\ \vdots & \vdots \\ {{{\mathit{\boldsymbol{x'}}}_N}}&{{{\mathit{\boldsymbol{y'}}}_N}} \end{array}} \right] $ | (7) |
| $ {\mathit{\boldsymbol{F}}_t} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{x}}_1}}&{{\mathit{\boldsymbol{y}}_1}}\\ {{\mathit{\boldsymbol{x}}_2}}&{{\mathit{\boldsymbol{y}}_2}}\\ \vdots & \vdots \\ {{\mathit{\boldsymbol{x}}_N}}&{{\mathit{\boldsymbol{y}}_N}} \end{array}} \right] $ | (8) |
通过粗匹配后,ICP算法达到收敛条件的迭代次数将会大大减小。最后, 当ICP算法达到收敛条件时,得到最终的变换矩阵Tt(xtT, ytT, θtT)。
2 基于动态阈值的局部尺度压缩搜索粗匹配完成之后,当前帧中的点和其匹配点的距离被大大缩小,所以本文中的匹配点搜索将通过局部搜索完成。同时,每次迭代完成之后,匹配点之间的距离都比上一次迭代时更小,此时便可以通过动态阈值达到尺度压缩,从而缩小匹配点搜索的范围。局部尺度压缩搜索不仅能加快匹配点搜索速度,还能提高匹配点搜索质量。同时在本文中,因为SLAM创建的地图为栅格地图,所以本小节将先阐述本文中采用的栅格地图的坐标表征方式,接着再详细剖析局部搜索和尺度压缩。
2.1 栅格地图的坐标表征SLAM创建栅格地图时,栅格地图中的某个单元格只能处于两种状态中的一种:被物体占据或没有被物体占据。当单元格被物体占据时用深色表示,单元格没有被物体占据时用浅色表示。在栅格地图中,水平面被分割为一个包含m×n个正方形单元格平面,记正方形单元格边长为L,并设栅格地图能表示的范围为x^min, x^max, y^min, y^max,同时把正方形单元格的几何中心作为该正方形单元格的坐标。在图 3中,阴影正方形单元格的坐标(xblack, yblack)可以表示为
| $ \left( {{\mathit{\boldsymbol{x}}_{{\rm{black}}}},{\mathit{\boldsymbol{y}}_{{\rm{black}}}}} \right) = \left( {3.5\mathit{\boldsymbol{L}},3.5\mathit{\boldsymbol{L}}} \right) $ | (9) |

|
图 3 栅格地图示意图 Fig.3 Grid map |
同时可以把该阴影正方形单元格在栅格地图中的标号(xi-black, yi-black)表示为
| $ \begin{array}{l} \left( {{\mathit{\boldsymbol{x}}_{i - {\rm{black}}}},{\mathit{\boldsymbol{y}}_{i - {\rm{black}}}}} \right) = \left( {\left\langle {{\mathop{\rm int}} } \right\rangle \left( {{\mathit{\boldsymbol{x}}_{{\rm{black}}}} - \mathit{\boldsymbol{x}}_{\min }^ \wedge } \right)/\mathit{\boldsymbol{L}},} \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {\left\langle {{\mathop{\rm int}} } \right\rangle \left( {{\mathit{\boldsymbol{y}}_{{\rm{black}}}} - \mathit{\boldsymbol{y}}_{\min }^ \wedge } \right)/\mathit{\boldsymbol{L}}} \right) \end{array} $ | (10) |
当有更多的点落入到某一个正方形单元格时,该正方形单元格的颜色会加深。
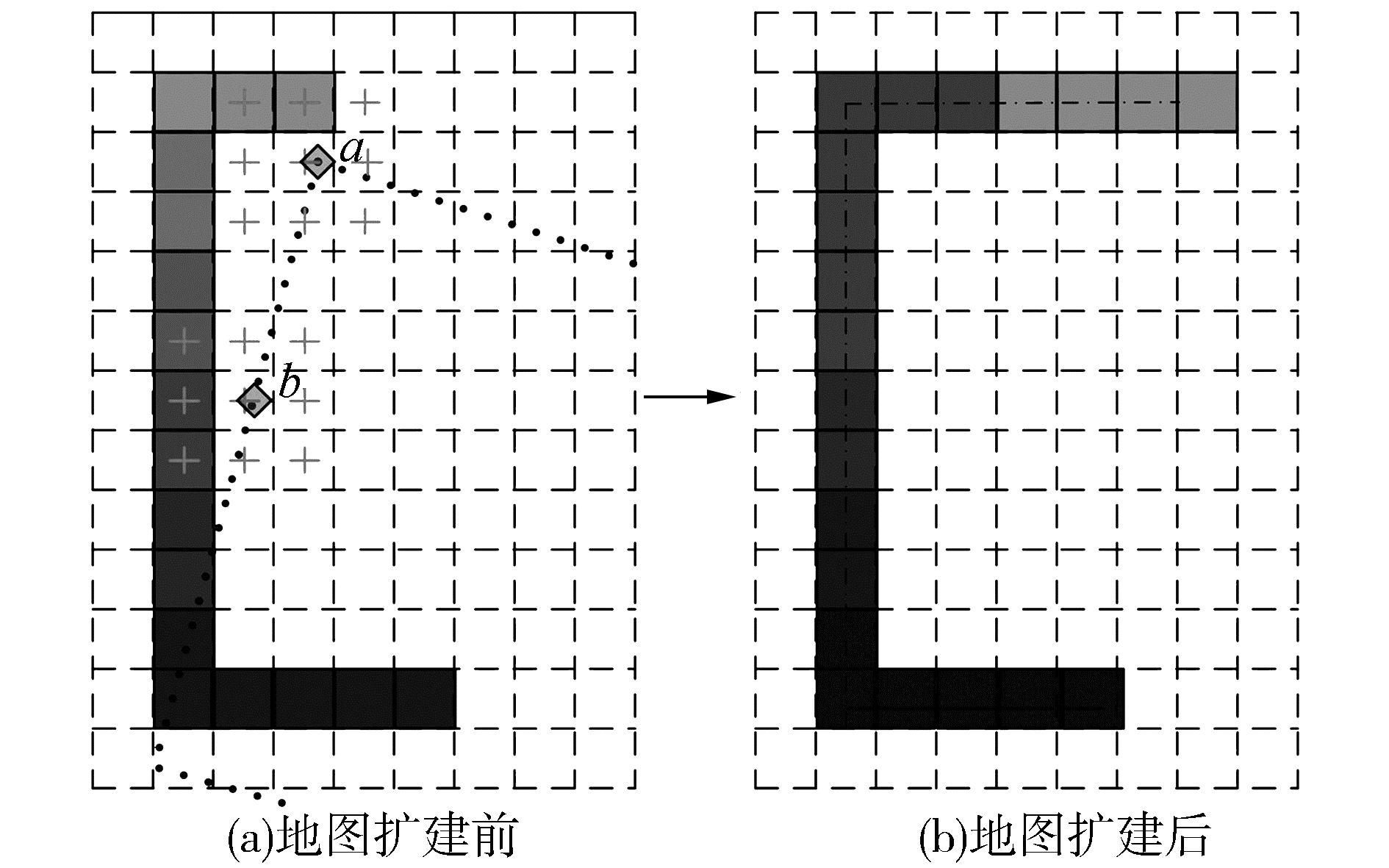
2.2 基于Point-to-Region的局部搜索局部搜索只有当完成粗匹配后才有意义。因为经过粗匹配后,当前帧中的某一点的匹配点只能出现在距离该点某一距离的范围内。所以为了能采用局部搜索,必须在匹配点搜索前,将Ft′通过Poset(xt, yt, θt)和(5) 式投影到Mglobal(记为Ft),然后再在Mglobal和Ft之间通过局部搜索完成匹配点搜索。以图 4中的a点和b点为例,通过式(9) 计算出a点和b点所在正方形单元的标号,记为(cxa, cya)和(cxb, cyb)。局部搜索的搜索范围可以表示为
|
图 4 扩建栅格地图 Fig.4 Grid map expansion |
| $ c\mathit{\boldsymbol{x}}_{\min }^ \wedge = c{\mathit{\boldsymbol{x}}_x} - {\rm{SearchingRange}} $ | (11) |
| $ c\mathit{\boldsymbol{x}}_{\max }^ \wedge = c{\mathit{\boldsymbol{x}}_x} + {\rm{SearchingRange}} $ | (12) |
| $ c\mathit{\boldsymbol{y}}_{\min }^ \wedge = c{\mathit{\boldsymbol{y}}_x} - {\rm{SearchingRange}} $ | (13) |
| $ c\mathit{\boldsymbol{y}}_{\max }^ \wedge = c{\mathit{\boldsymbol{y}}_x} + {\rm{SearchingRange}} $ | (14) |
其中SearchingRange的值是自己设定的, 在图 4中SearchingRange的值为1。在确定搜索范围后,下一步便计算出点a/b与所有落在搜索范围内的点的欧式距离di。当di满足:
| $ {d_i} < {\rm{thresholdDist}} $ | (15) |
则记该点为匹配点(Point-to-Region策略,即一个点可以存在多个匹配点)。比如Ft中的第j个点表示为Ft(j),则Ft(j)的第i个匹配点记为
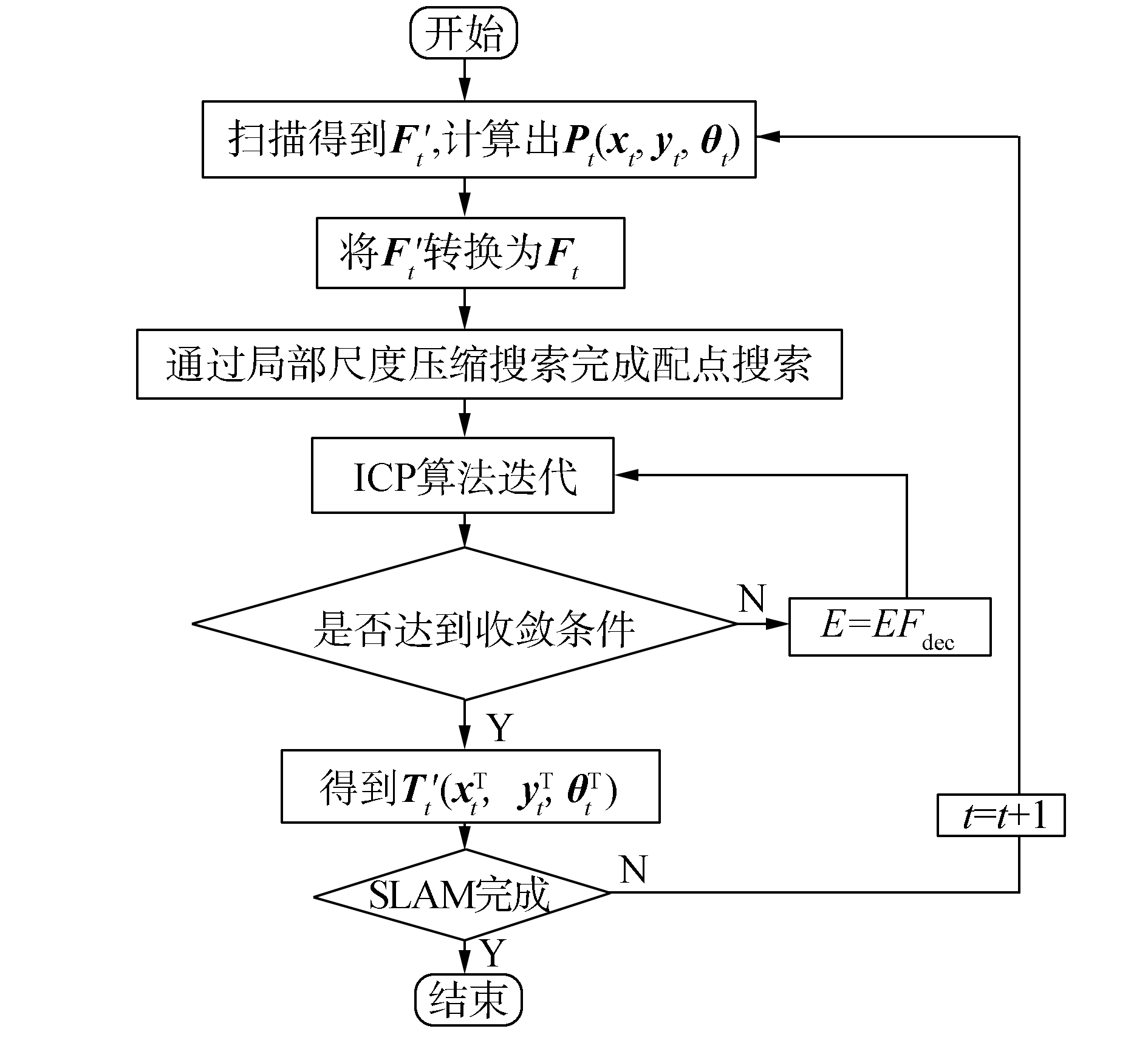
ICP算法的最终目的是为了得到一个平移矩阵和旋转角。所以当完成匹配点搜索后,下一步便是通过最小化匹配点误差方程得到平移矩阵和旋转角。但在得到最终的平移矩阵和旋转角之前,当ICP算法完成一次迭代之后,当前帧和全局地图的匹配能更加准确。这意味着,Ft中的点与其匹配点之间的距离缩短。所以ICP算法在下一次的匹配点搜索中,搜索范围可以缩小。这不但可以减小匹配点搜索的计算量,还能减少误匹配。完整的算法流程如图 5所示。
|
图 5 算法总流程图 Fig.5 Algorithm flow chart |
本文将选择匹配点之间的欧式距离作为匹配点误差方程,匹配点的欧式距离如式(16):
| $ \begin{array}{l} e_t^i\left( j \right) = {\left( {x\left[ {\mathop {\mathit{\boldsymbol{F}}_t^i\left( j \right)}\limits^{{\rm{match}}} } \right] - x\left[ {{\mathit{\boldsymbol{F}}_t}\left( j \right)} \right]} \right)^2} + \\ \;\;\;\;\;\;\;\;\;\;{\left( {y\left[ {\mathop {\mathit{\boldsymbol{F}}_t^i\left( j \right)}\limits^{{\rm{match}}} } \right] - y\left[ {{\mathit{\boldsymbol{F}}_t}\left( j \right)} \right]} \right)^2} \end{array} $ | (16) |
匹配点的权重通过式(17) 计算:
| $ w_t^i\left( j \right) = \left\{ \begin{array}{l} 0,\;\;\;\;\left| {e_t^i\left( j \right)} \right| \ge E\\ 1,\;\;\;\;\;其他 \end{array} \right. $ | (17) |
式中E为动态阈值。匹配点的数量为
| $ {n_t} = \sum\limits_{j = 0}^N {\sum\limits_i {w_t^i\left( j \right)} } $ | (18) |
当前帧与全局地图的重合度可以表示为
| $ {\rm{O}}{{\rm{L}}_t} = \frac{{{n_t}}}{{N + 1}} $ | (19) |
综上,最终的误差方程可以表示为
| $ {I_t} = \frac{{\sum\limits_{j = 0}^N {\sum\limits_i {\left[ {w_t^i\left( j \right)e_t^i\left( j \right)} \right]} } }}{{{n_t}{\rm{O}}{{\rm{L}}_t}}} $ | (20) |
通过求导可以完成(20) 式的最小化,得出变换矩阵(xtnew, ytnew, θtnew):
| $ \frac{{\partial {I_t}}}{{\partial {x_t}}} = 0 \Rightarrow x_t^{{\rm{new}}} $ | (21) |
| $ \frac{{\partial {I_t}}}{{\partial {\mathit{\boldsymbol{y}}_t}}} = 0 \Rightarrow \mathit{\boldsymbol{y}}_t^{{\rm{new}}} $ | (22) |
| $ \frac{{\partial {I_t}}}{{\partial {\mathit{\boldsymbol{\theta }}_t}}} = 0 \Rightarrow \mathit{\boldsymbol{\theta }}_t^{{\rm{new}}} $ | (23) |
完成一次迭代之后,E通过下式被缩小:
| $ E = E{F_{{\rm{dec}}}},\;\;\;{F_{{\rm{dec}}}} \in \left( {0,1} \right) $ | (24) |
当It达到阈值后,ICP算法停止并得到最终的变换矩阵Tt(xtT, ytT, θtT)。Ft通过该变换矩阵转换成Ftc(图 4中的虚线),并最终实现Mglobal的扩建。
3 实验结果与分析为了有效验证粗匹配和局部尺度压缩搜索对ICP-SLAM实时性的改善,本文搭建了一辆可定位的小车作为验证平台。该小车搭载了一个RobotPeak激光雷达、一个Uranus MEMS磁力计和一块Raspberry Pi主板,如图 6所示,各传感器规格见表 1。

|
图 6 实验平台 Fig.6 Experiment platform |
| 表 1 RobotPeak激光雷达和Uranus MEMS磁力计参数 Tab.1 Features of Robot Peak and Uranus MEMS |
本小节将从两方面验证快速ICP-SLAM。第一方面是快速ICP-SLAM实时性改善验证。首先,对比未进行粗匹配和进行粗匹配下ICP-SLAM的迭代次数和ICP算法运行时间,验证粗匹配对ICP-SLAM实时性的改善; 其次,记录Fdec的值从1到0.3变化过程中ICP-SLAM的迭代次数和ICP算法运行时间,观察其变化趋势,进而验证局部尺度压缩搜索对ICP-SLAM实时性的改善。第二方面是快速ICP-SLAM整体性改善验证。其不仅可以验证同时采用粗匹配和局部尺度压缩搜索时,ICP-SLAM实时性的改善情况,同时还可以验证ICP-SLAM在建模精度、鲁棒性和计算开销等方面的提升。
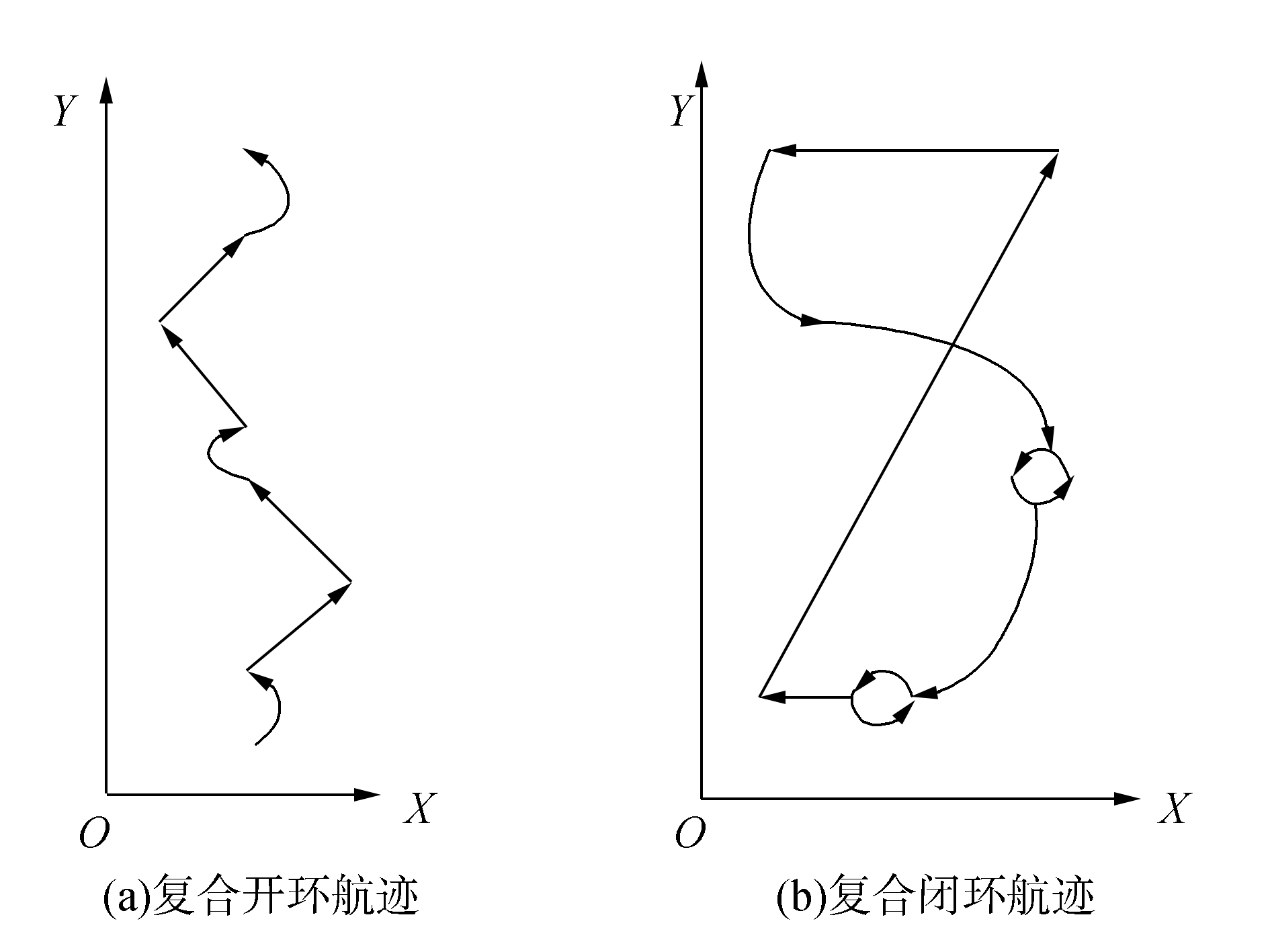
3.1 快速ICP-SLAM实时性改善验证通过第1节和第2节的分析可知,ICP-SLAM实时性受初始姿态矩阵、局部搜素和参数Fdec影响。本小节将采用复合开环航迹和复合闭环航迹,验证粗匹配和局部尺度压缩搜索对ICP-SLAM实时性的改善。复合开环航迹和复合闭环航迹分别如图 7中的(a)和(b)所示。
|
图 7 复合开环航迹和复合闭环航迹 Fig.7 Mix-open track and mix-close track |
粗匹配对迭代次数和ICP算法运行时间的改善如表 2和表 3所示。
| 表 2 小车在复合开环航迹下的实验结果 Tab.2 Result in mix-open track |
| 表 3 小车在复合闭环航迹下的实验结果 Tab.3 Result in mix-close track |
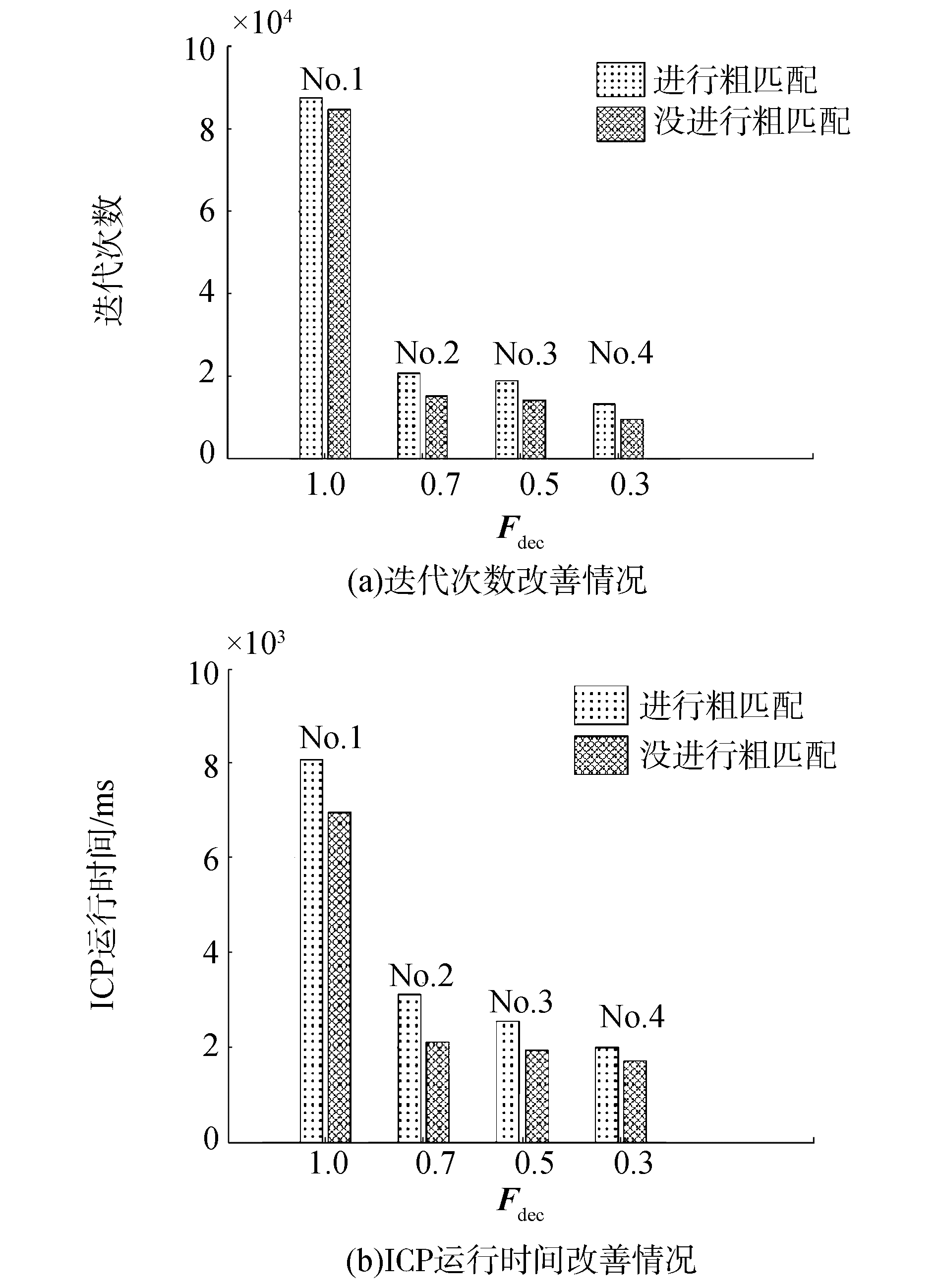
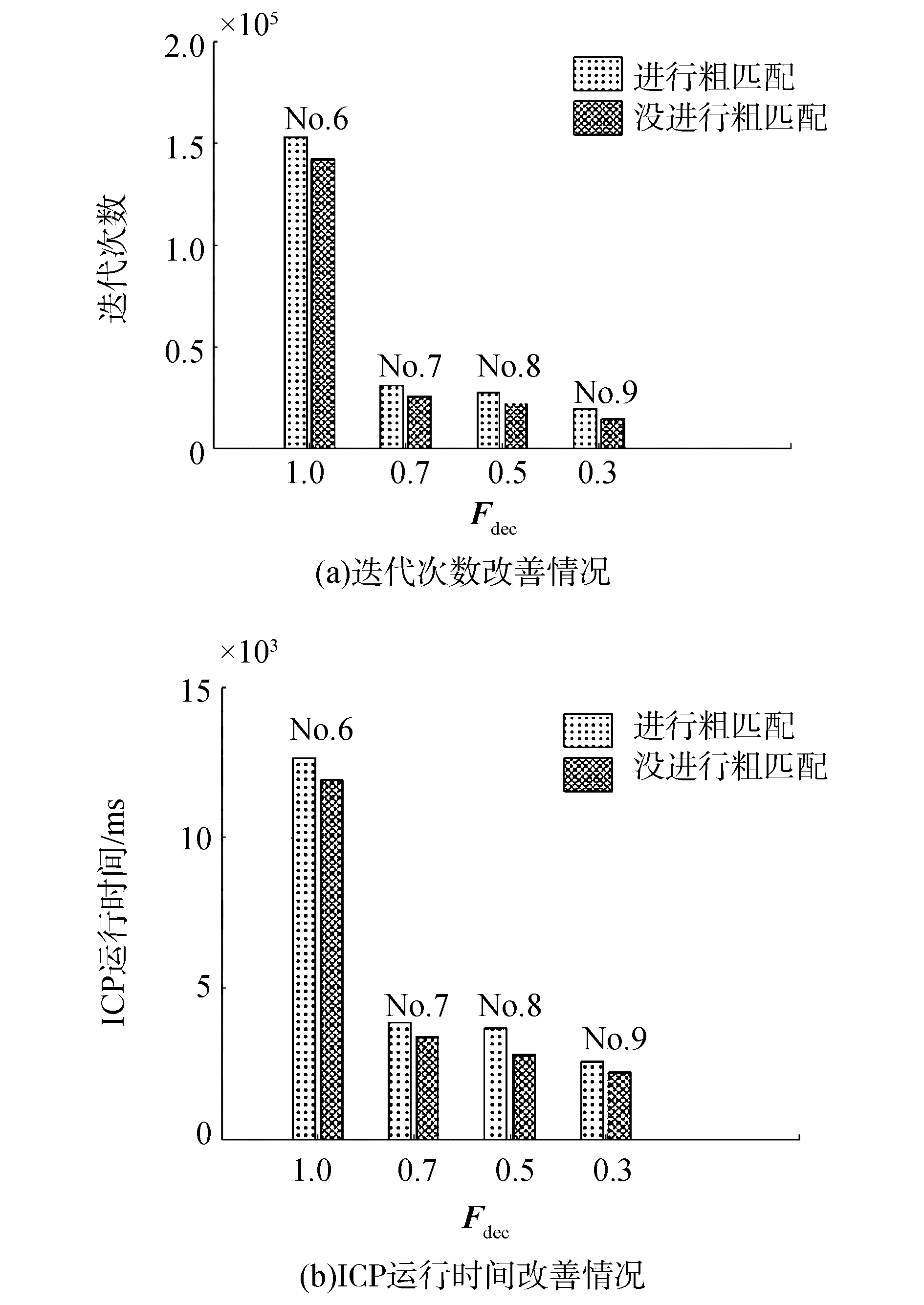
从表 2和表 3中可以看出,在每一组对比实验中,当进行粗匹配后,迭代次数和ICP算法运行时间都被大大减小。所以粗匹配改善了ICP-SLAM实时性。局部尺度搜索对迭代次数和ICP算法运行时间的提升结果如图 8和图 9所示, 从图中可以看出当Fdec从1渐变到0.3时,大大减少迭代次数,缩短了ICP算法的运行时间。
|
图 8 Fdec在复合开环航迹下的实验结果 Fig.8 Result of Fdec in mix-open track |
|
图 9 Fdec在复合闭环航迹下的实验结果 Fig.9 Result of Fdec in mix-close track |
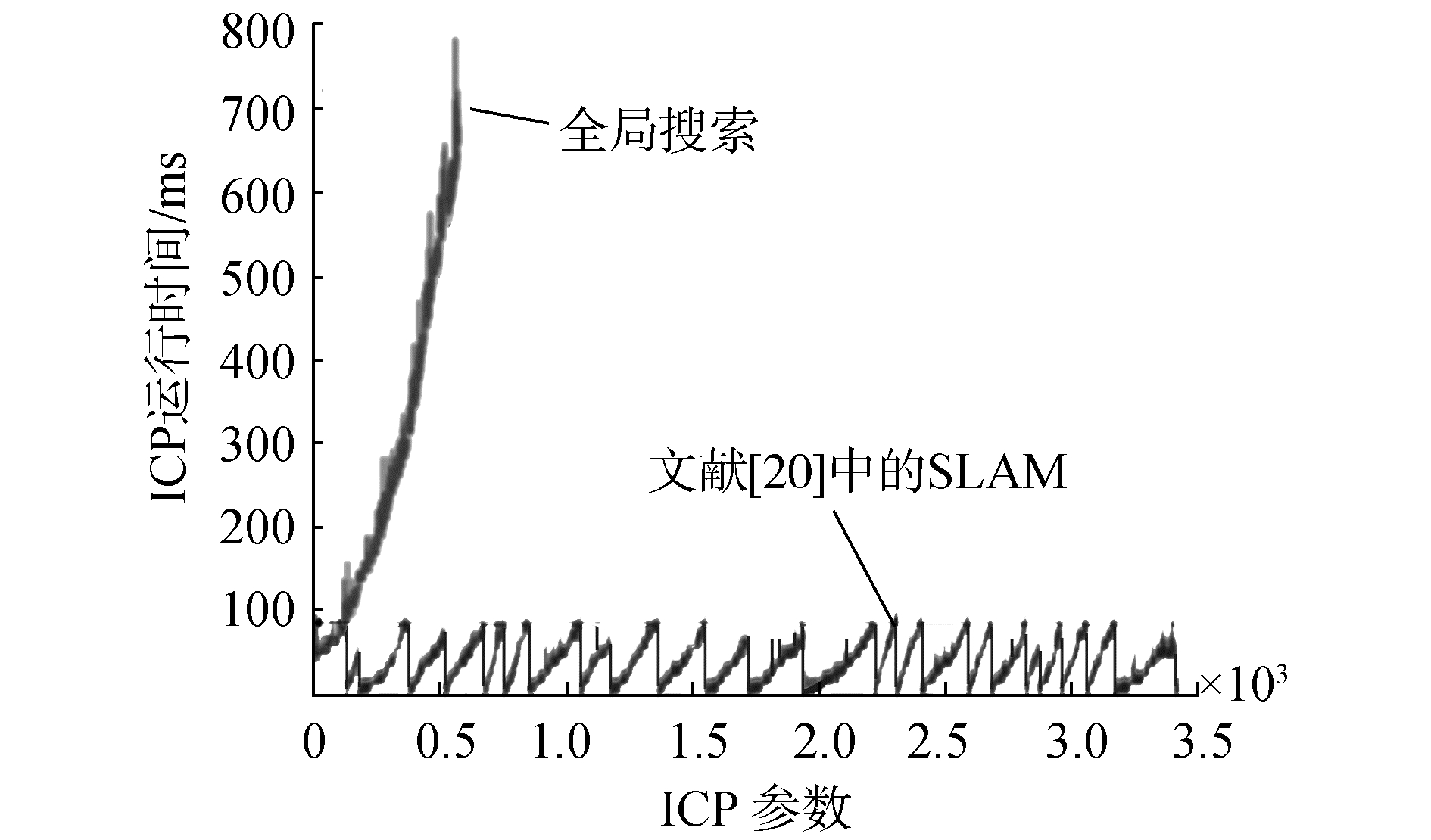
除此之外,采用全局搜索时,ICP-SLAM的计算开销会随着全局地图的增大而增大。但当采用局部尺度压缩搜索时,ICP-SLAM的计算开销被控制在稳定状态,如图 10所示。

|
图 10 ICP-SLAM的计算开销对比 Fig.10 Comparison of computation in ICP-SLAM |
从图 10中可以看出,当采用局部尺度压缩搜索时,随着ICP算法迭代次数的增加,ICP算法的运行时间被保持在一个稳定值,这表明ICP-SLAM的计算开销被控制在稳定状态。但采用全局搜索时,ICP-SLAM的计算开销却随着ICP算法迭代次数的增加而不断增加。所以局部尺度压缩搜索对提高ICP-SLAM实时性有着显著的效果。对比图 10和图 11可知,本文提出的ICP-SLAM比文献[20]的局部SLAM在计算负载的稳定性上更有优势。
3.2 快速ICP-SLAM整体性改善验证在该验证环节中,实验平台首先以低速走过一段弧度较小曲线,用来验证Pt(xt, yt, θt)的作用。然后快速走完一段直线,用来验证(xt, yt)的作用。接着作一个急速转弯,此时θt会产生巨大的变化。最后一段小车慢速走过一段短直线和慢速转弯。图 12为对比结果。在图 12(a)的方法中,ICP算法开始时会采用粗匹配,并且通过局部尺度压缩搜索来完成匹配点搜索(Fdec=0.5)。图 12(b)中的对照组为传统的ICP-SLAM算法。完成整个SLAM过程中,图 12(a)的方法总共进行了28 200次迭代,ICP算法运行时间为4 414 ms。图 12(b)中的方法进行了399 109次迭代,ICP算法运行时间为301 152 ms。可见, 图 12(a)的方法比图 12(b)的方法减少了92.34%的迭代次数和98.86%的运行时间。此外,在图 12(a)方法的结果中,累积误差被大大消除了,创建的地图精度也比图 12(b)的好,并且没有出现匹配ICP算法失锁。综上,图 12(a)的方法不仅提高了ICP-SLAM实时性,而且ICP-SLAM的整体性能得到很大的提升。

|
图 12 快速ICP-SLAM整体性改善验证结果 Fig.12 Overall improvement in fast ICP-SLAM |
针对传统ICP-SLAM实时性差,本文提出了粗匹配和局部尺度压缩搜索。在进行ICP算法开始之前,通过MEMS磁力计和全局地标计算出机器人当前位姿矩阵,并基于该位姿矩阵完成当前帧和全局地图的粗匹配,从而减少ICP算法的迭代次数。同时在ICP算法每次迭代中,采用局部尺度压缩搜索替代全局搜索完成匹配点搜索,加快匹配点搜索速度。实验结果表明ICP-SLAM实时性得到了很大提升,迭代次数和系统运行时间分别降低92.34%和98.86%。此外,ICP-SLAM的整体性能得到很大的提升。
| [1] |
LI Hai, CHEN Qijun. Towards a non-probabilistic approach to hybrid geometry-topological SLAM[C]//Proceedings of 2010 8th World Congress of IEEE on Intelligent Control and Automation. Jinan: IEEE, 2010: 1045-1050.
( 0) 0)
|
| [2] |
BARRAU A, BONNABEL S. Invariant filtering for Pose EKF-SLAM aided by an IMU[C]//Proceedings of 2015 IEEE Conference on Decision and Control. Osaka: IEEE, 2015: 2133-2138.
( 0) 0)
|
| [3] |
季晓玲, 贺青, 迟宗涛. 基于EKF的SLAM算法在机器人定位中的应用[J]. 科技经济导刊, 2016(13): 17-19. ( 0) 0)
|
| [4] |
ZANDARA S, RIDAO P, RIBAS D, et al. Probabilistic surface matching for bathymetry based SLAM[C]//Proceedings of 2013 IEEE International Conference on Robotics and Automation. Karlsruhe: IEEE, 2013: 40-45.
( 0) 0)
|
| [5] |
ALBERT P, RIDAO P, RIBAS D, et al. Bathymetry-based SLAM with difference of normals point-cloud subsampling and probabilistic ICP registration[C]//Proceedings of 2013 MTS/IEEE OCEANS-Bergen. Bergen: IEEE, 2013: 1-8.
( 0) 0)
|
| [6] |
TREHARD G, ALSAYED Z, POLLARD E, et al. Credibilist simultaneous Localization And Mapping with a LIDAR[C]//Proceedings of 2014 IEEE/RSJ International Conference on Intelligent Robots and Systems. Chicago, IL: IEEE, 2014: 2699-2706.
( 0) 0)
|
| [7] |
ARTH C, PIRCHHEIM C, VENTURA J, et al. Instant outdoor localization and SLAM initialization from 2.5D maps[J]. IEEE transactions on visualization and computer graphics, 2015, 21(11): 1309-1318. DOI:10.1109/TVCG.2015.2459772 ( 0) 0)
|
| [8] |
CHOUDHARY S, INDELMAN V, CHRISTENSEN H I, et al. Information-based reduced landmark SLAM[C]//Proceedings of 2015 IEEE International Conference on Robotics and Automation (ICRA). Seattle, WA: IEEE, 2015: 4620-4627.
( 0) 0)
|
| [9] |
陈兴秀, 张金艺, 晏理, 等. 三维复杂运动模式航迹推算惯性导航室内定位[J]. 应用科学学报, 2014, 32(4): 349-350. CHEN Xingxiu, ZHANG Jinyi, YAN Li, et al. Inertial indoor navigation with 3D complex motion mode of pedestrian dead reckoning[J]. Journal of appliend sciences-electronics and information engineering, 2014, 32(4): 349-350. (  0) 0)
|
| [10] |
张苍松, 郭军, 崔娇, 等. 基于RSSI的室内定位算法优化技术[J]. 计算机工程与应用, 2015, 51(3): 235-238. ZHANG Cangsong, GUO Jun, CUI Jiao, et al. Indoor positioning optimization techniques based on RSSI[J]. Computer engineering and applications, 2015, 51(3): 235-238. (  0) 0)
|
| [11] |
王益健. 蓝牙室内定位关键技术的研究与实现[D]. 南京: 东南大学, 2015. WANG Yijian.Research and implementation on key technologies of bluetooth indoor positioning[D].Nanjing:Southeast University, 2015. http: //cdmd. cnki. com. cn/Article/CDMD-10286-1016752963. htm (  0) 0)
|
| [12] |
BESL P J, MCKAY N D. Method for registration of 3-D shapes[J]. IEEE transactions on pattern analysis and machine intelligence, 1992, 14(2): 239-256. DOI:10.1109/34.121791 ( 0) 0)
|
| [13] |
RUSINKIEWICZ S, LEVOY M. Efficient variants of the ICP algorithm[C]//Proceedings of the Third International Conference on 3-D Digital Imaging and Modeling. Quebec City, Que: IEEE, 2001: 145.
( 0) 0)
|
| [14] |
BLANCO J L, GONZáLEZ-JIMéNEZ J, FERNáNDEZ-MADRIGAL J A. A robust, multi-hypothesis approach to matching occupancy grid maps[J]. Robotica, 2013, 31(5): 687-701. DOI:10.1017/S0263574712000732 ( 0) 0)
|
| [15] |
XU Haixia, ZHOU Wei, ZHU Jiang. 3D visual SLAM with a time-of-flight camera[C]//Proceedings of 2015 IEEE Workshop on Signal Processing Systems (SiPS). Hangzhou: IEEE, 2015: 1-6.
( 0) 0)
|
| [16] |
ULAS C, TEMELTAS H. A robust feature extraction method and semantic data association for 6D SLAM[C]//Proceedings of 2015 IEEE World Automation Congress (WAC). Mexico: IEEE, 2012: 1-6.
( 0) 0)
|
| [17] |
GONG Zizhen, HUA Xianghong, YI Chongzheng, et al. The research and implementation of ICP based on Delaunay triangulation[J]. Engineering of surveying and mapping, 2010, 19(5): 29-31. ( 0) 0)
|
| [18] |
HU Linjia, NOOSHABADI S, AHMADI M. Massively parallel KD-tree construction and nearest neighbor search algorithms[C]//Proceedings of 2015 IEEE International Symposium on Circuits and Systems (ISCAS). Lisbon: IEEE, 2015: 2752-2755.
( 0) 0)
|
| [19] |
ZHANG Lei, CHOI S I, PARK S Y. Polar-Cartesian hybrid transforms: a novel 2D range scan registration algorithm[J]. International journal of control automation and systems, 2013, 11(5): 1001-1008. DOI:10.1007/s12555-012-0172-4 ( 0) 0)
|
| [20] |
TIAR R, LAKROUF M, AZOUAOUI O. FAST ICP-SLAM for a bi-steerable mobile robot in large environments[C]//Proceedings of 2015 International Conference on Advanced Robotics (ICAR). Istanbul: IEEE, 2015: 1-6.
( 0) 0)
|
| [21] |
TIAR R, OUADAH N, AZOUAOUI O, et al. ICP-SLAM methods implementation on a bi-steerable mobile robot [C]//Proceedings of IEEE 11th International Workshop of Electronics, Control, Measurement, Signals and their Application to Mechatronics (ECMSM). Toulouse: IEEE, 2013: 1-6.
( 0) 0)
|
 2017, Vol. 12
2017, Vol. 12