2. 沈阳建筑大学 高档石材数控加工装备与技术国家地方联合工程实验室, 辽宁 沈阳 110168
2. National-Local Joint Engineering Laboratory of High-Grade Stone Numerical Control Machining Equipments and Technology, Shenyang Jianzhu University, Shenyang 110168, China
图像在切割及传输等过程中,不可避免地会受到各种噪声污染,其中最常见的就是由白色亮点盐噪声和黑色暗点胡椒噪声组成的黑白杂点,即椒盐噪声,也称脉冲噪声。图像降噪就是将被污染的噪声点去除,使其恢复原来图像的过程。图像降噪既要保证图像边缘细节信息不被破坏,又要对噪声点进行去除,使图像清晰,有较好的视觉效果。传统的降噪方法[1-3],如中值降噪在对图像降噪过程中对每一个像素点都进行滤波,致使图像纹理细节得到不同程度的破坏,从而影响了图像清晰度,没有使图像得到更好地恢复。
脉冲耦合神经网络[4-6](pulse coupled neural network,PCNN) 是第3代人工神经网络,由于它有着极强的生物学背景,因此显示出突出的图像处理能力,近年来,已广泛应用于图像分割[7-8]、图像识别[9]、图像降噪[10-12]等图像处理的各个领域[13-15]。文献[10]提出了一种自适应突触链接强度的PCNN降噪方法,对图像中的噪声点进行了有效去除;文献[11]提出了单向衰减阈值以及滤波窗口大小和滤波次数均自适应选择的图像降噪方法,其较传统降噪方法有显著优势,降噪效果较好;文献[12]提出一种结合形态学方法的滤波算法,更好地抑制混合噪声的干扰,到达了良好的降噪效果。为更好地提高图像质量,改善降噪效果,本文提出一种改进突触链接强度和改进阈值函数的PCNN模型。
1 PCNN神经元模型 1.1 PCNN介绍PCNN是由许多神经元相互链接形成的一种动态非线性神经网络。如图 1所示,一个PCNN神经元主要由接收外部刺激信号部分、对信号进行调制部分以及根据信号强弱决定能否产生脉冲部分这3部分组成。

|
| 图 1 基本PCNN神经元模型 Fig. 1 Basic PCNN neuron model |
接收外部刺激信号部分由F和L两条通道接收并传输信号,其中F通道的馈送输入Fij不仅与外部刺激信号Iij有关,还与其周围神经元的点火情况相关联,其值为神经元馈送权系数矩阵M与邻域内各神经元输出值点乘的和再乘以神经元馈送幅度系数VF,然后加上外部刺激信号,并且随时间按指数变化不断衰减。而L通道的链接输入Lij仅接收其周围神经元的链接信号,其值为神经元链接权系数矩阵W与邻域内各神经元输出值点乘的和再乘以神经元链接幅度系数VL,同时也随时间按指数形式逐渐衰减。
调制器的作用是调节F和L两条通道传递的信号,通过耦合调制得到内部活动项Uij。
脉冲发生器用来控制脉冲的产生与否,当Uij≥θij时,神经元点火发放脉冲,即输出Yij=1,否则神经元不点火,输出Yij=0。其中动态阈值θij按指数形式随时间衰减。
1.2 简化PCNN模型由上面介绍可知,基本PCNN神经元模型参数较多,对参数设置较为困难,运算起来也较为繁琐,因此,本文将基本PCNN模型简化。PCNN简化模型的数学形式可用下列方程来描述。
 |
(1) |
 |
(2) |
 |
(3) |
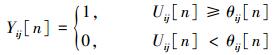 |
(4) |
 |
(5) |
式中:αθ为阈值衰减时间常数,Vθ为阈值幅度系数,Yij[n]为第n时刻神经元 (i, j) 的输出,其他符号代表的含义同1.1小节所介绍。
由式 (1)~(5) 能够知道,模型保持了原有特征,同时参数大大减少,并且馈送输入Fij和链接输入Lij均不再自身随时间衰减。此时的馈送输入Fij仅与外部刺激有关,其值为图像的灰度值,而链接输入Lij仅关联神经元的链接信号,其值为周围神经元的输出值与链接权系数矩阵点乘后求和。简化后PCNN模型的内部活动项没有改变,脉冲产生与否仍然由内部活动项与动态阈值大小来决定。因此,简化后PCNN模型保持了基本PCNN模型的一些特性。
2 改进PCNN模型降噪 2.1 改进突触链接强度基本PCNN模型所有神经元突触链接强度均为同一初始设置值。实际上,神经元接收不同信号刺激时,其对周围神经元影响的强弱是不同的,而传统PCNN模型没有更好地体现出不同神经元之间的差异性。因此,本文将突触链接强度加以改进,使其根据不同神经元的各异性而自适应取值。具体取值方式如下。
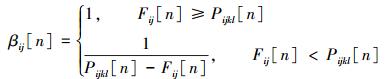 |
(6) |
式中:Fijkl[n]表示第n时刻神经元 (i, j) 邻域内神经元 (k, l) 的馈送输入,即Fkl;Pijkl[n]表示神经元 (i, j) 邻域内所有神经元 (k, l) 的馈送输入Fkl[n]的平均值。
由式 (6) 可以看出,每个神经元都有不同自适应取值的突触链接强度:如果当前神经元 (i, j) 的馈送输入值Fij[n]大于或等于其邻域神经元馈送输入值的平均值Pijkl[n],这时当前神经元 (i, j) 的突触链接强度βij[n]取值为1,即相当于当前神经元 (i, j) 对周围神经元 (k, l) 引起了共振响应;否则,当前神经元 (i, j) 的突触链接强度βij[n]取值为邻域内其他神经元馈送输入的平均值与当前神经元馈送输入差值的倒数。突触链接强度这样取值是因为神经元 (i, j) 受到的外界刺激与其邻域神经元 (k, l) 的外界刺激相似或较大时,其会带动邻域神经元 (k, l) 的活跃性,致使整个邻域内神经元的活跃性提高,从而增大了内部活动项Uij[n]的取值,促进神经元 (i, j) 提早点火发放脉冲;若神经元 (i, j) 的外界激励相对其邻域神经元 (k, l) 的外界激励较弱,即Pijkl[n]-Fij[n]在0~1取值时,可使突触链接强度βij[n]取值较大,这样邻域神经元 (k, l) 也会带动神经元 (i, j) 提前点火激活;但当神经元 (i, j) 的外界激励相对其邻域神经元 (k, l) 的外界激励很小,即Pijkl[n]-Fij[n]>1时,神经元 (i, j) 不易被点火激活而处于抑制状态。改进的突触链接强度体现出不同神经元之间链接程度大小的不同,能更真实地模拟生物神经元,从而准确地定位噪声位置,达到更好的降噪效果。
2.2 改进阈值函数简化PCNN模型阈值函数仍按指数形式衰减,而馈送输入Fij是一定值,链接输入Lij值较小,因此,对于灰度值较大的神经元内部活动项Uij[n]的值与馈送输入值较为接近。而指数衰减的阈值,当阈值较大时,阈值函数衰减的速度就会较快,随着阈值的减小,其衰减速度也逐渐减小,这样导致较大值神经元对应的图像区域有较小差异的大灰度值之间的分辨力较低,而较小值神经元对应的图像区域有较小差异的小灰度值的分辨力较高,从而导致灰度值大的区域噪声不易定位的缺点。因此,本文将动态阈值函数加以改进,其公式为
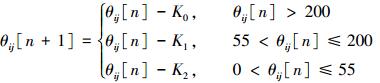 |
(7) |
式中:K0、K1和K2均为大于零的常数,且K1取值要大于K0与K2,以达到使动态阈值快速下降,加快算法运行速度的目的,而K0及K2取较小值时,可以提高算法对图像的分辨率。根据每次迭代的指数衰减阈值函数的改变大小,这里将灰度值大于200的看作大灰度值,小于55的看作小灰度值。
由图 2动态阈值的衰减曲线可以看出,改进后的阈值函数在灰度值较大和较小区域衰减速度均较慢,但灰度值在中间值附近时阈值函数衰减速度较快,从而保证了阈值函数衰减的平均速度不至于过慢。在保证准确分辨图像不同灰度值的同时,选择合适的K0、K1和K2值还会提高阈值衰减速率,从而提高降噪效率。此外,由图 2可知,随着时间的增加指数衰减阈值的衰减速度逐渐降低,且始终大于零,致使较小的灰度值很难达到点火状态,通过图 2及式 (7) 可以看出,改进阈值函数经过衰减,最后一次可以达到θij[n+1]≤0,这时即使灰度值最小的神经元也会点火发放脉冲,并且减少了算法运行时间。因此,改进阈值函数可以在有限时间内使所有神经元都点火输出脉冲。

|
| 图 2 动态阈值衰减曲线 Fig. 2 Dynamic threshold attenuation curve |
由2.2节知道,改进阈值函数后,可以使所有神经元在有限时间内均点火发放脉冲,因此可添加一个记录神经元点火时间的矩阵T,即神经元点火时间图,其与PCNN及图像相对应,大小相等。神经元点火时间矩阵T记录着每个神经元的初次点火时间,即当第n时刻神经元 (i, j) 首次点火,其对应的点火时间矩阵元素tij=n。
为了判断噪声位置,文献[15]采用一个全1的 (2m+1)×(2m+1) 窗口对点火时间矩阵T中的元素逐个扫描,并对相应的 (2m+1)×(2m+1) 个元素排序来判断噪声点。上述方法分析矩阵T中所有元素,算法运行时间较长。根据椒盐噪声的特点,噪声将出现在灰度值最大的亮点处或灰度值最小的暗点处,即矩阵T中元素为最大值或最小值对应的图像位置,因此,本文算法中仅分析矩阵T中最大和最小元素,大大缩减了算法的运行时间。本文对噪声定位的具体过程为:
将点火时间矩阵T中所有最大及最小元素tij均与各自的 (2m+1)×(2m+1) 邻域元素tkl相减,得到若干个 (2m+1)×(2m+1) 窗口大小的矩阵Dij,其中m为正整数。如果矩阵Dij中除中间元素外有一半以上元素小于-1,此时神经元 (i, j) 未能捕获邻域内大多数神经元 (k, l),与它们均有较大差异,因此,可判断神经元 (i, j) 对应的像素点为大值噪声点 (灰度最大值为255),即噪声点的灰度值为最大值,应使其减小;如果矩阵Dij中除中间元素外有一半以上元素大于1,此时神经元 (i, j) 未能被邻域内大多数神经元 (k, l) 捕获,与邻域内大多数神经元 (k, l) 亦均有较大差异,因此,可判断神经元 (i, j) 对应的像素点为小值噪声点 (灰度最小值为0),即噪声点的灰度值为最小值,应使其增大。其他情况均认定为不是噪声点。由文献[11]可知,根据噪声密度的不同,调节m的值来控制 (2m+1)×(2m+1) 窗口大小,能够更准确辨别噪声。
2.4 PCNN滤波算法本文方法可以将图像中噪声点准确定位,因此不必对每个像素点都做滤波处理,仅对被判定为噪声的像素点进行滤波。具体算法步骤如下:
1) 初始化PCNN,设置各个参数初始值,同时令神经元均处于熄火状态,即Yij=0。
2) 输入含噪图像,在PCNN中按式 (1)~(4) 及式 (6) 和式 (7) 循环迭代,直到所有神经元均点火发放脉冲,同时记录神经元初次点火时间于点火时间矩阵T中。
3) 应用2.3小节介绍的方式定位噪声。对大值噪声点和小值噪声点均采用 (2m+1)×(2m+1) 窗口局部中值滤波。除以上情况外,直接输出原灰度值。
4) 输出降噪后图像。
此外,对降噪后图像进行评价后,如果效果仍较差,可对降噪后图像再执行一次降噪。
3 实验验证与结果分析本文以常用Lena图像和作者拍摄的Deer图像来验证改进算法对图像降噪的性能。原始Lena图像和Deer图像如图 3所示,均为256×256大小的灰度图像。测试客观评价结果采用峰值信噪比 (PSNR)、均方误差 (MSE)、信噪比改善因子 (ISNR) 等指标对降噪性能进行客观评价并进一步分析。

|
| 图 3 测试图像的原始图像 Fig. 3 The original images for test |
参照文献[15]将测试参数选择为:θ0=260、W=[0.5 1 0.5;1 0 1;0.5 1 0.5],取K0=8、K1=15、K2=8。
图 4和图 5分别为Lena图像和Deer图像通过添加密度为10%的椒盐噪声,并采用不同降噪方法的测试结果的主观视觉图。

|
| 图 4 Lena图像添加密度10%的椒盐噪声降噪效果 Fig. 4 Noise reduction results for Lena image added the salt and pepper noise with a density of 10% |

|
| 图 5 Deer图像添加密度10%的椒盐噪声降噪效果 Fig. 5 Noise reduction results for Deer image added the salt and pepper noise with a density of 10% |
从图 3~图 5可以看出,本文提出的降噪方法能够有效地滤除图像中的噪声,通过降噪所得到的视觉效果要优于中值降噪及均值降噪,不仅去除了噪声点,同时保护了图像边缘细节等信息,使图像轮廓清晰,改善了图像质量。
图 6为Lena图像添加密度10%的椒盐噪声降噪后的局部效果图,从图中可以看出,本文方法较文献[10]更好地保持了图像的纹理信息。由于本文方法可对噪声准确定位,并且仅对噪声点进行中值滤波,不改变图像中原有的灰度值,从而减少了对图像灰度值的破坏,很好地保持了图像纹理。

|
| 图 6 降噪细节比较 Fig. 6 Detail comparison of noise reduction results |
为了进一步客观评价本文算法的降噪能力,笔者做了多次测试,并将客观评价结果列于表 1。表 1给出了Lena图像和Deer图像添加密度为10%的椒盐噪声PSNR、MSE、ISNR 3种评价指标的对比,表 2中数据为针对Lena图像受不同强度椒盐噪声污染情况降噪后的PSNR性能。
| 评价指标 | Lena | Deer | |||||
| PSNR | MSE | ISNR | PSNR | MSE | ISNR | ||
| 加噪图像 | 15.515 | 1826 | 0 | 15.048 | 2034 | 0 | |
| 均值降噪 | 23.450 | 290.5 | -8.04 | 20.813 | 539.3 | -5.70 | |
| 中值降噪 | 31.003 | 51.62 | -15.57 | 23.520 | 289.2 | -8.41 | |
| 本文算法 | 38.265 | 9.70 | -22.81 | 32.423 | 37.22 | -17.32 | |
表 1中两种图像均是本文降噪算法的PSNR值最大,且远高于中值降噪和均值降噪,验证了本文算法的降噪性能优于中值降噪及均值降噪。而MSE值最小说明本文算法有效滤除了噪声,ISNR有最小的负值也表明本文算法对噪声的抑制效果最好。
表 2中文献[10]与文献[15]的降噪评价指标为原文中数据。由表 2可知,随着噪声密度的增大,PSNR值逐渐减小,但在同一密度情况下,本文算法的PSNR值最大,滤波效果最佳。表明本文方法不仅优于传统降噪算法,而且较文献[10]与文献[15]所提方法也有较大的优势。从峰值信噪比来看,本文方法的峰值信噪比显著高于与之比较的其他方法,得到了更为接近原始图像的降噪图像。因此,通过表 2中的实验数据可以得出,尽管图像受污染的程度不同,但在比较的滤波算法中,本文所提出的改进算法在滤除图像椒盐噪声时去噪性能最强。
脉冲耦合神经网络能够辨识出噪声点,并针对噪声点进行有目的的滤波,文献[10]在改进突触链接强度后对滤波效果有所改善,而本文利用另一种策略改进PCNN的突触链接强度,使突触链接强度的取值更加合理,同时对阈值函数进行改进,提高了算法对图像大灰度值之间及小灰度值之间的分辨力,并且在一定程度上还能够降低算法运行时间。因此本文方法提高了对图像椒盐噪声定位的精确度,对噪声的滤除不改变图像中原有的灰度值,要较其他传统降噪方法以及文献[10]与文献[15]方法好的多。虽然在噪声密度较大时降噪性能有所下降,但依然较其他方法滤波有较高的峰值信噪比。
此外,笔者测试了参数K0、K1、K2选取不同值时对降噪效果的影响,参数取值见表 3。Lena图像添加10%椒盐噪声时的测试评价结果如表 4,其中算法运行时间单位为s,表 4中序号与表 3序号阈值函数参数取值相对应。
| 序号 | K0 | K1 | K2 |
| 1 | 4 | 8 | 4 |
| 2 | 8 | 15 | 8 |
| 3 | 16 | 30 | 16 |
| 4 | 4 | 15 | 4 |
| 5 | 8 | 30 | 8 |
| 序号 | PSNR | MSE | ISNR | TIME |
| 1 | 37.998 4 | 10.327 2 | -22.544 2 | 45.834 5 |
| 2 | 38.503 5 | 9.182 7 | -23.050 3 | 30.266 5 |
| 3 | 36.071 0 | 16.076 8 | -20.590 5 | 21.705 7 |
| 4 | 38.247 6 | 9.916 8 | -22.770 0 | 40.646 4 |
| 5 | 37.925 3 | 10.486 7 | -22.452 9 | 27.017 5 |
从表 4中能够看出,序号2中除了算法运行时间不是最优外,其他性能评价指标均较优,各参数取值越小,算法运行时间越长,而K0与K2取值较大时性能指标下降较大,但整体综合分析参数选择对性能影响不是很大。因此,在具体应用中,应综合分析、合理选择式 (7) 中的参数。
4 结束语本文提出了一种使突触链接强度自适应取值以及阈值函数随时间分段衰减的改进PCNN模型。该方法提高了分辨图像不同灰度值的能力,能够较准确地定位噪声,实现了更好的降噪效果。经过实验测试,验证了该方法能够准确地辨识图像椒盐噪声点,并有效地将噪声点滤除,降噪效果好于与其比较的其他方法,同时对图像的边缘细节有较好的保护效果。
| [1] | NAKARIYAKUL S. Fast spatial averaging: an efficient algorithm for 2D mean filtering[J]. The journal of supercomputing, 2013, 65(1): 262-273. DOI:10.1007/s11227-011-0638-9. |
| [2] | YUAN Xinxing, WEN Peng, FAN Xiuxiang, et al. A local pixel distribution based self-adaptive median filter for removal of pepper and salt noise[J]. IFAC proceedings volumes, 2013, 46(20): 63-67. DOI:10.3182/20130902-3-CN-3020.00179. |
| [3] | WANG Huiyan, ZHENG Jia. Comparative study of tongue image denoising methods[J]. Journal of computers, 2013, 8(3): 787-794. |
| [4] |
张文兴, 闫海鹏, 王建国. 基于改进脉冲耦合神经网络的数据降噪方法研究[J].
机械设计与制造, 2015(2): 25-28.
ZHANG Wenxing, YAN Haipeng, WANG Jianguo. Research on data noise reduction method based on modified PCNN[J]. Machinery design & manufacture, 2015(2): 25-28. |
| [5] | WANG Zhaobin, MA Yide, CHENG Feiyan, et al. Review of pulse-coupled neural networks[J]. Image and vision computing, 2010, 28(1): 5-13. DOI:10.1016/j.imavis.2009.06.007. |
| [6] | SUBASHINI M M, SAHOO S K. Pulse coupled neural networks and its applications[J]. Expert systems with applications, 2014, 41(8): 3965-3974. DOI:10.1016/j.eswa.2013.12.027. |
| [7] |
沈艳, 张晓明, 韩凯歌, 等. PCNN图像分割技术研究[J].
现代电子技术, 2014, 37(2): 38-41.
SHEN Yan, ZHANG Xiaoming, HAN Kaige, et al. Research of image segmentation technology based on PCNN[J]. Modern electronics technique, 2014, 37(2): 38-41. |
| [8] |
周东国, 高潮, 郭永彩. 一种参数自适应的简化PCNN图像分割方法[J].
自动化学报, 2014, 40(6): 1191-1197.
ZHOU Dongguo, GAO Chao, GUO Yongcai. Adaptive simplified PCNN parameter setting for image segmentation[J]. Acta automatica sinica, 2014, 40(6): 1191-1197. |
| [9] | 李翔. 基于脉冲耦合神经网络的图像识别和图像检索算法研究[D]. 昆明: 云南大学, 2014. LI Xiang. Research on image recognition and image retrieval algorithm based on pulse coupled neural network[D]. Kunming: Yunnan University, 2014. |
| [10] |
张文兴, 闫海鹏, 王建国. 一种基于脉冲耦合神经网络的图像降噪方法[J].
图学学报, 2015, 36(1): 47-51.
ZHANG Wenxing, YAN Haipeng, WANG Jianguo. A method for image de-noising based on pulse coupled neural network[J]. Journal of graphics, 2015, 36(1): 47-51. |
| [11] |
李海燕, 张榆锋, 施心陵, 等. 基于脉冲耦合神经网络的自适应图像滤波[J].
计算机应用, 2011, 31(4): 1037-1039.
LI Haiyan, ZHANG Yufeng, SHI Xinling, et al. Adaptive filtering method for images based on pulse-coupled neural network[J]. Journal of computer applications, 2011, 31(4): 1037-1039. |
| [12] |
张艳珠, 李媛, 李小娟. 简化型PCNN的混合噪声图像滤波算法研究[J].
控制工程, 2013, 20(5): 829-832.
ZHANG Yanzhu, LI Yuan, LI Xiaojuan. The research of hybrid noise filtering for images based on pulse coupled neural network[J]. Control engineering of China, 2013, 20(5): 829-832. |
| [13] | 刘勍. 基于脉冲耦合神经网络的图像处理若干问题研究[D]. 西安: 西安电子科技大学, 2011. LIU Qing. Research on several issues about image processing based on pulse coupled neural networks[D]. Xi'an: Xidian University, 2011. |
| [14] | 樊洪斌. 脉冲耦合神经网络在医学图像处理中的应用研究[D]. 桂林: 广西师范大学, 2009. FAN Hongbin. The applications in the medical image processing based on pulse coupled neural network[D]. Guilin: Guangxi Normal University, 2009. |
| [15] |
刘勍, 马义德. 一种基于PCNN赋时矩阵的图像去噪新算法[J].
电子与信息学报, 2008, 30(8): 1869-1873.
LIU Qing, MA Yide. A new algorithm for noise reducing of image based on PCNN time matrix[J]. Journal of electronics & information technology, 2008, 30(8): 1869-1873. |



