线性切换系统稳定性判断有几种方法,其中公共Lyapunov函数(common Lyapunov function, CLF)方法是在多Lyapunov函数方法之后被提出来的。其出发点是若切换系统所有子系统存在一个单Lyapunov函数,并且这个Lyapunov函数在整个状态空间中沿着特定的切换序列或者是任意切换都能递减,则整个系统稳定[1-2]。Beldiman等[3]指出通过对原来稳定的非线性切换系统线性化后,其线性化的系统是渐近稳定的。目前研究焦点是如何构造CLF,或者如何判断存在CLF。Dogruel首先提出了CLF方法,证明了切换系统如果存在一个Lyapunov函数
显然,CLF只是切换系统稳定的充分条件,反之,如果切换系统在任意切换信号下全局渐近稳定,是否存在CLF?针对这一问题,Dayawansa证明了若线性切换系统在任意切换信号下全局指数稳定,则线性切换系统存在CLF[8]。Cheng等[9]应用CLF分析了几类切换系统的稳定性,提出了确保闭环切换系统稳定的CLF。
CQLF的存在性必然有一定条件,而且和切换系统的分析和控制器设计密切相关。对CLF存在的充分和必要条件讨论可以参考文献[10]。CLF的构造方法也已经取得了许多成果。基本都是假设
本文将讨论不确定线性切换系统的稳定性判定CQLF问题。如果单独考虑带有不确定性的线性切换系统稳定性,即鲁棒稳定性问题,其CQLF的构造将会更加困难。为了克服这个困难,本文提出了公共鲁棒稳定矩阵集的概念,并进一步扩展推出鲁棒稳定矩阵集的CQLF矩阵的判定定理和构造定理。本文的结果对于任意切换规则下的不确定线性切换系统鲁棒控制问题具有以下重要意义:1)有了一套实用的搜寻CQLF的具体LMI算法;2)有了一个判断任意切换规则下系统鲁棒二次稳定的充分性条件。
1 问题描述考虑如下的不确定切换系统
| $\dot x(t) = ({{\mathit{\boldsymbol{A}}}_\sigma } + \Delta {{\mathit{\boldsymbol{A}}}_\sigma })x(t)$ | (1) |
式中:
| $\begin{array}{c}{\mathit{\boldsymbol{Q}}}: = {x_0};\left( {{i_0},{t_0}} \right),\left( {{i_1},{t_1}} \right), \cdots ,\left( {{i_N},{t_N}} \right), \cdots ,\\\forall {i_k} \in {\bf{N}},k \in {{\bf{Z}}^ + },\end{array}$ |
意味着当
| ${{\mathit{\boldsymbol{A}}}_\sigma } \buildrel \Delta \over = {{\mathit{\boldsymbol{A}}}_i},\Delta {{\mathit{\boldsymbol{A}}}_\sigma } \buildrel \Delta \over = \Delta {{\mathit{\boldsymbol{A}}}_i}$ |
因此,在第k次切换,对于
| $\dot x(t) = ({{\mathit{\boldsymbol{A}}}_i} + \Delta {{\mathit{\boldsymbol{A}}}_i})x(t)$ | (2) |
切换系统式(2)满足以下假设。
假设1[14] 不确定参数
| $\Delta {{\mathit{\boldsymbol{A}}}_i} = {{\mathit{\boldsymbol{H}}}_{a,i}}{{\mathit{\boldsymbol{F}}}_{a,i}}\left( t \right){{\mathit{\boldsymbol{E}}}_{a,i}}$ | (3) |
式中:
| ${\mathit{\boldsymbol{F}}}_{a,i}^{\rm{T}}\left( t \right){{\mathit{\boldsymbol{F}}}_{a,i}}\left( t \right) \leqslant {\mathit{\boldsymbol{I}}}$ |
接下来给出本文用到的常用引理。
引理1[13] (Schur补引理) 对于给定对称矩阵
1)
2)
3)
引理2[14] 设H和E是具有适当维数的实常数矩阵,
| ${\mathit{\boldsymbol{HF}}}\left( t \right){\mathit{\boldsymbol{E}}} + {{\mathit{\boldsymbol{E}}}^{\rm{T}}}{{\mathit{\boldsymbol{F}}}^{\rm{T}}}\left( t \right){{\mathit{\boldsymbol{H}}}^{\rm{T}}} \leqslant {\varepsilon ^{ - 1}}{\mathit{\boldsymbol{H}}}{{\mathit{\boldsymbol{H}}}^{\rm{T}}} + \varepsilon {{\mathit{\boldsymbol{E}}}^{\rm{T}}}{\mathit{\boldsymbol{E}}}$ |
假设稳定矩阵集
| ${{\mathit{\boldsymbol{P}}}_N}{{\mathit{\boldsymbol{A}}}_N} + {\mathit{\boldsymbol{A}}}_N^{\rm{T}}{{\mathit{\boldsymbol{P}}}_N} = - {{\mathit{\boldsymbol{P}}}_{N - 1}}$ |
引理3[12] 对于稳定矩阵集
| $\left\{ \begin{array}{l}{\rm{max}}\left( {\gamma _i^i} \right) < 2{\rm{min}}\left| {{\rm{Re}}\lambda \left( {{{\mathit{\boldsymbol{A}}}_N}} \right)} \right|\\ - {{\mathit{\boldsymbol{P}}}_{i,N - 1}} + \gamma _i^N{{\mathit{\boldsymbol{P}}}_{N - 1}} - \sum\limits_{k = 1,k \ne i}^{N - 1} {\gamma _i^k{{\mathit{\boldsymbol{P}}}_{k,N}} > 0} \end{array} \right.$ | (4) |
式中:
当稳定矩阵集
| $\left[ {{{\mathit{\boldsymbol{A}}}_N},{{\mathit{\boldsymbol{A}}}_j}} \right] = {{\mathit{\boldsymbol{C}}}_{N,j}},\;\forall j \in {\bf{N}}$ | (5) |
引理4[12] 对于稳定矩阵集
| ${{\mathit{\boldsymbol{P}}}_{i,N - 1}} + {{\mathit{\boldsymbol{P}}}_N}{{\mathit{\boldsymbol{C}}}_{N,i}} + {\mathit{\boldsymbol{C}}}_{N,i}^{\rm{T}}{{\mathit{\boldsymbol{P}}}_N} < 0$ | (6) |
则
引理5 若
| $\left[ {\begin{array}{*{20}{c}}{{{\mathit{\boldsymbol{P}}}_i}{{\mathit{\boldsymbol{A}}}_i} + {\mathit{\boldsymbol{A}}}_i^{\rm{T}}{\mathit{\boldsymbol{P}}} + {{\mathit{\boldsymbol{L}}}_i}} & {{{\mathit{\boldsymbol{P}}}_i}{{\mathit{\boldsymbol{H}}}_{a,i}}}\\* & { - {\varepsilon _i}{\mathit{\boldsymbol{I}}}}\end{array}} \right] < 0,\;\forall i \in {\bf{N}}$ | (7) |
有正定对称阵解
| ${{\mathit{\boldsymbol{G}}}_i} = \varepsilon _i^{ - 1}{{\mathit{\boldsymbol{H}}}_{a,i}}{\mathit{\boldsymbol{H}}}_{a,i}^{\rm{T}},{\rm{ }}{{\mathit{\boldsymbol{L}}}_i} = {\varepsilon _i}{\mathit{\boldsymbol{E}}}_{a,i}^{\rm{T}}{{\mathit{\boldsymbol{E}}}_{a,i}}$ | (8) |
证明 选取各子系统(2)的Lyapunov函数:
| ${V_i}\left( {{\mathit{\boldsymbol{x}}}(t)} \right) = {{\mathit{\boldsymbol{x}}}^{\rm{T}}}\left( t \right){{\mathit{\boldsymbol{P}}}_i}{\mathit{\boldsymbol{x}}}\left( t \right)$ |
沿子系统(2)求其时间导数:
| ${\dot V_i}\left( {{\mathit{\boldsymbol{x}}}(t)} \right) = {{\mathit{\boldsymbol{x}}}^{\rm{T}}}\left[ {{{\mathit{\boldsymbol{P}}}_i}{{\mathit{\boldsymbol{A}}}_i} + {\mathit{\boldsymbol{A}}}_i^{\rm{T}}{{\mathit{\boldsymbol{P}}}_i} + {{\mathit{\boldsymbol{P}}}_i}\Delta {{\mathit{\boldsymbol{A}}}_i} + \Delta {\mathit{\boldsymbol{A}}}_i^{\rm{T}}{{\mathit{\boldsymbol{P}}}_i}} \right]{\mathit{\boldsymbol{x}}}$ |
根据假设1和引理2,对于任意
| ${{\mathit{\boldsymbol{P}}}_i}\Delta {{\mathit{\boldsymbol{A}}}_i} + \Delta {\mathit{\boldsymbol{A}}}_i^{\rm{T}}{{\mathit{\boldsymbol{P}}}_i} \leqslant {{\mathit{\boldsymbol{G}}}_i} = \varepsilon _i^{ - 1}{{\mathit{\boldsymbol{P}}}_i}{{\mathit{\boldsymbol{H}}}_{a,i}}{\mathit{\boldsymbol{H}}}_{a,i}^{\rm{T}}{{\mathit{\boldsymbol{P}}}_i} + {\varepsilon _i}{\mathit{\boldsymbol{E}}}_{a,i}^{\rm{T}}{{\mathit{\boldsymbol{E}}}_{a,i}}$ |
成立。将其代入
| ${\dot V_i}\left( {{\mathit{\boldsymbol{x}}}(t)} \right) \leqslant {{\mathit{\boldsymbol{x}}}^{\rm{T}}}\left[ {{{\mathit{\boldsymbol{P}}}_i}{{\mathit{\boldsymbol{A}}}_i} + {\mathit{\boldsymbol{A}}}_i^{\rm{T}}{{\mathit{\boldsymbol{P}}}_i} + {{\mathit{\boldsymbol{P}}}_i}{{\mathit{\boldsymbol{G}}}_i}{{\mathit{\boldsymbol{P}}}_i} + {{\mathit{\boldsymbol{L}}}_i}} \right]{\mathit{\boldsymbol{x}}}$ |
成立。根据引理7,显然若满足,则有
| ${\dot V_i}\left( {{\mathit{\boldsymbol{x}}}(t)} \right) < - {{\mathit{\boldsymbol{x}}}^{\rm{T}}}\left( t \right){{\mathit{\boldsymbol{Q}}}_i}{\mathit{\boldsymbol{x}}}\left( t \right)$ |
成立,其中
切换系统(2)的系数矩阵满足如下假设。
假设2 稳定矩阵集
定义
| ${{\mathit{\boldsymbol{P}}}_{i,j}} = {\mathit{\boldsymbol{A}}}_i^{\rm{T}}{{\mathit{\boldsymbol{P}}}_j} + {{\mathit{\boldsymbol{P}}}_j}{{\mathit{\boldsymbol{A}}}_i},\;\forall i,j \in {\bf{N}}$ | (9) |
以及
| ${{\mathit{\boldsymbol{U}}}_{i,N}} = {{\mathit{\boldsymbol{P}}}_N}{{\mathit{\boldsymbol{G}}}_i}{{\mathit{\boldsymbol{P}}}_N} + {{\mathit{\boldsymbol{L}}}_i}$ | (10) |
若鲁棒稳定矩阵集
| ${{\mathit{\boldsymbol{P}}}_N}{{\mathit{\boldsymbol{A}}}_N} + {\mathit{\boldsymbol{A}}}_N^{\rm{T}}{{\mathit{\boldsymbol{P}}}_N}{\rm{ + }}{{\mathit{\boldsymbol{U}}}_{N,N}} = - {{\mathit{\boldsymbol{P}}}_{N - 1}}$ | (11) |
根据上述CQLF引理3,我们得到以下推论。
推论1 对于满足引理5的鲁棒稳定矩阵集
| $\left\{ \begin{array}{l}{\rm{max}}\left( {\gamma _i^i} \right) < 2{\rm{min}}\left| {{\rm{Re}}\lambda \left( {{A_N}} \right)} \right|{\rm{}}\\ - {{\mathit{\boldsymbol{P}}}_{i,N - 1}} + \gamma _i^N{{\mathit{\boldsymbol{P}}}_{N - 1}} - \sum\limits_{k = 1,k \ne i}^{N - 1} {\gamma _i^k{{\mathit{\boldsymbol{P}}}_{k,N}}} + \gamma _i^i{{\mathit{\boldsymbol{U}}}_{i,N}} + \\\quad\quad{\rm{ }}\gamma _i^N{{\mathit{\boldsymbol{U}}}_{N,N}} + {{\mathit{\boldsymbol{U}}}_{i,N}}{{\mathit{\boldsymbol{A}}}_N} + {\mathit{\boldsymbol{A}}}_N^{\rm{T}}{{\mathit{\boldsymbol{U}}}_{i,N}} - {\rm{ }}{{\mathit{\boldsymbol{U}}}_{N,N}}{{\mathit{\boldsymbol{A}}}_i} - \\[5pt]\quad\quad{\rm{ }}{\mathit{\boldsymbol{A}}}_i^{\rm{T}}{{\mathit{\boldsymbol{U}}}_{N,N}} > 0{\rm{}}\end{array} \right.$ | (12) |
则
| ${{\mathit{\boldsymbol{P}}}_N}{{\mathit{\boldsymbol{A}}}_i} + {\mathit{\boldsymbol{A}}}_i^{\rm{T}}{{\mathit{\boldsymbol{P}}}_N} + {{\mathit{\boldsymbol{P}}}_N}{{\mathit{\boldsymbol{G}}}_i}{{\mathit{\boldsymbol{P}}}_N} + {{\mathit{\boldsymbol{L}}}_i} < 0$ | (13) |
证明
| $\begin{array}{c}\left( {{{\mathit{\boldsymbol{P}}}_{i,N}} + {{\mathit{\boldsymbol{U}}}_{i,N}}} \right)\left( {{{\mathit{\boldsymbol{A}}}_N} + \gamma _i^i{\mathit{\boldsymbol{I}}}/2} \right) + {\left( {{{\mathit{\boldsymbol{A}}}_N} + \gamma _i^i{\mathit{\boldsymbol{I}}}/2} \right)^{\rm{T}}} \times \left( {{{\mathit{\boldsymbol{P}}}_{i,N}} + {{\mathit{\boldsymbol{U}}}_{i,N}}} \right) = \\[5pt]\left( {{{\mathit{\boldsymbol{P}}}_N}{{\mathit{\boldsymbol{A}}}_i} + {\mathit{\boldsymbol{A}}}_i^{\rm{T}}{{\mathit{\boldsymbol{P}}}_N} + {{\mathit{\boldsymbol{U}}}_{i,N}}} \right){{\mathit{\boldsymbol{A}}}_N} + {\mathit{\boldsymbol{A}}}_N^{\rm{T}}\left( {{{\mathit{\boldsymbol{P}}}_N}{{\mathit{\boldsymbol{A}}}_i} + } \right.\end{array}$ |
| $\begin{array}{c}\left. {{\mathit{\boldsymbol{A}}}_i^{\rm{T}}{{\mathit{\boldsymbol{P}}}_N} + {{\mathit{\boldsymbol{U}}}_{i,N}}} \right) + \gamma _i^i\left( {{{\mathit{\boldsymbol{P}}}_N}{{\mathit{\boldsymbol{A}}}_i} + {\mathit{\boldsymbol{A}}}_i^{\rm{T}}{{\mathit{\boldsymbol{P}}}_N} + {{\mathit{\boldsymbol{U}}}_{i,N}}} \right) = \\[5pt]{{\mathit{\boldsymbol{P}}}_N}\left( {{{\mathit{\boldsymbol{A}}}_N}{{\mathit{\boldsymbol{A}}}_i} - \sum\limits_{k = 1}^N {\gamma _i^k} {{\mathit{\boldsymbol{A}}}_k}} \right) + {\mathit{\boldsymbol{A}}}_i^{\rm{T}}{{\mathit{\boldsymbol{P}}}_N}{{\mathit{\boldsymbol{A}}}_N} + {\mathit{\boldsymbol{A}}}_N^{\rm{T}}{{\mathit{\boldsymbol{P}}}_N}{{\mathit{\boldsymbol{A}}}_i} + \\[5pt]\left( {{\mathit{\boldsymbol{A}}}_i^{\rm{T}}{\mathit{\boldsymbol{A}}}_N^{\rm{T}} - \sum\limits_{k = 1}^N {\gamma _i^k} {\mathit{\boldsymbol{A}}}_k^{\rm{T}}} \right){{\mathit{\boldsymbol{P}}}_N} + \gamma _i^i\left( {{{\mathit{\boldsymbol{P}}}_N}{{\mathit{\boldsymbol{A}}}_i} + {\mathit{\boldsymbol{A}}}_i^{\rm{T}}{{\mathit{\boldsymbol{P}}}_N}} \right. + \\[5pt]\left. {{{\mathit{\boldsymbol{U}}}_{i,N}}} \right) + {{\mathit{\boldsymbol{U}}}_{i,N}}{{\mathit{\boldsymbol{A}}}_N} + {\mathit{\boldsymbol{A}}}_N^{\rm{T}}{{\mathit{\boldsymbol{U}}}_{i,N}} = \\[5pt]\left( {{{\mathit{\boldsymbol{P}}}_N}{{\mathit{\boldsymbol{A}}}_N} + {\mathit{\boldsymbol{A}}}_N^{\rm{T}}{{\mathit{\boldsymbol{P}}}_N}} \right){{\mathit{\boldsymbol{A}}}_i} + {\mathit{\boldsymbol{A}}}_i^{\rm{T}}\left( {{{\mathit{\boldsymbol{P}}}_N}{{\mathit{\boldsymbol{A}}}_N} + {\mathit{\boldsymbol{A}}}_N^{\rm{T}}{{\mathit{\boldsymbol{P}}}_N}} \right) - \\[5pt]\gamma _i^N\left( {{{\mathit{\boldsymbol{P}}}_N}{{\mathit{\boldsymbol{A}}}_N} + {\mathit{\boldsymbol{A}}}_N^{\rm{T}}{{\mathit{\boldsymbol{P}}}_N}} \right) - \sum\limits_{k = 1,k \ne i}^{N - 1} {\gamma _i^k} \left( {{{\mathit{\boldsymbol{P}}}_N}{{\mathit{\boldsymbol{A}}}_k} + } \right.\\[5pt]\left. {{\mathit{\boldsymbol{A}}}_k^{\rm{T}}{{\mathit{\boldsymbol{P}}}_N}} \right) + {{\mathit{\boldsymbol{U}}}_{i,N}}\left( {{{\mathit{\boldsymbol{A}}}_N} + \gamma _i^i} \right) + {\mathit{\boldsymbol{A}}}_N^{\rm{T}}{{\mathit{\boldsymbol{U}}}_{i,N}} = \\[5pt] - {{\mathit{\boldsymbol{P}}}_{i,N - 1}} + \gamma _i^N{{\mathit{\boldsymbol{P}}}_{N - 1}} - \sum\limits_{k = 1,k \ne i}^{N - 1} {\gamma _i^k} {{\mathit{\boldsymbol{P}}}_{k,N}} + {\mathit{\boldsymbol{A}}}_N^{\rm{T}}{{\mathit{\boldsymbol{U}}}_{i,N}} + \\[5pt]{{\mathit{\boldsymbol{U}}}_{i,N}}\left( {{{\mathit{\boldsymbol{A}}}_N} + \gamma _i^i} \right) - {\rm{ }}{{\mathit{\boldsymbol{U}}}_{N,N}}\left( {{{\mathit{\boldsymbol{A}}}_i} - \gamma _i^N} \right) - {\mathit{\boldsymbol{A}}}_i^{\rm{T}}{{\mathit{\boldsymbol{U}}}_{N,N}}\end{array}$ |
若式(12)第2个条件
| ${{\mathit{\boldsymbol{P}}}_N}{{\mathit{\boldsymbol{A}}}_i} + {\mathit{\boldsymbol{A}}}_i^{\rm{T}}{{\mathit{\boldsymbol{P}}}_N} + {{\mathit{\boldsymbol{P}}}_N}{{\mathit{\boldsymbol{G}}}_i}{{\mathit{\boldsymbol{P}}}_N} + {{\mathit{\boldsymbol{L}}}_i} < 0$ | (14) |
成立,即
若鲁棒稳定矩阵集
推论2 对于鲁棒稳定矩阵集
| $\begin{array}{c}{{\mathit{\boldsymbol{P}}}_{i,N - 1}} + {{\mathit{\boldsymbol{P}}}_N}{{\mathit{\boldsymbol{C}}}_{N,i}} + {\mathit{\boldsymbol{C}}}_{N,i}^{\rm{T}}{{\mathit{\boldsymbol{P}}}_N} + {{\mathit{\boldsymbol{U}}}_{N,N}}{{\mathit{\boldsymbol{A}}}_i} + \\{\mathit{\boldsymbol{A}}}_i^{\rm{T}}{{\mathit{\boldsymbol{U}}}_{N,N}} - {{\mathit{\boldsymbol{U}}}_{i,N}}{{\mathit{\boldsymbol{A}}}_N} - {\mathit{\boldsymbol{A}}}_N^{\rm{T}}{{\mathit{\boldsymbol{U}}}_{i,N}} < 0\end{array}$ | (15) |
则
| ${{\mathit{\boldsymbol{P}}}_N}{{\mathit{\boldsymbol{A}}}_i} + {\mathit{\boldsymbol{A}}}_i^{\rm{T}}{{\mathit{\boldsymbol{P}}}_N} + {{\mathit{\boldsymbol{P}}}_N}{{\mathit{\boldsymbol{G}}}_i}{{\mathit{\boldsymbol{P}}}_N} + {{\mathit{\boldsymbol{L}}}_i} < 0$ | (16) |
证明
| $\begin{array}{c}\left( {{{\mathit{\boldsymbol{P}}}_{i,N}} + {{\mathit{\boldsymbol{U}}}_{i,N}}} \right){{\mathit{\boldsymbol{A}}}_N} + {\mathit{\boldsymbol{A}}}_N^{\rm{T}}\left( {{{\mathit{\boldsymbol{P}}}_{i,N}} + {{\mathit{\boldsymbol{U}}}_{i,N}}} \right) = \\[5pt]\left( {{{\mathit{\boldsymbol{P}}}_N}{{\mathit{\boldsymbol{A}}}_i} + {\mathit{\boldsymbol{A}}}_i^{\rm{T}}{{\mathit{\boldsymbol{P}}}_N} + {{\mathit{\boldsymbol{U}}}_{i,N}}} \right){{\mathit{\boldsymbol{A}}}_N} + \\[5pt]{\mathit{\boldsymbol{A}}}_N^{\rm{T}}\left( {{{\mathit{\boldsymbol{P}}}_N}{{\mathit{\boldsymbol{A}}}_i} + {\mathit{\boldsymbol{A}}}_i^{\rm{T}}{{\mathit{\boldsymbol{P}}}_N} + {{\mathit{\boldsymbol{U}}}_{i,N}}} \right) = \\[5pt]{{\mathit{\boldsymbol{P}}}_N}\left( {{{\mathit{\boldsymbol{A}}}_N}{{\mathit{\boldsymbol{A}}}_i} - {{\mathit{\boldsymbol{C}}}_{N,i}}} \right) + {\mathit{\boldsymbol{A}}}_i^{\rm{T}}{{\mathit{\boldsymbol{P}}}_N}{{\mathit{\boldsymbol{A}}}_N} + {\mathit{\boldsymbol{A}}}_N^{\rm{T}}{{\mathit{\boldsymbol{P}}}_N}{{\mathit{\boldsymbol{A}}}_i} + \\[5pt]\left( {{\mathit{\boldsymbol{A}}}_i^{\rm{T}}{\mathit{\boldsymbol{A}}}_N^{\rm{T}} - {\mathit{\boldsymbol{C}}}_{N,i}^{\rm{T}}} \right){{\mathit{\boldsymbol{P}}}_N} + {{\mathit{\boldsymbol{U}}}_{i,N}}{{\mathit{\boldsymbol{A}}}_N} + {\mathit{\boldsymbol{A}}}_N^{\rm{T}}{{\mathit{\boldsymbol{U}}}_{i,N}} = \\[5pt]\left( {{{\mathit{\boldsymbol{P}}}_N}{{\mathit{\boldsymbol{A}}}_N} + {\mathit{\boldsymbol{A}}}_N^{\rm{T}}{{\mathit{\boldsymbol{P}}}_N}} \right){{\mathit{\boldsymbol{A}}}_i} + {\mathit{\boldsymbol{A}}}_i^{\rm{T}}\left( {{{\mathit{\boldsymbol{P}}}_N}{{\mathit{\boldsymbol{A}}}_N} + {\mathit{\boldsymbol{A}}}_N^{\rm{T}}{{\mathit{\boldsymbol{P}}}_N}} \right) - \\[5pt]{{\mathit{\boldsymbol{P}}}_N}{{\mathit{\boldsymbol{C}}}_{N,i}} - {\mathit{\boldsymbol{C}}}_{N,i}^{\rm{T}}{{\mathit{\boldsymbol{P}}}_N} + {{\mathit{\boldsymbol{U}}}_{i,N}}{{\mathit{\boldsymbol{A}}}_N} + {\mathit{\boldsymbol{A}}}_N^{\rm{T}}{{\mathit{\boldsymbol{U}}}_{i,N}} = \\[5pt]- \left( {{{\mathit{\boldsymbol{P}}}_{i,N - 1}} + {{\mathit{\boldsymbol{P}}}_N}{{\mathit{\boldsymbol{C}}}_{N,i}} + {\mathit{\boldsymbol{C}}}_{N,i}^{\rm{T}}{{\mathit{\boldsymbol{P}}}_N} + {{\mathit{\boldsymbol{U}}}_{N,N}}{{\mathit{\boldsymbol{A}}}_i} + } \right.\\[5pt]\left. {{\mathit{\boldsymbol{A}}}_i^{\rm{T}}{{\mathit{\boldsymbol{U}}}_{N,N}} - {{\mathit{\boldsymbol{U}}}_{i,N}}{{\mathit{\boldsymbol{A}}}_N} - {\mathit{\boldsymbol{A}}}_N^{\rm{T}}{{\mathit{\boldsymbol{U}}}_{i,N}}} \right)\end{array}$ |
若不等式(15)条件成立,则
| $\left( {{{\mathit{\boldsymbol{P}}}_{i,N}} + {{\mathit{\boldsymbol{U}}}_{i,N}}} \right){{\mathit{\boldsymbol{A}}}_N} + {\mathit{\boldsymbol{A}}}_N^{\rm{T}}\left( {{{\mathit{\boldsymbol{P}}}_{i,N}} + {{\mathit{\boldsymbol{U}}}_{i,N}}} \right) > 0$ |
成立,表明两个矩阵
| ${{\mathit{\boldsymbol{P}}}_N}{{\mathit{\boldsymbol{A}}}_i} + {\mathit{\boldsymbol{A}}}_i^{\rm{T}}{{\mathit{\boldsymbol{P}}}_N} + {{\mathit{\boldsymbol{P}}}_N}{{\mathit{\boldsymbol{G}}}_i}{{\mathit{\boldsymbol{P}}}_N} + {{\mathit{\boldsymbol{L}}}_i} < 0$ | (17) |
那么
根据引理4,我们进一步得到稳定矩阵集的如下CQLF的构造算法定理。
定理1 若稳定矩阵集
| $\left\{ \begin{array}{l}{{\mathit{\boldsymbol{P}}}_{k,k}} < 0\\{\mathit{\boldsymbol{A}}}_i^{\rm{T}}{{\mathit{\boldsymbol{P}}}_{k,k}} + {{\mathit{\boldsymbol{P}}}_{k,k}}{{\mathit{\boldsymbol{A}}}_i} - {{\mathit{\boldsymbol{P}}}_k}{{\mathit{\boldsymbol{C}}}_{k,i}} - {\mathit{\boldsymbol{C}}}_{k,i}^{\rm{T}}{{\mathit{\boldsymbol{P}}}_k} > 0\end{array} \right.$ | (18) |
的正定对称阵
| ${{\mathit{\boldsymbol{C}}}_{i,j}} = {{\mathit{\boldsymbol{A}}}_i}{{\mathit{\boldsymbol{A}}}_j} - {{\mathit{\boldsymbol{A}}}_j}{{\mathit{\boldsymbol{A}}}_i}$ |
证明
| $\begin{array}{c}{{\mathit{\boldsymbol{P}}}_{i,k}}{{\mathit{\boldsymbol{A}}}_k} + {\mathit{\boldsymbol{A}}}_k^{\rm{T}}{{\mathit{\boldsymbol{P}}}_{i,k}} =\left( {{{\mathit{\boldsymbol{P}}}_k}{{\mathit{\boldsymbol{A}}}_i} + {\mathit{\boldsymbol{A}}}_i^{\rm{T}}{{\mathit{\boldsymbol{P}}}_k}} \right){{\mathit{\boldsymbol{A}}}_k} + \\[5pt] {\mathit{\boldsymbol{A}}}_k^{\rm{T}}\left( {{{\mathit{\boldsymbol{P}}}_k}{{\mathit{\boldsymbol{A}}}_i} + {\mathit{\boldsymbol{A}}}_i^{\rm{T}}{{\mathit{\boldsymbol{P}}}_k}} \right) = {{\mathit{\boldsymbol{P}}}_k}\left( {{{\mathit{\boldsymbol{A}}}_k}{{\mathit{\boldsymbol{A}}}_i} - {{\mathit{\boldsymbol{C}}}_{k,i}}} \right) +\\[5pt] {\mathit{\boldsymbol{A}}}_i^{\rm{T}}{{\mathit{\boldsymbol{P}}}_k}{{\mathit{\boldsymbol{A}}}_k} + {\mathit{\boldsymbol{A}}}_k^{\rm{T}}{{\mathit{\boldsymbol{P}}}_k}{{\mathit{\boldsymbol{A}}}_i} +{\rm{ }}{\left( {{{\mathit{\boldsymbol{A}}}_k}{{\mathit{\boldsymbol{A}}}_i} - {{\mathit{\boldsymbol{C}}}_{k,i}}} \right)^{\rm{T}}}{{\mathit{\boldsymbol{P}}}_k} = \\[5pt]\left( {{{\mathit{\boldsymbol{P}}}_k}{{\mathit{\boldsymbol{A}}}_k} + {\mathit{\boldsymbol{A}}}_k^{\rm{T}}{{\mathit{\boldsymbol{P}}}_k}} \right){{\mathit{\boldsymbol{A}}}_i} + {\mathit{\boldsymbol{A}}}_i^{\rm{T}}\left( {{{\mathit{\boldsymbol{P}}}_k}{{\mathit{\boldsymbol{A}}}_k} + {\mathit{\boldsymbol{A}}}_k^{\rm{T}}{{\mathit{\boldsymbol{P}}}_k}} \right) - \\[5pt]{\rm{ }}{{\mathit{\boldsymbol{P}}}_k}{{\mathit{\boldsymbol{C}}}_{k,i}} - {\mathit{\boldsymbol{C}}}_{k,i}^{\rm{T}}{{\mathit{\boldsymbol{P}}}_k} ={\mathit{\boldsymbol{A}}}_i^{\rm{T}}{{\mathit{\boldsymbol{P}}}_{k,k}} + {{\mathit{\boldsymbol{P}}}_{k,k}}{{\mathit{\boldsymbol{A}}}_i} - \\[5pt] {{\mathit{\boldsymbol{P}}}_k}{{\mathit{\boldsymbol{C}}}_{k,i}} - {\mathit{\boldsymbol{C}}}_{k,i}^{\rm{T}}{{\mathit{\boldsymbol{P}}}_k}\end{array}$ |
如果不等式(18)满足,则显然有
| ${{\mathit{\boldsymbol{P}}}_{i,k}}{{\mathit{\boldsymbol{A}}}_k} + {\mathit{\boldsymbol{A}}}_k^{\rm{T}}{{\mathit{\boldsymbol{P}}}_{i,k}} > 0$ |
因为
| ${{\mathit{\boldsymbol{P}}}_{i,k}} = {\mathit{\boldsymbol{A}}}_i^{\rm{T}}{{\mathit{\boldsymbol{P}}}_k} + {{\mathit{\boldsymbol{P}}}_k}{{\mathit{\boldsymbol{A}}}_i} < 0,{\rm{ }}\forall i = 1, 2, \cdots ,k$ |
成立。因此
假设一个鲁棒稳定矩阵集
定理2 假设鲁棒稳定矩阵集
| $\left\{ \begin{array}{l}{{\mathit{\boldsymbol{P}}}_{k,k}} + {{\mathit{\boldsymbol{U}}}_{k,k}} < 0,\\[5pt]{\mathit{\boldsymbol{A}}}_i^{\rm{T}}{{\mathit{\boldsymbol{P}}}_{k,k}} + {{\mathit{\boldsymbol{P}}}_{k,k}}{{\mathit{\boldsymbol{A}}}_i} - {{\mathit{\boldsymbol{P}}}_k}{{\mathit{\boldsymbol{C}}}_{k,i}} - {\mathit{\boldsymbol{C}}}_{k,i}^{\rm{T}}{{\mathit{\boldsymbol{P}}}_k} + \\[5pt]\quad\quad{{\mathit{\boldsymbol{U}}}_{i,k}}{{\mathit{\boldsymbol{A}}}_k} + {\mathit{\boldsymbol{A}}}_k^{\rm{T}}{{\mathit{\boldsymbol{U}}}_{i,k}} > 0\end{array} \right.$ | (19) |
的正定对称阵
| ${{\mathit{\boldsymbol{P}}}_k}{{\mathit{\boldsymbol{A}}}_i} + {\mathit{\boldsymbol{A}}}_i^{\rm{T}}{{\mathit{\boldsymbol{P}}}_k} + {{\mathit{\boldsymbol{U}}}_{i,k}} < 0$ | (20) |
其中是矩阵集中两两矩阵交换差。
证明
| $\begin{array}{c}\left( {{{\mathit{\boldsymbol{P}}}_{i,k}}{\rm{ + }}{{\mathit{\boldsymbol{U}}}_{i,k}}} \right){{\mathit{\boldsymbol{A}}}_k} + {\mathit{\boldsymbol{A}}}_k^{\rm{T}}\left( {{{\mathit{\boldsymbol{P}}}_{i,k}} + {{\mathit{\boldsymbol{U}}}_{i,k}}} \right) = \\[5pt]\left( {{{\mathit{\boldsymbol{P}}}_k}{{\mathit{\boldsymbol{A}}}_i} + {\mathit{\boldsymbol{A}}}_i^{\rm{T}}{{\mathit{\boldsymbol{P}}}_k} + {{\mathit{\boldsymbol{U}}}_{i,k}}} \right){{\mathit{\boldsymbol{A}}}_k} + \\[5pt]{\rm{ }}{\mathit{\boldsymbol{A}}}_k^{\rm{T}}\left( {{{\mathit{\boldsymbol{P}}}_k}{{\mathit{\boldsymbol{A}}}_i} + {\mathit{\boldsymbol{A}}}_i^{\rm{T}}{{\mathit{\boldsymbol{P}}}_k} + {{\mathit{\boldsymbol{U}}}_{i,k}}} \right) = \\[5pt]{{\mathit{\boldsymbol{P}}}_k}\left( {{{\mathit{\boldsymbol{A}}}_k}{{\mathit{\boldsymbol{A}}}_i} - {{\mathit{\boldsymbol{C}}}_{k,i}}} \right) + {\mathit{\boldsymbol{A}}}_i^{\rm{T}}{{\mathit{\boldsymbol{P}}}_k}{{\mathit{\boldsymbol{A}}}_k} + {\mathit{\boldsymbol{A}}}_k^{\rm{T}}{{\mathit{\boldsymbol{P}}}_k}{{\mathit{\boldsymbol{A}}}_i} + \\[5pt]{\rm{ }}{\left( {{{\mathit{\boldsymbol{A}}}_k}{{\mathit{\boldsymbol{A}}}_i} - {{\mathit{\boldsymbol{C}}}_{k,i}}} \right)^{\rm{T}}}{{\mathit{\boldsymbol{P}}}_k} + {{\mathit{\boldsymbol{U}}}_{i,k}}{{\mathit{\boldsymbol{A}}}_k} + {\mathit{\boldsymbol{A}}}_k^{\rm{T}}{{\mathit{\boldsymbol{U}}}_{i,k}}=\end{array}$ |
| $\begin{array}{c}\left( {{{\mathit{\boldsymbol{P}}}_k}{{\mathit{\boldsymbol{A}}}_k} + {\mathit{\boldsymbol{A}}}_k^{\rm{T}}{{\mathit{\boldsymbol{P}}}_k}} \right){{\mathit{\boldsymbol{A}}}_i} + {\mathit{\boldsymbol{A}}}_i^{\rm{T}}\left( {{{\mathit{\boldsymbol{P}}}_k}{{\mathit{\boldsymbol{A}}}_k} + {\mathit{\boldsymbol{A}}}_k^{\rm{T}}{{\mathit{\boldsymbol{P}}}_k}} \right) - \\[4pt]{\rm{ }}{{\mathit{\boldsymbol{P}}}_k}{{\mathit{\boldsymbol{C}}}_{k,i}} - {\mathit{\boldsymbol{C}}}_{k,i}^{\rm{T}}{{\mathit{\boldsymbol{P}}}_k} + {{\mathit{\boldsymbol{U}}}_{i,k}}{{\mathit{\boldsymbol{A}}}_k} + {\mathit{\boldsymbol{A}}}_k^{\rm{T}}{{\mathit{\boldsymbol{U}}}_{i,k}} = \\[4pt]{\mathit{\boldsymbol{A}}}_i^{\rm{T}}{{\mathit{\boldsymbol{P}}}_{k,k}} + {{\mathit{\boldsymbol{P}}}_{k,k}}{{\mathit{\boldsymbol{A}}}_i} - {{\mathit{\boldsymbol{P}}}_k}{{\mathit{\boldsymbol{C}}}_{k,i}} - {\mathit{\boldsymbol{C}}}_{k,i}^{\rm{T}}{{\mathit{\boldsymbol{P}}}_k} + \\[4pt]{\rm{ }}{{\mathit{\boldsymbol{U}}}_{i,k}}{{\mathit{\boldsymbol{A}}}_k} + {\mathit{\boldsymbol{A}}}_k^{\rm{T}}{{\mathit{\boldsymbol{U}}}_{i,k}}\end{array}$ |
如果不等式(19)满足,则显然有
| $\left( {{{\mathit{\boldsymbol{P}}}_{i,k}}{\rm{ + }}{{\mathit{\boldsymbol{U}}}_{i,k}}} \right){{\mathit{\boldsymbol{A}}}_k} + {\mathit{\boldsymbol{A}}}_k^{\rm{T}}\left( {{{\mathit{\boldsymbol{P}}}_{i,k}}{\rm{ + }}{{\mathit{\boldsymbol{U}}}_{i,k}}} \right) > 0$ |
因为
| ${{\mathit{\boldsymbol{P}}}_{i,k}}{\rm{ + }}{{\mathit{\boldsymbol{U}}}_{i,k}} = {\mathit{\boldsymbol{A}}}_i^{\rm{T}}{{\mathit{\boldsymbol{P}}}_k} + {{\mathit{\boldsymbol{P}}}_k}{{\mathit{\boldsymbol{A}}}_i}{\rm{ + }}{{\mathit{\boldsymbol{U}}}_{i,k}} < 0$ |
成立。因此
由于实际系统矩阵往往不容易两两可交换,或者说构成对合矩阵集。因此,在实际控制应用中,引理3、推论1并不实用。而引理4和本文给出的定理1、定理2、推论2满足大多数实际应用计算情况。
3.4 鲁棒二次Lyapunov函数矩阵寻找算法定理2在实际应用中更加广泛,因此我们进一步给出实用的鲁棒二次CLF寻找算法。
推论3 给定系统(2)的鲁棒稳定矩阵集
| $\left\{ \begin{array}{l}\left[ {\begin{array}{*{20}{c}}{{{\mathit{\boldsymbol{P}}}_k}{{\mathit{\boldsymbol{A}}}_k} + {\mathit{\boldsymbol{A}}}_k^{\rm{T}}{{\mathit{\boldsymbol{P}}}_k} + {{\mathit{\boldsymbol{L}}}_k}} & {{{\mathit{\boldsymbol{P}}}_k}{{\mathit{\boldsymbol{H}}}_{a,k}}}\\* & { - {\varepsilon _k}{\mathit{\boldsymbol{I}}}}\end{array}} \right] < 0,\\[9pt]\left[ {\begin{array}{*{20}{c}}{{\Xi _{i,k}}} & {\left( {{\mathit{\boldsymbol{I}}} - {\mathit{\boldsymbol{A}}}_k^{\rm{T}}} \right){{\mathit{\boldsymbol{P}}}_k}{{\mathit{\boldsymbol{H}}}_{a,i}}}\\* & {{\varepsilon _i}{\mathit{\boldsymbol{I}}}}\end{array}} \right] > 0,{\rm{ }}i = 1, 2, \cdots ,k - 1\end{array} \right.$ | (21) |
那么
| $\begin{array}{c}{\Xi _{i,k}} = {\mathit{\boldsymbol{A}}}_i^{\rm{T}}{{\mathit{\boldsymbol{P}}}_{k,k}} + {{\mathit{\boldsymbol{P}}}_{k,k}}{{\mathit{\boldsymbol{A}}}_i} - {{\mathit{\boldsymbol{P}}}_k}{{\mathit{\boldsymbol{C}}}_{k,i}} - \\[4pt]{\mathit{\boldsymbol{C}}}_{k,i}^{\rm{T}}{{\mathit{\boldsymbol{P}}}_k} + {{\mathit{\boldsymbol{L}}}_i}{{\mathit{\boldsymbol{A}}}_k} + {\mathit{\boldsymbol{A}}}_k^{\rm{T}}{{\mathit{\boldsymbol{L}}}_i}\end{array}$ | (22) |
证明 式(21)中第1个LMI证明
| ${\Xi _{i,k}} - \left( {{\mathit{\boldsymbol{I}}} - {\mathit{\boldsymbol{A}}}_k^{\rm{T}}} \right){{\mathit{\boldsymbol{P}}}_k}{{\mathit{\boldsymbol{G}}}_i}{{\mathit{\boldsymbol{P}}}_k}\left( {{\mathit{\boldsymbol{I}}} - {{\mathit{\boldsymbol{A}}}_k}} \right) > 0$ |
将式(22)代入,有不等式:
| $\begin{array}{c}{\mathit{\boldsymbol{A}}}_i^{\rm{T}}{{\mathit{\boldsymbol{P}}}_{k,k}} + {{\mathit{\boldsymbol{P}}}_{k,k}}{{\mathit{\boldsymbol{A}}}_i} - {{\mathit{\boldsymbol{P}}}_k}{{\mathit{\boldsymbol{C}}}_{k,i}} - {\mathit{\boldsymbol{C}}}_{k,i}^{\rm{T}}{{\mathit{\boldsymbol{P}}}_k} + \\[4pt]{{\mathit{\boldsymbol{L}}}_i}{{\mathit{\boldsymbol{A}}}_k} + {\mathit{\boldsymbol{A}}}_k^{\rm{T}}{{\mathit{\boldsymbol{L}}}_i} + {\mathit{\boldsymbol{A}}}_k^{\rm{T}}{{\mathit{\boldsymbol{P}}}_k}{{\mathit{\boldsymbol{G}}}_i}{{\mathit{\boldsymbol{P}}}_k} + \\[4pt]{{\mathit{\boldsymbol{P}}}_k}{{\mathit{\boldsymbol{G}}}_i}{{\mathit{\boldsymbol{P}}}_k}{{\mathit{\boldsymbol{A}}}_k} - {{\mathit{\boldsymbol{P}}}_k}{{\mathit{\boldsymbol{G}}}_i}{{\mathit{\boldsymbol{P}}}_k} - {\mathit{\boldsymbol{A}}}_k^{\rm{T}}{{\mathit{\boldsymbol{P}}}_k}{{\mathit{\boldsymbol{G}}}_i}{{\mathit{\boldsymbol{P}}}_k}{{\mathit{\boldsymbol{A}}}_k} > 0\end{array}$ |
再根据,上式即
| $\begin{array}{c}{\mathit{\boldsymbol{A}}}_i^{\rm{T}}{{\mathit{\boldsymbol{P}}}_{k,k}} + {{\mathit{\boldsymbol{P}}}_{k,k}}{{\mathit{\boldsymbol{A}}}_i} - {{\mathit{\boldsymbol{P}}}_k}{{\mathit{\boldsymbol{C}}}_{k,i}} - {\mathit{\boldsymbol{C}}}_{k,i}^{\rm{T}}{{\mathit{\boldsymbol{P}}}_k} + {{\mathit{\boldsymbol{U}}}_{i,k}}{{\mathit{\boldsymbol{A}}}_k} + \\[4pt]{\mathit{\boldsymbol{A}}}_k^{\rm{T}}{{\mathit{\boldsymbol{U}}}_{i,k}} - {{\mathit{\boldsymbol{P}}}_k}{{\mathit{\boldsymbol{G}}}_i}{{\mathit{\boldsymbol{P}}}_k} - {\mathit{\boldsymbol{A}}}_k^{\rm{T}}{{\mathit{\boldsymbol{P}}}_k}{{\mathit{\boldsymbol{G}}}_i}{{\mathit{\boldsymbol{P}}}_k}{{\mathit{\boldsymbol{A}}}_k} > 0\end{array}$ |
由式(8)可见,
| $\begin{array}{c}{\mathit{\boldsymbol{A}}}_i^{\rm{T}}{{\mathit{\boldsymbol{P}}}_{k,k}} + {{\mathit{\boldsymbol{P}}}_{k,k}}{{\mathit{\boldsymbol{A}}}_i} - {{\mathit{\boldsymbol{P}}}_k}{{\mathit{\boldsymbol{C}}}_{k,i}} - {\mathit{\boldsymbol{C}}}_{k,i}^{\rm{T}}{{\mathit{\boldsymbol{P}}}_k} + \\[4pt]{{\mathit{\boldsymbol{U}}}_{i,k}}{{\mathit{\boldsymbol{A}}}_k} + {\mathit{\boldsymbol{A}}}_k^{\rm{T}}{{\mathit{\boldsymbol{U}}}_{i,k}} > 0\end{array}$ |
成立。这样LMI(21)就等价于定理2中式(19)。那么推论3与定理2是等价的。
推论3给出了便于计算机计算寻找CQLF矩阵的递推算法。我们可以首先给出某一个子系统的鲁棒二次Lyapunov函数矩阵
需要指出的是,定理1、定理2、推论3均是充分条件,如果这些定理不能满足,并不能说明鲁棒二次CLF矩阵不存在。
4 应用仿真现代农业中,温室大棚提供了经济作物适宜的生长环境。其中温度和湿度是最为重要的因素,各类农作物的需求各不相同。因此,合理的温室温度和湿度控制成为智能温室大棚的主要和关键工程问题。文献[15]选择较为传统的近似线性化方法,在选取的温湿度工作点对非线性模型进行泰勒展开,这样就获得了所有工作点的线性化模型组。针对每个子模型设计相应的最优跟踪控制器,根据然后进行了跟踪切换控制。
本文依据文献[15],考虑大棚的温度
| $\begin{array}{c}{C_T}\displaystyle\frac{{{\rm{d}}{T_i}}}{{{\rm{d}}t}} = {C_1}\left( {{T_p} - {T_i}} \right) - \left( {{C_2}\left( {{C_3}G + {\varphi _1}} \right) + {C_4}} \right) \times \\[4pt]\left( {{T_i} - {T_o}} \right) + {C_5}\left( {{T_1} - {T_i}} \right) + {C_6}{T_{{\rm{rad}}}}\\[4pt]{C_H}\displaystyle\frac{{{\rm{d}}{\omega _i}}}{{{\rm{d}}t}} = {C_8}{C_9}\left( {{C_{10}}{C_{11}}{T_i} - {\omega _i}} \right) - {C_{12}}\left( {{T_p} - {T_i}} \right) - \\[4pt]\left( {{C_3}G + {\varphi _1}} \right)\left( {{\omega _i} - {\omega _o}} \right) + {C_H}\left( {{C_5}{T_1} + {C_{14}}} \right)\end{array}$ |
式中:管道加热温度G,通风率G,土壤表层温度T1,室外温度
| $\begin{array}{c}{{\dot x}_1} = - \left( {{b_1} + {b_3} + {b_4}} \right){x_1} + {b_1}{u_1} + \left( { - {b_2}{x_1} + {b_2}{v_2}} \right){u_2} + \\[2pt]{b_5}{v_3} + {b_3}{v_1} + {b_4}{v_4}\\[2pt]{{\dot x}_2} = {c_4}{x_1} + {c_1}{x_2} + {c_6}{v_2} + {c_8}{u_1} + {c_2}{u_2}{v_2} + {c_2}{u_2}{x_2} + \\[2pt]{c_5}{v_1} + {c_3}{v_4} + {c_7}\end{array}$ |
式中:
| $\begin{array}{c}{b_1} = {C_1}/{C_T},\;{b_2} = {C_2}{C_3}/{C_T}\\[4pt]{b_3} = \left( {{C_2}_1\varphi + {C_4}} \right)/{C_T},\;{b_4} = {C_5}/{C_T}\\[4pt]{b_5} = {C_6}/{C_T}\\[4pt]{c_1} = \left( {{C_{15}} - {C_8}{C_9} - {\varphi _1}} \right)/{C_H},\;{c_2} = {C_3}/{C_H}\\[4pt]{c_4} = {C_8}{C_9}{C_{10}}/{C_H},\;{c_5} = {C_{15}}/{C_H}\\[4pt]{c_6} = {\varphi _1}/{C_H}\end{array}$ |
各个参数物理意义及数值参考文献[15]。将上述模型在工作点
| $\begin{array}{c}{{\dot x}_1} = - \left( {{b_1} + {b_3} + {b_4}} \right){x_1} + {b_1}{u_1} + \left( { - {b_2}{x_{10}} + {b_2}{v_2}} \right){u_2} + \\[0pt]{b_5}{v_3} + {b_3}{v_1} + {b_4}{v_4}\\[0pt]{{\dot x}_2} = {c_4}{x_1} + {c_1}{x_2} + {c_8}{u_1} + {c_2}{v_2}{u_2} + {c_2}{x_{20}}{u_2} + {c_6}{v_2} + \\[0pt]{c_5}{v_1} + {c_3}{v_4} + {c_7}\end{array}$ |
根据文献[15],我们简单以温度、湿度的3个工作点:
(这里设计反馈控制系数与文献[15]不同)
(这里设计最优反馈控制系数与文献[15]相同)
这样,对于这个温室大棚的控制问题,我们看做是一个在不同工作点线性化后的线性不确定切换系统。在各个不同工作点进行了最优反馈控制设计后的闭环系统,是多个工作点附近的稳定子系统。这样,各个工作点闭环控制后的系统参数矩阵
注:这里闭环控制后的参数矩阵
| ${{\mathit{\boldsymbol{A}}}_1} = \left[ {\begin{array}{*{20}{c}}{0.148 \,\, 2} & {0.374 \,\, 6}\\{0.374 \,\, 6} & {1.892 \,\, 7}\end{array}} \right],\;{{\mathit{\boldsymbol{A}}}_2} = \left[ {\begin{array}{*{20}{c}}{0.148 \,\, 2} & {0.374 \,\, 6}\\{0.374 \,\, 6} & {1.892 \,\, 7}\end{array}} \right]$ |
的CLF是
| ${\mathit{\boldsymbol{P}}} = \left[ {\begin{array}{*{20}{c}}{0.148 \,\, 2} & {0.374 \,\, 6}\\{0.374 \,\, 6} & {1.892 \,\, 7}\end{array}} \right]$ |
但经过验证P不满足
我们把本文的理论和方法,进行应用,目标是判断在各个工作点线性化、最优反馈控制后的各个子系统构成的整体是否是鲁棒稳定的。我们把各个干扰部分进行取近似化为
| $\begin{array}{c}\Delta {{\mathit{\boldsymbol{A}}}_1} = \left[ {\begin{array}{*{20}{c}}{0.001\sin \, (0.02\pi t)} & 0\\0 & {0.014{{\rm{e}}^{ - 0.1t}}}\end{array}} \right],\\[8pt]\Delta {{\mathit{\boldsymbol{A}}}_2} = \left[ {\begin{array}{*{20}{c}}{0.000\;1\cos \, (0.01t)} & {0.000\;2\cos \, (0.01t)}\\0 & {0.005{{\rm{e}}^{ - 0.2t}}}\end{array}} \right],\\[8pt]\Delta {{\mathit{\boldsymbol{A}}}_3} = \left[ {\begin{array}{*{20}{c}}0 & 0\\0 & {0.026{{\rm{e}}^{ - 0.01{t^2}}}}\end{array}} \right].\end{array}$ |
根据假设1,将各个子系统不确定性分解。各个不确定性矩阵为
子系统1中:
| $\begin{array}{c}{{\mathit{\boldsymbol{H}}}_{a,1}} = \left[ {\begin{array}{*{20}{c}}{0.1} & 0\\0 & 1\end{array}} \right],{{\mathit{\boldsymbol{F}}}_{a,1}} = \left[ {\begin{array}{*{20}{c}}{\sin \, (0.02\pi t)} & 0\\0 & {{{\rm{e}}^{ - 0.1t}}}\end{array}} \right]\\[9pt]{{\mathit{\boldsymbol{E}}}_{a,1}} = \left[ {\begin{array}{*{20}{c}}{0.01} & 0\\0 & {0.014}\end{array}} \right]\end{array}$ |
子系统2中:
| $\begin{array}{c}{{\mathit{\boldsymbol{H}}}_{a,2}} = \left[ {\begin{array}{*{20}{c}}{0.01} & 0\\0 & {0.1}\end{array}} \right],{{\mathit{\boldsymbol{F}}}_{a,2}} = \left[ {\begin{array}{*{20}{c}}{\cos \, (0.01t)} & 0\\0 & {{{\rm{e}}^{ - 0.2t}}}\end{array}} \right]\\[9pt]{{\mathit{\boldsymbol{E}}}_{a,2}} = \left[ {\begin{array}{*{20}{c}}{0.01} & {0.02}\\0 & {0.05}\end{array}} \right]\end{array}$ |
子系统3中:
| ${{\mathit{\boldsymbol{H}}}_{a,3}} = \left[ {\begin{array}{*{20}{c}}0\\{0.1}\end{array}} \right],{{\mathit{\boldsymbol{F}}}_{a,3}} = {{\rm{e}}^{ - 0.01{t^2}}},{{\mathit{\boldsymbol{E}}}_{a,3}} = \left[ {\begin{array}{*{20}{c}}0 & {0.26}\end{array}} \right]$ |
k=2时子系统1、2的公共Lyapunuov矩阵为
k=3时子系统1、2、3的公共Lyapunuov矩阵为
这样,找到了温室大棚这3个工作点的鲁棒二次CLF,说明在任意切换规则下系统渐近稳定。
我们不考虑设计跟踪设定温度、湿度曲线问题,只考虑镇定问题。因此为了验证CQLF方法的有效和正确性,设系统的初始状态为
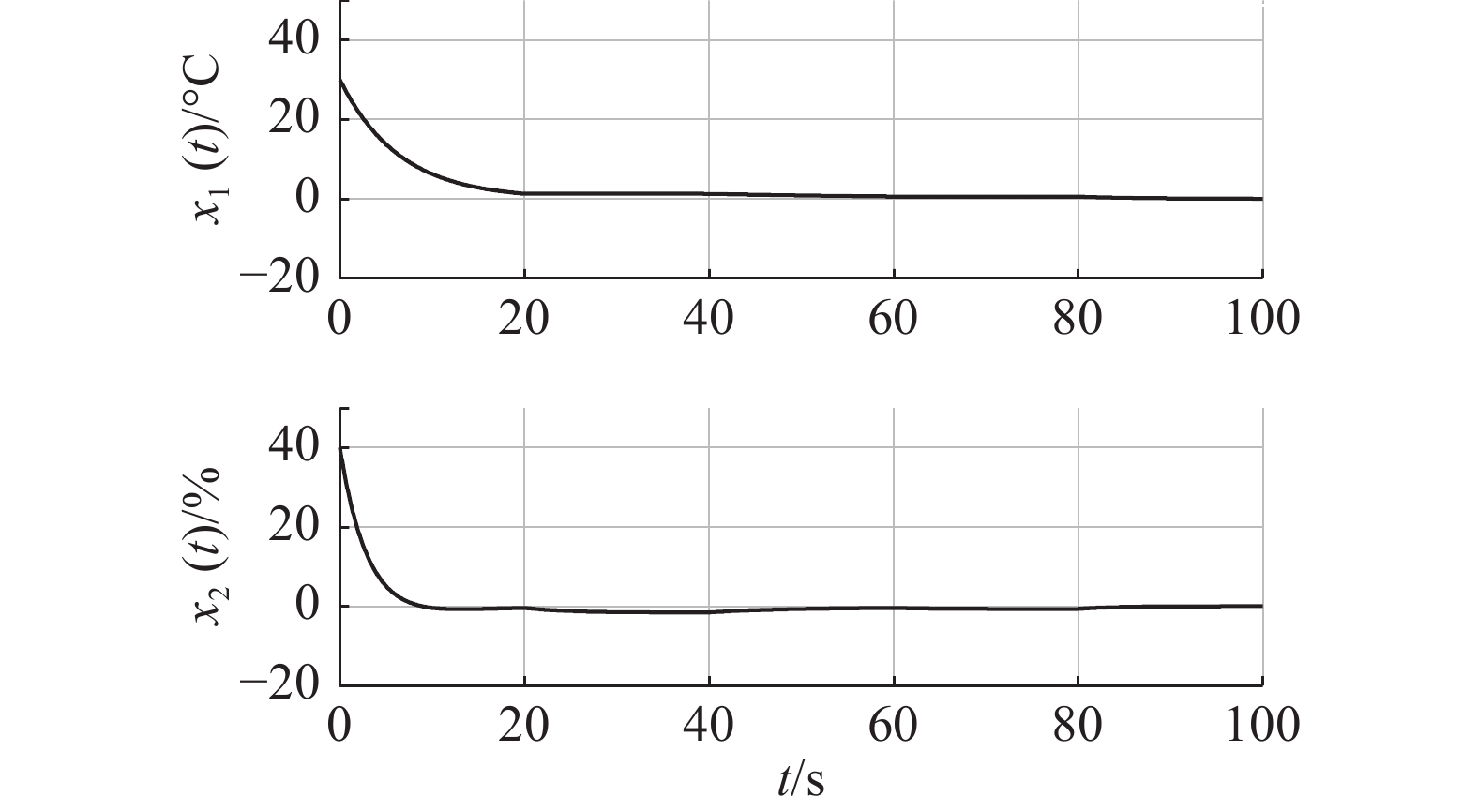
|
图 1 切换规则下系统状态曲线 Fig.1 The state curves under switching signal |
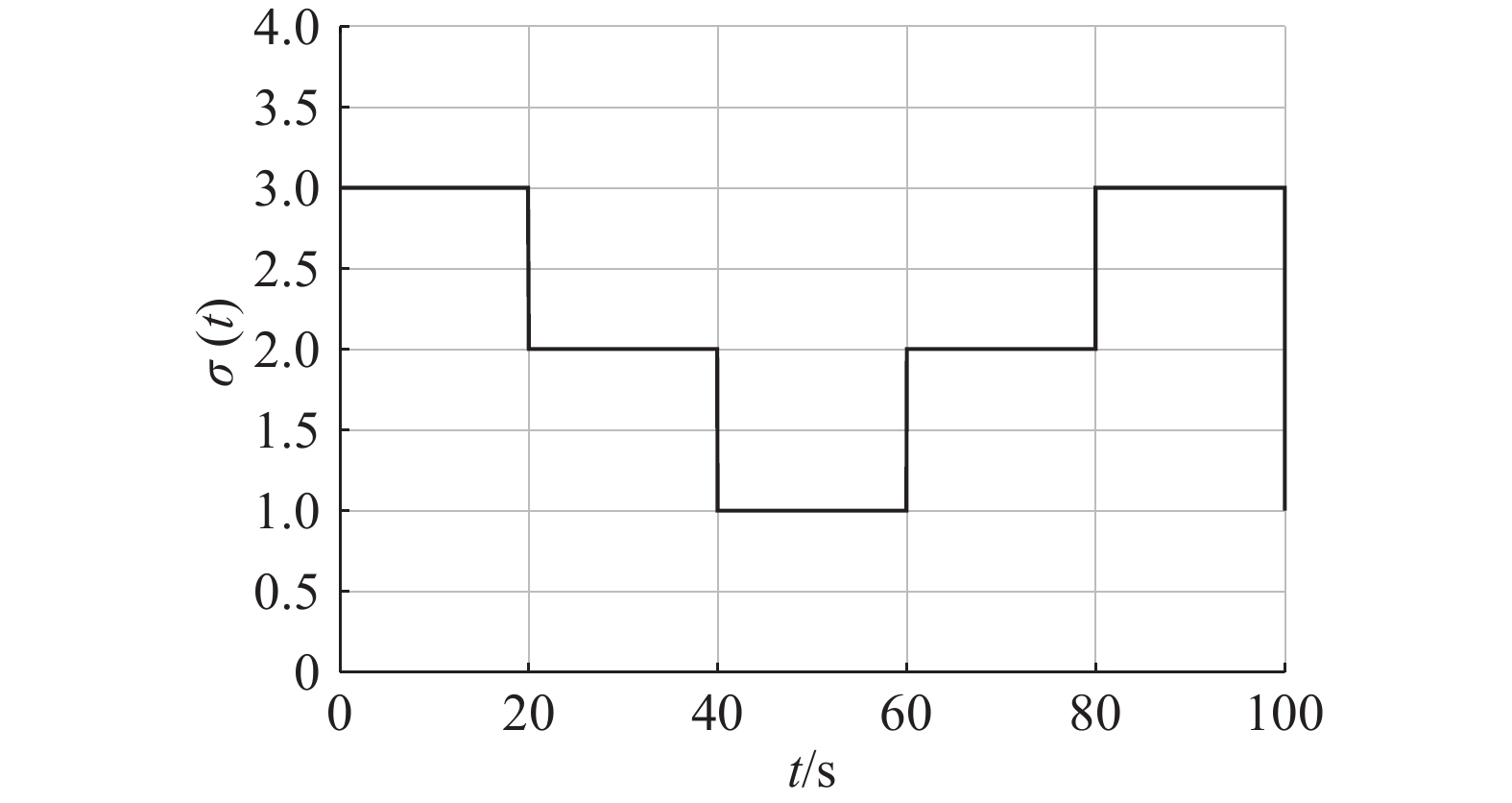
|
图 2 切换信号曲线 Fig.2 The switching signal curve |
对不确定线性切换系统的CLF问题进行了讨论。若系统矩阵构成鲁棒稳定矩阵集,给出了CQLF矩阵的递推判定方法和构造算法。构造算法是递推式的LMI形式,求解方便,实用性强。在温室大棚的温湿度控制问题的典型应用仿真验证了结果的可行性。
| [1] |
LIBERZON D, MORSE A S. Basic problems in stability and design of switched systems[J]. IEEE transaction on control systems, 1999, 19(5): 59-70. ( 0) 0)
|
| [2] |
DOGRUEL M, OZGUNER U. Stability of a set of matrices: an application to hybrid systems[C]//Proc of IEEE International Symposium on Intelligent Control. [S.l.], 1995: 59–64.
( 0) 0)
|
| [3] |
BELDIMAN O, BUSHNELL L. Stability, linearization and control of switched systems[C]//Proc of American Control Conference. San Diego, CA, 1999: 2950–2955.
( 0) 0)
|
| [4] |
OOBA T, FUNAHASHI Y. Two conditions concerning common quadratic Lyapunov functions for linear syste- ms[J]. IEEE trasactions on automatic control, 1997, 42(5): 719-721. ( 0) 0)
|
| [5] |
NARENDRA K S, BALAKRISHNAN J A. A common Lyapimov function for stable LTI systems with commuting A-matrices[J]. IEEE transactions on automatic control, 1994, 39(12): 2469-2471. ( 0) 0)
|
| [6] |
LIBERZON D, MORSE J P. Stability of switched systems: a Lie algebraic condition[J]. Systems and control letters, 1999, 37(3): 117-122. ( 0) 0)
|
| [7] |
MARGALIOTA M, LIBERZON D. Lie-algebraic stability conditions for nonlinear switched systems and differential inclusions[J]. Systems and control letters, 2006, 55(1): 8-16. ( 0) 0)
|
| [8] |
CHENG D Z, ZHU Y H, HU Q X. Stabilization of switched systems via common Lyapunov function[C]//Proc of the World Congress on Intelligent Control and Automation (WCICA). [S.l.], 2006: 183–187.
( 0) 0)
|
| [9] |
DAYAWANSA W P, MARTIN C F. A converse Lyapunov theorem for a class of dynamical systems which undergo switching[J]. IEEE transactions on automatic control, 1999, 44(4): 751-760. ( 0) 0)
|
| [10] |
LIN H, ANTSAKLIS P J. Stability and stabilizability of switched linear systems: a survey of recent results[J]. IEEE transactions on automatic control, 2009, 54(2): 308-322. ( 0) 0)
|
| [11] |
CHENG D Z, GUO L, HUANG J. On quadratic Lyapunov functions[J]. IEEE transactions on automatic control, 2003, 48(5): 885-890. ( 0) 0)
|
| [12] |
ZHU Y H, CHENG D Z, QIN H S. Constructing conmmon Lyapunov functions for a class of stable matrices[J]. Acta automatica sinica, 2007, 33(2): 202-204. ( 0) 0)
|
| [13] |
BOYD S, GHAOUI L E, FERON E, et al. Linear Matrix Inequalities in system and control theory[M]. Philadelphia: SIAM, 1994: 7–35.
( 0) 0)
|
| [14] |
俞立. 鲁棒控制—线性矩阵不等式处理方法[M]. 北京: 清华大学出版社, 2002. YU Li. Robust control-linear matrix inequality methods [M]. Beijing: Tsinghua University Press, 2002. (  0) 0)
|
| [15] |
王向东, 何南思. 温室大棚温湿度跟踪切换最优控制器[J]. 沈阳工业大学学报, 2014, 36(5): 543-549. WANG Xiangdong, HE Nansi. Tracking switching optimal controller for temperature and humidity of greenhouse[J]. Journal of Shenyang university of technology, 2014, 36(5): 543-549. (  0) 0)
|
 2017, Vol. 12
2017, Vol. 12


