视觉图像的分类与识别研究是计算机视觉研究、模式识别与机器学习领域内的一个非常活跃的方向,其在许多领域中应用广泛,如银行系统的人脸识别、防御系统的行人检测与跟踪、交通系统的车牌检测与车辆跟踪等。近年来,图像分类[1]吸引了研究者们的注意,关于视觉图像识别与分类的各种理论与算法层出不穷,如最近邻分类器[2]、神经网络分类器[3-4]、SVM支持向量机分类器[5]、卷积神经网络分类器[6]、ELM极限学习机[7]及稀疏编码方法等。为获得良好的图像分类效果,研究者们在设计图像分类方法及改进分类准确性方面都做了大量工作。例如,稀疏编码方法已被证实在图像分类中具有优秀的分类性能,基于该方法的许多改进的稀疏编码方法也被相继提出,如SRC方法[8]、CRC方法[9]、RSC方法[10]及RLRC方法[11]等。尽管现有的许多算法在图像分类方面表现突出,但目前已有的识别分类算法大多侧重于“区别”,忽视了“认识”,即侧重将某一类物体与有限类已学过物体进行区分。然而人类认识事物的过程侧重于对某一类物体与无限类未知物体的区分,只在细小之处重视“区别”(如区别桌子与椅子或者鱼与海豚等)。对于首次遇到的从未学习过的物体,传统的模式识别方法会将其归类于某一个已学习的类别。但是同样情况下,人类对首次遇到的新物体的直接反应是从未见过或者不认识该物体,而不是直接判断其属于哪一类已经学习过的物体。众所周知,计算机视觉研究的主要目标是使计算机能像人类一样轻易地识别视觉图像。神经生理学、心理学以及认知科学研究表明[12-13],人类能够轻易地将目标从周围环境中识别出来与人类记忆机制有着非常密切的联系。人们所看到的和所经历的都要经过记忆系统的处理。当认知新的事物时,与该事物相关的记忆信息就会被提取出来,从而加快认知的过程并适应新的环境。然而,在人脑记忆过程中信息是如何被加工、存储和提取的仍然不得而知。Murdock[14]认为现代人脑记忆建模理论至少要解释4个问题:信息是如何被表达、被存储与提取的信息的种类,存储与提取运算的本质以及信息存储的格式。围绕这些问题研究人员提出了包括情景记忆、语义记忆以及神经计算在内的记忆建模理论。Raaijmakers等[15]提出了SAM模型,所存储的信息用“记忆影像”表达,能解释记忆研究中的列表强度效应、列表长度效应以及近因效应等,但无法解释镜像效应;Hintzman等[16]提出的MINERVA 2模型首次将情景记忆与语义记忆联合用于提取建模,没有考虑列表强度效应以及镜像效应;Shiffrin等[17]提出的REM记忆模型,采用Bayesian理论计算线索与记忆影像的似然度,用于匹配搜索。上述情景记忆模型均假设识别判断是在整体匹配相似度强度的基础上完成的,其中REM记忆模型的突出性不仅因为其坚实的数学基础,也源于其可以解释情景记忆研究中出现的许多现象,如列表长度、列表强度与词汇频率效应等。REM模型对情景记忆研究中的列表强度效应、列表长度效应、词汇频率效应以及镜面效应与正态ROC斜率效应的解释不仅吸引了众多研究人员对REM模型的进一步研究[18-21],也引起了我们的思考——能否将记忆模型应用于图像识别分类中。目前大多数记忆模型均采用词汇列表的学习方式,对自然图像的学习和分类研究得很少,因此本文尝试将REM模型引入视觉图像的存储与识别,并提出一种基于REM记忆模型的视觉图像的学习、存储与提取方法。
1 图像特征表达图像特征提取在视觉图像学习过程中起着非常关键的作用。近几年来,许多特征提取算法被陆续提出并被应用于物体识别、如方向梯度直方图(HOG)等[22]、局部二值模式(LBP) [23]、尺度不变特征转换(SIFT)[24]、加速鲁棒特征(SURF)[25]等。其中HOG算子能很好地描述局部目标的表现与形状,LBP算子具有灰度尺度不变性和旋转不变性,本文将这两种算子同时应用于图像特征提取以描述图像的形状与纹理特征。
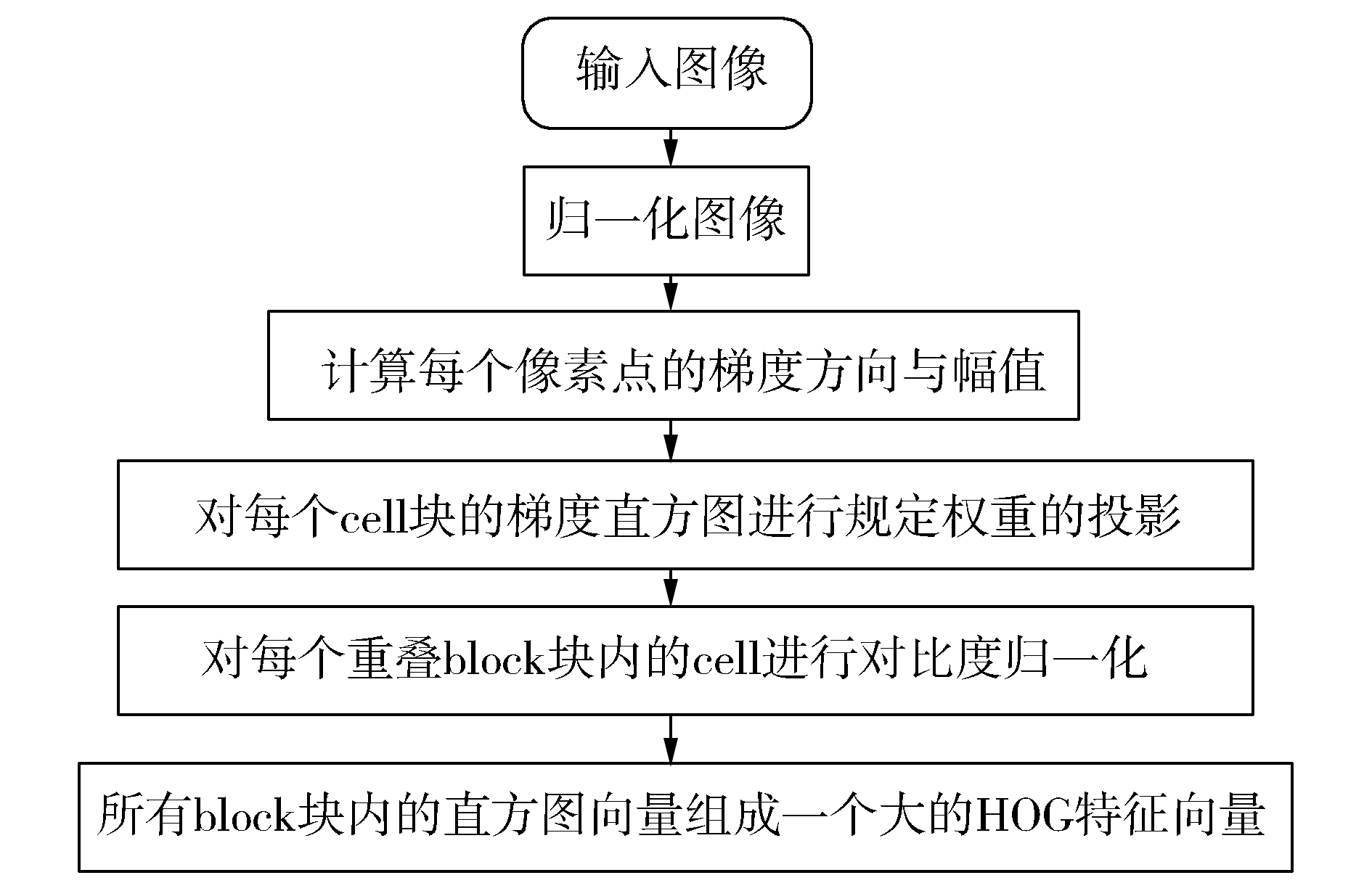
1.1 HOG特征方向梯度直方图(histogram of oriented gradient, HOG)特征是由N.Dalal等[22]提出的一种物体特征描述子,其通过计算和统计图像局部区域的梯度方向直方图来构成特征。HOG特征提取算法的具体实现过程如图 1所示。
|
图 1 HOG特征提取算法流程 Fig.1 The flow chart of HOG algorithm |
局部二值模式(LBP)是由T.Ojala、M.Pietikäinen和D. Harwood提出的一种灰度尺度不变性和旋转不变性的纹理算子[23]。原始LBP算子不能满足不同尺寸和频率纹理的需要,研究人员对其进行各种改进与优化,如半径为R的圆形区域内含有P个采样点的LBP算子及LBP旋转不变算子[26]。T. Ojala[27]定义了一个等价模式,模式数量减少为种,特征向量维数更少,减少了高频噪声带来的影响。
本文采用的LBP特征提取算法过程如下:
1) 对图像中的每一个像素点,定义圆形邻域窗口,每个像素的灰度值与其相邻的8个像素的灰度值比较,若周围像素值大于中心像素值,则该像素点的位置被标记为1,否则为0。这样可产生8位二进制数,即得到该窗口中心像素点的初始LBP值。
2) 不断旋转圆形邻域得到一系列初始定义的LBP值,取最小值作为该像素点的LBP值。
3) 统计LBP值对应的二进制数从0~1或1~0跳变的次数,根据跳变次数确定其属于哪一种LBP模式,共有P+1=9种模式,得到的模式数值即为像素点的LBP值。
4) 图像中所有像素点的LBP值组合起来形成一个LBP特征矩阵,即为该图像的LBP特征。
2 REM模型在视觉图像的表达、存储与提取中的应用认知记忆的快速提取模型——REM模型是Shiffrin等[17]1997年提出的一个用于识别单词的记忆模型,该模型采用Bayesian理论计算线索与记忆影像的似然度,用于匹配搜索。该模型能够解释许多情景记忆研究中的一些科学现象,如列表强度效应、列表长度效应、词汇频率效应、镜面效应与正态ROC斜率效应;其与SAM、MINERVA2模型的主要区别之一在于,其实现了似然率的贝叶斯计算, 是国际上公认的最好的记忆模型之一。
REM记忆模型被提出之后,研究人员陆续对REM模型进行研究。Stams等[18]通过对编码与提取过程中的项目强度的控制,对比研究了REM模型与BCDMEM模型对提取过程中项目强度对误报率降低的解释说明。Cox等[19]在REM与RCA-REM模型基础上提出一个新认知记忆模型,证实了即使在任务、学习因素、刺激及其他因子变化情况下,所提方法都有可能获得合理的认知决策。Criss等[20]对比了REM模型与SLiM(the subjective likelihood model)模型,发现REM模型预测的误报率较高;M.Montenegro等[21]研究了REM模型的解析表达式,文中引入Fourier变换,给出REM模型的FT积分方程,导出在给定参数值下模型预测的命中率与误报率的双积分形式的解析表达式,同时发现其具有与BCDMEM模型相同的一些性质:模型是不确定的,除非其中的一个参数固定为一个预设值,向量长度参数是不可忽略的参数。
2.1 特征表达与存储REM模型指出人脑记忆由图像构成,每幅图像是由一个特征值向量表示的,并且最终存储结果是对特征值向量的一个不完整且容易出错的复制。本文试图借鉴REM模型对单词的存储学习过程来模拟人脑对图像的学习过程,有概率地对图像的特征向量进行复制,同时在复制过程中允许出现错误值。
从图像库中选取图像,提取图像LBP与HOG特征,将其分别写成行向量形式并连接起来生成图像特征向量。HOG特征是由小数组成的,并不是非负整数,为方便REM模型的计算,在实验中简单地对该特征扩大10倍并四舍五入。每学习一次图像特征向量,对于那些还没有存储任何信息的位置,存储新信息的概率为u*。注意到,一旦某个值被存储,之后该值不会改变。如果对某个特征有存储,其特征值从已学向量中正确复制的概率是c,以1-c的概率根据P[V=j]=(1-g)j-1g, j=1, 2,…,∞随机取值,并允许偶然选取正确值的可能性。
用V={Vj}j=1, 2, …, N标记所有已学习图像的特征集,其中Vj表示已学习图像集合中第j副图像Ij的特征向量,N为已学习图像集合中的图像个数。
2.2 提取给定要检测的图像Itest,将其特征向量Vtest与V={Vj}j=1, 2, …, N进行匹配,匹配结果为D={Dj}j=1, 2, …, N,其中Dj为被检测图像特征与第j个视觉图像特征的匹配结果。用s图像表示与被检测图像相同的存储图像,d图像表示除被检测图像之外的其他视觉图像的存储图像。
被检测图像Itest与第j幅已存储图像Ij的匹配过程的关键步骤是,计算似然率λj,即在观测结果Dj基础上第j幅图像为s图像与d图像的概率比值:
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;{\lambda _j} = \frac{{P\left( {{D_j}\left| {{S_j}} \right.} \right)}}{{P\left( {{D_j}\left| {{N_j}} \right.} \right)}} = \\ {\left( {1-c} \right)^{{n_{jq}}}}\prod\limits_{k \in M} {\frac{{c + \left( {1-c} \right)g{{\left( {1-g} \right)}^{{V_{kj}} - 1}}}}{{g{{\left( {1 - g} \right)}^{{V_{kj}} - 1}}}}} \end{array} $ | (1) |
式中:Sj为第j副图像为s图像的事件; Nj为第j副图像为d图像的事件; M为非零特征值与被检测向量特征值匹配的目录; Vkj为第j副图像中第k个特征值; njq为Vj与Vtest不匹配的非零特征值个数; g为几何分布参数。
2.3 Bayesian决策给定探测图像Itest,将其与所有已学习图像I={Ij}j=1, 2, …, N进行匹配与不匹配比较,计算对应的似然值λ={λ1, λ2, …, λN},进而得到被检测图像为旧的而非新的概率为
| $ \begin{array}{l} \phi = \frac{{P\left( {O\left| D \right.} \right)}}{{P\left( {N\left| D \right.} \right)}} = \frac{{\frac{{P\left( O \right)P\left( {D\left| O \right.} \right)}}{{P\left( D \right)}}}}{{\frac{{P\left( N \right)P\left( {D\left| N \right.} \right)}}{{P\left( D \right)}}}} = \frac{{P\left( {D\left| O \right.} \right)}}{{P\left( {D\left| N \right.} \right)}} = \\ \;\;\;\;\;\;\sum\limits_{j = 1}^N {\frac{{P\left( {D\left| {{S_j}} \right.} \right)P\left( {{S_j}} \right)}}{{P\left( {D\left| N \right.} \right)}} = } \sum\limits_{j = 1}^N {\frac{1}{N}\frac{{P\left( {D\left| {{S_j}} \right.} \right)}}{{P\left( {D\left| N \right.} \right)}} = } \\ \;\;\;\;\;\;\frac{1}{N}\sum\limits_{j = 1}^N {\frac{{P\left( {{D_j}\left| {{S_j}} \right.} \right)\prod\limits_{i \ne j} {P\left( {{D_i}\left| {{N_i}} \right.} \right)} }}{{P\left( {{D_j}\left| {{N_j}} \right.} \right)\prod\limits_{i \ne j} {P\left( {{D_i}\left| {{N_i}} \right.} \right)} }} = } \\ \;\;\;\;\;\;\frac{1}{N}\sum\limits_{j = 1}^N {\frac{{P\left( {{D_j}\left| {{S_j}} \right.} \right)}}{{P\left( {{D_j}\left| {{N_j}} \right.} \right)}} = } \frac{1}{N}{\lambda _j} \end{array} $ |
若ϕ>1,那么认为被检测的图像为已学习的图像,同时认为该图像匹配最大λj值对应第j幅图像;反之认为被检测图像是新的,从未学习过。
如果被检测图像是已学习过图像的极小变化如旋转之后的图像,由于当前图像特征向量的提取技术限制, 被检测图像与对应的已学习过图像的特征向量中部分特征值并不一致。而原REM模型中的复制过程亦会导致不一致特征值的个数增加,计算似然率时会有很多1-c项相乘,使得λ≪1,故本文忽略了该复制过程。同时,由于所提取的特征值包含LBP特征,而LBP特征向量中值为8对应的是像素不变区域,故同时忽略特征值为0与8的区域。我们用图 2简单地解释该记忆模型过程,其中参数采用g=0.4,c=0.7。

|
图 2 改进的图像特征存储提取数值例子 Fig.2 An improved numerical example for the storage and retrieval of the image feature |
为验证本文所提方法的有效性,在Matlab编程环境下,先后对哥伦比亚大学Coil-20图像数据库[28]与加州福尼亚理工大学Caltech-256数据库[29]中的图像进行实验测试。
3.1 Coil-20数据库实验结果Coil-20数据库由20个不同对象的旋转图像构成,每个对象在水平方向上旋转360°,并每隔5°拍摄一张照片,故每个项目有72幅图像,每幅图像的像素为128×128。
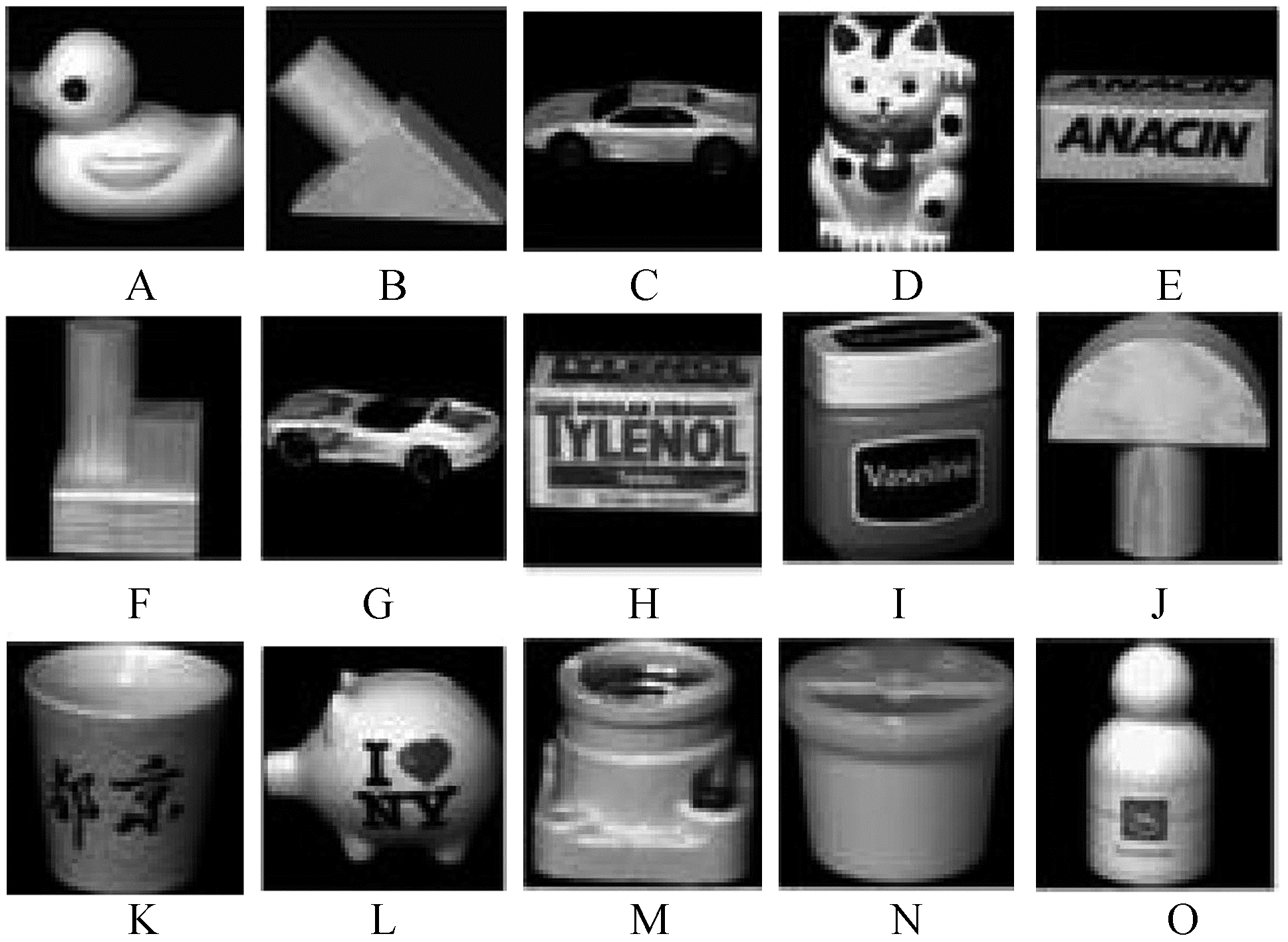
从Coil-20图像数据库中选取已学习图像,本文选择了15个不同项目的图像,构成图 3所示已学习图像集。图 3中大写英文字母(A~O)分别代表不同项目图像的序号。
|
图 3 已学习图像集 Fig.3 The studied images set |
接着从数据库中选取被测试图像,被测试图像根据实验需要选取图 4所示几组图像。

|
图 4 被测试图像集 Fig.4 The probe images set |
由于特征向量维数比原REM模型中单词特征维数大得多,计算似然率过程中会出现多个1-c项相乘,导致λ≪1,最终会影响到识别效果,故将ϕ值扩大到10100倍。表 1是利用本文所提算法对6组实验图像运行得到的识别结果。
| 表 1 Coil-20数据库实验结果 Tab.1 The experimental result on the Coil-20 database |
表 1中大写字母代表测试图象对应的已学习图像序号,“√”说明识别正确,“×”说明判别错误。很显然,图像组(a)、(b)识别效果不错;图像组(c)由5副已学习项目的旋转图像组成,只有2副图像被正确识别为已学习图像,即图像发生旋转时识别效果变差。通过对图像组(d)、(e)、(f)的测试实验发现,随着图像旋转角度增加,算法识别率降低。导致识别效果不理想的原因在于,尽管采用的LBP算子具有旋转不变性,但是当旋转角度超过一定范围之后算子不能很好地刻画图像特征。
3.2 Caltech-256数据库实验结果Caltech-256数据库来自加利福利亚理工学院,该数据库共有29 780副图像,包含了256个不同图像项目类别,每个图像类别包含不少于80幅属于该类别的不同图像,这些图像属于同一类,但并不是完全相同的项目,实验选择的已学习图像列表如图 5所示。

|
图 5 Caltech-256数据库中已学习图像集 Fig.5 The studied images set on the Caltech-256 database |
从数据库中选取20副被测试图像,包含10副已学习过类别的图像与10副新类别的图像, 如图 6所示。

|
图 6 Caltech-256数据库中被检测图像集 Fig.6 The probe images set on the Caltech-256 database |
利用本文所提算法并将LBP特征值扩大两倍,ϕ值扩大1075倍的实验结果由表 2给出。
| 表 2 Caltech-256数据库实验结果 Tab.2 The result on the Caltech-256 database |
对于前10副“旧”的图像,其中有7副图像被正确识别出来,其余3副图像被错误地判断为“新”,后10副图像都被正确地判断为“新”。该实验说明,本文所提的基于REM记忆模型的图像识别算法不止对同一个物体的识别有效,也为同一类物体的识别方法给出了一个新思路。
3.2.1 实验参数对识别率的影响为说明ϕ值和LBP特征向量的倍数变化对Caltech-256数据库实验结果的影响,本文采用多组ϕ值和LBP变化数据进行实验,实验结果如图 7。
|
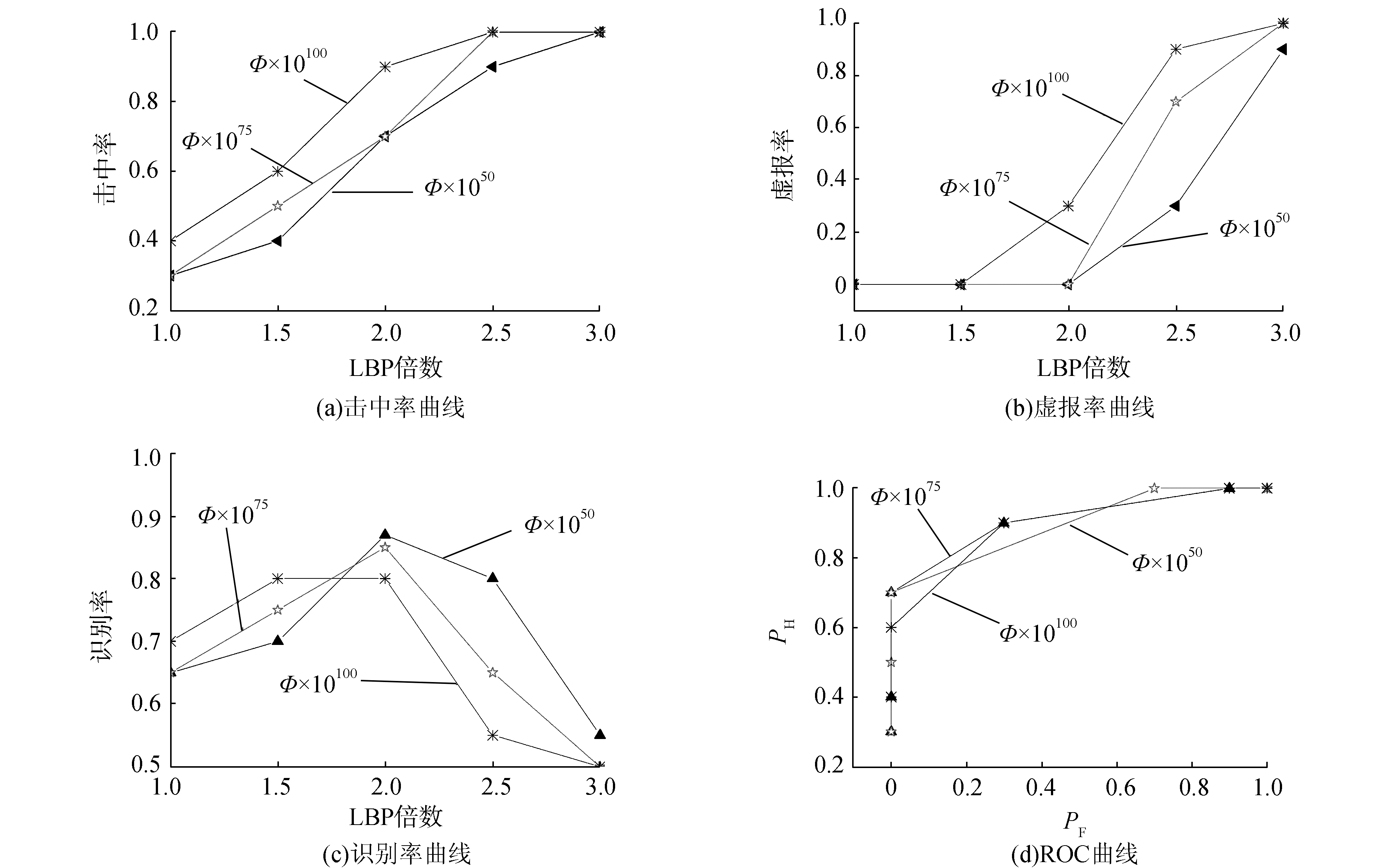
图 7 不同Φ值与LBP倍数变化下的实验曲线 Fig.7 The hit and false rate curve under the varying value of Φ and LBP |
图 7分别描述了在不同ϕ值和LBP特征倍数情况下的图像击中率PH、虚报率PF、识别率与ROC曲线。3种曲线分别代表ϕ值扩大1050,1072,10100倍之后的实验结果。不论ϕ值被扩大多少倍,随着LBP特征倍数的增加,击中率都在增加,但同时虚报率也在增加。当LBP倍数为2时,识别率取得最大值,即不论ϕ值被扩大多少倍,LBP特征被扩大2倍时图像识别率都最高。很明显,ϕ值被扩大10100倍时的识别率较其他情况的识别率低,其余两种情况下的识别率相近。观察3个实验的ROC曲线下的面积(AUC)进行比较,很明显ϕ值被扩大1075倍时ROC曲线下的面积最大,即实验准确性最佳。当LBP特征值被扩大两倍且ϕ值扩大1075倍时,实验识别效果达到最佳。
3.2.2 与SRC算法的实验性能对比实验采用的SRC算法[8]描述如下:所有已学习图像特征向量被标记为X,对每一个探测图像特征向量记为Y,求解如下最优问题:
| $ \mathop {\min }\limits_H \left\| {\mathit{\boldsymbol{Y}}-\mathit{\boldsymbol{X}}H} \right\|_2^2 $ | (3) |
然后计算F=‖Y-XiHi‖22, i=1, 2, …,并搜索最小值Fmin。给定阈值λ,若Fmin>λ,那么该被探测图像被认为是新的;若Fmin≤λ,则反馈结果为已学过的,并且与Fmin对应的图像匹配。
从表 3中可以看出,SRC算法在λ=290时的击中率PH与本文算法相同,但是其虚报率PF高达7/10,远高于本文算法的虚报率。
| 表 3 本文方法与SRC算法在Caltech-256数据库实验对比 Tab.3 Performance comparison between the proposed method and the SRC method on the Caltech-256 database |
为进一步说明所提方法的有效性,对比了本文所提算法与支持向量机(SVM)算法在Caltech-256数据库上的识别分类性能。实验中选取图 5所示的训练图像,即分别属于10个不同类别的10幅图像。对测试图像集,选取20个不同类别(10个已学习类别与10个新类别)的100幅图像,每个类别分别选取5幅图像,实验参数选取c=0.3,g=0.4,实验结果如表 4所示。
| 表 4 本文方法与SVM算法在Caltech-256数据库实验对比 Tab.4 Performance comparison between the proposed method and the SVM method on the Caltech-256 database |
很明显,对已学习过的类别,本文算法有着很好的识别率,并且对从未学习过的类别的虚报率为0,即拒识率达到100%,而SVM算法的虚报率高达100%。
4 结束语在人脑认知记忆模型启发下将图像学习识别与REM模型结合在一起,验证了REM记忆模型可以用于自然图像的存储与提取。实验结果证实了,所提方法能够实现在小幅度旋转情况下的简单图像的识别任务与简单类别图像的分类任务。同时与SRC、SVM算法的实验对比结果说明,本文方法的虚报率远低于SRC与SVM方法。但由于现有特征提取方法限制,及REM模型本身对特征表达采用非负整数的这种要求均限制了图像分类识别率。因此如何对大范围旋转变化图像提取恰当的特征向量改进图像特征表达,同时改进REM模型的特征表达存储方法,以提高图像识别率是下一步的研究重点。
| [1] |
XU Y, ZHANG B, ZHONG Z. Multiple representations and sparse representation for image classification[J]. Pattern recognition letters, 2015, 68: 9-14. DOI:10.1016/j.patrec.2015.07.032 ( 0) 0)
|
| [2] |
HELLMAN M E. The nearest neighbor classification rule with a reject option[J]. IEEE transactions on systems science and cybernetics, 1970, 6(3): 179-185. DOI:10.1109/TSSC.1970.300339 ( 0) 0)
|
| [3] |
DENOEUX T. A neural network classifier based on Dempster-Shafer theory[J]. IEEE transactions on systems man and cybernetics-Part A systems and humans, 2010, 30(2): 131-150. ( 0) 0)
|
| [4] |
DAVTALAB R, DEZFOULIAN M H, MANSOORIZADEH M. Multi-level fuzzy min-max neural network classifier[J]. IEEE transactions on neural networks and learning systems, 2014, 25(3): 470-482. DOI:10.1109/TNNLS.2013.2275937 ( 0) 0)
|
| [5] |
CHANG C C, LIN C J. LIBSVM: a library for support vector machines[J]. ACM transactions on intelligent systems and technology, 2011, 2(3): 389-396. ( 0) 0)
|
| [6] |
SIMONYAN K, ZISSERMAN A. Very deep convolutional networks for large-scale image recognition[J]. Computer science, 2014. ( 0) 0)
|
| [7] |
HUANG G B. What are extreme learning machines? Filling the gap between Frank Rosenblatt's dream and John von Neumann's puzzle[J]. Cognitive computation, 2015, 7(3): 263-278. DOI:10.1007/s12559-015-9333-0 ( 0) 0)
|
| [8] |
WRIGHT J, YANG A Y, GANESH A, et al. Robust face recognition via sparse representation[J]. IEEE transactions on pattern analysis and machine intelligence, 2008, 31(2): 210-227. ( 0) 0)
|
| [9] |
ZHANG L, YANG M, FENG X. Sparse representation or collaborative representation: Which helps face recognition[C]//International Conference on Computer Vision, 2011: 471-478. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=6126277
( 0) 0)
|
| [10] |
YANG M, ZHANG L YANG J, ZHANG D. Robust sparse coding for face recognition[C]//IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR), 2011, 42(7): 625-632. http://ieeexplore.ieee.org/xpls/icp.jsp?arnumber=5995393
( 0) 0)
|
| [11] |
SCHOLKOPF B, PLATT J, HOFMANN T. Sparse representation for signal classification[J]. Advances in neural information processing systems, 2007, 19: 609-616. ( 0) 0)
|
| [12] |
WANG Y. Formal description of the cognitive process of memorization[M]//Transactions on Computational Science V. Springer Berlin Heidelberg, 2009: 81-98.
( 0) 0)
|
| [13] |
WANG Y, CHIEW V. On the cognitive process of human problem solving[J]. Cognitive systems research, 2010, 11(1): 81-92. DOI:10.1016/j.cogsys.2008.08.003 ( 0) 0)
|
| [14] |
MURDOCK B B. A theory of the storage and retrieval of item and associative information[J]. Psychological review, 1982, 89(6): 609-626. DOI:10.1037/0033-295X.89.6.609 ( 0) 0)
|
| [15] |
RAAIJMAKERS J G W, SHIFFRIN R M. SAM: a theory of probabilistic search of associative memory[J]. Psychology of learning and motivation, 1980, 14: 207-262. DOI:10.1016/S0079-7421(08)60162-0 ( 0) 0)
|
| [16] |
HINTZMAN D L. Judgments of frequency and recognition memory in a multiple-trace model[J]. Psychological review, 1988, 95(4): 528-551. DOI:10.1037/0033-295X.95.4.528 ( 0) 0)
|
| [17] |
SHIFFRIN R M, STEYVERS M. A model for recognition memory: REM-retrieving effectively from memory[J]. Psychonomic bulletin and review, 1997, 4(2): 145-166. DOI:10.3758/BF03209391 ( 0) 0)
|
| [18] |
STARN J J, WHITE C N, RATCLIFF R. A direct test of the differentiation mechanism: REM, BCDMEM, and the strength-based mirror effect in recognition memory[J]. Journal of memory and language, 2010, 63(1): 18-34. DOI:10.1016/j.jml.2010.03.004 ( 0) 0)
|
| [19] |
COX G E, SHIFFRIN R M. Criterion Setting and the dynamics of recognition memory[J]. Topics in cognitive science, 2012, 4(1): 135-150. DOI:10.1111/tops.2012.4.issue-1 ( 0) 0)
|
| [20] |
CRISS A H, MCCLELLAND J L. Differentiating the differentiation models: a comparison of the retrieving effectively from memory model (REM) and the subjective likelihood model (SLiM)[J]. Journal of memory and language, 2006, 55(4): 447-460. DOI:10.1016/j.jml.2006.06.003 ( 0) 0)
|
| [21] |
MONTENEGRO M, MYUNG J I, PITT M A. Analytical expressions for the REM model of recognition memory[J]. Journal of mathematical psychology, 2014, 60(3): 23-28. ( 0) 0)
|
| [22] |
DALAL N, TRIGGS B. Histograms of oriented gradients for human detection[C]//Computer Vision and Pattern Recognition. IEEE Computer Society Conference, on, 2005: 886-893. http://doi.ieeecomputersociety.org/resolve?ref_id=doi:10.1109/CVPR.2005.177&rfr_id=trans/tp/2008/10/ttp2008101713.htm
( 0) 0)
|
| [23] |
OJALA T, HARWOOD I. A Comparative study of texture measures with classification based on feature distributions[J]. Pattern recognition, 1996, 29(1): 51-59. DOI:10.1016/0031-3203(95)00067-4 ( 0) 0)
|
| [24] |
LOWE D G. Distinctive image features from scale-invariant keypoints[J]. International journal of computer vision, 2004, 60(2): 91-110. DOI:10.1023/B:VISI.0000029664.99615.94 ( 0) 0)
|
| [25] |
BAY H, TUYTELAARS T, VAN GOOL L. SURF: speeded up robust features[J]. Computer vision and image understanding, 2006, 110(3): 404-417. ( 0) 0)
|
| [26] |
PIETIKAINEN M, OJALA T, XU Z. Rotation-invariant texture classification using feature distributions[J]. Pattern recognition, 2000, 33(1): 43-52. DOI:10.1016/S0031-3203(99)00032-1 ( 0) 0)
|
| [27] |
OJALA T, PIETIKAINEN, MAENPAA T. Multiresolution gray-scale and rotation invariant texture classification with local binary patterns[J]. IEEE transactions on pattern analysis and machine intelligence, 2002, 24(7): 971-987. DOI:10.1109/TPAMI.2002.1017623 ( 0) 0)
|
| [28] |
NENE A S, NAYAR S K, MURASE H. Columbia object image library (COIL-20)[R]. CUCS-005-96, 1996. http://www.researchgate.net/publication/2784735_Columbia_Object_Image_Library_
( 0) 0)
|
| [29] |
GRIFFIN G, HOLUB A, PERONA P. Caltech-256 object category dataset[R]. Pasadena: California Institute of Technology, 2007. https://www.researchgate.net/publication/30766223_Caltech-256_Object_Category_Dataset
( 0) 0)
|
 2017, Vol. 12
2017, Vol. 12


