2. 黑龙江工程学院 电气与信息工程学院, 黑龙江 哈尔滨 150050;
3. 长江大学 电子信息学院, 湖北 荆州 434000
2. The Institute of Electrical and Information Engineering, Heilongjiang Institute of Technology, Harbin 150050, China ;
3. College of Information and Communications Engineering, Harbin Engineering University, Harbin 150001, China
大型舰船总体要素优化设计是舰船总体设计中最基本也是最重要的工作之一。如何选择合适的总体要素将直接关系到大型舰船的安全性、经济性以及战斗性等。因此,设计好的优化方法具有十分重要的实际意义。由于大型舰船航行时具有多变性以及舰船自身技术具有复杂性,利用传统的设计方法[1-5]来求得最佳的舰船总体要素是十分困难的。目前有一些学者研究了进化算法在舰船优化设计中的应用,然而它们大多都是将大型舰船总体要素多目标优化设计问题转化为无约束单目标优化问题进行求解[6-10],所以无法求得分布均匀的Pareto解集,从而不能为设计者提供多样的优化方案。此外,有学者对大型舰船总体要素优化设计问题进行多目标优化[11],但所求解集仍存在分布不均匀、收敛不佳等问题,从而不能提供性能优异且多样的设计方案。为此,本文建立4目标的大型舰船总体要素优化模型,并根据模型特点,提出一种约束多目标分解进化算法用于大型舰船的总体要素优化设计,以改善现有方法的优化性能。
1 大型舰船总体要素优化模型大型舰船总体要素优化设计[10]是一个具有多变量、多目标以及多约束的优化问题,需要确定的总体要素有飞行甲板长Ld、飞行甲板宽Bd、水线长Lw、水线宽Bw、吃水深T、型深D和标准排水量Δ等。目前文献[10]提出的模型最为全面,但该模型只是将多目标优化问题转为成单目标优化问题进行求解,从而无法获得分布均匀的解集,不能为决策者提供良好分布的设计方案。文献[11]利用粒子群算法进行多目标优化,只考虑了舰船的经济性,而忽略了安全性,并且存在所求解集分布不均以及分布不广等问题。为此,在文献[10]和文献[11]的基础上,本文建立一种大型舰船总体要素多目标优化模型,优化目标包括最合理化初稳性高、最大化飞行甲板面积、最大化横摇固有周期和最小化阻力,综合考虑了经济性能和安全性能。
1.1 最合理化初稳性高在大型舰船方案设计中,必须确定最合理的初稳性高,从而确保舰船具有优良的扶正能力和安全性能。然而,大型舰船的初稳性高Ish(Initial stability height)并不是越小越好,也不是越大越好,过小将会导致受力倾斜后扶正缓慢,过大将会导致飞行甲板横摇剧烈。因此,最佳的初稳性高Ish应为一个处于允许范围内的最理想值。本文根据国外同类优秀舰型确定一个最佳参考值Ish0=3.0m[10],并以Ish最接近Ish0为目标。初稳性高Ish如式(1):
 |
(1) |
式中:T为吃水深,Bw为水线宽,D为型深,Cb=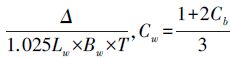
最大化飞行甲板面积是大型舰船方案设计的主要目标,飞行甲板面积可确定为飞行甲板长与飞行甲板宽的函数,如式(2)
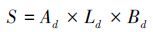 |
(2) |
式中:Ad为面积系数,根据相关舰船设计经验[10]令Ad=0.807, Ld为飞行甲板长,Bd为飞行甲板宽。
1.3 最大化横摇固有周期较大的横摇固有周期能够保证舰载机起降作业的安全系数较高。大型舰船横摇越缓和,即横摇周期TΦ越大,舰载机起降作业越安全。横摇固有周期如式(3):
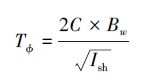 |
(3) |
式中: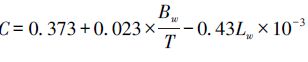
阻力在很大程度会影响大型舰船的快速性和战斗性,所以必须加以考虑。大型舰船阻力计算可转化为估算舰船的有效功率P,本文采用海军系数法确定,如式(4):
 |
(4) |
式中:Δ0=58 000 t,V0=29 kn,V0=200 000 hp,Δ为排水量。
为保障大型舰船的整体性能,还需要对各个要素进行限定,具体设定如下约束条件[10]:2.5 <Ish<4.5,T/Lw>0.035,TΦ>13,Ld<1.128Lw,Bd<1.84Bw。
综上所述,大型舰船总体要素优化设计模型如式(5):
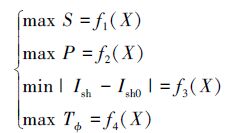 |
(5) |
式(5)中的大型舰船总体要素优化模型具有4个目标函数,各个目标函数是相互冲突的,并且约束条件较为简单,其实质是一个约束4目标优化问题,所以适用于约束多目标进化算法进行求解。
2 约束多目标分解进化算法2007年Zhang等[12]提出了一种基于分解的多目标进化算法(MOEA/D算法),该算法摒弃了常用的Pareto支配,转为采用不同的分解策略进行个体选择,从而为无约束多目标优化提供了一种新思路。目前,MOEA/D算法因其优越的分布性能在诸多进化算法中脱颖而出,成为求解无约束多目标优化问题中备受关注的一种进化算法。
MOEA/D算法的关键步骤包括权重向量的生成和分解策略的选择。
2.1 权重向量的生成初始权重向量的设置是MOEA/D算法的一个重要步骤,通常采用均匀分布的权重向量生成方式。最常用的是在超平面f1+f2+…+fi+…+fm=1(fi为第i维上的分量)上生成均匀分布的权重向量[12],每个权重向量λ=(λ1 ,λ2,… ,λm)满足式(6)的条件,λ的每一维分量λi满足式(7)的条件
 |
(6) |
 |
(7) |
式中:H是需要定义的正整数,m为优化目标数量生成权重向量的数量,其值为N=CH+m-1m-1,N为种群规模。
2.2 分解策略目前MOEA/D算法中应用效果最好的是Tchebycheff分解策略[13],它利用极大极小策略的思想将多目标优化问题分解成单目标子问题,具体可表示成式(8)的形式:
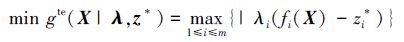 |
(8) |
式中:λi≥0且∑i=1mλi=1,i=1,2,…,m,z*=(z1*,z2*,…,zm*)为参考点,z*是由当前种群中所有个体在各个目标函数上的最优值构成的理想点。
然而,MOEA/D算法需要结合约束技术才能求解约束多目标优化问题。为此,本文提出一种新的约束处理技术,并通过结合MOEA/D算法,构成约束多目标分解进化算法。
2.3 约束处理技术约束处理技术是约束多目标进化算法中最关键的技术,它对于平衡可行解与不可行解的关系起着十分重要的作用。研究表明[14],优秀的不可行解在进化中扮演着重要角色,让它们参与进化不仅能够加大探索范围,而且能够使得进化从不可行域向可行域进化,从而提高种群多样性。然而,过多利用不可行解反而会影响收敛,降低算法效率。通过分析得知,在进化前期应该更多利用部分优秀不可行解的有效信息,以改善多样性维持能力,而在进化后期应该注重收敛性,以保证种群收敛到真实帕累托(Pareto)前沿。基于上述思想,提出一种新的约束处理技术,如式(9):
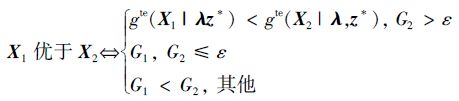 |
(9) |
式中:G1和G2分别代表个体X1和X2的约束违反度[14],ε随进化迭代次数的变化如式(10):
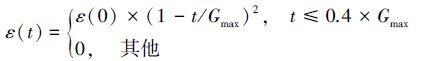 |
(10) |
式中:t为进化迭代次数,Gmax为最大进化迭代次数,ε(0)为初始值,其设置方式如式(11):
 |
(11) |
式中:N为种群规模,G(Xi)为初始种群个体的约束违反度,i=1,2,…,N。
式(10)和式(11)通过调节ε的取值,能够在容忍的约束违反度下扩大约束区域,让更多约束违反度较小的不可行解参与进化,从而加强对可行域边界的探索力度,来提高种群多样性。同时,ε随进化迭代次数的不断增大逐渐减小直至为零,从而不断缩小约束区域,促使进化达到可行域。因此,式(9)~(11)通过互相配合,在进化前期能够让优秀不可行解参与进化来提高多样性;在进化后期约束处理技术强调可行解优于不可行解,从而保障算法收敛到可行Pareto区域。
2.4 算法流程综上所述,约束多目标分解进化算法的具体流程如下:
1) 初始化阶段:生成N个均匀分布的权重向量λ1,λ2,…,λN;计算任意两个权重向量之间的欧氏距离,求出每一个权重向量的邻域集合B(i)={i1,i2,…,iT},{i1,i2,…,iT}代表距离权重向量λi最近的T个权重向量的索引;利用随机方式生成初始种群{X1,X2,…,XN},令FVi=F(X);构造参考点z*=(z1* z2* … zm*);设置初始进化迭代次数t=1。
2) 进化阶段:从每一个B(i),i=1,2,…,N中随机选取两个个体与Xi经过差分变异操作[15]和交叉操作[15]生成试验个体Y*;若Y的某一维分量超出定义域,则对该分量进行修补操作[15],让其重新在定义域内;计算新生个体的目标函数值F(Y)=(f1(Y)),f2(Y),…,fm(Y))。
3) 更新阶段:若zi* <fi(Y),则令zi*=fi(Y);利用2.3节方法进行个体比较,若Y优于Xi,令Xi=Y,FVi=F(X);
4) 判断终止条件。若t=Gmax,则算法停止并输出种群中的Pareto最优解;否则,t=t+1,返回2)。
2.5 算法的时间复杂度假设种群规模为N,目标数量为m,则本文算法迭代一次的最坏时间复杂度计算为:种群目标函数和约束违反度的时间复杂度为O(mN);差分变异和交叉操作的时间复杂度为O(2mN),修补操作的时间复杂度为O(mN);更新种群的最坏时间复杂度为O(mN),算法迭代一次的最坏时间复杂度为
O(mN)+O(2mN)+O(mN)+O(mN)=O(5mN)
由此可得,本文算法的时间复杂度为O(mN)。
3 大型舰船总体要素优化设计的实现综上所述,基于约束多目标分解进化算法的大型舰船总体要素优化设计的具体实现过程如下。
1) 初始化阶段
①设置参数,包括种群规模N,最大进化迭代次数Gmax,缩放因子F,交叉因子CR,确定舰船总体要素中变量的上限和下限;
②生成N个均匀分布的权重向量λ1,λ2,…,λN;
③计算任意两个权重向量之间的欧氏距离,求得每一个权重向量的邻域集合 B(i)={i1,i2,…,iT},{i1,i2,…,iT}代表距离权重向量λi最近的T个权重向量的索引;
④利用随机方式生成初始种群{X1,X2,…,XN},令FVi=F(Xi),其中,Xi={Ld Bd Lw Bw T D Δ},FVi={S,P,|Ish-Ish0|,TΦ};
⑤构造参考点z*=(z1* z2* … zm*),zi*=min{fi(X)|X∈Ω},i=1,2,…,m;
⑥设置初始进化迭代次数t=1。
2) 进化阶段
①从每一个B(i),i=1,2,…,N中随机选取两个个体与Xi经过差分变异操作[15]和交叉操作[15]生成试验个体Y*;
②若Y的某一维分量超出定义域,则对该分量进行修补操作[15],让其重新在定义域内;
③计算新生个体的目标函数值F(Y)=(f1(Y), f2(Y),…,fn(Y))。
3) 更新阶段
①更新参考点:若z1*<fi(Y),则令zi*=fi(Y),i=1,2,…,m;
②个体比较阶段:利用2.3节方法,若Y优于Xi,则令,Xi=Y,FVi=F(Y);
4) 判断终止条件。若t=Gmax,则算法停止并将种群中的Pareto最优解作为结果输出;否则,返回2)。
4 实验仿真与结果分析为验证本文提出算法的有效性和先进性,将其与目前优化性能较好的文献[10]算法、文献[11]算法进行对比实验。实验硬件环境为Intel Pentium、CPU:G620、4 GB内存、主频2.6 GHz的计算机,程序采用MATLAB R2010编写。本文算法的实验参数参考文献[12]设置为:种群规模N=200,最大进化迭代次数Gmax=1 500,缩放因子F=0.5,交叉因子CR=0.9。决策变量X=(Ld Bd Lw Bw T D Δ)的定义域如表 1所示。
| 变量 范围 |
Ld/m | Bd/m | Lw/m | Bw/m | T/m | D/m | Δ/t |
| 下限 | 280 | 60 | 250 | 35 | 8 | 25 | 60 000 |
| 上限 | 350 | 80 | 300 | 50 | 12 | 35 | 80 000 |
表 2给出了本文算法和文献[10]算法所求方案的对比结果。其中,文献[10]算法将4个目标聚合成一个目标进行单目标优化,一次运行只能得到一个解。本文算法是进行多目标优化,一次运行能够得到一组解(数量为种群规模)。限于篇幅,本文算法从200个(种群规模)解中随机选择3个与文献[10]算法进行对比。
从表 2可以看出,本文方案1支配文献[10]方案,并且本文方案1在所有目标上完全优于文献[10]方案,即具有更大的飞行甲板面积、更好的初稳性高、更小的阻力和更大的横摇固有周期。本文方案2和本文方案3与文献[10]方案互不支配,但本文方案2在飞行甲板面积、阻力和横摇固有周期上具有明显的优势,在初稳性高上略劣于文献[10]方案。本文方案3在阻力和横摇固有周期上具有更优的性能,而在飞行甲板面积和初稳性高上欠佳。综上分析可以得出,本文算法不仅能够为决策者提供多样分布的方案,而且所得方案具有较好的收敛性能。本文算法求得的大型舰船总体要素如表 3所示。
| 总体 要素 |
Ld/m | Bd/m | Lw/m | Bw/m | T/m | D/m | Δ/t |
| 方案1 | 338.4 | 79.9 | 299.9 | 44.5 | 11.6 | 32.6 | 60 056 |
| 方案2 | 282.5 | 77.9 | 251.3 | 45.3 | 10.2 | 34.9 | 60 312 |
| 方案3 | 307.1 | 79.6 | 272.7 | 45.3 | 10.4 | 34.9 | 60 624 |
表 4给出了本文算法和文献[11]算法所求方案的对比结果。其中,文献[11]算法和本文算法一样,对4个目标同时进行多目标优化。为便于公平比较,文献[11]算法和本文算法均选择在单个目标上最优的解。
从表 4可以看出,本文方案4与文献[11]方案1相比,具有更优的飞行甲板面积、初稳性高和阻力,而在横摇固有周期上劣于文献[11]方案1。本文方案5与文献[11]方案2相比,在4个目标上均获得最优结果,即具有更优的飞行甲板面积、初稳性高、阻力以及横摇固有周期。同样,本文方案6与文献[11]方案3相比,在4个目标上均最优,即前者支配后者。本文方案7与文献[11]方案4相比,除在横摇固有周期上略劣之外,在飞行甲板面积、初稳性高、阻力上均具有明显优势。综上分析可以得出,本文算法相比文献[11]算法具有更好的收敛性,能够为设计中提供更优的决策方案。本文算法所求的大型舰船总体要素如表 5所示。
| 总体 要素 |
Ld/m | Bd/m | Lw/m | Bw/m | T/m | D/m | Δ/t |
| 方案4 | 326.1 | 79.7 | 289.6 | 45.1 | 10.4 | 34.9 | 60 989 |
| 方案5 | 338.0 | 79.8 | 299.9 | 44.6 | 10.7 | 34.2 | 60 235 |
| 方案6 | 338.3 | 80.0 | 300.0 | 44.8 | 11.6 | 32.2 | 60 025 |
| 方案7 | 338.1 | 79.9 | 299.9 | 44.5 | 10.9 | 33.8 | 60 044 |
综上所述,本文提出的大型舰船总体要素优化方法能够获得性能优异且丰富多样的设计方案,使得大型舰船具备更好的初稳性高、更大的飞行甲板面积、更大的横摇固有周期以及更小的阻力,不失为一种简单和高效的新方法。
5 结论针对大型舰船方案优化设计的特点,建立了大型舰船总体要素优化模型,并将提出的约束多目标分解进化算法用于大型舰船的总体要素优化设计,通过仿真算例可以得到以下结论:
1) 提出的大型舰船总体要素优化方法是一种简便、高效的方法,能够用于大型舰船的优化设计。
2) 在分布性和收敛性上,提出的约束多目标分解进化算法相比其他优化方法均具有一定优势。
同时,在后续研究中将进一步完善舰船总体要素模型,加入更多的目标属性,以适应不断变化的实际需求。
| [1] | 冯佰威, 刘祖源, 常海超. 多学科设计优化技术在船舶初步设计中的应用[J]. 中国造船 , 2009, 50 (4) : 109-116 FENG Baiwei, LIU Zuyuan, CHANG Haichao. Application of multi-disciplinary design optimization techniques in ships' preliminary design[J]. Shipbuilding of China , 2009, 50 (4) : 109-116 |
| [2] | 周奇, 陈立, 许辉, 等. 舰船总体设计中的多学科优化技术[J]. 船舶与海洋工程 , 2013 (3) : 6-9 ZHOU Qi, CHEN Li, XU Hui, et al. Multi-disciplinary optimization method in ship overall design[J]. Naval architecture and ocean engineering , 2013 (3) : 6-9 |
| [3] | CAMPANA E F, LIUZZ G, LUCIDI S, et al. New global optimization methods for ship design problems[J]. Optimization and engineering , 2009, 10 (4) : 533-555 DOI:10.1007/s11081-009-9085-3 |
| [4] | 刘鹏, 付雪峰. 基于高精度近似模型的舰船线型优化[J]. 舰船科学技术 , 2015, 37 (6) : 92-94 LIU Peng, FU Xuefeng. A method of hull line optimization based on CFD and approximate model[J]. Ship science and technology , 2015, 37 (6) : 92-94 |
| [5] | 毕晓君, 刘国安. 基于云差分进化算法的约束多目标优化实现[J]. 哈尔滨工程大学学报 , 2012, 33 (8) : 1022-1031 BI Xiaojun, LIU Guoan. A cloud differential evolutionary algorithm for constrained multi-objective optimization[J]. Journal of Harbin engineering university , 2012, 33 (8) : 1022-1031 |
| [6] | 金雁, 赵耀. 基于改进蚁群算法的船舶主尺度优化[J]. 华中科技大学学报:自然科学版 , 2008, 36 (11) : 99-102 JIN Yan, ZHAO Yao. Optimization of ship principal parameters with improved ant colony algorithm[J]. Journal of Huazhong university of science & technology:natural science edition , 2008, 36 (11) : 99-102 |
| [7] | 柳存根, 裘泳铭, 姚震球, 等. 遗传进化算法在船舶初步设计中的应用[J]. 上海交通大学学报 , 2000, 34 (1) : 41-45 LIU Cungen, QIU Yongming, YAO Zhenqiu, et al. Application of genetic evaluative algorithm in ship preliminary design[J]. Journal of Shanghai jiaotong university , 2000, 34 (1) : 41-45 |
| [8] | PARSON M G, SCOTT R L. Formulation of multicriterion design optimization problems for solution with scalar numerical optimization methods[J]. Journal of ship research , 2004, 48 (1) : 61-76 |
| [9] | 李文龙, 谭家华. 集装箱船主尺度全局最优化的混沌算法[J]. 中国造船 , 2003, 44 (1) : 11-16 LI Wenlong, TAN Jiahua. Global optimization of container ships' principal parameters based on chaos optimization algorithm[J]. Shipbuilding of China , 2003, 44 (1) : 11-16 |
| [10] | 王文全, 黄胜, 侯远航, 等. 基于改进人工蜂群算法的大型舰船主尺度优化[J]. 武汉理工大学学报 , 2012, 34 (6) : 58-62 WANG Wenquan, HUANG Sheng, HOU Yuanhang, et al. Optimal principal parameters for large naval ship based on modified artificial bee colony algorithm[J]. Journal of Wuhan university of technology , 2012, 34 (6) : 58-62 |
| [11] | 侯磊. 基于多目标粒子群算法的船舶主尺度优化设计研究[J]. 船舶力学 , 2011, 15 (7) : 784-790 HOU Lei. Application of multi-objective particle swarm optimization (MOPSO) in study of ship's principal parameters[J]. Journal of ship mechanics , 2011, 15 (7) : 784-790 |
| [12] | ZHANG Qingfu, LI Hui. MOEA/D:a multiobjective evolutionary algorithm based on decomposition[J]. IEEE transactions on evolutionary computation , 2007, 11 (6) : 712-731 DOI:10.1109/TEVC.2007.892759 |
| [13] | WANG Zhenkun, ZHANG Qingfu, ZHOU Aimin, et al. Adaptive replacement strategies for MOEA/D[J]. IEEE transactions on cybernetics , 2016, 46 (2) : 474-486 DOI:10.1109/TCYB.2015.2403849 |
| [14] | 毕晓君, 张磊, 肖婧. 基于双种群的约束多目标优化算法[J]. 计算机研究与发展 , 2015, 52 (12) : 2813-2823 BI Xiaojun, ZHANG Lei, XIAO Jing. Constrained multi-objective optimization algorithm based on dual populations[J]. Journal of computer research and development , 2015, 52 (12) : 2813-2823 |
| [15] | 毕晓君, 张磊. 基于自适应ε截断策略的约束多目标优化算法[J]. 电子与信息学报 , 2016, 38 (8) : 2047-2053 BI Xiaojun, ZHANG Lei. Constrained multi-objective optimization algorithm with adaptive ε truncation strategy[J]. Journal of electronics & information technology , 2016, 38 (8) : 2047-2053 |



