预测是所有的科学学科所不能回避的问题。链路预测是数据挖掘的研究方向之一,尤其在计算机领域早有较深入的研究,其研究思路主要是基于马尔可夫链和机器学习[1-3]。网络中的链路预测是利用已知的网络节点以及网络结构等信息,预测网络中尚未产生连边的两个节点之间链接的可能性。这种预测包含了对网络中实际上存在但尚未被探测到的链路预测,即“未知链接”预测;也包含了目前不存在和应该存在或者未来可能会存在的链路预测,即“未来链接”预测。其中,基于相似性 (接近程度) 的链路预测是网络链路预测的主流方法。刻画节点的相似性有较多方法,最简单直接的就是利用节点的属性,网络中属性相似的节点之间更容易链接[4]。应用节点属性进行预测的效果良好,如刘宏鲲等[5]利用链路预测将结构 (共同邻居数目) 和节点属性 (地理位置、人口、GDP和第三产业产值) 进行耦合,研究中国城市航空网络演化机制;O'Madadhain等[6]利用网络的拓扑结构信息以及节点的属性建立了一个局部的条件概率模型,应用节点属性进行链路预测;Lin[7]基于节点的属性定义了节点间的相似性,直接用定义的属性进行链路预测。虽然应用节点外部信息可得到良好的预测效果,但很多情况这些信息非常难获取,包括信息是保密的、真假难辨等,甚至无法获得。相对于节点外部信息而言,获取网络内部结构信息较为容易也更加可靠。近几年,内部结构相似性的链路预测方法受到越来越多的关注,包括度分布、集聚性质、社团结构、节点中心性、节点间的路径长度等[8-10]。Liben-Nowell等[11]定义了网络拓扑结构的相似性方法,将相似性指标分为节点和路径,并且分析了多种指标在社会合作网络中的预测效果。周涛等[12]用9种相似性指标对6种现实网络进行了链路预测,进一步验证了Liben-Nowell等的研究结果,并且提出了两种精确度更高的指标:资源分配指标和局部路径指标。Clauset等[13]分析了利用网络的层次结构进行链路预测的方法,该方法在具有明显层次结构的网络中表现较好;Roger G等[14]提出了识别错误链路预测的方法,同时定义了网络错误连边的概念。
利用链路预测方法不仅在各种静态网络结构的研究成果众多,从动态角度揭示网络演化的机制、各种微观因素对网络结构形成的影响成果也较为丰富[15-18]。利用链路预测研究网络演化机制最常用的方法是直接建立演化模型从而预测影响网络演化的因素。例如Barabási-Albert (BA)[19]模型是基于节点度研究网络优先连接机制,针对某些影响因素建立对象网络并研究其统计特征,如果分析所得的统计特征具有和真实网络接近的性质,那么这些影响因素对网络的结构就有显著影响,即这些因素是网络演化的重要机制,否则认为这些影响因素对网络结构的影响不显著。但衡量模拟网络与真实网络相似度的影响因素指标可能会表现不一致,以致难以辨析哪些才是影响网络演化的主导因素,以及这些主导因素在网络演化过程中分别起到了多大的作用,这在一定程度上制约了演化模型的发展。
能源在我国社会发展中具有重要战略地位,能源问题已成为影响经济发展、国家安全等重大战略性问题。能源供应链是由多流程 (能源供应、加工、配送等)、多部门 (生产部门、运输部门等)、多资源 (人力、物力、技术等) 要素构成的开放系统,节点企业的协调和合作影响整个供应链的运营效率。自然灾害可导致煤电能源供应链脱节,重要电路供电中断。能源供应链断链的背后,映射出我国能源供应链各个环节需要进行整体规划,实现相互协调与合作。因此,对于现实中的能源供应链的合作演化机制有必要进行深入研究。
随着能源供应链面临的问题越来越多,供应链上节点企业的内外部环境越来越复杂,很多合作问题亟需解决,针对能源供应链合作演化,本文提供了一个全新的视角,即利用链路预测研究能源供应链合作演化机制问题。在分析链路预测法和评价指标的基础上,对能源供应链进行实证分析,将供应链似然成网络,在供应链网络中选取5个可以代表能源供应链的网络结构相似性指标,通过计算5种相似性指标的精确度,清晰直观地对各指标预测精确度进行辨别,找到最佳的预测指标,并将最佳指标和其他4种指标耦合,运用耦合指标算法更加精确地预测“未知链接”和“未来链接”,为挖掘能源供应链合作演化机制的重要驱动因素模型和公平评价模型优劣提供了可能性,链路预测在分析供应链网络演化机制上提供了科学的量化方法。
1 问题描述与评价指标国民生产和生活需要消耗大量的能源,每个节点企业协调一致保障着整个供应链的高效运营,一旦供应链发生问题,小则导致局部瘫痪,大则引起社会动荡。上游企业 (如煤炭、电力企业) 和下游企业 (如钢铁企业) 不仅是供求关系,同时也是一个整体,节点企业之间相互制约和相互合作。供应链中的合作是相互合作,不存在方向性,因此可将能源供应链节点企业之间的合作关系描述为一个完整无向网络,节点之间的连线代表企业间合作关系,利用无向网络一些特征和链路预测对其进行合作演化研究。
针对任意无向网络G,令N为网络的总节点数,U为总连边数,则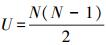
为了测试相似性指标预测的准确性,一般将已知的连边E分为两个部分:训练集ET和测试集EP。显然,E=ET∪EP,ET∩EP=∅。在此,将属于U但不属于E的边称为不存在的边,称为J,属于U但不属于ET的边为未知边,称为H。
衡量链路预测算法精确度的指标主要有AU、Precision和RankingScore。这3个指标对预测精确度衡量的侧重点不同,其中AUC是最常见的一种衡量指标,它从整体上衡量算法的精确度[20];Precision只考虑排在前L位的边是否预测准确[21];而RankingScore则更多考虑了所预测边的排序[22]。文中选择的衡量算法精确度的指标为AUC,AUC是在EP中随机选择一条边的分数值比随机选择的一条不存在的边的分数值高的概率[23]。每次随机从EP中选一条边,再从J中随机选择一条边,若EP中选择边的分数值大于J中选择边的分数,那么就加1分;若两个分数值相等就加0.5分;若小于就不加分。这样独立比较n次,如果有M次EP中的边分数值大于J分数值,有Z次两分数值相等,AUC的计算式如式 (1) 所示。
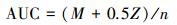 |
(1) |
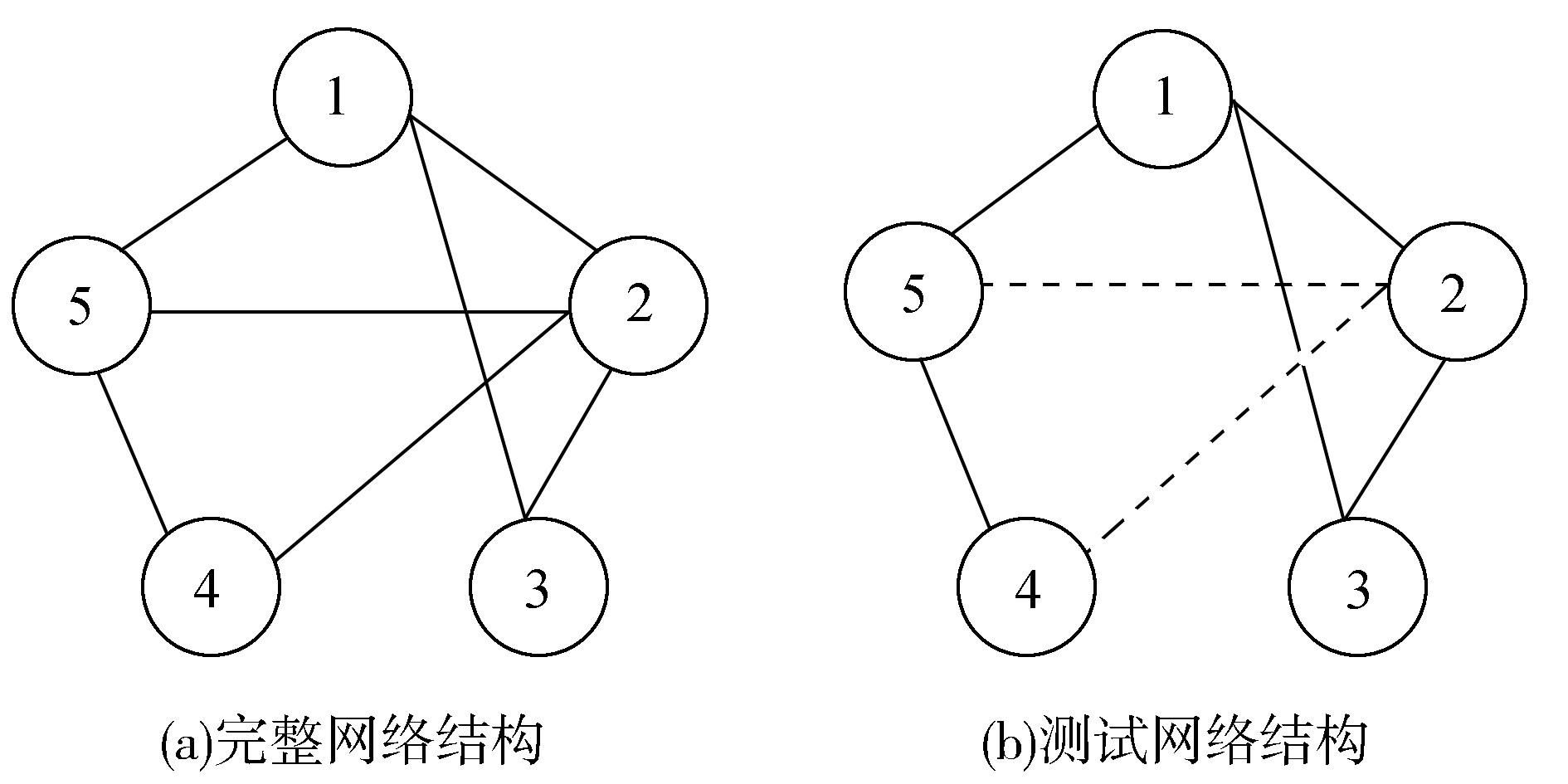
假设所有分数都是随机产生的,因此AUC≈0.5,当AUC≥0.5时,大于的程度衡量了算法在多大程度上比随机选择的方法要精确。为了进一步说明AUC指标的含义,假设由5个节点构成的能源供应链网络,其结构图如图 1所示。
|
| 图 1 5个节点能源供应链网络结构 Fig. 1 Network structure of five node energy supply chains |
图 1表示一个完整的供应链网络结构,实线表示训练集,虚线表示测试集。该网络中包含5个节点,该网络在理论上存在的连边数是5×(5-1)/2=10,其中7条是已知的,剩下3条为不存在的边。为了验证链路预测算法的精确性,需要在7条已知边中选择部分构成EP,假如选择边{2, 4}和{2, 5}作为测试边,如图 1(b)所示,则剩下的5条已知边则构成ET。在链路预测方法中,只应用ET中边的信息,上述中的EP中的边仅是随机从已知边中选取的,若再进行下一次验证精确性选择,则测试边不一定是{2, 4}和{2, 5},而是ET中的任何边都可能被选出作为测试边,ET中的边只是暂时被“待定”。根据链路预测算法得到剩下5条未知边的得分值分别为s25=4,s24=4.5,s14=3.8,s34=4.6,s35=4,那么在计算AUC时需将未知边按照其得分排序:s14 < s25=s35 < s24 < s34,再根据上述AUC计算公式,得AUC=(1+0.5+1+1)/(2×3)=0.583。
由此可以说明,当选择EP中的边个数发生变化时,AUC值会相应地变化,即使EP完全相同时,AUC值也会不同。因为AUC计算公式中的n是抽样次数,抽样方式有多种类型,如随机抽样、逐项遍历、滚雪球抽样等,由5个节点构成的能源供应链中n=6,其含义是测试边和不存在的边比较了6次。而在文中利用计算机程序计算AUC值时,比较的边 (预测边和不存在边的比较) 是随机抽取的,因此即便EP中信息完全一样,抽样次数和抽样比较对象不同导致AUC值变化,为了使得到的AUC越接近真实值,抽样次数n越大越好。
2 能源供应链网络合作演化分析本文运用链路预测对能源供应链合作演化进行研究,将能源供应链网络中节点内外部信息量化,对量化后的数据进行划分,再利用相似性指标对预测进行得分,最后使用AUC评价指标对预测的精确性进行对比分析。
2.1 能源供应链网络结构一个简单无向无权网络,由点和边构成,需要满足以下4个条件:
1) 节点自身不可以与自身连接;
2) 节点间最多只有一条连线,不可出现多条连边;
3) 连边不具有方向性;
4) 连边只代表节点间关系,代表的是合作的关系,没有对应的权重。
本文分析的能源供应链由20个节点企业构成,将其分别编号为1, 2, …, 20,其节点链接表示其长期合作情况,如表 1所示。
| 节点企业编号 | 合作节点企业编号 |
| 1 | 2, 3, 4, 5, 6, 7, 8, 11, 14, 16, 17, 20 |
| 2 | 1, 3, 4, 5, 6, 7, 8, 10, 12, 13, 15, 16, 18, 20 |
| 3 | 1, 2, 4, 5, 6, 7, 8, 10, 11, 16 |
| 4 | 1, 2, 3, 5, 6, 7, 8, 11, 14, 16 |
| 5 | 1, 2, 3, 4, 6, 7, 8, 9, 12, 18, 19, 20 |
| 6 | 1, 2, 3, 4, 5, 7, 8, 9, 14 |
| 7 | 1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 14, 15, 19 |
| 8 | 1, 2, 3, 4, 5, 6, 7, 17 |
| 9 | 5, 6, 7, 10 |
| 10 | 2, 3, 7, 9, 13 |
| 11 | 1, 3, 4 |
| 12 | 2, 5, 7, 13 |
| 13 | 2, 10, 12 |
| 14 | 1, 4, 6, 7, 19 |
| 15 | 2, 7 |
| 16 | 1, 2, 3, 4, 17, 18 |
| 17 | 1, 8, 16 |
| 18 | 2, 5, 16 |
| 19 | 5, 7, 14 |
| 20 | 1, 2, 5 |
由表 1中所示的节点企业的合作情况,将其合作转化成连边。在使用计算机分析时,用邻居矩阵来刻画网络,假设能源供应链网络的邻居矩阵为A,由上表可知A是一个20×20的方阵,如果节点vx、vy有合作关系,那么A的第x行y列上的元素就为1,否则为0。为了方便研究,在满足构建条件的同时,作出如下假设:
1) 传统的供应链管理是按照上下游关系将供应链中企业分为制造商、分销商、零售商等,而本文研究不考虑企业的类型,只是将企业作为网络中的一个节点;其次,一般供应链的末端都是消费者,为了方便统计,将零售商作为整个网络的边界点;
2) 企业间有相互的合作关系,则彼此之间存在一条连线,合作是指长期的合作,短期的或者偶尔的合作将不作为连线标准,同时认为合作是相互的,不考虑连边的方向性;
3) 将供应链企业合作关系抽象为无向网络,忽略企业间上下游的关系,默认企业间的传递信息是对称的,所以没有对边进行赋值。
2.2 基于网络结构相似性的指标利用节点间的相似性进行链路预测时,两个节点之间相似性越大,它们之间存在链接的可能性就会越大。相似性也为一种接近的程度。基于网络结构相似性可分为基于局部信息的相似性、基于路径的相似性和基于随机游走的相似性。
基于局部信息的最简单的相似性指标是共同邻居的相似性指标CN[24](common neighbors),又称为结构等价 (structural equivalence),即两个节点如果有很多的共同邻居节点,那么这两个节点相似。在链路预测中应用CN指标的基本假设是两个未链接的节点如果有更多的共同邻居,则它们更倾向于连边。CN指标是对于网络中的节点vx,定义其邻居集合为Γ(x),则两个节点vx和vy的相似性就定义为两者共同的邻居数,即
 |
(2) |
局部信息相似性指标除了共同邻居的相似性指标以外,还有基于偏好连接相似性[25](PA) 指标。偏好连接是指优先连接,即一条新边连接到节点vx的概率正比于该节点的度kx的大小。新链接节点vx和vy的概率正比于两个节点度的乘积。由此两个节点间的偏好连接相似性定义为
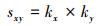 |
(3) |
局部信息的相似性指标的优势就在于计算复杂度较低,但是由于利用信息有限,预测精度受到了限制。周涛等[26]在共同邻居的基础上考虑三阶路径的因素,提出了基于局部路径相似性指标 (local path,LP)。其定义为
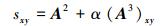 |
(4) |
式中:α为可调参数,A表示网络的邻接矩阵,(A3)xy表示节点vx和vy之间的长度为3的路径数目。当α=0时,LP指标退化为CN指标。CN指标本质上是考虑了二阶路径数目,当然LP指标也可以扩展到为更高阶形式,但是当阶数无穷大的时候,LP就会相当于考虑网络全部路径的Katz指标[27]。
Katz指标考虑了网络的所有路径,其定义为
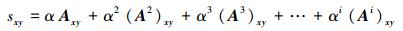 |
(5) |
式中:(Ai)xy表示连接节点vx和vy之间长度为i的路径数。由式 (5) 可知,当可调参数α很小时,高阶路径的贡献也很小,使得Katz指标的预测效果接近于LP指标。
有相当数量的相似性指标是基于随机游走的,譬如有重启的随机游走指标[28](Random walk with restart,RWR)。RWR指标假设随机游走粒子在每走一步的时候都以一定概率返回初始位置。设粒子返回概率为ρ,P为网络概率返回矩阵,其元素Pixy=axy/kx表示节点vx处的粒子下一步到节点vy的概率,如果两者相连axy=1,否则axy=0。某粒子初始时刻在节点vx处,那么t+1时刻该粒子到达网络每个节点概率向量为
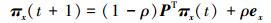 |
(6) |
式中:ex表示一个一维列向量且仅有第x个元素为1,其他元素都为0。不难得到式 (6) 的稳定解为
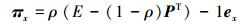 |
(7) |
式中:πxy为节点vx出发的粒子最终有多少概率走到节点vy,由此定义RWR相似性为
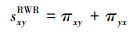 |
(8) |
表 1中所示该能源供应链共66条连边,不存在自环 (没有单独的点),而20个节点的网络在理论上的链接边数为20×[(20-1)/2]=190条,当前已知链接数为66,未知链接数为190-66=124。假设测试集比例为10%,训练集则为90%,对测试集和训练集进行一次性划分,在划分的同时需要保证训练集的连通性。测试集中的测试边的数目为66×10%≈7,最精确的方法是将所有的测试边和不存在的边都进行比较,共有比较次数为7×124=868次,因为计算机程序代码设计的是随机抽样,为了使得AUC尽可能接近真实值,本文采取抽样次数为200 000次,并进行200次独立实验,计算出的AUC值等于200 000次抽样200次独立实验的平均数。
计算AUC值的过程类似于伯努利实验,200 000次随机抽样的结果不相互影响,忽略比较得分相等的情况下,计算AUC值时得分为1的概率为p,则得分为0的概率为1-p。如此地进行n次抽样得到的AUC值为M/n,抽样次数越多AUC值越接近p。那么,最佳的抽样次数是能够接受的概率无限接近于p的最小n值。设LP指标和Katz指标中可调参数α=0.001,RWR指标中的粒子返回概率ρ=0.95,5种相似性算法在能源供应链中预测的AUC值平均值和方差如表 2所示。
| 算法名称 | 精确度 | 方差 |
| 共同邻居 (CN) | 0.737 4 | 0.009 3 |
| 偏好连接 (PA) | 0.759 3 | 0.010 4 |
| 局部路径 (LP) | 0.760 3 | 0.009 0 |
| 全部路径 (Katz) | 0.746 5 | 0.009 5 |
| 重启的随机游走 (RWR) | 0.795 2 | 0.007 1 |
由表 2看出,当单独以5种指标作为相似性算法时,RWR指标的精确度AUC为0.795 2是最高的,说明通过RWR指标进行能源供应链节点企业合作预测更符合网络特征,对于合作演化的机制具有较高的精确性,而且平均方差σ=0.007 1,在5种指标中也是最小的,意味着200组独立实验计算的AUC值波动幅度最小,提高了实验的准确性和可靠性;利用路径相似指标的LP指标预测效果好于Katz指标,也就是在该能源供应链网络中考虑局部路径的效果明显好于考虑全部路径,其中LP指标预测效果也是5组指标中精确度第2的指标;基于局部信息相似指标的PA指标预测的精确度大于CN指标的精确度,但是PA指标的实验数据方差较大,也就是再次进行实验时可能导致PA指标平均精确度值变化较大;CN指标预在能源供应链中预测合作的效果最差,和其他4个指标相比,精确度之差相差甚大。在此特别说明的是,表 2中精确度的平均值并不是绝对的,也就是说,假如再一次进行200组独立实验时,计算的结果可能会发生改变,但是通过各自方差可知变化浮动不会太大。
为了丰富算法的选择,将5种指标算法进行相互结合,以便观察两种指标耦合后预测效果好还是单独利用相似性指标效果好。本文设计的是:经过计算后的精确度最高的RWR指标与其他4种指标分别耦合从而进行链路预测,也就是将基于随机游走的指标与路径相似性指标、局部信息相似性指标进行耦合。采用的是最简单的线性方式,即
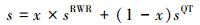 |
(9) |
式中:sRWR是基于RWR指标,sQT是基于其他4种结构性指标,参数x∈[0, 1],当x=1时,算法回归到sRWR,当x=0时,算法回归到sQT。
式 (9) 中实际上是对计算机程序中指标算法的得分进行重新计算,为了统一标准,将每种相似性指标得分值作归一化处理,即每组数据都除以组别数据中的最大值。值得注意的是,所有算法最后的链接边的得分都是在训练集的基础上计算出来的,也就是在训练集和测试集划分后,原网络的链接情况就是去掉测试集中的边剩下训练集的边,测试集中边和不存在链接一样不存在了,预测的时候只可以应用训练集中的信息。
参数x的区间为[0.1, 0.95],步长为0.05,分别计算4种耦合指标算法的精确度结果如表 3。
| x | RWR+CN | RWR+PA | RWR+LP | RWR+Katz |
| 0.1 | 0.769 6 | 0.767 5 | 0.770 7 | 0.797 9 |
| 0.15 | 0.762 8 | 0.774 4 | 0.777 0 | 0.799 7 |
| 0.2 | 0.758 1 | 0.779 8 | 0.780 8 | 0.797 8 |
| 0.25 | 0.755 7 | 0.768 1 | 0.764 0 | 0.801 4 |
| 0.3 | 0.762 6 | 0.778 3 | 0.773 0 | 0.790 1 |
| 0.35 | 0.767 5 | 0.784 6 | 0.780 6 | 0.804 0 |
| 0.4 | 0.777 3 | 0.774 4 | 0.772 9 | 0.795 1 |
| 0.45 | 0.772 9 | 0.784 1 | 0.777 7 | 0.786 5 |
| 0.5 | 0.785 5 | 0.778 5 | 0.775 4 | 0.793 8 |
| 0.55 | 0.770 0 | 0.782 3 | 0.780 9 | 0.783 8 |
| 0.6 | 0.779 9 | 0.784 4 | 0.782 5 | 0.799 6 |
| 0.65 | 0.786 9 | 0.788 3 | 0.788 2 | 0.788 7 |
| 0.7 | 0.784 0 | 0.776 0 | 0.777 1 | 0.791 5 |
| 0.75 | 0.789 0 | 0.784 5 | 0.783 4 | 0.788 7 |
| 0.8 | 0.779 1 | 0.789 8 | 0.790 7 | 0.797 3 |
| 0.85 | 0.783 3 | 0.801 5 | 0.802 8 | 0.804 8 |
| 0.9 | 0.786 1 | 0.790 4 | 0.790 4 | 0.801 5 |
| 0.95 | 0.805 7 | 0.800 7 | 0.800 1 | 0.799 1 |
根据表 3数据,确定耦合后算法精确度变化趋势如图 2所示。图3展现了4种耦合算法随着参数x变化,预测精确度的变化情况。
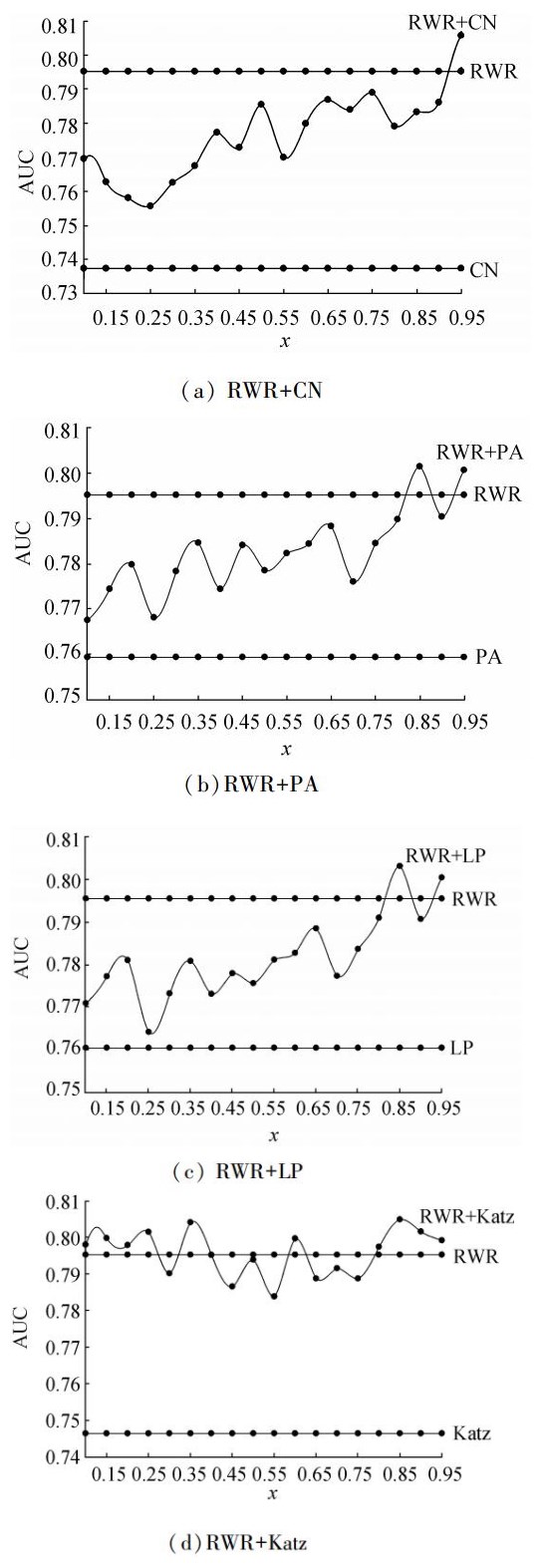
|
| 图 2 耦合算法精确度随着参数的变化情况 Fig. 2 The accuracy of coupling algorithms change with the parameter |
1) 将RWR指标与其他各4个指标相互耦合后预测能源供应链网络链路合作演化效果总比单独考虑其他4个指标预测效果要好,同时存在最优参数使得耦合指标算法预测精确度要高于单独考虑RWR指标。
2) 观察图 2(b)和图 2(c)可知,RWR指标分别耦合PA指标、LP指标后精确度变化趋势几乎是相同的,在单独考虑PA指标、LP指标时,其精确度就几乎相等,因此可以认为在能源供应链网络链路合作预测时,PA指标和LP指标是等价的,预测效果是相近的。
3) 当RWR+Katz耦合后,其精确度在单独考虑RWR指标时的精确度上下波动,而RWR与其他3个指标耦合精确度都有随着参数的增大而增大的趋势,也就是说,RWR+Katz耦合效果明显优于RWR指标与其他3个指标。
为了更为清晰地进一步观察3种耦合算法的预测效果,总结表 3和图 2中数据于表 4中。
| 耦合算法 | 最优参数 | 精确度 | 提高率/% (与RWR相比) | 提高率/% (与耦合对象相比) |
| RWR+CN | 0.95 | 0.807 5 | 1.547 | 9.506 |
| RWR+PA | 0.85 | 0.801 5 | 0.792 | 5.558 |
| RWR+LP | 0.85 | 0.808 2 | 1.300 | 6.300 |
| RWR+Katz | 0.85 | 0.804 8 | 1.207 | 7.810 |
从表 4预测精度对比得出,耦合算法的最优精确度都比5种单独指标精确度要高,但耦合算法只比利用RWR指标预测的精确度略微提高,分别提高了1.547%、0.792%、1.300%、1.207%。同时最优参数x*分别为0.95、0.85,说明了RWR指标在耦合算法中起到了决定性作用,对节点企业合作连边产生了较大的作用。尽管相比RWR指标耦合算法精确度提高不是很明显,但是不可以忽略耦合对象指标在耦合算法所起到的作用。
相比单独考虑其他4种指标,预测精确度分别提高了9.506%、5.558%、6.300%、7.810%,有显著提高。耦合算法提高了耦合中原本精确度较小的指标预测的效果,其中帮助CN提高了接近10%的精确度,说明了耦合算法达到了提高指标在能源供应链网络中预测合作连边的目的,也为链路预测中各类指标结合提高了可能性。
上述研究结论并不说明CN指标在能源供应链网络预测合作连边中不重要,文献[12]比较了9种基于共同邻居的局部接近性算法,结果显示CN指标表现较好,而且对航空网络的预测比较准确,AUC可达到0.9以上。本文是应用链路预测方法研究能源供应链网络中节点企业合作演化机制,由于计算程序中的随机性,因此各指标精确度对所有供应链网络预测不可一概而论。
3 结论能源供应链的合作问题凸显出合作演化机制研究的重要性,一般研究能源供应链网络合作演化机制的常用方法直接应用演化模型来推测影响供应链网络合作演化的因素,但由于可比较的结构特征量太多,不同的模型之间难以进行定量地比较,而链路预测方法推测网络演化的机制规避了传统方法的缺陷。本文应用基于网络结构的链路预测方法,研究能源供应链网络合作演化机制,研究结果表明:
1) 在5种相似性指标中,RWR指标预测供应链网络合作的效果最好;
2) 耦合其他4种指标时,耦合后的预测效果会优于单独考虑时,达到了耦合指标的目的;
3) RWR指标和Katz指标耦合效果要优于和CN指标、PA指标、LP指标耦合效果;
4) RWR指标在耦合算法中起到主导性作用,耦合对象指标在耦合中则是不可忽略的。
由于链路预测能够计算预测方法的准确度,能够清晰直观地利用量化结果对各种因素进行辨别为供应链网络合作演化机制研究提供了分析工具和全新的视角,推动复杂网络演化模型的理论研究。
为开拓链路预测,针对供应链网络结构的研究视角,增加供应链网络结构属性;将结构属性与外部属性相耦合等方面将是进一步研究内容,使得后续供应链网络合作演化机制研究更加全面和更具有深度。
| [1] | SARUKKAI R R. Link prediction and path analysis using Markov chains[J]. Computer networks, 2000, 33(1/2/3/4/5/6): 377-386. |
| [2] | ZHU Jianhan, HONG Jun, HUGHES J G. Using Markov chains for link prediction in adaptive web sites[M]//BUSTARD D, LIU Weiru, STERRITT R. Soft-Ware 2002: Computing in An Imperfect World. Berlin Heidelberg: Springer, 2002: 60-73. |
| [3] | POPESCUL A, UNGAR L H. Statistical relational learning for link prediction[C]//Proceedings of Workshop on Learning Statistical Models from Relational Data. New York: ACM Press, 2003: 81-87. |
| [4] | KOLACZYK E E. Some implications of path-based sampling on the Internet[C]//Proceedings of a Workshop on Statistics of Networks. Washington: National Academies Press, 2007: 207-226. |
| [5] |
刘宏鲲, 吕琳媛, 周涛. 利用链路预测推断网络演化机制[J].
中国科学:物理学力学天文学, 2011, 41(7): 816-823.
LIU Hongkun, LYU Linyuan, ZHOU Tao. Uncovering the network evolution mechanism by link prediction[J]. Scientia sinica: physica, mechanica & astronomica, 2011, 41(7): 816-823. |
| [6] | O'MADADHAIN J, HUTCHINS J, SMYTH P. Prediction and ranking algorithms for event-based network data[J]. ACM SIGKDD explorations newsletter, 2005, 7(2): 23-30. DOI:10.1145/1117454. |
| [7] | LIN Dekang. An information-theoretic definition of Similarity[C]//Proceedings of the Fifteenth International Conference on Machine Learning. San Francisco: Morgan Kaufmann Publishers, 1998: 296-304. |
| [8] |
吕琳媛. 复杂网络链路预测[J].
电子科技大学学报, 2010, 39(5): 651-661.
Lü Linyuan. Link prediction on complex networks[J]. Journal of university of electronic science and technology of China, 2010, 39(5): 651-661. |
| [9] | Lü Linyuan, ZHOU Tao. Link prediction in complex networks: a survey[J]. Physica A: statistical mechanics and its applications, 2011, 390(6): 1150-1170. DOI:10.1016/j.physa.2010.11.027. |
| [10] | GETOOR L, DIEHL C P. Link mining: a survey[J]. ACM SIGKDD explorations newsletter, 2005, 7(2): 3-12. DOI:10.1145/1117454. |
| [11] | LIBEN-NOWELL D, KLEINBERG J. The link prediction problem for social networks[J]. Journal of the American society for information science and technology, 2007, 58(7): 1019-1031. DOI:10.1002/(ISSN)1532-2890. |
| [12] | ZHOU Tao, Lü Linyuan, ZHANG Yicheng. Predicting missing links via local information[J]. The European physical journal B, 2009, 71(4): 623-630. DOI:10.1140/epjb/e2009-00335-8. |
| [13] | CLAUSET A, MOORE C, NEWMAN M E J. Hierarchical structure and the prediction of missing links in networks[J]. Nature, 2008, 453(7191): 98-101. DOI:10.1038/nature06830. |
| [14] | GUIMERà R, SALES-PARDO M. Missing and spurious interactions and the reconstruction of complex networks[J]. Proceedings of the national academy of sciences of the United States of America, 2009, 106(52): 22073-22078. DOI:10.1073/pnas.0908366106. |
| [15] | ADAMIC L A, HUBERMAN B A. Power-law distribution of the world wide web[J]. Science, 2000, 287(5461): 2115DOI:10.1126/science.287.5461.2115a. |
| [16] | NEWMAN M E J. The structure of scientific collaboration networks[J]. Proceedings of the national academy of sciences of the United States of America, 2001, 98(2): 404-409. DOI:10.1073/pnas.98.2.404. |
| [17] | ALBERT R, BARABáSI A L. Statistical mechanics of complex networks[J]. Reviews of modern physics, 2002, 74(1): 47-97. DOI:10.1103/RevModPhys.74.47. |
| [18] | DOROGOVTSEV S N, MENDES J F F. Evolution of networks[J]. Advances in physics, 2002, 51(4): 1079-1187. DOI:10.1080/00018730110112519. |
| [19] | BARABáSI A L, Albert R. Emergence of scaling in random networks[J]. Science, 1999, 286(5439): 509-512. DOI:10.1126/science.286.5439.509. |
| [20] | HANLEY J A, MCNEIL B J. The meaning and use of the area under a receiver operating characteristic (ROC) curve[J]. Radiology, 1982, 143(1): 29-36. DOI:10.1148/radiology.143.1.7063747. |
| [21] | HERLOCKER J L, KONSTAN J A, TERVEEN L G, et al. Evaluating collaborative filtering recommender systems[J]. ACM transactions on information systems, 2004, 22(1): 5-53. DOI:10.1145/963770. |
| [22] | ZHOU Tao, REN Jie, MEDO M, et al. Bipartite network projection and personal recommendation[J]. Physical review E, 2007, 76(4): 046115DOI:10.1103/PhysRevE.76.046115. |
| [23] | FAWCETT T. An introduction to ROC analysis[J]. Pattern recognition letters, 2006, 27(8): 861-874. DOI:10.1016/j.patrec.2005.10.010. |
| [24] | LORRAIN F, WHITE H C. Structural equivalence of individuals in social networks[J]. The journal of mathematical sociology, 1971, 1(1): 49-80. DOI:10.1080/0022250X.1971.9989788. |
| [25] | XIE Yanbo, ZHOU Tao, WANG Binghong. Scale-free networks without growth[J]. Physica A: statistical mechanics and its applications, 2008, 387(7): 1683-1688. DOI:10.1016/j.physa.2007.11.005. |
| [26] | Lü Linyuan, JIN Cihang, ZHOU Tao. Similarity index based on local paths for link prediction of complex networks[J]. Physical review E, 2009, 80(4): 046122DOI:10.1103/PhysRevE.80.046122. |
| [27] | KATZ L. A new status index derived from sociometric analysis[J]. Psychometrika, 1953, 18(1): 39-43. DOI:10.1007/BF02289026. |
| [28] | BRIN S, PAGE L. The anatomy of a large-scale hypertextual Web search engine[J]. Computer networks and ISDN systems, 1998, 30(1): 107-117. |



