聚类是将一批现实或抽象的数据对象分组成为多个类或簇的过程。随着计算机技术、网络技术和信息技术的迅速发展, 庞大、海量、复杂、高维的数据信息充斥在当前世界的各个领域。如何处理这些数据并从中快速、准确地提取有益的信息, 越来越引起人们的普遍关注。面对这些大规模复杂数据,聚类算法需要具有可伸缩性、处理不同类型的数据、发现任意形状的簇、处理高维数据等能力。而对于这些问题与要求,传统的聚类分析方法已然显得无力。
为解决这些问题,研究者们尝试引入各种群智能算法,其中粒子群优化算法(PSO)逐渐引起人们的注意,并在聚类分析中取得了比传统方法更好的效果。从粒子群算法被提出用来解决聚类问题开始,大批学者开展了对它的研究,如文献[1]提出了一种结合自适应惯性权重参数和无线折叠迭代混沌映射的混沌粒子群的模糊聚类方法;文献[2]中结合Newton移动规则提出了重心加速粒子群算法;文献[3]提出一种多优量子粒子群算法,以解决基因表达数据的聚类问题;文献[4]利用一种交互学习策略在两个种群中确定学习种群与被学习种群来增加粒子群算法的全局搜索能力;文献[5]将基于K均值的粒子群聚类算法应用于无线传感网能源节约的管理策略中;文献[6]将粒子群聚类算法应用于多级阈值转化法中,以解决传统计算复杂度指数性增长问题。
随着研究的不断深入,基于粒子群的聚类算法越来越成熟、可伸缩性越来越强、可处理的数据类型也越来也多、使用场合越来越广。同时,聚类精度也得到了极大的提高,已基本达到临界值,很难再有较大的提升。但是,这些研究也大都着眼于此,少有文献以提升聚类效率、降低聚类时间为目标,以期在处理大规模数据时也能将聚类时间控制在一个可接受的范围内。以上述文献为例,都是结合了新型策略的粒子群聚类算法,以提高聚类精度、扩大适应场景为目标,都未考虑聚类时间。针对这一问题,本文采用一种基于粒子群的模板缩减[4]法,用来发现并移除那些在之后的聚类周期中不会或者小概率会改变簇的模板,以此来提升聚类效率,减小聚类算法周期的执行时间。但是在此过程中不可避免地会使聚类精度有所下降,对此本文采用一种能够充分结合该模板缩减法的广义遗传算法来提升降低的精度。以期在基本不降低聚类品质的前提下,缩短大量的聚类时间。
1 基于模板缩减的粒子遗传聚类算法 1.1 粒子群聚类算法在粒子群聚类算法中,每一个聚类解可以看做搜索空间中的一个粒子。首先,生成初始群体,即在可行解空间中随机初始化m个粒子,每个粒子代表一种可行解,并由目标函数式(1)确定一个适应度值。
 |
(1) |
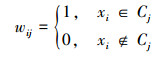 |
(2) |
式中:n为数据个数,k为聚簇的个数,d为数据的维数,xi为第i个数据点,zi为第i个簇Ci的中心,wij为数据xi对簇Cj的隶属度值。
每个粒子都将在解空间中运动,并由运动速度决定其飞行方向和距离。粒子通过式(3)、(4)不断调整自己的速度Vi和位置Xi来搜索新解。同时每个粒子自己搜索到的最优解Pid,以及整个粒子群经历过的最优位置Pgd。
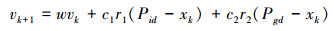 |
(3) |
 |
(4) |
粒子通过不断地学习更新,最终飞至解空间中最优解所在的位置,搜索过程结束,最后输出的Pgd就是全局最优解。
在粒子群聚类的每个周期中,粒子调整完速度和位置后,还需要通过最近邻聚类对模板进行分类,从而得到目标函数中的参数为wij。对于最近邻聚类而言,首先需要计算样本到每个簇心的距离,再取最小值以判断出模板所属簇,这一步需要耗费大量时间。但是,在不断的搜索过程中,必然会存在一些“静态模板”在搜索前期就处于“最优”状态,即在之后搜索过程中不改变其所属簇的模板。如果找到这些“静态模板”,并将其移除以避免再次的最近邻聚类就可以节省大量的聚类时间。
1.2 模板缩减模板缩减就是发现并压缩静态模板[7]的过程,而所谓的静态模板就是那些在之后的聚类过程中基本不会改变其所在簇的模板。这种模板缩减的方法,可分为两步:静态模板检测和静态模板压缩。
1.2.1 静态模板检测文献[8]采用两种方法结合的形式来检测模板是否有着大概率在下一周期聚类时不改变其所在簇:1) 模板到其簇心的距离在一个很小的范围内;2) 在几个连续的迭代周期内不改变簇的模板。
1) 通过判断模板到簇心的距离来确定静态模板。准确地说,该方法只认定每个簇中到簇心的距离小于γ的模板是静态的。
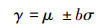 |
(5) |
式中:μ和σ分别表示簇Ci中所有模板到簇心的平均距离和标准偏差。
通常来说,γ不仅可以用来作为一个阈值来筛选静态模板,而且还是一个用来平衡准确度和算法收敛速度的参数。
2) 通过判断模板连续保持在相同簇的次数Sij来确定静态模板。直观上来讲,一个静态模板连续保持在同一个簇的迭代周期数Smax越大,则该模板是静态模板的可能性就越高。而设定多大的Smax作为阀值就取决于聚类算法的收敛速度或者是最终解的质量。
不难发现,对于方法2,需要对周期的每个粒子参数样本分类数据进行储存,才可以计算连续次数Sij。假设Smax=3,就至少需要参考之前两个迭代周期中的样本分类数据,才可以判断出哪些模板可视为“静态模板”。对于文献[8]的方法来说,Sij的储存不止麻烦而且对于算法而言没有任何帮助,只会增加算法的复杂度。但是本文基于广义遗传算法的粒子群聚类算法就可以很好地解决这一问题。对于广义遗传算法而言,本身就有保护分类数据的特点,而且还可以通过遗传算法来增加其样本多样性。因此,本文算法不仅可以对分类的数据用一种新型的方式进行储存,还可以很好地利用这些数据产生新的遗传粒子以替换适应值低的PSO粒子。
1.2.2 静态模板压缩静态模板压缩操作是为了记录、传送静态模板的信息给后期的其他操作,以确保没有多余的计算被执行。该操作的数学表达形式如式(6)所示。
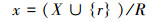 |
(6) |
式中:X表示所有输入模板集合,Q表示所有静态模板集合,q表示静态模板的压缩模板集合,x表示输入模板的压缩模板集合。
基于模板缩减法的粒子群聚类,每个迭代周期只需要对属于x的模板执行聚类操作。这种方式,可以确保Q中的静态模板不被重复计算。
对于静态压缩模板q,本文提出一种新型的编码方式,该方法可以很好地保存输入模板的信息,同时也可以完美地同复合了k-means的粒子群聚类相结合。
其中,每个静态压缩模板q中包含两种信息,分别为属于簇Ci的静态模板的平均特征值avi,如式(7)所示,和属于簇Ci的静态模板的个数si。
 |
(7) |
采用模板压缩方法减少计算时间的过程中,不可避免地会导致聚类精度的下降,也就是说会比传统PSO聚类更容易陷入“早熟”收敛。文献[8]采用一种“多星”操作来解决这一问题,即通过随机选取种群中粒子相互交叉产生新的粒子,类似于一种简易的“遗传”算法。但是,在粒子群寻优的过程中,所有粒子都不断地向着个体最优解和全局最优解靠近。也就是说,在迭代了许多代后,整个种群可能已经大部分收敛,但是还没有得到稳定的全局最优解。此时整个种群的平均适应度值较高,而且最优个体的适应度值与全体适应度均值间的差别不大,即使在种群中随机选取粒子进行交叉产生新的粒子,也没有足够的力量推动种群的寻优找到最优解,从而陷入到“局部”最优。
为了解决这一问题,本文更好地吸取了遗传算法的优点,修改了一种广义遗传算法来增加样本多样性,提高算法跳出“局部”最优的能力。考虑到在自然演化中,近亲繁殖往往不利于种群的繁荣,而远亲杂交往往会培育出更优良的品种;变异作为一种重要的进化方式,是保持物种多样性的必要手段。因此,我们首先对每个迭代周期产生的分类数据进行储存,以扩大遗传种群的数量,因为只有非常大的种群量才能更好地进行远亲杂交。再从中选取一组种群粒子与当前的“优质”粒子进行交叉、变异,生成新的粒子。此处,通过系数l来避免“近亲”繁殖,即不选择近代生成的种群粒子。该算法通过不断地补充、记录、生成新的种群粒子,在不断寻优的过程中,也增加了粒子群聚类的样本多样性。
1.4 基于模板缩减的新型粒子群遗传聚类算法该算法创新性地将一种修改后的新型广义遗传算法同基于模板缩减的粒子群聚类算法相结合,在充分同模板缩减相结合的同时,也提高了样本多样性。
基于模板缩减的粒子群聚类算法,其对于初始中心的敏感性不仅没有降低反而会更加敏感,将严重导致聚类精度的不稳定。本文通过选取10%的样本进行简单的k-means聚类,来初始簇心。同时,为了更好地提高由模板缩减而降低的聚类精度,本文在聚类迭代中并行k-means,即在重新分配完粒子后,使用式(8)来重新计算簇心。
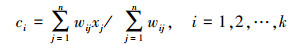 |
(8) |
考虑到迭代前期粒子群聚类不需要太多的遗传粒子,而后期特别是当粒子群聚类陷入局部最优时往往需要较大量的遗传粒子来增加其调出陷阱的能力。因此,对替换粒子量C采用一种递增策略来解决这一矛盾。
 |
(9) |
式中:prN代表压缩后模板的数量,PN表示模板的总数量。Φmin表示没有模板缩减时,最小替换个数;Φmax表示最大可以增加的替换个数;
该聚类算法的实现过程如下:
Begin
Initialize
输入样本数据集X, 聚类数据k;
设置粒子群数m, 替换粒子数C;
选取10%的X, 初始化种群P(0);
while不满足停止准则
根据式(1)计算每个粒子适应度
更新Pid和Pgd;
for i=1:M-C
根据式(3)、(4)更新粒子i的速度和位置;
for每个属于粒子i数据集x的样本
根据最近邻法则划分;
保存到广义遗传算法的种群中;
根据式(8)重新计算聚类中心;
检测生成静态压缩模板q;
根据式(6)生成新的x;
end for
end for
for i=1:C
在区间[1,n-l]中生成一个随机整数l;
选择第l代种群与当种群进行交叉、变异操作生成第n+1代种群;
end for
end while
输出最优Pgd对应的广义遗传算法种群中的最优分类;
End
1.5 计算复杂度分析从1.4中的算法流程中可以看出,每个周期需要进行以下5步计算:适应度计算、粒子更新、最近邻划分、静态模板检测和缩减、遗传粒子计算。其中,适应度计算和最近邻划分,由于需要对数据到各个簇心的距离,其计算复杂度最高,为O(mn′n2);减部分,只需要对划分后的数据进行求平均值、比较和删除操作,所以其计算复杂度为O(mn′n);其余操作,可忽略不计。综上,本文算法的计算复杂度为O(rmn′n2),其中r表示迭代周期数,n′表示非静态模板数。可以看出,随着静态模板数的增加其计算复杂度逐渐减小,从而达到了降低聚类时间的目的。
2 实验结果分析 2.1 实验环境目前,大部分对于粒子群聚类算法的改进基本都是从适应值函数、编码方式、参数调整等方面着手。而本文算法,只是从模板方面着手进行缩减,每个周期需要对多少个样本分类对目前的粒子群改进没有丝毫的影响,只需要调整不同编码方式就可以同这些改进措施完美衔接。同时,虽然很多改进措施是通过混合不同的策略来优化粒子群的聚类算法,但大多都是将采用的策略同粒子群并行使用,对每个周期需要对多少个样本进行操作没有要求。例如,文献[9]提出的基于模糊c均值和粒子群的模糊聚类方法;文献[10]提出了使用边界约束策略的自适应粒子群聚类;这类文献,只是引入一些改进策略混合并行使用来改善粒子群算法的一些缺陷,同样对每个周期对多少个样本进行操作也没有影响,同本文算法衔接没有任何问题;更典型的,像文献[11]这些针对粒子群聚类算法需要预先设定聚类中心个数的问题进行算法改进的策略,对粒子群算法本身没有什么变动,和本文算法就更谈不上什么冲突了;所以,本次试验只采用基本的粒子群聚类(PSO)和典型的混合k-means的kmPSO[12]混合聚类算法(记为KP)进行实验分析,并同文献[7]的MPREPSO算法(MP)比较来测试本文算法的性能。
仿真实验基于MATLAB2010b平台,计算机的硬件配置为:Intel Core i5-4200M CPU 2.5 GHz、4 GB RAM。选取UCI数据库中的8个典型数据集在该环境下对本文和比较算法进行测试。其中,数据集的特性如表 1所示。
| 数据集 | 数据集个数 | 类 | 维数 |
| Iris | 150 | 3 | 4 |
| Glass | 214 | 7 | 9 |
| Ionosphere | 351 | 2 | 34 |
| Balance Scale | 625 | 3 | 4 |
| CMC | 1 472 | 3 | 19 |
| Yeast | 1 484 | 10 | 8 |
| Wall following 2 | 5 456 | 4 | 2 |
| Wall following 4 | 5 456 | 4 | 4 |
根据聚类准确度、运行时间对本文的基于模板缩减的粒子群广义遗传聚类算法(PR-PSO-GGA)聚类性能进行分析比较,考虑到实验要求,4种基于粒子群的聚类算法参数一致,设置同文献[7]相同:w=0.72,c1=c2=2。每种算法独立运行20次,计算各自的适应度值、accuracy[8]、Rand Index[3]指标和运行时间, 聚类结果如表 2所示。其中,适应度值函数由式(1)定义。
| 数据集 | 算法 | 目标函数 | 精度 | Rand Index | 时间 |
| Iris | PSO | 105.44 | 0.90 | 0.89 | 5.21 |
| KP | 97.22 | 0.90 | 0.89 | 1.96 | |
| MP | 100.15 | 0.90 | 0.89 | 0.58 | |
| 本文 | 97.28 | 0.89 | 0.88 | 0.44 | |
| Glass | PSO | 276.54 | 0.49 | 0.62 | 7.55 |
| KP | 205.98 | 0.50 | 0.64 | 8.92 | |
| MP | 231.00 | 0.47 | 0.63 | 0.93 | |
| 本文 | 216.00 | 0.48 | 0.63 | 0.84 | |
| Ionosphere | PSO | 858.74 | 0.69 | 0.57 | 4.07 |
| KP | 796.17 | 0.71 | 0.58 | 2.96 | |
| MP | 815.67 | 0.70 | 0.58 | 1.14 | |
| 本文 | 796.25 | 0.71 | 0.58 | 0.92 | |
| Balance Scale | PSO | 1431.73 | 0.53 | 0.60 | 15.81 |
| KP | 1423.92 | 0.52 | 0.59 | 8.59 | |
| MP | 1436.78 | 0.53 | 0.60 | 2.35 | |
| 本文 | 1427.18 | 0.53 | 0.60 | 2.07 | |
| CMC | PSO | 5618.57 | 0.40 | 0.56 | 41.99 |
| KP | 5541.63 | 0.40 | 0.56 | 28.96 | |
| MP | 5559.27 | 0.40 | 0.56 | 6.38 | |
| 本文 | 5542.12 | 0.40 | 0.56 | 5.49 | |
| Yeast | PSO | 273.74 | 0.31 | 0.74 | 62.95 |
| KP | 235.73 | 0.36 | 0.75 | 214.55 | |
| MP | 249.21 | 0.34 | 0.74 | 8.58 | |
| 本文 | 241.67 | 0.35 | 0.75 | 8.11 | |
| Wall following2 | PSO | 1 299.33 | 0.62 | 0.72 | 355.72 |
| KP | 1 292.42 | 0.66 | 0.72 | 186.52 | |
| MP | 1 284.02 | 0.65 | 0.72 | 36.64 | |
| 本文 | 1 293.39 | 0.66 | 0.72 | 29.93 | |
| Wall following4 | PSO | 3 555.69 | 0.43 | 0.59 | 241.44 |
| KP | 3 381.33 | 0.41 | 0.58 | 211.98 | |
| MP | 3 371.74 | 0.41 | 0.58 | 32.67 | |
| 本文 | 3 381.89 | 0.41 | 0.58 | 29.05 |
2.2 实验分析
对于评价聚类算法的聚类品质而言,低适应度值一定代表着高品质,但较高accuracy值和Rand Index值却不一定意味着较高的品质。因为,基于粒子群的聚类算法都是围绕着适应度值在不断地寻优,以期找到最低的适应度值,这就意味着适应度值越低该聚类算法的寻优能力越强,聚类算法的聚类品质也就越高。accuracy和Rand Index指标作为外部评价指标和目标函数有着密切联系,只能大致评价聚类结果,不能完美地表现粒子群聚类算法寻优能力的优劣。因此,本文实验分析将根据适应度值来评价聚类结果,聚类accuracy和Rand Index值仅作为参考数据。
各数据集实验结果如表 2所示。
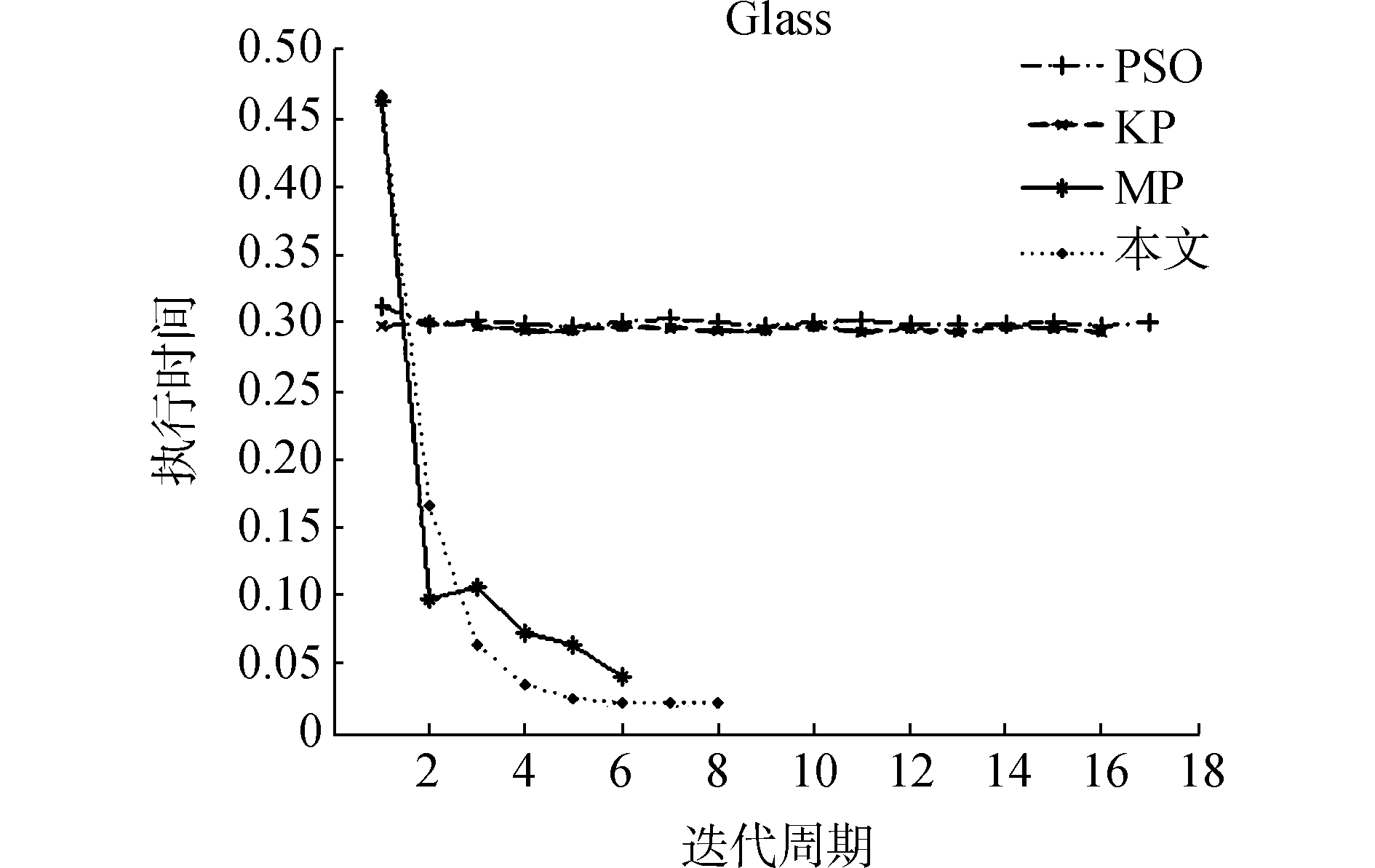
从表 2中可以看出,针对不同的数据集,基于模板缩减的粒子群广义遗传算法的聚类时间只需要原算法20%左右的时间,对有些数据集甚至只需要10%的聚类时间。这些缩短的聚类时间一部分是由于模板缩减法移除模板降低的周期执行时间所造成的,另一部分是由于串行了广义遗传算法减小了收敛周期所造成的, 具体可参考图 1和图 2。
|
| 图 1 周期执行时间图 Fig. 1 The graph of cycle time |
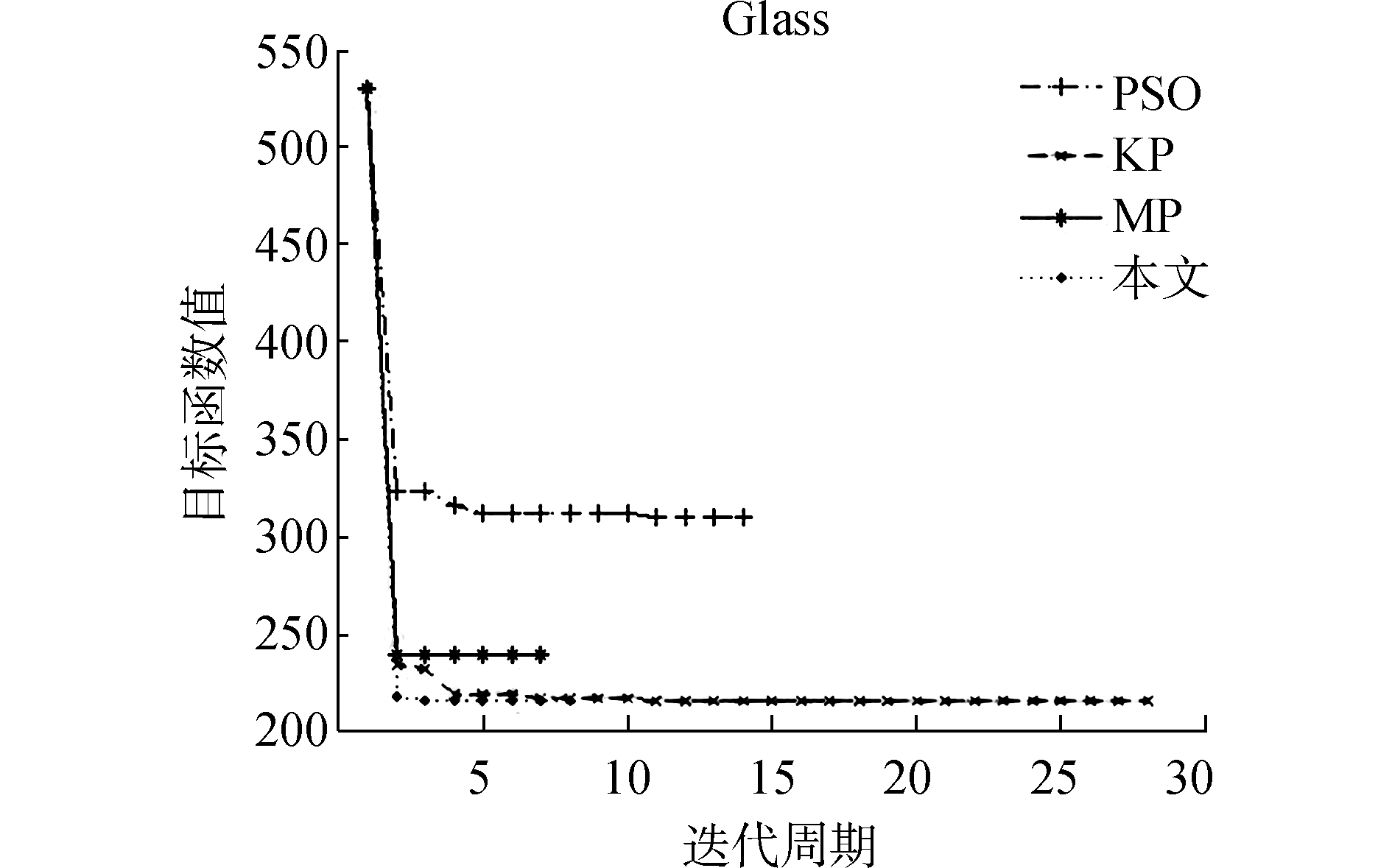
|
| 图 2 目标函数收敛图 Fig. 2 The convergence graph of objective function |
从图 1可以看出,MP和本文算法开始的周期执行时间高于PSO和KP算法,并随着迭代次数的增加周期执行时间迅速减小。这说明基于模板压缩法粒子群算法虽说会增加算法复杂度,但随着算法的运行其周期执行时间越来越短, 将大大节约总体聚类时间。从图 2可以看出,算法迅速下降到一个较低值并在短期内完成聚类。这表明较其他算法,本文算法有着较快收敛速度和较低收敛周期。
对表 2的数据具体分析,可以看出:
1) 比起典型的粒子群聚类而言,本文算法不仅缩短了大量的时间,而且聚类精度也有所提高。典型的粒子群聚类算法只通过粒子间的个体协作与竞争来搜索最优解,不可避免会陷入“局部最优”中,同时收敛周期也较长。因此,虽然模板缩减法会降低聚类精度,但是本文算法通过广义遗传算法等一系列的措施却可以在缩短聚类时间的基础上提高其聚类精度。
2) 对于并行k-means的粒子群聚类算法而言,本文算法的聚类结果对于Iris等数据集的目标函数值只下低了千分之几,却只需要其25%~30%的聚类时间。其中,对精度降低最高的Glass数据集而言,目标函数下降了4.8%,但是其聚类时间却缩短了90%以上。本文算法通过增加广义遗传算法来加快收敛速度,在减少了每个周期的聚类时间的前提下也缩短了其聚类周期数。但是本文算法却不能无限缩减每个聚类周期的时间,即使聚类后期“较优”的粒子模板已经大聚类后期“较优”的粒子模板已经大部分被压缩并移除只剩下静态模板的静态压缩模板的集合q,但是每个周期还会产生C个新的包含所有输入模板的粒子。如图 1所示,本文算法在后期的迭代周期中,周期执行时间逐渐收敛于一个固定值;
3) 比起MP聚类算法,本文算法对于Iris等数据集既能缩短聚类时间,也能提高聚类精度。而对于数据Wall following而言虽说本文算法降低了千分之几的精度,但是却缩短了1/10的聚类时间。同MP算法相比,本文算法虽然增加了广义遗产算法等一系列操作,但是这些操作大多能与模板缩减法相结合且不会增加太多计算复杂性,如图 1所示,本文算法同MP算法在开始的周期执行时间基本相等。所以本文算法能够在增强聚类精度的基础上提高部分聚类速度。
总体来看,本文算法能够在基本不降低聚类算法精度的前提下,缩短大量的聚类时间。
3 结束语随着规模庞大、结构复杂数据的不断出现,对其聚类往往需要耗费大量的时间。但是当今大量文献研究往往都着眼于提高其准确度,很少针对聚类速度。本文基于模板缩减的粒子群聚类算法,将其与一种改进的广义遗传算法充分结合,不仅能够提高种群的多样性而且能够对模板缩减过程中必要的信息进行存储保护。实验表明,本文算法能够在基本不降低聚类精度的前提下,显著地缩短聚类时间。但是本文基本模板缩减的粒子群聚类算法,精度不可避免带有些许的损失,特别是当类数增加时误差会较大。对于这一问题,应该是还没有将遗传算法的全部优点挖掘出来,下一步还有待改进。
| [1] | LI Chaoshun, ZHOU Jianzhong, KOU Pangao, et al. A novel chaotic particle swarm optimization based fuzzy clustering algorithm[J]. Neurocomputing , 2012, 83 : 98-109 DOI:10.1016/j.neucom.2011.12.009 |
| [2] | BEHESHTI Z, SHAMSUDDIN S M H. CAPSO:Centripetal accelerated particle swarm optimization[J]. Information sciences , 2014, 258 : 54-79 DOI:10.1016/j.ins.2013.08.015 |
| [3] | SUN Jun, CHEN Wei, FANG Wei, et al. Gene expression data analysis with the clustering method based on an improved quantum-behaved particle swarm optimization[J]. Engineering applications of artificial intelligence , 2012, 25 (2) : 376-391 DOI:10.1016/j.engappai.2011.09.017 |
| [4] | 秦全德, 李丽, 程适, 等. 交互学习的粒子群优化算法[J]. 智能系统学报 , 2012, 7 (6) : 547-553 QIN Quande, LI Li, CHENG Shi, et al. Interactive learning particle swarm optimization algorithm[J]. CAAI transactions on intelligent systems , 2012, 7 (6) : 547-553 |
| [5] | SOLAIMAN B F, SHETA A F. Energy optimization in wireless sensor networks using a hybrid K-means PSO clustering algorithm[J]. Turkish Journal of electrical engineering and computer sciences, 2015. https://www.researchgate.net/publication/271507441_Energy_optimization_in_wireless_sensor_networks_using_a_hybrid_K-means_PSO_clustering_algorithm |
| [6] | DASH P, NAYAK M. Multilevel thresholding using PSO clustering[J]. International journal of computer applications , 2014, 97 (18) : 27-32 DOI:10.5120/17107-7752 |
| [7] | CHIANG M C, TSAI C W, YANG C S. A time-efficient pattern reduction algorithm for k-means clustering[J]. Information sciences , 2011, 181 (4) : 716-731 DOI:10.1016/j.ins.2010.10.008 |
| [8] | TSAI C W, HUANG K W, YANG C S, et al. A fast particle swarm optimization for clustering[J]. Soft computing , 2015, 19 (2) : 321-338 DOI:10.1007/s00500-014-1255-3 |
| [9] | FILHO T M S, PIMENTEL B A, SOUZA R M C R, et al. Hybrid methods for fuzzy clustering based on fuzzy c-means and improved particle swarm optimization[J]. Expert systems with applications , 2015, 42 (17/18) : 6315-6328 |
| [10] | RANA S, JASOLA S, KUMAR R. A boundary restricted adaptive particle swarm optimization for data clustering[J]. International journal of machine learning and cybernetics , 2013, 4 (4) : 391-400 DOI:10.1007/s13042-012-0103-y |
| [11] | 张亮, 杨国正. 一种变维搜索的量子粒子群优化聚类算法[J]. 小型微型计算机系统 , 2012, 33 (4) : 804-808 ZHANG Liang, YANG Guozheng. A quantum particle swarm optimization clustering algorithm using variable dimensions searching[J]. Journal of Chinese computer systems , 2012, 33 (4) : 804-808 |
| [12] | AHMADYFARD A, MODARES H. Combining PSO and k-means to enhance data clustering[C]//Proceedings of International Symposium on Telecommunications. Tehran, Iran, 2008:688-691. |



