高分辨距离像(high range resolution profile, HRRP)是目标沿雷达视线方向的投影,反映了目标在纵向距离上的散射结构,即散射中心在空间的位置分布、强度和数量等,包含了丰富的目标物理结构信息,并且易于获取和处理,从而备受关注[1-6]。提取不同特征进行融合识别成为雷达目标识别领域研究的热点[1-5]。
由于HRRP存在姿态敏感性、平移敏感性和幅度敏感性问题,克服这三大敏感性问题是实现HRRP特征提取的关键。姿态和幅度敏感性问题可分别通过对一定角域内的距离像进行非相干平均和对距离像幅度进行归一化解决[1],平移敏感性可以通过提取平移不变特征来克服。文献[2]提取了HRRP的幅度特征、功率谱特征和频谱幅度特征, 分别使用最大相关分类器、支持向量机和关联向量机进行了多类分类,并用加权投票法对拒判和识别结果进行融合,提高了识别系统的性能; 文献[3]提取中心矩和双谱平移不变特征,通过将LS-SVM的输出进行DS证据理论融合,提高了目标识别性能和抗噪能力; 文献[4]利用多极化HRRP提供的目标特征信息,将混淆矩阵提供的基分类器可信度值与SVM后验概率结合到DS证据理论的基本概率赋值中,降低了融合分类的误识率; 文献[5]提取每种极化通道下6种平移不变特征,使用最近邻分类器进行分类,用DS证据理论进行了多极化多特征融合识别,使系统的识别率明显提升。
尽管上述方法从不同侧面获得了较好的识别结果,但仍然存在有待进一步解决的问题,比如,在现有融合识别方法中,用加权投票法进行融合存在如何确定权值和如何处理冲突判决的问题,而应用DS证据理论进行融合存在如何得到基本概率赋值等问题。本文在提取不同的平移不变特征的基础上,构建高性能RVM进行特征分类,并用DS证据理论融合分类结果以得到目标识别结果,提出一种基于RVM和DS的一维距离像融合识别方法。该方法充分利用了RVM输出的概率信息,解决了用DS证据理论进行融合时基本概率赋值获取困难的问题。
1 相关向量机相关向量机(relevance vector machine,RVM)[7-9]是M. E. Tipping在2000年提出的一种基于贝叶斯框架理论的机器学习方法。RVM具有与SVM相同的决策形式,但有效地克服了SVM存在的稀疏性不强、核函数必须满足Mercer条件、需要估计规则化系数、缺乏必要的概率信息等缺点,它可以在保证分类精度与SVM相同的情况下,提供样本的后验概率分布。目前,RVM已广泛应用于高光谱图像分类[10]、网络流量预测[11]、风能预测[12]等领域。
1.1 RVM分类模型对于二分类问题,给定一组训练样本X={xn}n=1N,对应的类别标号为t={tn}n=1N,其中N为样本个数,RVM的分类函数定义为
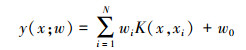 |
(1) |
式中:K(x, xi)为核函数,wi是模型的权值。把logistic sigmoid连接函数σ(y)=1/(1+e-y)应用于y(x),使得p(t|x)服从伯努利分布。假设训练样本独立同分布,那么整个样本集的似然函数为
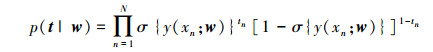 |
(2) |
式中:t=[t1 t2 … tN]T,w=[w0 w1 … wN]T。
在贝叶斯框架下,可以通过最大化似然函数来估计参数向量w,但为了避免过学习问题,RVM为每个权值定义了高斯先验概率分布来约束参数
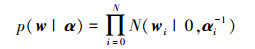 |
(3) |
式中:α=[α0 α1 … αN]是N+1维超参数,并假设α服从Gamma先验概率分布。对每一个权值配置超参数是RVM的最显著特点,最终导致了算法求解的稀疏特性。
1.2 参数推断给定了先验概率和似然分布,根据贝叶斯准则,得到如下后验概率:
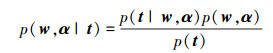 |
(4) |
若获得了p(w, α|t),则对于给定的测试样本x*,相应输出t*的预测分布为
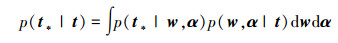 |
(5) |
但我们无法计算p(t)=∫p(t|w, α)p(w, α)dwdα,所以无法直接计算式(4)中的后验概率p(w, α|t),然而可以将后验概率分解为
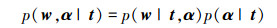 |
(6) |
关于权重的后验概率分布式如下:
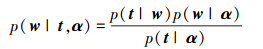 |
(7) |
由于后验概率p(w|t, α)和p(α|t)无法通过积分求解,因此利用拉普拉斯方法的逼近过程进行近似。首先对p(w|t, α)进行逼近。
1) 对当前固定的α值,求最大可能的权值wMP。
因为p(w|t, α)∝p(t|w)p(w|α),故可以将关于w的最大后验概率估计等价为最大化:
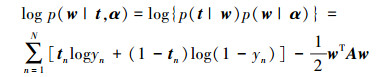 |
(8) |
式中:A=diag(α0, α1, …, αN),yn=σ{y(xn; w)}。
2) 利用拉普拉斯方法,将对数后验概率进行二次逼近。将式(8)两次求导得出
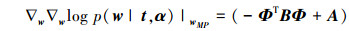 |
(9) |
式中:Φ=[φ(x1) φ(x2) … φ(xN)]T,是N×(N+1)的矩。
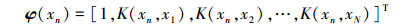 |
B=diag(β1,β2,…,βN)是一个对角阵,
 |
然后可得到协方差矩阵Σ和wMP:
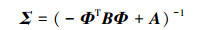 |
(10) |
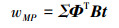 |
(11) |
由于p(α|t)∝p(t|α)p(α),所以对于p(α|t)的求解可以转化为超参数的后验分布p(α|t)关于α的最大化问题。我们仅需对p(t|α)最大化:
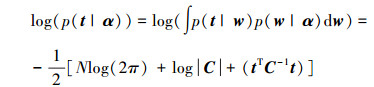 |
(12) |
式中:C=B+ΦA-1ΦT。采用拉普拉斯方法可得:
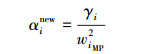 |
(13) |
式中:γi≡1-αiΣii,Σii是Σ的第i个对角元素。当αi很大,wi被它的先验概率严格约束,Σii≈αi-1,且γi≈0。相反,当αi很小,wi趋于稳定时,γi≈1。实际迭代过程中,通常发现许多αi趋于无穷,wiMP将为0。通过不断地迭代,少量的wiMP趋向于稳定有限值,对应的xi即为相关向量(relevant vectors),体现了数据中最核心的特征。
利用相关向量机进行分类的步骤如下:
1) 训练RVM:
①选择合适的核函数,将特征向量向高维空间映射。
②初始化α。因为α是由迭代过程获得的,所以需要对其进行初始化,但初始化的值对其结果的影响不大。
③利用式(10)、(11)计算Σ和wMP。
④利用式(13)重新估计α。
⑤重复③,直到达到合适的收敛尺度。
2) RVM分类准则
如果σ(yi)=1/(1+e-yi) < 0.5,ti=0,反之ti=1。
2 基于RVM和DS的HRRP融合识别方法通过RVM进行分类,得到的后验概率信息表示样本属于某个类别的可能性,是对分类结果不确定性的有效度量。同时,有效的特征提取是目标识别的关键,通过多特征融合可提升目标识别的性能。DS证据理论[13]作为一种有效的决策层融合方法,在对不确定信息的表示、处理及融合问题的解决中具有明显的优势,它能够有效区分“不确定”和“不知道”,并通过证据的不断积累缩小假设集,广泛应用于不确定信息融合,但如何获取基本概率赋值(basic probability assignment,BPA)是用DS证据理论进行不确定信息融合时需要解决的问题。本文将RVM与DS证据理论相结合,用于目标HRRP分类和融合识别,充分利用了RVM输出的概率信息,解决了用DS证据理论进行融合时基本概率赋值问题,提出一种基于RVM和DS的融合识别方法——RVM_DS。该方法在提取不同平移不变特征的基础上,通过交叉验证构建稳健的RVM基分类器进行特征分类,并结合RVM输出的样本后验概率信息与分类正确率构建BPA,最后用DS证据理论融合不同特征分类结果以得到目标识别结果。
2.1 HRRP特征提取特征提取是目标识别的重要步骤。HRRP的强散射中心结构特征、能量聚集区长度特征、稳定性特征是目标本质属性的反映,具有平移不变性,维数低、便于计算,在目标识别中被广泛使用。
1) 强散射中心结构特征
设目标HRRP为X(i)={x(i, j)}, j=1, 2, …, N,其中N是距离像的长度,i表示目标的第i次一维距离成像,x(i, j)表示该HRRP序列的第j个采样点的幅值。
强散射中心为HRRP幅度大于均值且为峰值的点,它不仅具有强散射功率,而且是散射功率变化趋势改变的散射点。在一定方位角范围内,目标强散射中心分布具有相似性,而且目标平动并不改变强散射中心之间的相对距离,因此强散射中心幅度和强散射中心的相对位置均可作为识别目标的平移不变特征。
综合强散射中心幅度和位置两种特征,定义强散射中心结构特征[14]为
 |
式中:当x(i, j)>max(x-(i), x(i, j-1), x(i, j+1))时,A(i, j)=x(i, j);否则,A(i, j)=0。POS(i, j)为强散射中心的相对位置,选择第一个强散射中心位置为基准点,取值为1。
2) 能量聚集区长度特征
能量聚集区长度[15]能反映目标的径向长度,具有平移不变性。其提取方法如下:
①求取HRRP序列X(i)的均值x-(i);
②设置阈值Th,使得:Th=ηx-(i)。
式中:η为置信系数, 可在0.8~2之间取值,它取决于HRRP的信噪比,当信噪比较大时,η可取较小值,反之则取较大值。
③对X(i)各距离单元的值从两端向中间搜索,当左右两端分别出现第1个大于阈值的点的时候,就停止搜索,并记下它们的位置, 分别为PL(i)、PR(i),则能量聚集区长度为
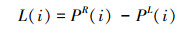 |
(19) |
3) 稳定性特征
计算HRRP的幅度谱差分:
 |
(20) |
它表征了HRRP幅度起伏情况。
定义HRRP的稳定性特征[14]为
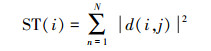 |
(21) |
显然ST(i)越小,HRRP在相邻距离单元上的幅度变化越小,说明目标在该方位角域总体稳定性越好,可以表征HRRP序列的形状信息。
2.2 基本概率赋值获取用DS证据理论进行不确定信息融合时,基本概率赋值是需要解决的关键问题。对于二分类问题,辨识框架为Θ={Ø, +, -, θ},本文基于各分类器的输出根据式(22)构造BPA:
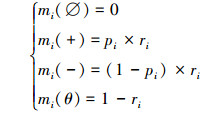 |
(22) |
式中:ri为第i个基分类器的分类精度,pij为第i个基分类器分类样本j时其属于正类的概率,mi(Ø)、mi(+)、mi(-)、mi(θ)分别表示空集、正类、负类和全集的BPA。
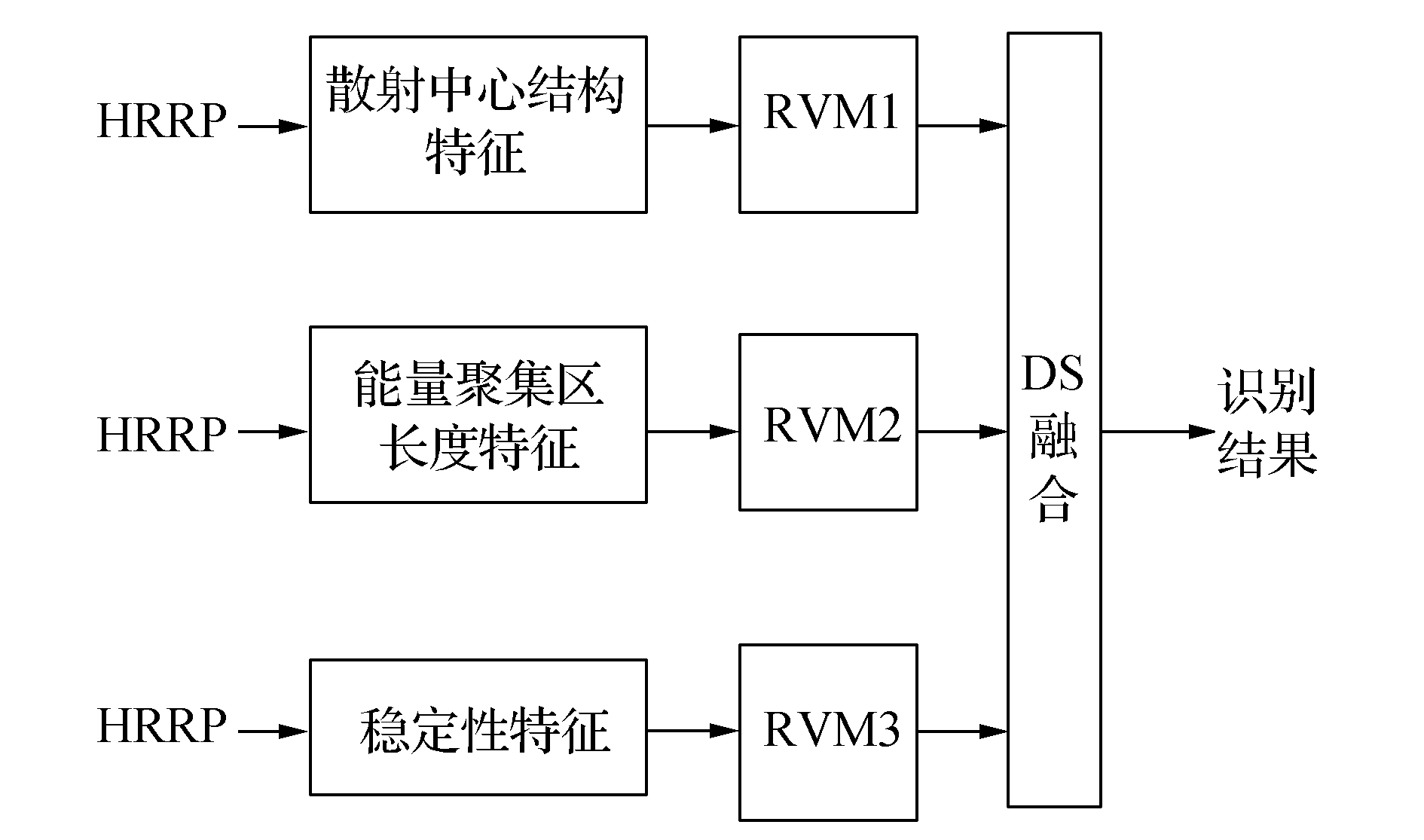
2.3 基于RVM和DS的HRRP融合识别方法基于RVM和DS的HRRP融合识别方法的流程如图 1所示。
|
| 图 1 基于RVM和DS的HRRP融合识别方法流程图 Fig. 1 Flowchart of HRRP fusion recognition based on RVM and DS |
RVM_DS方法主要包括训练阶段和融合识别阶段。具体步骤如下:
1) 训练阶段
①对HRRP训练数据,分别提取散射中心结构特征、能量聚集区长度特征、稳定性特征。
②分别通过交叉验证进行分类器参数优选,构建稳健的RVM基分类器。
2) 识别阶段
①对未知类别HRRP测试数据,提取散射中心结构特征、能量聚集区长度特征、稳定性特征;
②利用训练好的RVM基分类器分别进行特征分类;
③根据各RVM的分类结果:预测概率和分类正确率,利用式(22)构造BPA,用DS证据理论进行融合,得到最终目标识别结果。
3 实验及分析 3.1 实验数据为了验证本文方法的有效性,我们利用弹头和诱饵在步进频率雷达下的全姿态HRRP仿真数据进行了识别实验。雷达工作频率范围为8.75~10.75 GHz,步进频率间隔为15.748 MHz,共有128个频率采样点。目标俯仰角为90°,方位角范围为0~180°,方位角采样间隔为0.1°,采样数为1 801,每个角度的HRRP样本数据共256维。采用两类目标的0~20°,30~50°,60~80°,90~110°,120~140°,150~170°范围内的HRRP数据用于实验,每个训练数据集含有两类目标各201个样本,共402个样本,采用每个训练数据集相邻角度范围内平均HRRP作为测试样本,测试数据集含有两类目标各200个样本,共400个样本。
3.2 实验设计为了实现SVM与DS结合,实验中用SVM对所提取的3种特征进行分类,并采用Platt[16]提出的Sigmod函数将SVM的输出映射到[0,1],以获得SVM的后验概率输出,最后采用本文所提方法构造BPA,实现SVM与DS证据理论相结合的HRRP融合识别方法,并将此方法称为SVM_DS。SVM_DS方法的具体步骤与RVM_DS相同。
实验中RVM与SVM均选用常用的径向基核函数。由于参数会影响分类器的性能,为了提高RVM和SVM分类器的泛化能力和识别精度,实验中首先对两种分类器进行参数优化。参数优化方法很多,文献[17]定义理想核函数的Gram矩阵,提出采用基于距离测度的方法优化参数,并指出在特定的γ取值下,参数C趋向于取较大值能够保证较高的分类正确率。文献[18]提出的交叉验证网格搜索法尽管计算量大,却是一种行之有效的简单方法。
本文采用5折交叉验证的方法来获取SVM的最佳参数C和γ以及RVM的最佳参数γ,构造稳健的高性能SVM和RVM分类器。结合文献[17]与[18]的结论,实验中设置C取值范围为[2-5, 2-4, …, 29, 210],γ取值范围为[2-10, 2-9, …, 24, 25]。那么,SVM寻找最优参数的时间复杂度为O(N2),RVM仅为O(N),RVM通过交叉验证方法获取核函数参数计算量比SVM少的多,效率更高。实验基于LIBSVM[18]和RVM[19]工具箱在PC机上进行,PC机配置为8 G内存,3.6 GHz CPU,算法基于MATLAB7.14(R2012a)实现。
3.3 实验结果与分析1) SVM和RVM分类性能对比
通过交叉验证获取SVM和RVM的最优参数后,对SVM和RVM的训练时间、测试时间、稀疏性、及分类精度进行实验仿真与比较。表 1给出在0~20°角度范围内提取的特征数据集上的对比结果。
| 特征 | 分类器 | 训练时间/s | 支持向量/相关向量个数 | 识别正确率/% |
| 散射中心结构特征 | SVM | 0.078 0 | 382 | 61.00 |
| RVM | 0.140 4 | 9 | 62.25 | |
| 能量聚集区长度特征 | SVM | 0.062 4 | 218 | 89.00 |
| RVM | 0.358 8 | 3 | 89.50 | |
| 稳定性特征 | SVM | 0.078 0 | 362 | 68.75 |
| RVM | 0.312 0 | 8 | 68.75 |
分析表 1可知,RVM的训练时间比SVM长,RVM的相关向量远小于SVM的支持向量,RVM更稀疏,且极大地减少了核函数的计算量,所以测试时间更短,更适合于在线识别。由于本文提取的特征维数低,计算量小,在测试时间方面几乎都为0,无明显差别。在选择合适的参数情况下RVM与SVM的分类精度相当。
2) 融合识别性能对比
为了验证本文所提融合识别方法的有效性,将本文方法与多数投票融合法、加权投票融合法、SVM_DS进行比较。加权投票融合法采用文献[2]提出的混淆矩阵计算权值矩阵实现加权投票,多数投票法与加权投票法采用的基分类器都是3个SVM。在最优参数下设置下,分别对不同方位数据集提取的3种特征进行分类实验,表 2采用不同融合识别方法的实验结果。
| % | |||||||
| 角度范围 | 特征 | SVM | RVM | 多数投票融合法 | 加权投票融合法 | SVM_DS | RVM_DS |
| 0~20° | 散射中心结构 | 61.00 | 62.25 | 78.75 | 89.70 | 89.50 | 91.00 |
| 能量聚集区长度 | 89.00 | 89.50 | |||||
| 稳定性特征 | 68.75 | 68.75 | |||||
| 30°~50° | 散射中心结构 | 74.75 | 74.25 | 80.00 | 87.00 | 89.25 | 91.50 |
| 能量聚集区长度 | 88.25 | 88.75 | |||||
| 稳定性特征 | 66.00 | 65.00 | |||||
| 60°~80° | 散射中心结构 | 73.00 | 72.00 | 72.50 | 73.50 | 75.55 | 77.75 |
| 能量聚集区长度 | 59.75 | 54.50 | |||||
| 稳定性特征 | 69.25 | 67.25 | |||||
| 90°~110° | 散射中心结构 | 92.00 | 92.00 | 96.75 | 96.75 | 97.75 | 97.50 |
| 能量聚集区长度 | 94.00 | 92.50 | |||||
| 稳定性特征 | 91.75 | 91.25 | |||||
| 120°~140° | 散射中心结构 | 99.75 | 99.75 | 99.75 | 99.75 | 100 | 100 |
| 能量聚集区长度 | 95.50 | 94.75 | |||||
| 稳定性特征 | 95.50 | 98.75 | |||||
| 150°~170° | 散射中心结构 | 96.25 | 96.75 | 97.00 | 98.25 | 98.50 | 99.75 |
| 能量聚集区长度 | 82.75 | 83.75 | |||||
| 稳定性特征 | 93.50 | 93.00 | |||||
从表 2中可以看出,不同特征的分类效果不同,在不同角度范围内对目标的识别能力也不同。两种投票融合法的识别效果比RVM_DS和SVM_DS方法差,在0~20°和30~50°角域内,多数投票法甚至比单个基分类器的识别效果差,这主要是由于多数投票法忽略了各个分类器之间性能的差异, 给予各个分类器同等地位,易造成冲突判决。RVM_DS方法的融合识别效果明显优于SVM_DS方法,这充分说明了利用RVM输出的概率信息的重要性和优越性。事实上M.E.Tipping在文献[7]中早已指出SVM采用logistic sigmoid函数实现概率估计并不是一种好的后验概率近似,不能较好地表示预测值的概率分布,然而,获取后验概率估计信息对于加深分类结果的不确定性理解非常重要,通过RVM可以得到未知样本类别信息及样本后验概率分布。采用RVM输出的概率信息构造DS的BPA函数比SVM更加简便、合理、准确,进而导致RVM_DS的融合识别更好。RVM输出的后验概率可以为分类决策提供更精确、更有参考价值的信息,充分重视并有效利用这些信息对提高系统识别性能具有重要价值。
5 结束语基于HRRP多特征融合识别是提高雷达目标别正确率的一个重要手段,稳健、高效的分类器设计一直是HRRP识别的关键问题。本文利用RVM输出的概率信息,解决了用DS证据理论进行融合时基本概率赋值获取困难的问题,提出一种基于RVM和DS的一维距离像融合识别方法。该方法使用交叉验证进行参数选择,构造了稳健的高性能RVM分类器,利用RVM输出的概率信息对DS证据理论的BPA赋值,实现了HRRP分类过程中的不确定信息融合识别,实验结果验证了所提方法的有效性。
| [1] | 李丽亚.宽带雷达目标识别技术研究[D].西安:西安电子科技大学, 2009. LI Liya. Study on wideband radar target recognition[D]. Xi'an:Xidian University, 2009. http://cdmd.cnki.com.cn/Article/CDMD-10701-2009195450.htm |
| [2] | 张学峰, 王鹏辉, 冯博, 等. 基于多分类器融合的雷达高分辨距离像目标识别与拒判新方法[J]. 自动化学报 , 2014, 40 (2) : 348-356 ZHANG Xuefeng, WANG Penghui, FENG Bo, et al. A new method to improve radar HRRP recognition and outlier rejection performances based on classifier combination[J]. Acta automatica sinica , 2014, 40 (2) : 348-356 |
| [3] | 孙佳佳, 童创明. 基于一维距离像序列的弹道目标融合识别研究[J]. 微波学报 , 2013, 29 (3) : 72-76 SUN Jiajia, TONG Chuangming. Study on ballistic target fusion recognition based on HRRP[J]. Journal of microwaves , 2013, 29 (3) : 72-76 |
| [4] | 蕾蕾, 王晓丹, 邢雅琼, 等. 结合SVM和DS证据理论的多极化HRRP分类研究[J]. 控制与决策 , 2013, 28 (6) : 861-866 LEI Lei, WANG Xiaodan, XING Yaqiong, et al. Multi-polarized HRRP classification by SVM and DS evidence theory[J]. Control and decision , 2013, 28 (6) : 861-866 |
| [5] | 曹向海, 刘宏伟, 吴顺君. 多极化多特征融合的雷达目标识别研究[J]. 系统工程与电子技术 , 2008, 30 (2) : 261-264 CAO Xianghai, LIU Hongwei, WU Shunjun. Utilization of multiple polarization data and multiple features for radar target identification[J]. Systems engineering and electronics , 2008, 30 (2) : 261-264 |
| [6] | CHO H, CHUN J, SONG S, et al. Radar target classification using the relevance vector machine[C]//Proceedings of IEEE Radar Conference. Cincinnati, OH:IEEE, 2014:1333-1336. |
| [7] | TIPPING M E. Sparse Bayesian learning and the relevance vector machine[J]. The journal of machine learning research , 2001, 1 : 211-244 |
| [8] | TIPPING M E. The relevance vector machine[J]. Advances in neural information processing systems , 1999, 12 (3) : 652-658 |
| [9] | BISHOP C M, TIPPING M E. Variational relevance vector machines[C]//Proceedings of the 16th Conference on Uncertainty in Artificial Intelligence. San Francisco, CA, USA:ACM, 2000:46-53. |
| [10] | MIANJI F A, ZHANG Ye. Robust hyperspectral classification using relevance vector machine[J]. IEEE transactions on geoscience and remote sensing , 2011, 49 (6) : 2100-2112 DOI:10.1109/TGRS.2010.2103381 |
| [11] | MENG Qingfang, CHEN Yuehui, ZHANG Qiang, et al. Local prediction of network traffic measurements data based on relevance vector machine[M]//GUO Chengan, HOU Zengguang, ZENG Zhigang. Advances in Neural Networks-ISNN 2013. Berlin Heidelberg:Springer, 2013:606-613. |
| [12] | BAO Yan, WANG Hui, WANG Beining. Short-term wind power prediction using differential EMD and relevance vector machine[J]. Neural computing and applications , 2014, 25 (2) : 283-289 DOI:10.1007/s00521-013-1482-z |
| [13] | 韩德强, 杨艺, 韩崇昭. DS证据理论研究进展及相关问题探讨[J]. 控制与决策 , 2014, 29 (1) : 1-11 HAN Deqiang, YANG Yi, HAN Chongzhao. Advances in DS evidence theory and related discussions[J]. Control and decision , 2014, 29 (1) : 1-11 |
| [14] | 张玉玺, 王晓丹, 姚旭, 等. 基于Bagging-SVM动态集成的多极化HRRP识别[J]. 系统工程与电子技术 , 2012, 34 (7) : 1366-1371 ZHANG Yuxi, WANG Xiaodan, YAO Xu, et al. HRRP recognition for polarization radar based on Bagging-SVM dynamic ensemble[J]. Systems engineering and electronics , 2012, 34 (7) : 1366-1371 |
| [15] | 徐庆, 王秀春, 李青, 等. 基于高分辨一维像的目标特征提取方法[J]. 现代雷达 , 2009, 31 (6) : 60-63 XU Qing, WANG Xiuchun, LI Qing, et al. Extraction of target feature using high resolution range profile[J]. Modern radar , 2009, 31 (6) : 60-63 |
| [16] | PLATT J C. Probabilistic outputs for support vector machines and comparisons to regularized likelihood methods[M]//SMOLA A J, BARTLETT P L, SCHOLKOPF B, et al. Advances in Large Margin Classifiers. Cambridge:MIT Press, 1999:61-74. |
| [17] | 李晓宇, 张新峰, 沈兰荪. 一种确定径向基核函数参数的方法[J]. 电子学报 , 2005, 33 (12A) : 2459-2463 LI Xiaoyu, ZHANG Xinfeng, SHEN Lansun. A selection means on the parameter of radius basis function[J]. Acta electronica sinica , 2005, 33 (12A) : 2459-2463 |
| [18] | CHANG C C, LIN C J. LIBSVM:a library for support vector machines[ED/OL].[2013-03-04].http://www.csie.ntu.edu.tw/~cjlin/libsvm. |
| [19] | TIPPING M. Sparse Bayesian models (and the RVM)[EB/OL].[2006-10-12].http://www.relevancevector.com. |



