概念格[1]是对背景中属性、对象及其关系进行分析研究的理论。它提供了一种支持数据分析和知识处理的数学工具[2-3]。目前,概念格已经广泛应用于数据挖掘[4]、信息处理[5]、软件工程[6]和其他方面[7-8]。概念格理论的研究不仅能用于解决知识发现领域中所涉及的关联规则、蕴含规则、分类规则的提取,还能够实现对信息的有机组织、减少冗余度、简化信息表,所以对概念格理论及其算法的研究具有重要的意义。
概念是人类进行知识表达的一种手段,数据库知识发现的过程就是将数据库中蕴含的知识形式化成有用的概念的过程。对形式背景的表示及寻找背景下的所有概念是概念格理论研究的基本问题。近年来许多学者从图论的方面对概念格进行研究,例如,张涛等[9]提出用属性拓扑图来表示形式背景,并在此属性拓扑图的基础上进行概念计算;A.Berry等[10]将形式背景构造成二部图,利用团的思想生成概念;此外,李立峰等[11]利用弦二部图对概念格进行表示,其中判断弦二部图中是否有圈,是判断弦二部图的关键。这也证实图论特别是图中的圈,在概念格的研究中之重要。
本文结合图论的知识,将形式背景以属性拓扑图表示出来,通过构造弱化的属性拓扑图,然后寻找弱化的属性拓扑图中的权值w之最大圈,用以生成概念,从而构造出概念格,并结合实例分析了这一算法的有效性。
1 基本概念本节将回顾概念格与图论的一些性质和定义,关于概念格的更多内容参见文献[12],有关图论详细内容参见文献[13],并且简单描述形式背景的属性拓扑图表示方法,更多详细内容参见文献[9, 14]。
1.1 概念格定义1
1)形式背景(O,M,I)是一个三元组,其中O是对象集,M是属性集,I⊆O×M。O和M中的元素分别称为对象和属性。
2)设A⊆O且B⊆M,定义
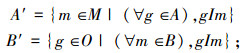 |
若A′=B且B′=A,则元素对(A,B)是一个概念。A为概念(A,B)的外延,B为概念(A,B)的内涵。形式背景(O,M,I)的所有概念的集合用β(O,M,I)表示,称β(O,M,I)为(O,M,I)的概念格。
3)对于β(O,M,I)中的概念(A1,B1)和(A2,B2),如果A1⊆A2,我们写作(A1,B1)≤(A2,B2)。很容易看到(β(O,M,I);≤)是一个完备格。
例1 形式背景(O,M,I),其中O={1,2,3,4,5,6},M={a,b,c,d,e,f,g},关系I如表 1所示。
| 对像 | a | b | c | d | e | f | g |
| 1 | × | × | × | ||||
| 2 | × | × | × | × | |||
| 3 | × | × | × | ||||
| 4 | × | × | × | × | |||
| 5 | × | × | |||||
| 6 | × |
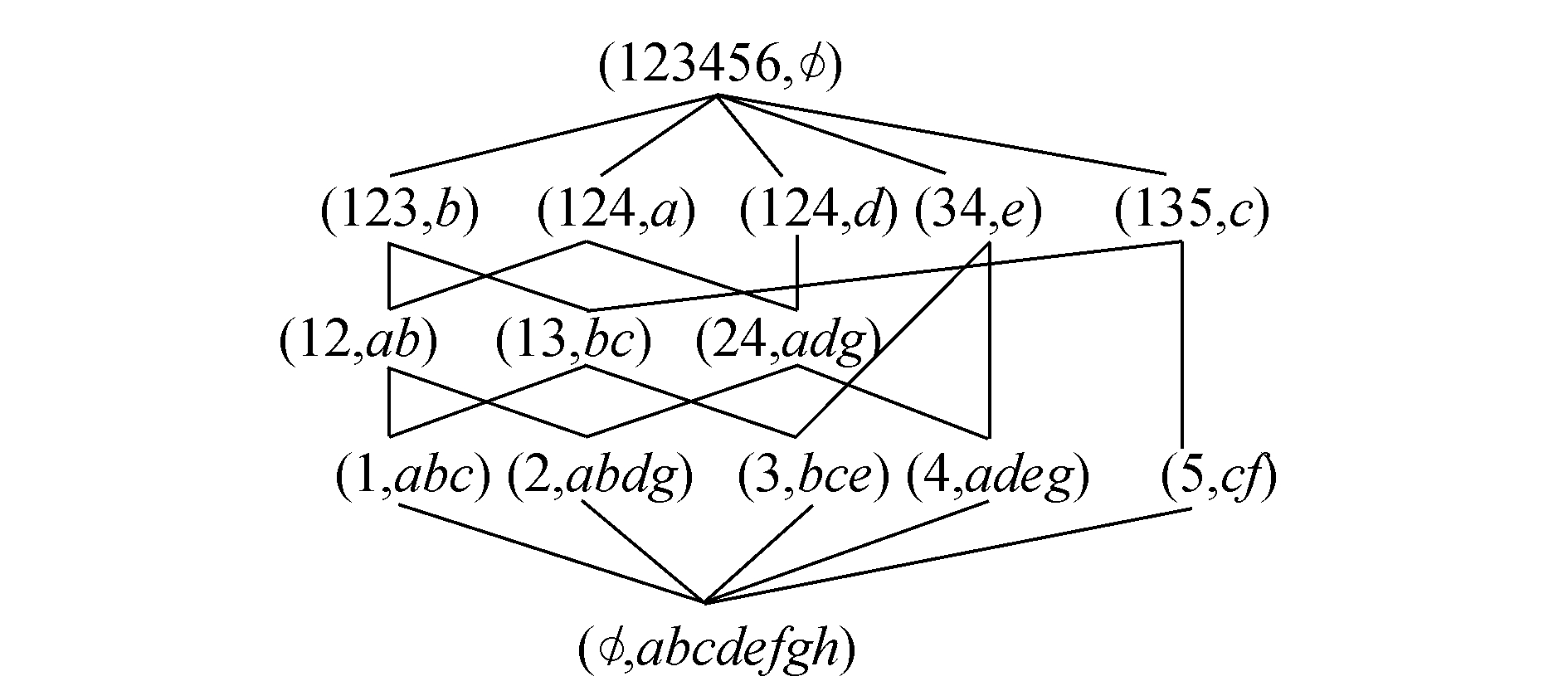
|
| 图 1 β(O,M,I) Fig. 1 β(O,M,I) |
说明1 本文所讨论的形式背景中不含有满足以下条件的属性和对象,m∈M,m′=O或m′=Ø;g∈O,g′=M或g′=Ø。
1.2 图论定义2 1)称数学结构G={V(G),E(G),ψG }为一个图,其中V(G)为非空集合,ψG 是从集合E(G)到V(G)× V(G)的一个映射,则称G是一个以V(G)为顶集合,以E(G)为边集合的有向图,V(G)中的元素称为G的顶点。E(G)中的元素称为G的边,ψG称为G的关联函数。若ψG(e)=(u,v),e∈E(G),(u,v)∈V(G)× V(G),简写成e=uv,称u是有向边e的尾,v是有向边e的头。擦掉有向图中的箭头,则得到无向图。
2)在顶边交错链P=v0e1v1e2…vkek中,ei∈E(G),i=1,2,…,k,vj∈V(G),j=1,2,…,k,且ei= vi-1 vi,则称P是G的一条道路,其中允许vi= vj或ei= ej,i≠ j。称v0是p的起点,vk是p的终点。各顶相异的道路称为轨道;起点与终点重合的轨道称为圈。
3)在一个无向图中,只有一个顶的圈叫做自环;ψG(e1)= ψG(e2)=(u,v),则称e1与e2是重边。
说明2 由上述定义可知自环、重边均为圈。
1.3 属性拓扑图定义3 设(O,M,I)是一个形式背景。按如下规则构造属性拓扑图(A(O,M,I),w):
1) 设m1,m2∈M且m1≠m2。
①若m′1⊄m′2,m′2⊄m′1且m′1∩m′2≠Ø,则用“↔”连接m1和m2;
②若m′1⊂m′2且m′1∩m′2≠Ø,则用“→” 连接m1和m2表示为m2→m1;
③若m′1∩m′2 =Ø,则m1和m2没有边连接。
2) 设(A(O,M,I),w)为(O,M,I)的属性拓扑图,e(mi,mj)∈E(A(O,M,I),w)),E(A(O,M,I),w)为(A(O,M,I),w)的边集,e(mi,mj)上的权值用w(mi,mj)表示,w(mi,mj)为属性mi和mj之间的公共对象{g1,g2,…,gn}的集合,称w(mi,mj)为mi和mj之间的权值。
3)设m∈M,b∈M,若与m连接的边均为非单向入边,即与m连接的边均为m→b或m↔b,则称m为顶层属性,顶层属性的集合用T表示。
例2 图 2为表 1形式背景(O,M,I)对应的属性拓扑图。
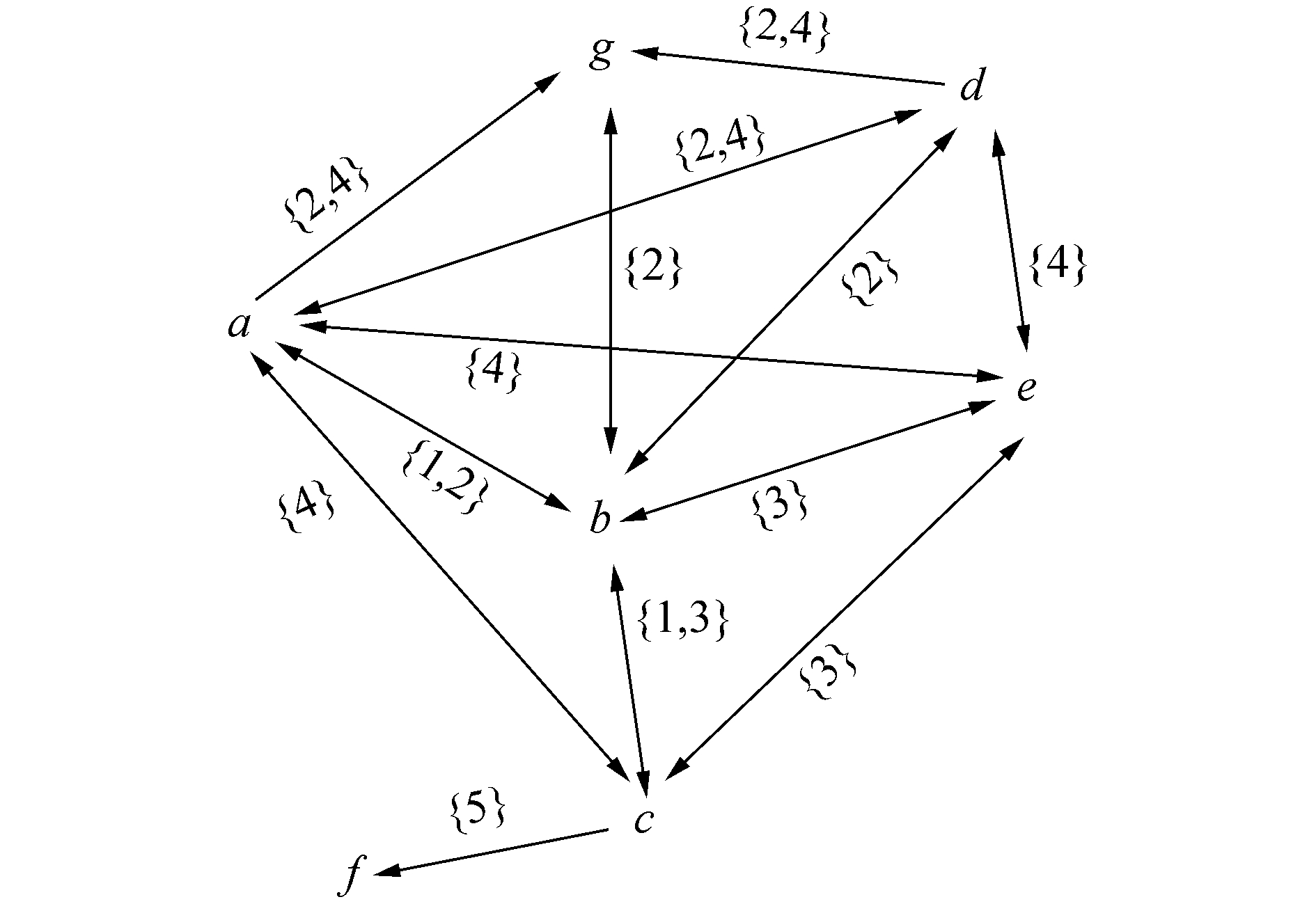
|
| 图 2 (A(O,M,I),w) Fig. 2 (A(O,M,I),w) |
引理1 设(O,M,I)是一个形式背景,(A(O,M,I),w)为(O,M,I)的属性拓扑图,若m∈T,则(m′,m)∈β(O,M,I)。
2 概念格的构造在搜索概念的过程中,为了不受方向的限制,首先进行属性拓扑图弱化,将有向图变为无向图,实际上目前结合图论生成概念格的算法,都是在无向图的基础上进行的。其次,给出弱化后属性拓扑图关于某个权值的最大圈的定义。最后,给出利用权值的最大圈构造概念算法,并进行算法分析。
2.1 弱化的属性拓扑图设(O,M,I)是一个形式背景,按照如下规则对属性拓扑图进行弱化:
1)去掉属性拓扑图中的方向,得一无向图。
2)若m 在(A(O,M,I),w)中为顶层属性,则在1)中的无向图中,加一个以m为顶点的自环。
3)若在1)中的无向图中,包含权值w(u,v)的只有一条边e,其中,u、v为e的两个端点,则在u与v之间再添加一条边e1 (图中用虚线表示),并且令e1的权值也为w(u,v)。
完成1)~3)后得到的加权无向图称为弱化的属性拓扑图,用(R(O,M,I),w)表示。
此外,显然,在上述3)中的e与e1是重边。
例3 下面图 3为图 2所对应的(A(O,M,I),w)之弱化的属性拓扑图。
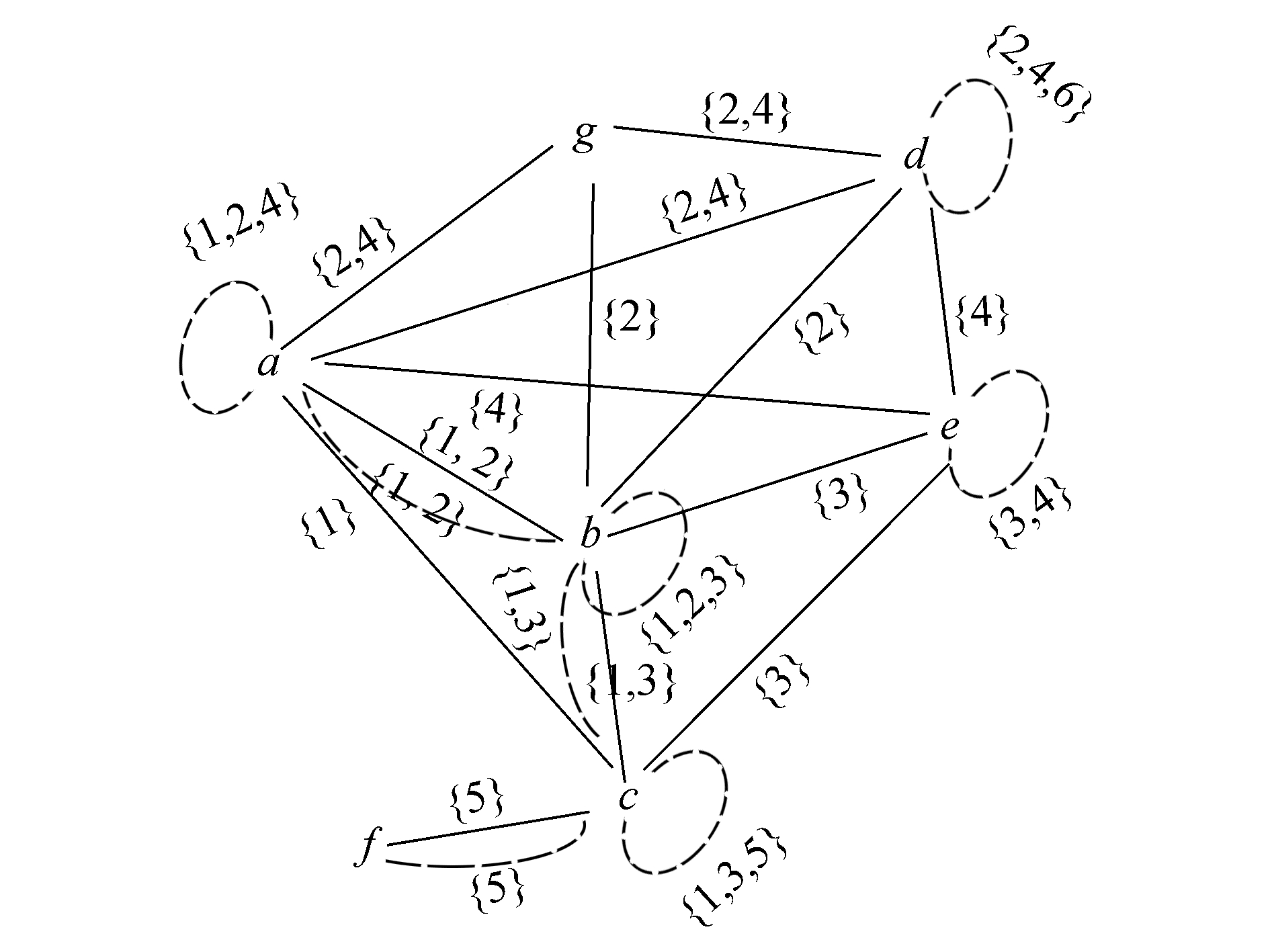
|
| 图 3 (R(O,M,I),w) Fig. 3 (R(O,M,I),w) |
定义4 设(O,M,I)是一个形式背景,(R(O,M,I),w)是(O,M,I)对应的弱化的属性拓扑图,{m1,m2,…,mh}⊆M且{m1,m2,…,mh}'≠Ø,若不存在任意ma∈M,ma∉{m1,m2,…,mh},使得{m1,m2,…,mh}'={m1,m2,…,mh,ma}',则称Y={m1,m2,…,mh}为权值w({m1,m2,…,mh}')的最大圈。
例如图 3中,Y={bdga}为权值{2}的最大圈。
说明3 为了描述方便,有时将w(mi,mj)简写为w。
2.2 算法过程对于给定的形式背景(O,M,I),构造概念格的过程如下:
输入 形式背景(O,M,I)以及W(R(O,M,I),w)={w1,w2,…,wn},wr≠ws,r,s,n=1,2,…,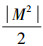
输出 所有概念β(O,M,I)\\{(O,Ø),(Ø,M)}。
1)对于(O,M,I),绘制属性拓扑图,根据属性拓扑图中的箭头指向,确定顶层属性集合T。
2)将属性拓扑图转化为弱化的属性拓扑图。
3)①初始将W(R(O,M,I),w)赋值给Wr,对任意wi,wj∈Wr,求wi∩wj, i,j=1,2,…,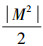
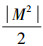
②若wi∩wj=wt,wt∉W(R(O,M,I),w),i,j,t=1,2,…,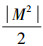
4)取max|ws|,开始寻找边上权值包含ws的最大圈,记录权值ws最大圈的顶点为Y,对应概念为C={(A,B): A=ws ,B= Y}。
5)①根据4)的原则,若W中存在ws+1,s=1,2,…,|M|2,则选定ws+1,重复4)。
②若W中不存在ws+1,则停止。
若W(R(O,M,I),w)中的元素满足3)中的①,若wi∩wj=Ø,或wi∩wj=wt,此处wi,wj,wt∈W(R(O,M,I),w),i,j,t=1,2,…,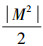
若W(R(O,M,I),w)中的元素满足wi∩wj=wt,wt∉W(R(O,M,I),w),i,j,t=1,2,…,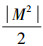
根据文献[9],可以看出1)的复杂度为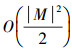
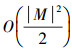
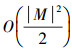
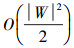
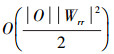
因此,整个算法的复杂度为O(2|M|×|O|)。
引理2 圈有且仅有以下3种情况:
1)由一条边构成,也即自环;
2)由两条边构成,也即重边;
3)由3条或3条以上的边构成,也即非自环非重边的圈。
证明 由定义2中3)可知,自环是只有一个顶点的圈;重边是由两个顶点的圈;由定义2中3)可知,非自环非重边的圈之顶点个数大于2。
当圈只有一个顶点时,根据定义2中3)可知,此时的圈为一个自环;
当圈有两个顶点时,根据定义2中3)可知,此时的圈为重边;
当圈的顶点个数大于2时,符合定义2中2)。
因此,圈有且仅有自环、重边、非自环非重边的圈3种情况。
定理1 设(O,M,I)是一个形式背景,(R(O,M,I),w)是(O,M,I)对应的弱化的属性拓扑图,权值最大圈一定能够生成一个概念。
证明 由引理2可知,弱化的属性拓扑图的权值w最大圈有且仅有3种情况,下面关于这3种情况分别说明。
1)当圈为自环时
m∈M,圈Y={m},由弱化的属性拓扑图的构造1)可知,有m∈T。根据引理1,(m′,m)∈β(O,M,I)。而m′=w(m,m),因此,(w(m,m),m)∈β(O,M,I)。
2)当圈为重边时
m1,m2∈M,圈Y={m1,m2},由弱化的属性拓扑图的构造2)可知,不存在其他权值为w(m1,m2)的边,即不存在其他顶mi ,mj∈M,使w(m1,m2)⊆w(mi ,mj),i≠j,i≥3,j≥1。这就是说,除m1,m2外,不存在其他属性所拥有的对象集包含w(m1,m2),所以(w(m1,m2),Y)∈β(O,M,I)。
3)=当圈的顶点个数大于等于3时
m1,m2,… ,mi ∈M,i≥3,若圈Y={ m1,m2,… mi},证明过程与第2种情况类似,易证(w(m1,m2),Y)∈β(O,M,I)。
引理3 设W(R(O,M,I),w)是一个集族,则任意的其中wi,wj,wt∈W(R(O,M,I),w),wu∉W(R(O,M,I),w),i,j,t,u=1,2,…,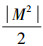
1)wi∩wj=Ø;
2)wi∩wj=wt;
3)wi∩wj=wu。
证明 根据文献[15],可得若W(R(O,M,I),w)是一个集族,则对于任意的wi,wj,wt∈W(R(O,M,I),w),wu∉W(R(O,M,I),w),i,j,t,u=1,2,…,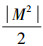
定理2 设(O,M,I)是一个形式背景,(R(O,M,I),w)是(O,M,I)对应的弱化的属性拓扑图,通过权值w最大圈算法一定能够得到β(O,M,I)\\{(O,Ø),(Ø,M)}。
证明 由引理3可知集族W(R(O,M,I),w)中的权值之间有且仅有3种情况,对于任意的wi,wj,wt∈W(R(O,M,I),w),wu∉W(R(O,M,I),w),i,j,t,u=1,2,…,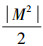
1)wi∩wj=Ø
说明任意3个属性之间没有公共对象,根据属性拓扑图的构造过程,其弱化的属性拓扑图为定理1的第2种情况,得到的W(R(O,M,I),w)能够包括所有概念的外延,因此,依次搜索W(R(O,M,I),w)中的每一个权值w最大圈,即可得到β(O,M,I)\{(O,Ø),(Ø,M)}。
2)wi∩wj=wt,wt∈W(R(O,M,I),w),i,j,t=1,2,…,|M|2,说明得到的W(R(O,M,I),w)能够包括所有概念的外延,符合定理的第2、3种情况。因此,依次搜索W(R(O,M,I),w)中的每一个权值w最大圈,即可得到β(O,M,I)\\{(O,Ø),(Ø,M)}。
3)若wi∩wj=wt,wt∉W(R(O,M,I),w),i,j,t=1,2,…,|M|2,则说明当前W(R(O,M,I),w)中不能包含所有概念的外延,将Wr ={wt:wi∩wj=wt,wt∉W(R(O,M,I),w)}添加到W中,只需对Wr中的任意两个元素取交集即可,由于|O|是有限的,因此一定会有wi∩wj=wt,wt∈W(R(O,M,I),w),i,j,t=1,2,…,|M|2,此时说明得到的W(R(O,M,I),w)能够包括所有概念的外延,并且W(R(O,M,I),w)中的元素对应的最大圈符合定理1的第2、3种情况。因此,依次搜索W(R(O,M,I),w)中的每一个权值w最大圈,即可得到β(O,M,I)\\{(O,Ø),(Ø,M)}。
以上说明了本算法的正确性。下面将通过与已有的图论方法构造概念格的相关著名算法或方法的比较,分析得出本算法的优势。
1)张涛等[14]在属性拓扑的基础上给出概念计算方法,实际上是将图论中已有的深度优先算法应用于概念的寻找,如此可能导致产生冗余概念。冗余概念的产生必然导致算法的储存空间的增加,引发空间复杂度的加大。
本文算法用图论中的权值与最大圈结合来寻找概念,由于不会重复对同一权值寻找其相应的最大圈,因此不会有冗余概念的产生。从而,必然在概念寻找中,降低数据的储存空间,空间复杂度较张涛等的方法减少成为显然之事。
2)Berry等[10]将形式背景构造成二部图,利用团的思想生成概念,其计算每个概念的复杂度为O(|M|2)。
对于弱化的属性拓扑图产生概念有:
1)对于只含有一个顶点属性的情况,由引理1可知,属性m为某个概念的内涵。在弱化的属性拓扑图中属性m构成一个自环时,本文计算每个概念的复杂度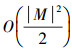
2)对于至少含有两个顶点属性的情况,本文计算每个概念的算法复杂度O(|M|2)。
以上两种情形说明,当情形1)时,本文算法的复杂度小于Berry等的;当情形2)时,本文算法的复杂度与Berry等的相同。这说明,对于情形1),本文的算法优于Berry等的,虽然在其他情况(也就是情形2)),本文的算法与Berry等的具有相同的时间复杂度。
再有,由图论知识可知,每一个团必包含至少一个圈,所以在判断团的过程中必然存在对圈的判断过程,当一个团中含有两个以上圈时,此时对团的判定过程会重复圈的判断过程。因此,Berry等的方法会造成数据存储量过大。而本文算法,不会对相同权值的圈进行重复判断与存储,因此,降低了数据存储空间复杂度。
3)李立峰等[11]仅是从理论方面指出弦二部图的概念格表示,并没有给出算法过程。所以他们的方法只是理论过程,而无法直接实现。
本文中不仅给出了理论分析,并且将理论的内容通过一个可行的算法加以实现,故此,本文的思想和方法可操作性强,易于直接理解与实现。
由以上1)~3)的分析可以看出,本文给出的算法与已有算法相比,计算出全部概念的时间复杂度并不低于以往的算法,基本相同。在数据存储空间方面,本文给出的算法与已有算法相比,空间复杂度降低。这样必然使得本算法在整个计算过程能在占用更小内存的情况下完成,同时也就对计算机器系统的运行空间降低了要求。因此本文算法要优于其他一些已有算法或方法。
3 实例结合实例,说明第2.2节中的算法有效性。以表 2为形式背景(O1,M1,I1),进行概念的搜索,该背景从UCI机器学习数据库中,随机选取BLOGGER数据集的前40个对象进行试验,整理后得到如表 2所示的形式背景。
| 对像 | a1 | a2 | a3 | a4 | a5 | a6 | a7 |
| 1 | × | × | × | ||||
| 2 | × | × | × | ||||
| 3 | × | × | × | ||||
| 4 | × | × | × | ||||
| 5 | × | × | × | ||||
| 6 | × | × | |||||
| 7 | × | × | |||||
| 8 | × | × | × | ||||
| 9 | × | × | |||||
| 10 | × | × |
其中,a1代表博主高学历,a2代表博主中等学历,a3代表博主低学历,a4代表政治立场为左派,a5代表政治立场中立,a6代表政治立场为右派,a7代表博客被当地媒体转载。
根据1),按照定义3中1)得到以表 2为形式背景的属性拓扑图,如图 4。根据2),按照定义4,构造出弱化的属性拓扑图(R(O1,M1,I1),w),如图 5。
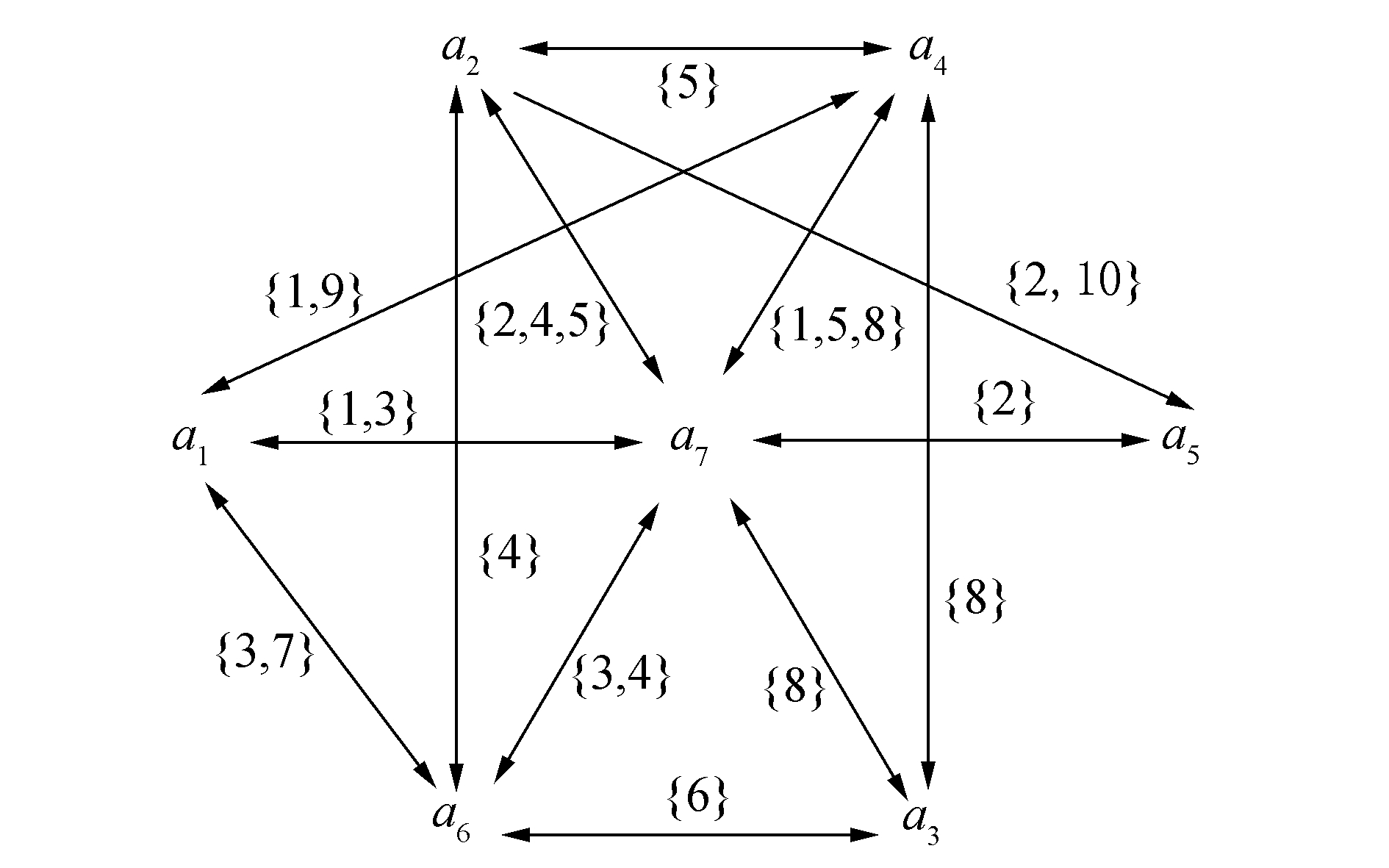
|
| 图 4 (A(O1,M1,I1),w) Fig. 4 (A(O1,M1,I1),w) |
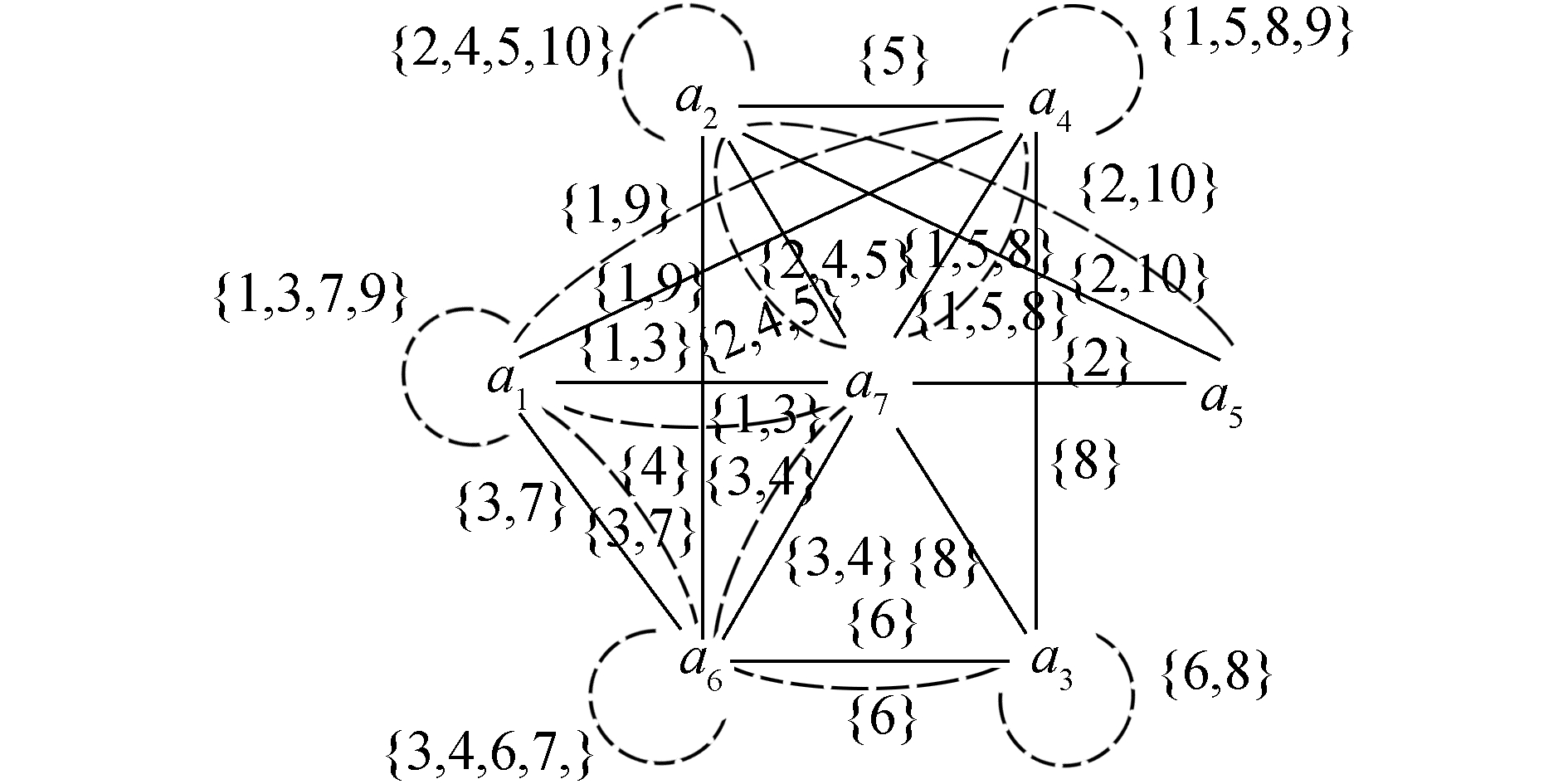
|
| 图 5 (R(O1,M1,I1),w) Fig. 5 (R(O1,M1,I1),w) |
根据3),W={w(a1,a1),w(a2,a2),w(a3,a3),w(a4,a4),w(a6,a6),w(a7,a7),w(a1,a4),w(a1,a6),w(a1,a7),w(a2,a4),w(a2,a5),w(a2,a6),w(a2,a7),w(a3,a4),w(a3,a6),w(a4,a7),w(a5,a7),w(a6,a7)}。
对于任意两个w(ai,aj)求交集,i,j=1,2,…,7,根据3)中②,可以发现存在w(a1,a1)∩ w(a4,a7)= w(a1,a4)∩ w(a4,a7)=…={1}及w(a1,a1)∩ w(a6,a7)= w(a1,a7)∩ w(a6,a7)=…={3},{1},{3}∉W,将{1}与{3}添加到W,重复3)。
对{{1},{3}}进行步骤3)中②,{1}∩{3}=Ø,进行4)。
根据4),W={w(a1,a1),w(a2,a2),w(a3,a3),w(a4,a4),w(a6,a6),w(a7,a7),w(a1,a4),w(a1,a6),w(a1,a7),w(a2,a4),w(a2,a5),w(a2,a6),w(a2,a7),w(a3,a4),w(a3,a6),w(a4,a7),w(a5,a7),w(a6,a7),{1},{3}}。
因为6=|w(a7,a7)| ≥4= |w(a1,a1)| = |w(a2,a2)|= |w(a4,a4)| = |w(a6,a6)| ≥3= |w(a2,a7)| = |w(a4,a7)| ≥2 |w(a1,a4)| = |w(a1,a6)|= |w(a1,a7)| =|w(a2,a5)| = |w(a3,a3)| =|w(a6,a7)| ≥1= |w(a2,a6)| = |w(a2,a4)| = |w(a3,a4)|= |w(a3,a6)| = |w(a5,a7)| = |{1}|= |{3}|,所首先寻找包含w(a7,a7)={1,2,3,4,5,8}的最大圈,Y1={ a7},对应的概念为(1 2 3 4 5 8,a7)。
根据5)中①,依次选择W中的其他元素重复4),概念分别为(1 3 7 9,a1),(2 4 5 10,a2),(1 5 8 9,a4),(3 4 6 7,a6),(2 4 5,a2 a7),(1 5 8,a4 a7),(1 9,a1a4),(3 7,a1 a6),(1 3,a1 a7),(2 10,a2 a5),(6 8,a3),(3 4,a6 a7),(4,a2 a6 a7),(5,a2 a4 a7),(8,a3 a4 a7),(6,a3 a6),(2,a2a5 a7),(1,a1a4 a7),(3,a1a6 a7)。
根据5)中②,停止。
最后添加(1 2 3 4 5 6 7 8 9 10,Ø)和(Ø,a1a2 a3 a4 a5 a6 a7)后,得到概念格β(O1,M1,I1)={(1 2 3 4 5 6 7 8 9 10,Ø),(1 2 3 4 5 8,a7),(1 3 7 9,a1),(2 4 5 10,a2),(1 5 8 9,a4),(3 4 6 7,a6),(2 4 5,a2 a7),(1 5 8,a4 a7),(1 9,a1a4),(3 7,a1 a6),(1 3,a1 a7),(2 10,a2 a5),(6 8,a3),(3 4,a6 a7),(4,a2 a6 a7),(5,a2 a4 a7),(8,a3 a4 a7),(6,a3 a6),(2,a2a5 a7),(1,a1a4 a7),(3,a1a6 a7) ,(Ø,a1a2 a3 a4 a5 a6 a7)}。
在本实例中,步骤2),弱化属性拓扑图,以w(a1,a1)为例进行复杂度计算,判断是否有w(a1,a1)⊆w(ai,aj),其中i,j=1,2,…,16,对于w(a1,a1)进行16次比较可得a1为顶层属性。对每个w∈W重复上述比较过程,可得到弱化的属性拓扑图。
3)对任意两个元素wi,wj∈W,i,j=1,2,…,16,取交集,此过程需要进行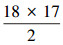
4)取W中的元素w(a7,a7),判断w(a7,a7)⊆w(ai,aj) 其中i,j=1,2,…,20,每个元素比较20次,寻找最大圈,得到概念(1 2 3 4 5 8,a7)。
5)依次取W中的其他元素,重复4),在此例W中的18个元素,4)需要重复18次。
在复杂度上,本文算法与张涛等的算法相同。并且利用张涛等的算法对(O1,M1,I1)进行概念的计算,得到的概念格与本文算法的结果相同。从而说明了本文算法的有效性与正确性。
4 结束语本文结合图论的知识,将形式背景对应的属性拓扑图弱化,提出了一种利用权值最大圈寻找概念的算法。与现有的算法比较,本文提出一种新的思路来搜索概念,此外通过弱化的属性拓扑图,对于概念的可视化也得到了很好的体现;通过实例可知,该方法能够有效地构造概念格,为知识获取和数据处理提供了一种有益的思想。通过分析可知,虽然本文提出的算法产生全部概念的空间复杂度降低,但由于其时间复杂度仍为指数级,因此对于数据量较大的情况,计算时间方面需要进一步研究,以便提高应用其进行数据分析的效率。
| [1] | WILLE R. Restructuring lattice theory:an approach based on hierarchies of concepts[M]//RIVAL I. Ordered Sets. Dordrecht:Springer, 1982. |
| [2] | BELOHLAVEK R, SIGMUND E, ZACPAL J. Evaluation of IPAQ questionnaires supported by formal concept analysis[J]. Information sciences , 2011, 181 (10) : 1774-1786 DOI:10.1016/j.ins.2010.04.011 |
| [3] | NGUYEN T T, HUI S C, CHANG Kuiyu. A lattice-based approach for mathematical search using formal concept analysis[J]. Expert systems with applications , 2012, 39 (5) : 5820-5828 DOI:10.1016/j.eswa.2011.11.085 |
| [4] | 王旭杨, 李明. 基于概念格的数据挖掘方法研究[J]. 计算机应用 , 2005, 25 (4) : 827-829 WANG Xuyang, LI Ming. Method of data mining based on concept lattice[J]. Computer applications , 2005, 25 (4) : 827-829 |
| [5] | SIFF M, REPS T. Identifying modules via concept analysis[C]//Proceedings of International Conference on Software Maintenance. Washington, DC, USA:IEEE Computer Society, 1997:170-179. |
| [6] | FERJANI F, ELLOUMI S, JAOUA A, et al. Formal context coverage based on isolated labels:an efficient solution for text feature extraction[J]. Information sciences , 2012, 188 : 198-214 DOI:10.1016/j.ins.2011.10.023 |
| [7] | 邓君, 马晓君, 张巨峰, 等. 基于概念格的实体档案馆用户行为研究[J]. 图书情报工作 , 2014, 58 (12) : 109-117 DENG Jun, MA Xiaojun, ZHANG Jufeng, et al. Study on entity archives' user behavior based on concept lattice[J]. Library and information service , 2014, 58 (12) : 109-117 |
| [8] | 张晓, 龙伟, 卢斌. 基于概念格的关联规则在排产管理的应用[J]. 计算机工程与应用 , 2014, 50 (9) : 264-270 v ZHANG Xiao, LONG Wei, LU Bin. Application of association rule based on concept lattice for scheduling management[J]. Computer engineering and applications , 2014, 50 (9) : 264-270 |
| [9] | 张涛, 任宏雷. 形式背景的属性拓扑表示[J]. 小型微型计算机系统 , 2014, 35 (3) : 590-593 ZHANG Tao, REN Honglei. Attribute topology of formal context[J]. Journal of Chinese computer systems , 2014, 35 (3) : 590-593 |
| [10] | BERRY A, SIGAYRET A. Representing a concept lattice by a graph[J]. Discrete applied mathematics , 2004, 144 (1/2) : 27-42 |
| [11] | 李立峰, 刘三阳, 罗清君. 弦二部图的概念格表示[J]. 电子学报 , 2013, 41 (7) : 1384-1388 LI Lifeng, LIU Sanyang, LUO Qingjun. Representing chordal bipartite graph using concept lattice theory[J]. Acta electronica sinica , 2013, 41 (7) : 1384-1388 |
| [12] | DAVEY B A, PRIESTLEY H A. Introduction to lattices and order[M]. 2nd ed New York: Cambridge University Press, 2002 : 66 -69. |
| [13] | 王树禾. 图论[M]. 北京: 科学出版社, 2009 . |
| [14] | ZHANG Tao, REN Honglei, WANG Xiaomin. A calculation of formal concept by attribute topology[J]. ICIC express letters part B:applications , 2013, 4 (3) : 793-800 |
| [15] | 方嘉琳. 集合论[M]. 长春: 吉林人民出版社, 1982 . |



