2. 四川长虹电器股份有限公司, 四川 成都 610041;
3. 江南大学, 江苏 无锡 214122;
4. 江南大学 智能系统与网络计算研究所, 江苏 无锡214122
2. Sichuan Changhong Electric Co., Ltd., Chengdu 610041, China ;
3. School of Science, Jangnan University, Wuxi 214122, China ;
4. Institute of Intelligence System & Network Computing, Jiangnan University, Wuxi 214122, China
二元随机序列在密码应用中占有举足轻重的地位。现在大量的计算机系统的安全性需要依赖于二元随机序列,比如各种密码算法中使用的密钥、非对称密码算法RSA加密、数字签名方案中大素数的生成以及挑战应答身份识别系统中的挑战数等,这些都充分体现了二元随机序列的实际使用价值。在应用密码学中,随机性检测采用概率统计的方法对随机数发生器等生成的二元序列的随机性进行分析和检测,判断待检序列在统计上是否难以和真随机数区分开来。不同的随机性检测算法从不同的侧面分析刻画待检二元序列与真随机序列之间的差距。经过多年的发展,随机性检测算法已取得丰硕成果,出现并颁布了大量的随机性检测算法和相关标准,与此同时,大量新的随机性检测算法还在源源不断地涌现。美国国家标准与技术研究院(National Institute of Standards and Technology,NIST)发布了SP 800-22标准[1],其中建议了16种用于随机性测试的统计检测方法。德国以此规范为基础发布了BSI AIS 30规范[2]。我国国家密码管理局于2009年颁布了适用于我国的随机性检测规范[3]。随机性检测在实际应用中有重要的实用价值,不仅可以用于测评按照密码算法或特定标准生成的伪随机数据的性质,如分组算法与某些工作模式相结合生成的数据流[4],还可以分析测试以杂凑算法为核心生成的数据流,如我国SM3杂凑算法[5] 生成的数据流。上述工作不仅可以帮助算法分析,减少分析的难度和复杂度,而且可以检测出其他检测方法难以检测出的某些安全性隐患。因此,国际上很多著名的密码算法竞赛均进行了大量的随机性检测评估,比如AES密码算法竞赛、欧洲的NISSIE竞赛、estream算法竞赛等,我国的祖冲之序列密码算法[6-7]也进行了大量相关的随机性检测。此外,还有大量文章对随机性检测算法和标准进行进一步的分析讨论,比如讨论随机性检测规范的各项检测项的快速实现,例如研究单比特检测以及块内频数的快速实现[8],尝试新的统计测试方法以便作为现有测试规范的有益补充[9],考虑统计测试算法的GPU并行化,搭建可并行计算的统计测试实现框架[10]。本文的研究重点是扑克检测的快速实现,因为扑克检测不仅是我国随机性检测规范的检测项,而且也是很多基本的随机性检测的必检项目之一,所以此项检测的快速实现研究具有非常重要的现实意义。
1 扑克检测我国的随机性检测规范有15项检测,包括:单比特频数检测、块内频数检测、扑克检测、重叠子序列检测、游程总数检测、块内最大1游程检测、矩阵秩检测、累积和检测、近似熵检测、线性复杂度检测、Maurer通用统计检测、离散傅里叶变换检测、游程分布检测、二元推导检测、自相关检测。扑克检测不仅出现在我国的随机性检测规范中,也出现在很多别的基本随机性检测中,比如作为5项基本检测项中的一项出现,5项基本检测包括单比特频数检测、序偶检测、扑克检测、游程分布检测、自相关检测。
我国随机性检测规范对扑克检测的执行流程分为4个步骤,描述如下[3]:
1) 将长度为n的二元待检序列ε1ε2…εn划分为N=n/m个长度为m的非重叠子序列,将多余的比特舍弃。统计第i种子序列模式出现的频数,用ni(1≤i≤2m)表示。我国随机性检测规范规定m取4和8。
2) 计算统计值:
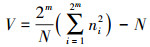 |
(1) |
3) 计算P值:
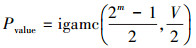 |
(2) |
4) 如果Pvalue≥α,则认为待检序列通过检测。
式(2)中使用的igamc是余不完全伽马函数,该函数的定义为
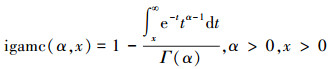 |
(3) |
式中:Γ(x)为伽马函数,该函数的定义为
 |
(4) |
扑克检测在很多基本的随机性检测中都会出现,因此这是一种基础检测项,在随机性检测中具有非常重要的作用。在实际应用中,该检测项需要具有较高的检测速度,以便快速剔除那些明显不满足随机性特征的样本。
2 原算法的检测效率分析在实际应用中,送入的待检序列数据多为字节序列,但传统的实现方式会根据算法描述先将待检数据转化为单比特表示,然后对m=4和m=8各执行一遍算法中的1)~4)的操作。扑克检测算法中3)和4)在一次样本检测中执行两次,1)的执行次数则为O(n);2)的执行次数则为O(1),所以其中最关键也最耗时操作为准备工作的字节转比特操作以及1)的统计各种频数。
在分析算法的计算量时,本文采用如下缩略符号:XOR表示异或运算;SHIFT表示左/右移位运算;ADD表示加法运算;AND表示与运算。
传统的扑克检测中最关键也最耗时的步骤是1),因此以下分析执行一组样本检测时1)所需的运算量。在m=4和m=8时1)需分别执行n次SHIFT、n次LOAD和2n次ADD,即合计总共需执行2n次SHIFT、2n次LOAD和4n次ADD。1)进行一组样本检测所需执行的操作数详情如表 1。
| 步骤1 | 运算量 |
| m=4 | nSHIFT + nLOAD +2nADD |
| m=8 | nSHIFT +nLOAD +2nADD |
| 合计 | 2nSHIFT +2nLOAD +4nADD |
按我国随机性检测规范规定一组样本的大小n为106 bit,因此由表 1的统计结果可知,算法的运算量不小,执行效率不会太快。在实际检测中,需要加快扑克检测的执行速度,以增强它的基础筛选作用。
3 优化思想和优化算法根据上一节的分析可知,扑克检测的效率不高的主要原因是计算统计量时出现了以下问题:
1)采用了单比特统计方式,每次仅仅处理一个比特,CPU的字长没有得到充分利用;如果一次处理多个比特则处理速度将有明显的提升;
2)对参数m=4和m=8,传统实现方式会各执行一遍算法中的1)~4)的操作,存在相同数据反复加载的情况;
3)算法的统计量计算和判断过程没有精简和优化,存在不必要的余不完全伽马函数的计算。
针对扑克检测原算法出现的效率不高问题,下面有针对性地提出几点优化想法。具体的优化想法如下:
1)一次处理多个比特,比如一个字节或半个字节,加快频数统计过程;
2)对m=4和m=8整合在一起实现,减少不必要的数据加载;
3)精简并优化统计量的计算和判断过程,事先计算Pvalue≥α时统计量V的阈值,让统计值直接和此阈值比较,避免每个样本都计算两次余不完全伽马函数。
记待检序列为n/8字节的字节数据Ei,Ei=ε8i+1‖ε8i+2‖…‖ε8i+8,0≤i≤n/8-1。为区分两种不同参数取值时各种序列模式出现的频数,记C4[i],0≤i≤15为m=4时各种序列模式出现的频数,记C8[i],0≤i≤255为m=8时各种序列模式出现的频数。
参数m=8时的频数统计方式为直接加载字节数据并更新频数,即
 |
(5) |
参数m=4时的频数统计方式为先加载字节数据,接着获取高半字节和低半字节,
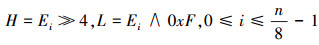 |
(6) |
最后利用获取的高半字节和低半字节更新对应的频数,即
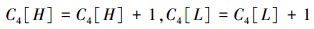 |
(7) |
参数m=4时和m=8时的统计过程分开实现会使得待检数据序列重复加载,这也是扑克检测效率不高的主要原因之一。如果能更进一步将参数在两种不同取值时的统计过程合并在一起,则可以减少大量的数据重复加载。参数m取4和8合并实现时的频数统计方式为先加载字节数据,然后获取高半字节和低半字节,最后更新m=4的频数和m=8的频数,合并式(5)~(7),可得
 |
(8) |
统计量的计算和判断过程还可以进行精简和优化:可根据余不完全伽马函数的性质预先求出Pvalue≥α时统计量V的阈值,让统计值V直接和此阈值比较,如此可以减少余不完全伽马函数的计算次数。
记m=4时的统计量为V4,即
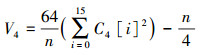 |
(9) |
记m=8时的统计量为V8,即
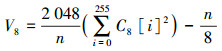 |
(10) |
计算统计值所用的余不完全伽马函数满足性质igamc(α,0)=1,igamc(α,∞)=0。经简单计算可知,当显著水平α=0.01,m=4时,统计量V4的阈值为λ4=30.577 914;当显著水平α=0.01,m=8时,统计量V8的阈值为λ8=310.457 388。即如果V4<λ4且V8<λ8则认为待检序列通过检测。根据以上描述,优化实现的扑克检测算法如下。
算法1 优化实现的扑克检测算法
输入 n/8字节的数据Ei,0≤i≤n/8-1;
输出 检测结果。
1) 初始化数据: i=0。
 |
2)当i<n/8时执行如下步骤;否则转3)。
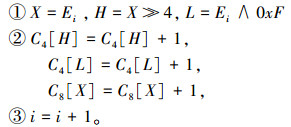 |
3)计算两个统计值V4和V8。
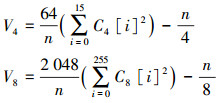 |
4)如果V4<λ4且V8<λ8,则认为待检序列通过检测。否则未通过。
算法1的主要优化方式是直接对输入的待检序列按字节而不是比特进行处理,减少了大量不必要的数据拆分为单比特等操作;并且将两种参数下的频数统计合并在一起,避免了大量的数据加载等操作。
4 优化前后计算量分析与对比本节对优化前的算法和优化后的算法的计算量进行定量评估与对比。
原算法的2)~4)的计算量都很小,因此本节在进行计算量评估对比时,只比较最关键最耗时的步骤统计频数所需要的运算量。为简化表示,将n比特二元序列的字节长度记为M,M=n/8。而且通常情况下输入的二元序列都是以字节表示,因此这里默认待检二元序列的比特长度n能被8整除。
根据第2节的分析结果知,对一个n=106 bit(M=125×103字节)的样本而言,原算法1)的计算量为16M次SHIFT、16M次LOAD和32M次ADD。扑克检测优化算法1的1)进行简单分析可知,对一个n=106 bit的样本而言,算法1的2)的计算量为M次SHIFT、M次LOAD、M次AND和3M次ADD。原算法和优化算法(算法1)的运算量详情以及对比情况见表 2。
| 运算 | 原算法 | 算法1 |
| LOAD | 16M | M |
| SHIFT | 16M | M |
| AND | 0 | M |
| ADD | 32M | 3M |
由表 2可知,优化后的扑克检测的计算量显著降低。
在现在的CPU中,常见的整数运算都比较快,如整数的加、减、比较、比特运算及移位等仅需一个时钟周期(cycle)。但数据加载的执行时间则有很多因素,无法以准确的值计量。这里仅做粗略估计,因此加速数据加载也仅需要一个时钟周期。这样一来原算法对一个样本进行检测的粗略估计时间为64M个时钟周期,算法1对一个样本进行检测的粗略估计时间为6M个时钟周期,以此法粗略估计,算法1的检测速度为原算法的10.7倍左右。当然,此处为不精确的粗略估计而已,具体的速度提升情况以实验为准。
5 模拟实验测试为更准确地说明本文提出的算法的效率,本节测试优化前后算法的执行效率。
测试数据是利用我国的分组密码算法SM4算法生成的109 bit的伪随机数据,按样本大小106比特划分为1 000个样本。
测试平台为Intel Core i3 @3400MHz处理器、4 GB DDR3 1600MHz内存、Windows XP SP3操作系统、Visual Studio 2008编译器。处理器的缓存情况为:一级缓存为每个核心32 KB,二级缓存为每个核心64 KB,三级缓存为多核共享3 MB。
模拟实验使用的代码情况如下。优化前的测试代码来源是先从NIST的官方网站取得检测代码,然后按原算法以及NIST代码思想对以比特表示的二元序列,按比特操作实现扑克检测,NIST代码完成字节序列转比特表示的二元序列的相关功能。优化后的代码(参见附录)是对以字节表示的序列按算法1的步骤以字节处理为主实现扑克检测。所有的算法都采用标准C实现。
实验采用欧洲estream算法竞赛的速度测试模型的简化版本,该测试模型不仅在estream算法竞赛中采用,后续许多算法的性能评估也常采用该测试模型。具体来讲速度测试流程如下。1)在被测试代码段的前后各设置一个时间计数器TS和TF;2)将两个计时器之差T=TF-Ts作为这段代码的耗时;3)重复1)和2)多次,为统计方便设定重复次数为奇数,记重复次数为C,得到一系列的耗时值T[i],1≤i≤C;4)将统计得到的耗时值序列按从大到小的顺序排列得到T′[1]≥T′[2]≥…≥T′[C],当然也可按从小到大的顺序排列;5)取新序列的中值T′[(C+1)/2]作为本段代码的统计耗时值。w为了保证测试结果的准确性,本测试模型中1)的时间计数器使用CPU频率计时器,直接调用汇编指令RDTSC,在Windows环境下也可调用__rdtsc()函数,该指令或函数返回CPU时钟周期值,按现代CPU的时钟频率计算,此计数器可精确到纳秒级。两次RDTSC指令返回的时钟周期之差再除以CPU频率,即可得到以s为单位的耗时值。
原算法和优化算法(算法1)对1 000个样本进行检测的性能统计结果见表 3。
| 性能对比 | 原算法 | 算法1 |
| 耗时/s | 2.244 | 0.236 |
| 速度比 | 1:1 | 9.508:1 |
理论评估时只估算了最重要也最耗时的步骤1),略去了后面的步骤的耗时。虽然步骤2)的计算过程和原算法一样,但优化算法对步骤3)也做了相应的优化。实验的结果表明,优化算法通过充分利用CPU字长一次处理多个比特,优化整合算法流程减少不必要的计算,精简统计量的计算和判断过程的技术方式和方法,的确可以显著地提升扑克检测的检测性能,且检测速度可提升9.5倍左右。
此外,算法性能提升显著的另外一个重要原因是扑克检测中的参数m取值较为特殊,m=8恰好是一个字节,m=4恰好是将一个字节拆分为两个“半字节”。这使得优化算法基于字节的处理方式得到了淋漓尽致的发挥。
6 结论本文对我国随机性检测规范采用的扑克检测算法进行优化实现。通过充分利用CPU字长一次处理多个比特,优化整合算法流程减少不必要的计算,精简统计量的计算和判断过程的技术方式和方法,可以显著地提升扑克检测的检测性能,实验结果表明检测速度可提升9.5倍左右。因此,建议在实际检测中采用软件实现时使用本文提出的扑克检测快速实现方式以提高扑克检测的检测效率。NIST和我国的随机性检测规范还有很多别的检测项,其中还有很多检测项可以做必要的性能优化,这将是今后工作的一个研究方向。另外,怎样利用并行化技术(如多线程技术、SIMD指令、GPU运算)快速实现这些检测项,也是今后研究的另一个方向。
附录 优化算法的代码
本节列出优化算法(算法1)的标准C代码。其中poker_test函数为扑克测试优化后的功能实现函数,poker_get_statistics函数为扑克检测中计算统计量的函数。
//扑克测试优化后代码
int poker_test(BYTE *p_u8,int n)
{
double v;
BYTE *p_bound = p_u8 + n / 8,d;
u32 c4[16] = {0},c8[256] = {0};
while( p_u8 < p_bound)
{
d = *p_u8++;
c8[d]++;
c4[d >> 4]++;
c4[d & 0xf]++;
}
//m = 8时计算统计量
v = poker_get_statistics(8,n,c8);
if(v >= POKER_BOUND_M_8)
{
return -8;
}
//m = 4 时计算统计量
v = poker_get_statistics(4,n,c4);
if(v >= POKER_BOUND_M_4)
{
return -4;
}
return 1;
}
//扑克检测计算统计量,n为序列比特长度
// m为参数,p_ctr为子序列频数
double poker_get_statistics(int m,int n,u32 *p_ctr)
{
int i,blk_sz,pow_m;
double blk_sz_inv,sum;
sum = 0.0;
pow_m = 1 << m;
blk_sz = n / m;
blk_sz_inv = 1.0 / blk_sz;
for( i = 0; i < pow_m; i++)
{
sum += p_ctr[i] * p_ctr[i] * blk_sz_inv;
}
return ( sum * pow_m) - blk_sz;
}
| [1] | National Institute of Standards and Technology. NIST SP 800-22, A statistical test suite for random and pseudorandom number generators for cryptographic applications[S]. Revision 1a. Washington DC, USA:Information Technology Laboratory of National Institute of Standards and Technology, 2010. |
| [2] | BSI AIS-20, AIS-30,. Application notes and interpretation of the scheme functionality classes and evaluation methodology for deterministic and physical random number generators[S]. Berlin, Germany:German Federal Office for Information Security, 2008. |
| [3] | 随机性检测规范[S]. 中国北京:国家密码管理局, 2009. Randomness test specification[S]. Beijing:National Cryptography Administration, 2009. |
| [4] | 罗影, 刘冬梅, 康红娟. NIST新分组密码工作模式及快速实现研究[J]. 通信技术 , 2014, 47 (9) : 1066-1070 LUO Ying, LIU Dongmei, KANG Hongjuan. , NIST new block cipher modes of operation and their fast implementationoperation modes and their fast implementations of nist new block cipher[J]. Communications technology , 2014, 47 (9) : 1066-1070 |
| [5] | 杨先伟, 康红娟. SM3杂凑算法的软件快速实现研究[J]. 智能系统学报 , 2015, 10 (6) : 9541-9597 YANG Xianwei, KANG Hongjuan. Fast software implementation of SM3 hash algorithm[J]. CAAI transactions on intelligent systems , 2015, 10 (6) : 9541-9597 |
| [6] | CCSA. Specification of the 3GPP confidentiality and integrity algorithms 128-EEA3& 128-EIA3. Document 2:ZUC specification[S]. Cedex, France:CCSA, 2011. |
| [7] | 冯秀涛. 3GPP LTE国际加密标准ZUC算法[J]. 信息安全与通信保密 , 2011, 9 (12) : 45-46 FENG Xiutao. ZUC algorithm:3GPP LTE international encryption standard[J]. Information security and communications privacy , 2011, 9 (12) : 45-46 |
| [8] | 罗影, 张文科, 尹一桦, 等. 单比特频数检测和块内频数检测的快速实现研究[J]. 通信技术 , 2015, 48 (9) : 1073-1077 LUO Ying, ZHANG Wenke, YIN Yihua, et al. Fast Implementation of monobit frequency test and frequency test within a block[J]. Communications technology , 2015, 48 (9) : 1073-1077 |
| [9] | Edro M, AALCOVER P M, GUILLAMóN A, RUIZ M D CAntonio G, et al. A new randomness test for bit sequences[J]. Informatica , 2013, 24 (3) : 339-356 |
| [10] | KAMINSKY A. GPU parallel statistical and cube test analysis of the SHA-3 finalist candidate hash functions. (2012-02-13). http://www.cs.rit.edu/~ark/parallelcrypto/sha3test01/. |



